The Influence of Extended Interactions on Spin Dynamics in One-dimensional Cuprates
Abstract
Quasi-one-dimensional (1D) materials provide a unique platform for understanding the importance and influence of extended interactions on the physics of strongly correlated systems due to their relative structural simplicity and the existence of powerful theoretical tools well-adapted to one spatial dimension. Recently, this was highlighted by anomalous observations in the single-particle spectral function of 1D cuprate chain compounds, measured by angle-resolved photoemission spectroscopy (ARPES), which were explained by the presence of a long-range attractive interaction. Such an extended interaction should leave its fingerprints on other observables, notably the dynamical spin structure factor , measured by neutron scattering or resonant inelastic x-ray scattering (RIXS). Starting from a simple Hubbard Hamiltonian in 1D and using time-dependent density matrix renormalization group (tDMRG) methods, we show that the presence of long-range attractive coupling, directly through an instantaneous Coulomb interaction or retarded electron-phonon (el-ph) coupling, can introduce significant spectral weight redistribution in across a wide range of doping. This underscores the significant impact that extended interactions can have on dynamical correlations among particles, and the importance of properly incorporating this influence in modeling. Our results demonstrate that can provide a sensitive experimental constraint, which complements ARPES measurements, in identifying key interactions in 1D cuprates, beyond the standard Hubbard model.
The origin of high-temperature superconductivity that has been found in layered, quasi-two-dimensional (2D) cuprates remains elusive despite concerted investigations over the last few decades. From the perspective of numerical simulations, although simplified Hamiltonians, such as the Hubbard model and related variants, have produced rich physics, seemingly relevant to the cuprates [1, 2, 3], insufficient evidence exists for the presence of -wave superconductivity in the ground state. Quasi-long-range superconductivity has been reported only on small width cylinders with a strong competition from coexisting charge order [4, 5, 6, 7, 8, 9, 10, 11, 12, 13]. Moreover, it seems superconducting correlations decay exponentially for wider clusters, indicating that superconductivity may be absent for parameters thought to be relevant to the hole-doped cuprate compounds.
While numerical difficulties in reaching the 2D limit may prevent us from saying anything definitive about superconductivity in these simplified models, additional ingredients may well be needed to provide the crucial boost for superconductivity. Assessing the impact of missing ingredients, such as phonons, whose influence has manifest as kinks or replica bands in photoemission measurements [14, 15, 16, 17, 18], or long-range interactions, is even more challenging in 2D modeling due to the additional numerical difficulty associated with adding more degrees of freedom and the associated expansion of the effective Hilbert space, and the growth of long-range entanglement. Our task may be made easier, with more numerical control and better theoretical understanding, by turning to the simpler, yet structurally similar, quasi-one-dimensional (1D) cuprates.
Recent synthesis progress on the doped 1D-chain cuprate [19] provides an excellent opportunity for testing theoretical models against experiments. Angle-resolved photoemission spectroscopy (ARPES) data on this doped 1D-chain in conjunction with numerical simulations revealed the presence of a strong, extended, attractive interaction [19]. Such an effective strong and extended attractive interaction likely originates from extended electron-phonon (el-ph) couplings [20]. It was found in later numerical work [21], that the extended el-ph coupling reproduces well the doping dependence of salient ARPES spectral features, which has been shown to enhance superconducting pairing correlations in 1D and have important implications for realizing a -wave superconducting ground state in the structurally similar layered 2D cuprates. This extended el-ph coupling can significantly suppress the static spin-spin correlation [21] otherwise obtained from the Hubbard model, while only slightly affecting the exponent of the single particle correlations. This motivates us to unravel the spin-spin correlation in frequency through the dynamical spin structure factor , which can be used to further refine how the el-ph interactions impact the spin dynamics beyond the simple Hubbard model. As we will show, may provide a sensitive probe on the presence and influence of extended el-ph interactions in the 1D cuprates.
In this work, we compute the dynamical spin structure factor influenced by extended, attractive couplings on a 1D chain for various hole doping concentrations . We demonstrate that the addition of such extended interactions can introduce significant qualitative and quantitative changes to as a function of . The two-spinon excitations at the zone edge significantly broaden and soften, even becoming gapless across the momentum range when the extended interactions come from el-ph coupling, while also leading to an apparent shift in the “2” momentum position towards , compared to the simple Hubbard model [] .
The Hubbard model (HM) is purely electronic
| (1) |
where () is the charge creation (annihilation) operator on site for spin , is the charge number operator on site for spin , and is the on-site repulsion. To avoid confusion with the time variable , we use to denote the hopping integral. We consider two forms of extended, attractive couplings to modify this simple HM. In one case, we introduce an effective nearest-neighbor attractive interaction, which has been used in prior work to well-reproduce the apparent single-particle spectra from ARPES experiments [19], to produce an extended-Hubbard model (HM+) given by
| (2) |
where and are total charge number operators on neighboring sites. In the other case, we add local optical phonons with coupling to the on-site and nearest-neighbor charge densities to the HM, resulting in a Hubbard-extended Holstein model (HM++) [20, 21]
| (3) | |||||
where and are the phonon ladder operators on site , is the total charge number operator on site , is the phonon frequency, is the on-site el-ph coupling, is the nearest-neighbor el-ph coupling, and sums over nearest-neighbors.
To solve for the ground states of these models, we use the density matrix renormalization group (DMRG) [22, 23] method; and for the HM++ we employ a local basis optimization (LBO) [24] for the phonon degrees of freedom in Eq. 3. We then use time-dependent DMRG (tDMRG) [25, 26, 27], with a dynamical LBO [28] for the HM++, to calculate the correlator
| (4) |
which is measured at uniformly spaced discrete time steps , , until reaching the maximum time . is then obtained by Fourier transform. To reduce the effect of the cutoff at finite time , a decaying window function , where , is multiplied to the time signal. The resulting spectra is
We use a window function , whose Fourier transformation is a Gaussian with standard deviation . This window function broadens the spectra
| (6) |
We compute and compare at various doping levels for the three models: HM, HM+ and HM++. Unless otherwise stated, the spectra have been evaluated for parameters and for the HM+ or , , and for the HM++. These parameters have been shown to well-reproduce features in the experimental single-particle spectra as measured by ARPES [19, 21].
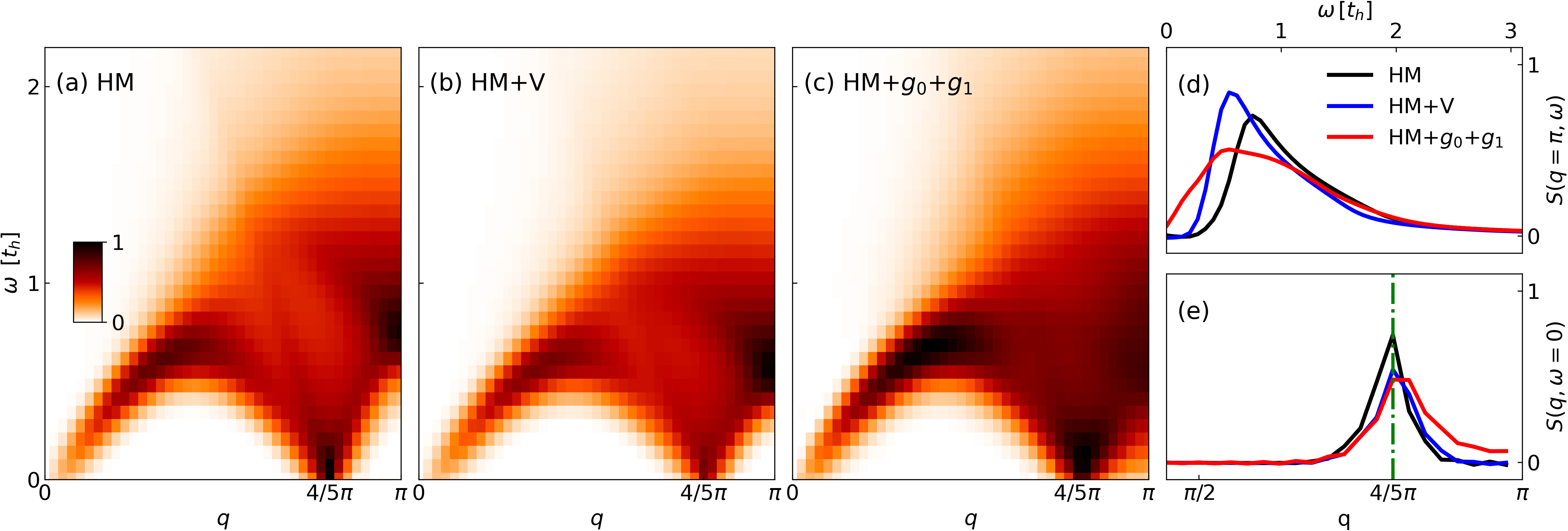
We first show results for relatively long chains with and relatively long total times to produce high resolution spectra with small finite-size effects to elucidate the spectral changes for representative doping . As shown in Figs. 1(a) and (b), both the simple HM and HM+ have gapless spectra at momentum , and with increasing momentum from to , the excitation gap grows monotonically. Similar to the overall renormalization of the single-particle bandwidth and Fermi velocity with the introduction of the extended Hubbard interaction [19, 21], the spectra for the HM+ [shown in panel (b)] between to are noticeably softer than the spectra of the simple HM. In other words, a spectral gap at extends to higher energies in the absence of extended interaction .
The introduction of extended el-ph coupling produces qualitative differences in compared to both the HM and HM+. For the HM++, shown in Fig. 1(c), the lowest excitation peak becomes significantly broadened across momenta , with spectral weight extending to very low energy (approaching ). As a comparison of the three models, we plot the energy distribution curves (EDC) at in Fig. 1(d), highlighting both the softening of the gap in the HM+ and the significant broadening and low energy spectral weight caused by the extended el-ph couplings.
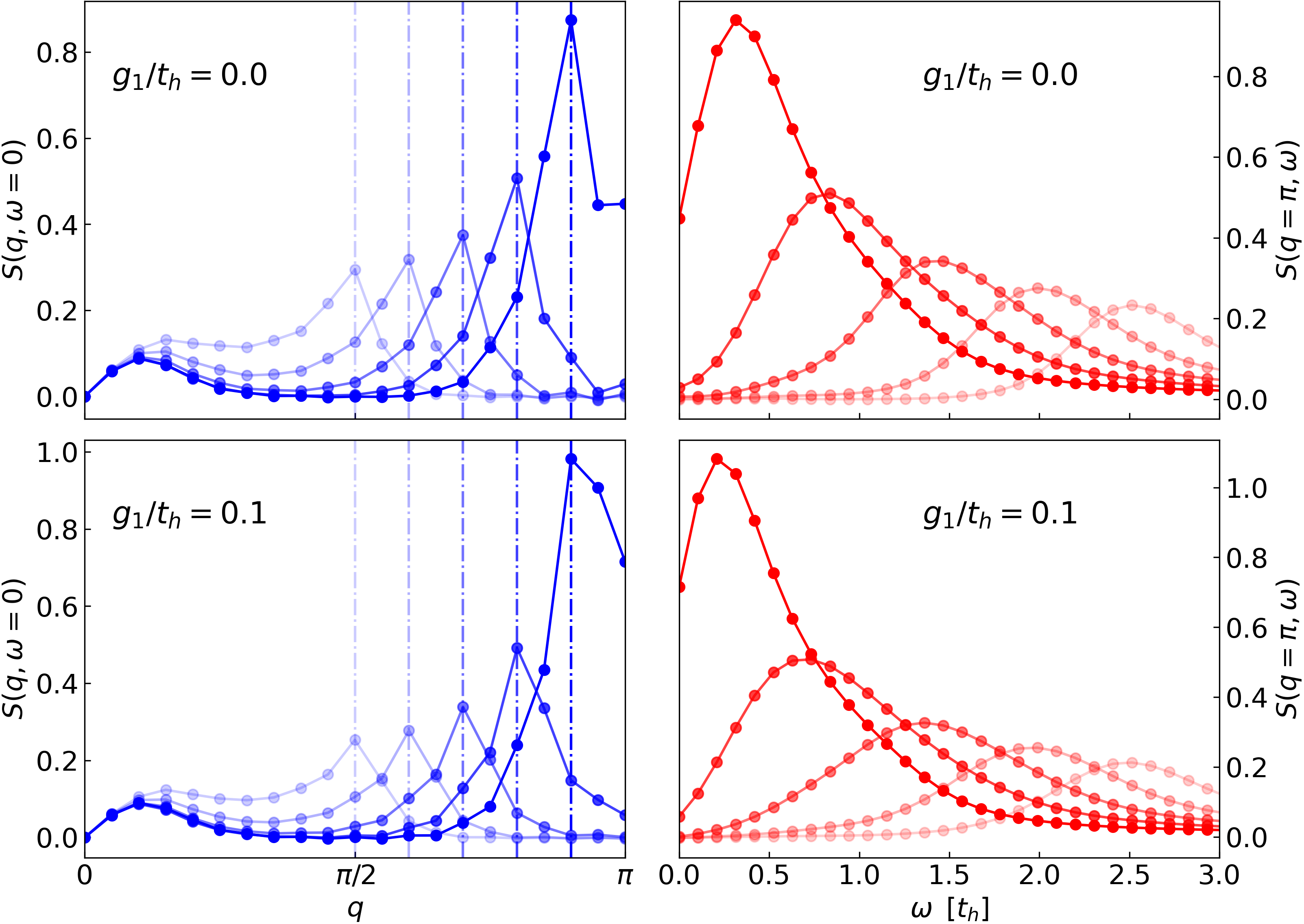
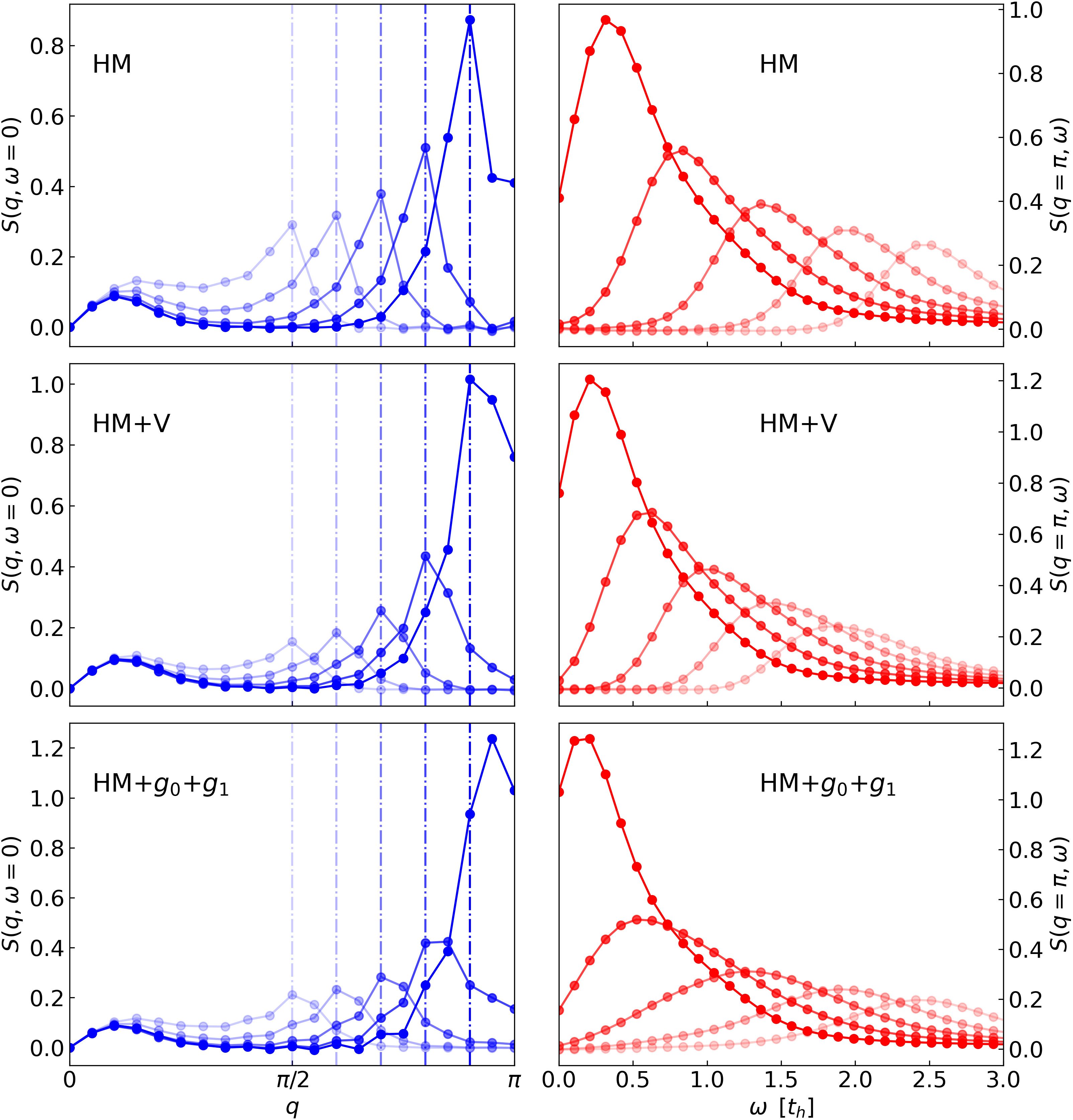
An additional, but not so obvious, difference induced by the extended el-ph coupling occurs in the apparent “” position. We show the momentum distribution curves (MDC) at in Fig. 1(e). For both the HM and HM+, the spectral peak position is well defined at . The introduction of extended el-ph coupling broadens and shifts the peak towards .
Due to the numerical complexities associated with the addition of phonons, we perform the remaining simulations on short 40-site chains. The resulting spectral resolution is sufficient to demonstrate the impact of extended interactions on as a function of hole doping , and the differences between an effective attractive interaction and extended el-ph coupling.
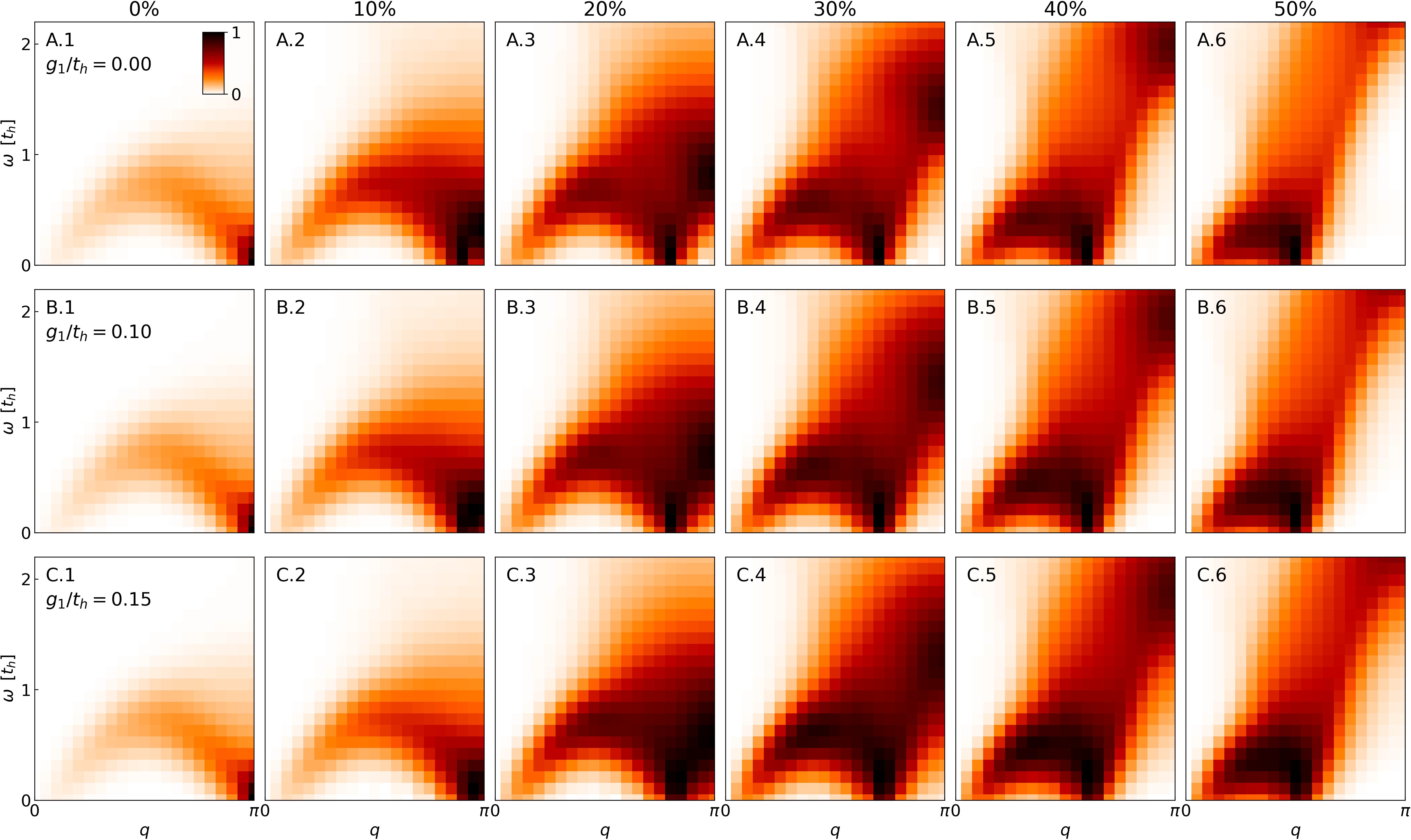
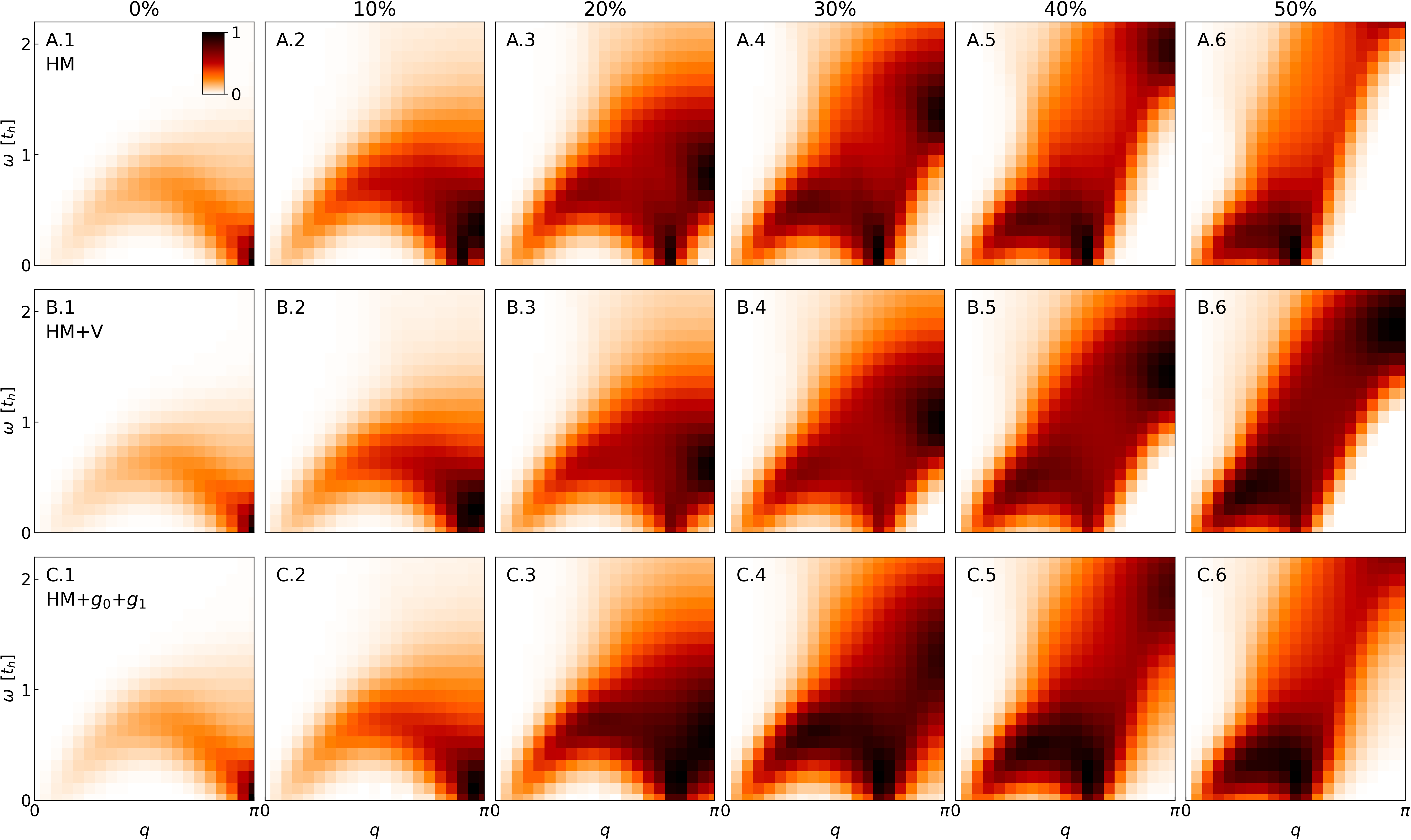
In Fig. 2, we show for different models (rows) with increasing doping (columns). The time-dependent spin-spin correlators in real-space can be found in Fig. S2 of the Supplementary Material. Even with the lower resolution afforded on the 40-site chain, one still sees that both the HM and HM+ at doping level possess gapless spectra at momentum . In each case, for momenta from to , this excitation gap grows monotonically. As doping increases, becomes smaller and the gap at becomes larger (see Fig. 2 rows A and B). Compared to the simple HM, the HM+ has a smaller excitation gap at across all doping levels, as also seen in the higher resolution spectra of Fig. 1.
For the HM++ with (Fig. 2 row C), the lowest excitation peak is significantly broadened across momentum at all doping levels, and there is noticeable spectral weight extending to very low energy (even approaching at low doping).
As a comparison of the three models, we plot the energy distribution curves (EDC) at in the right column of Fig. 3, demonstrating broadened peaks and low energy spectral weight caused by the extended el-ph couplings. In terms of the peak positions at , compared to the HM, the HM++ has lower energy peaks at low doping (), but the peak positions at higher doping are more comparable; however, at all doping levels the spectra of the HM++ are significantly broadened compared to both the HM and HM+. We also show the momentum distribution curves (MDC) at obtained from Fig. 2 in the left column of Fig. 3. For both the HM and HM+, the spectral peaks are well defined at . With extended el-ph coupling, the peaks broaden and shift toward at small doping, as observed with higher resolution on the 80-site chain.
We have shown that the extended el-ph coupling induces significant changes to the spin dynamics across a wide range of doping levels. Specifically, without the extended el-ph coupling, is gapless at momentum and has a gap that widens from to . The extended el-ph coupling significantly broadens the excitations across this momentum range and introduces noticeable spectral weight down to zero energy for doping levels up to at least 50%, as examined here. Compared to HM, the peak positions at are softened at smaller doping but remain comparable, yet broad, at higher doping levels. There is also a shift of from towards caused by the extended el-ph coupling. We also have demonstrated that an effective attractive interaction can not emulate well all these quantitative, or even qualitative changes in induced by the extended el-ph coupling.
Compared to the enhancement of the holon folding branch seen in the single particle spectral function , which is relatively weak and disappears quickly as the doping level increases, [19, 21] the impact of el-ph coupling can be more readily observed in across a wide range of doping due to the modification of spectral weight. The position of , the peak positions at , and the general shape of both MDC and EDC cuts at lower doping can provide vital clues about the strength of extended el-ph coupling in these materials. Our work points out that a promising and perhaps more sensitive experimental assessment of extended el-ph coupling in the doped 1D cuprates can come, for example, from measurements of by resonant inelastic X-ray scattering (RIXS) [29].
Acknowledgements.
We are grateful for detailed discussions with Jiarui Li, Wei-Sheng Lee, Z.-X. Shen, and Yao Wang. This work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under Contract No. DE-AC02-76SF00515. The computational results utilized the resources of the National Energy Research Scientific Computing Center (NERSC) supported by the U.S. Department of Energy, Office of Science, under Contract No. DE-AC02-05CH11231. Some of the computing for this project was performed on the Sherlock cluster. We would like to thank Stanford University and the Stanford Research Computing Center for providing computational resources and support that contributed to these research results.References
- Dagotto [1994] E. Dagotto, Correlated electrons in high-temperature superconductors, Reviews of Modern Physics 66, 763 (1994).
- Arovas et al. [2022] D. P. Arovas, E. Berg, S. A. Kivelson, and S. Raghu, The Hubbard Model, Annual Review of Condensed Matter Physics 13, 239 (2022).
- Qin et al. [2022] M. Qin, T. Schäfer, S. Andergassen, P. Corboz, and E. Gull, The Hubbard Model: A Computational Perspective, Annual Review of Condensed Matter Physics 13, 275 (2022).
- White and Scalapino [1997] S. R. White and D. J. Scalapino, Ground states of the doped four-leg - ladder, Physical Review B 55, R14701 (1997).
- Ehlers et al. [2017] G. Ehlers, S. R. White, and R. M. Noack, Hybrid-space density matrix renormalization group study of the doped two-dimensional Hubbard model, Physical Review B 95, 125125 (2017).
- LeBlanc et al. [2015] J. P. F. LeBlanc, A. E. Antipov, F. Becca, I. W. Bulik, G. K.-L. Chan, C.-M. Chung, Y. Deng, M. Ferrero, T. M. Henderson, C. A. Jiménez-Hoyos, E. Kozik, X.-W. Liu, A. J. Millis, N. V. Prokof’ev, M. Qin, G. E. Scuseria, H. Shi, B. V. Svistunov, L. F. Tocchio, I. S. Tupitsyn, S. R. White, S. Zhang, B.-X. Zheng, Z. Zhu, E. Gull, and (Simons Collaboration on the Many-Electron Problem), Solutions of the Two-Dimensional Hubbard Model: Benchmarks and Results from a Wide Range of Numerical Algorithms, Physical Review X 5, 041041 (2015).
- Jiang and Devereaux [2019] H.-C. Jiang and T. P. Devereaux, Superconductivity in the doped Hubbard model and its interplay with next-nearest hopping , Science 365, 1424 (2019).
- Chung et al. [2020] C.-M. Chung, M. Qin, S. Zhang, U. Schollwöck, and S. R. White (The Simons Collaboration on the Many-Electron Problem), Plaquette versus ordinary -wave pairing in the -Hubbard model on a width-4 cylinder, Phys. Rev. B 102, 041106 (2020).
- Jiang et al. [2020] Y.-F. Jiang, J. Zaanen, T. P. Devereaux, and H.-C. Jiang, Ground state phase diagram of the doped Hubbard model on the four-leg cylinder, Physical Review Research 2, 033073 (2020).
- Jiang et al. [2021] S. Jiang, D. J. Scalapino, and S. R. White, Ground-state phase diagram of the -- model, Proceedings of the National Academy of Sciences 118, e2109978118 (2021).
- Gong et al. [2021] S. Gong, W. Zhu, and D. N. Sheng, Robust -wave superconductivity in the square-lattice - model, Phys. Rev. Lett. 127, 097003 (2021).
- Jiang et al. [2022] S. Jiang, D. J. Scalapino, and S. R. White, Pairing properties of the --- model, Phys. Rev. B 106, 174507 (2022).
- Qin et al. [2020] M. Qin, C.-M. Chung, H. Shi, E. Vitali, C. Hubig, U. Schollwöck, S. R. White, S. Zhang, and (Simons Collaboration on the Many-Electron Problem), Absence of Superconductivity in the Pure Two-Dimensional Hubbard Model, Physical Review X 10, 031016 (2020).
- Lanzara et al. [2001] A. Lanzara, P. V. Bogdanov, X. J. Zhou, S. A. Kellar, D. L. Feng, E. D. Lu, T. Yoshida, H. Eisaki, A. Fujimori, K. Kishio, J.-I. Shimoyama, T. Noda, S. Uchida, Z. Hussain, and Z.-X. Shen, Evidence for ubiquitous strong electron–phonon coupling in high-temperature superconductors, Nature 412, 510 (2001).
- Cuk et al. [2005] T. Cuk, D. H. Lu, X. J. Zhou, Z.-X. Shen, T. P. Devereaux, and N. Nagaosa, A review of electron–phonon coupling seen in the high- superconductors by angle-resolved photoemission studies (ARPES), physica status solidi (b) 242, 11 (2005).
- Lee et al. [2006] J. Lee, K. Fujita, K. McElroy, J. A. Slezak, M. Wang, Y. Aiura, H. Bando, M. Ishikado, T. Masui, J.-X. Zhu, A. V. Balatsky, H. Eisaki, S. Uchida, and J. C. Davis, Interplay of electron–lattice interactions and superconductivity in Bi2Sr2CaCu2O8+δ, Nature 442, 546 (2006).
- He et al. [2018] Y. He, M. Hashimoto, D. Song, S.-D. Chen, J. He, I. M. Vishik, B. Moritz, D.-H. Lee, N. Nagaosa, J. Zaanen, T. P. Devereaux, Y. Yoshida, H. Eisaki, D. H. Lu, and Z.-X. Shen, Rapid change of superconductivity and electron-phonon coupling through critical doping in Bi-2212, Science 362, 62 (2018).
- Kulić [2000] M. L. Kulić, Interplay of electron–phonon interaction and strong correlations: The possible way to high-temperature superconductivity, Physics Reports 338, 1 (2000).
- Chen et al. [2021] Z. Chen, Y. Wang, S. N. Rebec, T. Jia, M. Hashimoto, D. Lu, B. Moritz, R. G. Moore, T. P. Devereaux, and Z.-X. Shen, Anomalously strong near-neighbor attraction in doped 1D cuprate chains, Science 373, 1235 (2021).
- Wang et al. [2021] Y. Wang, Z. Chen, T. Shi, B. Moritz, Z.-X. Shen, and T. P. Devereaux, Phonon-Mediated Long-Range Attractive Interaction in One-Dimensional Cuprates, Physical Review Letters 127, 197003 (2021).
- Tang et al. [2023] T. Tang, B. Moritz, C. Peng, Z.-X. Shen, and T. P. Devereaux, Traces of electron-phonon coupling in one-dimensional cuprates, Nature Communications 14, 3129 (2023).
- White [1992] S. R. White, Density matrix formulation for quantum renormalization groups, Physical Review Letters 69, 2863 (1992).
- White [1993] S. R. White, Density-matrix algorithms for quantum renormalization groups, Physical Review B 48, 10345 (1993).
- Zhang et al. [1998] C. Zhang, E. Jeckelmann, and S. R. White, Density Matrix Approach to Local Hilbert Space Reduction, Physical Review Letters 80, 2661 (1998).
- Vidal [2003] G. Vidal, Efficient Classical Simulation of Slightly Entangled Quantum Computations, Physical Review Letters 91, 147902 (2003).
- White and Feiguin [2004] S. R. White and A. E. Feiguin, Real-Time Evolution Using the Density Matrix Renormalization Group, Physical Review Letters 93, 076401 (2004).
- Paeckel et al. [2019] S. Paeckel, T. Köhler, A. Swoboda, S. R. Manmana, U. Schollwöck, and C. Hubig, Time-evolution methods for matrix-product states, Annals of Physics 411, 167998 (2019).
- Brockt et al. [2015] C. Brockt, F. Dorfner, L. Vidmar, F. Heidrich-Meisner, and E. Jeckelmann, Matrix-product-state method with a dynamical local basis optimization for bosonic systems out of equilibrium, Physical Review B 92, 241106 (2015).
- Ament et al. [2011] L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill, and J. van den Brink, Resonant inelastic x-ray scattering studies of elementary excitations, Reviews of Modern Physics 83, 705 (2011).
Supplementary Material
DMRG details for L=80
In the DMRG algorithm, we keep up to states for all models and a bare phonon basis and an optimal LBO phonon basis for the HM++.
To find the ground state, we perform up to 36 DMRG sweeps and then perform up to time evolution steps in tDMRG with time interval . For the simple HM, the DMRG ground state truncation error was around and the maximum truncation error for time evolution was around . For the HM+, the DMRG ground state truncation error was around and the maximum truncation error for time evolution was around .
Finally, for the HM++, the DMRG ground state truncation error with respect to was around , with an LBO phonon basis truncation error around ; and for time evolution of the HM++, the maximum truncation error with respect to was around , with a maximum truncation error of the dynamical LBO basis around .
DMRG details for L=40
For the 40-site chain, we kept a number of DMRG block basis states up to for all models, with a number of bare phonons up to and the number of optimal LBO phonons equal to for the HM++. We perform up to 30 DMRG sweeps to determine the ground state and then perform up to time evolution steps with time interval . For a doping level as an example, we list the truncation errors in our simulations. For the HM, the ground state truncation error was around , and the maximum truncation error for time evolution was around . For the HM+, the ground state truncation error was around , and the maximum truncation error for the time evolution was around . For the HM++, the ground state final sweep truncation error with respect to was around and the LBO phonon basis truncation error was around . During time evolution with the dynamical LBO, the maximum truncation error with respect to was around and the maximum truncation error of the phonon basis was around . The truncation errors at other doping levels are close to these values (within a factor of to 3).
Dependence on
To demonstrate the spectral dependence on the extended el-ph coupling, we plot full spectra as a function of doping in Fig. S3, and then extract MDCs at and EDCs at in Fig. S4, for different values of . For , the MDCs and EDCs are similar to the results of the HM, as the local Holstein coupling primarily renormalizes the effective on-site Hubbard interaction. One sees the previously discussed modifications to the spectra that appear as one increases to in the second row of Fig. S3 and further increases to in the third row, as in Fig. 2 of the main text. Corresponding real-space and time-dependent spectra can be found in Fig. S5.