The impact of asymmetric neutrino emissions on nucleosynthesis in core-collapse supernovae II – progenitor dependences –

As in our previous study (Fujimoto & Nagakura, 2019), we perform hydrodynamic simulations from core collapse to SN explosion of massive stars, employed with two codes, the GR1D code (O’Connor, 2015) and a modified Zeus 2D code (Stone & Norman, 1992a, b; Ohnishi et al., 2006, 2007; Fujimoto et al., 2011), in which a simplified $\nu$ transport, or a light-bulb scheme, is adopted and appropriate weak interactions are taken into account (see detailed in Appendix of Fujimoto et al. (2011)). We follow matter evolution from the core collapse to the shock stole with the GR1D code in spherical symmetry, and then the results are mapped in the polar coordinate $(r,\theta)$ on the Zeus 2D code. The computational domain in 2D simulations is from $50\rm$ to $50,000{\,\rm km}$ in $r$ and $0\leq\theta\leq\pi$, covered with $(500,128)$ meshes. The central part ($\leq 50{\,\rm km}$) of the proto-neutron star (proto-NS) is excised and is treated as the central point source with a mass of $M$, which continuously increases due to mass accretion through the inner boundary ($50{\,\rm km}$) of the computational domain of our 2D simulations. At the time of remapping from 1D to 2D, the mass of a central point source is $1.2M_{\odot}$, and we add non-radial ($l=1$) perturbations on radial velocities, whose magnitudes are $1\%$, to break the spherical symmetry.

In the present study, neutrinos are assumed to be emitted from the neutrinospheres with a thermal spectrum. We assume that the neutrino temperatures are spherical symmetric but luminosities have dipole components;

where $L_{\nu_{\rm e}}$ and $L_{{\bar{\nu}}_{\rm e}}$ are luminosity of $\nu_{\rm e}$ and ${\bar{\nu}}_{\rm e}$ and $L_{\nu_{\rm e},\rm ave}$ and $L_{\nu_{\rm e},\rm ave}$ are angular-averaged $L_{\nu_{\rm e}}$ and $L_{{\bar{\nu}}_{\rm e}}$, respectively. Here the evolution of $L_{\nu_{\rm e},\rm ave}$, $L_{{\bar{\nu}}_{\rm e},\rm ave}$ and $\nu$ temperatures are evaluated with a $\nu$-core model from the mass accretion rate at the inner boundary of the computational domain, as in Ugliano et al. (2012); Sukhbold et al. (2016) but with some modifications (Appendix A). As in our previous work (Fujimoto & Nagakura, 2019), we have tuned two parameters of the $\nu$-core model so that the $19.4M_{\odot}$ progenitor explodes as SN1987A-like (the explosion energy, $E_{\rm exp}$, $\sim 10^{51}\rm erg$ and the ejected mass of ${}^{56}\rm Ni$, $M$(${}^{56}\rm Ni$), of $(0.07-0.08)M_{\odot}$; ) for cases of spherical $\nu$ emission ($m_{\rm asy}=0\%$). We run the simulations by fixing those tunned parameters but changing $m_{\rm asy}$ as 0%, 10/3%, 10%, 30%, and 50%. We note that the typical asymmetry of neutrino emissions may be $m_{\rm asy}\leq 10\%$ (see e.g., Tamborra et al., 2014; Nagakura et al., 2019b; Vartanyan et al., 2019b), although it is not definitive; hence, we investigate cases with higher asymmetric, neutrino-emissions in this study.

In the present study, we investigate the impact of neutrino asymmetry on explosive nucleosynthesis in CCSNe of progenitors (Woosley & Heger, 2015; Woosley et al., 2002) with a mass of $9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot}$, and $25.0M_{\odot}$ in addition to the progenitor of $19.4M_{\odot}$, whose detailed nucleosynthetic results are presented in our previous study (Fujimoto & Nagakura, 2019) (see also §3.1).

Figure 1 shows density profiles of the progenitors of $M_{\rm ms}=9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot},19.4M_{\odot}$, and $25.0M_{\odot}$ as a function of a mass-coordinate $M_{r}$. The 9.5(15.0) $M_{\odot}$ progenitor has a density profile very similar to that of the 11.2(19.4)$M_{\odot}$ progenitor, but shallower at the mass coordinate, $M_{r}$, $\geq 1.5M_{\odot}$ ($2.0M_{\odot}$). At $M_{r}\geq 1.5M_{\odot}$, the density of the 13.0 and 17.0$M_{\odot}$ progenitors lie between those of the light (9.5 and 11.2$M_{\odot}$) progenitors and those of the 15.0 and 19.4$M_{\odot}$ progenitors, while the density is much higher for the 25.0$M_{\odot}$ progenitor. As we shall discuss below, the accretion component of neutrino luminosity is directly associated with the density profile at the onset of collapse, indicating that the difference of the density profile is responsible for the progenitor dependence of the impact of asymmetric neutrino emissions on the explosive nucleosynthesis (see Sec. 3 for more details).

It should be mentioned that a mass cut-off due to a black hole formation needs to be assumed in order to compute the IMF-averaged abundances. We refer Brown & Woosley (2013); Suzuki & Maeda (2018) which suggest that the mass cut-off with $\geq 25-40M_{\odot}$ is appropriate. A maximum mass of $25M_{\odot}$, therefore, seems to be adequate for the current study. It should be mentioned that the IMF-averaged [X/Fe] is insensitive to the mass cut-off in spherically symmetric neutrino emission models as long as it is $\geq 25-40M_{\odot}$ (see Fujimoto et al. (2021) in preparation); hence our choice of the mass cut-off would give fewer impacts on our present results. We also note that the seven progenitors employed in this study are enough to compute the averaged IMF abundances, since the relative contribution of the averaged [X/Fe] over the seven progenitors are comparable to that over more than 20 progenitors from $9.5M_{\odot}$ to $25.0M_{\odot}$ in our spherically symmetric neutrino emission models (Fujimoto et al. (2021) in preparation).

We terminate our CCSN simulations when the shock wave reaches to $\sim 10,000{\,\rm km}$. Figure 2 shows the time evolution of angular-averaged shock radii, $r_{\rm sh}$ (left panel), $L_{\nu_{\rm e},\rm ave}$ (top right panel), and $L_{{\bar{\nu}}_{\rm e},\rm ave}$ (bottom right panel) for case with symmetric neutrino emission ($m_{\rm asy}=0\%$) and for progenitors of $9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot},19.4M_{\odot}$, and $25.0M_{\odot}$ as a function of the time from the core bounce ($t_{\rm pb}$). Note that the evolution of $r_{\rm sh}$, neutrino luminosities, and temperatures weakly depend on $m_{\rm asy}$; hence, we display only the results with $m_{\rm asy}=0$ in these panels. For the light progenitors: $9.5M_{\odot}$, $11.2M_{\odot}$, $13.0M_{\odot}$ and, $17.0M_{\odot}$, shock revivals occur at relatively early time ($\sim$ 200  ms), while the shock wave for the other progenitors ($15.0M_{\odot}$, $19.4M_{\odot}$, and $25.0M_{\odot}$) revives at a later phase $\sim$ 300  ms. Neutrino luminosities are low for the light progenitors of $9.5M_{\odot}$ and $11.2M_{\odot}$, whereas they are higher for heavier progenitors due to larger mass accretion rates. In particular, for progenitors with high compactness ($M_{\rm ms}=15.0M_{\odot}$, $19.4M_{\odot}$, and $25.0M_{\odot}$), the luminosities and temperatures are remarkably higher than other models.

We follow Lagrangian thermodynamic histories of SN ejecta for nucleosynthetic computation with a tracer particle method (Nagataki et al., 1997; Seitenzahl et al., 2010; Harris et al., 2017), in which tracer particles evolve in accordance with the fluid-velocity of the CCSN simulations while storing their physical quantities such as density, temperature, and electron fraction, $Y_{e}$. We distribute 6,000 tracer particles in the regions from $1,000$km to $10,000$km (or an O-rich layer) at the beginning of the simulations, with being adaptively weighted to the mass of a layer where the particle is located. By virtue of the adaptive mass of tracer particles, the highest resolutions in the particle mass become $\sim(10^{-5}$-$10^{-4})M_{\odot}$ in the present study. We made a sensitivity study of nuclear abundances to the particle numbers in (Fujimoto et al., 2011), and a reasonable convergence is achieved at 6,000 particles; indeed, we found that the differences in ejected masses of nuclei between 3,000 and 6,000 particles cases are less than $\sim$ 1%, hence, we adopted 6,000 particles in this study. In our models, $\sim$ 3,000-4,500 particles are ejected by SN explosions, whose masses weakly depend on $m_{\rm asy}$ and are evaluated to be 0.09$M_{\odot}$, (0.20-0.22)$M_{\odot}$, (0.35-0.36)$M_{\odot}$, (0.44-0.47)$M_{\odot}$, (0.53-0.56)$M_{\odot}$, (0.52-0.58)$M_{\odot}$, and (0.78-0.81)$M_{\odot}$, for progenitors with $(9.5,11.2,13.0,15.0,17.0,19.4$, and $25.0)M_{\odot}$.

We follow the abundance evolution of 2,488 nuclides from $n$, $p$ to ${}^{196}\rm Nd$ in the CCSN ejecta by employing the Lagrangian thermodynamic histories of the ejecta and a nuclear reaction network as in our previous study (Fujimoto & Nagakura, 2019). Note that, when the ejecta become hotter than $9\times 10^{9}{\,\rm K}$, we set the abundances of the nuclides to be the chemical composition in nuclear statistical equilibrium. We also take into account abundance change via neutrino interactions for He and nuclei from C to Kr as in Fujimoto et al. (2011). In the nucleosynthetic computations, we recompute $Y_{e}$ following the weak interactions employed in the nuclear reaction network, albeit possessing $Y_{e}$ data from the hydrodynamic simulations. This is mainly because more elaborate weak reactions are incorporated in the nuclear reaction network than those used in 2D hydrodynamic simulations (Fujimoto et al., 2011), and the recomputation is necessary in particular for reversed-$L_{\nu}$ cases (see below) in nucleosynthetic computations.

We note that the deviation of the neutrino spectra from a Fermi-Dirac distribution has a negligible effect on the composition of the SN ejecta via $\nu$-processes. The impact was well investigated by the two simulations in Sieverding et al. (2019); a simulation of a piston-driven CCSN explosion of a $27M_{\odot}$ progenitor and $E_{\rm exp}=1.2\times 10^{51}\,{\rm erg}$ with a quasi-thermal energy distribution of $\nu$ and a spherically symmetric, artificially exploded CCSN simulation of the $27M_{\odot}$ progenitor, whose $\nu$ luminosities and spectra evaluated with a hydrodynamic code, in which an approximated neutrino transport is taken into account. We, hence, ignore the effect of deviations from the thermal spectrum in neutrino spectra in this study.

We find that in the region, $r_{\rm cc}\leq 10,000{\,\rm km}$, the peak temperature of the SN shock wave becomes higher than $\sim 1\times 10^{9}{\,\rm K}$, where nuclei heavier than C are abundantly synthesized. Here $r_{\rm cc}$ is the radius of the ejecta at the onset of the core collapse. We therefore conduct nucleosynthetic computation only for the tracer particles, which are located $r_{\rm cc}\leq 10,000{\,\rm km}$. For the initial abundances of the particles, we take abundances of 20 nuclei in the progenitors at the onset of the core collapse. The abundances are taken from the results of stellar evolution in Woosley et al. (2002). For $15.0M_{\odot}$ and $25.0M_{\odot}$ progenitors, we also adopt alternative abundance data of more than 1,300 nuclei (Rauscher et al., 2002), which consist of those with $Z\leq 83$ including odd $Z$ nuclei as well as $s$-process nuclei produced via the weak $s$-process. The chemical composition of the outer ejecta with $r_{\rm cc}>10,000{\,\rm km}$ is set to be the abundances in the progenitors at the onset of the core collapse, ignoring the $\gamma$-processes in $p$-process layers (Rayet et al., 1995) and the $\nu$-processes in the outer layers (Sieverding et al., 2019). We note that the ejected masses from the region $r>r_{\rm cc}$ are $7.73M_{\odot}$, $9.30M_{\odot}$, $9.49M_{\odot}$, $10.5M_{\odot}$, $11.7M_{\odot}$, $13.0M_{\odot}$, and $9.75M_{\odot}$ for progenitors with $9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot}$, $19.4M_{\odot}$, and $25.0M_{\odot}$.

Recent multi-D CCSN simulations reveal the correlation between the directions of stronger shock and the hemisphere with high-${\bar{\nu}}_{\rm e}$ emissions (the high-${\bar{\nu}}_{\rm e}$ hemisphere) (see, e.g., Tamborra et al. (2014); Nagakura et al. (2019b); Vartanyan et al. (2019b)). In some of our models, however, the direction of the high-${\bar{\nu}}_{\rm e}$ hemisphere does not correlate with that of the stronger shock expansion. It is attributed to the fact that the shock revival takes place in stochastic directions, meanwhile we set a priori the dipole direction of neutrino asymmetry. We find that ten models are mis-correlated; ($M_{\rm ms}/M_{\odot}$, $m_{\rm asy}/\%$) = $(9.5,10)$, $(9.5,30)$, $(13.0,10)$, $(13.0,30)$, $(13.0,50)$, $(15.0,30)$, $(17.0,10)$, $(17.0,30)$, $(17.0,50)$, and $(25.0,10)$. For the nucleosynthetic calculation in these mis-correlated models, we retain the matter data but reverse the direction of $\nu$ asymmetry in nucleosynthetic computations. We discuss the impact of the reversed-$L_{\nu}$ procedure in Appendix B, and confirm that it is a reasonable prescription to obtain qualitatively accurate results.

We briefly summarize the essential results of our previous study (Fujimoto & Nagakura, 2019): the impact of asymmetric neutrino emissions on explosive nucleosynthesis for a CCSN of the $19.4M_{\odot}$ progenitor. As shown in Sec. 2.1, the progenitor is tuned to reveal the SN1987A-like explosion with $E_{\rm exp}\sim 10^{51}\rm erg$ and $M($${}^{56}\rm Ni$$)\sim(0.07-0.08)M_{\odot}$. In our model, the shock wave is revived at $\sim 0.3$ s after the core bounce (Fig. 2) and then it expands quasi-spherically. The explosion exhibits the aspherical distribution of the density, temperature, and entropy of neutrino-driven inner ejecta. Although the fluid-dynamics is less sensitive to $m_{\rm asy}$, the distribution of $Y_{e}$ of SN ejecta strongly depends on $m_{\rm asy}$ due to a different amount of $\nu$ absorption through the different degree of the dipolar and anti-correlated $\nu$ emissions (Eqs. (1) and (2)); In the hemisphere of $\pi/2<\theta\leq\pi$ (the high-${\bar{\nu}}_{\rm e}$ hemisphere), the asymmetric emissions of $\nu$ tend to yield larger amounts of $n$-rich ejecta ($Y_{e}<0.49$), while $p$-rich matter ($Y_{e}>0.51$) are ejected in the opposite hemisphere of the higher $\nu_{\rm e}$ emissions ($0\leq\theta<\pi/2$; the high-$\nu_{\rm e}$ hemisphere). See also Fig. 1 in Fujimoto & Nagakura (2019) for more details.

For larger asymmetric cases with $m_{\rm asy}\geq 30\%$, the larger amounts of the $n$-rich ejecta are produced in the high-${\bar{\nu}}_{\rm e}$ hemisphere. As a result, there are too many elements heavier than Zn compared to the solar abundances (Fig. 4 in Fujimoto & Nagakura (2019)). For cases with small $m_{\rm asy}$ ($10/3\%$ and $10\%$), abundances of the elements are comparable to or slightly larger than those of the solar abundances. We also observed the characteristic features in elemental distribution; abundances lighter than Ca are insensitive to $m_{\rm asy}$ and the production of Ni, Zn, and Ge is much larger in the $n$-rich ejecta in the high-${\bar{\nu}}_{\rm e}$ hemisphere than those in the $p$-rich ejecta in the high-$\nu_{\rm e}$ hemisphere even for smaller asymmetric cases with $\leq 10\%$. With these results in mind, let us delve into the progenitor dependence, which is the main subject in this paper.

Figure 3 shows mass profiles of $dM_{\rm ej}$ in $Y_{\rm e,1}$ of the ejecta from the inner region ($r_{\rm cc}\leq 10,000{\,\rm km}$) for the progenitors with $M_{\rm ms}=9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot}$, and $25.0M_{\odot}$, and for cases with $m_{\rm asy}=$ 0%, 10/3%, 10%, 30%, and 50%. Here $Y_{\rm e,1}$ is the electron fraction evaluated when the temperature is equal to $1\times 10^{9}\rm K$ during the ejection and $dM_{\rm ej}$ is a mass of ejecta integrated with a bin of $dY_{\rm e,1}=0.005$. We note that $Y_{e}$ of the ejecta chiefly changes through the neutrino absorption near the proto-NS during the ejection, implying that it freezes out at the place with $Y_{e}\sim Y_{\rm e,1}$ where it is far away from proto-NS in this phase (see, e.g., Fig.4 in Fujimoto et al., 2011). The ejecta goes through the adiabatic cooling with expansions but $Y_{e}$ re-increases from a certain point due to subsequent $\beta$-decays of unstable nuclei in the ejecta. For larger $m_{\rm asy}$, $Y_{\rm e,1}$ distributions are widely varying, indicating that mass fractions of $n$- and $p$-rich ejecta become larger due to larger ${\bar{\nu}}_{\rm e}$ and $\nu_{\rm e}$ absorptions on nucleon in the ejecta. We also find that masses of $n$-rich ejecta tend to be larger with larger amounts of the inner ejecta and with larger ${\bar{\nu}}_{\rm e}$ luminosities. It should be mentioned, however, that the mass of $n$-rich ejecta is not a monotonic function of the progenitor mass; indeed, they are smaller in $17.0M_{\odot}$ ($11.2M_{\odot}$) than in $15.0M_{\odot}$ ($9.5M_{\odot}$). It is attributed to the fact that the mass density profile of progenitors just prior to the onset of gravitational collapse is a non-monotonic order to the zero age main-sequence mass. This can be seen in Fig. 1; there are regions where the density becomes lower in $17.0M_{\odot}$ ($11.2M_{\odot}$) than $15.0M_{\odot}$ ($9.5M_{\odot}$), which results in decreasing accretion components of neutrino luminosity (see also Fig.2). As a result, the impact of asymmetric neutrino emissions becomes weak, implying that the production of $n$-rich ejecta is less efficient.

Figure 4 shows the composition of the ejecta for our models in terms of [X/Fe] ¹¹1[A/B] = $\log\left[(X_{\rm A}/X_{\rm A,\odot})/(X_{\rm B}/X_{\rm B,\odot})\right]$, where $X_{\rm i}$ and $X_{\rm i,\odot}$ are a mass fraction of an element $\rm i$ and its solar value (Anders & Grevesse, 1989), respectively. of the ejecta as a function of an atomic number $Z$ for the progenitors with $M_{\rm ms}=9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot}$, and $25.0M_{\odot}$ and for cases with $m_{\rm asy}=$ 0%, 10/3%, 10%, 30%, and 50%. We present [X/Fe] for cases with initial abundances of 20 nuclei in the stellar evolution code (Woosley et al., 2002) (solid-lines with filled-squares) and those for cases with the alternative initial abundances of more than 1,300 nuclei (Rauscher et al., 2002) (dashed-lines with open-squares) only for the $15.0M_{\odot}$ and $25.0M_{\odot}$ progenitors. We find that [X/Fe] of odd-$Z$ elements and elements with $Z\geq 27$ are largely underproduced if we adopt the initial abundances of the 20 nuclei, while [X/Fe] of even-$Z$ elements with $Z\leq 26$ are comparable. Hence, the pronounced odd-even patterns of [X/Fe] for elements lighter than Fe would be due to the small number of initial abundances (20 nuclei) in our simulations. The comparison suggests that the odd-even patterns of [X/Fe] found in other progenitor models may disappear if we employ initial abundances computed with larger nuclear reaction network. Keeping in mind the systematic error, let us study the progenitor dependence of the impact of asymmetric neutrino emissions on the abundance pattern in the ejecta.

As in case with the $19.4M_{\odot}$ progenitor (see Fig.4 in Fujimoto & Nagakura, 2019), [X/Fe] for elements lighter than Ca are insensitive to $m_{\rm asy}$. For symmetric $L_{\nu}$ cases ($m_{\rm asy}=0$), elements heavier than Cu ($Z=29$) other than Sr, Y, and Zr are underproduced except for the progenitor of $9.5M_{\odot}$. The exceptional trend found in $9.5M_{\odot}$ model is mainly due to the fact that the fractions of $n$-rich ejecta are large even in the case with $m_{\rm asy}=0$ (see top left panel in Fig.3). It should be mentioned that isotopes of Sr, Y, and Zr with the neutron number $N=50$ are abundantly produced in $n$-rich ejecta ($Y_{\rm e,1}\leq 0.49$). which appear appreciably in 9.5, 15.0, and 17.0$M_{\odot}$ models even in the case with $m_{\rm asy}=0$. For larger $m_{\rm asy}$, on the other hand, [X/Fe] for elements heavier than Zn ($Z=30$) become larger due to larger fractions of $n$-rich elements. In particular, for cases with $m_{\rm asy}\geq 30\%$, these elements are overproduced compared with the solar abundances regardless of progenitors. We also note that Zn is synthesized in the p-rich ejecta but the contribution to Zn in the ejecta is minor because of the small abundances (mass fraction $<0.01$; see e.g., Fig.10 in Wanajo et al. (2018)).

It is also interesting to be mentioned that [Zn/Fe] for the case with $m_{\rm asy}=10/3\%$ in 9.5$M_{\odot}$ model is less than those for $m_{\rm asy}=0$, indicating that the abundance ratio is not always monotonic function with $m_{\rm asy}$. This peculiar trend can be understood as follows. Let us first point out that Zn is chiefly composed by ${}^{64}\rm Zn$ and ${}^{66}\rm Zn$ and abundantly synthesized in the ejecta with $Y_{e,1}\sim 0.45-0.48$ and $\leq 0.43$ (see, e.g., Fig.10 in Wanajo et al. (2018)), i.e., there is a hole between the two $Y_{e,1}$ regions. For the 9.5$M_{\odot}$ model, Zn is mainly produced in the region of $Y_{e,1}\sim 0.45-0.48$ in the case with $m_{\rm asy}=0$. With increasing $m_{\rm asy}$ to $10/3\%$, the ejecta tends to be shifted to the region of the lower $Y_{e,1}$ due to the higher ${\bar{\nu}}_{\rm e}$ absorptions, and some of them get into the hole (see in the top, left figure on Fig. 3), results in decreasing [Zn/Fe].

We now turn our attention to the comparison between IMF-averaged abundances of our results and the solar one. We average abundances of the ejecta with the Salpeter IMF weighted by their masses over the seven progenitors of $9.5M_{\odot},11.2M_{\odot},13.0M_{\odot},15.0M_{\odot},17.0M_{\odot},19.4M_{\odot}$, and $25.0M_{\odot}$, setting the minimum and maximum masses of CCSNe to be $9.5M_{\odot}$ and $25M_{\odot}$, respectively. The abundances of the other progenitors are computed by the linear interpolation of the results of our models with the progenitors of nearby $M_{\rm ms}$. Figure 5 shows IMF-averaged [X/Fe] of the ejecta for cases with $m_{\rm asy}=$ 0%, 10/3%, 10%, 30%, and 50% in panels from top to bottom. Solid-lines with filled-squares show averaged [X/Fe] for cases with the initial abundances of 20 nuclei in a stellar evolution code (Woosley et al., 2002), while dashed-lines with open-squares portray those with more than 1,300 nuclei (Rauscher et al., 2002) only for the $15.0M_{\odot}$ and $25.0M_{\odot}$ progenitors. We find that IMF-averaged [X/Fe] for elements with $30\leq Z\leq 40$ in cases with the smaller asymmetry of $m_{\rm asy}=10/3\%$ and $10\%$ are roughly consistent with the solar abundance, although Rb and Zr are slightly underproduced and overproduced, respectively. On the other hand, those for the elements with $30\leq Z\leq 40$ with $m_{\rm asy}\geq 30\%$ are remarkably overproduced compared with the solar abundances.

It should be mentioned that the contribution to [X/Fe] for elements with $30\leq Z\leq 40$ of the weak $s$-process, which is taken into account in cases with the initial abundances of more than 1,300 nuclei (dashed-lines with open-squares), dominates over that of the $n$-rich ejecta. We also emphasize that for the symmetric $\nu$-emission ($m_{\rm asy}=0$; top panel) elements heavier than Se ($Z=34$) are underproduced compared with the solar abundances, even if we consider the contribution of the weak $s$-process (dashed-lines with open-squares); hence the $n$-rich ejecta synthesized via the asymmetric neutrino emissions play a complementary role to approach the solar abundance.

In short, we conclude that $\nu$ asymmetry with $m_{\rm asy}\geq 30\%$ is excluded in light of the solar abundances. We must mention a caveat, however; $m_{\rm asy}$ for the light progenitors of $9.5M_{\odot}$ and $11.2M_{\odot}$ cannot be constrained from the investigation due to the small masses of the $n$-rich ejecta (top, left and center panels of Fig. 3) and thus a small contribution to elements with $Z\geq 31$.

There is another caveat in the above analysis; we need to take into account the contribution from Type Ia SN (SNIa) since it is the dominant contributor to the solar abundances of the iron-group elements. Hence, we add the contribution of SNIa to the IMF-averaged [X/Fe] of our CCSN ejecta so that [O/Fe] becomes zero. We note that the resultant [X/Fe] with the solar abundances, which correspond to, by definition, is set to be zero following the convention in the literature. Figure 6 shows [X/Fe] of the IMF-averaged CCSN ejecta added by the contribution of the SNIa ejecta of the W7 model (Leung & Nomoto, 2018), in which a Ni-overproduction problem is resolved (Kobayashi et al., 2020), for cases with $m_{\rm asy}=$ 0%, 10/3%, 10%, 30%, and 50% in panels from top to bottom. We find that IMF-averaged [X/Fe] with the SNIa contribution well reproduce the solar abundances of elements from $Z=6-39$ except for F for cases with the smaller asymmetry of $m_{\rm asy}=10/3\%$ and $10\%$ and cases with the initial abundances of more than 1,300 nuclei. We note that the underproduction of F would not be a problem, since it can be complemented by the AGB stars (Spitoni et al., 2018; Olive & Vangioni, 2019) and rotating massive stars (Limongi & Chieffi, 2018; Choplin et al., 2018) through $s$-processes.

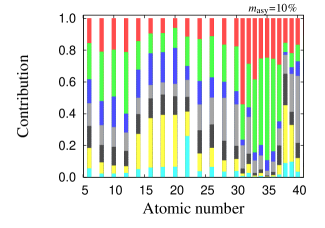
To see the importance of each progenitor to the IMF-averaged [X/Fe] of the CCSN ejecta quantitatively, we compute the relative contribution to the IMF-averaged [X/Fe] of the progenitors of as a function of $Z$ for cases with $m_{\rm asy}=$ 0% and 10% (see Figure 7). In the computation, we adopt abundances of ejecta for cases with the full initial compositions as the abundances of ejecta for the progenitors of $15M_{\odot}$ and $25M_{\odot}$ and thus the contribution of $s$-process elements is partially included. We evaluate the relative contribution of a progenitor with $M_{\rm ms}/M_{\odot}=m_{i}=[9.5,11.2,13.0,15.0,17.0,19.4,25.0]$ for $i=1,2,...,7$. as the IMF-averaged [X/Fe] over progenitors from $M_{l}$ to $M_{u}$, where we set $\{M_{l}/M_{\odot},M_{u}/M_{\odot}\}$ to $\{(m_{i-1}+m_{i})/2,(m_{i}+m_{i+1})/2\}$ for $i=2,3,...,6$, $\{9.5,(m_{i}+m_{i+1})/2\}$ for $i=1$, and $\{(m_{i-1}+m_{i})/2,25\}$ for $i=7$. We omit the contribution of odd-$Z$ elements with $Z<30$ in Figure 7. This is because the contribution is strongly inherited from the initial compositions adopted in each model and is incorrectly dominant over that for the progenitors of $15M_{\odot}$ and $25M_{\odot}$ in the current evaluation. We find that the relative contribution to elements lighter than Ni is insensitive to $m_{\rm asy}$. On the contrary, it is very sensitive to $m_{\rm asy}$ for each element of $Z=30-40$. Our result suggests that the appropriate multi-D treatments are required in both CCSN and nucleosynthesis computations to determine the primary CCSN progenitor producing each element in the range of $Z=30-40$.