The evolving role of astrophysical modelling in dark matter halo relaxation response

The IllustrisTNG simulations, conducted by the TNG collaboration, employed the arepo code [25], which utilizes a moving mesh approach defined by Voronoi tessellation [26]. These simulations incorporate an updated model of galaxy formation that includes cosmic magnetic fields in addition to major baryonic processes such as cooling, star formation, and stellar and AGN feedback [27, 28]. The suite comprises three cosmological boxes: TNG50, TNG100, and TNG300, with periodic box sizes of $35h^{-1}{\rm Mpc}$, $75h^{-1}{\rm Mpc}$, and $200h^{-1}{\rm Mpc}$, respectively, consistent with the cosmology from [29]. Initial conditions were generated at $z=127$ using the Zel’dovich approximation [30] with the N-GenIC code [31].

We utilize the highest resolution runs from all three boxes to study a wide range of halo responses to galaxy formation. Specifically, TNG50 offers sufficient resolution for low-mass haloes, while TNG300 provides an adequate number of cluster-scale haloes. Throughout our analysis, we utilize data from redshifts $z=0.01$ and $z=1$ from IllustrisTNG for both hydrodynamical and corresponding gravity-only runs. This allows us to examine the effects of baryonic processes on dark matter halo properties across different scales and epochs.

The EAGLE (Evolution and Assembly of GaLaxies and their Environments) cosmological simulations were conducted using a modified version of the gadget-3 code, which employs smoothed particle hydrodynamics [32]. Initial conditions were generated using the ic_2lpt_gen code following [33]. The main large-volume simulation was performed in a cosmological volume of $(100~{}\rm{Mpc})^{3}$ periodic box with its reference model of galaxy formation, incorporating sub-grid prescriptions for various baryonic processes such as cooling, star formation, and feedback mechanisms [4, 34]. This reference model of EAGLE simulations has been shown to produce realistic galaxies [35, 36, 37].

In addition, this suite includes multiple small-volume simulations with wide variations in the baryonic subgrid prescriptions for astrophysical processes. These simulations were performed at the same resolution as the large-volume reference simulation but in a $25~{}\rm{Mpc}$ periodic box. The variations include adjustments to the gas equation of state, the threshold for star formation, efficiency of stellar feedback, the viscosity of the black-hole accretion disk and the nature of stochastic heating caused by AGN feedback. In particular we study these following simulations:

• •

  Ref (Reference model): This simulation uses the standard EAGLE subgrid physics parameters but in this smaller box.

• •

  eos53 : This considers a gas equation of state with adiabatic index $\gamma=5/3$.

• •

  eos1 : This considers an isothermal gas equation of state with $\gamma=1$.

• •

  FixedSfThresh: This uses a constant threshold for star formation independent of the metallicity.

• •

  WeakFB: This follows a lower efficiency of stellar feedback that is scaled down by $50\%$ compared to the reference simulation.

• •

  StrongFB: This follows a higher efficiency of stellar feedback, twice that of the reference simulation.

• •

  NoAGN: AGN feedback is disabled in this simulation to study the effects of stellar feedback alone.

• •

  AGNdT8: In this, the temperature of gas raised by the AGN feedback heating is lower with $\Delta T_{\rm{AGN}}=10^{8}$K from the reference value of $\Delta T_{\rm{AGN}}=10^{8.5}$K.

• •

  AGNdT9: In this, the temperature of gas raised by the AGN feedback heating is higher with $\Delta T_{\rm{AGN}}=10^{9}$K from the reference value of $\Delta T_{\rm{AGN}}=10^{8.5}$K.

• •

  RefHR: This simulation uses the same EAGLE subgrid prescription as ‘Ref’ simulation but at a mass resolution higher by factor 8.

• •

  RecalHR: This simulation uses the same resolution as ‘RefHR’ but with recalibrated EAGLE subgrid prescription.

We use the redshift $z=0$ data from this set of simulations along with their corresponding gravity-only run to study the role of different astrophysical processes on the relaxation response of the halo.

The Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) project comprises a comprehensive suite of hydrodynamical simulations designed to explore the interplay between cosmological and astrophysical parameters in shaping the universe’s large-scale structure [38]. This large collection of simulations are performed in a relatively smaller cosmological volume of $(25\ \mathrm{Mpc}/h)^{3}$, containing $256^{3}$ dark matter particles and an equivalent number of baryonic particles [39].¹¹1In addition, simulations in larger volume of $(50\ h^{-1}{\rm Mpc})^{3}$ are also expected to be made available as part of CAMELS project. It will be interesting to see the implications of improved statistics and large scale effects in a future work.

In our study, we specifically utilize the CAMELS-TNG suite’s 1P set of simulations, a subset that methodically varies one parameter at a time to isolate the effects of individual parameters in the TNG model. For our analysis, we concentrate on astrophysical parameters related to supernova (SN) feedback and active galactic nucleus (AGN) feedback, each governed by the following two distinct parameters:

• •

  Supernova Feedback Parameters:

  • –

    $A_{\mathrm{SN1}}$: Varied between 0.25 to 4, this parameter controls the energy flux of the galactic winds. It is implemented as a prefactor for the overall energy output per unit star formation rate [28, 38].

  • –

    $A_{\mathrm{SN2}}$: Varied between 0.5 to 2, this parameter controls the speed of the galactic winds. For a fixed $A_{\mathrm{SN1}}$, changes in $A_{\mathrm{SN2}}$ affect the galactic wind speed in concert with the mass-loading factor to maintain a fixed energy output.

• •

  AGN Feedback Parameters:

  • –

    $A_{\mathrm{AGN1}}$: Varied between 0.25 to 4, this parameter controls the overall power injected in the kinetic feedback mode of AGN. It is implemented as a prefactor for the energy per unit black-hole accretion rate [27, 38].

  • –

    $A_{\mathrm{AGN2}}$: Varied between 0.5 to 2, this parameter controls the burstiness and the temperature of the heated gas during AGN feedback "bursts" by changing the wind speed of the AGN feedback.

All these parameters have a value of unity in the fiducial simulation, and there are five simulations with higher values and another five simulations with lower values for each of these parameters. In total, we utilize these 41 hydrodynamical simulations and compare them against the gravity-only simulation over the same cosmological volume.

In the simulations from IllustrisTNG and EAGLE suites, 3D friend-of-friends (FoF) algorithm [see 40, 7, for details] was used to obtain halo group catalogues, while the subfind code [41] was used to identify the subhaloes within these FoF group haloes as gravitationally bound substructures. Within each FoF group halo, the subhalo enclosing the gravitational potential minimum is assigned as its central subhalo. This trough in the gravitational potential is used to define the centre of that halo. Its size is characterized by the ‘virial’ radius $R_{\rm vir}\equiv R_{\rm 200c}$ defined as the radius of the sphere around its centre enclosing a mean matter density that is 200 times the cosmological critical density. Its mass is then defined as the corresponding total mass enclosed $M\equiv M_{200c}$. In the simulations from the CAMELS suite, the haloes were identified in the phase-space by a 6D FoF algorithm using the rockstar code. We characterize sizes and masses using the same quantities $R_{\rm 200c}$ and $M_{\rm 200c}$ respectively.

To study the relaxation response of dark matter, we match the haloes from the full hydrodynamic simulations with the haloes in the corresponding gravity-only runs performed over same cosmological volumes. We identify these matched halo pairs based on the amount of overlap in their proto-haloes characterized by the positions of their particles in the initial conditions. In particular, this involves identifying nearby haloes of similar sizes between the hydrodynamical and gravity-only simulations and then match them by simulation particles [see 23, for details].

In the catalogues of matched halo pairs, hydrodynamical ones with galaxies are considered relaxed, while the gravity-only counterparts represent unrelaxed dark haloes. The relaxation response of dark matter within a halo, is generally evaluated through variations in their radial mass profiles indicating contraction or expansion due to the galaxy. These spherically averaged dark matter profiles are computed by the cumulative sum of the mass contributed by all dark matter particles within concentric spherical shells. For the gravity-only halo, the cosmic dark matter fraction of the mass in each particle is considered as contributing to the dark matter.

We employ the quasi-adiabatic relaxation framework to characterize the relaxation from these profiles. The relaxation response in cold dark matter occurs entirely due to gravitational interactions with baryons. This is an aggregate effect of the baryonic mass flow resulting from galactic processes such as inflows and feedback. The quasi-adiabatic relaxation model is a physically motivated framework that relates the change in the spherically averaged dark matter distribution at a given time to the spherically averaged baryonic distribution at the same time. This baryonic profile encompasses all non-dark matter mass, including gas and stars.

Earlier models assumed spherical halo where the dark matter particles maintain their radial ordering while responding adiabatically to baryonic particle flows [12]. In this scenario, if a dark matter particle initially orbiting at radius $r_{i}$ in the unrelaxed halo moves to radius $r_{f}$ in the relaxed halo, the enclosed dark matter mass within these radii remains equal.

$$M_{f}^{d}(r_{f})=M_{i}^{d}(r_{i})\,.$$

(3.1)

However, due to the baryonic mass flow, the total mass enclosed within these spheres is not necessarily equal, $M_{i}(r_{i})\neq M_{f}(r_{f})$. Further assumption of angular momentum conservation for dark matter particles in circular orbits, implies that the change in total enclosed mass must be consistent with the amount of relaxation [12].

$\displaystyle r_{i}\,M_{i}(r_{i})=r_{f}\,M_{f}(r_{f})\implies\frac{r_{f}}{r_{i}}=\frac{M_{i}(r_{i})}{M_{f}(r_{f})}\,.$

(3.2)

The Quasi-adiabatic relaxation framework empirically extends this idealized scenario by considering the relaxation ratio $r_{f}/r_{i}$ as a function of the mass ratio $M_{i}/M_{f}$.

$\displaystyle\frac{r_{f}}{r_{i}}$

$\displaystyle=1+\chi\left(\frac{M_{i}(r_{i})}{M_{f}(r_{f})}\right)$

(3.3)

Various quasi-adiabatic models have been proposed, offering different approaches to this framework [9, 14, 23]. A minimal extension considered in some of the baryonification procedures [42, 43] incorporate dark matter response as a quasi-adiabatic relaxation with a single parameter

$$\chi(y)=q\,(y-1)\,.$$

(3.4)

Velmani & Paranjape (2023) [23] proposed a locally linear model of the relaxation relation as follows:

$\displaystyle\frac{r_{f}}{r_{i}}-1$

$\displaystyle=q_{1}(r_{f})\left[\frac{M_{i}(r_{i})}{M_{f}(r_{f})}-1\right]+q_{0}(r_{f}),.$

(3.5)

In that model, the relaxation is described by a linear relation however there is an additional explicit dependance on the halo centric distance.

In this section, we investigate the relaxation response in the radial distribution of dark matter in the main simulations of IllustrisTNG simulations at an earlier redshift of $z=1$ and compare it to the present redshift of $z=0$. Haloes at both these redshifts were identified and matched between hydrodynamical and the corresponding gravity-only runs as described in section 3.1. Additionally, we use the SubLink merger tree catalogues to trace the most massive progenitor haloes at $z=1$ of the haloes considered at $z=0$ [7]. While present epoch haloes are sampled only by their masses at the present time, we consider three different methods for sampling the early epoch haloes. This results in four distinct sets of halo samples:

1. 1.

   $z=1$ haloes sampled by their masses at $z=1$.

2. 2.

   $z=1$ haloes sampled by the masses of their descendants at $z=0$. Note that not all haloes with a given mass at the present time have valid progenitors with the same mass at $z=1$.

3. 3.

   $z=1$ haloes sampled by their masses at $z=1$, but the mass bins are defined by the median masses of the most massive progenitors of the $z=0$ haloes.

4. 4.

   $z=0$ haloes sampled by their masses at $z=0$.

In each case, we consider the nine mass bins starting from $\log(M/h^{-1}M_{\odot})=10$ to $14$ in steps of $0.5$ dex represented by the colors shown in figure 1. Additionally, this figure indicates the peak heights ($\nu$) corresponding to these halo masses at both $z=0$ and $z=1$. These values correspond to the rarity of haloes with that mass at that redshift with rarer haloes having larger values of $\nu$. This can be used to identify mass of the halo at $z=1$ that will have similar rarity as $z=0$ halo of a given mass.

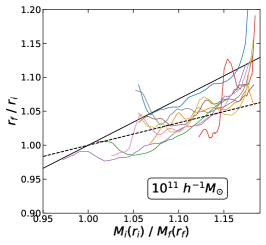
For each of these four sets of halo samples, the average relaxation relations ($r_{f}/r_{i}$ vs $M_{i}/M_{f}$) are shown in figure 2. We find that, for a given halo mass, relaxation is usually stronger at the earlier epoch (top left panel) compared to the present time $z=0$ (bottom right panel). In both cases, the trend in relaxation with halo mass is similar, with the strongest relaxation observed in $10^{12}h^{-1}M_{\odot}$ haloes. Interestingly, cluster-scale haloes with masses of $10^{14}h^{-1}M_{\odot}$ at redshift $z=1$ exhibit significant relaxation, unlike clusters of similar size at the present time.

The progenitors at redshift $z=1$ of the same haloes found at $z=0$ show even stronger relaxation, especially in Milky Way-scale and larger haloes, as shown in the top right panel of figure 2. The relaxation follows the simple quasi-adiabatic model (3.4) with $q=0.33$ among larger cluster-scale ($10^{14}h^{-1}M_{\odot}$) haloes, while group-scale haloes are consistent with the second-order polynomial relation proposed by Abadi et al. (2010) [9]. In the bottom left panel, the relaxation relation is shown for all haloes within a narrow mass bin around the median mass of the progenitors of the haloes selected at $z=0$. Notice that the relaxation relation shifts further lower in Milky Way-scale haloes and smaller clusters with the inclusion of those additional haloes.

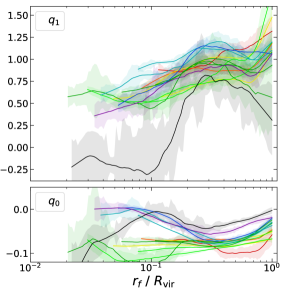
We have tested the locally linear model of relaxation relation (3.5) with our halo samples at $z=1$ and found it to hold reasonably well. For each halo sample, at each halo-centric distance $r_{f}$, the relationship between mass ratio and relaxation ratio across all haloes is best fitted by a linear curve with the slope and offset parameters namely $q_{1}(r_{f})$ and $q_{0}(r_{f})$. The radial profiles of these two relaxation parameters are shown for the four set of halo populations in figure 3 with the color-coding given by figure 1 for the associated halo mass.

Notice that the universality in these relaxation profiles extends to much larger mass haloes ($\sim 10^{13.5}h^{-1}M_{\odot}$) at $z=1$ (top left panel) compared to $z=0$ (bottom right panel). This is despite the fact that such massive haloes are even rarer at $z=1$ than at $z=0$, as indicated by the value of $\nu$ in figure 1. For all the halo samples selected at $z=0$, their traced progenitor populations at $z=1$ show nearly universal relaxation profiles, with the exception of $q_{0}(r_{f})$ in the inner halo (shown in the top right panel). This universality is even more apparent among the halo populations selected in narrow mass bins at $z=1$ based on the median masses of the progenitor populations (see bottom left panel).

The less universal and relatively noisier profiles in direct progenitors might be due to the inclusion of low mass fast accreting haloes together with high mass slow accreting haloes or simply a systematic issue such as a few misidentified progenitors. This difference between the direct progenitor populations and the haloes selected by the median progenitor masses seems to be more noticeable in the relaxation profiles than in the radially independent relaxation relations. For example, the black curves (corresponding to $10^{14}h^{-1}M_{\odot}$) are noticeably different especially in inner regions between top right and bottom left panels in figure 3, however, the overall relaxation relation shown in figure 2 is well-fitted by the linear $q=0.33$ model in both the panels. While the exact reason is not yet clear, we note that the radially-dependent relaxation might be more sensitive to this difference. Another interesting thing to note is that $q_{1}(r_{f})$ shows a small non-monotonic behavior in the outer haloes at all masses in $z=1$ (e.g., see lower left panel) that is not seen at $z=0$ (lower right panel). The range of halo-centric distances, over which $q_{1}(r_{f})$ is linearly increasing with $\log\left(\frac{r_{f}}{R_{\rm{vir}}}\right)$, referred to as the loglinear regime seem to increase with time. Investigations of dynamics of the response through time-series analysis (presented in a separate publication [44]) suggest that these are likely due to the astrophysical effects that are seen first in the inner halo and then in the outer halo.

The offset parameter $q_{0}$ shown in the lower sub-panels is relatively uniform across the halo, especially among the low-mass haloes. The figure 4 shows the mean of $q_{0}$ in all four sets of halo samples. The $q_{0}$ parameter is usually more negative across all $z=1$ halo populations compared to $z=0$, indicating a stronger relaxation offset. Additionally, the values are more universal with halo mass at $z=1$. A negative value of $q_{0}$ is expected to be a result of recent feedback outflows [23]. These feedback outflows are produced by a combination of AGN and stellar feedbacks. In the high mass haloes, powerful AGN feedbacks at earlier epochs lead to significant suppression in the star formation activity reducing the stellar feedbacks at present epoch. The reduction in the magnitude of $q_{0}$ from $z=1$ to $z=0$ in the high mass haloes could be simply due to the reduction in overall feedback among those haloes.

In this section, we investigate the role of various feedback parameters prescribed in the IllustrisTNG simulations using the set of CAMELS simulations performed with the IllustrisTNG model. This includes a set of 41 hydrodynamical simulations, with one replicating the reference TNG model in a smaller cosmological volume, and 10 simulations each by varying 4 different feedback parameters as described in section 2.3. To recall, this includes two supernovae feedback parameters ($A_{\mathrm{SN1}}$ and $A_{\mathrm{SN2}}$) and another two AGN feedback parameters ($A_{\mathrm{AGN1}}$ and $A_{\mathrm{AGN2}}$).

Due to the limited resolution and the smaller volumes of the CAMELS simulation, among all the mass bins shown in figure 1, we consider only $10^{11}h^{-1}M_{\odot}$, $10^{11.5}$, and $10^{12}h^{-1}M_{\odot}$ at both redshifts $z=0$ and $z=1$. Even in these mass bins, we consider only the outer well-resolved regions of the haloes. Also, since the cosmological volume is smaller than even the smallest TNG50 simulation, we have only a smaller sample of haloes at each of these halo mass bins. We find this sample size insufficient to estimate the radially-dependent relaxation parameters at each of these mass bins. We consider the following two approaches to alleviate this issue.

In this section, we present insights from small boxes of EAGLE simulations on the role of different feedback mechanisms on the relaxation response. These physics variation simulations from the EAGLE suite are described in section 2.2. Again, due to the significantly smaller box size and resolution, we only consider haloes in three different mass bins centered at $10^{10.5}h^{-1}M_{\odot}$, $10^{11}h^{-1}M_{\odot}$, and $10^{11.5}h^{-1}M_{\odot}$ as discussed in section 4.2. In these narrow mass bins, the mean relaxation relation obtained by stacking independent of the halo-centric distance is shown in figure 7 for these physics variation simulations.

We find that the deviation in the relaxation across different astrophysical modeling is usually much smaller than the differences from one halo mass to the other. However, notice that the gas equation of state has a strong influence on the relaxation relation, especially among low-mass haloes. In particular, stiffer equations of state lead to a very large $r_{f}/r_{i}$ indicating a stronger expansion of the dark matter shells in response to galaxy formation. Similar trends have been found in simpler self-similar systems of individual haloes [24].

In figure 8, we present the radially dependent relaxation parameters for a larger sample of haloes in a wider range of halo masses from $10^{10.5}h^{-1}M_{\odot}$ to $10^{11.5}h^{-1}M_{\odot}$. These results also reflect the strong influence of the equation of state of gas on the relaxation response of dark matter haloes. Additionally, these results highlight the effect of supernovae feedback modeling. In particular, the $q_{0}(r_{f})$ is more negative, indicating a stronger offset in the haloes found in the simulation with stronger supernova feedback implementation (brown curve vs. rose curve).