The electromagnetic form factors of heavy-light pseudo-scalar and vector mesons
Abstract
We systematically investigate the electromagnetic form factors of heavy-light pseudo-scalar and vector mesons within the Dyson-Schwinger/Bethe-Salpeter equations framework for the first time. It is found that the charge radius of vector meson is larger than that of its pseudo-scalar counterpart. In heavy-light systems, the flavor symmetry breaking will lead to a splitting of the form factor of different quark, and the distribution range of lighter and heavier quark gradually expands and contracts, respectively. The competition between them together generates the electromagnetic form factors of meson. Our results can be compared with other theoretical calculations and future experimental data.
I Introduction
The study of electromagnetic properties of mesons is a fundamental topic in hadron physics. The electromagnetic form factors (EFFs), which describe the response of composite particles to electromagnetic probes, provide an important tool for understanding the structure of bound states in QCD. Therefore, there have been numerous studies of the electromagnetic form factors of the mesons in experimental and theoretical [1, 2, 3, 4, 5, 6, 7, 8, 9].
Compared with , , …, heavy-light systems, such as , , , …, exhibit higher flavor asymmetry, thereby offering more information for the internal structure and dynamics of QCD’s bound states. However, due to the lack of experimental data and theoretical challenges, there are few studies about them. Recently, the electromagnetic form factors of heavy-light meson have attracted growing attention and various methods have been applied, for example, light-front framework (LFF) [10], constituent quark model (CQM) [11], contact interaction model (CI) [12], Algebraic model (AM) [13], Extended Nambu–Jona-Lasinio model (ENJL) [14], Lattice QCD (lQCD) [15] and others [16, 17, 18, 19, 20, 21]. Different or similar results have been reported.
On the other hand, the Dyson-Schwinger/Bethe-Salpeter equations (DSEs/BSEs) formalism provides a non-perturbative and Poincaré-covariant framework capable of simultaneously describing confinement and dynamical chiral symmetry breaking (DCSB). It has been successfully used to study hadron properties for thirty years [22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]. Therefore, investigating the electromagnetic form factors of heavy-light systems within the framework of DSEs/BSEs, including the extraction of physical information like charge radius and magnetic moment, is necessary and valuable for comparative analysis with results obtained from alternative approaches and future experiments. However, the current predictions of DSEs/BSEs for the meson’s EFFs have focused on flavor-symmetric or slightly asymmetric systems such as , , and mesons [34, 35, 36, 37, 38, 39].
In this work, we extend our previous work [37] to the heavy-light mesons, and an effective flavor-dependent BSE interaction kernel is applied [30]. Based on it, we systematically investigate the electromagnetic form factors of heavy-light quark-antiquark system within DSEs/BSEs framework for the first time. As a comparison, pseudo-scalar (PS) and vector (VC) channels are calculated uniformly.
This paper is organized as follows: In section. II, we introduce the DSEs/BSEs framework and the electromagnetic form factors of meson. In section. III, the numerical results of heavy-light pseudo-scalar/vector mesons’ EFFs are presented. Then we discuss the effect of flavor symmetry breaking, and the results are compared with those obtained by other approaches. Sec. IV provides a brief summary.
II The electromagnetic form factors within DSEs/BSEs framework
II.1 Quark propagators, quark-photon vertex and heavy-light meson’s BSAs
We work within DSEs/BSEs framework in Euclidean space. Under the rainbow-ladder (RL) approximation, the dressed-quark propagator can be obtained from the following gap equation,
| (1) |
and the general form of can be written as
| (2) |
Where and are scalar functions, is current quark mass, are the renormalization constants, in this work we employ a mass-independent momentum-subtraction renormalisation scheme [40] and choose renormalization scale GeV [41]. represents a translationally-invariant regularization of the four-dimensional integral with the regularization scale . For the dressed-gluon propagator , we employ the Qin-Chang model [26, 28]
| (3) |
where is transverse projection operator and the effective interaction is
| (4) |
with , GeV, , GeV, [41]. For model parameters and , a typical choice is GeV with for , quark, GeV with for , quark [41, 37]. In this work we follow these values except , ,, which are tweaked slightly to consider flavor dependence of the interaction [33], thus producing results closer to the experimental value (see Table. 1). More details of Eq. (1-4) are presented in Refs. [22, 24, 25, 26, 23].
| Quark | |||||
|---|---|---|---|---|---|
| 0.0068 | 0.135 | 0.095 | 0.755 | 0.150 | |
| 0.198 | 0.734 | 0.123 | 1.019 | 0.168 | |
| 1.739 | 2.984 | 0.270 | 3.114 | 0.290 | |
| 7.494 | 9.399 | 0.464 | 9.453 | 0.441 |
Correspondingly, the meson’s Bethe-Salpeter amplitudes (BSAs), , and the dressed quark-photon vertex, , can be obtained from (in)homogeneous BSEs, respectively,
| (5) |
and
| (6) |
where and denote the flavor of (anti-)quark, ; with the momentum partitioning parameter . Although the physical observables do not depend on , in the actual calculation111If we define the vertex of parabola contour in complex plane as and , we will have , and the best , where is meson’s mass., the selection of should be careful to avoid parabola include the pole for the accuracy of the contour integral [44, 45]. The general form of can be written as
| (7) |
where is basis and is scalar function. For the pseudo-scalar/vector meson, we choose [28]
| (8a) | |||||
| and | |||||
| (8b) | |||||
with . Then the decay constant can be obtained easily after normalization of the meson’ BSAs [28].
As for the quark-photon vertex , the general basis is
| (9) |
and should satisfy the vector Ward-Green-Takahashi identity (WGTI) [34, 39]
| (10) |
The only thing left is the BSE interaction kernel . In the case of flavor symmetry, the standard RL approximation kernel can be written as [41]
| (11) |
and generally, it works well for the flavor symmetric/slightly asymmetric ground state pseudo-scalar/vector mesons. However, for the highly flavor asymmetric system, such as , , , Eq. (11) is difficult to be applied because of the lack of flavor asymmetry [46]. To consider this effect, we effectively average the kernel as [30]
| (12) |
Here a weight factor is introduced, and Eq. (12) can be regarded as an extension of RL approximation, that is, weight-RL. For the flavor symmetric case, and it will degenerate to the RL kernel, therefore the solution of Eq. (6) still satisfy the vector WGTI, which will be used in the calculation of electromagnetic form factor [34].


For flavor asymmetric meson, an automatic average of this weight has been presented in Ref. [30]. In this work, we directly determine the by the pseudo-scalar meson’s mass to obtain a relatively realistic interaction. Once the weight factor is fixed, the decay constant of the pseudo-scalar meson, the mass and decay constant of the vector meson can all be well predicted (see Table. 2 and Figure. 1). It is worth noting that Eq. (12) should be considered as an effective kernel, the theoretical explore for flavor dependence and strict beyond-RL kernel is still ongoing [47, 48, 49, 33, 46, 50]. .
| Meson | Mass | Decay constant | ||||||
|---|---|---|---|---|---|---|---|---|
| Expt. | lQCD | This work | RL | Expt. | lQCD | This work | RL | |
| 0.495(1) | - | 0.495† | 0.495 | 0.110(1) | - | 0.108 | 0.112 | |
| 0.896(1) | 0.993(1) | 0.880 | 0.955 | 0.159(1) | - | 0.158 | 0.179 | |
| 1.868(1) | 1.868(3) | 1.868† | - | 0.144(4) | 0.150(4) | 0.140 | - | |
| 2.009(1) | 2.013(14) | 2.017 | - | - | 0.158(6) | 0.160 | - | |
| 5.279(1) | 5.283(8) | 5.279† | - | 0.133(18) | 0.134(1) | 0.123 | - | |
| 5.325(1) | 5.321(8) | 5.334 | - | - | 0.131(5) | 0.126 | - | |
| 1.968(1) | 1.968(4) | 1.968† | - | 0.182(3) | 0.177(1) | 0.164 | - | |
| 2.112(1) | 2.116(11) | 2.111 | - | - | 0.190(5) | 0.186 | - | |
| 5.367(1) | 5.366(8) | 5.367† | - | - | 0.163(1) | 0.149 | - | |
| 5.415(1) | 5.412(6) | 5.422 | - | - | 0.158(4) | 0.151 | - | |
| 6.275(1) | 6.276(7) | 6.275† | 6.388 | - | 0.307(10) | 0.300 | 0.429 | |
| - | 6.331(7) | 6.340 | 6.542 | - | 0.298(9) | 0.296 | 0.483 | |
II.2 The electromagnetic form factors of pseudo-scalar and vector mesons
The generalized impulse approximation allows electromagnetic processes to be described in terms of dressed quark propagators, bound state BSAs, and the dressed quark-photon vertex. These couplings are given by [34, 35, 37]
| (13) |
Where , and are incoming meson, outgoing meson and incoming photon momenta, which are constrained by on-shell condition
| (14) |
with is meson’s mass. The other elements in Eq. (13) are the dressed-quark propagators , the meson’s BSAs and dressed quark-photon vertex . In this work we determine them from homogeneous/inhomogeneous BSEs in the moving frame, correspondingly, , , , with is the momentum partitioning parameter of the outgoing meson and physical observables are independent of it. Then the need for interpolation or extrapolation of the meson’s BSAs/quark-photon vertex can be avoided [35].
Consider the coupling of a photon to the quark and antiquark, this interaction should be written as the sum of two terms (see Figure. 2)

| (15) |
where is the quark or antiquark electric charge. For pseudo-scalar meson, the only form factor is defined by [34]
| (16) |
and for vector meson, the three form factors are defined by [35]
| (17) | ||||
| (18) | ||||
| (19) |
with
| (20) | ||||
| (21) | ||||
| (22) | ||||
| (23) |
and . Where , defines the meson’s charge. In the impulse approximation, as long as the relation between the dressed quark propagator and the quark-photon vertex satisfies WGTI, and the BSE kernel is independent of the meson momentum, the conservation of electromagnetic current will be preserved after the meson’s BSAs are canonical normalized [34]. Besides, (0) and can be identified with the magnetic moment, , and the quadrupole moment, , of a vector meson [35, 37].
III Numerical results and discussion
III.1 Pseudo-scalar mesons
With all the above at hand, we first consider the electromagnetic form factor for ground state heavy-light pseudo-scalar mesons. These are the simplest quark-antiquark bound states embodying confinement, and the lightest pseudo-scalar meson, , is also the Goldstone mode of DCSB. In Figure. 3, we present a comparison of the electromagnetic form factors of the pion and kaon with current experimental results. Our predictions demonstrate a good agreement with the experimental data.


In the case of pseudo-scalar channel, the only electromagnetic form factor, , corresponds to the charge distribution of the system222Although the exact form of this relation is still up for debate [67, 68].. It is well known that the charge radius can be defined as
| (24) |
which denotes the distribution range of charge. The numerical results of Eq. (24) can be found in Table. 3. As a comparison, we also collected some predictions from other approaches.
| Meson | This work | LFF | PM | CI | AM | CQM | ENJL | IQCD | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| L | H | Full | |||||||||
| 0.646 | 0.646 | 0.646 | 0.666 | - | 0.45 | - | 0.665 | 0.57 | 0.648(15) | ||
| 0.659 | 0.491 | 0.608 | 0.591 | - | 0.42 | - | 0.551 | 0.54 | - | ||
| / | / | 0.253 | 0.260 | - | - | - | - | - | - | ||
| 0.706 | 0.187 | 0.435 | 0.429 | 0.510 | - | 0.680 | 0.505 | 0.46 | 0.450(24) | ||
| / | / | 0.556 | 0.551 | 0.673 | 0.36 | - | - | - | - | ||
| 0.757 | 0.071 | 0.619 | 0.615 | 0.732 | 0.34 | 0.926 | - | 0.74 | - | ||
| / | / | 0.435 | 0.432 | 0.516 | - | - | - | - | - | ||
| 0.547 | 0.192 | 0.352 | 0.352 | 0.465 | 0.26 | 0.372 | 0.377 | 0.39 | 0.465(57) | ||
| 0.588 | 0.072 | 0.337 | 0.345 | 0.463 | 0.24 | 0.345 | - | - | - | ||
| 0.260 | 0.089 | 0.219 | 0.208 | - | 0.17 | 0.217 | - | - | - | ||
For the full charge radius of these mesons, each approaches reports results of the same order of magnitude, that is, fm. It is no surprise because fm is the order of magnitude of a nucleon’s size. Nevertheless, the charge radii obtained from contact interaction model (CI) are lower than others, since CI is a relatively simple model [12]. However, it still provides useful qualitative results. CI predicts that the charge radius of is the largest of these ground state pseudo-scalar meson, and our results confirm this conclusion. This is interesting because is the one with the most significant DCSB effect, which seems to suggest that DCSB, while generating mass, also tends to increase the size of the system.
For slightly/moderately flavor asymmetric meson, such as , , , , , …, the charge radii predicted by these methods are generally consistent. However, In the case of extremely flavor symmetry breaking, such as , these results begin to deviate from each other. CI reports 0.34 fm for , but the result of AM is 0.926 fm, even larger than the proton radius, 0.841(1) fm [70]. In this work, the predicted charge radius of is rather close to light-front framework (LFF) fm. More comparison can be found in Table. 3.
According to Eq. (15), the contributions of different quarks to the system can be extracted, this gives us a glimpse into the internal structure of heavy-light meson. In Table. 3 and Figure. 4, both the separated contributions and full results are presented, we will discuss this in conjunction with vector mesons in the next subsection.


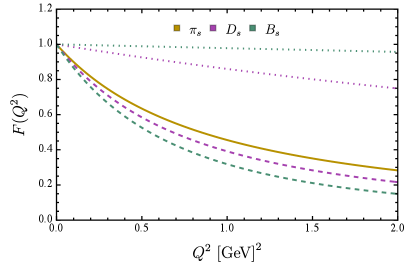
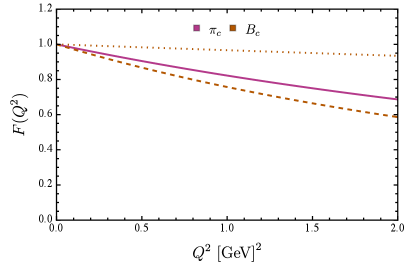



III.2 Vector mesons
Compared with the pseudo-scalar case, the heavy-light vector meson’s electromagnetic form factor have received much less attention. On the one hand, it is difficult to measure in experiment, on the other hand, its theoretical calculation is more complicated. However, noteworthy distinctions or unexpected similarities between pseudo-scalar and vector mesons, such as their charge radii, can help us to better understand the internal structure of these hadrons. Therefore, in this work, we calculate the EFFs of pseudo-scalar/vector mesons with momentum transfer uniformly, except because the pole of the quark propagator in the complex plane limits the computable region [36].
| Meson | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L | H | Full | L | H | Full | L | H | Full | ||
| 0.722 | 0.722 | 0.722 | 2.006 | 2.006 | 2.006 | -0.364 | -0.364 | -0.364 | ||
| 0.732 | 0.557 | 0.679 | 2.234 | 1.896 | 2.121 | -0.479 | -0.340 | -0.433 | ||
| / | / | 0.274 | / | / | -0.112 | / | / | 0.046 | ||
| 0.768 | 0.204 | 0.473 | 4.464 | 1.419 | 2.434 | -1.281 | -0.148 | -0.525 | ||
| / | / | 0.604 | / | / | -2.030 | / | / | 0.755 | ||
| 0.802 | 0.072 | 0.657 | 11.23 | 1.178 | 7.880 | -3.238 | -0.056 | -2.177 | ||
| / | / | 0.462 | / | / | -3.351 | / | / | 1.061 | ||
| 0.589 | 0.210 | 0.381 | 3.856 | 1.472 | 2.267 | -1.044 | -0.170 | -0.461 | ||
| 0.605 | 0.074 | 0.347 | 9.526 | 1.204 | -2.774 | -2.719 | -0.059 | 0.887 | ||
| 0.275 | 0.094 | 0.231 | 4.078 | 1.424 | 3.193 | -0.945 | -0.118 | -0.669 | ||
| Meson | This work | ENJL | LCSR | EBM | BM | NR | BSLT | ChPT | |
|---|---|---|---|---|---|---|---|---|---|
| 2.492 | 2.54 | - | 2.500 | - | - | - | - | ||
| 2.261 | 2.26 | - | 2.210 | - | - | - | - | ||
| -0.119 | - | - | -0.216 | - | - | - | - | ||
| 1.132 | 1.16 | 1.16(8) | 1.060 | 1.17 | 1.32 | - | |||
| -0.944 | - | 0.30(4) | -1.210 | -0.89 | -1.47 | - | - | ||
| 1.386 | 1.47 | 0.90(19) | 1.470 | 1.54 | 1.92 | - | |||
| -0.589 | - | -0.21(4) | -0.650 | -0.64 | -0.87 | - | - | ||
| 1.007 | 0.98 | 1.00(14) | 0.870 | 1.03 | 1.00 | - | |||
| -0.480 | - | -0.17(2) | -0.480 | -0.47 | -0.55 | - | - | ||
| 0.472 | - | - | 0.350 | 0.56 | 0.45 | 0.426 | - | ||
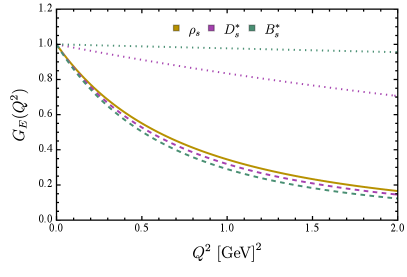
The electric form factor of vector meson, , can be compared with the pseudo-scalar meson’s , because both of them correspond to the charge distribution. The results of this comparison are presented in Figure. 4, and a clear pattern can be noticed immediately.
As mentioned earlier, Eq. (15) allows us to separate the contributions of the lighter and heavier dressed-quark. For , systems, with the increase of current quark mass of , the form factor of the lighter quark becomes steeper while the form factor of the heavier quark flattens out (see Figure. 4, upper panel). The extracted charge radii are presented in the Table. 3 (PS) and Table. 4 (VC). Obviously, the distribution range of and (anti-)quarks gradually expands and contracts. Especially, for quark in system, 0.618 fm (PS), 0.655 fm (VC), it is very close to the charge radius of and , that is, 0.619 fm and 0.657 fm. This reveals that, in systems, the quark is basically stationary, with the charge distribution almost entirely contributed by the quark.
For the , systems, in the middle panel of Figure. 4 we constructed four fictitious states, , which are constituted from -like quarks with current masses equal to and quarks. Again, flavor symmetry breaking leads to the splitting of the form factor, the distribution range of lighter and heavier quarks gradually expands and contracts, respectively. We note that similar conclusions have also been reported by the ENJL model [14].
The full results of the electric form factors of heavy-light mesons are presented in the lower panel of Figure. 4. Qualitatively, the results of pseudo-scalar and vector channel are not much different, however, the charge radius of vector meson is larger than that of its pseudo-scalar counterpart (see Table. 3 and Table. 4). This suggests that spin-dependent interactions will expand the size of the meson, which is consistent with the conclusion in the case of flavor symmetry [37].





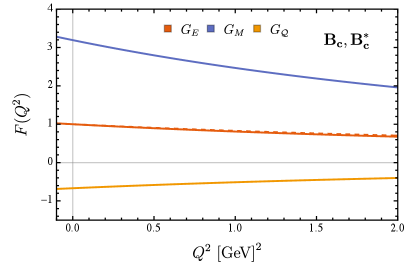

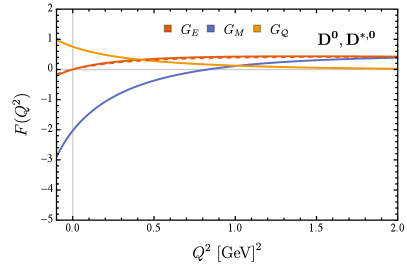


Differing from pseudo-scalar mesons, vector mesons have two more form factors, and , corresponding to magnetic moment and quadrupole moment, respectively. The full results are plotted in Figure. 5 (charged mesons) and Figure. 6 (neutral mesons). For heavy-light mesons, the form factor is qualitatively consistent as the flavor asymmetry increases. However, in the case of charge neutrality, the significant deviation from zero has been exhibited, which reveals a non-trivial internal structure.
The extracted magnetic moments and quadrupole moments are presented together in Table. 4. It is easy to see that when the charge radius of dressed-quark rises, the corresponding magnetic moment and quadrupole moment also increases. In Table. 5, the magnetic moments are listed in the unit of nuclear magneton to compare with the results of other approaches. Once again, the results given by each model/framework are basically the same for slightly/moderately flavor asymmetric meson, but in the extremely flavor asymmetric case, there are significant differences between them. Our predictions of the magnetic moment are basically consistent with the ENJL model’s results. The possible reason is that NJL is a similar framework to DSEs/BSEs, and the magnetic moment is not sensitive to the form of interaction. However, due to the absence of experimental data, these predictions still need to be verified by more approaches.
IV Summary
In this work, we systematically investigate the electromagnetic form factors of heavy-light pseudo-scalar/vector mesons within DSEs/BSEs framework for the first time, including , , , , and systems. Based on it, we extract the charge radii of pseudo-scalar mesons, the charge radii, magnetic moments and the quadrupole moments of the vector mesons, then compare our results with those obtained by other approaches.
The numerical results show that, the flavor symmetry breaking will lead to a splitting of the form factor of different quark in heavy-light system, and the distribution range of lighter and heavier quark gradually expands and contracts, respectively. In the case of vector meson, when the charge radius of dressed-quark increases, so do its corresponding magnetic moment and quadrupole moment. The competition between the contributions of the lighter and heavier quark together generates the electromagnetic form factors of heavy-light meson.
The results presented in this work can be compared with the experimental data and further theoretical calculations, such as applying more elaborate beyond-RL kernel, in the future. We expect that it will be useful for the understanding of the internal structure and dynamics of QCD’s bound states.
Acknowledgements.
We would like to thank Jorge Segovia, Khépani Raya, José Rodríguez-Quintero, Craig D. Roberts for useful discussions/suggestions. This work has been partially funded by Ministerio Español de Ciencia e Innovación under grant Nos. PID2019-107844GB-C22 and PID2022-140440NB-C22; Junta de Andalucía under contract Nos. Operativo FEDER Andalucía 2014-2020 UHU-1264517, P18-FR-5057 and also PAIDI FQM-370. The authors acknowledge, too, the use of the computer facilities of C3UPO at the Universidad Pablo de Olavide, de Sevilla.References
- Altmannshofer et al. [2019] W. Altmannshofer et al. (Belle-II), The Belle II Physics Book, PTEP 2019, 123C01 (2019), [Erratum: PTEP 2020, 029201 (2020)], arXiv:1808.10567 [hep-ex] .
- Aguilar et al. [2019] A. C. Aguilar et al., Pion and Kaon Structure at the Electron-Ion Collider, Eur. Phys. J. A 55, 190 (2019), arXiv:1907.08218 [nucl-ex] .
- Horn [2017] T. Horn, Meson Form Factors and Deep Exclusive Meson Production Experiments, EPJ Web Conf. 137, 05005 (2017).
- Bijnens and Talavera [2002] J. Bijnens and P. Talavera, Pion and kaon electromagnetic form-factors, JHEP 03, 046, arXiv:hep-ph/0203049 .
- Boyle et al. [2008] P. A. Boyle, J. M. Flynn, A. Juttner, C. Kelly, H. P. de Lima, C. M. Maynard, C. T. Sachrajda, and J. M. Zanotti, The Pion’s electromagnetic form-factor at small momentum transfer in full lattice QCD, JHEP 07, 112, arXiv:0804.3971 [hep-lat] .
- Kwee and Lebed [2008] H. J. Kwee and R. F. Lebed, Pion form-factors in holographic QCD, JHEP 01, 027, arXiv:0708.4054 [hep-ph] .
- Gao et al. [2017] F. Gao, L. Chang, Y.-X. Liu, C. D. Roberts, and P. C. Tandy, Exposing strangeness: projections for kaon electromagnetic form factors, Phys. Rev. D 96, 034024 (2017), arXiv:1703.04875 [nucl-th] .
- Miramontes and Bashir [2023] A. S. Miramontes and A. Bashir, Timelike electromagnetic kaon form factor, Phys. Rev. D 107, 014016 (2023), arXiv:2212.10800 [hep-ph] .
- Sauli [2022] V. Sauli, Timelike behavior of the pion electromagnetic form factor in the functional formalism, Phys. Rev. D 106, 034030 (2022), arXiv:2204.08424 [hep-ph] .
- Hwang [2002] C.-W. Hwang, Charge radii of light and heavy mesons, Eur. Phys. J. C 23, 585 (2002), arXiv:hep-ph/0112237 .
- Moita et al. [2021] R. M. Moita, J. P. B. C. de Melo, K. Tsushima, and T. Frederico, Exploring the flavor content of light and heavy-light pseudoscalars, Phys. Rev. D 104, 096020 (2021), arXiv:2104.02787 [hep-ph] .
- Hernández-Pinto et al. [2023] R. J. Hernández-Pinto, L. X. Gutiérrez-Guerrero, A. Bashir, M. A. Bedolla, and I. M. Higuera-Angulo, Electromagnetic form factors and charge radii of pseudoscalar and scalar mesons: A comprehensive contact interaction analysis, Phys. Rev. D 107, 054002 (2023), arXiv:2301.11881 [hep-ph] .
- Almeida-Zamora et al. [2024] B. Almeida-Zamora, J. J. Cobos-Martínez, A. Bashir, K. Raya, J. Rodríguez-Quintero, and J. Segovia, Algebraic model to study the internal structure of pseudoscalar mesons with heavy-light quark content, Phys. Rev. D 109, 014016 (2024), arXiv:2309.17282 [hep-ph] .
- Luan et al. [2015] Y.-L. Luan, X.-L. Chen, and W.-Z. Deng, Meson electro-magnetic form factors in an extended Nambu–Jona-Lasinio model including heavy quark flavors, Chin. Phys. C 39, 113103 (2015), arXiv:1504.03799 [hep-ph] .
- Li and Wu [2017] N. Li and Y.-J. Wu, Lattice study of D and Ds meson form factors with twisted boundary conditions, Eur. Phys. J. A 53, 56 (2017).
- Das et al. [2016] T. Das, D. K. Choudhury, and N. S. Bordoloi, Charge radii of heavy flavored mesons in a potential model, (2016), arXiv:1608.06896 [hep-ph] .
- Aliev et al. [2020] T. M. Aliev, S. Bilmis, and M. Savci, Multipole Moments of Heavy Vector and Axial-Vector Mesons in QCD, Phys. Rev. D 101, 054009 (2020), arXiv:1912.05988 [hep-ph] .
- Šimonis [2016] V. Šimonis, Magnetic properties of ground-state mesons, Eur. Phys. J. A 52, 90 (2016), arXiv:1604.05894 [hep-ph] .
- Bose and Singh [1980] S. K. Bose and L. P. Singh, Magnetic Moments of Charmed and Flavored Hadrons in MIT Bag Model, Phys. Rev. D 22, 773 (1980).
- Lahde [2003] T. A. Lahde, Exchange current operators and electromagnetic dipole transitions in heavy quarkonia, Nucl. Phys. A 714, 183 (2003), arXiv:hep-ph/0208110 .
- Wang et al. [2019] B. Wang, B. Yang, L. Meng, and S.-L. Zhu, Radiative transitions and magnetic moments of the charmed and bottom vector mesons in chiral perturbation theory, Phys. Rev. D 100, 016019 (2019), arXiv:1905.07742 [hep-ph] .
- Roberts and Williams [1994] C. D. Roberts and A. G. Williams, Dyson-Schwinger equations and their application to hadronic physics, Prog. Part. Nucl. Phys. 33, 477 (1994), arXiv:hep-ph/9403224 .
- Maris and Tandy [1999] P. Maris and P. C. Tandy, Bethe-Salpeter study of vector meson masses and decay constants, Phys. Rev. C 60, 055214 (1999), arXiv:nucl-th/9905056 .
- Maris and Roberts [2003] P. Maris and C. D. Roberts, Dyson-Schwinger equations: A Tool for hadron physics, Int. J. Mod. Phys. E 12, 297 (2003), arXiv:nucl-th/0301049 .
- Maris and Roberts [1997] P. Maris and C. D. Roberts, Pi- and K meson Bethe-Salpeter amplitudes, Phys. Rev. C 56, 3369 (1997), arXiv:nucl-th/9708029 .
- Qin et al. [2011] S.-x. Qin, L. Chang, Y.-x. Liu, C. D. Roberts, and D. J. Wilson, Interaction model for the gap equation, Phys. Rev. C 84, 042202 (2011), arXiv:1108.0603 [nucl-th] .
- Rodriguez-Quintero [2011] J. Rodriguez-Quintero, On the massive gluon propagator, the PT-BFM scheme and the low-momentum behaviour of decoupling and scaling DSE solutions, JHEP 01, 105, arXiv:1005.4598 [hep-ph] .
- Qin et al. [2012] S.-x. Qin, L. Chang, Y.-x. Liu, C. D. Roberts, and D. J. Wilson, Investigation of rainbow-ladder truncation for excited and exotic mesons, Phys. Rev. C 85, 035202 (2012), arXiv:1109.3459 [nucl-th] .
- Xu et al. [2020] Y.-Z. Xu, C. Shi, X.-T. He, and H.-S. Zong, Chiral crossover transition from the Dyson-Schwinger equations in a sphere, Phys. Rev. D 102, 114011 (2020), arXiv:2009.12035 [nucl-th] .
- Qin et al. [2020] P. Qin, S.-x. Qin, and Y.-x. Liu, Heavy-light mesons beyond the ladder approximation, Phys. Rev. D 101, 114014 (2020), arXiv:1912.05902 [hep-ph] .
- Xu et al. [2023a] Y.-Z. Xu, S.-X. Qin, and H.-S. Zong, Chiral symmetry restoration and properties of Goldstone bosons at finite temperature*, Chin. Phys. C 47, 033107 (2023a), arXiv:2106.13592 [hep-ph] .
- Li et al. [2023] Q. Li, C.-H. Chang, T. Wang, and G.-L. Wang, Strong decays of to J/(c)p and within the Bethe-Salpeter framework, JHEP 06, 189, arXiv:2301.02094 [hep-ph] .
- da Silveira et al. [2023] R. C. da Silveira, F. E. Serna, and B. El-Bennich, Strong two-meson decays of light and charmed vector mesons, Phys. Rev. D 107, 034021 (2023), arXiv:2211.16618 [hep-ph] .
- Maris and Tandy [2000] P. Maris and P. C. Tandy, The pi, K+, and K0 electromagnetic form-factors, Phys. Rev. C 62, 055204 (2000), arXiv:nucl-th/0005015 .
- Bhagwat and Maris [2008] M. S. Bhagwat and P. Maris, Vector meson form factors and their quark-mass dependence, Phys. Rev. C 77, 025203 (2008), arXiv:nucl-th/0612069 .
- Chen et al. [2018] M. Chen, M. Ding, L. Chang, and C. D. Roberts, Mass-dependence of pseudoscalar meson elastic form factors, Phys. Rev. D 98, 091505 (2018), arXiv:1808.09461 [nucl-th] .
- Xu et al. [2019] Y.-Z. Xu, D. Binosi, Z.-F. Cui, B.-L. Li, C. D. Roberts, S.-S. Xu, and H. S. Zong, Elastic electromagnetic form factors of vector mesons, Phys. Rev. D 100, 114038 (2019), arXiv:1911.05199 [nucl-th] .
- Xu and Segovia [2023] Y.-Z. Xu and J. Segovia, An Assessment of Pseudoscalar and Vector Meson Electromagnetic Form Factors, Few Body Syst. 64, 62 (2023).
- Xu et al. [2023b] Y.-Z. Xu, M. Ding, K. Raya, C. D. Roberts, J. Rodríguez-Quintero, and S. M. Schmidt, Pion and kaon electromagnetic and gravitational form factors, (2023b), arXiv:2311.14832 [hep-ph] .
- Chang et al. [2009] L. Chang, Y.-x. Liu, C. D. Roberts, Y.-m. Shi, W.-m. Sun, and H.-s. Zong, Chiral susceptibility and the scalar Ward identity, Phys. Rev. C 79, 035209 (2009), arXiv:0812.2956 [nucl-th] .
- Xu et al. [2021] Y.-Z. Xu, S. Chen, Z.-Q. Yao, D. Binosi, Z.-F. Cui, and C. D. Roberts, Vector-meson production and vector meson dominance, Eur. Phys. J. C 81, 895 (2021), arXiv:2107.03488 [hep-ph] .
- Tanabashi et al. [2018] M. Tanabashi et al. (Particle Data Group), Review of Particle Physics, Phys. Rev. D 98, 030001 (2018).
- McNeile et al. [2012] C. McNeile, C. T. H. Davies, E. Follana, K. Hornbostel, and G. P. Lepage, Heavy meson masses and decay constants from relativistic heavy quarks in full lattice QCD, Phys. Rev. D 86, 074503 (2012), arXiv:1207.0994 [hep-lat] .
- Fischer et al. [2005] C. S. Fischer, P. Watson, and W. Cassing, Probing unquenching effects in the gluon polarisation in light mesons, Phys. Rev. D 72, 094025 (2005), arXiv:hep-ph/0509213 .
- Blank [2011] M. Blank, Properties of quarks and mesons in the Dyson-Schwinger/Bethe-Salpeter approach, Ph.D. thesis, Graz U. (2011), arXiv:1106.4843 [hep-ph] .
- Chen and Chang [2019] M. Chen and L. Chang, A pattern for the flavor dependent quark-antiquark interaction, Chin. Phys. C 43, 114103 (2019), arXiv:1903.07808 [nucl-th] .
- Ivanov et al. [1999] M. A. Ivanov, Y. L. Kalinovsky, and C. D. Roberts, Survey of heavy meson observables, Phys. Rev. D 60, 034018 (1999), arXiv:nucl-th/9812063 .
- Rojas et al. [2014] E. Rojas, B. El-Bennich, and J. P. B. C. de Melo, Exciting flavored bound states, Phys. Rev. D 90, 074025 (2014), arXiv:1407.3598 [nucl-th] .
- Gómez-Rocha et al. [2016] M. Gómez-Rocha, T. Hilger, and A. Krassnigg, Effects of a dressed quark-gluon vertex in vector heavy-light mesons and theory average of the meson mass, Phys. Rev. D 93, 074010 (2016), arXiv:1602.05002 [hep-ph] .
- Qin and Roberts [2021] S.-X. Qin and C. D. Roberts, Resolving the Bethe–Salpeter Kernel, Chin. Phys. Lett. 38, 071201 (2021), arXiv:2009.13637 [hep-ph] .
- Edwards et al. [2001] K. W. Edwards et al. (CLEO), Study of B decays to charmonium states B — eta(c) K and B — chi(c0) K, Phys. Rev. Lett. 86, 30 (2001), arXiv:hep-ex/0007012 .
- Mathur et al. [2018] N. Mathur, M. Padmanath, and S. Mondal, Precise predictions of charmed-bottom hadrons from lattice QCD, Phys. Rev. Lett. 121, 202002 (2018), arXiv:1806.04151 [hep-lat] .
- Cichy et al. [2016] K. Cichy, M. Kalinowski, and M. Wagner, Continuum limit of the meson, meson and charmonium spectrum from twisted mass lattice QCD, Phys. Rev. D 94, 094503 (2016), arXiv:1603.06467 [hep-lat] .
- Dowdall et al. [2012] R. J. Dowdall, C. T. H. Davies, T. C. Hammant, and R. R. Horgan, Precise heavy-light meson masses and hyperfine splittings from lattice QCD including charm quarks in the sea, Phys. Rev. D 86, 094510 (2012), arXiv:1207.5149 [hep-lat] .
- Fu and Wang [2016] Z. Fu and L. Wang, Studying the resonance parameters with staggered fermions, Phys. Rev. D 94, 034505 (2016), arXiv:1608.07478 [hep-lat] .
- Dudek et al. [2014] J. J. Dudek, R. G. Edwards, C. E. Thomas, and D. J. Wilson (Hadron Spectrum), Resonances in coupled scattering from quantum chromodynamics, Phys. Rev. Lett. 113, 182001 (2014), arXiv:1406.4158 [hep-ph] .
- Donald et al. [2014] G. C. Donald, C. T. H. Davies, J. Koponen, and G. P. Lepage (HPQCD), from semileptonic decay and full lattice QCD, Phys. Rev. D 90, 074506 (2014), arXiv:1311.6669 [hep-lat] .
- Lubicz et al. [2017] V. Lubicz, A. Melis, and S. Simula (ETM), Masses and decay constants of D*(s) and B*(s) mesons with N twisted mass fermions, Phys. Rev. D 96, 034524 (2017), arXiv:1707.04529 [hep-lat] .
- Donald et al. [2012] G. C. Donald, C. T. H. Davies, R. J. Dowdall, E. Follana, K. Hornbostel, J. Koponen, G. P. Lepage, and C. McNeile, Precision tests of the from full lattice QCD: mass, leptonic width and radiative decay rate to , Phys. Rev. D 86, 094501 (2012), arXiv:1208.2855 [hep-lat] .
- Follana et al. [2008] E. Follana, C. T. H. Davies, G. P. Lepage, and J. Shigemitsu (HPQCD, UKQCD), High Precision determination of the pi, K, D and D(s) decay constants from lattice QCD, Phys. Rev. Lett. 100, 062002 (2008), arXiv:0706.1726 [hep-lat] .
- Bazavov et al. [2018] A. Bazavov et al., - and -meson leptonic decay constants from four-flavor lattice QCD, Phys. Rev. D 98, 074512 (2018), arXiv:1712.09262 [hep-lat] .
- Colquhoun et al. [2015a] B. Colquhoun, R. J. Dowdall, C. T. H. Davies, K. Hornbostel, and G. P. Lepage, and Leptonic Widths, and from full lattice QCD, Phys. Rev. D 91, 074514 (2015a), arXiv:1408.5768 [hep-lat] .
- Colquhoun et al. [2015b] B. Colquhoun, C. T. H. Davies, R. J. Dowdall, J. Kettle, J. Koponen, G. P. Lepage, and A. T. Lytle (HPQCD), B-meson decay constants: a more complete picture from full lattice QCD, Phys. Rev. D 91, 114509 (2015b), arXiv:1503.05762 [hep-lat] .
- Amendolia et al. [1986a] S. R. Amendolia et al. (NA7), A Measurement of the Space - Like Pion Electromagnetic Form-Factor, Nucl. Phys. B 277, 168 (1986a).
- Volmer et al. [2001] J. Volmer et al. (Jefferson Lab F(pi)), Measurement of the Charged Pion Electromagnetic Form-Factor, Phys. Rev. Lett. 86, 1713 (2001), arXiv:nucl-ex/0010009 .
- Amendolia et al. [1986b] S. R. Amendolia et al., A Measurement of the Kaon Charge Radius, Phys. Lett. B 178, 435 (1986b).
- Epelbaum et al. [2022] E. Epelbaum, J. Gegelia, N. Lange, U. G. Meißner, and M. V. Polyakov, Definition of Local Spatial Densities in Hadrons, Phys. Rev. Lett. 129, 012001 (2022), arXiv:2201.02565 [hep-ph] .
- Miller [2019] G. A. Miller, Defining the proton radius: A unified treatment, Phys. Rev. C 99, 035202 (2019), arXiv:1812.02714 [nucl-th] .
- Gao et al. [2021] X. Gao, N. Karthik, S. Mukherjee, P. Petreczky, S. Syritsyn, and Y. Zhao, Pion form factor and charge radius from lattice QCD at the physical point, Phys. Rev. D 104, 114515 (2021), arXiv:2102.06047 [hep-lat] .
- Workman et al. [2022] R. L. Workman et al. (Particle Data Group), Review of Particle Physics, PTEP 2022, 083C01 (2022).
- Povh and Hufner [1990] B. Povh and J. Hufner, Systematics of strong interaction radii for hadrons, Phys. Lett. B 245, 653 (1990).
- Krutov et al. [2016] A. F. Krutov, R. G. Polezhaev, and V. E. Troitsky, The radius of the rho meson determined from its decay constant, Phys. Rev. D 93, 036007 (2016), arXiv:1602.00907 [hep-ph] .