The effect of initial nuclear deformation on dielectron photoproduction
in hadronic heavy-ion collisions
Abstract
Significant excesses of pair production at very low transverse momentum ( 0.15 GeV/c) were observed by the STAR collaboration in hadronic heavy-ion collisions. Such enhancement is assumed to be a sign of photon-photon production in heavy-ion collisions with hadronic overlap, based on comparisons with model calculations for spherical Au + Au collisions. However, there is a lack of calculations for pair production from coherent photon-photon interactions in hadronic U + U collisions, due to the deformity of Uranium nuclei. In this article, we present calculations for pair photoproduction at = 193 GeV in both spherical and deformed U + U collisions within STAR detector acceptance using the equivalent photon approximation (EPA). We conduct event-by-event analysis to investigate the effects of initial nuclear deformation on pair production. Our numerical results show good agreement with experimental data for the 40%–60% and 60%–80% centrality classes in U + U collisions, and the differences between spherical and deformed configurations are approximately 3%. We also calculate the yields of the photoproduced pair in hadronic deformed Ru + Ru and Zr + Zr collisions at = 200 GeV. The results reveal that the ratios of the yields of Ru to Zr exhibit very small differences ( 1%) between spherical and deformed cases.
I Introduction
One of the major aims of the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National laboratory (BNL) is to simulate the extreme conditions in the first microseconds of the Universe and search for the deconfined state of partonic matter, commonly known as quark-gluon plasma (QGP), in a laboratory [1, 2]. Dileptons, which carry pure information about the hot and dense nuclear matter, are considered to be important probes for studying the properties of QGP since they are produced in the whole evolution of the collision and not involved in strong interactions [3]. Conventionally, dileptons are typically produced by the decays of known hadronic sources, QGP thermal radiation, and in-medium broadening of the spectral function [4, 5].
In addition, dileptons can also be generated via photon-photon interactions in relativistic heavy-ion collisions [6]. The almost transverse electromagnetic fields accompanied by the colliding nuclei can be viewed as an equivalent swarm of high-energy quasireal photons [7, 8]. Emitted virtual photons from one nucleus can interact with those emitted by the other nucleus, leading to dilepton production, known as photoproduction process. Two-photon processes have been widely studied in ultraperipheral collisions (UPCs), where the impact parameter () is larger than twice the nuclear radius (), and hadronic interactions do not occur [9, 10, 11].
Recently, significant enhancements of pair production were observed by the STAR collaboration [12] in peripheral Au + Au and U + U collisions (). All detected excesses are found below 0.15 GeV/c, whereas the upper limit of the transverse momentum of virtual photons is around 30 MeV/c () [13, 14]. Hence, this may indicate that the excesses likely result from photoproduction in violent hadronic heavy-ion collisions. Furthermore, model calculations of photon-photon interactions in spherical Au + Au collisions also support this idea [15, 16]. However, there are no calculations available on the photoproduced pair in hadronic U + U collisions to date due to initial nuclear deformation.
The equivalent photon spectrum of a relativistic ion depends quadratically on its charge number [13], and for this reason, the pair produced by two-photon interactions should be proportional to . To further confirm that the excesses of the pair at very low- are attributable to photon-photon processes, it is crucial to investigate the dependence of the observed excesses on the nuclear charge number. The isobaric collisions ( + and + ) at = 200 GeV, proposed to search for the presence of the chiral magnetic effect [17], also provide a unique opportunity to verify the theory of photoproduction because similar hadronic backgrounds are expected due to the same nucleon number [18, 19].
In this paper, we present the invariant mass dependence of the photoproduced
pair for both spherical and deformed U + U collisions at = 193 GeV and
compare our results with the excesses observed by STAR collaboration. We also calculate the
pair production in hadronic deformed Ru + Ru and Zr + Zr collisions at
= 200 GeV, and the ratios of the yields of Ru to Zr between spherical and
deformed cases are also shown.
II Methodology
II.1 Initial nuclear deformation
The charge density for a spherical heavy ion is typically given by the Woods-Saxon distribution:
| (1) |
where represents the normalization factor and denotes the density at the center of the nucleus. The radius and skin depth are obtained from elastic electron scattering [20, 21]. However, for deformed nuclei, an alternative way to describe their charge density is to extend the two-parameter Fermi distribution by introducing deformation parameters:
| (2) |
where and are quadrupole and hexadecupole deformation expressed in the spherical-harmonics expansion, respectively [22]. It is noteworthy that this charge density is independent of the azimuthal angle, allowing us to derive .
Deformation parameters for the nucleus are taken from Ref. [23]. Nuclear density distributions are not clear for deformed and because e-A scattering experiments [24, 25] and comprehensive model deductions [26] present significantly different results. In this study, we adopt larger values to evaluate the maximum impact of initial nuclear deformation on pair photoproduction in hadronic heavy-ion collisions. The parameters for both spherical and deformed nuclei used in our analysis are listed in Table 1. Additionally, the shape of the deformed nucleus is a prolate spheroid when , and the direction of the major axis in Eq. (2) is along the axis.
| Nucleus | Spherical | Deformed | ||||
|---|---|---|---|---|---|---|
| (fm) | (fm) | (fm) | (fm) | |||
| 6.8054 | 0.605 | 6.8054 | 0.605 | 0.2863 | 0.093 | |
| 5.085 | 0.46 | 5.085 | 0.46 | 0.158 | 0 | |
| 5.02 | 0.46 | 5.02 | 0.46 | 0.217 | 0 | |
In deformed heavy-ion collisions, the directions of the major axis of colliding nuclei are expected to be random and irrelevant. Our calculations adopt the following reference frame: where the beam direction corresponds to the axis, and the direction of the impact parameter corresponds to the axis.
The charge density of a deformed nucleus with a specific can then be expressed as:
| (3) |
| (4) |
| (5) |
| (6) |
where and are rotation matrices, and and denote the polar angle and azimuthal angle of , respectively. We assume that is isotropic in the surface of the unit sphere, which means that cos is uniform in and is uniform in . In our calculations, the surface of the unit sphere is divided into 400 bins, leading to = 160000 collision configurations when two deformed nuclei collide. Conventionally, configurations with and are referred to as tip-tip and body-body collisions, respectively [27, 28], where subscripts 1 and 2 represent the two colliding nuclei. Selecting central tip-tip events and central body-body events based on experimental observables is possible [29], so we will also present calculations for the two limiting cases in deformed U + U collisions.
II.2 Photon flux and form factor
In relativistic heavy-ion collisions, the electric and magnetic fields accompanied by nuclei are mutually perpendicular and have the same absolute magnitudes. These almost transverse electromagnetic fields are very similar to the electromagnetic fields of photons and can be viewed as an equivalent swarm of quasireal photons [8]. According to the equivalent photon approximation (EPA) method, the induced photon flux with energy at transverse position from the center of the nucleus is given by [7]:
| (7) |
| (8) |
where is the fine-structure constant, is the Lorentz factor of the nucleus, is the nuclear charge number, and is the transverse momentum of the photon. The form factor , carrying the information about the charge distribution inside the nucleus, can be obtained by performing a Fourier transformation to the charge density :
| (9) |
For a spherical nucleus, the form factor can be expressed as follows:
| (10) |
For a spheroidal nucleus, the form factor depends on the direction of momentum transfer as well:
| (11) |
| (12) |
where denotes the angle between momentum transfer and major axis . Utilizing Eq. (7), we can calculate the photon flux for a deformed nucleus with a given .
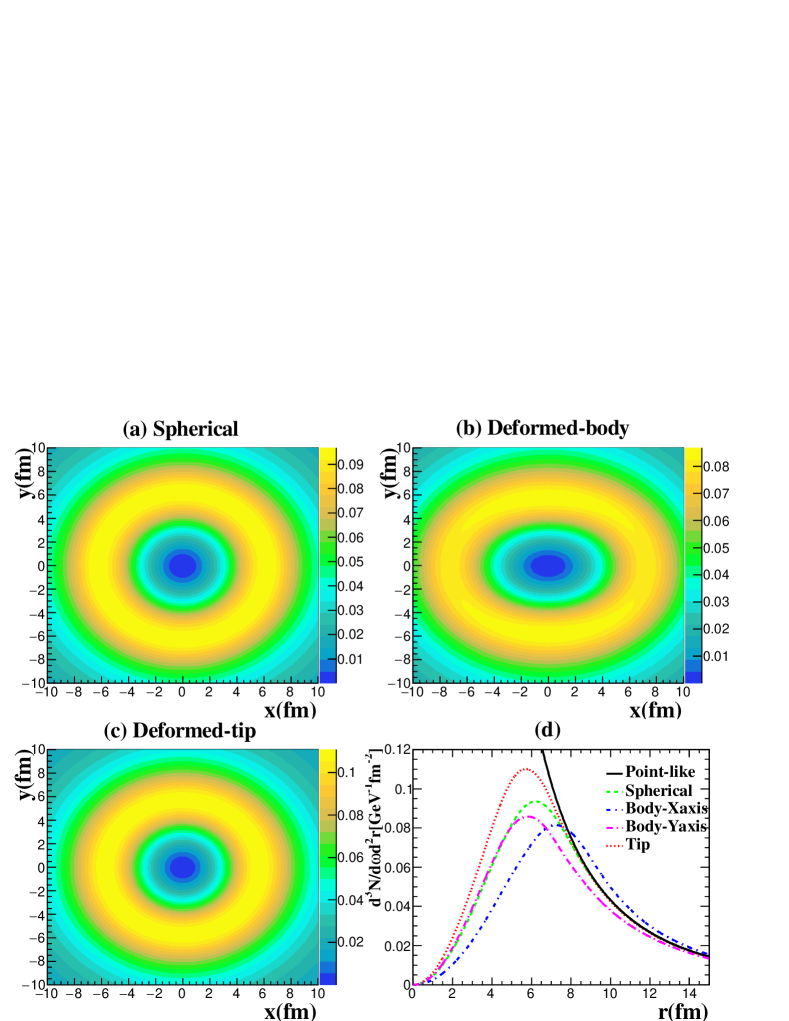
Fig. 1 shows the photon flux distributions with energy = 1 GeV in U + U collisions at = 193 GeV as a function of transverse position from the center of the nucleus. The photon flux for the spherical nucleus is shown in panel (a), and those in the case of body and tip orientations for the deformed nucleus are presented in panels (b) and (c). The results from different configurations as a function of distance from the center of the nucleus are illustrated in panel (d), and one can observe that the differences are concentrated around . The photon flux from the tip orientation is greater than that for the spherical nucleus, while the maximum region (orange circular band) presents a smaller radius. The pattern from the body orientation exhibits an ellipse, where the extreme points of photon flux along the -axis and -axis differ, corresponding to the polar (major) radius and equatorial radius of the prolate spheroid, respectively.
II.3 pair photoproduction
According to the equivalent photon approximation, the cross section of the pair produced by the two-photon process in relativistic heavy-ion collisions can be expressed as [13]:
| (13) |
where is the photon-photon reaction cross section for the pair. The energy of the produced particles is , while their longitudinal momentum becomes as the velocity of the moving heavy ion approaches the speed of light. The final- state particles have a small transverse momentum, which can be negligible compared to longitudinal momentum. Consequently, the invariant mass and rapidity of the pair can be obtained as follows:
| (14) |
| (15) |
Therefore, in Eq. (II.3) can be converted to . The cross section for producing a pair of electrons with invariant mass is given by the Breit-Wheeler formula [30]:
| (16) |
where is the mass of the electron.
| Centrality | Configuration | range(fm) | range | |
|---|---|---|---|---|
| 40%–60% | Spherical | 10.4–12.7 | 29.7–93.8 | 57.6 |
| Tip-tip | 9.8–12.0 | 28.5–93.1 | 57.6 | |
| Body-body | 11.8–14.4 | 35.1–102.8 | 65.1 | |
| Deformed | 30.1–94.2 | 58.0 | ||
| 60%–80% | Spherical | 12.7–14.7 | 5.9–29.7 | 15.3 |
| Tip-tip | 12.0–13.8 | 5.6–28.5 | 15.2 | |
| Body-body | 14.4–16.7 | 7.1–35.1 | 18.4 | |
| Deformed | 6.0–30.1 | 15.6 |
| Centrality | Spherical | Deformed | |||
|---|---|---|---|---|---|
| range (fm) | range | range | |||
| 0–10% | 0–3.7 | 128.0–180.9 | 152.7 | 127.6–180.1 | 152.0 |
| 10%–20% | 3.7–5.2 | 90.8–128.0 | 108.4 | 90.7–127.6 | 108.2 |
| 20%–30% | 5.2–6.3 | 63.3–90.8 | 76.4 | 63.2–90.7 | 76.3 |
| 30%–40% | 6.3–7.3 | 42.5–63.3 | 52.3 | 42.5–63.2 | 52.3 |
| 40%–50% | 7.3–8.2 | 27.1–42.5 | 34.3 | 27.1–42.5 | 34.3 |
| 50%–60% | 8.2–9.0 | 16.1–27.1 | 21.2 | 16.1–27.1 | 21.2 |
| 60%–70% | 9.0–9.7 | 8.7–16.1 | 12.1 | 8.8–16.1 | 12.1 |
| 70%–80% | 9.7–10.4 | 4.3–8.7 | 6.3 | 4.3–8.8 | 6.3 |
| 80%–90% | 10.4–11.1 | 1.7–4.3 | 2.9 | 1.7–4.3 | 2.9 |
| Centrality | Spherical | Deformed | |||
|---|---|---|---|---|---|
| range (fm) | range | range | |||
| 0–10% | 0–3.6 | 128.3–181.1 | 153.0 | 127.6–179.5 | 151.7 |
| 10%–20% | 3.6–5.1 | 91.0–128.3 | 108.7 | 90.7–127.6 | 108.2 |
| 20%–30% | 5.1–6.3 | 63.3–91.0 | 76.5 | 63.2–90.7 | 76.4 |
| 30%–40% | 6.3–7.3 | 42.4–63.3 | 52.4 | 42.5–63.2 | 52.4 |
| 40%–50% | 7.3–8.1 | 27.0–42.4 | 34.3 | 27.1–42.5 | 34.3 |
| 50%–60% | 8.1–8.9 | 16.0–27.0 | 21.1 | 16.1–27.1 | 21.2 |
| 60%–70% | 8.9–9.6 | 8.7–16.0 | 12.0 | 8.7–16.1 | 12.1 |
| 70%–80% | 9.6–10.3 | 4.3–8.7 | 6.2 | 4.2–8.7 | 6.3 |
| 80%–90% | 10.3–11.0 | 1.7–4.3 | 2.8 | 1.7–4.3 | 2.9 |
The model calculations of pair photoproduction have been presented in hadronic Au + Au collisions [15], and we utilize a similar approach to conduct model calculations of pair photoproduction in randomly oriented collisions of deformed heavy ions. The yield for the photoproduced pair with the orientation in a selected centrality bin can be expressed as:
| (17) |
where and are the minimum and maximum impact parameters for a given centrality class, and is the probability of hadronic interactions:
| (18) |
where is the nucleon number, is the inelastic nucleon-nucleon cross section, which is dependent on collision energy [31], and the nuclear thickness function is the projection of nuclear charge density with orientation on the - plane:
| (19) |
In this way, we can directly obtain the pair yields in tip-tip and body-body collisions, but the calculations of all = 160000 collision configurations are required to obtain the average yields in deformed heavy-ion collisions. Our results are filtered to match the fiducial acceptance ( 0.2 GeV/c, 1, 1) to compare with experimental data from the STAR collaboration [12]. As discussed in Refs. [15, 32], the impact of violent hadronic interactions occurring in the overlap region on photoproduction is negligible for peripheral collisions. In central collisions, this effect on differences between spherical and deformed configurations should be small. Therefore, we neglect the possible disruptive effects from hadronic interactions in our calculations.
II.4 Centrality definition
In deformed heavy-ion collisions, we will employ the Glauber model [31, 33] to define centrality and provide corresponding impact parameters. For a random collision configuration with the orientation , the centrality can be expressed as a percentage of the interaction probability:
| (20) |
In tip-tip and body-body collisions, this approach is suitable, but it is not sufficient when calculating average yields because all configurations occur with the same probability. Instead, the two-component approach is a better choice [33, 34, 35], where is the number of participating nucleons, and is the number of nucleon-nucleon collisions [33]:
| (21) |
| (22) |
The relative weight is usually small [31, 34, 35, 36, 37], and thus we set = 0 for simplicity. Therefore, the centrality in deformed heavy-ion collisions is defined by the cumulative distribution function of :
| (23) |
| (24) |
where is the average probability distribution of and is the probability distribution for a special configuration, which can be calculated using Eqs. (20) and (II.4):
| (25) |
It is noteworthy that monotonically decreases with impact parameter . Once the range of in a given centrality class is obtained from Eq. (23), the corresponding range of the impact parameter for a random configuration can be determined from Eq. (II.4). Then, the yield for the photoproduced pair can be calculated using Eq. (17). Table 2 presents the centrality definitions in 40%–60% and 60%–80% for U + U collisions as well as the tip-tip and body-body configurations. The average number of participants is also listed in the table. Tables 3 and 4 report the centrality definitions for Ru + Ru and Zr + Zr collisions, respectively, under both spherical and deformed configurations. Despite the systematic differences of observed when compared with the Glauber Monte Carlo approach [33], the variation in impact parameter between the two calculations is found to be minor.
III Results
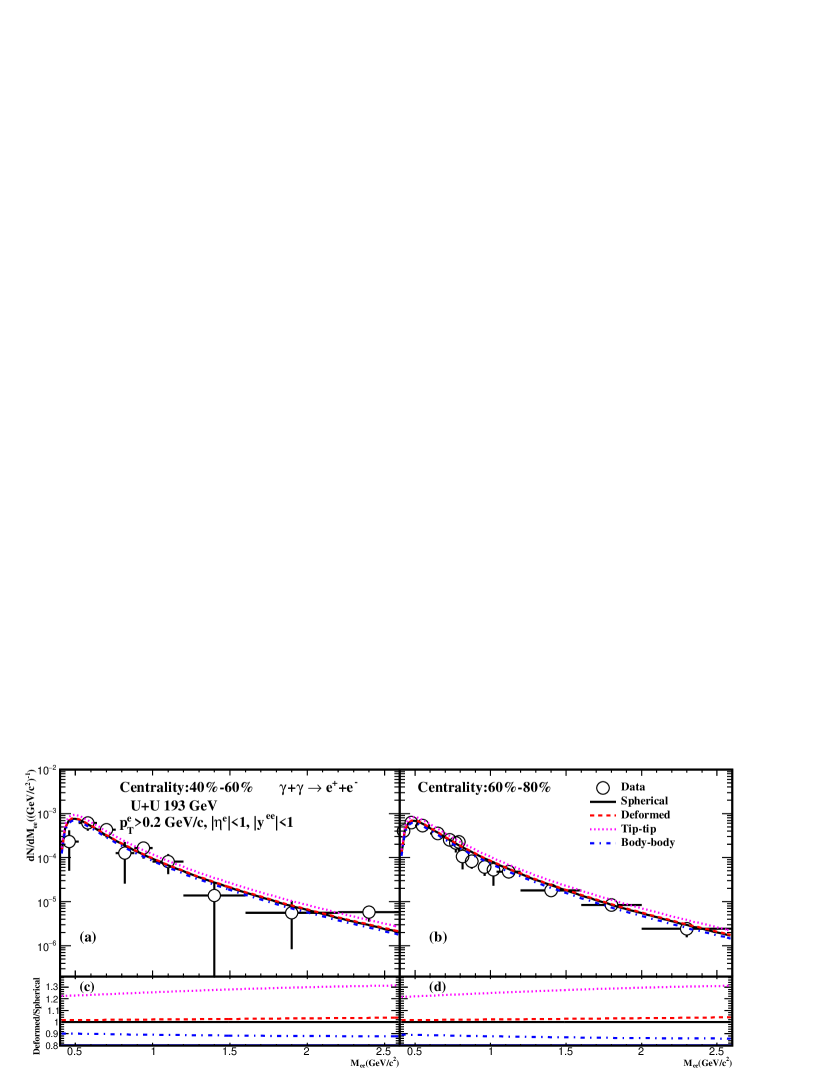
Fig. 2 shows the pair mass spectra within the STAR acceptance in (a) 40%–60% and (b) 60%–80% for spherical, tip-tip and body-body U + U collisions at = 193 GeV. The spectra are contrasted with previously reported excess yields at low from the STAR collaboration [12], while the average yields in deformed heavy-ion collisions are also presented and denoted as “Deformed”. The ratios of pair mass spectra from different configurations to those from the spherical case are shown in panels (c) and (d). The result in tip-tip collisions is approximately 25% higher than that in spherical collisions. The difference becomes more significant as the invariant mass increases due to the higher energy of photons induced in tip-tip collisions. Meanwhile, the pair mass spectrum in body-body collisions is approximately 10% lower than that in spherical collisions. Both the deformed and spherical configurations can describe the data well, and the former is slightly higher by approximately 3% than the latter.
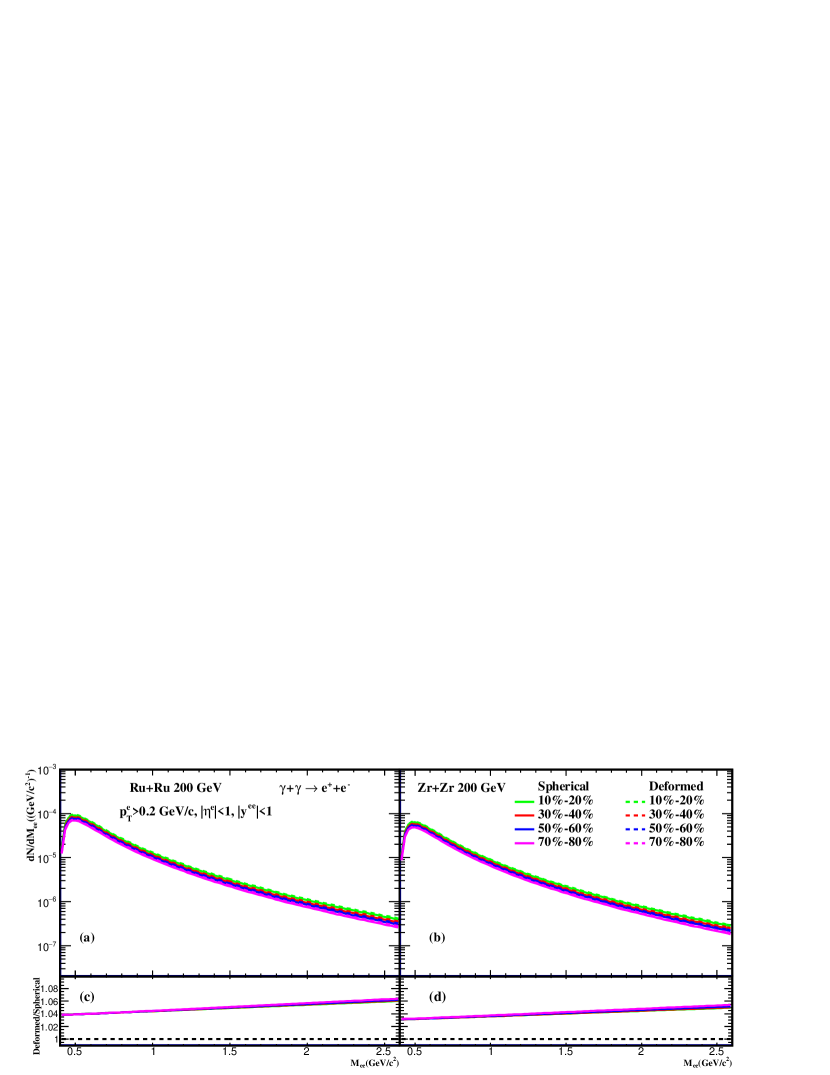
Fig. 3 shows the pair mass spectra in (a) Ru + Ru and (b) Zr + Zr collisions at = 200 GeV for different centrality classes within the STAR acceptance. Likewise, the ratios of pair mass spectra in deformed collisions to those in spherical collisions are shown in panels (c) and (d). Compared to the Zr + Zr collisions, the pair yields for Ru + Ru collisions are higher due to the larger charge number. The pair mass spectra with the deformed configuration exhibit approximately 5% increases compared to the spherical case in Ru + Ru collisions, while the differences become slightly smaller in Zr + Zr collisions. Although the yields of pair yields increase in more central collisions, the ratios do not seem to exhibit dependence on centrality.
We further present the centrality dependence of integrated yields of photoproduced pair in the mass region of 0.4–2.6 GeV/ in Ru + Ru and Zr + Zr collisions with both spherical and deformed configurations in Fig. 4. The corresponding ratios of pair yields in deformed collisions to those in spherical collisions are shown in panel (b), and indeed, the impact of initial nuclear deformation on pair photoproduction does not have centrality dependence.
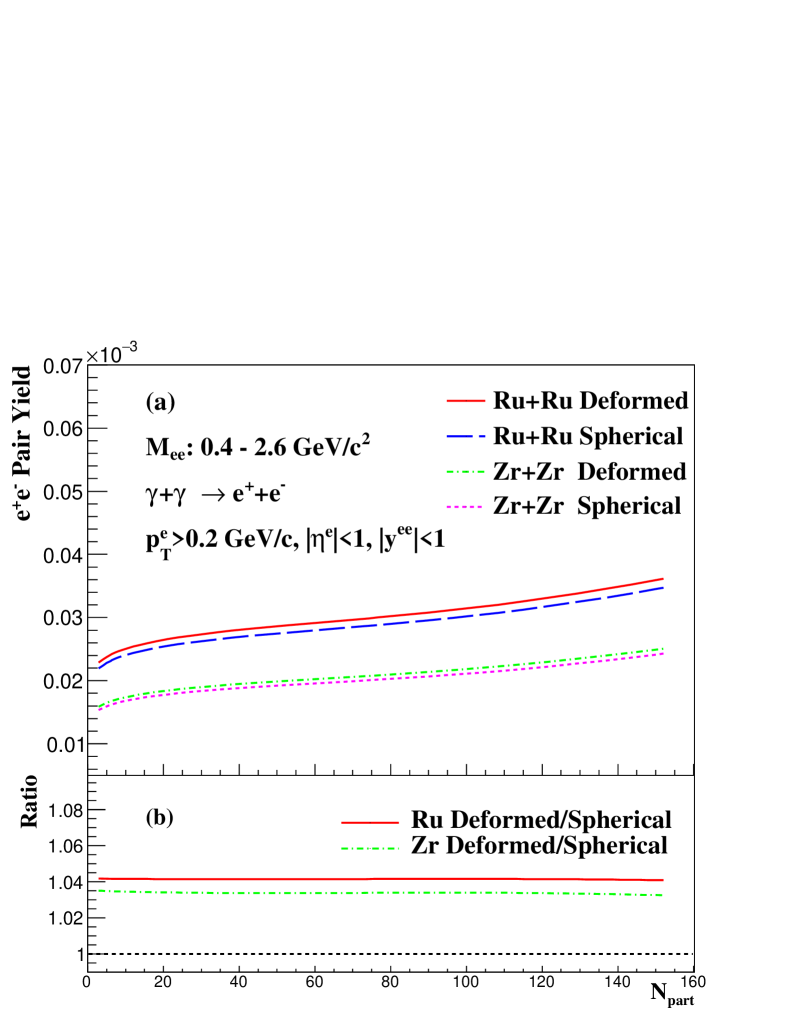
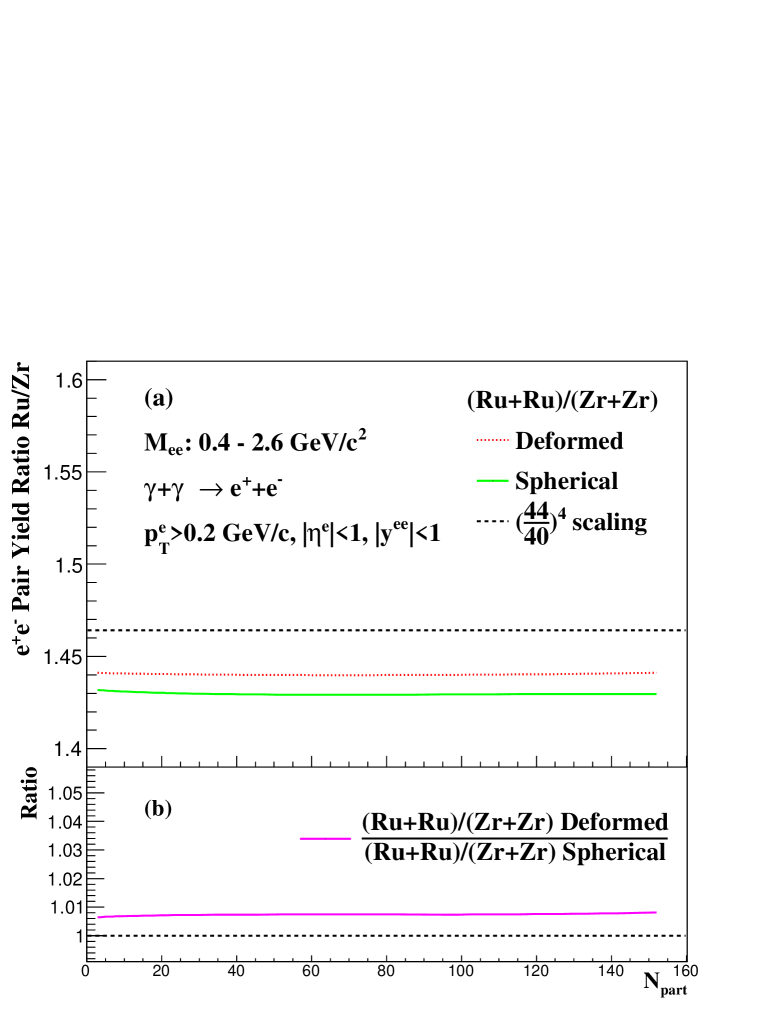
Fig. 5 illustrates the ratios of pair yields in Ru + Ru collisions to those in Zr + Zr collisions as a function of . The ratios are slightly smaller than the scaling, which is due to the slightly different Woods-Saxon parameters for Zr and Ru nuclei. And one can observe that the difference between the two ratios for spherical and deformed configurations is very small ( 1%), which demonstrates that the impact of initial nuclear deformation on the ratios of pair photoproduction between Ru + Ru and Zr + Zr collisions is negligible.
IV Summary
In summary, we employ the Glauber model and equivalent photon approximation to
investigate the impact of initial nuclear deformation on pair photoproduction in
hadronic U + U, Ru + Ru and Zr + Zr collisions. In this study, we present the equivalent photon
flux distributions as a function of transverse position for deformed colliding nuclei with a
random orientation. We conduct calculations of pair photoproduction in hadronic
heavy-ion collisions considering both spherical and deformed configurations. Our results can
describe the experimental data well for 40%–60% and 60%–80% centrality classes in U +
U collisions. We also observe approximately 3% differences between spherical and deformed
configurations. The impact of initial nuclear deformation on the ratios of pair
photoproduction between Ru + Ru and Zr + Zr collisions is negligible ( 1%). This
observation may alleviate difficulties for future study of pair photoproduction in
isobaric collisions.
V Acknowledgments
This work is supported in part by the National Key Research and Development Program of China under Contract No. 2022YFA1604900 and the National Natural Science Foundation of China (NSFC) under Contract No. 12175223 and 12005220. W. Zha is supported by Anhui Provincial Natural Science Foundation No. 2208085J23 and Youth Innovation Promotion Association of Chinese Academy of Sciences.
References
- Braun-Munzinger and Stachel [2007] P. Braun-Munzinger and J. Stachel, The quest for the quark-gluon plasma, Nature 448, 302 (2007).
- Adams et al. [2005] J. Adams et al. (STAR), Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions, Nucl. Phys. A 757, 102 (2005), arXiv:nucl-ex/0501009 .
- Shuryak [1980] E. V. Shuryak, Quantum Chromodynamics and the Theory of Superdense Matter, Phys. Rept. 61, 71 (1980).
- van Hees and Rapp [2008] H. van Hees and R. Rapp, Dilepton Radiation at the CERN Super Proton Synchrotron, Nucl. Phys. A 806, 339 (2008), arXiv:0711.3444 [hep-ph] .
- Rapp [2013] R. Rapp, Dilepton Spectroscopy of QCD Matter at Collider Energies, Adv. High Energy Phys. 2013, 148253 (2013), arXiv:1304.2309 [hep-ph] .
- Baltz [2008] A. J. Baltz, The Physics of Ultraperipheral Collisions at the LHC, Phys. Rept. 458, 1 (2008), arXiv:0706.3356 [nucl-ex] .
- Bertulani and Baur [1988] C. A. Bertulani and G. Baur, Electromagnetic Processes in Relativistic Heavy Ion Collisions, Phys. Rept. 163, 299 (1988).
- Klein et al. [2017] S. R. Klein, J. Nystrand, J. Seger, Y. Gorbunov, and J. Butterworth, STARlight: A Monte Carlo simulation program for ultra-peripheral collisions of relativistic ions, Comput. Phys. Commun. 212, 258 (2017), arXiv:1607.03838 [hep-ph] .
- Adams et al. [2004] J. Adams et al. (STAR), Production of e+ e- pairs accompanied by nuclear dissociation in ultra-peripheral heavy ion collision, Phys. Rev. C 70, 031902 (2004), arXiv:nucl-ex/0404012 .
- Afanasiev et al. [2009] S. Afanasiev et al. (PHENIX), Photoproduction of J/psi and of high mass e+e- in ultra-peripheral Au+Au collisions at s**(1/2) = 200-GeV, Phys. Lett. B 679, 321 (2009), arXiv:0903.2041 [nucl-ex] .
- Abbas et al. [2013] E. Abbas et al. (ALICE), Charmonium and pair photoproduction at mid-rapidity in ultra-peripheral Pb-Pb collisions at =2.76 TeV, Eur. Phys. J. C 73, 2617 (2013), arXiv:1305.1467 [nucl-ex] .
- Adam et al. [2018] J. Adam et al. (STAR), Low- pair production in AuAu collisions at = 200 GeV and UU collisions at = 193 GeV at STAR, Phys. Rev. Lett. 121, 132301 (2018), arXiv:1806.02295 [hep-ex] .
- Krauss et al. [1997] F. Krauss, M. Greiner, and G. Soff, Photon and gluon induced processes in relativistic heavy ion collisions, Prog. Part. Nucl. Phys. 39, 503 (1997).
- Vidovic et al. [1993] M. Vidovic, M. Greiner, C. Best, and G. Soff, Impact parameter dependence of the electromagnetic particle production in ultrarelativistic heavy ion collisions, Phys. Rev. C 47, 2308 (1993).
- Zha et al. [2018a] W. Zha, L. Ruan, Z. Tang, Z. Xu, and S. Yang, Coherent lepton pair production in hadronic heavy ion collisions, Phys. Lett. B 781, 182 (2018a), arXiv:1804.01813 [hep-ph] .
- Klein [2018] S. R. Klein, Two-photon production of dilepton pairs in peripheral heavy ion collisions, Phys. Rev. C 97, 054903 (2018), arXiv:1801.04320 [nucl-th] .
- Adam et al. [2021] J. Adam et al. (STAR), Methods for a blind analysis of isobar data collected by the STAR collaboration, Nucl. Sci. Tech. 32, 48 (2021), arXiv:1911.00596 [nucl-ex] .
- Voloshin [2010] S. A. Voloshin, Testing the Chiral Magnetic Effect with Central U+U collisions, Phys. Rev. Lett. 105, 172301 (2010), arXiv:1006.1020 [nucl-th] .
- Abdallah et al. [2022] M. Abdallah et al. (STAR), Search for the chiral magnetic effect with isobar collisions at =200 GeV by the STAR Collaboration at the BNL Relativistic Heavy Ion Collider, Phys. Rev. C 105, 014901 (2022), arXiv:2109.00131 [nucl-ex] .
- De Jager et al. [1974] C. W. De Jager, H. De Vries, and C. De Vries, Nuclear charge and magnetization density distribution parameters from elastic electron scattering, Atom. Data Nucl. Data Tabl. 14, 479 (1974), [Erratum: Atom.Data Nucl.Data Tabl. 16, 580–580 (1975)].
- De Vries et al. [1987] H. De Vries, C. W. De Jager, and C. De Vries, Nuclear charge and magnetization density distribution parameters from elastic electron scattering, Atom. Data Nucl. Data Tabl. 36, 495 (1987).
- Moller et al. [1995] P. Moller, J. R. Nix, W. D. Myers, and W. J. Swiatecki, Nuclear ground state masses and deformations, Atom. Data Nucl. Data Tabl. 59, 185 (1995), arXiv:nucl-th/9308022 .
- Shou et al. [2015] Q. Y. Shou, Y. G. Ma, P. Sorensen, A. H. Tang, F. Videbæk, and H. Wang, Parameterization of Deformed Nuclei for Glauber Modeling in Relativistic Heavy Ion Collisions, Phys. Lett. B 749, 215 (2015), arXiv:1409.8375 [nucl-th] .
- Raman et al. [2001] S. Raman, C. W. G. Nestor, Jr, and P. Tikkanen, Transition probability from the ground to the first-excited 2+ state of even-even nuclides, Atom. Data Nucl. Data Tabl. 78, 1 (2001).
- Pritychenko et al. [2014] B. Pritychenko, M. Birch, M. Horoi, and B. Singh, B(E2) Evaluation for Transitions in Even-Even Nuclei, Nucl. Data Sheets 120, 111 (2014), arXiv:1302.6881 [nucl-th] .
- Möller et al. [2008] P. Möller, R. Bengtsson, B. G. Carlsson, P. Olivius, T. Ichikawa, H. Sagawa, and A. Iwamoto, Axial and reflection asymmetry of the nuclear ground state, Atom. Data Nucl. Data Tabl. 94, 758 (2008).
- Haque et al. [2012] M. R. Haque, Z.-W. Lin, and B. Mohanty, Multiplicity, average transverse momentum and azimuthal anisotropy in U+U collisions at = 200 GeV using AMPT model, Phys. Rev. C 85, 034905 (2012), arXiv:1112.2340 [nucl-ex] .
- Schenke et al. [2014] B. Schenke, P. Tribedy, and R. Venugopalan, Initial-state geometry and fluctuations in Au + Au, Cu + Au, and U + U collisions at energies available at the BNL Relativistic Heavy Ion Collider, Phys. Rev. C 89, 064908 (2014), arXiv:1403.2232 [nucl-th] .
- Nepali et al. [2007] C. Nepali, G. I. Fai, and D. Keane, Selection of special orientations in relativistic collisions of deformed heavy nuclei, Phys. Rev. C 76, 051902 (2007), [Erratum: Phys.Rev.C 76, 069903 (2007)], arXiv:0709.1497 [hep-ph] .
- Brodsky et al. [1971] S. J. Brodsky, T. Kinoshita, and H. Terazawa, Two Photon Mechanism of Particle Production by High-Energy Colliding Beams, Phys. Rev. D 4, 1532 (1971).
- d’Enterria and Loizides [2021] D. d’Enterria and C. Loizides, Progress in the Glauber Model at Collider Energies, Ann. Rev. Nucl. Part. Sci. 71, 315 (2021), arXiv:2011.14909 [hep-ph] .
- Zha et al. [2018b] W. Zha, S. R. Klein, R. Ma, L. Ruan, T. Todoroki, Z. Tang, Z. Xu, C. Yang, Q. Yang, and S. Yang, Coherent J/ photoproduction in hadronic heavy-ion collisions, Phys. Rev. C 97, 044910 (2018b), arXiv:1705.01460 [nucl-th] .
- Miller et al. [2007] M. L. Miller, K. Reygers, S. J. Sanders, and P. Steinberg, Glauber modeling in high energy nuclear collisions, Ann. Rev. Nucl. Part. Sci. 57, 205 (2007), arXiv:nucl-ex/0701025 .
- Masui et al. [2009] H. Masui, B. Mohanty, and N. Xu, Predictions of elliptic flow and nuclear modification factor from 200 GeV U + U collisions at RHIC, Phys. Lett. B 679, 440 (2009), arXiv:0907.0202 [nucl-th] .
- Kharzeev and Nardi [2001] D. Kharzeev and M. Nardi, Hadron production in nuclear collisions at RHIC and high density QCD, Phys. Lett. B 507, 121 (2001), arXiv:nucl-th/0012025 .
- Abelev et al. [2013] B. Abelev et al. (ALICE), Centrality determination of Pb-Pb collisions at = 2.76 TeV with ALICE, Phys. Rev. C 88, 044909 (2013), arXiv:1301.4361 [nucl-ex] .
- Back et al. [2004] B. B. Back et al. (PHOBOS), Collision geometry scaling of Au+Au pseudorapidity density from s(NN)**(1/2) = 19.6-GeV to 200-GeV, Phys. Rev. C 70, 021902 (2004), arXiv:nucl-ex/0405027 .