The DT-instanton equation on almost Hermitian -manifolds
Abstract.
This article investigates a set of partial differential equations, the DT-instanton equations, whose solutions can be regarded as a generalization of the notion of Hermitian-Yang-Mills connections. These equations owe their name to the hope that they may be useful in extending the DT-invariant to the case of symplectic -manifolds.
In this article, we give the first examples of non-Abelian and irreducible DT-instantons on non-Kähler manifolds. These are constructed for all homogeneous almost Hermitian structures on the manifold of full flags in . Together with the existence result we derive a very explicit classification of homogeneous DT-instantons for such structures. Using this classification we are able to observe phenomena where, by varying the underlying almost Hermitian structure, an irreducible DT-instanton becomes reducible and then disappears. This is a non-Kähler analogue of passing a stability wall, which in string theory can be interpreted as supersymmetry breaking by internal gauge fields.
1. Introduction
1.1. Summary
The notions of holomorphic bundles and Hermitian Yang Mills connections have proven to be very fruitful in complex geometry. When considering Hermitian vector bundles, the Hitchin-Kobayashi correspondence [D, UY, LT] yields a relation between the algebro-geometric notion of a stable holomorphic vector bundle and the more differential geometric one of a Hermitian-Yang-Mills (HYM) connection. The goal of the present paper is to study some natural generalizations of these objects in almost complex geometry. The most well known of such generalizations are pseudo-holomorphic and pseudo-Hermitian-Yang-Mills (pHYM) connections. In specific situations, these have been studied by several authors, see [Charbonneau2016] and [Bryant2006] for example. The major goal of the current paper is to study a system of partial differential equations whose solutions give a further generalization of the notion of a HYM connection on real -dimensional almost Hermitian manifolds. To the authors’ knowledge such equations first appeared in Richard Thomas’s thesis [Thomas1997] (page 29). These equations have also independently appeared in the physics literature, for instance in [Baulieu1998, Baulieu1998b, Iqbal2008] and references therein. More recently, the same equations were studied by Yuuji Tanaka ([Tanaka2008], [Tanaka2013], [Tanaka2014]) who constructed the only known (nontrivial) examples of solutions in [Tanaka2008]. These rely on a very general version of the Hitchin-Kobayashi correspondence and require the underlying almost Hermitian manifold to actually be Kähler. In that direction, our results give the first nontrivial solutions to these equations on non-Kähler almost Hermitian manifolds. For instance, one of the examples explored in this paper focuses on , the manifold of full flags in . In that example, we give nontrivial solutions to these equations for several almost Hermitian structures compatible with the nearly Kähler almost complex structure.
1.2. The DT-instanton equations
Let be an almost Hermitian manifold, a compact semisimple111Similar equations to those considered here can be written if not semisimple. However, for the sake of simplifying some statements we shall restrict to this case. Lie group, and a principal -bundle. A connection on is called pseudo-holomorphic if its curvature is of type and pHYM if we further have
| (1.1) |
where denotes contraction with respect to the associated -form . These notions are word by word adaptations of the respective notions in the case where is Hermitian. However, for the general almost Hermitian structure there may not exist (even locally) solutions to these equations, see [Bryant2006]. Similarly, in the non-integrable case there is no analogue of the function theory relating the existence of a (pseudo)-holomorphic connection with local holomorphic framings. When is real -dimensional, there is a further generalization of the HYM equations which has a better general existence theory. This is an equation for a pair , consisting of a connection on and a Higgs field , required to satisfy
| (1.2) | |||||
| (1.3) |
where and denotes the -linear extension of the Hodge- operator associated with . In this paper we shall refer to these as the DT-instanton equations, and call a pair solving them a DT-instanton. The reason for this nomenclature is the point of view adopted in Richard Thomas and Yuuji Tanaka’s work, where these equations are regarded as the basis for a possible differential geometric approach to the Donaldson-Thomas invariants, constructed by Thomas for Calabi-Yau -folds using algebraic geometry, see [Thomas1997] and [Thomas2001]. Such a program is still far from being completed, but its success would extend the theory of DT-invariants to symplectic (or even almost Hermitian) real -dimensional manifolds.
As it will become clear in the course of the article, a particular case for these equations happens when admits a certain compatible -structure. In that situation, the equations can be rewritten as in proposition 3, leading to a simplification of the analysis which can be carried out in several particular cases of interest. For instance, when the -structure is Calabi-Yau or nearly Kähler, the DT-instanton equations actually reduce to the pHYM ones, see proposition 5. These vanishing theorems further motivate the DT-instanton equations as being a natural generalization of the HYM ones which, for the generic almost Hermitian structure, we expect to have more solutions then the pHYM equations. To test these ideas, in this paper we solve these equations in very specific examples, namely for invariant almost Hermitian structures on the manifold of full flags in . In particular, we obtain the first examples of DT-instantons on a compact manifold with , and these are also the first non-trivial examples on non-Kähler manifolds. For future reference, DT-instantons with an irreducible connection and will be called irreducible.
1.3. Main results
As mentioned before, the specific examples we shall study focus on , the manifold of full flags in . This is an homogeneous space of the form and we consider -invariant almost Hermitian structures on it. The space of such almost Hermitian structures, which we shall denote by , has two connected components , , both of which can be identified with . These components respectively correspond to those almost Hermitian structures which are compatible with the standard integrable almost complex structure and to one other non-integrable almost complex structure which is in fact compatible with a nearly Kähler structure. Indeed, admits two homogeneous Einstein metrics: the Kähler-Einstein one with ; and another one so that is nearly Kähler. For future reference, given we shall denote by the associated fundamental -form and we note here that for all the -form is exact and thus gives an associated cohomology class on .
In fact, of these two almost complex structures, is the only one with topologically trivial canonical bundle. As a consequence of this observation, for the almost Hermitian structures in we will be able to simplify the search for solutions to the DT-instanton equations 2.4–2.5 by making use of proposition 3. Indeed, in this case we are able to classify -invariant DT-instantons with gauge group . To state this classification we start with some preparation. Let be an integral weight of and the induced group homomorphism. Then, denote by the homomorphism obtained by composing with the degree one embedding of as the maximal torus of . This can be used to construct the -homogeneous -bundles
All the -homogeneous -bundles on are of this form, and in our first main result we classify -invariant DT-instantons on such bundles. As way of preparing for the statement it is important to note that the bundles are all reducible to the -bundles associated with the homomorphism . The Hitchin-Kobayashi correspondence, and also our analysis, yields that for an irreducible HYM connection on the bundle exists if and only if . In other words, for invariant Hermitian structures , the quantity controls the existence of HYM connections on the bundle . Here, by , i.e. the degree of , we mean the value of evaluated against the fundamental class of , which we regard as a real valued function on both and . Our main result, stated below, shows that, for invariant almost Hermitian structures , the same quantity controls the existence of invariant DT-instantons on .
Theorem 1.
Let and be a -invariant DT-instanton on . Then, must be a root of and
Moreover, the resulting DT-instanton is irreducible if and only if strict inequality holds.
The previous result, i.e. Theorem 1, is a summarized version of our main result stated as Theorem 3 which constructs these DT-instantons and the functions explicitly. In particular, this gives the first existence theorem for solutions of the equations 2.4–2.5 with , which are also the first nontrivial examples outside the Kähler world.
We must further mention on the appearance of the restriction that the integral weights are roots of follows in our case from the imposition that the DT-instantons be -invariant. In fact, we do not expect that this condition must hold for general DT-instantons, but of course we do not know if these exist on other .
An immediate consequence of the explicit nature of our formulas for the degrees as functions on is that it is very easy to check that they cannot all be simultaneously negative. Furthermore, they all vanish if and only if is the metric compatible with the nearly Kähler structure. This gives the result below, which will be presented in a more detailed manner as corollary 5.
Corollary 1.
Let be a -invariant almost Hermitian structure compatible with . Then, either:
-
(i)
There is a root together with an irreducible -invariant DT-instanton on , or
-
(ii)
is the nearly-Kähler metric and there is a reducible pHYM connection on all the bundles . In this case, the corresponding connection is reducible to .
In fact, one can explicitly pick a -parameter family of compatible -forms so that for some root crosses zero. Then, one can check that as , the DT-instanton constructed by theorem 1 become obstructed and reducible. See examples 4–5 and the accompanying figures for illustrations of this phenomena. From a Physics point of view, this phenomenon can be interpreted as analogous to crossing a wall from the supersymmetric region in to a non-supersymmetric one. Namely, it can be thought of as analogous to supersymmetric breaking by internal gauge fields. See [Anderson2009] for the description of this phenomenon in the Kähler case.
In section 6 we turn to the problem of classifying the -invariant pHYM connections with gauge group . In theorem 2 we prove that the existence of such irreducible pHYM connections requires the almost complex structure to be integrable and we write down the resulting HYM connections explicitly.
Acknowledgements
We would like to thank Benoit Charbonneau, Gäel Cousin and Lorenzo Foscolo for helpful conversations regarding this article. We are particularly thankful for Benoit Charbonneau’s comments and carefully reading a previous version of this article.
Gonçalo Oliveira is supported by Fundação Serrapilheira 1812-27395, by CNPq grants 428959/2018-0 and 307475/2018-2, and FAPERJ through the program Jovem Cientista do Nosso Estado E-26/202.793/2019.
2. Preliminaries
2.1. Almost Hermitian 6-manifolds and -structures
An almost Hermitian -manifold is a triple , where is real -dimensional smooth manifold equipped with an almost complex structure and a compatible Riemannian metric , i.e . In this situation, the associated -form is given by . The pair determines a reduction of the structure group of the frame bundle of from to . Thus, when convenient, we refer to the pair as an -structure. In this manner, a -structure compatible with a given consists of the extra data of a real -form satisfying
where . In particular, the complex valued -form is of type with respect to . Indeed, such a triple determines a reduction of the structure group of the frame bundle to . In order to settle on the nomenclature we now recall various different kinds of -structures we will be considering
Definition 1.
A -structure , or equivalently , will be called
-
(a)
Calabi-Yau if ;
-
(b)
Nearly Calabi-Yau if ;
-
(c)
Nearly Kähler if , and ;
-
(d)
Half-flat if .
Notice that a Calabi-Yau structure is also nearly Calabi-Yau and half-flat, while a nearly Kähler structure is also half-flat.
Remark 1.
Consider the product equipped with the -structure (and the orientation such that . This -structure is closed if and only if the -structure is nearly Calabi-Yau, and coclosed if and only if it is half-flat. This justifies our choice of rather than in the definition of nearly Calabi-Yau.
2.2. Pseudo-holomorphic and pHYM connections
Throughout this paper will be a compact Lie group, with Lie algebra , and a principal -bundle over . The adjoint bundle of will be denoted by . Recall, for example from [Bryant2005], that
Definition 2.
Let be an Hermitian connection on and denote its curvature. Then, is said to be pseudo-holomorphic if
| (2.1) |
and pseudo Hermitian-Yang-Mills (pHYM), if
| (2.2) | |||||
| (2.3) |
where , is a constant, and is a constant central element.
When is an Hermitian manifold, the notions of pseudo-holomorphic and pHYM connections obviously coincide with the usual ones of holomorphic and HYM connections respectively. This motivates the definitions above in the setting of general almost Hermitian structures where much less is known. See for example [Charbonneau2016, Bryant2005], and references therein, for the case of nearly Kähler manifolds.
Remark 2.
For a nearly Kähler structure any pseudo-holomorphic connection is immediately pHYM. Indeed, the curvature of a pseudo holomorphic connection is of type . Hence, for any compatible -structure vanishes. Thus, for a nearly Kähler structure we have and differentiating this equation gives , so is also pHYM.
2.3. DT-instantons
The conclusion of remark 2 is a shadow of the first of the following two interesting facts about nearly Kähler structures, see [Bryant2005, Foscolo2016, Verbitsky2011]:
-
(a)
All closed -forms of type are primitive, i.e satisfy . This follows from the computation in remark 2 by replacing the curvature by any such -form.
-
(b)
All closed, -forms of type are harmonic. This follows easily from the previous bullet and the fact that any primitive -form satisfies , hence
as is of type .
Robert Bryant identified in [Bryant2005] a class of Hermitian-structures on a -manifold for which closed -forms of type are primitive. Bearing in mind the previous remark, it would not be surprising if they had a good local existence theory for pseudo-holomorphic and pHYM connections. Indeed, these structures are called quasi-integrable and were shown in [Bryant2005] to locally admit as many pseudo-holomorphic and pHYM connections as the integrable ones.
However, for the general almost Hermitian structure, the pHYM equations are overdetermined modulo gauge. Motivated by this we shall now introduce an elliptic equation (modulo gauge) whose solutions we regard as generalizing the notion of pHYM equation to the generic almost Hermitian structure.
Definition 3.
A pair where is a connection on and is called a DT-instanton if
| (2.4) | |||||
| (2.5) |
where and denotes the -linear extension of the Hodge- operator. A DT-instanton will be called irreducible if the connection is irreducible.
To the authors’ knowledge, these equations first appeared in [Thomas1997] and were considered in this set-up already in [Donaldson2009]. They have been studied by Donaldson-Segal [Donaldson2009] and Yuuji Tanaka [Tanaka2008], [Tanaka2013], [Tanaka2014] who suggest these equations as a possible analytic approach to DT-invariants. On noncompact Calabi-Yau manifolds they were studied by the second named author in [Oliveira2014] and [Oliveira2016]. The same equations have also been studied by physicists such as in [Baulieu1998] and [Iqbal2008].
3. DT-instantons in special cases
In this subsection we study the DT-instanton equations in several particular cases. We give a few vanishing theorems which further motivate the view of the DT-instanton equations as a generalization of the HYM equations.
3.1. On Hermitian manifolds
If is compact and integrable, then any DT-instanton induces a holomorphic structure on any associated complex vector bundle. Indeed, it follows from the fact that is of type and the Bianchi identity that
Taking the inner product with and integrating by parts we get that . Thus and so solves
| (3.1) | ||||
In particular, this proves the following.
Proposition 1.
If is compact and integrable, then any DT-instanton solves 3.1. In particular, induces an holomorphic structure on any associated complex vector bundle.
In fact, notice that as is of type we have that , so that , where .
3.2. On Kähler manifolds
For Kähler manifolds we can prove that if the scalar curvature is positive then and the equations 3.1 coincide with the HYM equations. We state this as follows.
Proposition 2.
Let be compact and be a Kähler metric with nonnegative scalar curvature on . Then, any DT-instanton on has being HYM and .
Proof.
Using the Weitzenböck formula
and the last equation we compute
Thus, if the scalar curvature of the Kähler metric is nonnegative we must have and the equations above reduce to the HYM ones. ∎
Remark 3.
Suppose , which is a natural assumption from the variational point of view and also follows from the assumption that and Moser iteration as shown in [Tanaka2013]. Then, integrating the computation above shows that .
3.3. For compatible -structures
One other interesting case when the equations simplify is when the almost Hermitian structure admits a compatible -structure. Of course, this is a very restrictive condition. Indeed, an almost Hermitian structure admits a compatible -structure if and only if the canonical bundle is (topologically) trivial. When this is the case we shall say that a compatible -structure is pseudo-holomorphcially trivial if there is a so that . Under this further restriction we can rewrite the equations as follows.
Proposition 3.
Proof.
We shall use the notation . We start by inserting as in the statement into the first equation 2.4
where we used and the hypothesis that . Next, wedge this equation with
where we used the fact that the projection can be written as , for . Then, separate this equation into types and use the fact that
to obtain equations 3.2 and 3.4. Finally, equation 3.3, which follows from inserting , using and . ∎
In several cases the DT-instanton equations 2.4–2.5 reduce to the pHYM equations, which further motivates studying the DT-instantons as an extension of the pHYM connections for the general almost Hermitian structure. In this direction, we start by proving that if there is a compatible half-flat -structure, then the DT instanton equations 3.2–3.3 reduce to a simpler equation with only one Higgs field.
Proposition 4.
Let be compact and be a half-flat -structure. Then, any irreducible DT-instanton for a simple Lie group , satisfies and
| (3.5) | |||||
| (3.6) |
or, rewriting the first equation, .
Proof.
First, notice that if the structure is half flat then and so is real. However, by type decomposition is of type , where is the Nijenhuis tensor. Hence, and we can write the DT instanton equations as in 3.2–3.3. Now, equip the bundle with an -invariant metric compatible with , and compute
Using equation 3.2 together with the Bianchi identity and , we have
where in the last equality we used equation 3.3. Hence and so
is subharmonic. As is compact, is constant and so the previous equation yields and . Hence, given that the connection is irreducible, fixing a trivialization of at a point , is a central element, However, as is semisimple, we must have . The remaining equations follows simply from inserting into equations 3.2–3.3. ∎
For a compact Calabi-Yau manifold the DT-instanton equation further reduces to the HYM equations. Indeed, if the -structure is Calabi-Yau it also is half-flat and the DT instanton equations can be written as 3.6–3.6, with . Moreover, from the Bianchi identity and it follows that
Thus , and again, if is compact, semisimple and is irreducible must have . Hence, equations yields 3.6–3.6, so that is actually HYM. In the case of noncompact Calabi-Yau manifolds, irreducible DT-instantons with for semisimple Lie groups do exist, and are expected to be related to special Lagrangian submanifolds, see [Oliveira2014] for more on this. On nearly Kähler manifolds, a similar vanishing result holds true, as we now state.
Proposition 5.
Let be compact222Any nearly Kähler manifold is Einstein with positive scalar curvature. Hence, if it is complete, must actually be compact. and be compatible with a nearly Kähler structure. Then, any DT-instanton satisfies
| (3.7) | |||||
| (3.8) |
and , with as in proposition 3. In particular, is a pHYM connection.
Proof.
As any nearly Kähler structure is half-flat, the same proof as before yields that proposition 3 applies and can be written as in 3.2–3.3 (In fact, also proposition 4 applies and we could start applying the result therein). Here, we proceed in three steps from equations 3.2–3.4.
Step 1: We prove that
This follows from equation 3.4, the Bianchi identity and the equations for a nearly Kähler -structure. Indeed,
and inserting here equation 3.3 gives
| (3.9) |
The case of follows from a similar, but easier, computation, close to the Calabi-Yau case in lemma of [Oliveira2014].
Step : We prove that
As before, we shall only prove the case of . This follows from inserting 3.9 into the following computation
where we used the -invariance of the inner product on .
Step 3: We finish the proof by noticing that, from step , both , are subharmonic and since is compact, they must actually be constant. Hence, their Laplacians vanish and once again step gives that and the DT-instanton equations reduce to the pHYM ones. ∎
Remark 4.
In the Kähler case the Dolbeaut splitting passes to cohomology and Hodge theory proves that there is a unique (up to gauge) HYM connection on any complex line bundle whose first Chern class if of type . This has degree in the case when is primitive. In fact, the curvature of this HYM connection is the harmonic representative of . Similarly, it follows from a result of Lorenzo Foscolo [Foscolo2016] that on a nearly Kähler manifold the harmonic representative of any degree- cohomology class is primitive of type . Hence, by a repeated use of the Poincaré lemma, one proves that for any on a nearly Kähler manifold there is a complex line bundle with and which can be equipped with a pHYM connection unique up to gauge.
4. Invariant almost-Hermitian structures on
The manifold of full flags in is the homogeneous manifold , where is the subgroup of diagonal matrices, a maximal torus in As in [Bryant2005], we use the Maurer-Cartan form on given by
Consider the set of simple roots such that the are given by
and set , to be the real component of the root spaces. These are respectively
Then, we fix the complement to the isotropy so that .
We would like to consider -invariant almost complex structures . Evaluating any such at the identity coset and extending it by left invariance one obtains an -invariant map with . From Schur’s lemma any such map must preserve the root spaces and we shall now describe them by fixing a trivialization for the pullback of to .
For each and , we define the complex valued -forms
We then consider the -invariant almost complex structures so that the span the pullback of to . Using the Maurer-Cartan equations we compute the Nijenhuis tensor of . This is diagonal in the basis , of and respectively, being given by with
| (4.1) |
Remark 5 (Weyl group and symmetries).
The Weyl group of acts on and so on the almost complex structures determined by . Having in mind that we easily find that the Weyl group is generated by the reflections such that and similarly for and . In particular, is an element of order which cyclically permutes the roots .
In particular, from equations 4.1, the almost complex structure is integrable if and only if
| (4.2) |
In particular, up to action of the Weyl group there are only two invariant almost complex structures and with respectively determined by and . In particular, inserting these into equation 4.2 we find that while is integrable is not. Indeed, we shall see shortly that is compatible with a nearly Kähler structure on . Now we consider the almost Hermitian structures determined by setting
| (4.3) |
which always satisfies the equation
| (4.4) |
In fact, a tedious but otherwise straightforward computation shows that , where
| (4.5) |
As the terms and cannot all vanish at the same time, it follows that is symplectic if and only if
| (4.6) |
In particular, the cannot all have the same sign and we conclude that cannot tame any symplectic form. On the other hand, is compatible with a real -parameter family of symplectic structures determined by solving 4.6. In fact, these are all nonequivalent as for any such there are three different holomorphic spheres of different areas. These correspond to three orbits of the subgroup tangent to each of the root spaces at the origin, which have area and so must be different for any two such up to changes of sign.
Example 1 (Kähler-Einstein structure).
The Kähler structure determined by and with can be seen to be Einstein. This is the standard homogeneous Kähler-Einstein Fano structure on .
The -form on given by
| (4.7) |
is semi-basic and of type . For , i.e. , it is actually basic and so descends to a nowhere vanishing -form on . In particular, and determines a -structure on compatible with .
Example 2 (Nearly Kähler almost complex structure).
For , i.e. we have that the -form in 4.5, so that , is given by
Thus, any -compatible invariant almost Hermitian structure satisfies
| (4.8) |
As a consequence, for any we have , which together with equation 4.4 shows that any -structure in this real -dimensional family is half flat. In particular, when
and so the -structure is the homogeneous nearly Kähler structure.
5. pHYM connections on -bundles over
In this section we prove proposition 6 and corollary 2 below which describe -invariant pseudo-holomorphic and pHYM connections on complex line bundles over .
We shall start by describing homogeneous circle bundles, invariant connections and Higgs fields. Topologically any circle bundle is determined by a class in , the first Chern class of the complex line bundle associated with the standard representation. The Serre spectral sequence for the fibration then gives an isomorphism
| (5.1) |
where is the weight lattice. Then, given such an integral weight we view it as an -form in which we extend to , using the orthogonal splitting induced by the Killing form. Finally, using left invariance we further extend to a -form in . In fact, the valued -form in is a connection on the complex line bundle
Its first Chern class can be computed from its curvature, using the identifications in equation 5.1, this is once again
which corresponds to under the isomorphism 5.1.
Recall that for all almost Hermitian structures under consideration and so yields a well defined cohomology class. Thus it makes sense to define
and the slope
Writing we have from the Maurer-Cartan equation
| (5.2) |
Thus, we immediately compute that
| (5.3) |
For circle bundles, the adjoint bundle is a trivial real line bundle and so a Higgs field is simply a real valued function. Moreover, the induced connection on the adjoint bundle is also trivial. If we assume that the Higgs field is invariant under the action of , then must be constant, and thus any invariant DT-instanton must actually be a pHYM connection together with a constant Higgs field. As a consequence, in considering invariant DT instantons on circle bundles, there is no loss of generality in simply considering the pHYM equations.
Proposition 6.
Given a complex line bundle , the connection described above is always pseudo-holomorphic. Furthermore, it is pHYM with degree if and only if
If for , this condition can be equivalently written as
Proof.
For the group homomorphism is . Recall the bundle is constructed via . Wang’s theorem [Wang1958] shows that any invariant connection on differs from by the addition of the left invariant extension of a morphism of -representations . As the later one is trivial and has no trivial components, Schur’s lemma yields that is the only invariant connection. Its curvature is as computed in equation 5.2. We see that is of type and so the connections are all pseudo-holomorphic. For to be pHYM of degree we must have which implies that
∎
In particular, the bundle need not be trivial for it to admit a pHYM connection of degree . In fact, the equation vanishes for all if and only if . For instance, the must all have the same sign and so the almost complex structure must be the non-integrable one in which case we have and the almost Hermitian is the nearly Kähler one up to scaling. This proves the following result.
Corollary 2.
Remark 6.
In the Kähler case, follows easily from Hodge theory that a HYM connection on a complex line bundle always exists and is unique. In that case, it has degree if and only if the bundle itself has degree . In the nearly Kähler case, any complex line bundle has degree as is exact. Also in that case one can use Hodge theory to prove that a pHYM connection always exists and is unique (up to gauge), see [Foscolo2016].
6. DT-instantons on -bundles over
In this section we classify -invariant pHYM connections and DT-instantons with gauge group .
The isomorphism classes of homogeneous -bundles are parametrized by group homomorphisms . Thinking of as any such homomorphism is of the form
and the corresponding homogeneous -bundle is
Proposition 7.
Let be an integral weight and be an irreducible -invariant triple on whose pullback to satisfies equations 3.2–3.3. Then, is a root of and is given by:
-
•
If , in which case and , i.e. . In this case
-
•
If , in which case and , i.e. . In this case
-
•
If , in which case and , i.e. . In this case
Moreover, when equality, rather than strict inequality, holds in any of the above cases the corresponding DT instanton becomes reducible and is one of the pHYM connections from proposition 6.
Proof.
For each , with , the group homomorphism is given by
The canonical invariant connection on is determined by the -form in with values in given by
By Wang’s theorem, other invariant connections on are determined by morphisms of -representations . The left and right hand sides respectively decompose into irreducible components as and . Hence, other invariant connections exist only in the case when for some . In all other cases the canonical invariant connection is the unique one, and the Ambrose-Singer theorem shows that any such connection is reducible, so that we would be back in the case analysed in proposition 6. It is then enough to restrict ourselves to the three cases above. We shall start with the case so and . In this case the most general invariant connection can be written as
| (6.1) |
for . Its curvature can be computed as and we can write it as with
Again, it follows from the Ambrose-Singer theorem that for such a connection to be irreducible we need . We turn now to invariant Higgs fields . We view these as functions in with values in , equivariant with respect to the action of on by multiplication on the right and on via . For to be left-invariant it must be constant, and so valued in the trivial component of . Thus, we may write our two invariant Higgs fields as , for , where , are real numbers. Their covariant derivative with respect to the connection , as in equation 6.1, can be computed to be
Now recall the DT instanton equations 3.2–3.3, which we rewrite here for convenience
| (6.2) | |||||
| (6.3) |
We start with the second equation 6.3. In our case we have that and so the equation turns into . The component of is given by
while the equations and hold automatically. It then follows that we must have
and so a solution exists if and only if , in which case
| (6.4) |
Moreover, by the previous comment, the resulting connection is irreducible if and only if strict inequality holds.
We now turn to the first of the DT instaton equations, i.e. equation 6.2. To compute the right hand side we must start by computing the Hodge star operator. Given that in the frame and that , we compute that and . Thus, the left hand side of equation 6.2 is
As for the right hand side, i.e. , the component along is simply which vanishes identically, while the other components are
So the remaining equations turn into
Then, either:
- •
-
•
or , in which case we can then impose the remaining equations. When the connection is irreducible, i.e. when is given by equation 6.4, the two remaining equations above are compatible if and only if
In that case we can solve for yielding
The cases when is either or are similar and in fact can be obtained from this one by applying , the element of order in the Weyl group of .
∎
Remark 7.
Notice that in each case the two connections differing from a choice of sign in are actually gauge equivalent. The gauge transformation exchanging these is given by .
6.1. pHYM connections
We shall start by using the results of proposition 7 to analyse the existence of -invariant pHYM connections with structure group . We shall use these same results to analyse the existence of DT-Instantons and compare them with those we now obtain for HYM connections. Indeed, as we will now see, the existence of irreducible pHYM connections implies the almost complex structure is actually integrable and so the pHYM connections are actually HYM.
Proposition 8.
Let be an integral weight and an irreducible pHYM connection on for equipped with an invariant almost Hermitian structure. Then, the almost complex structure is in fact integrable and either
-
•
, in which case , and , i.e. , and
-
•
, in which case and and , i.e. , and
-
•
If , in which case , and , i.e. . In this case
Moreover, when equality, rather than strict inequality, holds in any of the above cases the connection becomes reducible.
Proof.
The computations for an invariant pHYM connection are contained, as a subcase, in the DI-instanton ones. They correspond to the DT-instantons for which . As can be seen from the statement of proposition 7, this happens if and only if for some . In the proof we shall only deal with the case of as the other ones follow similar lines. Then, the condition that vanishes in proposition 7 yields that , while the condition that turns into and so with respectively. Inserting this into the inequality involving the metric structure, i.e. the , we must have , which is the inequality in the statement.
All the almost complex structures to which this result applies, i.e. those satisfying , and , are in fact integrable. Indeed, it is easy to check that for any such, the Nijenhuis tensor computed in equation 4.1, vanishes identically.
∎
Using the action of the Weyl group we may fix the invariant integrable complex structure to be , i.e. , and so Theorem 2 implies that for irreducible invariant HYM to exist on , must either be or and substituting into the previous theorem we obtain the following.
Theorem 2.
For any invariant Hermitian structure on there are, up to gauge, at most two invariant irreducible HYM connections with gauge group . Using the action of the Weyl group so that , these are the following:
-
•
The connection
on which exists in case , i.e. .
-
•
The connection
on , which exists in case , i.e. .
Moreover, when equality, rather than strict inequality, holds in any of the above cases the connection becomes reducible.
Suppose that one can find an invariant Hermitian structure which admits no invariant irreducible HYM connection with gauge group , then we would have that both and . Summing these two equations we obtain
which is obviously impossible. Thus we conclude the following
Corollary 3.
All invariant Hermitian structures on admit invariant, irreducible HYM connections with gauge group .
Remark 8.
This result also follows as an application of the universal Hitchin-Kobayashi correspondence [LT].
Example 3.
Finally we shall now prove one last consequence of Theorem 2.
Corollary 4.
There is a family of invariant Kähler structures with the following property. There is , such that: for the bundle has two irreducible, invariant HYM connections; these converge to the same reducible and obstructed HYM connection, as ; and for there are no irreducible, invariant HYM connections.333The two irreducible HYM connections existing for are actually gauge equivalent, see remark 7. However, the gauge transformation exchanging them fixed the reducible HYM connection existing at .
Proof.
We shall explicitly construct a family explicitly. Let be positive and , then we set
and , which is positive (and less than ) for . Then, by the proof of the first part we have that for there are two irreducible, invariant HYM connections on ; while for there are no invariant HYM connections with gauge group . The fact that the connections become obstructed an reducible as follows from a straightforward computation. ∎
6.2. DT-instantons
Recall that in general the -form is only semibasic. However, it is basic for , which corresponds to the almost complex structure is . We shall now analyse the consequences of proposition 7 for the existence theory of DT-instantons for invariant almost Hermitian structures.
Theorem 3.
Equip with an invariant almost Hermitian structure compatible with . Let be an integral weight and an irreducible DT-instanton on . Then, is a root of and the DT-Instanton can be written, as in proposition 3, in terms of given by:
-
•
If , and , i.e. . In this case
-
•
If , and , i.e. . In this case
-
•
If , and , i.e. . In this case
Moreover, when equality, rather than strict inequality, holds in any of the above cases the corresponding DT-instanton becomes reducible and is one of the pHYM connections described in proposition 6.
Proof.
First we note that, as remarked before, for any -invariant almost Hermitian structure. Moreover, when the almost complex structure is , i.e. when we can compute that is of type and so we can apply proposition 3 and write the DT-instanton equations as in 3.2–3.3. The computations of these equations have been performed in the proof of proposition 7 and the current theorem is simply a particular case of that result. ∎
Remark 9.
Corollary 5.
For any invariant almost Hermitian structure on compatible with there exists at least one -bundle equipped with a DT-instanton. These DT-instantons are reducible, in which case is a pHYM connection, if and only if the almost Hermitian structure is nearly Kähler (up to scaling).
Proof.
Suppose there is no such DT-instanton, not even the reducible ones when equality is achieved in the strict inequalities of theorem 3. Then, we must have that
and adding these up we arrive at a contradiction. Hence, at least one of the inequalities above is violated and either: for one or two permutations of , or equality is achieved in all. In the first case, theorem 3 yields the existence of a bundle supporting at least one DT-instanton. In the second case we must have that all the equalities hold. This implies that and so, up to scaling, the metric is equivalent to the nearly Kähler one. ∎
Example 4.
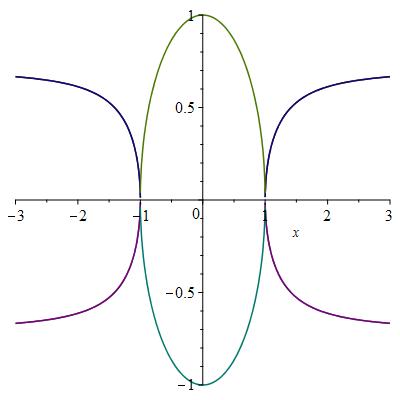
Consider the family of almost Hermitian structures with determined by and . For this is the almost Hermitian structure compatible with the nearly Kähler one. In figure 1, we have depicted on the horizontal axis, and in the vertical axis the value of (as in the proof of 7). This component of the connection has the property that it is nonzero if and only if the DT instanton is irreducible, with each pair of colors corresponding to the values of for the different weights . Analysing this figure we see that for any value of , other than the DT-instantons are irreducible. When , i.e. when the metric is the nearly Kähler one, these become obstructed and reducible to one of the Abelian pHYM connections in proposition 6.
Example 5.
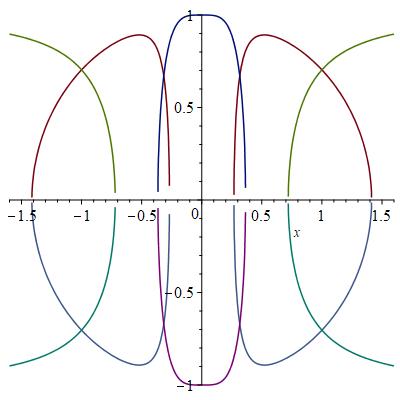
Now consider the family of almost Hermitian structures with determined by , and . In figure 2 we produce a similar plot as in the previous case. In this case we see that there are irreducible DT-instantons for any value of the parameter .
Appendix A The topology of the bundles
Recall that the bundles are constructed via , where
Let be the vector bundle associated with respect to the standard representation -representation, and consider the bundle
where
and the ismorphism. This has the property that the -adjoint bundle of splits as and
We shall now compute the Chern classes of the bundles using Chern-Weyl theory. For this we must equip with a connection which we choose to be the standard invariant connection given by
This has curvature and so
Furthermore, a computation using the Maurer-Cartan equations shows that
and so in we have
So, writing we compute that
while
In particular, when is one of the roots , , we respectively obtain
so these three bundles are all topologically different.