The Devil is in the Data: Learning Fair Graph Neural Networks
via Partial Knowledge Distillation
Abstract.
Graph neural networks (GNNs) are being increasingly used in many high-stakes tasks, and as a result, there is growing attention on their fairness recently. GNNs have been shown to be unfair as they tend to make discriminatory decisions toward certain demographic groups, divided by sensitive attributes such as gender and race. While recent works have been devoted to improving their fairness performance, they often require accessible demographic information. This greatly limits their applicability in real-world scenarios due to legal restrictions. To address this problem, we present a demographic-agnostic method to learn fair GNNs via knowledge distillation, namely FairGKD. Our work is motivated by the empirical observation that training GNNs on partial data (i.e., only node attributes or topology data) can improve their fairness, albeit at the cost of utility. To make a balanced trade-off between fairness and utility performance, we employ a set of fairness experts (i.e., GNNs trained on different partial data) to construct the synthetic teacher, which distills fairer and informative knowledge to guide the learning of the GNN student. Experiments on several benchmark datasets demonstrate that FairGKD, which does not require access to demographic information, significantly improves the fairness of GNNs by a large margin while maintaining their utility.111Our code is available via: https://github.com/ZzoomD/FairGKD/.
1. Introduction
Graph neural networks (GNNs) have demonstrated superior performance in various applications (Fan et al., 2019; Aykent and Xia, 2022; Jiang and Luo, 2022). However, the increasing application of GNNs in high-stakes tasks, such as credit scoring (Wang et al., 2021) and fraud detection (Liu et al., 2020), has raised concerns regarding their fairness, as highlighted by recent works (Rahman et al., 2019; Dong et al., 2022). A widely accepted view is that the source of biases that result in the fairness problem of GNNs is the training data (Beutel et al., 2017; Dai and Wang, 2021; Dong et al., 2022). GNNs inherit or even amplify these biases through message passing (Dai and Wang, 2021), leading to biased decision-making toward certain demographic groups divided by sensitive attributes such as race, gender, etc. As a result, such discriminatory decisions may potentially cause economic problems and even social problems (Mukerjee et al., 2002; Mehrabi et al., 2021).
Over the past few years, efforts (Dai and Wang, 2021; Jiang et al., 2022; Spinelli et al., 2021) have been made to improve the fairness performance of GNNs. A well-studied approach is to mitigate fairness-related biases by modifying the training data, such as reducing the connection of nodes within the same demographic group (Spinelli et al., 2021) or preprocessing data to minimize the distribution distance between demographic groups (Dong et al., 2022). In this regard, the trained GNNs inherit less bias from unbiased training data. Furthermore, another popular approach is to address the fairness problem from a training perspective such as adversarial learning, which aims to learn a fair GNN model to generate node embedding independent of the sensitive attribute (Bose and Hamilton, 2019; Dai and Wang, 2021). Despite significant progress, prior works often assume that sensitive attributes (i.e., demographic information), are fully or partially accessible. However, due to privacy and legal restrictions (Chai et al., 2022; Hashimoto et al., 2018a) on sensitive attributes, such an assumption may not always hold in real-world scenarios. Although recent advances (Zhu and Wang, 2022; Lahoti et al., 2020a) have explored improving fairness without demographic information for independent and identically distributed (IID) data, these works cannot be directly applied to graph data due to complicated relations between instances. To this end, a natural question arises:How can we learn fair GNNs without demographic information?
We find that previous efforts focus on mitigating group-level biases, i.e., biases defined by the difference between demographic groups, resulting in the requirement for accessing the sensitive attribute. For example, FairDrop (Spinelli et al., 2021) reduces the connections between intra-group nodes, i.e., nodes within the same demographic group. Here, “intra-group” implicitly means bias mitigation at the group level. As such, prior approaches are highly dependent on the accessible sensitive attribute. In the preliminary study of Section 4, we find that mitigating the higher-level biases, i.e., bias in node attributes or the graph topology, also improves fairness but without accessing the sensitive attribute. Here, higher-level biases emphasize a wider range of biases than group-level biases, and in this paper refer to biases in node attributes or graph topology. Specifically, considering that the trained model inherits biases from the training data (Dai and Wang, 2021; Ling et al., 2023), using a portion of the data for training may be a straightforward solution to mitigate the higher-level biases. Thus, we compare fairness performance across three model training strategies, i.e., using only graph topology, only node attributes, and full graph data. The first two training strategies are referred to as partial data training, representing mitigating biases in node attributes, and graph topology, respectively. As shown in Figure 1, our comparison demonstrates that partial data training improves fairness performance but inevitably sacrifices utility. This observation indicates that mitigating higher-level biases also improves fairness but without accessing the sensitive attribute.

In light of our observation, we propose the utilization of partial data training as a means to alleviate higher-level biases, thereby enhancing fairness in a demographic-agnostic manner. However, the suboptimal utility performance associated with partial data training renders it impractical for training inference GNNs using such an approach. Drawing inspiration from the notable success of knowledge distillation (Hinton et al., 2015), employing partial data training to optimize fairer teacher models for guiding the learning process of GNN students emerges as a potentially effective solution. Thus, we propose a demographic-agnostic fairness method built upon partial data training and knowledge distillation paradigm, namely FairGKD. Specifically, FairGKD employs a set of fairness experts (i.e., models trained on partial data) to construct a synthetic teacher for distilling fair knowledge. Then, FairGKD learns fair GNN students with the guidance of fair knowledge. Additionally, FairGKD uses an adaptive algorithm to further achieve the trade-off between fairness and utility. Our contributions can be summarized as follows:
-
•
We study a novel problem for learning fair GNNs without demographic information. To the best of our knowledge, our work is the first to explore fairness without demographic information on graph-structured data.
-
•
We propose FairGKD, a simple yet effective method that learns fair GNNs with the guidance of a fair synthetic teacher to mitigate their higher-level biases.
-
•
We conduct experiments on several real-world datasets to verify the effectiveness of the proposed method in improving fairness while preserving utility.
2. Related Work
2.1. Fairness in Graph
Fairness in the graph attracts increasing attention due to the superior performance of GNNs in different scenarios (Kipf and Welling, 2016; Hamilton et al., 2017; Xu et al., 2018). Commonly used fairness notions can be summarized as group fairness, individual fairness, and counterfactual fairness (Dwork et al., 2012; Kang et al., 2020; Ma et al., 2022). In this paper, we focus on group fairness which highlights that the model neither favors nor harms any demographic groups defined by the sensitive attribute. Efforts to improve group fairness have incorporated mitigating biases in graph-structured data (Current et al., 2022; Laclau et al., 2021) and constructing a fair GNNs learning framework (Agarwal et al., 2021). Mitigating data biases involves modifying the graph topology (i.e., adjacency matrix) (Li et al., 2021) and node attributes (Dong et al., 2022), which provides clean data for training GNNs. For example, FairDrop (Spinelli et al., 2021) proposes an edge dropout algorithm to reduce connection between nodes within the same demographic group. EDITS (Dong et al., 2022) modifies both graph topology and node attributes with an objective that minimizes distribution distance between several demographic groups. In the fair GNN learning framework construction, adversarial learning (Goodfellow et al., 2014) is a commonly used approach to learning a fair GNN for generating node representations or making decisions independent of the sensitive attribute. For example, FairGNN (Dai and Wang, 2021) utilizes an adversary to learn a fair GNN classifier which makes predictions independent of the sensitive attribute. FairVGNN (Wang et al., 2022) proposes mitigating the sensitive attribute leakage through generative adversarial debiasing. However, these two types of approaches make a strong assumption that the sensitive attribute is accessible, i.e., the sensitive attribute is known. Such an assumption may not hold in real-world scenarios due to legal restrictions. Although (Dai and Wang, 2021) studies fair GNNs in limited sensitive attributes, it still requires the sensitive attribute.
Different from previous works, this work aims to learn fair GNNs without accessing sensitive attributes. This requires novel techniques to overcome the challenges of learning in the absence of sensitive attributes. In addition, our proposed method, FairGKD, employs knowledge distillation to learn fair GNNs. It should be noted that (Dong et al., 2023b) has focused on addressing the fairness problem in GNN-based knowledge distillation frameworks by adding a learnable proxy of bias for the shallow student model. In contrast, FairGKD learns fair GNN students through a fairer teacher model, which is quite different from Dong et al. (Dong et al., 2023b).
2.2. Fairness without Demographics
Since the legal and privacy limitations for accessing sensitive attributes, there are some progresses (Yan et al., 2020; Zhao et al., 2022a) to focus on fairness without demographic information in machine learning. For example, DRO (Hashimoto et al., 2018b) proposes a method based on distributionally robust optimization without access to demographics, which achieves fairness by improving the worst-case distribution. As the authors point out, DRO struggles to reduce the impact of noisy outliers, e.g., outliers from label noise. To avoid this impact, ARL (Lahoti et al., 2020b) improves fairness by addressing computationally-identifiable errors and proposes adversarially reweighted learning to improve the utility of worst-case groups. Inspired by label smoothing improving fairness, (Chai et al., 2022) utilizes knowledge distillation to generate soft labels instead of label smoothing. Although prior works improve fairness without demographics, these works design algorithms based on IID data, and their effectiveness in non-IID data, e.g., graph data, remains unknown. Thus, this work focuses on improving the fairness of GNNs working in graph-structured data without accessing sensitive attributes. Different from (Chai et al., 2022), FairGKD aims to construct the fairer teacher and regards intermediate results (Romero et al., 2014) as soft targets.
3. Preliminaries
3.1. Notations
For clarity in writing, consistent with prior works (Dai and Wang, 2021; Wang et al., 2022), we contextualize our proposed method and relevant proofs within the framework of a node classification task involving binary sensitive attributes and binary label settings. We represent an attributed graph by where is a set of nodes, is a set of edges. is the node attribute matrix where is the node attribute dimension. is an all-one node attribute matrix. represents the binary sensitive attribute. is the node attribute matrix without the sensitive attribute. is the adjacency matrix. represents that there exists edge between the node and the node , and otherwise. For node and node , if , these two nodes are within the same demographic group. GNNs update the node representation vector through aggregating messages of its neighbors. As such, existing GNNs consist of two steps: (1) message propagation and aggregation; (2) node representation updating. Thus, the -th layer of GNNs can be defined as:
| (1) | ||||
| (2) |
where and represent aggregation function and update function in -th layer, respectively. represents the set of nodes adjacent to node .
3.2. Fairness Metrics
We focus on group fairness which highlights the outputs of the model are not biased against any demographic groups. For group fairness, demographic parity (Dwork et al., 2012) and equal opportunity (Hardt et al., 2016) are two widely used evaluation metrics. In this paper, we utilize these two metrics to evaluate the fairness of models in the node classification task. Demographic parity (DP) requires that the prediction is independent of the sensitive attribute and equal opportunity (EO) requires the same true positive rate for each demographic group. Let denote the node label prediction result of the classifier. denotes the node label ground truth. The DP and EO difference between the two demographic groups can be defined as:
| (3) | ||||
| (4) |
where small and imply fairer decision-making of GNNs.
3.3. Problem Definition
This work aims to learn a fair GNN classifier which does not require accessing to demographics. With and as evaluation metrics, a fair GNN achieves minimum value for these two metrics. The problem of this paper can be formally defined as:
Problem Definition. Given a graph , but non-accessible sensitive attributes, and partial node label , learn a fair GNN for node classification task while maintaining utility.
| (5) |
4. Impact of Partial Data Training
Prior efforts (Spinelli et al., 2021; Dai and Wang, 2021; Dong et al., 2022) to improve fairness have a strong assumption that demographic information is available. This is due to the fact that they aim to mitigate group-level biases, i.e., biases defined by the difference between demographic groups. Then, demographic-based data modifications or training strategies, such as reducing connections within intra-group nodes, are employed to mitigate such biases. As such, this results in the requirement for accessible demographic information. A natural question is raised: Can we alleviate other biases while mitigating group-level biases?
Inspired by the fact that GNNs may inherit biases from training data (Dai and Wang, 2021; Ling et al., 2023), we speculate that training models on partial data, i.e., only node attributes or topology data, may be a natural solution. As shown in Figure 2, we make a preliminary analysis for the fairness performance of different training strategies to verify our insight. We train GNNs on data with different components, which are described as follows: (1) Full data. Train a 2-layer graph convolutional network (GCN) (Kipf and Welling, 2016) classifier (i.e., a GCN layer followed by a linear layer) using the complete graph data with the binary cross-entropy (BCE) function as the loss function. (2) Nodes-only. Train a 2-layer GCN classifier using only node attributes (i.e., the adjacent matrix is an identity matrix) with BCE as the loss function. This model can be regarded as a multi-layer perceptron (MLP). (3) Topology-only. Train a 2-layer GCN classifier, which is the same as the classifier in Full data, using only graph topology (i.e., all-one node attributes matrix) with BCE as the loss function. Here, we refer to nodes-only and topology-only as partial data training.


We conduct the node classification experiment on three real-world datasets, i.e., German (Agarwal et al., 2021), Recidivism (Agarwal et al., 2021), and NBA (Dai and Wang, 2021). We run this experiment 10 times to report results. All hyperparameters follow experimental settings in Section 6. The experimental results on all datasets are shown in Figure 2. We only show the accuracy (ACC) and performance due to the similar results on other metrics. From Figure 2, we make the following observations:
-
•
Fairness. Compared with full data training, partial data training (i.e., only node attributes or only graph topology) achieves a remarkable performance on fairness.
-
•
Utility. Although partial data training performs better in fairness, it sacrifices utility performance.
The possible reason for the first observation is that: As the deep learning model inherits biases from training data (Dai and Wang, 2021; Jiang and Nachum, 2020), models trained on partial data only inherit biases in node attribute or graph topology, which results in better fairness performance. For example, graph topology in real-world scenarios exhibits the homophily of sensitive attributes, which is one of the sources of bias resulting in fairness problems (Spinelli et al., 2021; Dong et al., 2023a). Topology-only models are trained on such data to capture graph patterns but inevitably inherit bias from these patterns. In contrast, Nodes-only models avoid such bias by not taking into account graph topology. The same principle applies to node attributes. Here, partial data training makes trained models avoid inheriting biases in node attributes or graph topology, including fairness-relevant biases and fairness-irrelevant biases. Thus, we refer to all biases hidden in partial data (node attributes or graph topology) as higher-level biases which also encompass group-level biases. Mitigating group-level biases improves the fairness performance of GNNs (Spinelli et al., 2021; Dong et al., 2022). As such, alleviating higher-level biases also eliminates group-level biases, resulting in fairness performance improvement. For the second observation, there are two possible reasons to explain this: (1) GNNs are more powerful than MLP in representation and reasoning capacity, which is empirically proved by prior efforts (Zhang et al., 2021; Xu et al., 2018). (2) with partial data for training, the model misses part of the information in full data, which leads to the model utility sacrifice.
Experimental results indicate that models trained on partial data present superior performance on fairness but sacrifice utility. To achieve the trade-off between fairness and utility, we propose FairGKD which is built upon knowledge distillation (Hinton et al., 2015) with partial data training, as shown in Section 5.
5. Methodology
Inspired by the preliminary analysis, we propose a method for learning fair GNNs, namely FairGKD. Here, we first give an overview of FairGKD. Then, we make a detailed description for each component of FairGKD, followed by the optimization objective. Finally, we present the theoretical proof and the complexity analysis in Appendix.
5.1. Overview
In this subsection, we provide an overview of FairGKD, which is illustrated in Figure 3. FairGKD is motivated by our empirical observation on partial data training. The goal of FairGKD is to learn a fair GNN without accessing sensitive attributes. To achieve this, several issues need to be tackled: (1) improving fairness without accessing the sensitive attribute; (2) avoiding utility sacrifice resulting from partial data training; (3) achieving a trade-off between fairness and utility. To overcome the first two challenges, FairGKD employs the partial data training strategy to mitigate higher-level biases. Then, following the knowledge distillation paradigm (Romero et al., 2015; Hinton et al., 2015), FairGKD employs two fairness experts (i.e., models trained on only node attributes or topology) to construct a synthetic teacher for distilling fair and informative knowledge. To overcome the third challenge, FairGKD utilizes an adaptive optimization algorithm to balance loss terms of fairness and utility.
As shown in Figure 3 (a), FairGKD consists of a synthetic teacher and a GNN student model denoted by and , respectively. is a GNN classifier for the node classification task, mimicking the output of . The synthetic teacher aims to distill fair and informative knowledge for the student model. Specifically, is comprised of two fairness experts, and , and a projector . Here, and , which are trained on only node attributes and only topology, alleviate higher-level biases without requiring access to sensitive attributes. Due to partial data training, and may generate fair yet uninformative node representations denoted by , . To bridge this gap, the projector is used to combine these uninformative representations and performs mapping to generate informative representation . will be regarded as additional supervision to assist the learning of . Mimicking fair and informative representation , tends to generate fair node representation while preserving utility. During each training epoch, takes full graph-structured data as input and predicts node labels. With a trained and fixed synthetic teacher as the teacher, is supervised by node label to maintain utility and node representation from the synthetic teacher to improve fairness. To further achieve the trade-off between fairness and utility for , an adaptive optimization algorithm (Zhao et al., 2022b) is employed to balance the training influence between the utility loss term (hard loss) and the knowledge distillation loss term (soft loss).
In summary, FairGKD is a demographic-agnostic framework that facilitates the learning of fair GNNs without sacrificing utility. Specifically, FairGKD is built upon knowledge distillation with partial data training. Different from the traditional teacher-student framework, FairGKD employs a synthetic teacher , which is the combination of multiple models, to distill fair knowledge for learning fair GNNs. Benefiting from partial data training, FairGKD can learn fair GNNs without accessing sensitive attributes. Meanwhile, FairGKD can achieve fairness improvement for multiple sensitive attributes with just a single training session, as empirically demonstrated in Section 6.
5.2. Synthetic Teacher
In this subsection, we introduce the components of synthetic teacher and its optimization objective. The goal of is to distill fair and informative node representation for the student model. consists of two fairness experts , , and a projector . The MLP fairness expert takes only node attributes without the sensitive attribute as input while outputting node representations . Meanwhile, the GNN fairness expert takes graph with all-one node attributes matrix as input and outputs . Note that can be regarded as only graph topology due to the all-one node attributes matrix. The processing for obtaining the node representation and is as follows:
| (6) | ||||
| (7) |
and are trained on partial data, i.e., only node attributes and only topology, respectively. According to observation in Section 4, and only inherit bias in node attributes or topology. As a result, , are fairer node representations due to mitigating higher-level biases. However, these two representations may be uninformative due to partial data training of and , which can lead to poor performance in downstream tasks. With such representations as the additional supervised information, it is challenging to train a fair student model that preserves utility. To address this issue, FairGKD employs a projector to merge these two representations to generate fair and informative representations . Specifically, takes the concatenation of and as input and outputs . This can be summarized as:
| (8) |
where denotes the concatenate operation. Since partial data training mitigates higher-level biases, and generated by the trained model display more fairness. To maintain such fairness, aims to seek bias neutralization between and , which results in fair representations . Eq. (8) combines the information from node attributes and graph topology while transforming and to a unified embedding space, similar to obtaining node representations with full data as input. As such, can output informative yet fair representations .
To ensure the implementation of the above design, FairGKD leverages a multi-step training scheme with a contrastive objective to train . As shown in Figure 3(b), the multi-step training scheme can be divided into two steps, i.e., fairness experts training and projector training. (1) Fairness experts training aims to make fairness experts inherit less biases through partial data training. Given a full graph without the sensitive attribute, we have two partial versions of , i.e., and . Then, , generate node representations , according to Eq. (6)-(7). Taking , as input, the classifier, e.g., a linear classification layer, is employed to predict node labels , . Based on the predicted node labels and the ground truth, BCE function is utilized as the loss function to optimize weights of two fairness experts, respectively. (2) Projector training ensures the projector generates informative node representations through a contrastive objective and a trained GNN . Here, has the same network structure as our GNN student but is directly trained on the full graph . After fairness experts training, we fix the model parameters of , and generate , . As shown in Eq. (8), the projector takes the concatenation of , as input and generates the node representations . This process can be summarized as . With node representations generated by as the ground truth, we optimize the projector by minimizing the contrastive objective. This maximizes the similarity between the representation of the same node in and , which means the synthetic model learns the informative node representations like .
For the contrastive objective, we follow the setting in Zhu et al. (Zhu et al., 2020). and denote the node representation of node in and . can be considered as a positive pair and the remaining ones are all negative pairs. Given a similarity function to computing node representations similarity, the contrastive objective for any positive pair can be defined as:
| (9) |
where and are the negative pairs. is a scalar temperature parameter. We consider the similarity function as , where is the consine similarity and is a projector. We compute the contrastive objective over all positive pairs to obtain the overall contrastive objective:
| (10) |
With Eq. (10) as the objective function, the trained synthetic teacher can generate fair and informative node representations for guiding the student model. As shown in Theorem ‣ A, we find that minimizing our contrastive objective is equivalent to maximizing the mutual information between and the original graph . This proves that the node representation generated by is informative. As a result, FairGKD learns fair and informative GNN students with a such teacher model.
Theorem 1.
Let , denote node representations generated by the trained GNN and the synthetic teacher , respectively. Given an original graph , the contrastive objective is a lower bound of mutual information between the node representations generated by and the original graph :
| (11) |
5.3. Learning Fair GNNs Student
With a trained synthetic model as the teacher model, FairGKD trains a fair GNN student . Following the knowledge distillation paradigm (Hinton et al., 2015), the GNN student learns to mimic the output of the synthetic teacher. Assuming that is a -layer model with a single linear layer as the classifier, i.e., the first layer constitutes the GNN backbone, while the -th layer serves as the classifier. Given a full graph , generates node representations in (-1)-th layer and predicts node labels in -th layer. With two partial versions of as input, the trained distills the knowledge as the additional supervised information in soft loss. Node labels ground truth is regarded as the ground truth in hard loss to make maintain high accuracy in the node classification task. Specifically, the objective function of training can be defined as:
| (12) |
where is the hard loss, which aims to maintain utility on the node classification task. We refer to as the binary cross-entropy function. is the soft loss to optimize the GNN backbone for generating node representations similar to the output of , which ensures that FairGKD learns fair GNNs. Similar to the optimization of the projector , we refer to as the contrastive objective shown in Eq. (9), (10) during the knowledge distillation process. and , which are adaptive coefficients for balancing the influence of these two loss terms, are calculated by the adaptive algorithm shown in Section 5.4.
5.4. Adaptive Optimization
Due to the multi-loss of FairGKD, it can be challenging to achieve a balance between different loss terms, which indicates a trade-off between utility and fairness. To address this issue, an adaptive algorithm is used to calculate two adaptive coefficients (i.e., and ) which balance the influence of the two loss terms. Inspired by the adaptive normalization loss in MTARD (Zhao et al., 2022b), we use this algorithm to balance and instead of loss terms in multi-teacher knowledge distillation. The core idea behind this algorithm is to amplify the impact of the disadvantage term (i.e., loss term with slower reduction) on the overall loss function. In this regard, the disadvantage term will be assigned a larger coefficient and then contribute more to the overall model update. Specifically, let denote the loss at epoch , Eq. (12) can be formulated as:
| (13) |
We compute and at each epoch through the loss decrease relative to the initial epoch, i.e., . Here, we utilize the relative loss to measure the loss decrease of loss . A small value of means a better optimization for the training model. Based on , and can be computed by the following formulation:
| (14) | ||||
| (15) |
where is the learning rate of the hard loss term, is a hyperparameter to enhance the disadvantaged loss which represents the loss term with a lower loss decrease.
In our scenarios, this algorithm suppresses the significantly decreasing loss term by assigning a smaller coefficient. Conversely, a bigger coefficient will promote the loss term that is slightly decreased. Meanwhile, and are dynamically changing with model optimization. Thus, the GNN student is optimized by balancing two loss terms, resulting in the trade-off between utility and fairness. Additionally, we give a brief complexity analysis for our proposed method FairGKD in Appendix B.
6. Experiments
In this section, we conduct experiments on three datasets, namely, (Agarwal et al., 2021), -, - (Takac and Zábovský, 2012). The statistical information of these datasets is shown in Table 1. Limited by space, we present the detailed experimental settings in Appendix D.
| Dataset | Recidivism | Pokec-z | Pokec-n |
|---|---|---|---|
| #Nodes | 18,876 | 67,796 | 66,569 |
| #Edges | 321,308 | 617,958 | 583,616 |
| #Attributes | 18 | 277 | 266 |
| Sens. | Race | Region | Region |
| Labels | Bail Prediction | Working Field | Working Field |
| Methods | Recidivism | Pokec-z | Pokec-n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ACC () | () | () | ACC () | () | () | ACC () | () | () | ||
| GCN | Vanilla | 84.23 ± 0.71 | 7.54 ± 0.59 | 5.20 ± 0.52 | 69.74 ± 0.27 | 5.02 ± 0.56 | 4.15 ± 0.81 | 68.75 ± 0.36 | 1.58 ± 0.57 | 2.56 ± 1.07 |
| FairGNN | 82.93 ± 1.17 | 6.65 ± 0.80 | 4.50 ± 0.90 | 68.96 ± 1.52 | 7.95 ± 1.53 | 6.29 ± 2.00 | 67.53 ± 1.75 | 2.36 ± 1.25 | 2.87 ± 1.05 | |
| FairVGNN | 85.92 ± 0.57 | 6.00 ± 0.75 | 4.69 ± 1.19 | 68.30 ± 0.94 | 3.51 ± 3.01 | 3.67 ± 1.88 | 69.25 ± 0.29 | 6.91 ± 1.74 | 8.93 ± 1.85 | |
| FDKD | 84.12 ± 0.52 | 7.33 ± 0.77 | 6.40 ± 1.14 | 69.71 ± 0.26 | 4.36 ± 0.68 | 3.25 ± 0.66 | 68.70 ± 0.53 | 1.03 ± 0.58 | 1.92 ± 0.83 | |
| FairGKD | 86.10 ± 1.09 | 7.12 ± 1.15 | 5.86 ± 1.30 | 69.21 ± 0.41 | 4.16 ± 0.80 | 3.15 ± 0.85 | 67.85 ± 0.30 | 0.87 ± 0.50 | 1.25 ± 1.04 | |
| FairGKDS | 86.09 ± 1.05 | 5.98 ± 0.47 | 4.47 ± 0.72 | 69.42 ± 0.37 | 7.72 ± 0.90 | 5.90 ± 0.99 | 68.04 ± 0.54 | 2.46 ± 0.86 | 3.62 ± 0.94 | |
| GIN | Vanilla | 72.53 ± 4.95 | 8.96 ± 3.13 | 6.62 ± 2.21 | 68.37 ± 0.55 | 4.29 ± 1.84 | 4.65 ± 1.85 | 68.48 ± 0.40 | 2.75 ± 1.45 | 4.81 ± 2.84 |
| FairGNN | 78.34 ± 1.56 | 8.93 ± 1.63 | 6.65 ± 1.77 | 68.48 ± 0.79 | 3.96 ± 1.47 | 5.22 ± 1.51 | 67.50 ± 1.11 | 2.25 ± 1.33 | 2.68 ± 1.59 | |
| FairVGNN | 80.76 ± 1.22 | 6.95 ± 0.41 | 6.97 ± 1.18 | 68.35 ± 0.71 | 1.93 ± 1.23 | 2.71 ± 1.20 | 67.55 ± 1.33 | 6.13 ± 1.59 | 7.00 ± 1.80 | |
| FDKD | 61.29 ± 6.17 | 5.95 ± 2.90 | 4.93 ± 3.54 | 68.40 ± 0.50 | 3.39 ± 1.19 | 4.16 ± 1.52 | 66.56 ± 1.57 | 1.60 ± 1.04 | 2.90 ± 2.27 | |
| FairGKD | 78.09 ± 4.53 | 8.37 ± 1.52 | 5.57 ± 1.63 | 67.63 ± 2.10 | 1.60 ± 1.07 | 2.26 ± 1.66 | 67.90 ± 1.09 | 1.59 ± 0.99 | 1.81 ± 1.59 | |
| FairGKDS | 79.98 ± 2.45 | 5.89 ± 1.56 | 4.53 ± 0.96 | 68.87 ± 0.35 | 4.78 ± 1.03 | 5.44 ± 1.38 | 68.48 ± 0.63 | 2.10 ± 0.81 | 4.57 ± 1.32 | |
6.1. Comparison with Baseline Methods
With two different GNNs (GCN, GIN) as backbones, we compare FairGKD with three baseline methods on the node classification task. Specifically, we implement two FairGKD variants with the same network structure, i.e., FairGKD and FairGKDS, which represent training on graph-structured data with and without the sensitive attribute. Note that we denote the proposed method in Section 5 as FairGKDS for convenience. Table 2 presents the utility and fairness performance of two FairGKD variants and all baseline methods.
The following observations can be made from Table 2: (1) the proposed method FairGKD improves fairness while maintaining or even improving utility across all three datasets, highlighting the effectiveness of FairGKD in learning fair GNNs. (2) FairGKD achieves state-of-the-art performance in most cases. While it is not the best-performing method in some cases, FairGKD presents a small performance gap with the best result. This implies the superior performance of FairGKD on both fairness and utility. (3) FairGKD can improve the fairness of GNNs even without sensitive attribute information, and in some cases outperforms all baseline methods. This observation implies that FairGKD is a demographic-agnostic fairness method.
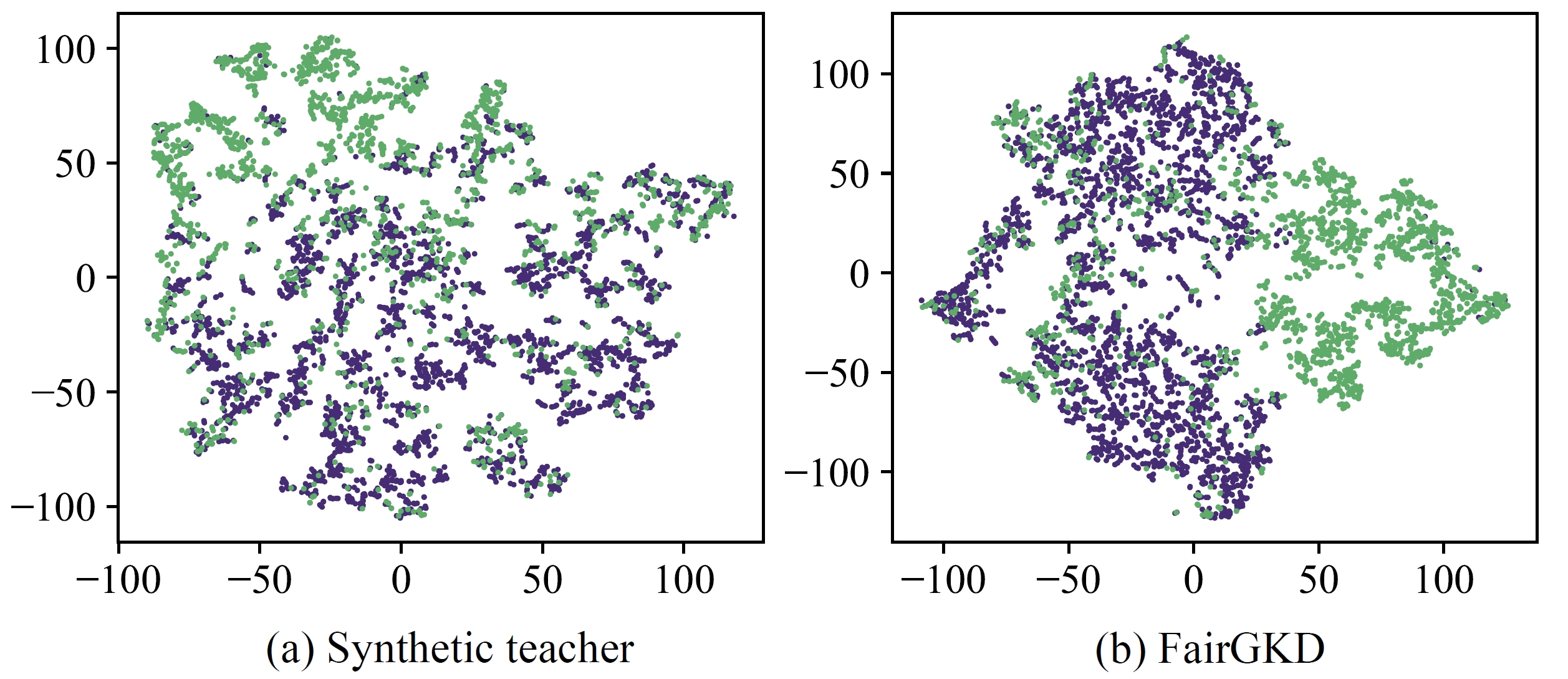
We also find that FairGKDS does not improve fairness on - and - dataset, but rather performs worse than Vanilla. However, comparing FairGKDS with VanillaS trained on data without the sensitive attribute, we observe FairGKDS improves the fairness of GNNs. One potential reason could be that non-sensitive attributes, which are highly correlated to the sensitive attribute, leak sensitive information and are more prone to make the training GNN inherit bias. We also observe that FairGKD is effective for two commonly used GNNs. To further understand FairGKD, we visualize the node representation generated by the synthetic teacher and the trained GNN student of FairGKD on using t-SNE in Figures 4 and 5. Figure 4 shows indistinguishable node representations with respect to the sensitive attribute, which demonstrates fair knowledge distilled by the synthetic teacher and fair student learned by FairGKD. Figure 5 shows clear clustering of node representations with respect to the node label, indicating the superior utility performance of FairGKD.

6.2. Ablation Study
We conduct ablations on datasets with the sensitive attribute. Specifically, we investigate how each of the following four components individually contributes to learning fair GNNs, i.e., fairness GNN expert, fairness MLP expert, the projector, and the adaptive optimization algorithm. We remove these four components separately and their results denoted by FairGKDG, FairGKDM, FairGKDP, and FairGKDA, respectively. For FairGKDG and FairGKDM, we regard the output of the remaining expert as the input of the projector. FairGKDP replaces the projector with mean operation. FairGKDA fixes and in Eq. (12) as 0.5.

We show ablation results of FairGKD learning GCN student model on -, and - datasets in Figure 6. We observe that FairGKD is stable in utility performance even if lacks some components. This is due to the fact that FairGKD trains the GNN student with full data as input and the knowledge distilling from the synthetic teacher is informative. The removal of any components, especially the fairness GNN expert and the fairness MLP expert, weakens the fairness improvement of FairGKD. This observation indicates that the synthetic teacher and the adaptive algorithm for loss coefficients are necessary for learning a fair GNN. Moreover, results of FairGKDA show higher value and standard deviations, which means worse fairness and more unstable performance. Thus, the adaptive algorithm for calculating loss coefficients is effective in achieving the trade-off between fairness and utility. Overall, the results show that all components of FairGKD are beneficial for the model fairness performance, while the adaptive algorithm also ensures the model fairness performance remains stable.
6.3. Various Sensitive Attributes Evaluation
Due to the partial data training to mitigate higher-level biases, FairGKD can be employed in fairness scenarios involving various sensitive attributes within a single training session. To verify this, we conduct FairGKD with GCN as the student and evaluate the fairness performance of this student on different sensitive attributes. We study the fairness performance of FairGKD w.r.t. three sensitive attributes, i.e., region, gender, and age. Here, we set all sensitive attributes to be binary. We set age 25 as 1 and age 25 as 0.
The results of various sensitive attributes are shown in Table 3. We observe that a single implementation of FairGKD improves fairness under different sensitive attributes in most cases. This is due to the fact that FairGKD is not tailored for a specific sensitive attribute and mitigates higher-level biases. Due to such a design, FairGKD exhibits a weaker impact on fairness in sensitive attributes like gender. Moreover, we also find that vanilla outperforms FairGKD on utility performance by a small margin which can be ignored. Overall, experimental results demonstrate that FairGKD is a one-size-fits-all approach for improving fairness under different sensitive attributes.
| Metrics | Pokec-z | Pokec-n | |||
| Vanilla | FairGKD | Vanilla | FairGKD | ||
| F1 | 70.23 ± 0.29 | 69.59 ± 0.36 | 65.33 ± 0.45 | 64.47 ± 0.47 | |
| ACC | 69.74 ± 0.27 | 69.21 ± 0.41 | 68.75 ± 0.36 | 67.85 ± 0.30 | |
| Region | 5.02 ± 0.56 | 4.16 ± 0.80 | 1.58 ± 0.57 | 0.87 ± 0.50 | |
| Gender | 3.07 ± 0.51 | 2.56 ± 0.72 | 6.03 ± 0.89 | 6.42 ± 0.45 | |
| Age | 57.03 ± 0.62 | 55.41 ± 2.82 | 62.41 ± 1.01 | 59.24 ± 2.08 | |
| Region | 4.15 ± 0.81 | 3.15 ± 0.85 | 2.56 ± 1.07 | 1.25 ± 1.04 | |
| Gender | 5.03 ± 0.37 | 5.01 ± 0.90 | 12.84 ± 0.99 | 12.43 ± 1.06 | |
| Age | 44.88 ± 0.53 | 43.52 ± 3.28 | 51.53 ± 1.10 | 48.72 ± 2.04 | |


6.4. Parameters Sensitivity
We conduct hyperparameter studies of two parameters, i.e., and . Specifically, we only show the parameter sensitivity results on dataset due to similar observations on other datasets. Using GCN as the student model, we vary and within the range of 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 0.001, 0.01, 0.1, 0.3, 0.5, 0.7, 1, 10, 100, respectively. As shown in Figure 7, we make the following observations: (1) the overall performance of FairGKD remains smooth despite the wide range of variation in and . Specifically, the performance of FairGKD is stable in terms of utility as well as fairness when varies within the range of 0.001 to 10 or varies within the range of 0.1 to 0.9. (2) When , FairGKD further improves fairness but the utility performance decreases rapidly. Due to a larger strengthening the disadvantaged loss, this observation indicates that the soft loss is the disadvantaged one in training. In this regard, a larger improves fairness but sacrifices utility. To better achieve the trade-off between utility and fairness, a suitable is necessary. (3) When , the fairness and utility performance of FairGKD both decrease. This suggests that the GNN student is not accurately replicating the output of the synthetic teacher. Overall, FairGKD remains stable with respect to the wide range variation of and . A suitable , e.g., , is beneficial for the trade-off between utility and fairness.
7. Conclusion
In this paper, we propose FairGKD, a simple yet effective method to learn fair GNNs on graph-structured data through knowledge distillation. To our best knowledge, FairGKD is the first effort to improve GNN fairness on graph-structured data without demographic information. The key insight behind our approach is to guide the GNN student training through the fair synthetic teacher, which mitigates higher-level biases via partial data training, i.e., training models on only node attributes or graph topology. As a result, FairGKD leverages the benefits of knowledge distillation and partial data training, improving fairness while eliminating the dependence on demographics. Experiments on three real-world datasets demonstrate that FairGKD outperforms strong baselines in most cases. Furthermore, we demonstrate that FairGKD is effective in learning fair GNNs even when demographic information is absent or in multiple sensitive attribute scenarios.
8. Acknowledgements
The research is supported by the National Key RD Program of China under grant No. 2022YFF0902500, the Key-Area Research and Development Program of Shandong Province (2021CXGC010108), the Guangdong Basic and Applied Basic Research Foundation, China (No. 2023A1515011050).
References
- (1)
- Agarwal et al. (2021) Chirag Agarwal, Himabindu Lakkaraju, and Marinka Zitnik. 2021. Towards a unified framework for fair and stable graph representation learning. In Proceedings of the Thirty-Seventh Conference on Uncertainty in Artificial Intelligence (Proceedings of Machine Learning Research, Vol. 161), Cassio de Campos and Marloes H. Maathuis (Eds.). PMLR, 2114–2124.
- Aykent and Xia (2022) Sarp Aykent and Tian Xia. 2022. GBPNet: Universal Geometric Representation Learning on Protein Structures. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Washington DC, USA) (KDD ’22). Association for Computing Machinery, New York, NY, USA, 4–14.
- Beutel et al. (2017) Alex Beutel, Jilin Chen, Zhe Zhao, and Ed H. Chi. 2017. Data Decisions and Theoretical Implications when Adversarially Learning Fair Representations. arXiv:1707.00075 [cs.LG]
- Bose and Hamilton (2019) Avishek Bose and William Hamilton. 2019. Compositional Fairness Constraints for Graph Embeddings. In Proceedings of the 36th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 97), Kamalika Chaudhuri and Ruslan Salakhutdinov (Eds.). PMLR, 715–724.
- Chai et al. (2022) Junyi Chai, Taeuk Jang, and Xiaoqian Wang. 2022. Fairness without Demographics through Knowledge Distillation. In Advances in Neural Information Processing Systems, S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh (Eds.), Vol. 35. Curran Associates, Inc., 19152–19164.
- Current et al. (2022) Sean Current, Yuntian He, Saket Gurukar, and Srinivasan Parthasarathy. 2022. FairEGM: Fair Link Prediction and Recommendation via Emulated Graph Modification. In Equity and Access in Algorithms, Mechanisms, and Optimization, EAAMO 2022, Arlington, VA, USA, October 6-9, 2022 (Arlington, VA, USA) (EAAMO ’22). Association for Computing Machinery, New York, NY, USA, Article 3, 14 pages.
- Dai and Wang (2021) Enyan Dai and Suhang Wang. 2021. Say No to the Discrimination: Learning Fair Graph Neural Networks with Limited Sensitive Attribute Information. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining (Virtual Event, Israel) (WSDM ’21). Association for Computing Machinery, New York, NY, USA, 680–688.
- Dong et al. (2022) Yushun Dong, Ninghao Liu, Brian Jalaian, and Jundong Li. 2022. EDITS: Modeling and Mitigating Data Bias for Graph Neural Networks. In Proceedings of the ACM Web Conference 2022 (Virtual Event, Lyon, France) (WWW ’22). Association for Computing Machinery, New York, NY, USA, 1259–1269.
- Dong et al. (2023a) Yushun Dong, Jing Ma, Song Wang, Chen Chen, and Jundong Li. 2023a. Fairness in graph mining: A survey. IEEE Transactions on Knowledge and Data Engineering (2023).
- Dong et al. (2023b) Yushun Dong, Binchi Zhang, Yiling Yuan, Na Zou, Qi Wang, and Jundong Li. 2023b. RELIANT: Fair Knowledge Distillation for Graph Neural Networks. CoRR abs/2301.01150 (2023). arXiv:2301.01150
- Dwork et al. (2012) Cynthia Dwork, Moritz Hardt, Toniann Pitassi, Omer Reingold, and Richard Zemel. 2012. Fairness through Awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference (Cambridge, Massachusetts) (ITCS ’12). Association for Computing Machinery, New York, NY, USA, 214–226.
- Fan et al. (2019) Wenqi Fan, Yao Ma, Qing Li, Yuan He, Eric Zhao, Jiliang Tang, and Dawei Yin. 2019. Graph Neural Networks for Social Recommendation. In The World Wide Web Conference (San Francisco, CA, USA) (WWW ’19). Association for Computing Machinery, New York, NY, USA, 417–426.
- Goodfellow et al. (2014) Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative Adversarial Nets. In Advances in Neural Information Processing Systems, Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence, and K.Q. Weinberger (Eds.), Vol. 27. Curran Associates, Inc.
- Hamilton et al. (2017) Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive Representation Learning on Large Graphs. In Advances in Neural Information Processing Systems, I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett (Eds.), Vol. 30. Curran Associates, Inc.
- Hardt et al. (2016) Moritz Hardt, Eric Price, and Nati Srebro. 2016. Equality of Opportunity in Supervised Learning. In Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, December 5-10, 2016, Barcelona, Spain, Daniel D. Lee, Masashi Sugiyama, Ulrike von Luxburg, Isabelle Guyon, and Roman Garnett (Eds.), Vol. 29. 3315–3323.
- Hashimoto et al. (2018a) Tatsunori Hashimoto, Megha Srivastava, Hongseok Namkoong, and Percy Liang. 2018a. Fairness Without Demographics in Repeated Loss Minimization. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 80), Jennifer Dy and Andreas Krause (Eds.). PMLR, 1929–1938.
- Hashimoto et al. (2018b) Tatsunori Hashimoto, Megha Srivastava, Hongseok Namkoong, and Percy Liang. 2018b. Fairness Without Demographics in Repeated Loss Minimization. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 80), Jennifer Dy and Andreas Krause (Eds.). PMLR, 1929–1938.
- He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, June 27-30, 2016. IEEE Computer Society, 770–778.
- Hinton et al. (2015) Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. 2015. Distilling the Knowledge in a Neural Network. arXiv:1503.02531 [stat.ML]
- Jiang and Nachum (2020) Heinrich Jiang and Ofir Nachum. 2020. Identifying and correcting label bias in machine learning. In International Conference on Artificial Intelligence and Statistics. PMLR, 702–712.
- Jiang and Luo (2022) Weiwei Jiang and Jiayun Luo. 2022. Graph neural network for traffic forecasting: A survey. Expert Systems with Applications 207 (2022), 117921.
- Jiang et al. (2022) Zhimeng Jiang, Xiaotian Han, Chao Fan, Zirui Liu, Na Zou, Ali Mostafavi, and Xia Hu. 2022. FMP: Toward Fair Graph Message Passing against Topology Bias. arXiv:2202.04187 [cs.LG]
- Kang et al. (2020) Jian Kang, Jingrui He, Ross Maciejewski, and Hanghang Tong. 2020. InFoRM: Individual Fairness on Graph Mining. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 379–389.
- Kipf and Welling (2016) Thomas N. Kipf and Max Welling. 2016. Semi-Supervised Classification with Graph Convolutional Networks. arXiv:1609.02907 [cs.LG]
- Laclau et al. (2021) Charlotte Laclau, Ievgen Redko, Manvi Choudhary, and Christine Largeron. 2021. All of the Fairness for Edge Prediction with Optimal Transport. In Proceedings of The 24th International Conference on Artificial Intelligence and Statistics (Proceedings of Machine Learning Research, Vol. 130), Arindam Banerjee and Kenji Fukumizu (Eds.). PMLR, 1774–1782.
- Lahoti et al. (2020a) Preethi Lahoti, Alex Beutel, Jilin Chen, Kang Lee, Flavien Prost, Nithum Thain, Xuezhi Wang, and Ed Chi. 2020a. Fairness without demographics through adversarially reweighted learning. Advances in neural information processing systems 33 (2020), 728–740.
- Lahoti et al. (2020b) Preethi Lahoti, Alex Beutel, Jilin Chen, Kang Lee, Flavien Prost, Nithum Thain, Xuezhi Wang, and Ed Chi. 2020b. Fairness without Demographics through Adversarially Reweighted Learning. In Advances in Neural Information Processing Systems, H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin (Eds.), Vol. 33. Curran Associates, Inc., 728–740.
- Li et al. (2021) Peizhao Li, Yifei Wang, Han Zhao, Pengyu Hong, and Hongfu Liu. 2021. On dyadic fairness: Exploring and mitigating bias in graph connections. In International Conference on Learning Representations.
- Ling et al. (2023) Hongyi Ling, Zhimeng Jiang, Youzhi Luo, Shuiwang Ji, and Na Zou. 2023. Learning Fair Graph Representations via Automated Data Augmentations. In The Eleventh International Conference on Learning Representations.
- Liu et al. (2020) Zhiwei Liu, Yingtong Dou, Philip S. Yu, Yutong Deng, and Hao Peng. 2020. Alleviating the Inconsistency Problem of Applying Graph Neural Network to Fraud Detection. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval (Virtual Event, China) (SIGIR ’20). Association for Computing Machinery, New York, NY, USA, 1569–1572.
- Ma et al. (2022) Jing Ma, Ruocheng Guo, Mengting Wan, Longqi Yang, Aidong Zhang, and Jundong Li. 2022. Learning Fair Node Representations with Graph Counterfactual Fairness. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining (Virtual Event, AZ, USA) (WSDM ’22). Association for Computing Machinery, New York, NY, USA, 695–703.
- Mehrabi et al. (2021) Ninareh Mehrabi, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, and Aram Galstyan. 2021. A survey on bias and fairness in machine learning. ACM Computing Surveys (CSUR) 54, 6 (2021), 1–35.
- Mukerjee et al. (2002) Amitabha Mukerjee, Rita Biswas, Kalyanmoy Deb, and Amrit P Mathur. 2002. Multi–objective evolutionary algorithms for the risk–return trade–off in bank loan management. International Transactions in operational research 9, 5 (2002), 583–597.
- Rahman et al. (2019) Tahleen Rahman, Bartlomiej Surma, Michael Backes, and Yang Zhang. 2019. Fairwalk: Towards Fair Graph Embedding. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (Macao, China) (IJCAI’19). AAAI Press, 3289–3295.
- Romero et al. (2014) Adriana Romero, Nicolas Ballas, Samira Ebrahimi Kahou, Antoine Chassang, Carlo Gatta, and Yoshua Bengio. 2014. FitNets: Hints for Thin Deep Nets. arXiv:1412.6550 [cs.LG]
- Romero et al. (2015) Adriana Romero, Nicolas Ballas, Samira Ebrahimi Kahou, Antoine Chassang, Carlo Gatta, and Yoshua Bengio. 2015. FitNets: Hints for Thin Deep Nets. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings.
- Spinelli et al. (2021) Indro Spinelli, Simone Scardapane, Amir Hussain, and Aurelio Uncini. 2021. Fairdrop: Biased edge dropout for enhancing fairness in graph representation learning. IEEE Transactions on Artificial Intelligence 3, 3 (2021), 344–354.
- Takac and Zábovský (2012) L. Takac and Michal Zábovský. 2012. Data analysis in public social networks. International Scientific Conference and International Workshop Present Day Trends of Innovations (01 2012), 1–6.
- Wang et al. (2021) Daixin Wang, Zhiqiang Zhang, Jun Zhou, Peng Cui, Jingli Fang, Quanhui Jia, Yanming Fang, and Yuan Qi. 2021. Temporal-Aware Graph Neural Network for Credit Risk Prediction. In Proceedings of the 2021 SIAM International Conference on Data Mining, SDM 2021, Virtual Event, April 29 - May 1, 2021, Carlotta Demeniconi and Ian Davidson (Eds.). SIAM, 702–710.
- Wang et al. (2022) Yu Wang, Yuying Zhao, Yushun Dong, Huiyuan Chen, Jundong Li, and Tyler Derr. 2022. Improving Fairness in Graph Neural Networks via Mitigating Sensitive Attribute Leakage. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Washington DC, USA) (KDD ’22). Association for Computing Machinery, New York, NY, USA, 1938–1948.
- Xu et al. (2018) Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. 2018. How Powerful are Graph Neural Networks? arXiv:1810.00826 [cs.LG]
- Yan et al. (2020) Shen Yan, Hsien-te Kao, and Emilio Ferrara. 2020. Fair Class Balancing: Enhancing Model Fairness without Observing Sensitive Attributes. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management (Virtual Event, Ireland) (CIKM ’20). Association for Computing Machinery, New York, NY, USA, 1715–1724.
- Zhang et al. (2021) Shichang Zhang, Yozen Liu, Yizhou Sun, and Neil Shah. 2021. Graph-less Neural Networks: Teaching Old MLPs New Tricks via Distillation. arXiv:2110.08727 [cs.LG]
- Zhao et al. (2022b) Shiji Zhao, Jie Yu, Zhenlong Sun, Bo Zhang, and Xingxing Wei. 2022b. Enhanced Accuracy and Robustness via Multi-teacher Adversarial Distillation. In Computer Vision - ECCV 2022 - 17th European Conference, Tel Aviv, Israel, October 23-27, 2022, Proceedings, Part IV (Lecture Notes in Computer Science, Vol. 13664), Shai Avidan, Gabriel J. Brostow, Moustapha Cissé, Giovanni Maria Farinella, and Tal Hassner (Eds.). Springer, Cham, 585–602.
- Zhao et al. (2022a) Tianxiang Zhao, Enyan Dai, Kai Shu, and Suhang Wang. 2022a. Towards Fair Classifiers Without Sensitive Attributes: Exploring Biases in Related Features. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining (Virtual Event, AZ, USA) (WSDM ’22). Association for Computing Machinery, New York, NY, USA, 1433–1442.
- Zhu and Wang (2022) Huaisheng Zhu and Suhang Wang. 2022. Learning Fair Models without Sensitive Attributes: A Generative Approach. arXiv:2203.16413 [cs.LG]
- Zhu et al. (2020) Yanqiao Zhu, Yichen Xu, Feng Yu, Qiang Liu, Shu Wu, and Liang Wang. 2020. Deep Graph Contrastive Representation Learning. arXiv:2006.04131 [cs.LG]
Appendix A Proof of theorem 1
Theorem 0 (Restated).
Let , denote node embedding generated by the trained GNN and the synthetic teacher , respectively. Given an original graph , the contrastive objective is a lower bound of mutual information between the node embedding generated by and the original graph :
| (16) |
Here is the proof of Theorem ‣ A:
Proof.
Based on the data processing inequality, given three random variables X, Y, Z satisfying a Markov chain , we have the inequality . In FairGKD, and are generated by and using the original graph as input. This gives rise to a Markov chain . and are conditionally independent after given , so this Markov chain is equivalent to . Thus, we obtain the following inequality:
| (17) |
According to the proof in (Ling et al., 2023; Zhu et al., 2020), the lower bound of the true mutual information between and is the contrastive objective , which can be summarized as:
| (18) |
This completes the proof of Theorem ‣ A, and we have shown that . ∎
Appendix B Complexity Analysis
We briefly discuss the space and time complexity of our proposed FairGKD. For space complexity, FairGKD computes the pairwise similarity in the contrastive objective to train fair GNNs. Thus, the space complexity of FairGKD, which is related to the number of nodes in graph , is . Fortunately, we can use the graph sampling-based training method or replace the contrastive objective with mean square error (MSE) to further reduce the space complexity. For time complexity, FairGKD conducts the forward of the synthetic teacher once to obtain soft targets and the rest of the training process is the same as the normal training of GNNs. Thus, the time complexity of FairGKD is .
Appendix C Algorithm
To help better understand FairGKD, we present the training algorithm of FairGKD in Algorithm 1. Note that the trained GNN has the same network structure as the GNN student but is directly trained on the full graph .
Input: , node labels , a -layer GNN student , a synthetic teacher , a trained GNN , and hyperparameters , , .
Output: Trained GNN student model with parameters .
Appendix D Experimental Settings
D.1. Datasets
We conduct node classification experiments on three commonly used datasets, namely, (Agarwal et al., 2021), -, - (Takac and Zábovský, 2012). To maintain consistency with previous research (Dai and Wang, 2021; Wang et al., 2022; Dong et al., 2022), the sensitive attribute and node labels of the above-mentioned datasets are binary. We present a brief description of these three datasets as follows:
-
•
Recidivism (Agarwal et al., 2021) is a defendants dataset including those defendants released on bail during 1990-2009 in U.S states. Nodes represent defendants and are connected based on the similarity of past criminal records and demographics. Considering “race” as the sensitive attribute, the task is to classify defendants into bail vs. no bail, i.e., predicting whether defendants will commit a crime after being released.
-
•
Pokec - and - (Takac and Zábovský, 2012) are derived from a popular social network application in Slovakia, which shows different data in two different provinces. A node denotes a user with features such as gender, age, interest, etc. A connection represents the friendship information between nodes. Regarding “region” as the sensitive attribute, we predict the working field of the users.
D.2. Evaluation Metrics
We regard the F1 score and the accuracy as utility evaluation metrics. For fairness performance, we use two group fairness metrics (i.e., and ) shown in Section 3.2. A smaller fairness metric indicates a fairer model decision.
D.3. Baseline Methods
We compare FairGKD with the following baseline methods, including FairGNN (Dai and Wang, 2021), FairVGNN (Wang et al., 2022), and FDKD (Chai et al., 2022):
-
•
FairGNN. FairGNN focuses on the group fairness of graph-structured data with limited sensitive attribute information. Based on adversarial learning, FairGNN aims to train a fair GNN classifier to generate results for which the discriminator cannot distinguish sensitive attributes.
-
•
FairVGNN. FairVGNN improves the fairness of GNNs by mitigating sensitive attribute leakage. Specifically, it aims to mask features and clamp encoder weights highly relevant to the sensitive attribute.
-
•
FDKD. FDKD, which is inspired by the fairness impact of label smoothing, focuses on fairness without demographics on IID data via soft labels from an overfitted teacher model. Both FDKD and FairGKD follow knowledge distillation, but they are quite different. To employ FDKD in graph-structured data, we replace the original backbone (ResNet (He et al., 2016)) in FDKD with the commonly used GNN backbones, e.g., GCN (Kipf and Welling, 2016) and GIN (Xu et al., 2018).
D.4. Implemental Details
We conduct all experiments 10 times and reported average results. For FairGKD, we fix the learning rate as 1.0 for all datasets. We set and for the , - dataset. For - dataset, we set and for GCN, GIN backbone. For FairGNN and FairVGNN, we train models while all hyperparameters follow the author’s suggestions. For FDKD, we tune the trade-off hyperparameter to find the best model performance in utility and fairness. For all models, we utilize the Adam optimizer with a learning rate of and a weight decay scheme for 1000 epochs, where the weight decay is set to .
Since baseline methods (i.e., FairGNN, FairVGNN) cannot be used in a scenario without sensitive attributes, all FairGKD implementations in experiments use the sensitive attribute for a fair comparison.
We use two commonly used GNNs (i.e., GCN, and GIN) as the GNN students in FairGKD. For GCN and GIN, a 1-layer GCN and GIN convolution, respectively, serve as the backbone, with a single linear layer positioned on top of the backbone as the classifier. For the synthetic teacher, FairGKD uses a 2-layer MLP as the fairness MLP expert, a 1-layer GCN as the fairness GNN expert, and a 3-layer MLP as the projector. Meanwhile, the hidden dimensions of all GNNs and MLPs for three datasets are 16. Moreover, we conduct all experiments on one NVIDIA TITAN RTX GPU with 24GB memory. All models are implemented with PyTorch.