The Deformation Spaces of Geodesic Triangulations of Flat Tori
Abstract.
We prove that the deformation space of geodesic triangulations of a flat torus is homotopy equivalent to a torus. This solves an open problem proposed by Connelly et al. in 1983, in the case of flat tori. A key tool of the proof is a generalization of Tutte’s embedding theorem for flat tori. When this paper is under preparation, Erickson and Lin proved a similar result, which works for all convex drawings.
Key words and phrases:
geodesic triangulations, Tutte’s embedding1. Introduction
This paper is a continuation of the previous work [13], where we proved that the deformation space of geodesic triangulations of a surface with negative curvature is contractible. The purpose of this paper is to identify the homotopy type of the deformation space of geodesic triangulations of a flat torus. This solves an open question proposed by Connelly et al. in [4]. The main result of this paper is
Theorem 1.1.
The deformation space of geodesic triangulations of a flat torus is homotopic equivalent to a torus.
It is conjectured in [4] that the space of geodesic triangulations of a closed orientable surface with constant curvature deformation retracts to the group of orientation preserving isometries of homotopic to the identity. This paper affirms this conjecture in the case of flat tori. The case of hyperbolic surfaces has been proved in [13]. In a very recent work, Erickson-Lin [8] proved independently a generalized version of our Theorem 1.1 for general graph drawings on a flat torus.
The study of the homotopy types of spaces of geodesic triangulations stemmed from the work by Cairns [2]. A brief history of this problem can be found in [13]. These spaces are closely related to diffeomoprhism groups of surfaces. Bloch-Connelly-Henderson [1] proved that the space of geodesic triangulations of a convex polygon is contractible. The space of geodesic triangulations of a planar polygon is equivalent to the space of simplexwise linear homeomorphisms. Hence, the Bloch-Connelly-Henderson theorem can be viewed as a discrete analogue of Smale’s theorem, which states that the diffeomorphism group of the closed -disk fixing the boundary pointwise is contractible. Earle-Eells [7] proved that the group of orientation-preserving diffeomorphisms of a torus isotopic to the identity is homotopy equivalent to a torus. Theorem 1.1 can be regarded as a discrete version of this theorem.
Similar to the previous work [13], our key idea to prove Theorem 1.1 originates from Tutte’s embedding theorem.
1.1. Set Up and the Main Theorem
Let be the flat torus constructed by gluing the opposite sides of the unit square in .
A topological triangulation of can be identified as a homeomorphism from to , where is the carrier of a 2-dimensional simplicial complex with the vertex set , and the edge set , and the face set . For convenience, we label the vertices as where is the number of the vertices. Denote as the number of the edges, and as the directed edge from the vertex to its neighbor , and as the set of directed edges, and as the indices of neighbored vertices of .
A geodesic triangulation with the combinatorial type is an embedding from the one-skeleton to satisfying that
-
(a)
the restriction of on each edge , identified with a unit interval , is a geodesic of constant speed, and
-
(b)
is homotopic to the restriction of on .
Let denote the set of all such geodesic triangulations, which is so-called a deformation space of geodesic triangulations of . This space can be defined for other flat tori in a similar fashion. Perturbing each vertex locally, we can construct a family of geodesic triangulations from an initial geodesic triangulation. Therefore, the space is naturally a -dimensional manifold.
For any geodesic triangulation , we can always translate on to make the image of the first vertex be at the (quotient of the) origin . By this normalization, we can decompose as , where
Since there are affine transformations between any two flat tori, and an affine transformation always preserves the geodesic triangulations, Theorem 1.1 reduces to the following.
Theorem 1.2.
Given a topological triangulation of , the space is contractible.
1.2. Key Tool: Generalized Tutte’s Embedding Theorem
Let be a map from to . Assume maps every edge in to a geodesic arc parametrized by constant speed on . A positive assignment on the set of directed edges is called a weight of . We say is -balanced at if
where . Then indicates the direction of the edge and equals to the length of . A map is called -balanced if it is -balanced at each vertex in . We have the following version of Tutte’s embedding theorem, which is a special case of Gortler-Gotsman-Thurston’s embedding result in [11] and Theorem 1.6 in [13].
Theorem 1.3.
Assume is a topological triangulation of , and is a map from to such that is homotopic to and the restriction of on each edge is a geodesic parametrized by constant speed. If is -balanced for some weight , then is an embedding, or equivalently is a geodesic triangulation.
To be self-contained, we will give a simple proof for Theorem 1.3 , which is adapted from Gortler-Gotsman-Thurston’s argument in [11].
The classical Tutte’s embedding theorem [14] states that a straight-line embedding of a simple 3-vertex-connected planar graph can be constructed by fixing an outer face as a convex polygon and solving interior vertices on the condition that each vertex is in the convex hull of its neighbors. Various new proofs of Tutte’s embedding theorem have been proposed by Floater [9], Gortler-Gotsman-Thurston [11], et al.
Tutte’s embedding theorem has been generalized by Colin de Verdière [5], Delgado-Friedrichs [6], and Hass-Scott [12] to surfaces with non-positive Gaussian curvatures. They showed that the minimizer of a discrete Dirichlet energy is a geodesic triangulation. Here the fact that is a minimizer of a discrete Dirichlet energy means that is -balanced for some symmetric weight in with . Their result also implies that is not an empty set for any topological triangulation . Recently, Luo-Wu-Zhu [13] proved a new version of Tutte’s embedding theorem, for nonsymmetric weights and triangulations of orientable closed surfaces with non-positive Gaussian curvature.
Gortler-Gotsman-Thurston [11] generalized Tutte’s embedding theorem to flat tori. In contrast to the case of convex polygons and surfaces of negative curvatures, it is not always possible to construct a geodesic triangulation of such that it is -balanced with respect to a given non-symmetric weight . See [3] Section 1.1 for a detailed discussion.
1.3. Outline of the Proof
Fix a lifting of for each . Then for any , there exists a unique lifting of such that . Then
for some lattice point .
A geodesic triangulation in can be represented by for with . Under this representation, is the quotient of the linear map
and the equations for -balanced conditions at all the vertices can be written as
In a closed matrix form, we can write
| (1) |
where the weight matrix is
and
Here we denote if .
A weight in is called admissible if the equation (1) is solvable. Let be the space of admissible weights. For any , a solution to the equation (1) uniquely determines the coordinates of the vertices, and a -balanced map that is homotopic to . By Theorem 1.3, such is an embedding, and . Noticing that is weakly diagonal dominant and the graph is connected, the solution to equation (1) is unique up to a 2-dimensional translation, and is unique if we require . Define the Tutte map as
sending an admissible weight to the unique -balanced geodesic triangulation in . The Tutte map is continuous by the continuous dependence of the solutions to the coefficients in a linear system.
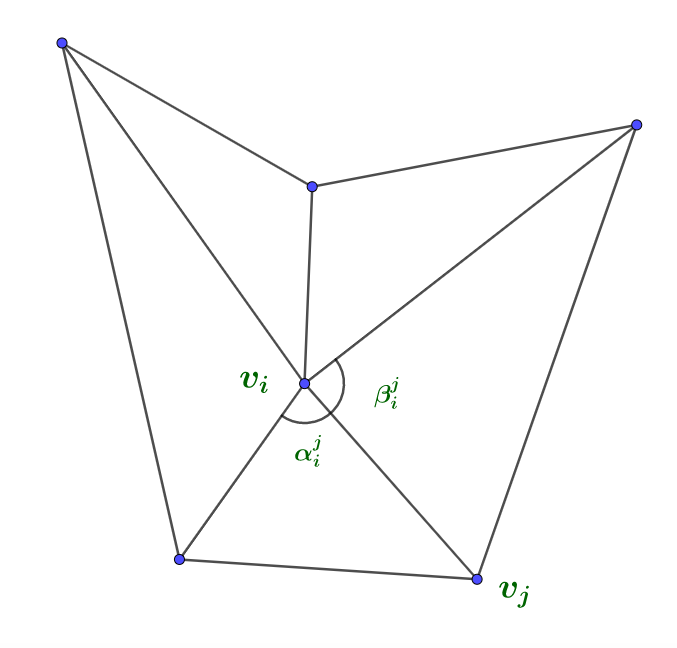
The Tutte map is also surjective, since there exists a smooth map from to by the “mean value coordinates”
introduced by Floater [10]. Here are two inner angles adjacent to at the vertex , and is the edge length of . See Figure 1 for an illustration. Floater [10] showed that any geodesic triangulation is -balanced, i.e., .
Having the knowledge of the Tutte map and the mean value coordinates, Theorem 1.2 reduces to the following proposition.
Proposition 1.4.
There exists a continuous map such that
1.4. Organization of this Paper
1.5. Acknowledgement
We really appreciate Professor Jeff Erickson for providing valuable insights and references about this problem.
2. Proof of Proposition 1.4
Set an energy function on the weight space as
where the norm is the Frobenius norm of a matrix. The second minimization problem above is a least square problem with real variables and a non-degerate coefficient matrix. By the standard formula in linear least squares (LLS) or quadratic programming (QP), the minimizer, denoted as , is a smooth function of , and thus is also a smooth function of . Note that if and only if is admissible, and intuitively measures the deviation of from being admissible. The key idea of the proof is to construct a flow on to minimize , as in the following Lemma 2.1.
Lemma 2.1.
There exists a smooth function and a continuous function on such that for any initial value , the flow defined by
| (2) |
satisfies that for any in the maximum existing interval ,
-
(a)
and
-
(b)
Proposition 1.4 is proved in Section 2.1, assuming this Lemma 2.1. Then we construct a flow in Section 2.2, and in Section 2.3 show that this flow is satisfactory for Lemma 2.1.
2.1. Proof of Proposition 1.4 Assuming Lemma 2.1
Assume and are as in Lemma 2.1. Given , assume is the flow defined by equation (2), and is the maximum existing interval.
We claim that and converge to some as . Since
we have that
and
which implies
Since
we have that
| (3) |
Then by the monotone convergence theorem, converge to some . By the maximality of , has to be in . Let be such that if , and if .
Now we prove that is continuous, i.e., for any and , there exists such that for any with . We consider the two cases and .
2.1.1.
Since is continous, there exists and such that for any with . Since is continuous, there exists such that
if . Then we will show that is satisfactory. Assume satisfies that . If , then . If ,
So by the inequality (3),
2.1.2.
Assume . Then by the result of the previous case, there exists such that for any with . Assume is the flow determined by the equation (2) with the initial value . Then there exists some , such that . By the continuous dependence of the solutions of ODEs on the initial values, there exists such that if , then , where is the flow determined by equation (2) with the initial value . So if , we have and
2.2. Construction of the Flow
Denote as the minimizer of the second minimization problem in the definition of the energy function . Define the residual as
where
The vector is the residual at the vertex , and , are the projections of the total residual in the directions of the -axis and the -axis respectively. Then by the minimality of ,
Equivalently,
Since , . So , and for any . Here means that vectors and are parallel, i.e., linearly dependent.
Lemma 2.2.
Assume and the following properties holds for .
-
(a)
The vectors have the same direction, namely,
-
(b)
If
then
Proof.
Without loss of generality, after a rotation we can assume that all the vectors are parallel to -axis, namely .
To prove part (a), assume that for some . Then one can find a non-zero vector so that . Then and there exists with . Then if for some ,
and thus if . By this maximum principle and the connectedness of the graph, for any , and . This contradicts with that is nonzero.
If part (b) is not true, ordering the set based on the values of monotonically, one can find a non-empty proper subset such that
Choose a vector such that if , and otherwise. Then the contradiction follows from
∎
Assume is the unit vector that is parallel to and . Define for each directed edge,
where is given by the minimizer . Note that
Lemma 2.3.
There exists a constant such that for any , there exists such that .
Proof.
Since for any , it suffices to find such that . Assume . Then or .
If , let be a horizontal simple loop in . Then is a simple loop in the carrier of , and it is not difficult to show that there exists a sequence of vertices such that for any , and the union is a piecewise linear loop in , which is homotopy equivalent to . By choosing an appropriate orientation, we have that
So
and there exists some such that . Notice that here is a constant depends only on and .
Similarly, if , there exists some such that for some constant . ∎
We define the smooth flow on the domain on each edge as follows
| (4) |
where and are smooth non-increasing functions such that
-
(a)
The function on and on , and
-
(b)
The function on , and on , and
-
(c)
Roughly speaking, the function tends be positive if , meaning that will decrease so as to reduce the residual . The function controls the difference between and . is smooth and very small. Specifically we have that
| (5) |
where is a continuous function on . Denote
which is another continous function on .
Lemma 2.4.
Assume the flow satisfies the equation (4). Then we have the following.
-
(a)
.
-
(b)
implies . Then for all directed edges.
-
(c)
implies .
-
(d)
is non-decreasing and is non-increasing.
-
(e)
For any edge ,
-
(f)
The residual vectors satisfies
-
(g)
The residual vectors satisfies
(6)
2.3. Proof of Lemma 2.1
Proof.
Let
where and are continous functions on , on which is also continuous. We claim that such function and the flow defined as equation (4) are satisfactory. Assume and is a flow defined by equation (4). By part (a) of Lemma 2.4 we only need to prove the Part (b) of Lemma 2.1. By part (d) of Lemma 2.4, it is easy to see that is non-decreasing on . So we only need to prove that
2.3.1. Case 1:
2.3.2. Case 2:
| (8) |
The last step (inequality ) uses the fact that , which is equivalent to that .
By the fact that , and the assumption ,
and thus . Notice that
and
Then
and
∎
3. Proof of Theorem 1.3
We will first introduce the concept of discrete one forms, and the Index Theorem proposed by Gortler-Gotsman-Thurston [11].
3.1. Discrete One Forms and the Index Theorem
A discrete one form is a real-valued function on the set of directed edges such that it is anti-symmetric on each undirected edge. Specifically, let be the value of on the directed edge from to , then we have
For a discrete one form, an edge is degenerate (resp. non-vanishing) if the one form is zero (resp. non-zero) on it. A vertex is degenerate (resp. non-vanishing) if all of edges connected to it are degenerate (resp. non-vanishing). A face is degenerate (resp. non-vanishing) if all of its three edges are degenerate (resp. non-vanishing). A one-form is degenerate (resp. non-vanishing) if all the edges are degenerate (resp. non-vanishing). Each edge is either degenerate or non-vanishing. However, vertices or faces can be degenerate, non-degenerate but vanishing on some edges, or non-vanishing.
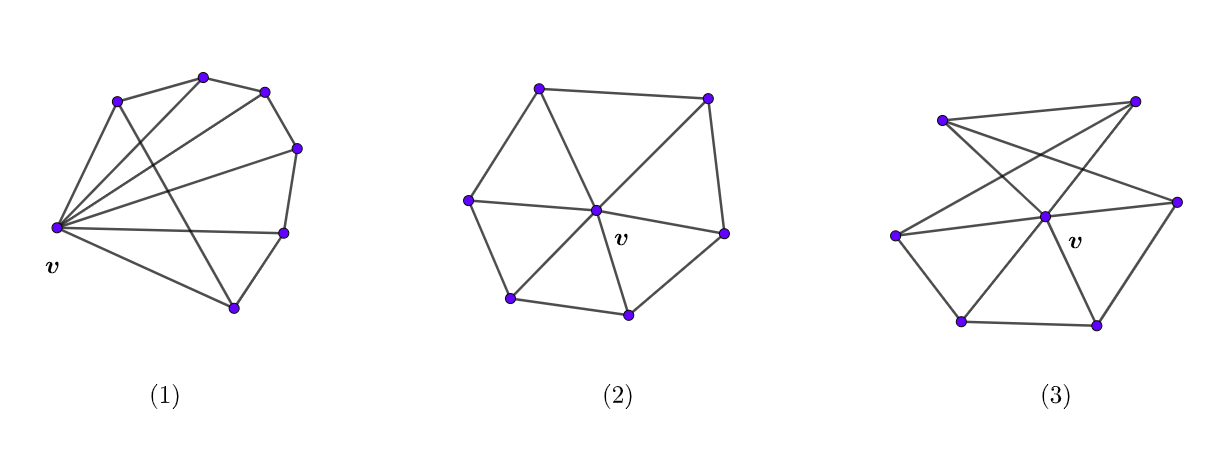
Assumet is a discrete one form. Deonote as the number of sign changes of the non-zero values of on the directed edges starting from , counted in counter-clockwise order. For a vertex , define the index of as . Similarly, for a non-degenerate face , the index of is , where is the number of sign changes of the non-zero values of on the three edges of , counted in counter-clockwise order.
The following theorem is a special case of the Index Theorem from [11], which is a discrete version of the Poincare-Hopf theorem for discrete one forms.
Theorem 3.1.
Let be a non-vanishing discrete one form on a triangulation of a torus. Then
Assume satisfies the assumption in Theorem 1.3, then for any unit vector we can naturally construct a discrete one form , by letting . If , a generic unit vector determines a non-vanishing discrete one form . Further, if and such constructed is non-vanishing, it is not difficult to show that all the indices of the vertices and faces are zero. Figure 2 illustrates how the neighborhood of looks like if it has positive, or zero, or negative index, for the case .
Based on this construction, we have
Lemma 3.2.
Given a triangulation of , denote as the triangle with three vertices , , and . There exists a non-vanishing discrete one form such that and . Moreover, all the indices of the vertices and faces of are zero.
Proof.
By the result of Colin de Verdière [5] and Hass-Scott [12], the space is not empty for any . Let be a geodesic triangulation in . Then it is not difficult to find a unit vector such that and . Define the discrete one form as . We can perturb the unit vector a little bit to make non-vanishing, and then such is satisfactory. ∎
3.2. The Proof of Theorem 1.3
Assume satisfies the assumption of Theorem 1.3, then there exists a unique extension such that the restriction of to every face is linear. Such is homotopic to , and is a geodesic triangulation in if and only if is a homeomorphism.
For any triangle , we say that is degenerate if is contained in some geodesic . If is not degenerate, we can naturally define its inner angle at . We claim that
-
(a)
is not degenerate for any , and
-
(b)
is locally a homeomorphism.
Then is a proper local homeomorphism, and thus is a covering map. Since is homotopic to the homeomorphism , is indeed a degree-one covering map, i.e., a homeomorphism.
3.2.1. Proof of Claim (a)
Assume there is some triangle such that is degenerate and hence contained in a geodesic . Here is assumed to be a closed geodesic, or a densely immersed complete geodesic. Let be the union of all triangles such that . Then is not the whole complex , otherwise is not homotopic to the homeomorphism . So, we can find a vertex . Denote as the star-neighborhood of in . Then is not in , but for some triangle in .
Let be a unit vector that is orthogonal to the geodesic , and define as . Then the vertex is non-degenerate with respect to , but the face is degenerate. Let be a discrete one form in Lemma 3.2 with the triangle and . Scale to make it very small so that has the same signs with on the non-degenerate edges of .
Notice that , or equivalently , otherwise all the edges connecting lie on a half-space, which contradicts to the assumption that is balanced. Since is degenerate in , taking the opposite instead of if necessary, we can assume that , and thus .
Noticing that is non-vanishing, we will derive a contradiction with the Index Theorem 3.1, by showing that the index of is nonpositive for any vertex and face.
If a face is degenerate in , then . If a face is non-degenerate in , then . In fact, the index of any non-degenerate face is zero.
If a vertex is degenerate in , then . If a vertex is non-vanishing, then . Since is balanced, .
If a vertex is non-degenerate but vanishing at some edges in , then
since adding can only introduce more sign changes.
3.2.2. Proof of Claim (b)
Since is -balanced, it is not difficult to show that for any vertex ,
and the equality holds if and only if all the edges around do not “fold” under the map . By the Gauss-Bonnet theorem,
So
for any vertex , and all the edges in do not fold. Thus, is a local homeomorphism.
References
- [1] Ethan D Bloch, Robert Connelly, and David W Henderson, The space of simplexwise linear homeomorphisms of a convex 2-disk, Topology 23 (1984), no. 2, 161–175.
- [2] Stewart S Cairns, Isotopic deformations of geodesic complexes on the 2-sphere and on the plane, Annals of Mathematics (1944), 207–217.
- [3] Erin Wolf Chambers, Jeff Erickson, Patrick Lin, and Salman Parsa, How to morph graphs on the torus, arXiv preprint arXiv:2007.07927 (2020).
- [4] Robert Connelly, David W Henderson, Chung Wu Ho, and Michael Starbird, On the problems related to linear homeomorphisms, embeddings, and isotopies, Continua, decompositions, manifolds, 1983, pp. 229–239.
- [5] Y Colin de Verdière , Comment rendre géodésique une triangulation d’une surface, L’Enseignement Mathématique 37 (1991), 201–212.
- [6] Olaf Delgado-Friedrichs, Equilibrium placement of periodic graphs and convexity of plane tilings, Discrete & Computational Geometry 33 (2005), no. 1, 67–81.
- [7] Clifford J Earle, James Eells, et al., A fibre bundle description of Teichmüller theory, Journal of Differential Geometry 3 (1969), no. 1-2, 19–43.
- [8] Jeff Erickson and Patrick Lin, Planar and toroidal morphs made easier, arXiv:2106.14086 (2021).
- [9] Michael Floater, One-to-one piecewise linear mappings over triangulations, Mathematics of Computation 72 (2003), no. 242, 685–696.
- [10] Michael S Floater, Mean value coordinates, Computer Aided Geometric Design 20 (2003), no. 1, 19–27.
- [11] Steven Gortler, Craig Gotsman, and Dylan Thurston, Discrete one-forms on meshes and applications to 3d mesh parameterization, Computer Aided Geometric Design (2006).
- [12] Joel Hass and Peter Scott, Simplicial energy and simplicial harmonic maps, arXiv preprint arXiv:1206.2574 (2012).
- [13] Yanwen Luo, Tianqi Wu, and Zhu Xiaoping, The deformation spaces of geodesic triangulations and generalized Tutte’s embedding theorem, arXiv:2105.00612 (2021).
- [14] William Thomas Tutte, How to draw a graph, Proceedings of the London Mathematical Society 3 (1963), no. 1, 743–767.