The comparison of methods for anisotropic flow measurements with the MPD Experiment at NICA

The Multi-Purpose Detector (MPD) at NICA collider has a substantial discovery potential concerning the exploration of the QCD phase diagram in the region of high net-baryon densities and moderate temperatures [1, 2]. The anisotropic collective flow, as manifested by the anisotropic emission of particles in the plane transverse to the beam direction, is one of the important observable sensitive to the properties of the strongly interacting matter: the equation of state (EOS), the specific shear and bulk viscosity [5]. It can be quantified by the Fourier coefficients $v_{n}$ in the expansion of the particles azimuthal distribution as: $dN/d\phi\propto 1+\sum_{n=1}2v_{n}\cos(n(\phi-\Psi_{n}))$, where $n$ is the order of the harmonic, $\phi$ is the azimuthal angle of particles of a given type, and $\Psi_{n}$ is the azimuthal angle of the $n$th-order event plane. In this work, we briefly review the available experimental results for the collision energy dependence of directed ($v_{1}$) and elliptic ($v_{2}$) flow and discuss the anticipated performance of MPD detctor for flow measurements at NICA energies. The directed flow ($v_{1}$) can probe the very early stages of the collision as it is generated during the passage time of the two colliding nuclei $t_{pass}=2R/(\gamma_{s}\beta_{s})$, where $R$ is the radius of the nucleus at rest, $\beta_{s}$ is the spectator velocity in c.m. and $\gamma_{s}$ the corresponding Lorentz factor, respectively. Both hydrodynamic and transport model calculations indicate that the $v_{1}$ signal of baryons, is sensitive to the equation of state [15] and predict a minimum in $dv_{1}/dy$ for the first order phase transition between hadronic matter and sQGP [15]. The recent results from the Beam Energy Scan (BES-I) program of STAR experiment at RHIC show a minimum at $\sqrt{s_{NN}}$ = 10-20 GeV for $dv_{1}/dy$ for protons and $\Lambda$ hyperons from midcentral Au+Au collisions [16]. Further progress in the area of model calculations and high-statistics differential measurements of $v_{1}$ is needed to find the reason for such non-monotonic behavior.
The published data from STAR experiment shows that $v_{2}(p_{T})$ for charged hadrons changes relatively little as a function of beam energy in the range $\sqrt{s_{\small{NN}}}$ = 11.5 - 62.4 GeV [13] and this may result from the interplay of the hydrodynamic and hadronic transport phase [17]. In the energy range $\sqrt{s_{\small{NN}}}$ = 11 - 2 GeV, the passage time $t_{pass}$ increases from 2 fm/c to 16 fm/c and the shadowing effects by the spectator matter start to play an important role for the generation of elliptic flow [18]. The left part of Fig. 1 shows $v_{2}(p_{T})$ of protons from 10-40% midcentral Au+Au collisions at $\sqrt{s_{NN}}=7.7$ GeV. Blue closed circles represent the published data from STAR experiment [13] and other symbols the results from event plane analysis of generated events from the current state of the art models of heavy-ion collisions: UrQMD [9, 10], SMASH [11], JAM [18], DCM-QGSM-SMM [20], AMPT [19] and hybrid vHLLE+UrQMD [17]. We found that, hybrid models with QGP formation: viscous hydro + hadronic cascade vHLLE+UrQMD model [17] or string melting version of AMPT [19] provide a relatively good description of $v_{2}(p_{T})$ of protons in Au+Au collisions at $\sqrt{s_{NN}}=7.7$ GeV and above. Pure hadronic transport models: UrQMD, SMASH, JAM and DCM-QGSM-SMM: generally underpredicts the $v_{2}$ values. However, the situation is different for Au+Au collisions at $\sqrt{s_{NN}}=4.5$ GeV, see right part of Fig. 1. Here, the pure hadronic transport system (as described by the UrQMD and SMASH models) appear to explain the measurements for $v_{2}(p_{T})$ of protons from the STAR experiment [14]. The high-statistics differential measurements of $v_{n}$ anticipated from the MPD experiment at NICA expected to provide valuable information about this parton-hadron transient energy domain.

The MPD detector system (Fig. 2, left) consists of a barrel part and two endcaps located inside the magnetic field. Time Projection Chamber (TPC) will be the central MPD tracking detector [2]. TPC will provide 3D tracking of charged particles, as well as the measurement of specific ionization energy loss dE/dx for particle identification for $|\eta|<$ 1.2. The TPC will be surrounded by a cylindrical barrel of the Time-of-Flight (TOF) detector with a timing resolution of the order of 50 ps. The combined system TPC+TOF will allow the efficient charged pion/kaon separation up to 1.5 GeV/c and protons/meson separation up to 2.5 GeV/c. The Forward Hadronic Calorimeter (FHCal), placed at 2$<|\eta|<$ 5, will be used for centrality determination as well for the reconstruction of event plane from the directed flow of particles.

In this work, we use cascade version of UrQMD model [9, 10] to simulate the heavy-ion collisions at NICA energies. In total, the sample of 120 M of minimum bias Au+Au events at $\sqrt{s_{NN}}=7.7$ and 11.5 GeV was used for directed and elliptic flow performance study using different methods of analysis. We used term ‘‘true’’ $v_{n}$ data for these results. At the next step, a sample of 10-25 M UrQMD minimum bias events, depending on the analysis, was used as an input for the full chain of the realistic simulations of the MPD detector subsystems’ based on the GEANT4 platform and reconstruction algorithms build in the MPDROOT. We named these $v_{n}$ results as the ‘‘reco’’ $v_{n}$ data. The main workflow for the analysis of identified charged hadrons with the reconstructed data is similar to the previous work [12]. For $K_{s}^{0}$ and $\Lambda$ particles analysis the secondary vertexes are reconstructed using a Kalman filtering algorithm based on the MpdParticle paradigm by combining identified decay products with set of topological cuts to optimize the signal [3].

In this section, we discuss how the event plane, scalar product and direct cumulant methods can be used for the measurements of anisotropic flow of the produced particles with MPD detector system at NICA.
The event plane method correlates azimuthal angle $\phi$ of each particle with the azimuthal angle $\Psi_{n}$ of event plane determined from the anisotropic flow itself [4]. The event flow vector ($Q_{n}$) and the azimuthal angle of event plane $\Psi_{n}$ can be defined for each harmonic, $n$, of the Fourier expansion by:

$\displaystyle Q_{n,x}=\sum\limits_{i}\omega_{i}\cos(n\varphi_{i}),\ Q_{n,y}=\sum\limits_{i}\omega_{i}\sin(n\varphi_{i}),\Psi_{n}=\frac{1}{n}\tan^{-1}\left(\frac{Q_{n,y}}{Q_{n,x}}\right),$

(1)

where the sum runs over all particles $i$ used in the event plane calculation, and $\varphi_{i}$ and $\omega_{i}$ are the laboratory azimuthal angle and the weight for the particle $i$. In this work we use two estimators for event plane: $\Psi_{1,\textrm{FHCal}}$ determined from the directed flow (n=1) of particles detected in the FHCal (2$<|\eta|<$ 5) and $\Psi_{2,\textrm{TPC}}$ determined from the elliptic flow (n=2) of produced particles detected in the TPC ($|\eta|<$ 1.5). The reconstructed $\Psi_{1,\textrm{FHCal}}$ can be used for the measuremented of directed (n=1) and elliptic (n=2) flow $v_{n}^{\Psi_{1,\text{FHCal}}}$ of the produced particles, detected in TPC. $\Psi_{2,\textrm{TPC}}$ allows to get an independent estimate of elliptic flow $v_{2}^{\Psi_{2,\text{TPC}}}$.

$$v_{2}^{\Psi_{2,\text{TPC}}}=\frac{\langle\cos(2(\phi_{i}-\Psi_{2,\text{TPC}}))\rangle}{R_{2}(\Psi_{2,\text{TPC}})},\>v_{n}^{\Psi_{1,\text{FHCal}}}=\frac{\langle\cos(n(\phi_{i}-\Psi_{1,\text{FHCal}}))\rangle}{R_{n}(\Psi_{1,\text{FHCal}})},$$

(2)

where $\rm R_{2}(\Psi_{2,\textrm{TPC}})$ and $\rm R_{n}(\Psi_{1,\textrm{FHCal}})$ represent the resolution of the event planes.

The right part of Fig. 3 shows the centrality dependence of $\rm R_{1}(\Psi_{1,\textrm{FHCal}})$ for the directed flow measurements with respect to $\Psi_{1,\textrm{FHCal}}$ plane for Au+Au collisions at $\sqrt{s_{NN}}$ = 4.5, 7.7 and 11 GeV. The results are based on the analysis of the fully reconstructed UrQMD events. The centrality dependence of $\rm R_{2}(\Psi_{2,\textrm{TPC}})$ and $\rm R_{2}(\Psi_{1,\textrm{FHCal}})$ for elliptic flow measurements in presented in Fig. 3.
In the scalar product method (SP) for differential flow $v_{n}(p_{T})$ measurements one uses the magnitude of the flow vector ($Q_{n}$) as a weight [4]:

$\displaystyle v_{n}^{\textrm{SP}}\{Q_{n,\textrm{TPC}}\}(p_{T})=\left\langle u_{n,i}(p_{T})Q_{n}^{*}\right\rangle/2\sqrt{\left\langle Q_{n}^{a}Q_{n}^{b*}\right\rangle},$

(3)

where $u_{n,i}$ is the unit vector of the $i^{th}$ particle (which is not included in $Q_{n}$ vector) and $a$ and $b$ are two subevents. If $Q_{n}$ vector is replaced by its unit vector, the scalar product method reduces to event plane method. In this work we present the $v_{2}$ results obtained by SP method.
For $K_{s}^{0}$ and $\Lambda$ particles, the $v_{n}^{SB}$ of selected sample contains both $v_{n}^{S}$ of the signal and the $v_{n}^{B}$ of background [6]. Therefore, the $v_{n}^{SB}$ is measured as a function of invariant mass ($M_{inv}$) and $p_{T}$:

$\displaystyle v_{n}^{SB}(M_{inv},p_{T})=v_{n}^{S}(p_{T})\frac{N^{S}(M_{inv},p_{T})}{N^{SB}(M_{inv},p_{T})}+v_{n}^{B}(M_{inv},p_{T})\frac{N^{B}(M_{inv},p_{T})}{N^{SB}(M_{inv},p_{T})}$

(4)

where $N^{S}(M_{inv},p_{T})$, $N^{B}(M_{inv},p_{T})$ and $N^{SB}(M_{inv},p_{T})$ are signal, background and total yields obtained for each $p_{T}$ interval from fits to the $K_{s}^{0}$ and $\Lambda$ invariant mass distributions, see left panels of Fig. 4. As an example the right panels of Fig. 4 illustrate the procedure of extraction of $v_{2}^{S}$. Values for $v_{2}^{S}$ signal for $K_{S}^{0}$ and $\Lambda$ particles were extracted via direct fit to the $v_{2}^{SB}(M_{inv})$ for each $p_{T}$ selection by Eq.4, see right panels of Fig. 4. That is, the background $v_{2}^{B}(M_{inv})$ was parametrized as a linear function of $M_{inv}$ and $v_{2}^{S}$ was taken as a fit parameter.

In the Q-cumulant method the two- and four- particle cumulants (for each harmonic $n$) can be calculated directly from a $Q_{n}$ vector, constructed using particles from the TPC acceptance $|\eta|<$ 1.5, $Q_{n}\equiv\sum_{i}^{M}exp\left(in\varphi_{i}\right)$ [7]:

	$$\displaystyle\left\langle 2\right\rangle_{n}=(\left|Q_{n}\right|^{2}-M)/M(M-1),$$		(5)
	$$\displaystyle\left\langle 4\right\rangle_{n}=\frac{\left|Q_{n}\right|^{4}+\left|Q_{2n}\right|^{2}-2\Re[Q_{2n}Q_{n}^{*}Q_{n}^{*}]-4(M-2)\left|Q_{n}\right|^{2}-2M(M-3)}{M(M-1)(M-2)(M-3)}.$$		(6)

M denotes the multiplicity in each event used in the analysis. The elliptic flow ($n=2$) can be defined via the Q-cumulant method as follows:

$\displaystyle v_{2}\{2\}=\sqrt{\left\langle\left\langle 2\right\rangle\right\rangle},\ v_{2}\{4\}=\sqrt[4]{2\left\langle\left\langle 2\right\rangle\right\rangle^{2}-\left\langle\left\langle 4\right\rangle\right\rangle},$

(7)

where the double brackets denote weighted average over all events. Equations for the $p_{T}$-differential elliptic flow can be found in [7].

Different methods of analysis can be affected by nonflow and flow fluctuations in different ways. The nonflow effects are mainly due to few particle correlations, not associated with the reaction plane: Bose-Einstein correlations, resonance decays, momentum conservation. In this work we discuss the comparison of different methods for elliptic flow only. The estimates of $v_{2}$ based on multi-particle cumulants have the advantage of significant reduction of contribution $\delta_{2}$ from nonflow effects: $\left\langle 2\right\rangle_{2}=v_{2}^{2}+\delta_{2},\ \left\langle 4\right\rangle_{2}=v_{2}^{4}+4v_{2}^{2}\delta_{2}+2\delta_{2}^{2}$. In order to suppress nonflow effects in $v_{2}$ results from two particle correlation methods one can use rapidity gaps between correlated particles. For $v_{2}\{\Psi_{2,\textrm{TPC}}\}$, $v_{2}^{\textrm{SP}}\{Q_{2,\textrm{TPC}}\}$, $v_{2}\{2\}$ we use the $\eta$-gap of $\Delta\eta>$ 0.1 between the two sub-events. The $v_{2}\{\Psi_{1,\textrm{FHCal}}\}$ results are expected to be less affected by nonflow due to larger $\eta$-gap between particles in TPC and FHCal: $\Delta\eta>$ 0.5.
Anisotropic flow can fluctuate event to event. We define the elliptic flow fluctuations by $\sigma_{v2}^{2}=\left\langle v_{2}^{2}\right\rangle-\left\langle v_{2}\right\rangle^{2}$. Here, the resulting flow signal, averaged over all events is denoted as $\left\langle v_{2}\right\rangle$. In the case of the Q-cumulants ($v_{2}\{2\}$ and $v_{2}\{4\}$), for a Gaussian model of fluctuations and in the limit $\sigma_{v2}\ll\left\langle v_{2}\right\rangle$ one can write [8, 4]:

$\displaystyle v_{2}\{2\}=\left\langle v_{2}\right\rangle+0.5\cdot\sigma_{v2}^{2}/\left\langle v_{2}\right\rangle,\ v_{2}\{4\}=\left\langle v_{2}\right\rangle-0.5\cdot\sigma_{v2}^{2}/\left\langle v_{2}\right\rangle.$

(8)

One of the important sources of $v_{2}$ flow fluctuations are participant eccentricity fluctuations in the initial geometry of the overlapping region of two colliding nuclei. Therefore, the $v_{2}\{\Psi_{1,\textrm{FHCal}}\}$ values are expected to be smaller than $v_{2}\{\Psi_{2,\textrm{TPC}}\}$ measured with respect to the participant plane $\Psi_{2,\textrm{TPC}}$ [8, 4]:

$\displaystyle v_{2}\{\Psi_{1,\textrm{FHCal}}\}\simeq\left\langle v_{2}\right\rangle,\ v_{2}\{\Psi_{2,\textrm{TPC}}\}\simeq\left\langle v_{2}\right\rangle+0.5\cdot\sigma_{v2}^{2}/\left\langle v_{2}\right\rangle.$

(9)

Figure 5 shows the $p_{T}$ dependence of $v_{2}$ of inclusive charged hadrons, charged pions and protons from 10-40% midcentral Au+Au collisions at $\sqrt{s_{NN}}=7.7$ GeV. Different symbols correspond to the the $v_{2}$ results obtained by event plane ($v_{2}\{\Psi_{1,\textrm{FHCal}}\}$, $v_{2}\{\Psi_{2,\textrm{TPC}}\}$), scalar product $v_{2}^{SP}\{Q_{2,\textrm{TPC}}\}$) and Q-cumulant ($v_{2}\{2\}$, $v_{2}\{4\}$) methods of analysis of events from UrQMD model. The ratios of $v_{2}$ signal to the $v_{2}\{2\}$ are shown on the bottom panels and show good agreement between $v_{2}$ results obtained by $v_{2}\{\Psi_{2,\textrm{TPC}}\}$, $v_{2}^{SP}\{Q_{2,\textrm{TPC}}\}$ and $v_{2}\{2\}$ methods. Both $v_{2}\{4\}$ and $v_{2}\{\Psi_{1,\textrm{FHCal}}\}$ methods give a smaller $v_{2}$ signal as one expect from elliptic flow fluctuations and nonflow effects.

The event plane ($v_{n}\{\Psi_{1,\textrm{FHCal}}\}$, $v_{n}\{\Psi_{2,\textrm{TPC}}\}$) and Q-cumulant ($v_{n}\{2\}$, $v_{n}\{4\}$) methods were implemented in the MPDROOT framework.

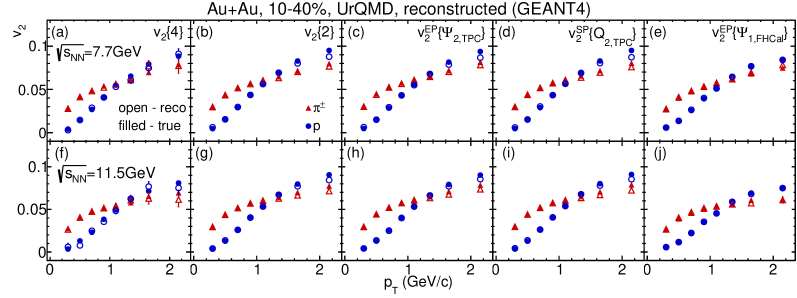
Figure 6 shows the $p_{T}$ dependence of $v_{2}$ of charged pions and protons from 10-40% midcentral Au+Au collisions at $\sqrt{s_{NN}}=7.7$ GeV (upper panels) and $\sqrt{s_{NN}}=11.5$ GeV (lower panels). The perfect agreement between $v_{2}$ results from the analysis of fully reconstructed ("reco") and generated ("true") UrQMD events is observed.

Figure 7 illustrates the MPD detector system’s performance for the $p_{T}$ differential directed and elliptic flow measurements of $K_{S}^{0}$ and $\Lambda$ particles from 10-40% midcentral Au+Au collisions at $\sqrt{s_{NN}}=11$ GeV. The results were obtained from the event plane analysis of 25M minimumbias fully reconstructed UrQMD events using the invariant-mass fit method, illustrated in the Fig. 4.

Figure 8 shows the MPD detector system’s performance for the directed $v_{1}$ (left) and elliptic $v_{2}$ (right) flow measurements of charged pions and protons from 10-40% midcentral Au+Au (open symbols) and Bi+Bi (filled symbols) collisions at $\sqrt{s_{NN}}=7.7$ GeV. The $v_{n}$ results were obtained by event plane method: using the first order event plane ($\Psi_{1,\textrm{FHCal}}$) from FHCal. In both cases, one can see the expected small difference between results for the event plane resolution and $v_{n}$ between two colliding systems.

The MPD detector system’s performance for the diected ($v_{1}$) and elliptic $v_{2}$ flow measurements of charged pions, protons, $K_{s}^{0}$ and $\Lambda$ particles is studied with Monte-Carlo simulations using collisions of Au+Au and Bi+Bi ions employing UrQMD heavy-ion event generator. We have shown how the various experimental measures of elliptic flow are affected by fluctuations and nonflow at NICA energies. The detailed comparison of the $v_{n}$ results obtained from the analysis of the fully reconstructed data and generator-level data allows to conclude that MPD system will allow reconstruction of $v_{n}$ coefficients with high precision.

This work is supported by the RFBR according to the research project No. 18-02-40086, the European Union‘s Horizon 2020 research and innovation program under grant agreement No. 871072, by the Ministry of Science and Higher Education of the Russian Federation, Project "Fundamental properties of elementary particles and cosmology" No 0723-2020-0041.