The bifurcation structure within robust chaos for two-dimensional piecewise-linear maps.
Abstract
We study two-dimensional, two-piece, piecewise-linear maps having two saddle fixed points. Such maps reduce to a four-parameter family and are well known to have a chaotic attractor throughout open regions of parameter space. The purpose of this paper is to determine where and how this attractor undergoes bifurcations. We explore the bifurcation structure numerically by using Eckstein’s greatest common divisor algorithm to estimate from sample orbits the number of connected components in the attractor. Where the map is orientation-preserving the numerical results agree with formal results obtained previously through renormalisation. Where the map is orientation-reversing or non-invertible the same renormalisation scheme appears to generate the bifurcation boundaries, but here we need to account for the possibility of some stable low-period solutions. Also the attractor can be destroyed in novel heteroclinic bifurcations (boundary crises) that do not correspond to simple algebraic constraints on the parameters. Overall the results reveal a broadly similar component-doubling bifurcation structure in the orientation-reversing and non-invertible settings, but with some additional complexities.
1 Introduction
Complex dynamics are caused by nonlinearity, and many physical systems involve an extreme form of nonlinearity: a switch. Examples include engineering systems with relay or on/off control which involve distinct modes of operation [5, 23, 43]. Mathematical models of systems with switches are naturally piecewise-smooth, where different pieces of the equations correspond to different positions of a switch.
Piecewise-smooth maps arise as discrete-time models of systems with switches [16, 33] and as Poincaré maps or stroboscopic maps of continuous-time models [7]. For multi-dimensional piecewise-smooth maps there are many abstract ergodic theory results stating that if an attractor satisfies certain properties (e.g. expansion) then it is chaotic in a certain sense (e.g. has an SRB measure) [6, 30, 35, 42, 45]. This paper in contrast provides explicit results for a physically-motivated family of maps. We study the four-parameter family
| (1.1) |
where . This is known as the two-dimensional border-collision normal form (BCNF) [26]. This family provides leading-order approximations to border-collision bifurcations where a fixed point of a piecewise-smooth map collides with a switching manifold as parameters are varied [36]. As such (1.1) can be used to capture the change in dynamics as parameters are varied to pass through border-collision bifurcations. In this regards it has been applied to mechanical oscillators with stick-slip friction [41], DC/DC power converters [47], and various models in economics [33]. We stress that unlike Poincaré maps of smooth invertible flows, the piecewise-smooth maps arising from these applications are mostly non-invertible. We distinguish four generic cases based on the signs of the determinants and :
- •
- •
- •
- •
Despite its apparent simplicity (1.1) has an incredibly complex bifurcation structure that remains to be fully understood [2, 10, 38, 40, 47]. The most significant bifurcations are those at which the attractor splits into pieces. In [12] we used renormalisation to uncover an infinite sequence of codimension-one bifurcations. However, this only accommodated the orientating-preserving setting of Banerjee et al [4]. In this paper we identify similar sequences of bifurcations in the orientation-reversing and non-invertible parameter regimes. Again we use renormalisation to find bifurcations, but now this approach misses some bifurcations. For this reason we combine the analytical framework with brute-force numerical simulations that compute the number of connected components from the behaviour of forward orbits.
The remainder of this paper is organised as follows. We start in §2 by reviewing the bifurcation structure of one-dimensional piecewise-linear maps (skew tent maps) and how this structure can be generated through renormalisation. This corresponds to the BCNF in the special case , and it is helpful to view the bifurcation structures described in later sections as extensions or perturbations from the structure that arises in one dimension. Then in §3 we review the parameter region where the BCNF has two saddle fixed points. We describe special points on the stable and unstable manifolds of the fixed points whose relation to one another can be used to characterise the occurrence of homoclinic and heteroclinic bifurcations where the attractor is destroyed. In §4 we introduce the renormalisation scheme and describe some basic aspects of this scheme that hold for all values of and . Then in §5 we summarise the results of [12] for the orientation-preserving setting.
Next in §6 we describe an algorithm for numerically determining the number of connected components of attractor. The algorithm outputs the greatest common divisor of a set of iteration numbers required for an orbit to return close to its starting point. The algorithm is effective when the components of attractor are not too close to one another and the dynamics on the attractor is ergodic. Applied to the orientation-preserving setting it reproduces the bifurcation structure obtained by renormalisation.
In §7, §8, and §9 we study the orientation-reversing and non-invertible cases and explain why the same renormalisation scheme should be expected to work in these settings. Formal proofs are beyond the scope of this study because, as evident from [12], these require a detailed analysis of the four-dimensional nonlinear renormalisation operator, plus will involve additional complexities because now stable period-two and period-four solutions are possible. Also if and then the bifurcations that destroy the attractor are different and more difficult to characterise. In §10 we describe a special case unique to the non-invertible settings where the dynamics reduces to one dimension. Concluding remarks are provided in §11.
2 Skew tent maps
With the -dynamics of (1.1) is trivial and the -dynamics reduces to
| (2.1) |
This is a two-parameter family of skew tent maps. For any values of the parameters and for which (2.1) has an attractor, this attractor is unique. Fig. 1 shows typical examples of the attractor using and with which (2.1) is piecewise-expanding, so the attractor is chaotic in a strict sense by the results of Lasota and Yorke [21] and Li and Yorke [22]. Fig. 1 shows typical examples of the chaotic attractor. In panel (a) the attractor is the interval whose endpoints are the first and second iterates of the switching value . In panel (b) the attractor is a disjoint union of four intervals whose endpoints are the first through eighth iterates of .
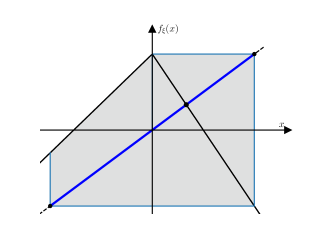 |
 |
| (a) . | (b) . |
For all values of and the nature of the attractor is well understood [24, 27, 39]. Fig. 2 shows how the part of the -plane that is relevent to us divides into regions according to the number of intervals that comprise the attractor. In the top-left region labelled the map has a stable period-two solution. This solution has one point in the left half-plane and one point in the right half-plane, so is termed an -cycle. This region is bounded by the curve , where
| (2.2) |
which is where the -cycle loses stability by attaining a stability multiplier of . The boundary in the lower-right part of the figure is a homoclinic bifurcation where maps in two iterations to the fixed point of (2.1) in . This occurs on the curve , where
| (2.3) |

As shown by Ito et al [17, 18] the remaining boundaries can be identified through renormalisation as follows. Suppose there exists an interval neighbourhood of that maps into , then, on the second iteration, back into . In this case the restriction of the second iterate of (2.1) to is piecewise-linear with two pieces. The piece corresponds to iterates with symbolic itinerary and has slope , while the piece corresponds to iterates with symbolic itinerary and has slope . Thus the second iterate of (2.1) on is conjugate to (2.1) with in place of and in place of . This corresponds to the substitution rule , and induces the renormalisation operator
| (2.4) |
By using the preimages of the homoclinic bifurcation boundary we define the sequence of regions
| (2.5) |
shown in Fig. 2. These are non-empty for all and converge to as . In the attractor consists of one interval:
Theorem 2.1.
For any with , the interval is the unique attractor.
A simple proof of Theorem 2.1 can be found in Veitch and Glendinning [44]. The condition is needed because for some and the attractor is periodic. This condition can be weakened but this is not needed for our purposes.
To characterise the attractor in the other regions we first make the following observation that follows simply from the definitions of and .
Proposition 2.2.
If with , then .
Thus if then . Theorem 2.1 can be applied at this parameter point because any point below maps under to the right of . Moreover, the above conjugacy can be shown to hold under all applications of , see Ito et al [17, 18], thus the -iterate of (2.1) has an interval attractor. The images of this interval under (2.1) give disjoint intervals and hence the following result.
Theorem 2.3.
If with , then (2.1) has a unique attractor comprised of disjoint intervals.
3 Two-dimensional piecewise-linear maps with two saddle fixed points
We now return to the BCNF (1.1) with non-zero values of and . In this section we identify two saddle fixed points and compute some important points on their stable and unstable manifolds.
Motivated by Banerjee et al [4] we focus on the following subset of four-dimensional parameter space:
| (3.1) |
It is a simple exercise to show that is the set of all parameter values for which (1.1) has two saddle fixed points [11]. These fixed points are
| (3.2) | ||||
| (3.3) |
where is in the open right half-plane , and is in the open left half-plane . Let
| (3.4) |
denote the Jacobian matrices associated with and respectively. With the matrix has eigenvalues and , while has eigenvalues and .
Since and are saddles their stable and unstable manifolds are one-dimensional, and since the map is piecewise-linear these manifolds are piecewise-linear. Their stable manifolds and have kinks on the switching manifold and at preimages of these points, while their unstable manifolds and have kinks on the image of the switching manifold and at images of these points. For instance, as we grow outwards from , in one direction its first kink occurs at the point
| (3.5) |
on , see Fig. 3. Similarly as we grow outwards from , in one direction its first kink occurs at
| (3.6) |
A third point will be also central to our later calculations. This point is where , when grown outwards from to the right, first intersects at a point with and is given by
| (3.7) |
Fig. 3 indicates the points , , and for four example phase portraits, one for each of the four cases for the signs of and . Notice if (upper plots) the left half-plane maps to the upper half-plane, while if (lower plots) the left half-plane maps to the lower half-plane. Similarly if (left plots) the right half-plane maps to the lower half-plane, while if (right plots) the right half-plane maps to the upper half-plane.
 |
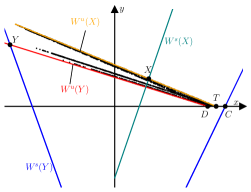 |
| (a) | (b) |
 |
 |
| (c) | (d) |
4 Renormalisation in two dimensions
In §2 we saw that renormalisation based on the substitution rule explains the bifurcation structure of the one-dimensional skew tent map family shown in Fig. 2. For the BCNF (1.1) this rule defines the renormalisation operator
| (4.1) |
The four values on the right-hand side of (4.1) are the traces and determinants of and . In this section we extend the basic aspects of this renormalisation operator beyond the orientation-preserving setting of our earlier work [12]. Renormalisation has also been applied to subfamilies of (1.1) by Pumariño et al [31, 32] and Ou [29].
We first identify the subset of where the BCNF has a stable -cycle. Generalising (2.2) we have that the matrix (whose eigenvalues are the stability multipliers of the -cycle) has an eigenvalue when , where
| (4.2) |
If this eigenvalue is greater than . For the -cycle to be stable we also need , where , so we define
| (4.3) |
Proposition 4.1.
If then has an asymptotically stable -cycle.
Proof.
Let and be the trace and determinant of . All eigenvalues of have modulus less than if and only if and . Certainly by assumption, and by the definition of ; also
by the definition of .
The composed map is affine with unique fixed point
Let
Notice the first component of is negative while the first component of is positive, thus is a periodic solution of . Above we showed all eigenvalues of have modulus less than , hence is asymptotically stable. ∎
If the -cycle is unstable. This is always the case if :
Proposition 4.2.
If with then .
Proof.
Suppose with . If then
using the definition of in the first inequality. If instead or then because , so
∎
Now we show that if then the renormalisation operator produces another instance of the BCNF in .
Proposition 4.3.
If and then .
Proof.
Let , let , and let and be as in the proof of Proposition 4.1; then . Observe because , and because , thus . Also because and , and , by assumption, thus . ∎
Now let
| (4.4) |
be the set of all points that map to the right half-plane. On the second iterate has only two pieces:
| (4.5) |
For any (4.5) is affinely conjugate to . Specifically on , where
| (4.6) |
is the necessary change of coordinates. As an example Fig. 4-a shows (in the phase space of ) at the parameter point
| (4.7) |
while Fig. 4-b shows (in the phase space of ). The map has an invariant set , so, as shown below, is an invariant set of . Moreover, the union of and its image under is an invariant set of . It is easy to infer the number of connected components in this set from the number of connected components of , and this forms the basis of the renormalisation scheme.
 |
 |
| (a) | (b) |
Proposition 4.4.
Suppose is an invariant set of . Then is an invariant set of . Moreover, if then the number of connected components of is twice the number of connected components of .
Proof.
Let . Since ,
| (4.8) |
But and , so the right-hand side of (4.8) is . Thus is invariant under , so is invariant under . Since is invertible the number of components of is the same as the number of components of . If then also has this many components (for otherwise would not be possible because is continuous). ∎
5 The orientation-preserving case
In this section we summarise the main results of our earlier work [12]. Let
| (5.1) |
be the subset of for which the BCNF is orientation-preserving. In a large part of an attractor is destroyed when the points and (shown in Fig. 3-a) coincide. This is a homoclinic bifurcation, or homoclinic corner [37], where the stable and unstable manifolds of the fixed point attain non-trivial intersections. Straight-forward algebra gives
| (5.2) |
where
| (5.3) |
Fig. 5 shows an example. In panel (a) the closure of the unstable manifold of ,
| (5.4) |
is a chaotic attractor. As the value of is increased the attractor approaches the point and is destroyed at when , panel (b). At larger values of almost all forward orbits diverge, panel (c).



In some parts of the attractor is not destroyed at . This occurs when it does not approach as ; instead the attractor is destroyed in a subsequent heteroclinic bifurcation involving a period-three solution [13].
With we have , so in this case the bifurcation surface reduces to the homoclinic bifurcation of the skew tent map family. This motivates the definition
| (5.5) |
for all . The constraint is not needed in this definition because, by Proposition 4.2, if then automatically . As shown in [12] the regions are disjoint and cover the subset of for which . These regions are more difficult to visualise than those in §2 because they are four-dimensional. Fig. 6 shows two-dimensional slices of parameter space defined by fixing and . In these slices only finitely many are visible because as they converge to (a fixed point of ). The following result describes for parameter values in . For a proof see [12].
 |
 |
| (a) . | (b) . |
Theorem 5.1.
For any ,
-
(i)
is bounded, connected, and invariant under ,
-
(ii)
has a positive Lyapunov exponent, and
-
(iii)
if there exists a forward invariant set with non-empty interior such that
(5.6)
Item (ii) says is chaotic in the sense of having a positive Lyapunov exponent. We believe it satisfies Devaney’s definition of chaos throughout , but have only proved this in a subset of [13]. Item (iii) says is a Milnor attractor. We believe the condition is unnecessary and is in fact a topological attractor throughout .
To understand the dynamics in all other regions we use the renormalisation operator . The following result follows simply from Proposition 4.3 and the definition of .
Proposition 5.2.
If with , then .
So if then where the attractor is connected. Then by applications of Proposition 4.4, has an attractor with connected components as long as the assumptions of Proposition 4.4 are satisfied in each application. This is indeed the case, as shown in [12] through a series of careful calculations, and gives the following result.
Theorem 5.3.
For any with , has a chaotic Milnor attractor with exactly connected components.
For example Fig. 4-a uses belonging to so the attractor has two connected components, as shown. The renormalisation allows us to say more about this attractor. Specifically each piece of the attractor is an affine transformation of the one-component attractor of (1.1) with belonging to , shown in Fig. 4-b.
6 A component counting algorithm.
To support an extension of the theoretical results of §5 to the orientation-reversing and non-invertible settings, we perform numerical simulations to count the number of connected components of the attractors. There are many methods for estimating the number of connected components of a set from a finite collection of points in . For example Robins et al [34] connect all pairs of points in with line segments to form a complete graph, then base their estimation from a minimal spanning tree. In our setting is generated by a map, so it is more effective to use a method that utilises the dynamics. For this reason we compute the number of components as the greatest common divisor of a certain set of computed values. This method originates with Eckstein [9] and is described by Avrutin et al [1]. As explained at the end of this section, the effectiveness of the method relies on the following result.
Lemma 6.1.
Suppose a compact invariant set of a continuous map has connected components, and has an orbit that visits all components. Then the components can be labelled as such that , and .
Thus the components of are ordered cyclically, each has one ‘predecessor’ and one ‘successor’. The following proof is adapted from [1, 9]. It uses a small quantity to avoid reference to path-connectedness.
Proof of Lemma. 6.1.
By assumption there exists whose forward orbit enters all components. Let be the component containing . Suppose for a contradiction contains points in two different components, and . Since is compact there exists such that any point in and any point in are at least a distance apart. Since is connected for any there exist with such that and . But so this is not possible because is continuous, hence is a subset of one component of . This component is not (because then would be forward invariant and the forward orbit of could not reach the other components), let us call it . So .
By a similar argument is a subset of one component, and if this component is neither nor , call it . Inductively we obtain with . Also is a subset of one component.
But is invariant, meaning . Thus , and further , and as required. ∎
Now fix and suppose has an attractor with connected components. To compute the value , which is assumed to be unknown to us a priori, the algorithm proceeds as follows. Fix (we used or ) and (we used ) and let . Choose some initial point assumed to be in the basin of attraction of and iterate it under a reasonably large number of times (we used iterations) to remove transient dynamics and obtain a point in , or extremely close to , call it . Iterate further, and for all evaluate the distance (Euclidean norm in ) between and . If this distance is less than , append the number to the set . Finally evaluate the greatest common divisor of the elements in — this is our estimate for the value of .
For example using , as in Fig. 4-a, the algorithm generated a set of numbers
whose elements have greatest common divisor (and indeed at this parameter point the attractor has two components).
Fig. 6 shows the output of this algorithm over a grid of parameter points. The results show excellent agreement to the theory described in §5. For example parameter points where the greatest common divisor of the numbers in is two have boundaries indistinguishable from the true bifurcation boundaries and .
Two principles underlie the effectiveness of the algorithm. First, if the distance between any two components of is greater than , then implies that and belong to the same component of (assuming ). By Lemma 6.1 this is only possible if is a multiple of . Thus the elements of are all multiples of .
Second, assuming is ergodic on , the set of all giving will not be expected to share a multiple larger than . This is because ergodicity implies the dynamics of on any component are well mixed (see Haydn et al [15] and references within for theory on the probability distribution of the values of when is small). In our setting seems to generate large enough sets to ensure the greatest common divisor of the numbers in is , instead a multiple of . One can also modify the algorithm, as described in [1, 9], to search for a close return to several reference points, instead of the single point .
7 The orientation-reversing case
Let
| (7.1) |
be the subset of for which the BCNF is orientation-reversing. As shown originally by Misiurewicz [25], the closure of the unstable manifold of the fixed point can be a chaotic attractor. This attractor contains the point , as shown in Fig. 3-d, so under parameter variation is destroyed when . This is a heteroclinic bifurcation beyond which the unstable manifold of is unbounded. From the formulas (3.5) and (3.7) we obtain
| (7.2) |
where
| (7.3) |
An example illustrating the destruction of the attractor is shown in Fig. 7. As the value of is increased the attractor is destroyed when at .



Analogous to the orientation-preserving case, if the expression reduces to . Thus the heteroclinic bifurcation reduces to the familiar homoclinic bifurcation of the skew tent map family in the limit .
We are now ready to subdivide into regions based upon the renormalisation operator , (4.1). But implies , so we again use the preimages of under to define the region boundaries. Specifically we let
| (7.4) | ||||
| (7.5) |
Fig. 8 shows these regions in two typical two-dimensional slices of parameter space. Unlike in the orientation-preserving setting we need to impose in these regions so that they don’t overlap where a stable -cycle exists.
 |
 |
| (a) . | (b) . |
We conjecture that throughout the map has a unique chaotic attractor with one connected component equal to the closure of the unstable manifold of , as in Fig. 7-a. In earlier work [11] we proved this to be true on a subset of . In the special case and of the Lozi family of maps, the constraint reduces to equation (3) of Misiurewicz [25].
Proposition 7.1.
If with , then .
This suggests that for any the BCNF has an attractor with connected components. For example
| (7.6) |
belongs to and indeed the attractor shown in Fig. 9-a appears to have two connected components. One component belongs to so Proposition 4.4 applies. Hence this component is an affine transformation of the attractor of (1.1) at the parameter point that belongs to , and we know its attractor has one component by Theorem 5.1.
Fig. 8 shows that our conjecture is supported by the output of the greatest common divisor algorithm. The boundaries of the closely approximate the places with the value of the greatest common divisor changes. This value changes slightly above because here the two components of the attractor are very close and is insufficient to detect this difference. Also has pixels erroneously corresponding to more than one component because here the attractor is relatively large and iterations are insufficient for the algorithm to consistently obtain a greatest common divisor of .
8 The non-invertible case , .
Here we study the parameter region
| (8.1) |
where (1.1) is non-invertible. In this region an attractor of (1.1) can be destroyed by crossing the homoclinic bifurcation or the heteroclinic bifurcation . This is because near these boundaries the attractor contains the point and is close to the point so is destroyed when one of these points collides with . For example in Fig. 10 lies to the left of , so the attractor is destroyed when , i.e. when . In contrast in Fig. 11 lies to the right of , so the attractor is destroyed when , i.e. when . For this reason we define
| (8.2) |
and
| (8.3) |
for all . Two-dimensional slices of these regions are shown in Fig. 12. We conjecture that throughout the first region the BCNF has a unique chaotic attractor with one connected component, and this is supported by the numerical results shown in Fig. 12. To explain the dynamics in the remaining regions we use the following analogy to Propositions 5.2 and 7.1. Here, however, the result is not trivial, so we provide a proof.






 |
 |
| (a) . | (b) . |
Proposition 8.1.
If with , then .
Proof.
Choose any with and write as in the proof of Proposition 4.3. By Proposition 4.3 we have . Further, because and . Also and . Finally where , , , and . By substituting and (true because ) we obtain (after simplification)
So if then (because ). If instead then because , so again by Proposition 4.2 applied to the parameter point . ∎
Proposition 8.1 suggests that throughout each with the BCNF has an attractor with exactly connected components, and Fig. 12 supports this conjecture. Fig. 13-a provides an example using the parameter point
| (8.4) |
which belongs to . The attractor has two pieces, one of which belongs to , so as above this piece is an affine transformation of the attractor of shown in Fig. 13-b.
9 The non-invertible case ,
It remains for us to consider
| (9.1) |
where (1.1) is non-invertible. In this region the attractor is usually destroyed before the boundaries and in a heteroclinic bifurcation that cannot be characterised by an explicit condition on the parameter values. This occurs when the attractor contains points on that lie to the right of and and is destroyed when its right-most point collides with .
Fig. 14 shows an example. In panel (a) the attractor is the closure of the unstable manifold of . As we grow the unstable manifold outwards from it develops points on that lie further and further to the right, but not beyond . This occurs as a consequence of the geometric configuration afforded by being orientation-preserving and being orientation-reversing. As the value of is increased the attractor is destroyed when its right-most point collides with , panel (b). With a slightly value of , panel (c), typical forward orbits diverge even though and still lie to the left of . Fig. 15 provides a second example. Here the parameter values are such that and are switched around but the attractor is destroyed in the same way.






 |
 |
| (a) . | (b) . |
Fig. 16 shows the results of numerical simulations applied to two slices of . The white areas just to the left of and correspond to the phenomenon that we have just described. These areas are bounded on the left by a curve of heteroclinic bifurcations. Since we cannot identify this curve with hand calculations, it is natural to attempt to compute the curve numerically with numerical continuation methods. However, we do not show the result of such a computation because we suspect this curve highly irregular, e.g. non-differentiable at infinitely many points, as explained by Osinga [28].
In each plot in Fig. 16 the attractor does in fact persist up to where the boundaries and meet. This is because on the curve the right-most point of the attractor is and , which are equal. Also near the top of Fig. 16-a the attractor persists slightly beyond because here the attractor fails to approach so is not destroyed when at .
Despite the extra complexities in it still appears that renormalisation is helpful for explaining the bifurcation structure. Let
| (9.2) |
Based on Fig. 16 we conjecture that for any , if (1.1) has an attractor then this attractor is chaotic with one connected component. Now let
| (9.3) |
Unlike in previous sections here we have included the extra constraint so that the do not include the region , defined to be where (1.1) has a stable period-four solution with symbolic itinerary . This region is visible in Fig. 16-b and shown more clearly in the magnification, Fig. 17. Note that here we do not show the result of the numerics because the component counting algorithm does not work efficiently close to the curve . The following result is a trivial consequence of our definitions.
Proposition 9.1.
If with , then .

Based on this we conjecture that for any with the map (1.1) has a chaotic attractor with exactly connected components, and this is supported by the numerics in Fig. 16. Fig. 18-a shows the attractor of (1.1) for a typical parameter point in , specifically
| (9.4) |
As expected it has two connected components, one of which is contained in , and both of which are affine transformations of the single-component attractor of (1.1) with shown in Fig. 18-b.
10 Reduction to one dimension
Finally we address a novelty of the non-invertible settings. In these settings the stable eigenvalues and have the same sign (they are both positive if and , and both negative if and ), so it is possible for them to be equal. From the formulas (3.5) and (3.6) for the points and we have
| (10.1) |
Thus and coincide when the stable eigenvalues are equal. Thus the boundaries and , where and respectively, intersect where , and this is evident in Figs. 12 and 16. Also for each the boundaries and intersect where .
We now show that if then the pertinent dynamics reduces to one dimension, as in Fig. 19.
 |
 |
| (a) | (b) corresponding cobweb diagram |
Proposition 10.1.
If with and , then is forward invariant on the line segment from to . Moreover, on this segment is conjugate to the skew tent map
| (10.2) |
on .
Proof.
The line segment from to is
because putting gives by (3.5), while putting gives which is identical to (since and ). If then
while if then
and the result follows. ∎
Notice and , which corresponds in Fig. 2 to a point in some , with . Thus, with this value of , the attractor of the skew tent map (10.2) is comprised of disjoint intervals. Consequently the attractor of is comprised of disjoint line segments. Places where the value of changes can be computed by solving for where in Fig. 2. We computed these points numerically and have plotted them as black dots in Figs. 12 and 16 from which we see that, as expected, these points are where and . In this way the conjectures in §8 and §9 on the number of connected components of the attractors are confirmed in the special codimension-one scenario that the stable stability multipliers associated with and are equal.
11 Discussion
It has long been known that symmetric tent maps and skew tent maps readily admit attractors with connected components, and that for any given slopes for the two pieces of the map the value of can be determined through renormalisation. Here we have shown how this can be realised for two-dimensional maps and uncovered some novel complexities relating to the possibility of stable period-two and period-four solutions. We have also shown how the attractor can be destroyed at heteroclinic bifurcations (boundary crises) that cannot be characterised algebraically.
It remains to verify the conjectures in §7–§9 on the number of connected components of the attractor in the various parameter regions we have defined. We feel this should be possible by following the methodology used in [12] but suspect it will be a substantial undertaking. Chaos in higher-dimensional piecewise-linear maps has applications to cryptography [19], and it remains to see what aspects of the renormalisation can be described for the -dimensional border-collision normal form [36] with no restriction on . Also it remains to see if renormalisation schemes based on other symbolic substitution rules can be used to explain parameter regimes where (1.1) has attractors with other numbers of components, e.g. three components, as described in [14].
Finally we note that Proposition 10.1 provides a rare example of dimension reduction in a piecewise-smooth setting. Dimension reduction is core element of smooth bifurcation theory whereby centre manifolds allow us to explain the dynamics of high dimensional systems with low dimensional equations [20]. In general the bifurcation theory of piecewise-smooth systems is hampered by an inability to do this usually centre manifolds usually do not exist [7]. It remains to see how far Proposition 10.1 can be generalised to help us understand border-collision bifurcations involving two eigenvalues that are identical, or are nearly identical.
Acknowledgements
This work was supported by Marsden Fund contracts MAU1809 and MAU2209 managed by Royal Society Te Apārangi.
References
- [1] V. Avrutin, B. Eckstein, and M. Schanz. On detection of multi-band chaotic attractors. Proc. R. Soc. A, 463(2081):1339–1358, 2007.
- [2] S. Banerjee and C. Grebogi. Border collision bifurcations in two-dimensional piecewise smooth maps. Phys. Rev. E, 59(4):4052, 1999.
- [3] S. Banerjee and G.C. Verghese, editors. Nonlinear Phenomena in Power Electronics. IEEE Press, New York, 2001.
- [4] S. Banerjee, J.A. Yorke, and C. Grebogi. Robust chaos. Phys. Rev. Lett., 80(14):3049–3052, 1998.
- [5] R.S. Burns. Advanced Control Engineering. Butterworth-Heinemann, Oxford, 2001.
- [6] J. Buzzi. Absolutely continuous invariant measures for generic multi-dimensional piecewise affine expanding maps. Int. J. Bifurcation Chaos, 9(9):1743–1750, 1999.
- [7] M. di Bernardo, C. Budd, A.R. Champneys, and P. Kowalczyk. Piecewise-smooth dynamical systems: theory and applications, volume 163. Springer-Verlag, New York, 2008.
- [8] M. di Bernardo and C.K. Tse. Chaos in power electronics: An overview. Chaos in circuits and systems, pages 317–340, 2002.
- [9] B. Eckstein. Bandcounter: counting bands of multiband chaotic attractors. Universitätsbibliothek der Universität Stuttgart, 2006.
- [10] H.O. Fatoyinbo and D.J.W. Simpson. A synopsis of the non-invertible, two-dimensional, border-collision normal form with applications to power converters. Int. J. Bifurcation Chaos, 33(8):2330019, 2023.
- [11] I. Ghosh, R.I. McLachlan, and D.J.W. Simpson. Robust chaos in orientation-reversing and non-invertible two-dimensional piecewise-linear maps. arXiv preprint arXiv:2307.05144, 2023.
- [12] I. Ghosh and D. J. W. Simpson. Renormalization of the two-dimensional border-collision normal form. Int. J. Bifurcation Chaos, 32(12):2250181, 2022.
- [13] I. Ghosh and D.J.W. Simpson. Robust Devaney chaos in the two-dimensional border-collision normal form. Chaos, 32(4):043120, 2022.
- [14] P. A. Glendinning and D. J. W. Simpson. Robust chaos and the continuity of attractors. Trans. Math. Appl., 4(1):tnaa002, 2020.
- [15] N. Haydn, Y. Lacroix, and S. Vaienti. Hitting and return times in ergodic dynamical systems. Ann. Probab., 33(5):2043–2050, 2005.
- [16] B. Ibarz, J.M. Casado, and M.A.F. Sanjuán. Map-based models in neuronal dynamics. Phys. Rep., 501:1–74, 2011.
- [17] S. Ito, S. Tanaka, and H. Nakada. On unimodal linear transformations and chaos. Proc. Japan Acad., 55, Ser. A(71):231–236, 1979.
- [18] S. Ito, S. Tanaka, and H. Nakada. On unimodal linear transformations and chaos II. Tokyo J. Math., 2(2):241–259, 1979.
- [19] L. Kocarev and S. Lian, editors. Chaos-Based Cryptography: Theory, Algorithms and Applications. Springer, New York, 2011.
- [20] Y.A. Kuznetsov. Elements of applied bifurcation theory, volume 112. Springer, 2004.
- [21] A. Lasota and J.A. Yorke. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc., 186:481–488, 1973.
- [22] T. Li and J.A. Yorke. Ergodic transformations from an interval into itself. Trans. Amer. Math. Soc., 235(1):183–192, 1978.
- [23] D. Liberzon. Switching in Systems and Control. Birkhauser, Boston, 2003.
- [24] Yu.L. Maistrenko, V.L. Maistrenko, and L.O. Chua. Cycles of chaotic intervals in a time-delayed Chua’s circuit. Int. J. Bifurcation Chaos., 3(6):1557–1572, 1993.
- [25] M. Misiurewicz. Strange attractors for the Lozi mappings. Nonlinear dynamics, Annals of the New York Academy of Sciences, 357(1):348–358, 1980.
- [26] H.E. Nusse and J.A. Yorke. Border-collision bifurcations including “period two to period three” for piecewise smooth systems. Phys. D: Nonlinear Phenomena, 57(1-2):39–57, 1992.
- [27] H.E. Nusse and J.A. Yorke. Border-collision bifurcations for piecewise-smooth one-dimensional maps. Int. J. Bifurcation Chaos., 5(1):189–207, 1995.
- [28] H. M. Osinga. Boundary crisis bifurcation in two parameters. J. Diff. Eq. Appl., 12(10):997–1008, 2006.
- [29] D. Ou. Critical points in higher dimensions, I: Reverse order of periodic orbit creations in the Lozi family. arXiv preprint arXiv:2203.02326, 2022.
- [30] Ya.B. Pesin. Dynamical systems with generalized hyperbolic attractors: hyperbolic, ergodic and topological properties. Ergod. Th. & Dynam. Sys., 12:123–151, 1992.
- [31] A. Pumariño and E. Rodríguez, J. Á.and Vigil. Renormalization of two-dimensional piecewise linear maps: Abundance of 2-D strange attractors. Discrete Contin. Dyn. Syst., 38:941–966, 2018.
- [32] A. Pumariño, J. Á. Rodríguez, and E. Vigil. Persistent two-dimensional strange attractors for a two-parameter family of expanding baker maps. Discrete Contin. Dyn. Syst. Ser. B, 24(2):657–670, 2019.
- [33] T. Puu and I. Sushko. Business Cycle Dynamics: Models and Tools. Springer-Verlag, New York, 2006.
- [34] V. Robins, J.D. Meiss, and E. Bradley. Computing connectedness: Disconnectedness and discreteness. Phys. D, 139(3–4):276–300, 2000.
- [35] M. Rychlik. Invariant Measures and the Variational Principle for Lozi Mappings., pages 190–221. Springer, New York, 2004.
- [36] D.J.W Simpson. Border-collision bifurcations in . SIAM Rev., 58(2):177–226, 2016.
- [37] D.J.W. Simpson. Unfolding homoclinic connections formed by corner intersections in piecewise-smooth maps. Chaos, 26(7):073105, 2016.
- [38] D.J.W. Simpson and J.D. Meiss. Neimark-Sacker bifurcations in planar, piecewise-smooth, continuous maps. SIAM J. Appl. Dyn. Sys., 7(3):795–824, 2008.
- [39] I. Sushko, V. Avrutin, and L. Gardini. Bifurcation structure in the skew tent map and its application as a border collision normal form. J. Diff. Eq. Appl., 22(8):1040–1087, 2016.
- [40] I. Sushko and L. Gardini. Center bifurcation for two-dimensional border-collision normal form. Int. J. Bifurcation Chaos, 18(4):1029–1050, 2008.
- [41] R. Szalai and H.M. Osinga. Arnol’d tongues arising from a grazing-sliding bifurcation. SIAM J. Appl. Dyn. Sys., 8(4):1434–1461, 2009.
- [42] M. Tsujii. Absolutely continuous invariant measures for expanding piecewise linear maps. Invent. Math., 143:349–373, 2001.
- [43] Ya.Z. Tsypkin. Relay Control Systems. Cambridge University Press, New York, 1984.
- [44] D. Veitch and P. Glendinning. Explicit renormalisation in piecewise linear bimodal maps. Phys. D, 44(1-2):149–167, 1990.
- [45] L.-S. Young. Bowen-Ruelle measures for certain piecewise hyperbolic maps. Trans. Amer. Math. Soc., 287(1):41–48, 1985.
- [46] Z.T. Zhusubaliyev and E. Mosekilde. Bifurcations and Chaos in Piecewise-Smooth Dynamical Systems. World Scientific, Singapore, 2003.
- [47] Z.T. Zhusubaliyev, E. Mosekilde, S. Maity, S. Mohanan, and S. Banerjee. Border collision route to quasiperiodicity: Numerical investigation and experimental confirmation. Chaos, 16(2):023122, 2006.





