The 10 antipodal pairings of strongly involutive polyhedra on the sphere

We quickly recall some notions on the group of spherical isometries (we refer the reader to [3] for further details and where our notation is taken from). An isometry of $\mathbb{S}^{2}$ is either a rotation or a reflection or a composition of these two. Let $\mbox{Isom}(\mathbb{S}^{2})$ be the group of isometries of the 2-sphere. We remark that any orientation reversing isometry is either a reflection or a product of three reflections. Also, it can be checked that $\mbox{Isom}(\mathbb{S}^{2})$ is generated by only reflections. Moreover, any isometry is a product of at most three reflections:

$\bullet$ [one reflection] Let $H$ be a plane passing through the center of $\mathbb{S}^{2}$. The reflection $\gamma$ w.r.t. $H$ is an involutive isometry and therefore of order 2. This group is denoted by $[1]$.

$\bullet$ [two reflections] Let $H_{1}$ and $H_{2}$ be two planes with angle $\angle(H_{1},H_{2})=\frac{\pi}{q}$. The reflection $\gamma_{1}$ and $\gamma_{2}$ w.r.t. these planes generate the group $[q]$ (isomorphic to the dihedral group $D_{q}$) having presentation $\gamma_{1}^{2}=\gamma_{2}^{2}=(\gamma_{1}\gamma_{2})^{q}=id$.

$\bullet$ [three reflections] Let $H_{1},H_{2}$ and $H_{3}$ be three planes inducing a spheric triangle with angles $\frac{\pi}{p},\frac{\pi}{q}$ and $\frac{\pi}{r}$, denoted by $[p,q]$.

It is known that the sum of the angles of a spheric triangle is strictly larger that $\pi$, therefore $\frac{1}{p}+\frac{1}{q}+\frac{1}{r}>1$ implying that $\min\{p,q,r\}=2$. We take $r=2$, obtaining that $\frac{1}{p}+\frac{1}{q}>\frac{1}{2}$ yielding to $(p-2)(q-2)<4$. By analyzing the latter, it can be found that the possible cases are :

- $[3,3]$ (corresponding to the tetrahedron),

- $[3,4]$ (corresponding to the cube and octahedron),

- $[3,5]$ (corresponding to the dodecahedron and icosahedron),

- $[2,q]$ (corresponding to a diamond polyhedron which dual is a prism with a $q$-polygon as a base).

The group $[p,q]$ or $[q,p]$ is defined by $\gamma_{1}^{2}=\gamma_{2}^{2}=\gamma_{3}^{2}=(\gamma_{1}\gamma_{2})^{p}=(\gamma_{2}\gamma_{3})^{q}=(\gamma_{1}\gamma_{3})^{2}=id$ having as a fundamental region the spherical triangle with angles $\frac{\pi}{p},\frac{\pi}{q}$ and $\frac{\pi}{2}$. Each of these groups has a rotational group consisting only of the possible rotations generated by pairs of reflections:

- The rotational subgroup of $[q]$, consisting of the powers of $\gamma_{1}\gamma_{2}$, is denoted by $[q]^{+}$ (clearly $[1]^{+}$ is the trivial group),

- the rotational subgroup of $[p,q]$, generated by the rotations $\gamma_{1}\gamma_{2},\gamma_{2}\gamma_{3}$ and $\gamma_{3}\gamma_{1}$, is denoted by $[p,q]^{+}$ (these subgroups are of order 2),

- the rotational subgroup of $[p,q]$ when $q$ is even, generated by $\gamma_{1}\gamma_{2}$ which is a rotation of order $p$ followed by the reflection $\gamma_{3}$, is denoted by $[p^{+},q]$ or $[q,p^{+}]$ (these subgroups are of order 2),

- the rotational subgroup of $[2^{+},q]$, generated by $\gamma_{1}\gamma_{2}\gamma_{3}$, is denoted by $[2^{+},q^{+}]$ (which turns out to be a cyclic group of index 2) generated by the rotatory reflection $\rho\gamma_{3}$.

We first present the following lemma that identifies which groups contain the antipodal function.

Proof. Since $\alpha$ is an isometry without fixed points then (1) is verified. Moreover, since $\alpha$ inverts orientation then (2) and (4) hold. Notice that (2) also follows since $[q]^{+}$ is a subgroup of $[q]$. We can establish (3) by observing that any prism has central symmetry if and only if it has a polygon with an even number of sides as a base and similarly we see that the cube and the octahedron are the only platonic solids on the list with central symmetry.

In order to illustrate the proof of (5) and (6), let us see that $\alpha\in[2^{+},6]$. The group $[2,6]$ is generated by the reflections $\gamma_{1},\gamma_{2}$ and $\gamma_{3}$ such that $\gamma_{1}^{2}=\gamma_{2}^{2}=\gamma_{3}^{2}=(\gamma_{1}\gamma_{2})^{2}=(\gamma_{3}\gamma_{1})^{2}=(\gamma_{2}\gamma_{3})^{2}=id$. The subgroup $[2^{+},6]$ is generated by the reflection $\gamma=\gamma_{1}$ and the rotation $\rho=\gamma_{2}\gamma_{3}$. The element $\rho\gamma$ is a rotatory reflection or a step, satisfying $(\rho\gamma)^{6}=id$ and $(\rho\gamma)^{3}=\alpha$ (See Figure 3).

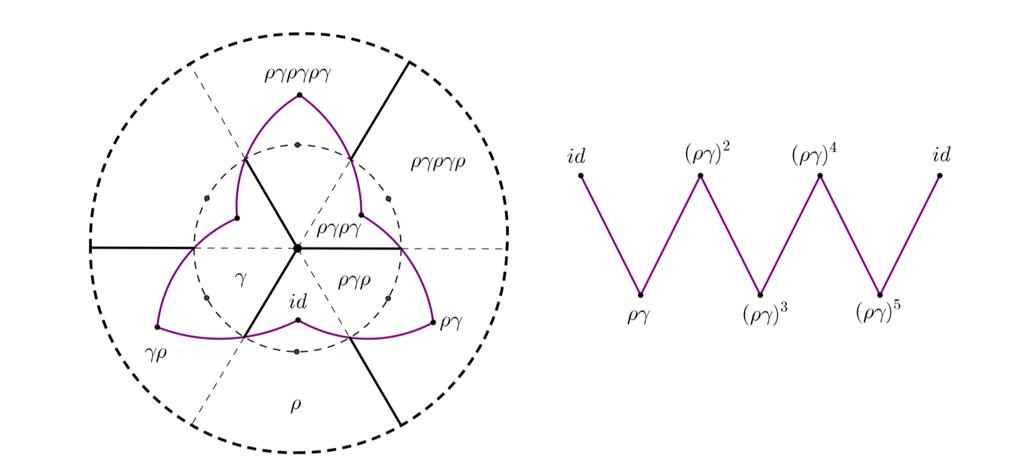
In the general case $[2^{+},q]$, if $q$ is even and $\frac{q}{2}$ is odd, then we have that $(\rho\gamma)^{q}=id$ and $(\rho\gamma)^{\frac{q}{2}}=\alpha$. Conversely, if $(\rho\gamma)^{\frac{q}{2}}=\alpha$, then $q$ is even and $\frac{q}{2}$ must be odd in order to express $\alpha$ as a product of generators with an odd number of reflections, otherwise $\alpha$ would preserve orientation, which is not the case. From this fact we can conclude also 6 since $[2^{+},q^{+}]$ is precisely the cyclic group generated by the step $\rho\gamma$. Finally, by considering (3), we just need to check the subgroup $[3^{+},4]$, which is generated by a reflection $\gamma$ and a rotation $\rho$. In this case, it can be verified that $\alpha=(\rho\gamma)^{3}$. $\square$

We may now prove Theorem 1.

Proof of Theorem 1. We may use Lemma 1 to identify those self-dual pairings $\mbox{Dual}(G)\rhd\mbox{Aut}(G)$ such that $\alpha\in\mbox{Dual}(G)$ and $\alpha\notin\mbox{Aut}(G)$. In Table 1 we examine each case. $\square$

Given $\sigma\in\mbox{Dual}(G)$ and a point $p\in\mathbb{S}^{2}$ we have that $\sigma\cdot p=\sigma(p)$, that is, $\mbox{Dual}(G)$ acts as an evaluation function in $\mathbb{S}^{2}$. The orbit of $R$ is the set of regions congruent to $R$ covering the sphere (the number of such regions is as many as the elements in $\mbox{Dual}(G)$. The stabilizer of $p$ consist of all the elements in $\mbox{Dual}(G)$ fixing $p$. An orbifold is defined as the fundamental region $R$ together with the points with nontrivial stabilizer.

Let $\Gamma\triangleleft\Delta$ be a self-duality pairing where $\Gamma$ and $\Delta$ are finite groups of isometries of the sphere, such that $\Gamma$ is an index 2 subgroup of $\Delta$. In order to describe each orbifold we need fundamental regions $R_{1}$ and $R_{2}$ corresponding to the groups $\Gamma$ and $\Delta$, respectively as well as their corresponding generators. We observe that since $\Delta$ is an extension of index 2, region $R_{2}$ is contained in $R_{1}$ and it will have half of its area.

In what follows we describe the fundamental regions for each antipodal self-dual pairing. We have drawn with :

- a thick line the singular elements of $\Gamma$, i.e., sets of fixed points under the action of $\Gamma$

- a double line the singular elements of $\Delta$

- continuous lines denote reflection lines

- dotted lines delimit the regions without considering a reflection and

- points marked with a circle denote a center of rotation by the marked angle.

Let $q$ and $l$ be natural numbers. The $q$-multi hyperwheel with $l$ levels is the graph $\mathcal{O}_{q}^{l}$ consisting of the cycles:

as well as a vertex $c=b_{i}^{l+1}$ called the cusp and the edges $a_{i}^{j}a_{i}^{j+1}$ and $b_{i}^{j}b_{i}^{j+1}$ for $j=1,\ldots,l$; see Figure 4.

If $q=2k\geq 4$ then $\mathcal{O}_{q}^{l}$ is a strongly involutive self-dual polyhedron. Indeed, let us check this for $\mathcal{O}_{q}^{l}$ where the strong involution $\alpha$ is given as follows:

Note that $\alpha$, as duality isomorphism, associates the vertex set of the dual face to each point $p$, while, as an isometry of the sphere, it associates the antipodal point $-p$ to each point $p$.

We may now construct the 4-multi hyperwheel $G=\mathcal{O}_{4}^{1}$ which is just the 4-hyperwheel as illustrated in Figure 1 (right) by means of the action of its antipodal pairing. Figure 5 gives the fundamental region $R$ and its doodle. This doodle can generate a family of self-dual polyhedra whose pairing is $[q]\triangleleft[2,q]$.

The external circle with dotted line represents the north pole, the circle with double line represents the equator and the central point is the south pole. The graphs $G$ and $G^{*}$ appear in blue and red, respectively and there is a black vertex in each intersection of an edge in $G$ with an edge in $G^{*}$. The join of these graphs (including the black vertices) is the graph of squares $G_{\square}$ whose all faces are quadrilaterals of the form $(vafb)$ for some $v\in V(G),f\in V(G^{*})$ and $a,b\in E(G)=E(G^{*})$.

We suppose that $\phi$ is the reflection in a spherical line $l$ which intersects the square $(vafb)$. If $\phi\in\mbox{Iso}(G)$ then $l$ must pass through $a$ and $b$ and must interchange $v$ and $f$. In this case, the reflection in the equator is a duality isomorphism since it interchanges vertices blue and red. Each automorphism can be obtained as a composition of reflections in four lines through the poles. The reflections through these lines generates the group $[4]$ and each one of them works as an automorphism, so we can write $\mbox{Aut}(G)=[4]$. The group $\mbox{Dual}(G)$ is $[2,4]$ and it can be obtained by adding the reflection through the equator. In this way, $\mbox{Dual}(G)$ is generated by the reflections in three planes $H_{1},H_{2}$ and $H_{3}$. Planes $H_{1}$ and $H_{2}$ intersect with angle $\frac{\pi}{4}$ and we can assume they are vertical planes through the poles, while $H_{3}$ is the equatorial plane and it forms angles of $\frac{\pi}{2}$ with each $H_{1},H_{2}$. The fundamental region is the spherical triangle with angles $\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{4}$. The self-dual pairing for this graph is $[4]\triangleleft[2,4]$ and it is determined by this triangle with three isometries: two reflections in $\mbox{Aut}(G)$ (black lines) and one in $\mbox{Iso}(G)$ (double line).

The above construction can be extended for each even $q$ and any $l$: For $q=4$ and $l=1$ we have the doodle of $G=\mathcal{O}_{4}^{1}$ (Figure 5). Then for $l=2$ and $3$ we have the doodles and the graphs in Figure 6. Here the doodle is drawn on the region between two planes forming an angle $\frac{\pi}{q}$: the fundamental region of the group $[q]$.

In Figure 7, we consider the embedding of both: the graph in blue and its dual graph in red. Here the reflection through the double line interchanges colors blue and red since it is a duality isomorphism of $[q]\triangleleft[2,q]$. If we let the group $[q]$ act on the sphere, we will have a generalization of the $q$-multi hyperwheel. Figure 7 illustrates the case $q=4$ and $l=3$.

Let $q$ and $l$ be natural numbers. The $q$-multi wheel with $l$ levels is the graph $\mathcal{P}_{q}^{l}$ consisting of the $l$ cycles

a central vertex $c=a_{i}^{0}$ called the cusp and edges $a_{i}^{j}a_{i}^{j+1}$. Figure 9 illustrates $\mathcal{P}_{5}^{3}$.

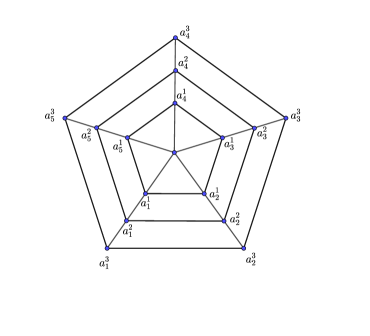
We notice that $\mathcal{P}_{q}^{1}$ is actually the $q$-wheel (a graph consisting of a $q$-cycle with a center joined to each vertex of the cycle).

If $q=2k+1\geq 3$ then $\mathcal{P}_{q}^{l}$ is a strongly involutive self-dual polyhedron. Indeed, let us check this for $\mathcal{P}_{q}^{l}$ where the strong involution $\alpha$ is given as follows:

We may now construct the 3-multi wheel $G=\mathcal{P}_{3}^{1}$ by means of the action of its antipodal pairing. Figure 5 gives the fundamental region $R$ and its doodle. This doodle can be naturally extended to generate a family of self-dual polyhedra whose pairing is $[q]\triangleleft[2,q]$.

Let us consider an isometric embedding of the graph $G=\mathcal{P}_{3}$ given in Figure 9.

In this embedding, the vertices $a,b$ and $c$ are in a circle while $d,e$ and $f$ are in another circle. These circles are concentric to the center $o$, which we can assume to be the south pole. The red vertices correspond to the dual graph and they are also in concentric circles, in this case $D,E$ and $F$ are connected with the central vertex $O$ located in the north pole (dotted external line in the figure).

We can observe that the reflection on the equator does not work as duality but the rotation by $\pi$ around the circle in double lines in the shaded region is a duality isomorphism. This rotation is color reversing: $e$ goes to $F$, the red point $C$ goes to $b$ and the central vertex $o$ goes to $O$. If we call this rotation $\rho$, then the group $\mbox{Dual}(\mathcal{P}_{3}^{1})$ is generated by $\gamma_{1},\gamma_{2},\rho$ and in Coxeter notation it corresponds to $[2^{+},6]$. The duality pairing is $[3]\triangleleft[2^{+},6]$.

The above construction can be extended for each odd $q$ and any $l$. We can start by restricting the graph $P_{5}^{1}$, which is the 5-wheel, to a fundamental region and then we can add more levels in order to obtain a simple, planar and 3-connected graph. See Figure 10.

In Figure 11 we have a fundamental region $R$ for the group $[q]$. It is between two vertical planes forming an angle of $\frac{\pi}{q}$. The circle in the center of the region denotes a rotation by $\pi$. This rotation sends the blue lines in the doodle to the red lines in the doodle and viceversa since it is a duality isomorphism in the pairing $[q]\triangleleft[2^{+},2q]$. If we let $[q]$ act on $\mathbb{S}^{2}$ we may obtain $\mathcal{P}_{q}^{l}$.