Textual Adversarial Attack using Metric-Guided Rewrite and Rollback

Lei Xu Alfredo Cuesta-Infante Laure Berti-Equille Kalyan Veeramachaneni
MIT LIDS
MA, USA

Abstract

Adversarial examples are helpful for analyzing and improving the robustness of text classifiers. Generating high-quality adversarial examples is a challenging task as it requires generating fluent adversarial sentences that are semantically similar to the original sentences and preserve the original labels, while causing the classifier to misclassify them. Existing methods prioritize misclassification by maximizing each perturbation’s effectiveness at misleading a text classifier; thus, the generated adversarial examples fall short in terms of fluency and similarity. In this paper, we propose a rewrite and rollback (R&R) framework for adversarial attack. It improves the quality of adversarial examples by optimizing a critique score which combines the fluency, similarity, and misclassification metrics. R&R generates high-quality adversarial examples by allowing exploration of perturbations that do not have immediate impact on the misclassification metric but can improve fluency and similarity metrics. We evaluate our method on 5 representative datasets and 3 classifier architectures. Our method outperforms current state-of-the-art in attack success rate by +16.2%, +12.8%, and +14.0% on the classifiers respectively. Code is available at https://github.com/DAI-Lab/fibber

1 Introduction

Recently, adversarial attacks in text classification have received a great deal of attention. Adversarial attacks are defined as subtle perturbations in the input text such that a classifier misclassifies it. They can serve as a tool to analyze and improve the robustness of text classifiers, thus being more and more important because security-critical classifiers are being widely deployed wu2019misinformation; torabi2019big; zhou2019fake.

Refer to caption — Figure 1: R&R generates adversarial examples by rewrite and rollback. The rewrite step explores possible perturbations stochastically and is guided by similarity metric and fluency metric to ensure better quality of the example. The rollback operation further improves the similarity.

Existing attack methods either adopt a synonym substitution approach (Jin2019IsBR; zang2019word) or use a pre-trained language model to propose substitutions for better fluency and naturalness (li2020bert; garg2020bae; li2021CLARE). They follow a similar framework: first, construct some candidate perturbations, and then, use the perturbations that most effectively mislead the classifier to modify the sentence. This process is repeated multiple times until an adversarial example is found. This framework prioritizes misclassification by picking perturbations that most effectively mislead the classifier. Despite the success in changing the classifier prediction, it has two main disadvantages. First, it is prone to modify words that are critical to the sentence’s meaning which decreases the similarity and is more likely to change the true label of the sentence, or introduce low-frequency words causing the fluency to decrease. Second, some perturbations do not have immediate impacts on misclassification, but can trigger it when combined with other perturbations, and these frameworks cannot find adversarial examples with these perturbations.

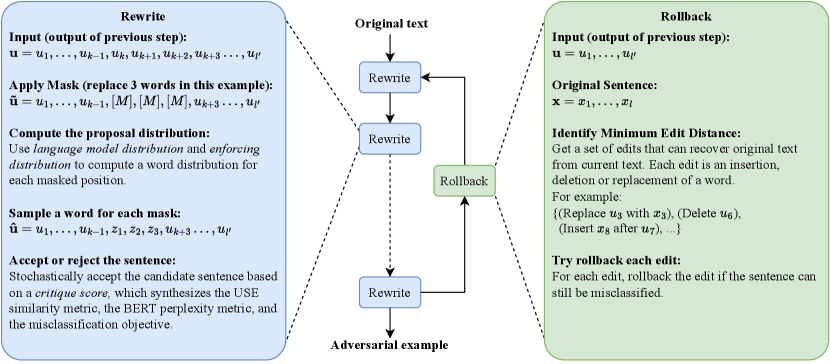
To overcome these problems, the attack method needs to consider fluency, similarity, and misclassification jointly, while also efficiently exploring various perturbations that do not show direct impacts on the latter. We define a critique score that combines fluency, similarity and misclassification metrics. Then, we present our design for a Rewrite and Rollback framework (R&R) which optimizes this score to generate better adversarial examples. In the rewrite stage, we explore multi-word substitutions proposed by a pre-trained language model. We accept or reject a substitution according to the critique score. We can generate a high-quality adversarial example after multiple iterations of rewrite. Rewrite may introduce changes that do not contribute to misclassification and may also reduce similarity and fluency. Therefore, we periodically apply the rollback operation to reduce the number of modifications without changing the misclassification result. Figure 1 illustrates the process using an example.

2 Problem Formulation

Let $\mathbf{x}=x_{1},\ldots,x_{l}$ be a sentence of length $l$ , $y$ be its classification label, and $f(\mathbf{x})$ be a text classifier that predicts a probability distribution over classes. The objective of an attack method $\mathcal{A}(\mathbf{x},y,f)$ is to \linenomathAMS

	$\displaystyle\text{construct }\mathbf{u}=u_{1},\ldots,u_{l^{\prime}}\text{ satisfying 3 conditions:}$
	$\displaystyle\begin{cases}\text{$\mathbf{u}$ is misclassified, i.e., $f(\mathbf{u})\neq y$,}\\ \text{Human considers $\mathbf{u}$ as a fluent sentence,}\\ \text{Human considers $\mathbf{u}$ to be semantically similar to $\mathbf{x}$.}\\ \text{Human considers $\mathbf{u}$ preserves the true label $y$.}\end{cases}$

where $l^{\prime}$ is the length of the adversarial sentence. However, this formulation requiring human evaluation is intractable for large-scale data. Therefore, we approximate the sentence fluency with the perplexity of the sentence. It is defined as

\textstyle\text{ppl}(\mathbf{x})=\exp\big{[}-\frac{1}{l}\sum_{i=1}^{l}\log p(x_{i}|x_{1}\ldots x_{i-1})\big{]},

where $p(x_{i}|x_{1}\ldots x_{i-1})$ is measured by a language model. Low perplexity means the sentence is predictable by the language model, which usually indicates the sentence is fluent. Sentence similarity can be quantified as $\cos\big{(}H(\mathbf{x}),H(\mathbf{u})\big{)}$ , where $H(\cdot)$ is a pre-trained sentence encoder that encodes the meaning of a sentence into a vector. We assume that high sentence similarity implies preservation of the sentence label. Thus, finding the adversarial sentence $\mathbf{u}$ is formulated as a multi-objective optimization problem as follows: \linenomathAMS

	Construct	$\displaystyle\mathbf{u}=u_{1},\ldots,u_{l^{\prime}}\text{ to }\text{minimize }\text{ppl}(\mathbf{u})$
		$\displaystyle\text{ and }\text{maximize }\cos\big{(}H(\mathbf{x}),H(\mathbf{u})\big{)}$
		$\displaystyle\text{ subject to }f(\mathbf{u})\neq y.$

We use a fine-tuned BERT-base model (Devlin2019BERTPO) to measure perplexity and use Unversal Sentence Encoder (USE) (cer2018universal) to measure sentence similarity. Ultimately, fluency, similarity, and the preservation of original label need to be verified by humans. We discuss human verification in Section 4.

Threat Model.

We assume the attacker can query the classifier for the prediction (i.e., the probability distribution over all classes). But they do not have knowledge on architecture of the classifier nor query for the gradient. They can also access some unlabeled text in the domain of the classifier.

3 Metric-Guided Rewrite and Rollback

In this section, we first give an overview, then introduce the rewrite and rollback components respectively. Finally, we give a summary of pre-trained models used in the framework.

3.1 Overview

R&R contains the rewrite and rollback steps. In the rewrite step, we randomly mask several consecutive words, and compute a proposal distribution, which is a distribution over the vocabulary on each masked position defined as Eq. (1). We construct a multi-word substitution¹¹1The number of words in each substitution, the number of rewrite steps between two rollback steps, the maximum number of rewrite steps, and the batch size are hyperparamters. for the masked positions according to the distribution, then compute the critique score defined as Eq. (3)-(5). If the score increases, we accept the substitution. If the score decreases, we accept it with a probability depending on the degree of decrease. The rewrite step contains randomness to encourage exploration of different modifications, while the critique score will guide the rewritten sentence to a high-quality adversarial example. After several steps of rewriting1, we apply a rollback operation on the sentences that have already been misclassified to reduce the number of changes introduced in the rewriting. In the rollback step, we identify a minimum set of edits required to change the current sentence back to the original sentence. We rollback an edit if it does not affect the misclassification.

We implement the framework to simultaneously rewrite a batch of sentences. We make multiple copies of an input text and create a batch1. The proposal distributions and critique scores for these copies can be computed in parallel on a GPU, while the randomness in the rewrite step leads to different rewritten sentences. The loop terminates when either the maximum number of rewrite steps is reached1 or half of the sentences in the batch are misclassified. Figure 2 shows the R&R framework.

3.2 Rewrite

In each rewrite, we mask then substitute a span of words. It is composed of the following steps.

Apply mask in the sentence.

First, we randomly pick $m$ consecutive words in the sentence, and replace them with $t$ mask, where $t$ can be $m$ , $m-1$ , or $m+1$ meaning replace, shrink, and expand operation respectively. Compared with CLARE li2021CLARE which masks one word at a time (i.e., $m=1$ ), masking multiple words can make it easier to modify common phrases. We use $\tilde{\mathbf{u}}$ to denote the masked sentence.

Compute proposal distribution.

Then, we compute proposal distribution for $t$ masks in the sentence. This distribution assigns a high probability to words that can construct a fluent and legitimate paraphrase. Let $z_{1},\ldots z_{t}$ be the words to be placed at the masked positions. The distribution is

\textstyle p_{\text{proposal}}(z_{i}|\tilde{\mathbf{u}},\mathbf{x})\propto p_{\text{lm}}(z_{i}|\tilde{\mathbf{u}})\times p_{\text{enforce}}(z_{i}|\tilde{\mathbf{u}},\mathbf{x})

(1)

where $p_{\text{lm}}$ is a language model distribution that give high probability to words that can make a fluent sentence, and $p_{\text{enforce}}$ is the enforcing distribution, which give high probability to words that can lead to semantically similar sentences. $p_{\text{lm}}$ and $p_{\text{enforce}}$ should be considered as two different weights of words and are multiplied together to get $p_{\text{proposal}}$ so that if either $p_{\text{lm}}$ or $p_{\text{enforce}}$ is low, the word will have low probability in $p_{\text{proposal}}$ . This is a desired property because we want the adversarial sentence to have good fluency (i.e., high $p_{\text{lm}}$ ) and high similarity (i.e., high $p_{\text{enforce}}$ ). $p_{\text{lm}}$ is computed by sending $\tilde{\mathbf{u}}$ into BERT and taking the predicted word distribution on masked positions. Depending on the position, the word distributions for $t$ masks are different. The enforcing distribution is measured by word embeddings. We use the sum of word embeddings $R(\mathbf{u})=\sum_{u_{k}}E(u_{k})$ as a sentence embedding, where $E(\cdot)$ is the counter-fitted word embedding (mrkvsic2016counter). Then we define the enforcing distribution as \linenomathAMS

	$\displaystyle p_{\text{enforce}}$	$\displaystyle(z_{i}\|\tilde{\mathbf{u}},\mathbf{x})\propto\exp\big{[}w_{\text{enforce}}$
		$\displaystyle\times(\cos(R(\mathbf{x})-R(\tilde{\mathbf{u}}),E(z_{i}))-1)\big{]}.$		(2)

$w_{\text{enforce}}$ is a hyper-parameter with a positive value. Larger $w_{\text{enforce}}$ penalizes more on dissimilar words. The $\exp$ ensures the value to be positive thus the values can be converted to a probability distribution over words. We use the conventional cosine similarity to compute the distance of two vectors. If the embedding of a word $E(z)$ perfectly aligns with the sentence representation difference $R(\mathbf{x})-R(\tilde{\mathbf{u}})$ , it gets the largest probability. The enforcing distribution aims at making the candidate modification more similar to the original sentence. Note that enforcing distribution is identical on all $t$ masks.

Sample a candidate sentence.

We sample a candidate word for each masked position by $z_{i}\sim p_{\text{proposal}}(z_{i}|\tilde{\mathbf{u}},\mathbf{x})$ . We do not consider the effect of sampling one word on other masked positions (i.e., we do not recompute proposal distribution for the remaining masks after sampling a word) because language model distribution already considers the position of the mask and assigns a different distribution for each mask, meanwhile recomputing is inefficient. We use $\hat{\mathbf{u}}$ to denote the candidate sentence.

Critique score and decision function.

We decide whether to accept the candidate sentence using a decision function. The decision function computes a heuristic critique score \linenomathAMS

$\displaystyle\textstyle C$	$\displaystyle(\mathbf{u})=\big{(}w_{\text{ppl}}\min(1-\text{ppl}(\mathbf{u})/\text{ppl}(\mathbf{x}),0)$	(3)
	$\displaystyle+w_{\text{sim}}\min(\cos\big{(}H(\mathbf{u}),H(\mathbf{x})\big{)}-\phi_{\text{sim}},0)$	(4)
	$\displaystyle+w_{\text{clf}}\min(\max_{y^{\prime}\neq y}f(\mathbf{u})_{y^{\prime}}-f(\mathbf{u})_{y},0)\big{)}$	(5)

Eq. (3) penalizes sentences with high perplexity, where $\text{ppl}(\mathbf{x})$ is perplexity measured by a BERT model. Eq. (4) penalizes sentences with sentences with cosine similarity lower than $\phi_{\text{sim}}$ , where $H(\cdot)$ is the sentence representation by USE. Eq. (5) penalizes sentences that cannot be misclassified where $f(\mathbf{u})_{y}$ means the log probability of class $y$ predicted by the classifier. $w_{\text{ppl}}$ , $w_{\text{sim}}$ and $w_{\text{clf}}$ are hyperparameters.

The decision is made based on

\textstyle\alpha=\exp[C(\hat{\mathbf{u}})-C(\mathbf{u})].

(6)

If $\alpha>1$ , the decision function accepts $\hat{\mathbf{u}}$ ; otherwise it accepts $\hat{\mathbf{u}}$ with probability $\alpha$ . The computation of $\alpha$ is motivated by the Metropolis–Hastings algorithm (hastings1970monte) (See Appendix 7). The critique score is a straightforward way to convert the multi-objective optimization problem into a single objective. Although it introduces several hyper-parameters, R&R is no more complicated than conventional methods, which also require hyper-parameter setting.

3.3 Rollback

In the rollback step, we eliminate modifications that do not correct the misclassification. It contains the following steps.

Find a minimum set of simple edits.

We first find a set of simple edits that change the current rewritten sentence back to the original sentence. Simple edits mean the insertion, deletion or replacement of a single word, which is different from the modification in the rewrite step.

Rollback edits.

For each edit, if reverting it does not correct the misclassification, then we revert the edit. For convenience, we scan each word in the sentence from right to left, and try to rollback each edit. Note that rollback may introduce grammar errors, but they can be fixed in future rewrite steps.

3.4 Vocabulary Adaptation

Computing $p_{\text{propose}}$ is challenging because of the inconsistent vocabulary. The counter fitted word embeddings in $p_{\text{enforce}}(\cdot)$ works on a 65k-word vocabulary, while the BERT language model used in $p_{\text{lm}}(\cdot)$ uses a 30k-word-piece vocabulary which contains common words and affixes. Rare words are handled as multiple affixes. For example “hyperparameter” does not appear in the BERT vocabulary, so it is handled as “hyper”, “##para”, and “##meter”. Since the BERT model is more complicated, we keep it as is and transfer word embeddings to BERT vocabulary. We train the word-piece embeddings as follows. Let $\mathbf{w}=\{w_{1},\ldots,w_{L}\}$ be a plain text corpus tokenized by words. Let $T(w)$ be word-piece tokenization of a word. Let $E(w)$ be the original word embeddings and $E^{\prime}(x)$ be the transferred embeddings on word-piece. We train the word-piece embeddings $E^{\prime}$ by minimizing the absolute error $\sum_{w\in\mathbf{w}}||E(w)-\sum_{x\in T(w)}E^{\prime}(x)||_{1}$ . We initialize $E^{\prime}$ by copying the embedding on words shared by two vocabularies and set other embeddings to $0$ . We optimize the absolute error using stochastic gradient descent. In each step, we sample 5000 words from $\mathbf{w}$ , then update $E^{\prime}$ accordingly. Figure 9 in Appendix illustrates the algorithm.

3.5 Summary of pre-trained models in R&R

In R&R, we employ several pre-trained models. Choices are made according to the different characteristics of these pre-trained models.

BERT for masked word prediction and perplexity. Because BERT is originally trained for masked word prediction, it can predict the word distribution given context from both sides. Thus, BERT is preferable for generating $p_{\text{lm}}$ . Estimating the perplexity for a sentence requires BERT to run in decoder mode and be fine-tuned. Perplexity can also be measured by other language models such as GPT2 radford2019language. We use BERT mainly for the consistent vocabulary with $p_{\text{lm}}$ .

Word embedding and USE for similarity. Word embedding is more efficient as it only computes the sum of vectors and cosine similarity. In enforcing distribution, we need to replace the selected position with all possible $z$ ’s and measure the similarity, so we use word embeddings for efficiency. In the critique score, only the proposal sentence needs to be measured, so we can afford more computation time of USE.

4 Experiments

We conducted experiments on a wide range of datasets and multiple victim classifiers to show the efficacy of R&R. We first evaluate the quality of adversarial examples using automatic metrics. Then, we conducted human evaluation to show the necessity to generate highly similar and fluent adversarial examples. Finally, we conduct an ablation study to analyze each component of our method, and discuss defense against the attack.

Datasets. We use 3 conventional text classification datasets: topic classification, sentiment classification, and question type classification. We also use 2 security-critical datasets: hate speech detection and fake news detection. Dataset details are given in Table 1.

Name	#C	Len	Description
AG	4	43	News topic classification by zhang2015character.
MR	2	32	Moview review dataset by pang2005seeing.
TREC	6	8	Question type classification by li2002learning.
HATE	2	23	Hate speech detection dataset by kurita20acl.
FAKE	2	30	Fake news detection dataset by yang2017satirical. We use the first sentence of the news for classification.

Table 1: Dataset details. #C means number of classes. Len is the average number of words in a sentence.

	AG	MR	TREC	HATE	FAKE
BERT-base	92.8	88.2	97.8	94.0	81.2
RoBERTa-large	92.7	91.6	97.3	95.0	75.5
FastText	89.2	79.5	85.8	91.5	72.4
Log Perplexity	3.38	5.27	3.91	3.56	4.92

Table 2: Accuracy of 3 classifers and sentence log perplexity on the clean test set.

		AG			MR			TREC			HATE			FAKE
	Attack	ASR	Sim	PPL	ASR	Sim	PPL	ASR	Sim	PPL	ASR	Sim	PPL	ASR	Sim	PPL
\multirow3* BERT	TextFooler	16.8	0.98	4.00	26.0	0.97	5.92	1.8	0.97	5.30	30.6	0.97	3.53	29.9	0.98	5.44
	CLARE	28.8	0.97	3.60	48.4	0.97	5.70	2.5	0.96	5.58	31.0	0.97	3.99	48.9	0.98	5.02
	R&R (Ours)	54.1	0.98	3.64	63.4	0.98	5.36	10.8	0.97	5.29	55.3	0.98	4.06	57.0	0.98	5.05
\multirow3* RoBERTa	TextFooler	15.6	0.98	5.21	18.0	0.97	6.06	0.4	0.96	7.09	24.0	0.98	4.20	26.6	0.98	5.45
	CLARE	23.3	0.97	5.24	45.9	0.97	5.67	2.5	0.97	6.53	35.7	0.97	4.37	46.0	0.98	5.20
	R&R (Ours)	41.2	0.98	3.73	48.5	0.97	5.53	12.5	0.97	5.17	55.7	0.97	4.07	59.6	0.98	5.25
\multirow3* FastText	TextFooler	25.8	0.98	4.16	33.1	0.98	5.85	6.5	0.98	5.04	21.7	0.98	3.44	35.3	0.98	5.46
	CLARE	28.9	0.97	3.91	41.5	0.97	5.79	8.5	0.97	6.06	35.6	0.97	4.24	76.0	0.98	5.15
	R&R (Ours)	37.8	0.98	3.84	48.9	0.98	5.48	44.1	0.98	4.68	53.3	0.98	4.03	76.4	0.98	5.10

Table 3: Automatic evaluation results. “Sim” and “PPL” represent similarity measured by USE and the log perplexity measured by BERT respectively.

Victim Classifiers. For each dataset, we use the full training set to train three victim classifiers: (1) BERT-base classifier Devlin2019BERTPO; (2) RoBERTa-large classifier liu2019roberta, and (3) FastText classifier joulin2017fasttext.

Baselines. We compare our method against two strong baseline attack methods: TextFooler (Jin2019IsBR) and CLARE (li2021CLARE).

Hyperparameters. In R&R, we use the BERT-base language model for $p_{\text{lm}}$ . For each dataset, we fine-tune the BERT language model using 5k batches on the training set²²2We use the plain text to fine-tune the language model, and do not use the label. In the threat model, we assume the attacker can access plain text data from a similar domain. with batch size 32 and learning rate 0.0001, so it is adapted to the dataset. We set the enforcing distribution hyper-parameters $w_{\text{enforce}}=5$ . The decision function hyper-parameters $w_{\text{ppl}}=5$ , $w_{\text{sim}}=20$ , $\phi_{\text{sim}}=0.95$ , $w_{\text{clf}}=2$ . To generate each paraphrase, we set maximum rewrite iterations to be $200$ , and replace a 3-word span in each iteration. We implement R&R in a 50-sentence batch and apply early-stop when half of the batch are misclassified. We apply rollback operation every 10 steps of rewrite. Then, we return the adversarial example with the best critique score.

Hardware and Efficiency. We conduct experiments on Nvidia RTX Titan GPUs. We measure the efficiency using average wall clock time. On the MR dataset, one attack on a BERT-base classifier using R&R takes 15.8 seconds on average. CLARE takes 14.4 seconds on average. TextFooler is the most efficient algorithm which takes 0.45 seconds.

Automatic Metrics. We evaluate the efficacy of the attack method using 3 automatic metrics:

Similarity ( $\uparrow$ ): We use Universal Sentence Encoder to encode the original and adversarial sentence, then use the cosine distance of two vectors to measure the similarity. We set a similarity threshold at 0.95, so the similarity of a legitimate adversarial example should be greater than 0.95.

Log Perplexity ( $\downarrow$ ) shows the fluency of adversarial sentences.

Attack success rate (ASR) ( $\uparrow$ ) shows the ratio of correctly classified text that can be successfully attacked.

Human Metrics: Automatic metrics are not always reliable. We use Mechanical Turk to verify the similarity, fluency, and whether the label of the text is preserved with respect to human evaluation.

Sentence similarity ( $\uparrow$ ): Turkers are shown pairs of original and adversarial sentences, and are asked whether the two sentences have the same semantic meaning. They annotate the sentence in a 5-likert, where 1 means strongly disagree, 2 means disagree, 3 means not sure, 4 means agree, and 5 means strongly agree.

Sentence fluency ( $\uparrow$ ): Turkers are shown a random shuffle of adversarial sentences, and are asked to rate the fluency in a 5-likert, where 1 describes a bad sentence, 3 describes a meaningful sentence with a few grammar errors, and 5 describes a perfect sentence.

Label match ( $\uparrow$ ): Turkers are shown a random shuffle of adversarial sentences and are asked whether it belongs to the class of the original sentence. They are asked to rate 0 as disagree, 0.5 as not sure, and 1 as agree.

We sample 100 adversarial sentences from each method, and each task is annotated by 2 Turkers. We do not annotate label matches on the FAKE dataset because identifying fake news is too challenging for Turkers. We require the location of the Turkers to be in the United States, and their Hit Approval Rate to be greater than 95%. The screenshots of the annotation tasks are shown on Figure 7 in Appendix.

Examples. Table 4 shows some examples. We find R&R makes natural modifications to the sentence and preserves the semantic meanings.

	AG			MR			TREC			HATE			FAKE
	S.	F.	M.	S.	F.	M.	S.	F.	M.	S.	F.	M.	S.	F.
TextFooler	3.93	3.58	0.90	3.3	3.49	0.92	3.25	2.88	0.88	3.76	3.61	0.46	3.58	3.58
CLARE	3.75	3.65	0.93	2.44	3.33	0.74	3.00	3.00	0.75	3.89	4.41	0.81	3.67	3.65
R&R (Ours)	4.12	3.87	0.99	3.48	3.61	0.85	3.59	3.14	0.89	3.59	3.94	0.76	3.81	3.87

	AG		FAKE
	+Filter	+SHIELD	+Filter	+SHIELD
TextFooler	6.2	8.2	13.8	16.7
CLARE	5.6	18.2	19.0	51.1
R&R (ours)	22.3	30.6	23.1	59.4

Textual Adversarial Attack using Metric-Guided Rewrite and Rollback

Abstract

1 Introduction

2 Problem Formulation

Threat Model.

3 Metric-Guided Rewrite and Rollback

3.1 Overview

3.2 Rewrite

Apply mask in the sentence.

Compute proposal distribution.

Sample a candidate sentence.

Critique score and decision function.

3.3 Rollback

Find a minimum set of simple edits.

Rollback edits.

3.4 Vocabulary Adaptation

3.5 Summary of pre-trained models in R&R

4 Experiments

4.1 Is R&R effective in attacking classifiers?

4.2 Does R&R generate semantically similar and fluent adversarial sentences?

4.3 Do adversarial sentences preserve the original labels?

4.4 How does each component in R&R contribute to the good performance?

Decision Function

Rollback

Multiple-Word Masking

4.4.1 How do existing defense methods work against R&R?

5 Related Work

6 Conclusion

Ethical Considerations

Acknowledgments

History of this Paper

7 Relation to Metropolis-Hastings Sampling