TeV Scale Resonant Leptogenesis with Gauge Symmetry
in the Light of Muon
Abstract
Motivated by the growing evidence for the possible lepton flavour universality violation after the first results from Fermilab’s muon measurement, we revisit one of the most widely studied anomaly free extensions of the standard model namely, gauged model, to find a common explanation for muon as well as baryon asymmetry of the universe via leptogenesis. The minimal setup allows TeV scale resonant leptogenesis satisfying light neutrino data while the existence of light gauge boson affects the scale of leptogenesis as the right handed neutrinos are charged under it. For gauge boson mass at GeV scale or above, the muon favoured parameter space is already ruled out by other experimental data while bringing down its mass to sub-GeV regime leads to vanishing lepton asymmetry due to highly restrictive structures of lepton mass matrices at the scale of leptogenesis. Extending the minimal model with two additional Higgs doublets can lead to a scenario consistent with successful resonant leptogenesis and muon while satisfying all relevant experimental data.
Introduction: The recent measurement of the muon anomalous magnetic moment, = , by the E989 experiment at Fermilab for the first time shows a discrepancy with respect to the theoretical prediction of the Standard Model (SM) Abi et al. (2021)
| (1) | |||
| (2) |
which, when combined with the previous Brookhaven determination of
| (3) |
leads to a 4.2 observed excess of 111The latest lattice results Borsanyi et al. (2020) however, predict a larger value of muon bringing it closer to experimental value. Tension of measured muon with global electroweak fits from to hadron data has also been reported in Crivellin et al. (2020).. The status of the SM calculation of muon magnetic moment has been updated recently in Aoyama et al. (2020). For more details, one may refer to Zyla et al. (2020). The latest Fermilab measurements have also led to several recent works on updating possible theoretical models with new data, a comprehensive review of which may be found in Athron et al. (2021). Gauged lepton flavour models like provide a natural origin of muon in a very minimal setup while also addressing the question of light neutrino mass simultaneously. Recent studies on this model related to muon may be found in Borah et al. (2020); Zu et al. (2021); Amaral et al. (2021); Zhou (2021); Borah et al. (2021). While this could be due to lepton flavour universality (LFU) violation, similar anomalies, that too in the context of muon, comes from the measurement of . While the hint for this anomaly, like muon was there for several years, recent update from the LHCb collaboration Aaij et al. (2021) has led to the most precise measurement ever with more than deviation from the SM predictions. In the light of growing evidences for such LFU violations, need for beyond standard model physics around the TeV corner has become very prominent.
Here we consider the popular and minimal model based on the gauged symmetry which is anomaly free He et al. (1991a, b). Apart from the SM fermion content, the minimal version of this model has three heavy right handed neutrinos (RHN) leading to to type I seesaw origin of light neutrino masses Minkowski (1977); Mohapatra and Senjanovic (1980); Yanagida (1979); Gell-Mann et al. (1979); Glashow (1980); Schechter and Valle (1980). The same RHNs can lead to leptogenesis Fukugita and Yanagida (1986); Davidson et al. (2008) via out-of-equilibrium decay into SM leptons. However, with hierarchical RHN spectrum, there exists a lower bound on the scale of leptogenesis, known as the Davidson-Ibarra bound GeV Davidson and Ibarra (2002). Several earlier works Adhikary (2006); Chun and Turzynski (2007); Ota and Rodejohann (2006); Asai et al. (2017, 2020) considered different scenarios like supersymmetry, high scale leptogenesis within type I seesaw framework of this model. However, it is also possible to have TeV scale leptogenesis via resonant enhancement due to tiny mass splitting between RHNs, known as the resonant leptogenesis Pilaftsis (1999); Pilaftsis and Underwood (2004); Moffat et al. (2018); Dev et al. (2018a). It should be noted that earlier works on leptogenesis in gauged model considered high scale breaking of such gauge symmetry and compatibility with muon explanation from a low scale vector boson was missing. We intend to perform a general analysis as well as to bridge this gap showing the possibility of TeV scale leptogenesis along with muon from a light vector boson.
Motivated by the recent measurements of the muon , in this work we consider the possibility of low scale leptogenesis and constrain the gauge sector from the requirements of successful leptogenesis and . Since the decaying RHNs can have this new gauge interaction which can keep them in equilibrium for a longer epochs and can also initiate some washout processes, the requirement of successful leptogenesis for a fixed scale of leptogenesis around a TeV can lead to constraints on the gauge sector parameter space. Since leptogenesis is a high scale phenomena and the requirement of needs a low scale breaking gauge symmetry, one can not realise both in the minimal version of the model. We first discuss the minimal model from the requirement of satisfying neutrino data and baryon asymmetry from leptogenesis and then consider an extended model which can accommodate muon as well. While we do not pursue the study of anomalies in this model, one may refer to Biswas and Shaw (2019) for common origin of muon and anomalies along with dark matter in extensions of minimal model. Explanation of similar flavour anomalies along with muon in this model have also been studied Crivellin et al. (2015); Altmannshofer et al. (2016). Recently, a dark matter extension of the model was also found to provide a common origin of muon and electron recoil excess reported by the XENON1T collaboration Borah et al. (2020, 2021).
|
|
|
||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Minimal Gauged Model: The SM fermion content with their gauge charges under gauge symmetry are denoted as follows.
The new field content apart from the SM ones are shown in table 1. Only the second and third generations of leptons are charged under the gauge symmetry. The relevant Lagrangian can be written as
| (4) |
where is the SM Higgs doublet. The covariant derivatives for RHNs are defined by
| (5) | |||||
| (6) |
While the neutral component of the Higgs doublet breaks the electroweak gauge symmetry, the singlets break gauge symmetry after acquiring non-zero vacuum expectation values (VEV). Denoting the VEVs of singlets as , the new gauge boson mass can be found to be with being the gauge coupling. Clearly the model predicts diagonal charged lepton mass matrix and diagonal Dirac Yukawa of light neutrinos. Thus, the non-trivial neutrino mixing will arise from the structure of right handed neutrino mass matrix only which is generated by the chosen scalar singlet fields. The right handed neutrino mass matrix, Dirac neutrino mass matrix and charged lepton mass matrix are given by
| (7) |
Here is the VEV of neutral component of SM Higgs doublet . We can find the light neutrino mass matrix can be found by the type I seesaw formula as
| (8) | |||||
| (9) |
The mass matrices for RHN as well as light neutrinos in this model do not possess any specific structure and hence it is straightforward to fit the neutrino oscillation data. In the presence of only one scalar singlet , the RHN mass matrix has zero entries at and entries leading to a two-zero minor structure Asai et al. (2017) in . The light neutrino mass matrix, although does not contain any zeros, leads to two constraints among its elements. In view of tight constraints on neutrino parameters from global fit data Esteban et al. (2019); de Salas et al. (2021); Zyla et al. (2020) as well as cosmology bounds on sum of light neutrino masses from Planck 2018 data Aghanim et al. (2018), it is difficult to satisfy the data using the constrained structure of mass matrices. Similar conclusion was also arrived at in earlier works Asai et al. (2017, 2020). This becomes more restrictive when we constrain two of the RHNs to be in TeV regime with tiny mass splittings for resonant leptogenesis. Therefore, we have introduced another singlet scalar which gives rise to general structures of and .
It should be noted that, a kinetic mixing term between of SM and of the form can exist in the Lagrangian where are the field strength tensors of respectively and is the mixing parameter. Even if this mixing is considered to be absent in the Lagrangian, it can arise at one loop level with particles charged under both the gauge sectors in the loop. We consider this mixing to be . While the phenomenology of muon , leptogenesis in our model is not much dependent on this mixing, the experimental constraints on the model parameters can crucially depend upon this mixing. We therefore choose it to be small, around the same order as its one loop value.
Anomalous Muon Magnetic Moment: The magnetic moment of muon is defined as
| (10) |
where is the gyromagnetic ratio and its value is for an elementary spin particle of mass and charge . However, higher order radiative corrections can generate additional contributions to its magnetic moment and is parameterised as
| (11) |
As mentioned earlier, the anomalous muon magnetic moment has been measured very precisely in the recent Fermilab experiment while it has also been predicted in the SM to a great accuracy. In the model under consideration in this work, the additional contribution to muon magnetic moment arises dominantly from one loop diagram mediated by gauge boson . The corresponding one loop contribution is given by Brodsky and De Rafael (1968); Baek and Ko (2009)
| (12) |
where . Note that in the presence of additional Higgs doublets (a scenario which we will discuss in the upcoming sections) we can have another one-loop diagram mediated by charged component of such additional scalar doublet and right handed neutrino . However, since such particles in loop couple only to the left handed muons, the required chirality flip has to occur in external muon legs, leading to a suppressed contribution to muon . While there can be a very fine-tuned parameter space with large Yukawa couplings and specific loop particle masses Calibbi et al. (2018), it is unlikely to be in agreement with light neutrino mass data along with successful TeV scale leptogenesis requirements. We therefore do not study this fine-tuned possibility here and focus on the light neutral gauge boson contribution alone.
Resonant Leptogenesis: In this section we study the possibility of leptogenesis from the out of equilibrium decays of RHNs neutrinos . The generated asymmetry can be converted into a baryon asymmetry by the sphaleron processes which conserves asymmetry but violet asymmetry. The sphaleron processes are active between temperatures of GeV to GeV in the early Universe. At high temperatures the sphalerons are in thermal equilibrium and subsequently they freeze-out just before the electroweak symmetry breaking (EWSB) at around . Usually the mass of required to generated the observe asymmetry lies above the scale of GeV in conventional vanilla leptogenesis Plumacher (1997); Buchmuller et al. (2002). However, the detection of these very heavy right handed neutrinos is beyond the reach of LHC and other near future colliders. That is why we are mainly focusing on TeV scale leptogenesis in this work by exploiting the resonance enhancement condition (). This framework is known as resonant leptogenesis Pilaftsis (1997); Pilaftsis and Underwood (2004); Heeck and Teresi (2016). The relevant Yukawa matrix for leptogenesis can be identified to be
| (13) |
where are the elements of the matrix which diagonalises .
| (14) |
The CP asymmetry parameter corresponding to the CP violating decay of RHN (summing over all lepton flavours) is given by Pilaftsis and Underwood (2004)
| (15) | |||||
| (16) |
Since we are mainly focusing on the parameter space where such that the leptogenesis is mainly governed by the resonant enhancement between and and the CP asymmetry coming from the decay of is negligible. The resonance condition is satisfied when where is the decay width of the lightest RHN . The relevant asymmetry parameters namely, and crucially depend upon and respectively. From equation (13) one can write
From equation (LABEL:eq:complex1) the importance of the phases appearing in the elements of the matrix can be seen. These phases are appearing in the diagonalising matrix from the complex parameters in .
The relevant Boltzmann equations for our setup can be written as
| (18) | |||||
| (19) | |||||
| (20) | |||||
where and denote the comoving number densities of and respectievly. The equilibrium no densities of ’s are defined by , (with being the modified Bessel function of -th kind) and (for resonant leptogenesis). In , denotes any final state particle to which ’s can annihilate into. are the decay terms and are the inverse decay terms for and decays respectively, which are measures of the rate of decay and inverse decay with respect to the background expansion of the universe parametrised by Hubble expansion rate . They are defined as
| (21) | |||||
| (22) |
with being the decay parameter. The term on the right hand side of the equation (20) takes account of all the scattering processes that can act as possible washouts for the generated asymmetry. We identify the following scattering washouts in our model, , , , , , and . We take all of them into account in our numerical analysis and defined as,
| (23) |
Thus, apart from the usual Yukawa or SM gauge coupling related processes, we also have washout processes involving gauge boson. Since interactions involving can cause dilution of abundance as well as wash out the generated lepton asymmetry, one can tightly constrain the gauge sector couplings from the requirement of successful leptogenesis at low scale. Similar discussions on impact of such Abelian gauge sector on leptogenesis can be found in Iso et al. (2011); Okada et al. (2012); Heeck and Teresi (2016); Dev et al. (2018b); Mahanta and Borah (2021); Fileviez Pérez et al. (2021).
After solving the above Boltzmann equations, we convert the final asymmetry just before electroweak sphaleron freeze-out into the observed baryon to photon ratio by the standard formula
| (24) |
where is the sphaleron conversion factor (taking into account two Higgs doublets). Here denote the relativistic degrees of freedom at scale of leptogenesis and scale of recombination respectively. The final baryon to photon ratio is then compared with Planck 2018 data Zyla et al. (2020); Aghanim et al. (2018)
| (25) |
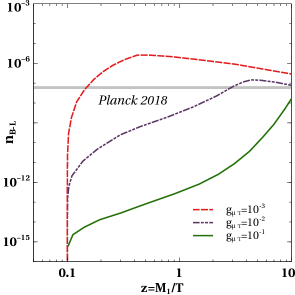
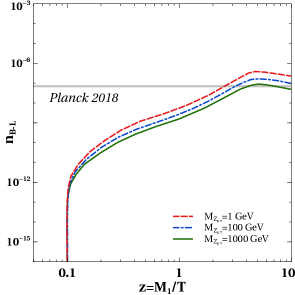
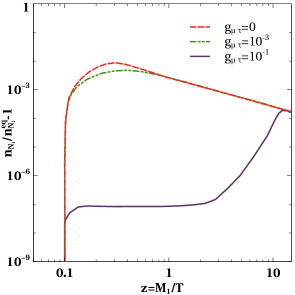
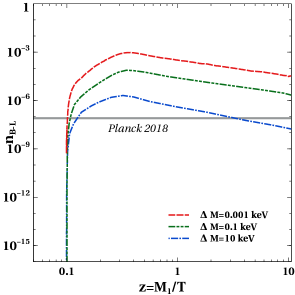
and constraints on the model parameters are obtained. In figure 1, we show the evolution of lepton asymmetries for different benchmark values of gauge coupling (left panel) and gauge boson mass (right panel) while keeping other parameters fixed. We can see that the asymmetry decreases with the increase in . It is because with the increase in the annihilations of through and to a pair of increases, which tries to bring the number densities close to their equilibrium densities. Thus, depletion in number densities of leads to a decrease in the final asymmetry.
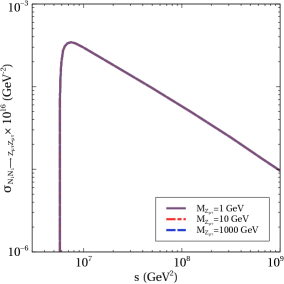
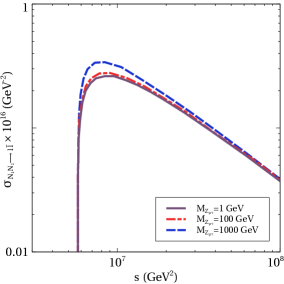
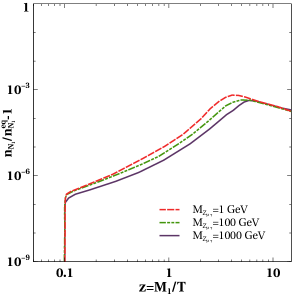
Again, from figure 1, we can see that the asymmetry decreases with increase in . This is because we have two types of annihilation of involving , the first one being the annihilation into a pair of leptons and the second one is the annihilation into a pair of . Out of these two processes, the dominant one is the annihilation into a pair of leptons as can be seen in figure 2 where the two annihilation cross-sections are shown as a function of center of mass energy squared for comparison. The annihilation of into a pair of lepton is possible through a s-channel diagram mediated by and through a t-channel diagram mediated by scalar doublet. The s-channel diagram mediated by singlet scalar due to mixing with the SM like Higgs is ignored as such mixing is generated only after electroweak symmetry breaking. As we are working in the region of parameter space where , therefore with increase in the cross sections for the mediated processes increase as seen from the right panel plot of figure 2. This tends to bring the number density closer to its equilibrium density and therefore leading to a decrease in asymmetry. We show this effect in figure 3. Clearly, increase in gauge coupling takes the number density of closer to its equilibrium number density, as seen from the left panel plot of figure 3 . Increase in also has a similar but milder effect, as seen from the right panel plot of figure 3.
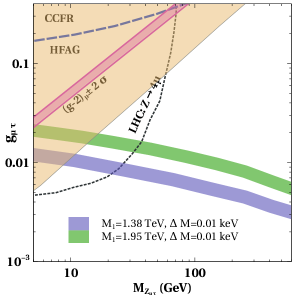
In figure 4, we summarise the results in parameter space considering mass larger than a GeV. The pink coloured band is the favoured region in plane from the Fermilab’s result on muon (g-2). The yellow coloured region is excluded by the upper bound on neutrino trident process measured by the CCFR collaboration Altmannshofer et al. (2014). Therefore one can clearly see that the muon favoured region in the high mass regime of is completely excluded from the bound on neutrino trident process. Additionally, the LHC bounds searches for multi-lepton final states signatures also rule out some part of the parameter space . We show the exclusion region from LHC measurements of Sirunyan et al. (2019) in terms of the dotted line. The region below the blue dashed line is allowed by HFAG lepton universality test at level Amhis et al. (2021). The leptogenesis favoured parameter space for two different scales of leptogenesis TeV, TeV are shown in blue and green coloured bands respectively. As increases, the annihilation rates of decreases, allowing slightly larger values of for fixed mass. On the other hand, as mass is increased towards , the annihilation rate of mediated by increases, requiring smaller values of in order to take out of equilibrium resulting in generation of lepton asymmetry.
If sub-GeV regime of is explored, there exists an allowed region in parameter space consistent with muon and other experimental bounds as discussed recently in Borah et al. (2020); Zu et al. (2021); Amaral et al. (2021); Zhou (2021); Borah et al. (2021). As we will see below, this allowed region correspond to MeV, . However, such sub-GeV will correspond to low scale breaking of gauge symmetry around 100 GeV, even below the sphaleron transition temperature. Prior to the symmetry breaking scale, the RHN mass matrix has very restrictive structure as can be realised by considering vanishing singlet scalar VEVs in given in (7). The fact that the model is inconsistent with successful leptogenesis in the symmetric limit was also noted in earlier works Adhikary (2006). Thus, one needs to go beyond the minimal setup in order to find a consistent picture accommodating both leptogenesis and muon while agreeing with experimental data including light neutrino mass and mixing.
Non-minimal Gauged Model:
|
|
|
|||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
In order to achieve successful leptogenesis with sub-GeV , we extend the minimal model with two additional Higgs doublets as shown in table 2. The presence of these additional Higgs doublets are required to allow corresponding Dirac Yukawa couplings with whose charges are chosen as with . While the Higgs doublet is neutral under this additional gauge symmetry, are charged. Singlet scalar charges are chosen to be respectively. Since gauge boson mass will be proportional to as well, in addition to and singlet VEVs, one can have symmetry breaking scale above the scale of leptogenesis while having in the desired range for explaining muon by choosing small .
With this new particle content in table 2, the singlet fermion Lagrangian remain same as before (except the new gauge charges of ) while the neutrino Dirac Yukawa terms change to the following
| (26) |
While the right handed neutrino mass matrix has the same structure as before, the Dirac neutrino mass matrix is changed to
| (27) |
Here we define , where , and are the VEV of neutral components of Higgs doublets , and respectively. We are assuming for simplicity so that GeV. While deviation from this assumption can lead to different phenomenology of such multi-Higgs doublet models, we do not expect leptogenesis results to change significantly and hence stick to this simple limit. Similarly, assuming the singlet VEVs to be identical to , the mass can be derived as
| (28) |
The model we adopt here has two SM-singlet scalars and three Higgs doublets. Since leptogenesis occurs below the scale of symmetry breaking, the singlet scalars are massive at the scale of leptogenesis. While they do not play any role in leptogenesis, their masses can still be constrained from experimental data. Bounds on such singlet scalars arise primarily due to its mixing with the SM like Higgs boson Robens and Stefaniak (2015); Chalons et al. (2016). The strongest bound on singlet scalar-SM like Higgs mixing angle () comes form boson mass correction López-Val and Robens (2014) at NLO for GeV as () where is the mass of singlet scalar . On the other hand, for GeV, the bounds from the requirement of perturbativity and unitarity of the theory turn dominant which gives . For lower values singlet masses GeV, the LHC and LEP direct search Khachatryan et al. (2015); Strassler and Zurek (2008) and measured Higgs signal strength Strassler and Zurek (2008) restrict the mixing angle dominantly (). The bounds from the measured value of EW precision parameter are mild for TeV. Since singlet scalars do not play any role in leptogenesis, we can tune their couplings with the SM like Higgs so that the mixing angle remains as small as required. On the other hand, the physical scalars arising from Higgs doublets are also constrained from experiments. While they remain massless at the scale of leptogenesis due to unbroken electroweak symmetry, several studies like Mühlleitner et al. (2017); Haller et al. (2018); Misiak and Steinhauser (2017); Arhrib et al. (2018) and references therein, have studied the phenomenology of such multi-Higgs doublet models. While the bounds from existing experiments depend upon the type of such models, the lower bounds on additional scalar masses, arising out of such additional Higgs doublets can range from around 100 GeV to a few hundred GeVs. Since we can satisfy these bounds by appropriate tuning of scalar potential parameters and without affecting the results related to leptogenesis, we do not elaborate them further in this work.
We then follow the same procedure as above by diagonalising and rewrite in the diagonal basis followed by solving the Boltzmann equations numerically to find the asymmetry. We keep the values of and in the region favoured by muon . With such small values of and while keeping the singlet VEVs above the masses of the RHNs, the required value of parameter becomes less than unity reducing the interaction strength of the RHNs with compared to the earlier model. As a consequence, the annihilation of RHNs into a pair of or other annihilation mediated by remain sub-dominant and hence do not play any significant role in our analysis. Therefore, abundances are primarily determined by their decays.
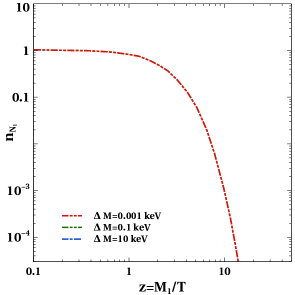
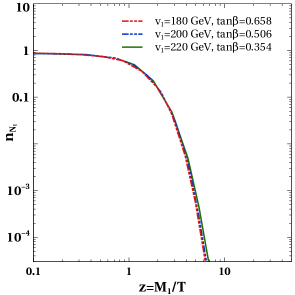
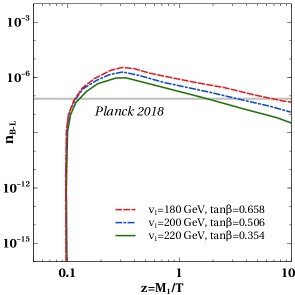
Similarly, in the muon favoured regime of , the washouts involving are very feeble and do not produce any significant effect on asymmetry. The dominant washout processes in this regime are the inverse decays and the scattering . In figure 5 we show the evolution of abundance for different benchmark parameters. Since abundance is primarily governed by decays in this regime, we do not see much differences due to change in model parameters like mass splitting or . Similarly, in figure 6, we show the evolution of for different combination of mass splitting (left panel) and (right panel). Clearly, the asymmetry is maximum for smallest mass splitting. It is because of the resonance enhancement of the asymmetry. The decay widths are of the order of GeV, within the parameter space we are interested in and as the mass splitting reaches near that value the CP asymmetry increases sharply to due to the resonance enhancement condition mentioned earlier. On the right panel of figure 6 it is seen that asymmetry increases for larger values of . Once we fix the entries of the Dirac mass matrix from neutrino oscillation data, the Yukawa couplings ( and ) relevant for leptogensis are very tightly constrained to . Since , one requires smaller values of Yukawa couplings ( and ) for larger values of to satisfy light neutrino data, for a fixed scale of leptogenesis. As a consequence of that the decay widths of decrease and also the corresponding inverse decay rates. The small difference in the decay rates of is marginally visible in the evolution plots of of figure 5 (right panel) as well. Since lepton asymmetry is generated primarily due to resonant enhancement, decrease in Yukawa coupling (or increase in ) decreases the inverse decay rates which increases the asymmetry as can be seen from the right panel plot of figure 6.
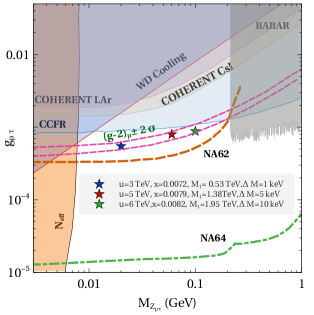
Due to the feeble gauge portal interactions in the low mass regime of , we do not find any strong correlation in plane from leptogenesis unlike in the previous model. Nevertheless, it is observed that low scale leptogenesis is possible in the region of plane favoured by muon (). We show a summary plot in figure 7 showing the allowed parameter space in plane and show three possible benchmark points for TeV scale leptogenesis which also satisfy the light neutrino data.
In equation (29) we show the numerical value of the Yukawa matrix for first benchmark point of figure 7.
| (29) |
Since the viability of resonant leptogenesis crucially depends upon quasi-degenerate right handed neutrinos, we show the structure of the RHN mass matrix too corresponding to the first benchmark point of figure 7 as
| (30) |
in the units of TeV. Accordingly, the bare mass terms as well as the singlet scalar Yukawa couplings with the RHNs can be tuned. The above mass matrix gives rise to two quasi-degenerate RHNs with masses TeV with mass splitting keV and TeV.
In summary plot of figure 7, the parameter space corresponding to Fermilab’s muon data is shown between the dashed pink coloured lines. Several experimental constraints are also shown in the summary plot of figure 7. The cyan coloured exclusion band labelled as CCFR correspond to the upper bound on neutrino trident process measured by the CCFR collaboration Altmannshofer et al. (2014). In the high mass regime for the exclusion region labelled as BABAR corresponds to the limits imposed on four muon final states by the BABAR collaboration Lees et al. (2016). The astrophysical bounds from cooling of white dwarf (WD) Bauer et al. (2020); Kamada et al. (2018) excludes the upper left triangular region. Very light is ruled out from cosmological constraints on effective relativistic degrees of freedom Aghanim et al. (2018); Kamada et al. (2018); Ibe et al. (2020); Escudero et al. (2019). This arises due to the late decay of such light gauge bosons into SM leptons, after standard neutrino decoupling temperatures thereby enhancing . More stringent constraints apply if DM is in the sub-GeV regime and its thermal relic is dictated by annihilation mediated by . However, in our case, such additional constraints do not arise as DM is much heavier and uncharged under gauge symmetry. The observation of coherent elastic neutrino-nucleus cross section in liquid argon (LAr) and cesium-iodide (CsI) performed by the COHERENT Collaboration Akimov et al. (2017, 2021) also leads to constraint on parameter space. Adopting the analysis of Cadeddu et al. (2021); Banerjee et al. (2021), we impose these bounds, labelled as COHERENT LAr and COHERENT CsI respectively in figure 7. Clearly, even after incorporating all existing experimental bounds, there still exists a small parameter space between a few MeV to around 100 MeV consistent with all bounds and the requirement of explaining muon . The three points denoted by stars correspond to benchmark values of parameters for which the correct baryon asymmetry can be generated via resonant leptogenesis. Therefore, we can have successful TeV scale resonant leptogenesis while also satisfying the Fermilab’s data on muon (g-2). This allowed region from muon (g-2) and also TeV scale leptogenesis remains within the reach of future experiments like NA62 at CERN Krnjaic et al. (2020) (Orange dashed line in figure 7), the NA64 experiment at CERN (dot-dashed line of green colour in figure 7) Gninenko et al. (2015); Gninenko and Krasnikov (2018). Possible future confirmation of this muon favoured parameter space will also indicate the possible scale of leptogenesis in this model.
Conclusion: We have studied the possibility of TeV scale resonant leptogenesis in gauged model with type I seesaw origin of light neutrino masses. While the minimal version of such a model has only one scalar singlet, we found it too constrained from light neutrino data specially if we demand two of the right handed neutrinos to be quasi-degenerate from the requirement of resonant leptogenesis. We then considered the two singlet scalars version of this model and showed the possibility of TeV scale leptogenesis while satisfying light neutrino data. We also found interesting correlations between gauge sector parameters from the criteria of successful leptogenesis. Since the requirement of successful leptogenesis at TeV scale requires broken gauge symmetry, this minimal setup requires heavy gauge boson above GeV scale. On the other hand, the muon favoured parameter space for such heavy is already ruled out by neutrino trident data and (partially) by the LHC constraints on . We then consider an extended version of this model with the possibility of sub-GeV even with TeV scale gauge symmetry breaking due to singlet scalars having fractional gauge charge less than unity. This requires two right handed neutrinos to have fractional charges too requiring the presence of additional Higgs doublets to allow the required Dirac neutrino Yukawa couplings. We show that, successful TeV scale resonant leptogenesis is possible in this model while satisfying muon and light neutrino data and also evading other experimental constraints on such sub-GeV leptophillic gauge sector. The presence of additional Higgs doublets can also give rise to interesting phenomenology, similar to two Higgs doublet models discussed extensively in the literature Branco et al. (2012).
Acknowledgements.
DB acknowledges the support from Early Career Research Award from DST-SERB, Government of India (reference number: ECR/2017/001873).References
- Abi et al. (2021) B. Abi et al. (Muon g-2), Phys. Rev. Lett. 126, 141801 (2021), eprint 2104.03281.
- Borsanyi et al. (2020) S. Borsanyi et al. (2020), eprint 2002.12347.
- Crivellin et al. (2020) A. Crivellin, M. Hoferichter, C. A. Manzari, and M. Montull, Phys. Rev. Lett. 125, 091801 (2020), eprint 2003.04886.
- Aoyama et al. (2020) T. Aoyama et al. (2020), eprint 2006.04822.
- Zyla et al. (2020) P. A. Zyla et al. (Particle Data Group), PTEP 2020, 083C01 (2020).
- Athron et al. (2021) P. Athron, C. Balázs, D. H. Jacob, W. Kotlarski, D. Stöckinger, and H. Stöckinger-Kim (2021), eprint 2104.03691.
- Borah et al. (2020) D. Borah, S. Mahapatra, D. Nanda, and N. Sahu (2020), eprint 2007.10754.
- Zu et al. (2021) L. Zu, X. Pan, L. Feng, Q. Yuan, and Y.-Z. Fan (2021), eprint 2104.03340.
- Amaral et al. (2021) D. W. P. Amaral, D. G. Cerdeño, A. Cheek, and P. Foldenauer (2021), eprint 2104.03297.
- Zhou (2021) S. Zhou (2021), eprint 2104.06858.
- Borah et al. (2021) D. Borah, M. Dutta, S. Mahapatra, and N. Sahu (2021), eprint 2104.05656.
- Aaij et al. (2021) R. Aaij et al. (LHCb) (2021), eprint 2103.11769.
- He et al. (1991a) X. He, G. C. Joshi, H. Lew, and R. Volkas, Phys. Rev. D 43, 22 (1991a).
- He et al. (1991b) X.-G. He, G. C. Joshi, H. Lew, and R. R. Volkas, Phys. Rev. D 44, 2118 (1991b).
- Minkowski (1977) P. Minkowski, Phys. Lett. B 67, 421 (1977).
- Mohapatra and Senjanovic (1980) R. N. Mohapatra and G. Senjanovic, Phys. Rev. Lett. 44, 912 (1980).
- Yanagida (1979) T. Yanagida, Conf. Proc. C7902131, 95 (1979).
- Gell-Mann et al. (1979) M. Gell-Mann, P. Ramond, and R. Slansky, Conf. Proc. C 790927, 315 (1979), eprint 1306.4669.
- Glashow (1980) S. Glashow, NATO Sci. Ser. B 61, 687 (1980).
- Schechter and Valle (1980) J. Schechter and J. Valle, Phys. Rev. D 22, 2227 (1980).
- Fukugita and Yanagida (1986) M. Fukugita and T. Yanagida, Phys. Lett. B174, 45 (1986).
- Davidson et al. (2008) S. Davidson, E. Nardi, and Y. Nir, Phys. Rept. 466, 105 (2008), eprint 0802.2962.
- Davidson and Ibarra (2002) S. Davidson and A. Ibarra, Phys. Lett. B535, 25 (2002), eprint hep-ph/0202239.
- Adhikary (2006) B. Adhikary, Phys. Rev. D 74, 033002 (2006), eprint hep-ph/0604009.
- Chun and Turzynski (2007) E. J. Chun and K. Turzynski, Phys. Rev. D 76, 053008 (2007), eprint hep-ph/0703070.
- Ota and Rodejohann (2006) T. Ota and W. Rodejohann, Phys. Lett. B 639, 322 (2006), eprint hep-ph/0605231.
- Asai et al. (2017) K. Asai, K. Hamaguchi, and N. Nagata, Eur. Phys. J. C 77, 763 (2017), eprint 1705.00419.
- Asai et al. (2020) K. Asai, K. Hamaguchi, N. Nagata, and S.-Y. Tseng, JCAP 11, 013 (2020), eprint 2005.01039.
- Pilaftsis (1999) A. Pilaftsis, Int. J. Mod. Phys. A14, 1811 (1999), eprint hep-ph/9812256.
- Pilaftsis and Underwood (2004) A. Pilaftsis and T. E. J. Underwood, Nucl. Phys. B692, 303 (2004), eprint hep-ph/0309342.
- Moffat et al. (2018) K. Moffat, S. Pascoli, S. T. Petcov, H. Schulz, and J. Turner, Phys. Rev. D98, 015036 (2018), eprint 1804.05066.
- Dev et al. (2018a) P. S. B. Dev, M. Garny, J. Klaric, P. Millington, and D. Teresi, Int. J. Mod. Phys. A33, 1842003 (2018a), eprint 1711.02863.
- Biswas and Shaw (2019) A. Biswas and A. Shaw, JHEP 05, 165 (2019), eprint 1903.08745.
- Crivellin et al. (2015) A. Crivellin, G. D’Ambrosio, and J. Heeck, Phys. Rev. Lett. 114, 151801 (2015), eprint 1501.00993.
- Altmannshofer et al. (2016) W. Altmannshofer, M. Carena, and A. Crivellin, Phys. Rev. D 94, 095026 (2016), eprint 1604.08221.
- Esteban et al. (2019) I. Esteban, M. C. Gonzalez-Garcia, A. Hernandez-Cabezudo, M. Maltoni, and T. Schwetz, JHEP 01, 106 (2019), eprint 1811.05487.
- de Salas et al. (2021) P. F. de Salas, D. V. Forero, S. Gariazzo, P. Martínez-Miravé, O. Mena, C. A. Ternes, M. Tórtola, and J. W. F. Valle, JHEP 02, 071 (2021), eprint 2006.11237.
- Aghanim et al. (2018) N. Aghanim et al. (Planck) (2018), eprint 1807.06209.
- Brodsky and De Rafael (1968) S. J. Brodsky and E. De Rafael, Phys. Rev. 168, 1620 (1968).
- Baek and Ko (2009) S. Baek and P. Ko, JCAP 10, 011 (2009), eprint 0811.1646.
- Calibbi et al. (2018) L. Calibbi, R. Ziegler, and J. Zupan, JHEP 07, 046 (2018), eprint 1804.00009.
- Plumacher (1997) M. Plumacher, Z. Phys. C 74, 549 (1997), eprint hep-ph/9604229.
- Buchmuller et al. (2002) W. Buchmuller, P. Di Bari, and M. Plumacher, Nucl. Phys. B643, 367 (2002), [Erratum: Nucl. Phys.B793,362(2008)], eprint hep-ph/0205349.
- Pilaftsis (1997) A. Pilaftsis, Phys. Rev. D 56, 5431 (1997), eprint hep-ph/9707235.
- Heeck and Teresi (2016) J. Heeck and D. Teresi, Phys. Rev. D 94, 095024 (2016), eprint 1609.03594.
- Iso et al. (2011) S. Iso, N. Okada, and Y. Orikasa, Phys. Rev. D 83, 093011 (2011), eprint 1011.4769.
- Okada et al. (2012) N. Okada, Y. Orikasa, and T. Yamada, Phys. Rev. D 86, 076003 (2012), eprint 1207.1510.
- Dev et al. (2018b) P. S. B. Dev, R. N. Mohapatra, and Y. Zhang, JHEP 03, 122 (2018b), eprint 1711.07634.
- Mahanta and Borah (2021) D. Mahanta and D. Borah (2021), eprint 2101.02092.
- Fileviez Pérez et al. (2021) P. Fileviez Pérez, C. Murgui, and A. D. Plascencia (2021), eprint 2103.13397.
- Altmannshofer et al. (2014) W. Altmannshofer, S. Gori, M. Pospelov, and I. Yavin, Phys. Rev. Lett. 113, 091801 (2014), eprint 1406.2332.
- Sirunyan et al. (2019) A. M. Sirunyan et al. (CMS), Phys. Lett. B 792, 345 (2019), eprint 1808.03684.
- Amhis et al. (2021) Y. S. Amhis et al. (HFLAV), Eur. Phys. J. C 81, 226 (2021), eprint 1909.12524.
- Robens and Stefaniak (2015) T. Robens and T. Stefaniak, Eur. Phys. J. C75, 104 (2015), eprint 1501.02234.
- Chalons et al. (2016) G. Chalons, D. Lopez-Val, T. Robens, and T. Stefaniak, PoS ICHEP2016, 1180 (2016), eprint 1611.03007.
- López-Val and Robens (2014) D. López-Val and T. Robens, Phys. Rev. D 90, 114018 (2014), eprint 1406.1043.
- Khachatryan et al. (2015) V. Khachatryan et al. (CMS), JHEP 10, 144 (2015), eprint 1504.00936.
- Strassler and Zurek (2008) M. J. Strassler and K. M. Zurek, Phys. Lett. B661, 263 (2008), eprint hep-ph/0605193.
- Mühlleitner et al. (2017) M. Mühlleitner, M. O. P. Sampaio, R. Santos, and J. Wittbrodt, JHEP 08, 132 (2017), eprint 1703.07750.
- Haller et al. (2018) J. Haller, A. Hoecker, R. Kogler, K. Mönig, T. Peiffer, and J. Stelzer, Eur. Phys. J. C 78, 675 (2018), eprint 1803.01853.
- Misiak and Steinhauser (2017) M. Misiak and M. Steinhauser, Eur. Phys. J. C 77, 201 (2017), eprint 1702.04571.
- Arhrib et al. (2018) A. Arhrib, R. Benbrik, S. Moretti, A. Rouchad, Q.-S. Yan, and X. Zhang, JHEP 07, 007 (2018), eprint 1712.05332.
- Lees et al. (2016) J. Lees et al. (BaBar), Phys. Rev. D 94, 011102 (2016), eprint 1606.03501.
- Bauer et al. (2020) M. Bauer, P. Foldenauer, and J. Jaeckel, JHEP 18, 094 (2020), eprint 1803.05466.
- Kamada et al. (2018) A. Kamada, K. Kaneta, K. Yanagi, and H.-B. Yu, JHEP 06, 117 (2018), eprint 1805.00651.
- Ibe et al. (2020) M. Ibe, S. Kobayashi, Y. Nakayama, and S. Shirai, JHEP 04, 009 (2020), eprint 1912.12152.
- Escudero et al. (2019) M. Escudero, D. Hooper, G. Krnjaic, and M. Pierre, JHEP 03, 071 (2019), eprint 1901.02010.
- Akimov et al. (2017) D. Akimov et al. (COHERENT), Science 357, 1123 (2017), eprint 1708.01294.
- Akimov et al. (2021) D. Akimov et al. (COHERENT), Phys. Rev. Lett. 126, 012002 (2021), eprint 2003.10630.
- Cadeddu et al. (2021) M. Cadeddu, N. Cargioli, F. Dordei, C. Giunti, Y. F. Li, E. Picciau, and Y. Y. Zhang, JHEP 01, 116 (2021), eprint 2008.05022.
- Banerjee et al. (2021) H. Banerjee, B. Dutta, and S. Roy (2021), eprint 2103.10196.
- Krnjaic et al. (2020) G. Krnjaic, G. Marques-Tavares, D. Redigolo, and K. Tobioka, Phys. Rev. Lett. 124, 041802 (2020), eprint 1902.07715.
- Gninenko et al. (2015) S. Gninenko, N. Krasnikov, and V. Matveev, Phys. Rev. D 91, 095015 (2015), eprint 1412.1400.
- Gninenko and Krasnikov (2018) S. Gninenko and N. Krasnikov, Phys. Lett. B 783, 24 (2018), eprint 1801.10448.
- Branco et al. (2012) G. C. Branco, P. M. Ferreira, L. Lavoura, M. N. Rebelo, M. Sher, and J. P. Silva, Phys. Rept. 516, 1 (2012), eprint 1106.0034.