Testing Autonomous Systems with Believed Equivalence Refinement

Let $f:\mathcal{D}_{in}\rightarrow\mathcal{D}_{out}$ be the function under analysis, where $\mathcal{D}_{in}$ and $\mathcal{D}_{out}$ are the input and the output domain respectively. Let $evl:\mathcal{D}_{in}\times\mathcal{D}_{out}\rightarrow\mathcal{D}_{evl}$ be an evaluation function that assigns an input-output pair with a value in the evaluation domain $\mathcal{D}_{evl}$. Let $\mathcal{C}=\{C_{1},\ldots,C_{m}\}$ be the set of categories, where for $i\in\{1,\ldots,m\}$, each category $C_{i}=\{c_{i,1},\ldots,c_{i,|C_{i}|}\}$ has a set of elements with the set size being $|C_{i}|$. In our example, we may use $C_{i}.c_{i,j}$ to clearly indicate the element and its belonging category. Each element $c_{i,j}:\mathcal{D}_{in}\rightarrow\{{\small\textsf{{false}}},{\small\textsf{{true}}}\}$ evaluates any input in the domain to true or false. We assume that for any input ${\small\textsf{{in}}}\in\mathcal{D}_{in}$, for every $i$ there exists exactly one $j$ ($\exists!j\in\{1,\ldots,|C_{i}|\}$) such that $c_{i,j}({\small\textsf{{in}}})={\small\textsf{{true}}}$, i.e., for each category, every input is associated to exactly one element.

In the following, we define believed equivalence over the test set. Intuitively, for any two data points in the test set, so long as their corresponding element information are the same, demonstrating believed equivalence requires that the results of the evaluation function are also the same.

Consider the example illustrated in Figure 1. Given $\mathcal{D}_{in}$ to be all possible pixel values in an image from the vehicle’s mounted camera, we build a highly simplified input categorization in the autonomous driving perception setup. Let $\mathcal{C}=\{{\small\textsf{{Time}}},{\small\textsf{{Front-Vehicle}}}\}$, where Time = $\{{\small\textsf{{day}}},{\small\textsf{{night}}}\}$, Front-Vehicle = {exist, not-exist} indicates whether in the associated ground truth, there exists a vehicle in the front. Consider $f$ to be a DNN that performs front-vehicle detection. The first output of $f$, denoted as $f_{1}$, generates 1 for indicating “DETECTED” (a front vehicle is detected, as shown in Figure 1 with dashed rectangles) and 0 for “UNDETECTED”. Based on the input image, let $evl$ be the function that checks if the detection result made by the DNN is consistent with the ground truth, i.e., $evl({\small\textsf{{in}}},f({\small\textsf{{in}}}))={\small\textsf{{true}}}$ iff $({\small\textsf{{Front-Vehicle.exist}}}({\small\textsf{{in}}})={\small\textsf{{true}}}\leftrightarrow f_{1}({\small\textsf{{in}}})={\small\textsf{{1}}})$.

As illustrated in Figure 1, let $\mathcal{D}_{test}=\{{\small\textsf{{in}}}_{1},\ldots,{\small\textsf{{in}}}_{9}\}$. For ${\small\textsf{{in}}}_{1}$ and ${\small\textsf{{in}}}_{2}$, one can observe from Figure 1 that $evl({\small\textsf{{in}}}_{1},f({\small\textsf{{in}}}_{1}))=evl({\small\textsf{{in}}}_{2},f({\small\textsf{{in}}}_{2}))$. Then $f$ demonstrates believed equivalence over $\mathcal{C}$ under $\mathcal{D}_{test}$, provided that the following conditions also hold.

• •

  $evl({\small\textsf{{in}}}_{3},f({\small\textsf{{in}}}_{3}))=evl({\small\textsf{{in}}}_{4},f({\small\textsf{{in}}}_{4}))$,

• •

  $evl({\small\textsf{{in}}}_{5},f({\small\textsf{{in}}}_{5}))=evl({\small\textsf{{in}}}_{6},f({\small\textsf{{in}}}_{6}))\\ =evl({\small\textsf{{in}}}_{7},f({\small\textsf{{in}}}_{7}))$,

• •

  $evl({\small\textsf{{in}}}_{8},f({\small\textsf{{in}}}_{8}))=evl({\small\textsf{{in}}}_{9},f({\small\textsf{{in}}}_{9}))$.

Test coverage can measure the degree that a system is tested against the provided test set. In the following lemma, we associate our formulation of believed equivalence with the combinatorial explosion problem of achieving full test coverage. Precisely, the size of the test set to demonstrate believed equivalence while completely covering all combinations as specified in the categories is exponential to the number of categories.

As the number of categories can easily achieve $50$, even when each category has only $2$ elements, achieving full coverage using the condition in Eq. 1 requires at least $2^{50}$ different test cases; this is in most applications unrealistic. Therefore, we consider asserting full coverage using $\gamma$-way combinatorial testing [16], which only requires the set of test cases to cover, for every pair ($\gamma=2$) or triple ($\gamma=3$) of categories, all possible combinations. The following lemma states the following: Provided that $\gamma$ is a constant, the number of test cases to achieve full coverage can be bounded by a polynomial with $\gamma$ being its highest degree.

Figure 2 illustrates an example for coverage with $2$-way combinatorial testing, where $C=\{C_{1},C_{2},C_{3}\}$ with each $C_{i}$ ($i\in\{1,2,3\}$) having $c_{i,1}$ and $c_{i,2}$ accordingly. Let $\mathcal{D}_{test}=\{{\small\textsf{{in}}}_{1},\ldots,{\small\textsf{{in}}}_{6}\}$ (i.e., excluding ${\small\textsf{{in}}}_{7}$ and ${\small\textsf{{in}}}_{8}$). Apart from $\mathcal{D}_{test}$ demonstrating believed equivalence, $\mathcal{D}_{test}$ also satisfies the condition as specified in Lemma 2. By arbitrary picking $2$ categories among $\{C_{1},C_{2},C_{3}\}$, for instance $C_{1}$ and $C_{2}$, all combinations are covered by elements in $\mathcal{D}_{test}$ ($c_{1,1}c_{2,1}\mapsto{\small\textsf{{in}}}_{5},{\small\textsf{{in}}}_{6}$; $c_{1,1}c_{1,2}\mapsto{\small\textsf{{in}}}_{3}$; $c_{1,2}c_{2,1}\mapsto{\small\textsf{{in}}}_{4}$; $c_{1,2}c_{2,2}\mapsto{\small\textsf{{in}}}_{1},{\small\textsf{{in}}}_{2}$).

As the definition of believed equivalence is based on the test set $\mathcal{D}_{test}$, upon new test cases outside the test set, i.e., $\mathcal{D}_{in}\setminus\mathcal{D}_{test}$, the function under analysis may not demonstrate consistent behavior. We first present a formal definition on consistency.

The following result show that, under a newly encountered consistent test case, one can add it to the existing test set while still demonstrating believed equivalence.

Consider again the example in Figure 2. Provided that $\mathcal{D}_{test}=\{{\small\textsf{{in}}}_{1},\ldots,{\small\textsf{{in}}}_{6}\}$, one can observe that ${\small\textsf{{in}}}_{8}$ is consistent with $f\models^{evl}_{\mathcal{D}_{test}}\mathcal{C}$ (as for $c_{1,1}c_{2,2}c_{3,1}$, there exists no test case from $\mathcal{D}_{test}$), while ${\small\textsf{{in}}}_{7}$ is inconsistent (the evaluated result for ${\small\textsf{{in}}}_{7}$ is not the same as ${\small\textsf{{in}}}_{1}$ and ${\small\textsf{{in}}}_{2}$).

Encountering a new test case ${\small\textsf{{in'}}}\in\mathcal{D}_{in}\setminus\mathcal{D}_{test}$ that generates inconsistency, there are two methods to resolve the inconsistency depending on whether $f$ is implemented correctly.

• •

  (When $f$ is wrong - function modification) Function modification refers to the change of $f$ to $f^{\prime}$ such that the evaluation over in’ turns consistent; it is used when $f$ is engineered wrongly. For the example illustrated in Figure 2, a modification of $f$ shall ensure that ${\small\textsf{{in}}}_{1}$, ${\small\textsf{{in}}}_{2}$, and ${\small\textsf{{in}}}_{7}$ have the same evaluated value (demonstrated using the same color).

• •

  (When $f$ is correct - refining the believed equivalence class) When $f$ is implemented correctly, it implies that our believed equivalence, based on the currently defined category $\mathcal{C}$, is too coarse. Therefore, it is necessary to refine $\mathcal{C}$ such that the created believed equivalence separates the newly introduced test case from others. To ease understanding, consider again the example in Figure 1. When one encounters an image where the front vehicle is a white trailer truck, and under heavy snows, we envision that the front vehicle can be undetected. Therefore, the currently maintained categories shall be further modified to

  • –

    differentiate images by snowy conditions (preferably via proposing a new category), and

  • –

    differentiate images having front vehicles in white from front vehicles having non-white colors (preferably via refining an existing element in a category).

In the next section, we mathematically define the concept of refinement to cope with the above two types of changes in categories.

To ease understanding, Figure 3 shows the visualization for two such cuts.²²2Note that Figure 3, the cut using a plane is only for illustration purposes; the condition as specified in Definition 3 allows to form cuts in arbitrary shapes. The cut in the left refines $c_{2,2}$ to $c_{2,2,1}$ and $c_{2,2,2}$, and the cut in the right refines $c_{1,2}$ to $c_{1,2,1}$ and $c_{1,2,2}$. One can observe that the left cut can enable a refined believed equivalence, as the cut has separated ${\small\textsf{{in}}}_{7}$ from ${\small\textsf{{in}}}_{1}$ and ${\small\textsf{{in}}}_{2}$. This brings us to the definition of effective refinement cuts.

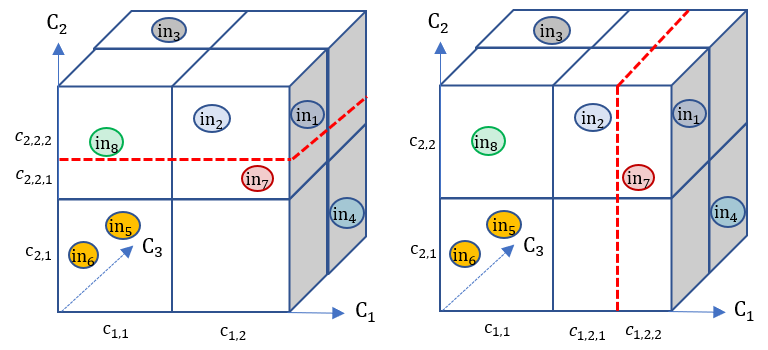
Apart from cuts, the second type of refinement is to add another category.

In contrast to refinement cuts where effectiveness is subject to how cuts are defined, the following lemma paraphrases that refinement-by-expansion is by-definition effective.

For $\gamma$-way combinatorial testing, in the worst case, the newly introduced element ($c_{m+1,2}$ in the refinement-by-expansion case; $c_{i,j,1}$ or $c_{i,j,2}$ in the refinement-by-cut case) will only be covered by the newly encountered test case ${\small\textsf{{in'}}}\not\in\mathcal{D}_{test}$. As one element has been fixed, the number of additional test cases to be introduced to recover full coverage can be conservatively polynomially bounded by ${{m}\choose{\gamma-1}}S^{\gamma}$, where $S=\max\{|C_{1}|,\ldots,|C_{m}|\}$. Under the case of $\gamma$ being a constant, the polynomial is one degree lower than the one as constrained in Lemma 2.

Finally, we omit technical formulations, but as refinement is operated based on the set of categories, it is possible to define the hierarchy of coverage accordingly utilizing the refinement concept. As a simple example, consider the element vehicle being refined to ${\small\textsf{{vehicle}}}_{{\small\textsf{{car}}}}$, ${\small\textsf{{vehicle}}}_{{\small\textsf{{truck}}}}$ and ${\small\textsf{{vehicle}}}_{{\small\textsf{{others}}}}$ to reflect different types of vehicle and their different performance profile. The coverage on vehicle can be an aggregation over the computed coverage from three refined elements.

Finally, we address the special case where the refinement can be computed analytically. Precisely, we consider the input domain $\mathcal{D}_{in}$ being $\mathbb{R}^{m}$, i.e., the system takes $m$ inputs $x_{1},\ldots,x_{m}$ over reals, where $m$ matches the size of the category set. We also consider that every category $C_{i}=\{c_{i,1},\ldots,c_{i,i_{k}}\}$ is characterized by $k+1$ ascending values $\alpha_{i,0},\alpha_{i,1},\ldots,\alpha_{i,i_{k}}$, such that $C_{i}$ performs a simple partitioning over the $i$-th input, i.e., for ${\small\textsf{{in}}}=(x_{1},\ldots,x_{m})$, $c_{i,j}({\small\textsf{{in}}})={\small\textsf{{true}}}$ iff $x_{i}\in(\alpha_{i,j-1},\alpha_{i,j}]$. Figure 4 illustrates the idea. The above formulation fits well for analyzing systems such as deep neural networks where each input is commonly normalized to a value within the interval $[-1,1]$.

Using Definition 3, a refinement-by-cut $RC(\mathcal{C},i,j)$ implies to find a value $\beta_{i,j}\in(\alpha_{i,j-1},\alpha_{i,j}]$ such that (1) $c_{i,j,1}={\small\textsf{{true}}}$ iff $x_{i}\in(\alpha_{i,j-1},\beta_{i,j}]$ and (2) $c_{i,j,2}={\small\textsf{{true}}}$ iff $x_{i}\in(\beta_{i,j},\alpha_{i,j}]$. Provided that ${\small\textsf{{in'}}}=(x_{1}^{\prime},\ldots,x_{m}^{\prime})$ being the newly encountered test case, we present one possible analytical approach for finding such a cut, via solving the following optimization problem:

subject to:

In the above stated optimization problem, apart from constraints as specified in Equation 4 which follows the standard definition as regulated in Definition 4 (illustrated in Figure 5a), we additionally impose two optional constraints Eq. 5 and Eq. 6.

• •

  First, we wish to regulate the size of the newly created element such that the new believed equivalence class generalizes better by keeping a minimal distance $\epsilon$ to the boundary $\beta_{i,j}$ (illustrated in Figure 5b).

• •

  Secondly, we also specify that all inputs within the $\epsilon$-ball centered by in’ demonstrate consistent behavior, thereby demonstrating robustness via behavioral equivalence (illustrated in Figure 5c).

The following lemma states the condition where the optimization problem can be solved analytically using integer linear programming. For general cases, nonlinear programming is required.

Finally, as the local robustness condition in Equation 6 is computationally hard to be estimated for state-of-the-art neural networks, we consider an alternative proposal that checks robustness using the direction as suggested by $k$-nearest neighbors. The concept is illustrated using Figure 5d, where one needs to find a cut when encountering in’. The method proceeds by searching for its closest neighbors ${\small\textsf{{in}}}_{1}$, ${\small\textsf{{in}}}_{2}$ and ${\small\textsf{{in}}}_{3}$ (i.e., $k=3$), and builds three vectors pointing towards these neighbors. Then perturb in’ alongside the direction as suggested by these vectors using a fixed step size $\Delta$, until the evaluated value is no longer consistent (in Figure 5d; all rectangular points have consistent evaluated value like in’). Finally, decide the cut ($\beta_{i,j}$) by taking the minimum distance as reflected by perturbations using these three directions.

The generated cut may further subject to refinement (i.e., newly encountered test cases may lead to further inconsistency), but it can be viewed as a lazy approach where (1) we take only finite directions (in contract to local robustness that takes all directions) and (2) we take a fixed step size (in contract to local robustness that has an arbitrary step size). By doing so, the granularity of refinement shrinks on-the-fly when encountering new-yet-inconsistent test cases.

Integrating the above mindset, we present in Algorithm 1 lazy cut refinement for constructing believed equivalence from scratch. Line 3 builds an initial categorization for each variable by using the corresponding bound. We use the set $\mathcal{D}_{exp}$ to record all data points that have been considered in building the believed equivalence, where $\mathcal{D}_{exp}$ is initially set to empty (line 4). For every new data in to be considered, it is compared against all data points in $\mathcal{D}_{exp}$; if exists ${\small\textsf{{in'}}}\in\mathcal{D}_{exp}$ such that the believed equivalence is violated (line 7), then find the nearest neighbors in $D_{exp}$ (line 8) and pick one dimension to perform cut by refinement (line 8 mimicking the process in Figure 5(d)). Whenever the generated cut proposal $C_{i}^{\prime}$ satisfies the distant constraint as specified in Equation 5 (line 12), the original $C_{i}$ is replaced by $C_{i}^{\prime}$. Otherwise (lines 18-20), every proposed cut can not satisfy the distant constraint as specified in Equation 5 so the algorithm raises a warning (line 19). Finally, the data point in is inserted to $\mathcal{D}_{exp}$, representing that it has been considered. The presentation of the algorithm is simplified to ease understanding; in implementation one can employ multiple optimization methods (e.g., use memory hashing to avoid running the inner loop at line 6 completely) to speed up the construction process.