Terahertz waves generation using the isomorphs of PPKTP crystal: a theoretical investigation
Abstract
Highly efficient terahertz (THz) wave sources based on difference frequency generation (DFG) process in nonlinear optical crystals play an important role for the applications of THz wave. In order to find more novel nonlinear crystals, here we theoretically investigate the generation of THz wave using the isomorphs of periodically poled (PPKTP), including periodically poled RTP, KTA, RTA and CTA. By solving the cascaded difference frequency coupled wave equations, it is found that the intensities of the THz wave generated from the cascaded difference frequency processes are improved by 5.27, 2.87, 2.82, 3.03, and 2.76 times from the non-cascaded cases for KTP, RTP, KTA, RTA and CTA, respectively. The effects of the crystal absorption, the phase mismatch and the pump intensity are also analyzed in detail. This study might help to provide a stronger THz radiation source based on the nonlinear crystals.
1 Introduction
High-power and high-stability terahertz (THz) wave sources have received extensive attention due to their important applications in time-domain spectroscopy system, imaging, material detection, biomedical science, etc [1, 2, 3, 4, 5]. There are several methods to generate THz radiation, for example, optical parametric oscillation [6], photoconductive antenna [7], optical rectification [8] and optical difference frequency generation (DFG) [9]. Among these methods, optical DFG is widely used due to its advantages of wide tuning range, high output power, and running at room temperature, etc. In an optical DFG process, two tunable near-infrared lasers with similar frequencies are combined and interact in a nonlinear crystal. However, the traditional DFG method is limited by the order of difference frequency, and the conversion efficiency of THz wave is very low, even lower than the absorption effect of the crystal. To solve this problem, the method of cascaded DFG was proposed [10] and this method has the merits of higher quantum conversion efficiency and overcoming the limitation of Manley-Rowe condition [11]. Manley-Rowe condition means the highest achievable conversion efficiency is the quotient of output and input frequencies in the conventional optical conversion [12].
The periodically poled KTP crystal (PPKTP) is one of the most widely used crystals in nonlinear optics because it has wide transparency in the range of visible light and THz wave, and a relatively high nonlinear coefficient (15.4 pm/V at 1064 nm) and a high light damage threshold (10 J/cm2 at 1064 nm)[13]. PPKTP has many isomorphic crystals, such as RTP, KTA, RTA and CTA, which have similar properties as their "parent" KTP. PPKTP and its isomorphs have been applied for extended phase matching [14, 15], the generation of spectrally pure single photons sources at telecom wavelength [16, 17, 18] and for mid-infrared single photon generation [19].
Recently, the generation THz wave using PPKTP and PPRTP in cascade DFG process has been theoretically investigated and achieved the THz intensity enhancement of 5.53 and 2.95 times, respectively [20, 21]. These studies provide new possibilities in the direction of searching for new crystals with higher nonlinear coefficient for higher quantum efficiency. Inspired by the previous works [22, 23, 24, 25], here we study the THz generation from the other three isomorphs of KTP, namely KTA, RTA and CTA. We compare these three isomorphs with KTP and RTP in Table 1. Some optical properties of these three crystals are even better than KTP and RTP, especially the effective nonlinear coefficient of KTA, RTA and CTA are larger than KTP and RTP. So, we theoretically expect these crystals can also achieve high quantum conversion efficiency for generating THz wave. These isomorphic crystals may provide more options for the preparation of terahertz wave in experiment in the future.
This article consists of the following parts: Section 1 is the introduction part; In Section 2, we establish the theoretical model of cascaded DFG in the form of coupled wave equations. In Section 3, we first calculate the wave vector mismatch and THz intensity under cascade conditions, and then we compare the effects of different conditions on the THz intensity and the quantum conversion efficiency. We provide comprehensive discussions in Section 4, and finally summarize the article in Section 5.
| Name | PPKTP | PPRTP | PPKTA | PPRTA | PPCTA |
|---|---|---|---|---|---|
| Composition | |||||
| () | 0.0005 | 0.05 | 0.005 | ||
| () | 1.69 | 4.04 | 3.79 | 3.59 | 4.31 |
| (pm/V) | 15.4 | 17.1 | 16.2 | 17.4 | 18.1 |
| @282 THz | 1.8297 | 1.85302 | 1.86764 | 1.88087 | 1.91924 |
| @281 THz | 1.82956 | 1.85286 | 1.86749 | 1.88072 | 1.91908 |
| @1 THz | 3.80761 | 3.34908 | 4.02779 | 4.29029 | 3.97803 |
| (m) | 236.854 | 219.902 | 236.129 | 241.549 | 225.387 |
| References | [26, 27, 28, 29, 30, 31] | [31, 32, 33, 34] | [33, 35, 36, 37, 38, 39] | [33, 40, 41, 42, 43] | [41, 44, 45, 46] |
2 Theory
2.1 Characteristics of PPKTP and its isomorphic crystals
The five crystals that we use to generate THz radiation from the PPKTP family are listed in Table 1. They have the same point group (mm2) in structure, similar lattice constants (a1.281 nm, b0.6404 nm, c1.0616 nm) and similar transparency (in the range of 0.35-5.3m). They are isomorphic to each other, so they are close in characteristics. The isomorphs of PPKTP crystal have higher light damage thresholds than conventional nonlinear optical crystals (e.g. PPLN, ZnTe, and GaAs) [47, 48, 49]. In addition, PPKTP and its isomorphic crystals have lower refractive indexes in the THz band, which is conducive to the generation of high-power THz waves in the DFG processes.
In order to simulate the performance of these five crystals in THz generation, we summarize the key parameters in Table 1, where the initial frequency of pump and signal laser are 282 and 281 THz, corresponding to wavelength of about 1064 nm and 1067 nm respectively, THz wave frequency is 1 THz. Note, the absorption coefficients for KTP, RTP and KTA are obtained from previous experimental data, while the for RTA and CTA in optical band are still not reported in previous literatures. So, we theoretically assumed that RTA and CTA have the same value as KTA. The RTA and CTA are chosen to have closer absorption coefficients as KTA instead of RTP and KTP, because RTA, CTA, and KTA have the same chemical unit of . The refractive indices of the pump, the signal, and the THz wave in the crystal are obtained by using the Sellmeier equations respectively.

2.2 Theory of cascaded DFG
We assume the frequencies of the incident pump light, the signal light, and the THz wave are , and , respectively. Under the nonlinear interactions in a cascaded DFG, a series of waves with frequencies of …, , , , , … are generated, and their mutual interval is . The light with frequency higher than the incident frequency (, …) are called anti-Stokes light, and the light with frequency (…, ) lower than the incident frequency called Stokes light, as shown in Fig.1.
The coupled wave equations of cascaded DFG can be derived from the nonlinear parametric interaction coupled wave equations[50], with a specific form as follow[20]:
| (1) |
and
| (2) |
where and respectively represent the electric fields of the pump light and the THz wave. The second and third terms on the right hand side of Eq. (2) represent the Stokes process (generating THz photons) and the anti-Stokes process (consuming THz photons), respectively. In our theory, the direction of the electric field of the pump light, signal light and THz wave are the same (see Fig. 1), and are the absorption coefficients of the pump light and the THz wave in the crystal respectively, represents the phase mismatch in the cascade process, and are the coupling coefficients. The phase mismatch and the coupling coefficient can be calculated using the following equations [20]:
| (3) |
| (4) |
| (5) |
where is the effective nonlinear coefficient, ( = p, s) and are the refractive indices of pump (signal) light and THz wave, respectively, and is the poling period of the nonlinear crystal. Combined with the equations (1) and (2), the THz power density in the cascaded difference frequency processes can be calculated.
3 Numerical simulations
First, we consider the parameter of coherence length, which is defined as the distance of the second harmonic intensity reaching its maximum for the first time. Coherence length is an important parameter for optical pulses. The coherence length and the phase mismatch in PPKTP and its isomorphic crystals can be calculated according to Eq. (3). The relationship between and can be described by the following equation[21]:
| (6) |

The simulation for and is shown in Fig.2. In the simulation, the frequencies of the pump light and the signal light are set to be 282 and 281 THz, respectively; the THz wave frequency is 1 THz and the range of frequency is from 227 THz to 322 THz. See Mathematica codes in Supplementary Information.
In Fig.2, the value of approaches 0 near the initial frequency; the part lower than the initial frequency (, 227-280 THz) represents the Stokes process, and the part higher than the initial frequency (, 283-322 THz) represents the anti-Stokes process. As the cascade process continues, the gap between the pump wave vector () and the signal wave vector () increases, and the absolute value of also increases gradually. Simultaneously, the coherence length reaches the maximum near the initial frequency, and then decreases rapidly. Here, is shown in an exponent with a base of 10.

In order to observe the influence of cascaded DFG on THz wave intensity, we compare the THz wave intensity generated by PPKTP, PPRTP, PPKTA, PPRTA, and PPCTA in the case of non-cascaded DFG and cascaded DFG in Fig.3 (, , , , and order), respectively. It can be seen that the intensity of the THz wave in the case of no cascade (i.e. the order line) is very low. And it can be calculated that the THz intensity at -order cascaded DFG is 5.27, 2.82, 2.87, 3.03 and 2.76 times of the case of non-cascaded DFG, respectively. The results indicate that utilizing the isomorphs of PPKTP crystal and cascaded DFG method is feasible for increasing the intensity of the THz wave.
In Fig.3, the curves of the -order cascade and the -order cascade are almost overlapped, indicating that the THz wave intensity at the -order reaches the maximum. In this calculation, we give a same initial value 1 MW/mm2 of the pump and the signal intensity to calculate the THz intensity. In addition, the maximal THz intensity in Fig. 3(b, c, d, e) are comparable, i.e., between 0.02 and 0.03 MW/mm2, lower than the value in Fig. 3(a), which is mainly due to the absorption coefficient of PPKTP crystal in THz band is smaller than other crystals. Another interesting phenomenon is that a second peak appears when the cascade process continues in the PPKTP crystal (the phenomenon also exists in four crystals). This is because the THz wave is converted to pump light (sum frequency) when its intensity reaches the first peak in the cascade process, and then the difference frequency process continues to generate THz wave, but owing to the crystal absorption, the second peak is much weaker than the first one.
In the process of cascaded DFG, the crystal absorption and the phase mismatch are two most important factors affecting the THz intensity, so next we compare the variation of THz intensity as a function of propagation distance under three different combinations of these two factors in Fig.4. It can be noticed in Fig.4 that the effect of crystal absorption on the THz intensity is more significant than the phase mismatch, i.e., the phase mismatch has almost no effect on the THz intensity when the propagation distance is not long enough. Since the absorption coefficient of PPKTP crystal in THz band is only 1.69 cm-1 [28], much lower than the values of its isomorphic crystals, the THz intensity in the PPKTP crystal is much higher than the value in other crystals.
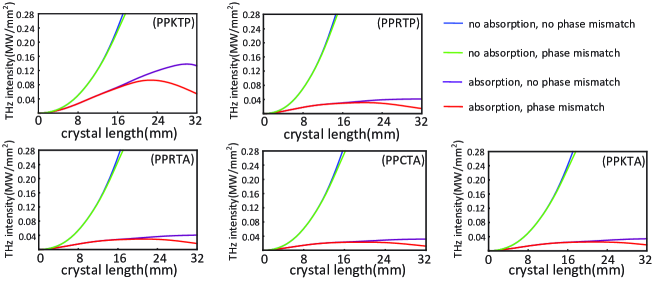

.
In the processes of generating THz wave from periodically poled crystals, quantum conversion efficiency is a very important parameter. The higher the quantum conversion efficiency, the greater the THz intensity, and the more useful for practical applications. Next, we simulate the quantum conversion efficiency in the cascaded DFG processes as a function of pump intensity in Fig.5 (considering 7th order condition). The pump intensity is directly related to the THz intensity and quantum conversion efficiency in the cascaded processes. As the cascade process continues, the pump intensity in the crystal gradually decreases. According to our and previous studies, the THz intensity will not change significantly after the 7th cascade process. We change the intensity of the pump light from 1 MW/mm2 to 20 MW/mm2 with an interval of 1 MW/mm2.
It can be noticed from Fig.5 that as the pump light intensity increases, the THz intensity and the quantum conversion efficiency are also enhanced. When the pump light intensity reaches 20 MW/mm2, the THz intensity and quantum conversion efficiency also reached their maximum. According to the calculation, the quantum conversion efficiency of PPKTP, PPRTP, PPKTA, PPRTA and PPCTA at 20 MW/mm2 pump intensity can reach 438.5%, 160.5%, 144.7%, 167.1%, and 135.1%, respectively, all exceed the Manley-Rowe limit. There are two reason reasons for this THz wave amplification during the DFG process: the first one is that one pump photon can generate multiple THz photons in the cascaded DFG process, and the second reason is that the three waves have a stronger interaction in the periodically poled crystal, due to the quasi-phase matching technology.
4 Discussion
In Fig. 3, we only investigate the cases where the cascaded DFG is under the 9th-order. For higher order cases, it can be calculated that the THz intensity does not increase any more. This is mainly due to the following fact: when the propagation distance increases, the Stokes (anti-Stokes) process decreased, at the same time, the crystal absorption of THz wave remains at a stable level.
The theoretical study in this article is based on room temperature. For periodically polarized crystals, temperature is a factor that cannot be ignored [51, 52, 53, 46]. The variation of temperature affects the refractive indices of the crystals, and thus changes the quasi-phase matching conditions of the crystal. Besides, temperature changes also affect the absorption coefficient of the pump light and the THz wave in the crystal, which are still in the stage of unexplored. It is promising to select appropriate conditions by controlling the temperature to make the THz intensity more efficient and stable.
KTP family have approximately 118 isomorphs [54, 55, 56], including 29 pure crystals and 89 doped crystals, all of which have a uniform form and can be written as , where M = K, Rb , Na, Cs, TI, NH4; = Ti, Sn, Sb, Zr, Ge, AI, Cr, Fe, V, Nb, Ta, Ga; X = P, As, Si, Ge. Only five of these crystals are studied in this paper, and most of the other crystals have not been thoroughly studied. Their Sellmeier equations, effective nonlinear coefficient and absorption coefficient are still unknown. Therefore, exploring the nonlinear optical properties of these crystals is necessary and may lead to more stable and stronger THz wave sources.
Here we discuss the limitation of this work. In the calculation, we mainly focus on the absorption effect of the different isomorphs in THz wave generation. However, some other effects also need to be taken into account. For example, the phase mismatch is affected by the dispersion of the pump in the medium. Furthermore, at high pump intensity, other limitations will occur, such as self-phase modulation (SPM) and cascaded effects. In the future, the theoretical model needs to be expanded to include these effects.
5 Conclusion
In conclusion, we have theoretically investigated the generation of THz wave from the isomorphs of PPKTP crystal, including PPRTP, PPKTA, PPRTA and PPCTA. The process of generating THz wave by cascaded DFG is studied in detail, and the influences of different conditions on THz wave intensity are analyzed comprehensively. The results show that cascaded DFG method can effectively improve the intensity of THz wave; quantum conversion efficiency that exceeding the Manley-Rowe condition can be achieved at high pump intensity. In addition, we find that the impact of crystal absorption on THz wave intensity is more important than the phase mismatch. This study may provide more and stronger THz light sources based on the nonlinear optics crystals for future practical applications.
6 Acknowledgments
We thank Dr. Fabian Laudenbach for help full discussions. This work is partially supported by the National Natural Science Foundations of China (Grant Nos. 91836102, 11704290, 12074299, 61775025).
Conflict of interest statement: The authors declared that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Supplementary Information: Mathematica codes for the figures in the main text.
References
- [1] X.-C. Zhang and J. Xu, Introduction to THz Wave Photonics (Springer, 2010), 2010th ed.
- [2] Y.-S. Lee, Principles of Terahertz Science and Technology (Springer, 2009), 1st ed.
- [3] K. Zhong, J.-Q. Yao, D.-G. Xu, H.-Y. Zhang, and P. Wang, “Theoretical research on cascaded difference frequency generation of terahertz radiation (in Chinese),” \JournalTitleActa Phys. Sin. 60, 034210 (2011).
- [4] K. Kawase and S. Hayashi, “Terahertz wave parametric generation and applications,” \JournalTitleProc. of SPIE 6772, 677202–(1–5) (2007).
- [5] K. Murate and K. Kawase, “Perspective: Terahertz wave parametric generator and its applications ,” \JournalTitleJ. Appl. Phys. 124, 160901 (2018).
- [6] Z. Li, P. Bing, D. Xu, and J. Yao, “High-power tunable terahertz generation from a surface-emitted THz-wave parametric oscillator based on two MgO:LiNbO3 crystals,” \JournalTitleChin. Phys. B 124, 4884–4886 (2013).
- [7] N. M. Burford and M. O. El-Shenawee, “Review of terahertz photoconductive antenna technology,” \JournalTitleOpt. Eng. 56, 010901 (2017).
- [8] H.-W. Du, H. Hoshina, and C. Otani, “Thz generation from optical rectification tilted-pulse-front pumping scheme with laser pulse focused to a line,” \JournalTitleProc. SPIE 9671, 96710M (2015).
- [9] Y. J. Ding, “Progress in terahertz sources based on difference-frequency generation,” \JournalTitleJ. Opt. Soc. Am. B 31, 2696–2711 (2014).
- [10] P. Liu, D. Xu, H. Yu, H. Zhang, Z. Li, K. Zhong, Y. Wang, and J. Yao, “Coupled-mode theory for cherenkov-type guided-wave terahertz generation via cascaded difference frequency generation,” \JournalTitleJ. Lightwave Technol. 31, 2508–2514 (2013).
- [11] K. Saito, T. Tanabe, and Y. Oyama, “Cascaded terahertz-wave generation efficiency in excess of the Manley-Rowe limit using a cavity phase-matched optical parametric oscillator,” \JournalTitleJ. Opt. Soc. Am. B 32, 617–621 (2015).
- [12] I. Waldmueller, M. C. Wanke, and W. W. Chow, “Circumventing the Manley-Rowe quantum efficiency limit in an optically pumped terahertz quantum-cascade amplifier,” \JournalTitlePhys. Rev. Lett. 99, 117401 (2007).
- [13] A. Hildenbrand, F. R. Wagner, H. Akhouayri, J.-Y. Natoli, M. Commandré, F. Théodore, and H. Albrecht, “Laser-induced damage investigation at 1064 nmin KTiOPO4 crystals and its analogy with RbTiOPO4,” \JournalTitleAppl. Opt. 48, 4263–4269 (2009).
- [14] T. Kim and K. J. Lee, “Extended phase matching properties of periodically poled potassium titanyl phosphate isomorphs,” \JournalTitleJ. Korean Phys. Soc. 67, 837–842 (2015).
- [15] I. Kim, D. Lee, and K. J. Lee, “Numerical investigation of high-purity polarization-entangled photon-pair generation in non-poled ktp isomorphs.” \JournalTitleAppl. Sci. 11, 565 (2021).
- [16] R.-B. Jin, P. Zhao, P. Deng, and Q.-L. Wu, “Spectrally pure states at telecommunications wavelengths from periodically poled MTiOXO4 (M = K, Rb, Cs; X = P, As) crystals,” \JournalTitlePhys. Rev. Appl. 6, 064017 (2016).
- [17] F. Laudenbach, R.-B. Jin, C. Greganti, M. Hentschel, P. Walther, and H. Hubel, “Numerical investigation of photon-pair generation in periodically poled TiOO4 (=K, Rb, Cs; =P, As),” \JournalTitlePhys. Rev. Appl. 8, 024035 (2017).
- [18] R.-B. Jin, G.-Q. Chen, F. Laudenbach, S. Zhao, and P.-X. Lu, “Thermal effects of the quantum states generated from the isomorphs of PPKTP crystal,” \JournalTitleOpt. Laser Technol. 109, 222–226 (2019).
- [19] R. A. McCracken, F. Graffitti, and A. Fedrizzi, “Numerical investigation of mid-infrared single-photon generation,” \JournalTitleJ. Opt. Soc. Am. B 35, C38–C48 (2018).
- [20] Z.-Y. Li, S.-L. Wang, M.-T. Wang, and W.-S. Wang, “Terahertz generation based on cascaded difference frequency generation with periodically-poled KTiOPO4,” \JournalTitleCurr. Opt. Photon. 1, 138–142 (2017).
- [21] Z.-Y. Li, M.-T. Wang, S.-L. Wang, D.-G. Xu, and J.-Q. Yao, “Highly efficient terahertz generation from periodically-poled RbTiOPO4,” \JournalTitleOptoelectron. Lett. 13, 127–130 (2017).
- [22] P. Liu, D. Xu, H. Yu, H. Zhang, Z. Li, K. Zhong, Y. Wang, and J. Yao, “Theoretical analysis of terahertz generation in periodically inverted nonlinear crystals based on cascaded difference frequency generation process,” \JournalTitleJ. Lightwave Technol. 31, 2508–2514 (2013).
- [23] C.-F. Hu, K. Zhong, J.-L. Mei, M.-R. Wang, S.-B. Guo, W.-Z. Xu, P.-X. Liu, D.-G. Xu, Y.-Y. Wang, and J.-Q. Yao, “Theoretical analysis of terahertz generation in periodically inverted nonlinear crystals based on cascaded difference frequency generation process,” \JournalTitleMod. Phys. Lett. B 29, 1450263 (2015).
- [24] W. Lu, A. Fallahi, K. Ravi, and F. K?rtner, “High efficiency terahertz generation in a multi-stage system,” \JournalTitleOpt. Express 26, 29744–29768 (2018).
- [25] W. Tian, G. Cirmi, H. T. Olgun, P. Mutter, and etc, “J-level multi-cycle terahertz generation in a periodically poled Rb: KTP crystal,” \JournalTitleOpt. Lett. 46, 761–764 (2021).
- [26] P. E. Perkins and T. S. Fahlen, “20-W average-power KTP intracavity-doubled Nd:YAG laser,” \JournalTitleJ. Opt. Soc. Am. B 4, 1066–1071 (1987).
- [27] D. J. Gettemy, W. C. Harker, G. Lindholm, and N. P. Barnes, “Some optical properties of KTP, LiIO3, and LiNbO3,” \JournalTitleIEEE J. Quantum Electron. 24, 2231–2237 (1988).
- [28] G. E. Kugel, F. Brehat, B. Wyncke, M. D. Fontana, G. Marnier, C. Carabatos-Nedelec, and J. Mangin, “The vibrational spectrum of a KTiOPO4 single crystal studied by Raman and infrared reflectivity spectroscopy,” \JournalTitleJ. Phys. C: Solid State Phys. 21, 5565 (1988).
- [29] I. Shoji, T. Kondo, A. Kitamoto, M. Shirane, and R. Ito, “Absolute scale of second-order nonlinear-optical coefficients,” \JournalTitleJ. Opt. Soc. Am. B 14, 2268–2294 (1997).
- [30] K. Kato and E. Takaoka, “Sellmeier and thermo-optic dispersion formulas for KTP,” \JournalTitleAppl. Opt. 41, 5040–5044 (2002).
- [31] M. Sang, J.-H. Qiu, T.-X. Yang, X.-C. Lu, and W.-L. Zhang, “Optical phonon resonance characteristics comparsion of KTP and RTP crystals in terahertz time-domain sperctroscopy,” \JournalTitleChin. J. Lasers 37 (2010).
- [32] L. K. Cheng, L. T. Cheng, J. Galperin, P. A. M. Hotsenpiller, and J. D. Bierlein, “Crystal growth and characterization of KTiOPO4 isomorphs from the self-fluxes,” \JournalTitleJ. Cryst. Growth 137, 107–115 (1994).
- [33] G. Hansson, H. Karlsson, S. Wang, and F. Laurell, “Transmission measurements in KTP and isomorphic compounds,” \JournalTitleAppl. Opt. 39, 5058–5069 (2000).
- [34] T. Mikami, T. Okamoto, and K. Kato, “Sellmeier and thermo-optic dispersion formulas for RbTiOPO4,” \JournalTitleOpt. Mater. 31, 1628–1630 (2009).
- [35] G. H. Watson, “Polarized raman spectra of KTiOAsO4 and isomorphic nonlinear-optical crystals,” \JournalTitleJ. Raman Spectrosc. 22, 705–713 (1991).
- [36] G. M. Loiacono, D. N. Loiacono, and J. J. Zola, “Optical properties and ionic conductivity of KTiOAsO4 crystals,” (1992), p. CThD5.
- [37] L. K. Cheng, L. T. Cheng, J. D. Bierlein, F. C. Zumsteg, and A. A. Ballman, “Properties of doped and undoped crystals of single domain KTiOAsO4,” \JournalTitleAppl. Phys. Lett. 62, 346–348 (1993).
- [38] K. Kato, N. Umemura, and E. Tanaka, “ phase-matched mid-infrared parametric oscillation in undoped KTiOAsO4,” \JournalTitleJpn. J. Appl. Phys. 36, L403 (1997).
- [39] P. Mounaix, L. Sarger, J. Caumes, and E. Freysz, “Characterization of non-linear Potassium crystals in the Terahertz frequency domain,” \JournalTitleOpti. Commun. 242, 631 – 639 (2004).
- [40] L. T. Cheng, L. K. Cheng, and J. D. Bierlein, “Linear and nonlinear optical properties of the arsenate isomorphs of KTP,” \JournalTitleProc. SPIE 1863, 43–53 (1993).
- [41] A. R. Guo, C. S. Tu, R. Tao, R. S. Katiyar, R. Guo, and A. S. Bhalla, “Temperature dependent raman scattering in RbTiOAsO4 and CsTiOAsO4 single crystals,” \JournalTitleFerroelectrics 188, 143–156 (1996).
- [42] Y. Yang and C. S. Yoon, “Dielectric properties of RbTiOAsO4 single crystals,” \JournalTitleAppl. Phys. Lett. 75, 1164–1166 (1999).
- [43] K. Kato, E. Takaoka, and N. Umemura, “Thermo-optic dispersion formula for RbTiOAsO4,” \JournalTitleJpn. J. Appl. Phys. 42, 6420 (2003).
- [44] L. T. Cheng, L. K. Cheng, J. D. Bierlein, and F. C. Zumsteg, “Nonlinear optical and electro-optical properties of single crystal CsTiOAsO4,” \JournalTitleAppl. Phys. Lett. 63, 2618–2620 (1993).
- [45] G. M. Loiacono, D. N. Loiacono, and R. A. Stolzenberger, “Crystal growth and characterization of ferroelectric CsTiOAsO4,” \JournalTitleJ. Cryst. Growth 131, 323 – 330 (1993).
- [46] T. Mikami, T. Okamoto, and K. Kato, “Sellmeier and thermo-optic dispersion formulas for CsTiOAsO4,” \JournalTitleJ. Appl. Phys. 109, 023108 (2011).
- [47] H.-W. Du and N. Yang, “Theoretical investigation on thz generation from optical rectification with tilted-pulse-front excitation,” \JournalTitleChin. Phys. Lett. 31, 124201 (2014).
- [48] M. Cronin-Golomb, “Cascaded nonlinear difference-frequency generation of enhanced terahertz wave production,” \JournalTitleOpt. Lett. 29, 2046–2048 (2004).
- [49] J. E. Schaar, K. L. Vodopyanov, P. S. Kuo, M. M. Fejer, X. Yu, A. Lin, J. S. Harris, D. Bliss, C. Lynch, V. G. Kozlov, and W. Hurlbut, “Terahertz sources based on intracavity parametric down-conversion in quasi-phase-matched gallium arsenide,” \JournalTitleIEEE J. Sel. Top. Quantum Electron. 14, 354–362 (2008).
- [50] K. Ravi, M. Hemmer, G. Cirmi, F. Reichert, D. N. Schimpf, O. D. Mücke, and F. X. Kärtner, “Cascaded parametric amplification for highly efficient terahertz generation,” \JournalTitleOpt. Lett. 41, 3806–3809 (2016).
- [51] R.-B. Jin, G.-Q. Chen, F. Laudenbach, S. Zhao, and P.-X. Lu, “Thermal effects of the quantum states generated from the isomorphs of PPKTP crystal,” \JournalTitleJ. Opt. Laser Technol. 109, 222–226 (2019).
- [52] S. Emanueli and A. Arie, “Temperature-dependent dispersion equations for KTiOPO4 and KTiOAsO4,” \JournalTitleAppl. Opt. 42, 6661–6665 (2003).
- [53] I. Yutsis, B. Kirshner, and A. Arie, “Temperature-dependent dispersion relations for RbTiOPO4 and RbTiOAsO4,” \JournalTitleAppl. Phys. B 79, 77–81 (2004).
- [54] G. D. Stucky, M. L. F. Phillips, and T. E. Gier, “The potassium titanyl phosphate structure field: a model for new nonlinear optical materials,” \JournalTitleChem. Mater. 1, 492–509 (1989).
- [55] N. I. Sorokina and V. I. Voronkova, “Structure and properties of crystals in the potassium titanyl phosphate family: A review,” \JournalTitleCryst. Rep. 52, 80–93 (2007).
- [56] A. P. Gazhulina and M. O. Marychev, “Pseudosymmetric features and nonlinear optical properties of potassium titanyl phosphate crystals,” \JournalTitleCryst. Struct. Theory Appl. 2, 106–119 (2013).