Tensor network for interpretable and efficient quantum-inspired machine learning
Abstract
It is a critical challenge to simultaneously gain high interpretability and efficiency with the current schemes of deep machine learning (ML). Tensor network (TN), which is a well-established mathematical tool originating from quantum mechanics, has shown its unique advantages on developing efficient “white-box” ML schemes. Here, we give a brief review on the inspiring progresses made in TN-based ML. On one hand, interpretability of TN ML is accommodated with the solid theoretical foundation based on quantum information and many-body physics. On the other hand, high efficiency can be rendered from the powerful TN representations and the advanced computational techniques developed in quantum many-body physics. With the fast development on quantum computers, TN is expected to conceive novel schemes runnable on quantum hardware, heading towards the “quantum artificial intelligence” in the forthcoming future.
I Introduction
Deep machine learning (ML) such as those based on deep neural network (NN) has achieved tremendous successes in, e.g., computer vision and natural language process. However, the dilemma between the interpretability and efficiency, which is a long-concerned topic [1, 2, 3, 4], has caused several severe challenges. Generally speaking, interpretability is defined as the degree to which a human can understand the cause of a decision, which is critical to question, understand, and trust the deep ML methods [4].
Though universal characterizations of interpretability are still controversial, it is widely recognized that the powerful deep NN models are non-interpretable. Due to their high non-linearity, rigorous understanding of the underlying mathematics of such models is mostly unlikely. Interpretations in these cases are usually “post hoc” (see, e.g., a recent work in Ref. [5]), in contrast to the “intrinsic” interpretation with “white-box” ML models or by knowing how the models work [3, 6]. Consequently, the investigations are generally conducted in an inefficient trial-and-error manner that consumes significant human and computational resources. Another serious issue brought by the non-interpretability concerns the robustness. For instance, a well-trained deep NN model might be severely disturbed by noises or intentional attacks (see, e.g., Ref. [7]). Currently, there exist no general theories to quantitatively characterize how far the deep NN models can be trusted or how significant different disturbances can affect the predictions. From the perspective of applications, interpretability concerns several vital issues such as fairness and privacy [8, 1].
Among the potential ways of opening the black boxes in deep ML, the (classical) probabilistic theories have drawn wide attentions. From a “revisionist” perspective, the deep NN has been incorporated with, e.g., the mutual information, relative entropy, or the physics-inspired renormalization groups [9, 10, 11, 12, 13], to show how the models process information. These interpretations are mostly post hoc, and help to understand the learning decision-making processes to certain extent. But the results or conclusions might strongly depend on data or the specifics of models.
The probabilistic ML models [14], such as Bayesian networks [15] and Boltzmann machines [16] (a type of Markov random fields), are regarded to be “white-box” and intrinsically interpretable. These models promise to interpret in the statistical ways that human minds can follow, where we have, e.g., the probabilistic reasoning to unveil the hidden casual relations [17, 18, 19]. Unfortunately, the gaps between the performance of these probabilistic models and state-of-the-art deep NN’s are quite huge. It seems that high efficiency and interpretability cannot be reached simultaneously with the ML models at hand 111For the efficiency of a ML method, we mainly mean the accuracy with a proper computational complexity depending on its academic or industrial uses. For the classical “white-box” ML schemes, it seems that their accuracy could not beat that of the deep NN’s even if we immensely increase their complexity..
II Tensor network: a powerful “white-box” mathematical tool from quantum physics
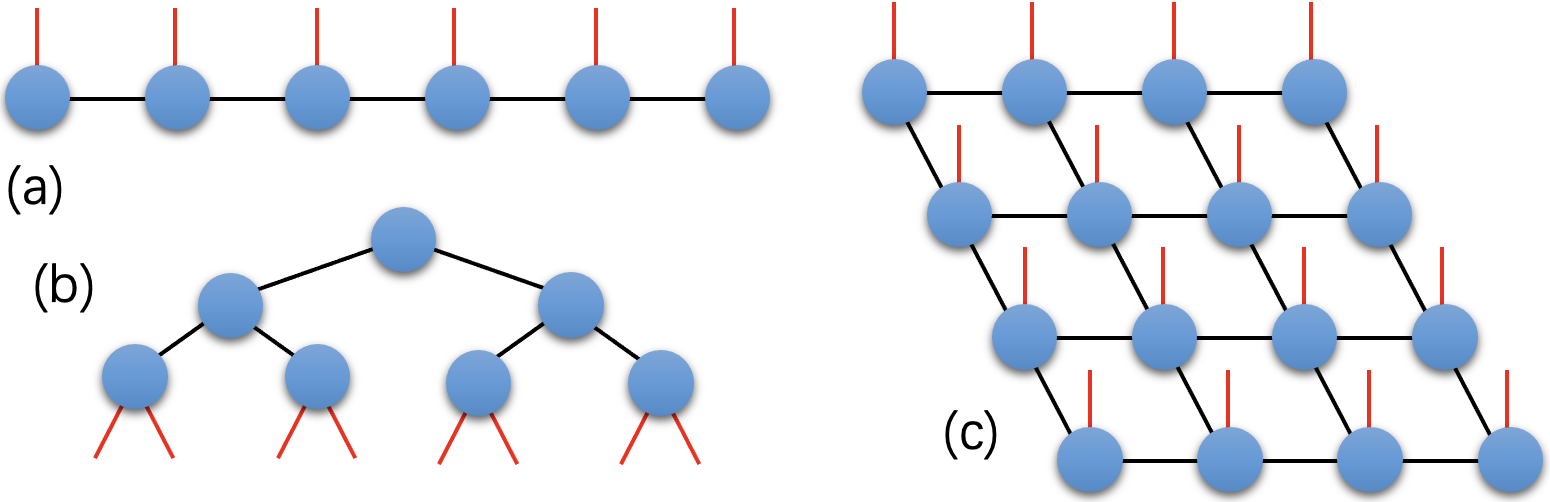
With the fast development of both the classical and quantum computations, tensor network (TN) sheds new light on getting out of the dilemma between interpretability and efficiency. A TN is defined as the contraction of multiple tensors. Its network structure determines how the tensors are contracted. Fig. 1 gives the diagrammatic representations of three kinds of TN’s, namely matrix product state [21] (MPS, which is also known as the tensor-train form [22] with the open boundary condition), tree TN [23], and projected entangled pair state [24]. Taking an MPS formed by tensors as an example, it results in an -th order tensor after contracting the virtual indexes [the black bonds in Fig. 1 (a)] that satisfies
| (1) |
TN has achieved significant successes in quantum mechanics as an efficient representation of the states for the large-scale quantum systems [25, 26, 27, 28, 29]. From the perspective of classical computation of quantum problems, the dimension of Hilbert space 222Hilbert space is a generalization of Euclidean space. We can define vectors, operators, and the measures of their distances in a Hilbert space, while the dimensions can be infinite. Hilbert space has been used to describe the space for quantum states and operators. and the parameter complexity of quantum states scale exponentially with the size of the quantum system, which is known as the “curse of dimensionality” or “exponential wall”. This makes large quantum systems inaccessible by the conventional methods such as exact diagonalization 333Exact diagonalization is a widely used approach by fully diagonalizing the matrix (say quantum Hamiltonian) that contains the full information for the physics of the considered model.. TN reduces the parameter complexity of representing a quantum state to be just polynomial, thus efficient simulations of a large class of quantum systems became plausible. Taking MPS as an example again, the number of parameters are reduced from (the number of elements in the -th order tensor ) to (the total number of parameters in the tensors ()), with and .

Among the TN theories, it has been revealed that the states satisfying the “area laws” 444We may consider a land consisting of many villages as an example to understand the area law. If every person in this land can only communicate with the persons in a short range nearby, the people who can communicate to a different village should live near the boarders. Therefore, the amount of exchanged information between a village and the rest ones should scale with the length of its boarders. In this case, the (two-dimensional) area law is applied. If phones are introduced, people are able to communicate with anyone in this land. The amount of exchanged information of a village should scale with its population or approximately the size of its territory. This is the volume law, where obviously the amount of exchanged information increases much faster than the area-law cases as the village expands. of entanglement entropy [57] can be efficiently approximated by the TN representations with finite bond dimensions [24, 58, 59, 29]. Entanglement entropy [60] is a fundamental concept in quantum sciences 555Entanglement can be understood as a description of quantum correlations. A strong entanglement between two quantum particles means significant affections to the state of one particle by operating another. Entanglement entropy is a measure of the strength of entanglement. For instance, zero entanglement entropy between two particles means that their state should be described by a product state. Even these two particles might be correlated, the correlations should be fully described by the classical correlations.. From a statistic perspective, the entanglement entropy between two subparts of a system characterizes the amount of the gained information on one subpart by knowing the information on the rest part. Luckily, most of the states that we care about satisfy such area laws, meaning the entanglement entropy scales not with the volume of the subpart but with the length of the boundary. For instance, MPS obeys the one-dimensional area law, where the boundary is represented by two zero-dimensional points and the entanglement entropy is a constant. Such an area law is satisfied by the low-lying eigenstates of many one- and quasi-one-dimensional quantum lattice models [62, 63, 64, 65, 66, 67, 68], including those with non-trivial topological properties [33, 34]. Therefore, the MPS-based algorithms including density matrix renormalization group (DMRG) [36, 37] and time-evolving block decimation (TEBD) [38, 39] exhibit remarkable efficiency for simulating such systems.
Moreover, a large class of artificially constructed states widely used in quantum information processing and computing can also be represented by MPS, such as Greenberger-Horne-Zeilinger (GHZ) states (also known as the cat states) [32] and W-state [35] (see the orange circles in Fig. 2). The multi-scale entanglement renormalization ansatz (MERA) is designed to exhibit the logarithmic scaling of the entanglement entropy, which efficiently represent the critical states [69, 70, 71]. The projected entangled pair state (PEPS) is proposed to obey the area laws in two and higher dimensions, which gained tremendous successes in studying higher-dimensional quantum systems [24, 72, 73, 74]. In short, the area laws of entanglement entropy provide intrinsic interpretations on the representational or computational power of TN for simulating quantum systems. Such interpretations also apply to the TN ML. Furthermore, the TN representing quantum states can be interpreted by Born’s quantum-probabilistic interpretation (also known as Born rule) [75]. Thus, TN is regarded as a “white-box” numerical tool (called Born machine [44]), akin to the (classical) probabilistic models for ML. We will focus on this point in the next section.
III Tensor network for quantum-inspired machine learning
Equipped with the well-established theories and efficient methods, TN illuminates a new avenue on tackling the dilemma of interpretability and efficiency in ML. To this end, two entangled lines of researches are under hot debate, which are
-
1.
How do the quantum theories serve as the mathematical foundation for the interpretability of TNML?
-
2.
How do the quantum-mechanical TN methods and quantum computing techniques conceive the TNML schemes with high efficiency?
Focusing around these two questions, below we will introduce the recent inspiring progresses on TN for quantum-inspired ML from three aspects: feature mapping, modeling, and ML by quantum computation. These are closely related to the advantages of TN for ML on gaining both efficiency and interpretability. As the theories, models, or methods are taken from or inspired by those in quantum physics, these ML schemes are often called “quantum-inspired” (see, e.g.,a recent work in Ref. [76]). But be noted that significantly more efforts are required to make towards a systematic framework of interpretability based on quantum physics. The main methods in the TN ML mentioned below, with their relations to efficiency and interpretability, are summarized in Table 1.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/d3484476-7f9b-4d8d-a79f-5e5c08186a34/table.png)
III.1 Quantum feature mappings and kernel functions
Previous works have provided us with stimulative hints on the quantum-inspired ML based on TN. A fundamental step for a quantum treatment of ML is to map the data to the Hilbert space, i.e., to encode them in quantum states [77]. A sample in machine learning can be an image, a sentence, a piece of time series, or etc., which can normally be regarded as a vector. The vector elements are called the features of the sample. The encoding of samples to quantum states is flexible [78, 79, 80, 81, 82]. A straightforward encoding way is to treat the features as the amplitudes of a quantum state. For instance, a sample with features can be considered as the state of a -level “qudit” with the normalization factor and a set of complete basis states 666With a set of quantum states that form a complete basis set in a Hilbert space, any quantum state in this space can be written as a weighted summation of the basis states.. The Born rule says that the probability of having the state from equals to the norm of the corresponding amplitudes, satisfying . It was also proposed to encode to the amplitudes of the state of qubits [82], to avoid the usage of high-level qudits 777As the quantum analog of a classical bit, a qubit represents a two-level quantum system such as a quantum spin. If the number of levels is higher than two, such quantum systems are often referred as “qudits”..
A different way is to encode samples to the Hilbert space of quantum many-body states, which is dubbed as quantum many-body feature mapping (QMFM). Each feature (that is a scalar) is mapped onto a two-component vector, which can be treated as the state of one qubit [80] as
| (2) |
where () can be chosen as the two eigenstates of Pauli operator 888The Pauli operators (, , and ) are three operators whose coefficients are given by three matrices known as Pauli matrices. They are applied to describe the interactions, operations, and algebras of quantum spins. A frequently-used complete and orthogonal set of spin states is the eigenstates of one of the Pauli operators. and we normally assume . In other words, is mapped to a normalized two-component complex vector. The probability of having the state from satisfies , with and . One may also choose an equivalent mapping with a rotation operator and the rotational angle, for the propose of quantum computation. By means of QMFM, a sample (vector) is mapped to a -qubit product state
| (3) |
with the number of features (or qubits in the state). One can see that a non-linear feature-mapping function will definitely introduce non-linearity in processing the sample , despite the following-up treatments on the encoded state in the Hilbert space might be linear. This non-linearity in principle would not harm the interpretability but might bring the quantum-inspired ML schemes with an accuracy competitive to the non-linear ML models if the non-linearity is key to gaining high accuracy. Developing new quantum feature mapping for high accuracy is currently an open issue.
There are in general two ways to process the encoded data. One follows the ideas of the kernel-based methods such as K-means [86], K-nearest neighbors [87, 88], and support vector machine (SVM) [89]. The kernel function in the quantum-inspired ML is determined by both the feature-map function [e.g., Eq. (2)] and the chosen measure of similarity (or distance) in the Hilbert space. A frequently-used measure of similarity between two quantum states is fidelity, which is defined as the norm of the inner product of the two states [60]. With the QMFM in Eq. (2), the fidelity between two encoded states becomes the cosine similarity between the two samples, where the kernel function reads
| (4) |
The above measure of similarity decays exponentially with the number of features (or qubits) , which is known as the “catastrophe of orthogonality”. Modifications on the measure were proposed, such as the rescaled logarithmic fidelity [90], to avoid such a catastrophe for better stability and performance. Exploring proper measures or kernel functions in the Hilbert space remains an open question in the field of quantum-inspired ML.
Besides the catastrophe of orthogonality, the dimension of the Hilbert space increases exponentially with the number of qubits. TN algorithms can be employed to efficiently represent the encoded data and evaluate the similarity including fidelity [91]. For instance, developing valid methods to distinguish quantum phases 999In the condensed matter physics and quantum many-body physics, quantum phases are defined to distinguish the states of quantum matter that possess intrinsically different properties (such as symmetries; one may refer to Sachdev S. Physics World 1999;12:33). Quantum phases are akin to the classical phases such as solids, liquids, and gases. In the paradigm of Landau and Ginzburg (see, e.g., a review article in Hohenberg P and Krekhov A. Physics Reports 2015;572:1–42), different phases of matter are separated by the phase transitions that generally exhibit certain singular properties. A phase transition can occur by changing the physical parameters, such as temperature for the solid-liquid transition of water, and the magnetic fields for the phase transitions of quantum magnets. is a long-concerned issue, to which quantum-inspired ML brought new clues. Ref. [93] considered the unsupervised recognition of quantum phases and phase transitions. The ground states of quantum spin models with different physical parameters (such as external magnetic fields), which can be regarded as the “quantum data” (obtained by DMRG [36, 37]), are represented efficiently by MPS’s. The phase transitions are clearly recognized unsupervisedly by visualizing the distribution of these MPS’s with non-linear dimensionality reduction [94], where the ground states in the same quantum phase tend to cluster towards a same sub-region of the Hilbert space. In this way, prior knowledge on the quantum phases, such as order parameters 101010In the Landau-Ginzburg paradigm, one way to identify quantum phases is to look at the corresponding order parameters. For instance, one may calculate the uniform magnetization to identify the ferromagnetic phase (where all spins are pointed in the same direction) for quantum magnets. Thus, such schemes for phase identification require the prior knowledge on which order parameter to look at. Developing the schemes with no need of such prior knowledge is an important topic to study quantum phases., is not required for identifying quantum phases.
Similar observations were reported for the ML of images and texts, where the encoded states (by QMFM) of the samples in the same category tend to cluster in the Hilbert space [90]. Clustering and the exponential vastness of the Hilbert space make the classification boundary easier to locate [96, 46, 90, 97]. This shares a similar spirit with the SVM’s [98]. Another work showed that the classification boundary can be efficiently parametrized by the generative MPS [99], which we will talk about later in this paper. These works drew forth an open question on how different quantum kernels [78, 100] would affect the ML efficiency for different kinds of data (such as images, texts, multimodal data, and quantum data) and for different ML tasks (supervised learning, unsupervised learning, reinforcement learning, etc.).
III.2 Parameterized modeling and quantum probabilistic interpretation with tensor network for machine learning
We now turn our focus on training the quantum-inspired ML models parameterized by TN. This provides another pathway of processing the quantum data (including the ground states for quantum phase recognition and the encoded states mapped from ML samples). Some relatively early progresses were made on the data clustering based on the quantum dynamics satisfying the Schrödinger equation 111111Schrödinger equation is one of the most fundamental equations in quantum physics. It is a partial differential equation of multiple variables for the time-dependent problems, or eigenvalue equation for static problems. The complexity of solving Schrödinger equation in general increases exponentially with the size of quantum system. with a data-determined potential [102, 103]. This concerns to inversely solve the differential equations, which can be efficiently done with a small number of variables [104, 105, 106]. For dealing with the quantum many-body states whose dimension scales exponentially, TN has been utilized to develop ML models with polynomial complexity [80, 99, 107, 108, 45, 46, 109], thanks to its high efficiency in representing quantum many-body states and operators.
By taking the advantages of its connections to Born rule and quantum information theories, intrinsically interpretable ML based on TN was developed, which is referred as the quantum-inspired TN ML. The key here is to build the probabilistic ML framework from quantum states, which can be efficiently represented and simulated by TN. In this sense of probabilities, the intrinsic interpretability of such TN ML is akin to or possibly beyond the interpretability of the classical probabilistic ML. In Ref. [99], MPS was suggested to formulate the joint probabilistic distribution of features provided with a dataset, and is used to implement generative tasks. Provided with a trained MPS , the probability of a given sample is determined by the quantum probability of obtaining [Eq. (3)] by measuring , satisfying
| (5) |
Following Born’s quantum probabilistic rule, the marginal and conditional probabilities can be naturally defined. For instance, the marginal probability distribution of the -th feature satisfies
| (6) |
where is defined by Eq. (2) and is the reduced density operator of the -th qubit by tracing over the degrees of freedom of all other qubits except for the -th. The marginal probability distributions can be used for, e.g., generation [99] and simulating onsite entanglement [110, 111] (which we will introduce below).
The conditional probabilities are useful for, e.g., classification [112] and data fixing [99, 113]. The conditional probability distribution of with knowing the values of the rest features satisfies
| (7) |
where is the quantum state by collapsing all the qubits but the -th to according to the known values.
The quantum probabilistic interpretation gave birth to various quantum-inspired ML schemes for, e.g., model optimization [80, 99, 108, 114], data generation [99, 45], anomaly detection [115], compressed sampling [113], solving differential equations [116] and constrained combinatorial optimization [117, 118, 119]. Some important ML proposals based on MPS are illustrated in Fig. 2 (see the green circles). These schemes are based on the probabilities obeying Born rule, where the probabilistic distributions can be efficiently represented and calculated with TN.
The calculation of the above probability distributions involve all coefficients of the quantum state , whose number increases exponentially with the number of features (). Note we normally have or more (say for the MNIST dataset of the images of hand-writing digits [120]), meaning coefficients in the state . The advantage of TN on efficiency here is the same as that for using TN for quantum simulations. Taking again MPS as an example, its parameter complexity for representing the probability distributions scale just linearly with (one may refer to Eq. (1) and the texts below). With the MNIST dataset, accurate generation can be made by the MPS with about parameters [99, 113]. Similar advantages on efficiency can be gained with other kinds of TN, such as MERA and PEPS, using the corresponding TN contraction algorithms [27]. We shall stress that the high efficiency of TN we refer to here is for representing or simulating the quantum states in the quantum-inspired ML. Another aspect of efficiency is from the power of the quantum computation, which we will discuss about later in Sec. III.3.
In the construction of generative models for ML, the quantum state satisfying could be the equal super-position of the encoded product states [Eq. (3)] as
| (8) |
with the number of samples. The equal probabilistic distribution can be deduced from above equation with the “catastrophe” of orthogonality for large [one may refer to Eq. (4)]. Taking the phase factors , such a state is called the lazy-learning state [46] since it contains no variational parameters, and is directly constructed by the training samples when it is used for classification.
The generative MPS proposed in Ref. [99] is essentially an approximation of the lazy-learning state with variationally-determined phase factors and bounded dimensions of the virtual indexes [ in Eq. (1)]. The approximation restricts the upper bound of the entanglement in the TN state by discarding the small elements in the entanglement spectrum, which is a widely recognized method in the TN approaches for quantum physics. The reported results on supervised learning for classifying images showed that the generative MPS exhibits lower accuracy on the training set but magically higher accuracy for the testing set than the lazy-learning state [46]. In other words, the approximation made in the generative MPS suppresses over-fitting. This implies possible connections of the quantum super-position rule and quantum entanglement to generalization ability and over-fitting in ML [121, 122], which is worth exploring in the future.
The quantum probabilistic nature allows to introduce the physical concepts and statistic properties of the TN models to the investigations of ML. For instance, the entanglement entropy has been used for feature selection [110, 111]. The importance of a feature can be characterized by how strongly the corresponding qubit is entangled to others, using the onsite entanglement entropy [110]
| (9) |
with the reduced density matrix of for the -th qubit. Note the onsite entanglement entropy is the von Neumann entropy of the marginal probabilities in Eq. (6).
Other quantities and theories in quantum sciences, such as quantum mutual information [123], quantum correlations [124], decoherence [125], and controllability of quantum systems [126] also help to enhance the ML interpretability. These issues are still in hot debate, illuminating a promising path to characterize the ML-relevant capabilities, such as the learnability and generalization powers. The entanglement scaling was applied to unveil the properties of quantum ML models such as the quantum NN’s [127, 128]. The controllability of quantum mechanical systems based on the dynamical Lie algebra was applied to understand and handle the over-parameterization [129] and gradient vanishing [130] (also known as barren plateaus [131]), which are critical issues for ML based on classical or quantum methods.
To give a brief summary of this subsection, we introduced the probabilistic framework for the quantum-inspired TN ML. This framework allows us to borrow the theories and techniques from both the classical and quantum information sciences, so that the quantum-inspired ML can possess equal or better interpretability than the classical probabilistic ML. But many issues have not been sufficiently explored, and more efforts need to be made in the future in this newly emergent area.
III.3 Quantum-inspired tensor network machine learning with quantum computation
In this subsection, we will concentrate on the combination of the quantum-inspired TN ML with the quantum computational methods and techniques, mainly for the purpose of high efficiency. The key here is the ability of TN as an efficient representation of quantum operations, which is essential for simulating the physical processes in quantum mechanics such as dynamics and thermodynamics [132, 133, 134, 135, 136, 137, 138]. For the TN ML with quantum computation, TN can serve as a mathematical representation of the quantum circuit models [139]. As the quantum counterpart of the classical logical circuits, a quantum circuit is composed of multiple quantum gates 121212A quantum gate is a specific operation on quantum state, and thus can be given by a quantum operator. When considering the quantum computation in practice, the quantum gates realizable on different quantum platforms (such as super-conducting circuits, ultra-cold atoms, and single photons) are different. that are usually unitary operators executable on the quantum computers. Efficient ways of deriving the quantum circuits for implementing quantum algorithms are key to quantum computation and to the ML by quantum computers.
However, the quantum algorithms where the circuits can be analytically derived (e.g., Shor’s algorithm for factoring [141], Grover’s algorithm for searching [142], and the disentangling circuits recently proposed for preparing MPSs [143]) are extremely rare. This puts strong limitations to quantum computation, including its applications to ML.
Variational quantum algorithms (VQAs) [144] were proposed, significantly extending the scope of problems that quantum computation can handle. Among others, the quantum circuits containing variational parameters, dubbed as the variational quantum circuits (VQCs), have been used for, e.g., state preparation and tomography [145, 146]. Variational quantum eigensolvers [147] were developed and applied to a wide range of areas such as quantum chemistry and quantum materials (one may refer to a recent review in Ref. [148]).
VQAs concern the hybrid classical-quantum optimizations [149], which also suffer from the “curse of dimensionality”. Naturally, TN has been employed as an efficient mathematical tool for classical computation, allowing to stably access equal or even much larger numbers of qubits than what the current quantum computers can handle [150, 151, 152, 146, 153, 154, 155, 156]. The relevant works provided valuable information on the races between the powers of classical and quantum computations in the noisy intermediate-scale quantum (NISQ) era [157], such as the efficiency of random-circuit sampling by the quantum computer of Google [158] and by the TN simulations [159, 153, 160, 161, 155, 162].
The previous works on TN and quantum computation have unveiled the underlying connections among quantum mechanics, quantum computing, and ML, which makes TN a uniquely suitable tool to explore ML incorporated with quantum computation [163]. As an example, let us compare the state preparation by VQC with the supervised ML by NN. The task of state preparation is to obtain the given target state () on a quantum computer with high fidelity, say with a unitary transformation. The VQC is used to represent the mapping , similar to the feed-forward mapping defined by the NN. As the building blocks of VQC, the quantum gates with variational parameters are analogous to the neurons in NN. The preparation error can be evaluated by the infidelity (, a measure of distance in quantum Hilbert space) [60] between the target state and the one prepared by the VQC, analogous to the loss function (or error) in ML. The gradients and the gradient-descent process for optimizing the parameters in VQC can be implemented by the TN methods or automatic differentiation technique [143, 146, 164, 165, 166, 167], analogous to the backward propagation of ML. The optimized circuit, after necessary compilation [168], can be distributed to quantum computers for their further uses.
TN has been extensively used in the quantum-inspired ML combined with quantum computation methods including VQC [108, 169, 170, 171, 172, 112, 173, 174]. The utilizations of TN in this sense can be generally summarized into three different but relevant ways. First, the TNs with unitary constraints are used as the parameterized ML model runnable on quantum platforms [108, 139, 170, 112, 173]. Here, the equivalence between the unitary TNs and the quantum circuits are utilized. It is expected that the computational power (with, e.g., parallel quantum computing 131313Quantum computing is expected to possess higher parallelism over classical computing. One operation on an entangled quantum state can manage to process all the exponentially-many coefficients, even this operation might be just on one qubit or a local part of the state. In comparison, such parallelism cannot be gained if the state has no entanglement (i.e., a product state). This is one reason for regarding entanglement as the source for the superior power of quantum computing.) would bring high efficiency to the ML schemes running on the quantum platforms. Second, TN methods are employed to classically optimize or simulate the VQCs for machine learning [173, 172, 47]. Such classical TN simulations have already been widely applied to the races between the powers of classical and quantum computers [159, 153, 160, 161, 155, 162], and are expected to provide useful information to guide the future investigations of the ML running on the quantum platforms. Third, TN are used for data preprocessing before entering the quantum computational procedures. For example, data compression by TN was suggested to lower the requirement of quantum hardware [169]. TN is also used as an efficient representation of the quantum data (such as the states of quantum systems and the quantum states encoded from the classical data) for, e.g., classification and ML-based quantum control [81, 47]. These researches are particularly useful for the quantum computation of ML in the NISQ era when the power of quantum hardware (number of qubits, stability, and etc.) is for the moment limited.
IV Tensor network enhancing classical machine learning
As a fundamental mathematical tool, the wide applications of TN to ML are not limited to those obeying the quantum probabilistic interpretation. With the fact that TN can be used to efficiently represent and simulate the partition functions of classical stochastic systems, such as Ising and Potts models (see, e.g., Refs. [176, 177, 178]), the relations between TN and Boltzmann machines [16] have been extensively studied [179, 180, 181, 182]. The relevant works also promoted the investigations of quantum many-body physics and ML from the perspective of, e.g., the area laws of entanglement entropy and the representation ability of TN as quantum state ansatz [127, 183, 182, 184].
TN were also used to enhance NN or develop novel ML models [185], ignoring any probabilistic interpretations. Tensor-train [22] and tensor-ring [186] forms (which correspond to the MPS’s with open and periodic boundary conditions, respectively) are applied to develop novel support vector machines [46, 187, 188], dimensionality reduction schemes [189], and parameterized ML models [190, 191, 192, 193, 194, 195]. Significant reductions of parameter complexity were reported, thanks to the efficiency of TN for representing higher-order tensors, which is essentially the same reason for the high efficiency of TN in describing quantum many-body systems.
Based on the same ground, model compression methods were proposed to decompose the variational parameters of NN’s to TN’s, or directly to represent the variational parameters as TN’s [196, 48, 49, 197, 50, 51, 52, 53, 198, 54, 199, 55]. Explicit decomposition procedures might not be necessary for the latter, where the parameters of NN’s are not restored as tensors but directly as the tensor-train (tensor-ring) forms [196], matrix product operators [51, 52], or deep TN’s [55]. Non-linear activation functions were incorporated with TN to improve the performance for ML [54, 194, 55], generalizing TN from a type of multi-linear models to non-linear ones.
V Discussion

Methodologies to solve the dilemma between efficiency and interpretability in artificial intelligence (AI) and particularly deep ML have been long concerned. We here review the inspiring progresses made in TN for interpretable and efficient quantum-inspired ML. The advantages of TN for ML are listed in the “TN-ML butterfly” in Fig. 3. For the quantum-inspired ML, the advantages of TN can be summarized into two critical points: quantum theories for interpretability, and quantum methods for efficiency. On one hand, TN enables us to apply quantum theories and statistics, such as the entanglement theories, to build a probabilistic framework for interpretability that might be beyond the description of the classical information or statistic theories. On the other hand, the powerful quantum-mechanical TN algorithms and the explosively boosted quantum computational technologies will empower the quantum-inspired TN-ML methods with high efficiency on both the classical and quantum computational platforms.
Particularly with the striking progresses recently made in the generative pre-trained transformer (GPT) [200], unprecedented surges in model complexity and computational power have occurred, which bring new opportunities and challenges to TN ML. The interpretability will become increasingly valuable when facing the emergent AI of GPT for not just investigations with higher efficiency but also their better use and safer control. In the current NISQ era and the forthcoming era of genuine quantum computing, TN is rapidly growing into a featured mathematical tool to explore the quantum AI from the perspective of theories, models, algorithms, software, hardware, and applications.
Acknowledgment
This work is supported in part by the NSFC (Grant No. 11834014 and No. 12004266), Beijing Natural Science Foundation (Grant No. 1232025), the National Key R&D Program of China (Grant No. 2018FYA0305804), the Strategetic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB28000000), and Innovation Program for Quantum Science and Technology (No. 2021ZD0301800).
References
- Gilpin et al. [2018] L. H. Gilpin, D. Bau, B. Z. Yuan, A. Bajwa, M. Specter, and L. Kagal, Explaining explanations: An overview of interpretability of machine learning, in 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA) (IEEE, 2018) pp. 80–89.
- Zhang and Zhu [2018] Q.-s. Zhang and S.-C. Zhu, Visual interpretability for deep learning: a survey, Frontiers of Information Technology & Electronic Engineering 19, 27 (2018).
- Lipton [2018] Z. C. Lipton, The mythos of model interpretability, Communications of The ACM 61, 36–43 (2018).
- Carvalho et al. [2019] D. V. Carvalho, E. M. Pereira, and J. S. Cardoso, Machine learning interpretability: A survey on methods and metrics, Electronics 8, 10.3390/electronics8080832 (2019).
- Madsen et al. [2022] A. Madsen, S. Reddy, and S. Chandar, Post-hoc interpretability for neural nlp: A survey, ACM Computing Surveys 55, 10.1145/3546577 (2022).
- Rudin [2019] C. Rudin, Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead, Nature Machine Intelligence 1, 206 (2019).
- Su et al. [2019] J. Su, D. V. Vargas, and K. Sakurai, One pixel attack for fooling deep neural networks, IEEE Transactions on Evolutionary Computation 23, 828 (2019).
- Doshi-Velez and Kim [2017] F. Doshi-Velez and B. Kim, Towards a rigorous science of interpretable machine learning (2017), arXiv:1702.08608 [stat.ML] .
- Battiti [1994] R. Battiti, Using mutual information for selecting features in supervised neural net learning, IEEE Transactions on Neural Networks 5, 537 (1994).
- Shwartz-Ziv and Tishby [2017] R. Shwartz-Ziv and N. Tishby, Opening the black box of deep neural networks via information (2017), arXiv:1703.00810 [stat.ML] .
- Koch-Janusz and Ringel [2018] M. Koch-Janusz and Z. Ringel, Mutual information, neural networks and the renormalization group, Nature Physics 14, 578 (2018).
- Saxe et al. [2019] A. M. Saxe, Y. Bansal, J. Dapello, M. Advani, A. Kolchinsky, B. D. Tracey, and D. D. Cox, On the information bottleneck theory of deep learning, Journal of Statistical Mechanics: Theory and Experiment 2019, 124020 (2019).
- Erdmenger et al. [2022] J. Erdmenger, K. T. Grosvenor, and R. Jefferson, Towards quantifying information flows: relative entropy in deep neural networks and the renormalization group, SciPost Physics 12, 41 (2022).
- Ghahramani [2015] Z. Ghahramani, Probabilistic machine learning and artificial intelligence, Nature 521, 452 (2015).
- Bishop [2006] C. M. Bishop, Pattern recognition and machine learning (Springer, 2006).
- Ackley et al. [1985] D. H. Ackley, G. E. Hinton, and T. J. Sejnowski, A learning algorithm for boltzmann machines, Cognitive Science 9, 147 (1985).
- Glymour [2003] C. Glymour, Learning, prediction and causal bayes nets, Trends in Cognitive Sciences 7, 43 (2003).
- Tenenbaum et al. [2006] J. B. Tenenbaum, T. L. Griffiths, and C. Kemp, Theory-based bayesian models of inductive learning and reasoning, Trends in Cognitive Sciences 10, 309 (2006), special issue: Probabilistic models of cognition.
- Lucas and Griffiths [2010] C. G. Lucas and T. L. Griffiths, Learning the form of causal relationships using hierarchical bayesian models, Cognitive Science 34, 113 (2010).
- Note [1] For the efficiency of a ML method, we mainly mean the accuracy with a proper computational complexity depending on its academic or industrial uses. For the classical “white-box” ML schemes, it seems that their accuracy could not beat that of the deep NN’s even if we immensely increase their complexity.
- Pérez-García et al. [2007] D. Pérez-García, F. Verstraete, M. M. Wolf, and J. I. Cirac, Matrix product state representations, Quantum Information & Computation 7, 401 (2007).
- Oseledets [2011] I. V. Oseledets, Tensor-train decomposition, SIAM Journal on Scientific Computing 33, 2295 (2011).
- Shi et al. [2006] Y.-Y. Shi, L.-M. Duan, and G. Vidal, Classical simulation of quantum many-body systems with a tree tensor network, Physical Review A 74, 022320 (2006).
- Verstraete et al. [2006] F. Verstraete, M. M. Wolf, D. Perez-Garcia, and J. I. Cirac, Criticality, the area law, and the computational power of projected entangled pair states, Physical Review Letters 96, 220601 (2006).
- Verstraete et al. [2008] F. Verstraete, V. Murg, and J. I. Cirac, Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems, Advances in Physics 57, 143 (2008).
- Cirac and Verstraete [2009] J. I. Cirac and F. Verstraete, Renormalization and tensor product states in spin chains and lattices, Journal of Physics A-Mathematical and Theoretical 42, 504004 (2009).
- Ran et al. [2020a] S.-J. Ran, E. Tirrito, C. Peng, X. Chen, L. Tagliacozzo, G. Su, and M. Lewenstein, Tensor network contractions: methods and applications to quantum many-Body systems (Springer, Cham, 2020).
- Orús [2019] R. Orús, Tensor networks for complex quantum systems, Nature Reviews Physics 1, 538 (2019).
- Cirac et al. [2021] J. I. Cirac, D. Pérez-García, N. Schuch, and F. Verstraete, Matrix product states and projected entangled pair states: Concepts, symmetries, theorems, Reviews of Modern Physics 93, 045003 (2021).
- Note [2] Hilbert space is a generalization of Euclidean space. We can define vectors, operators, and the measures of their distances in a Hilbert space, while the dimensions can be infinite. Hilbert space has been used to describe the space for quantum states and operators.
- Note [3] Exact diagonalization is a widely used approach by fully diagonalizing the matrix (say quantum Hamiltonian) that contains the full information for the physics of the considered model.
- Greenberger et al. [1989] D. M. Greenberger, M. A. Horne, and A. Zeilinger, Going beyond bell’s theorem, in Bell’s Theorem, Quantum Theory and Conceptions of the Universe, edited by M. Kafatos (Springer Netherlands, Dordrecht, 1989) pp. 69–72.
- Affleck et al. [1987] I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki, Rigorous results on valence-bond ground states in antiferromagnets, Physical Review Letters 59, 799 (1987).
- Affleck et al. [1988] I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki, Valence bond ground states in isotropic quantum antiferromagnets, Communications in Mathematical Physics 115, 477 (1988).
- Dür [2001] W. Dür, Multipartite entanglement that is robust against disposal of particles, Physical Review A 63, 020303 (2001).
- White [1992] S. R. White, Density matrix formulation for quantum renormalization groups, Physical Review Letters 69, 2863 (1992).
- White [1993] S. R. White, Density-matrix algorithms for quantum renormalization groups, Physical Review B 48, 10345 (1993).
- Vidal [2003] G. Vidal, Efficient classical simulation of slightly entangled quantum computations, Physical Review Letters 91, 147902 (2003).
- Vidal [2004] G. Vidal, Efficient simulation of one-dimensional quantum many-body systems, Physical Review Letters 93, 040502 (2004).
- Vidal et al. [2003] G. Vidal, J. I. Latorre, E. Rico, and A. Kitaev, Entanglement in quantum critical phenomena, Physical Review Letters 90, 227902 (2003).
- Pollmann et al. [2009] F. Pollmann, S. Mukerjee, A. M. Turner, and J. E. Moore, Theory of finite-entanglement scaling at one-dimensional quantum critical points, Physical Review Letters 102, 255701 (2009).
- Tagliacozzo et al. [2008] L. Tagliacozzo, T. R. de Oliveira, S. Iblisdir, and J. I. Latorre, Scaling of entanglement support for matrix product states, Physical Review B 78, 024410 (2008).
- Pollmann and Moore [2010] F. Pollmann and J. E. Moore, Entanglement spectra of critical and near-critical systems in one dimension, New Journal of Physics 12, 025006 (2010).
- Cheng et al. [2018a] S. Cheng, J. Chen, and L. Wang, Information perspective to probabilistic modeling: Boltzmann machines versus born machines, Entropy 20, 10.3390/e20080583 (2018a).
- Cheng et al. [2019] S. Cheng, L. Wang, T. Xiang, and P. Zhang, Tree tensor networks for generative modeling, Physical Review B 99, 155131 (2019).
- Sun et al. [2020a] Z.-Z. Sun, C. Peng, D. Liu, S.-J. Ran, and G. Su, Generative tensor network classification model for supervised machine learning, Physical Review B 101, 075135 (2020a).
- Metz and Bukov [2023] F. Metz and M. Bukov, Self-correcting quantum many-body control using reinforcement learning with tensor networks, Nature Machine Intelligence 5, 780 (2023).
- Tjandra et al. [2017] A. Tjandra, S. Sakti, and S. Nakamura, Compressing recurrent neural network with tensor train, in 2017 International Joint Conference on Neural Networks (IJCNN) (2017) pp. 4451–4458.
- Yuan et al. [2019] L. Yuan, C. Li, D. Mandic, J. Cao, and Q. Zhao, Tensor ring decomposition with rank minimization on latent space: An efficient approach for tensor completion, Proceedings of the AAAI Conference on Artificial Intelligence 33, 9151 (2019).
- Pan et al. [2019] Y. Pan, J. Xu, M. Wang, J. Ye, F. Wang, K. Bai, and Z. Xu, Compressing recurrent neural networks with tensor ring for action recognition, Proceedings of the AAAI Conference on Artificial Intelligence 33, 4683 (2019).
- Gao et al. [2020] Z.-F. Gao, S. Cheng, R.-Q. He, Z. Y. Xie, H.-H. Zhao, Z.-Y. Lu, and T. Xiang, Compressing deep neural networks by matrix product operators, Physical Review Research 2, 023300 (2020).
- Sun et al. [2020b] X. Sun, Z.-F. Gao, Z.-Y. Lu, J. Li, and Y. Yan, A model compression method with matrix product operators for speech enhancement, IEEE/ACM Transactions on Audio, Speech, and Language Processing 28, 2837 (2020b).
- Wang et al. [2020a] D. Wang, G. Zhao, G. Li, L. Deng, and Y. Wu, Compressing 3dcnns based on tensor train decomposition, Neural Networks 131, 215 (2020a).
- Wang et al. [2021a] D. Wang, G. Zhao, H. Chen, Z. Liu, L. Deng, and G. Li, Nonlinear tensor train format for deep neural network compression, Neural Networks 144, 320 (2021a).
- Qing et al. [2023] Y. Qing, P.-F. Zhou, K. Li, and S.-J. Ran, Compressing neural network by tensor network with exponentially fewer variational parameters (2023), arXiv:2305.06058 [cs.LG] .
- Note [4] We may consider a land consisting of many villages as an example to understand the area law. If every person in this land can only communicate with the persons in a short range nearby, the people who can communicate to a different village should live near the boarders. Therefore, the amount of exchanged information between a village and the rest should scale with the length of its boarders. In this case, the area law is obeyed. Someday, phones are introduced to this land, and people are able to communicate with anyone in this land. The amount of exchanged information of a village should scale with its population or approximately the size of its territory. This is named as the volume law, where obviously the amount of exchanged information increases much faster than the area-law cases if the village expands its territory.
- Eisert et al. [2010] J. Eisert, M. Cramer, and M. B. Plenio, Colloquium: Area laws for the entanglement entropy, Reviews of Modern Physics 82, 277 (2010).
- Tagliacozzo et al. [2009] L. Tagliacozzo, G. Evenbly, and G. Vidal, Simulation of two-dimensional quantum systems using a tree tensor network that exploits the entropic area law, Physical Review B 80, 235127 (2009).
- Piroli and Cirac [2020] L. Piroli and J. I. Cirac, Quantum cellular automata, tensor networks, and area laws, Physical Review Letters 125, 190402 (2020).
- Nielsen and Chuang [2002] M. A. Nielsen and I. Chuang, Quantum computation and quantum information (American Association of Physics Teachers, 2002).
- Note [5] Entanglement can be understood as a description of quantum correlations. A strong entanglement between two quantum particles means significant affections to the state of one particle by operating another. Entanglement entropy is a measure of the strength of entanglement. For instance, zero entanglement entropy between two particles means that their state should be described by a product state. Even these two particles might be correlated, the correlations should be fully described by the classical correlations.
- Hastings [2007a] M. B. Hastings, An area law for one-dimensional quantum systems, Journal of Statistical Mechanics: Theory and Experiment 2007, P08024 (2007a).
- Hastings [2007b] M. B. Hastings, Entropy and entanglement in quantum ground states, Physical Review B 76, 035114 (2007b).
- Schuch et al. [2008] N. Schuch, M. M. Wolf, F. Verstraete, and J. I. Cirac, Entropy scaling and simulability by matrix product states, Physical Review Letters 100, 030504 (2008).
- Verstraete and Cirac [2006] F. Verstraete and J. I. Cirac, Matrix product states represent ground states faithfully, Physical Review B 73, 094423 (2006).
- de Beaudrap et al. [2010] N. de Beaudrap, T. J. Osborne, and J. Eisert, Ground states of unfrustrated spin hamiltonians satisfy an area law, New Journal of Physics 12, 095007 (2010).
- Pirvu et al. [2012] B. Pirvu, J. Haegeman, and F. Verstraete, Matrix product state based algorithm for determining dispersion relations of quantum spin chains with periodic boundary conditions, Physical Review B 85, 035130 (2012).
- Friesdorf et al. [2015] M. Friesdorf, A. H. Werner, W. Brown, V. B. Scholz, and J. Eisert, Many-body localization implies that eigenvectors are matrix-product states, Physical Review Letters 114, 170505 (2015).
- Vidal [2007] G. Vidal, Entanglement renormalization, Physical Review Letters 99, 220405 (2007).
- Vidal [2008] G. Vidal, Class of quantum many-body states that can be efficiently simulated, Physical Review Letters 101, 110501 (2008).
- Evenbly and Vidal [2009] G. Evenbly and G. Vidal, Entanglement renormalization in two spatial dimensions, Physical Review Letters 102, 180406 (2009).
- Jordan et al. [2008] J. Jordan, R. Orús, G. Vidal, F. Verstraete, and J. I. Cirac, Classical simulation of infinite-size quantum lattice systems in two spatial dimensions, Physical Review Letters 101, 250602 (2008).
- Gu et al. [2009] Z.-C. Gu, M. Levin, B. Swingle, and X.-G. Wen, Tensor-product representations for string-net condensed states, Physical Review B 79, 085118 (2009).
- Buerschaper et al. [2009] O. Buerschaper, M. Aguado, and G. Vidal, Explicit tensor network representation for the ground states of string-net models, Physical Review B 79, 085119 (2009).
- Born [1926] M. Born, Zur quantenmechanik der stoßvorgänge, Zeitschrift für Physik 37, 863 (1926).
- Felser et al. [2021] T. Felser, M. Trenti, L. Sestini, A. Gianelle, D. Zuliani, D. Lucchesi, and S. Montangero, Quantum-inspired machine learning on high-energy physics data, npj Quantum Information 7, 111 (2021).
- Biamonte et al. [2017] J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, and S. Lloyd, Quantum machine learning, Nature 549, 195 (2017).
- Le et al. [2011] P. Q. Le, F. Dong, and K. Hirota, A flexible representation of quantum images for polynomial preparation, image compression, and processing operations, Quantum Information Processing 10, 63 (2011).
- Yan et al. [2016] F. Yan, A. M. Iliyasu, and S. E. Venegas-Andraca, A survey of quantum image representations, Quantum Information Processing 15, 1 (2016).
- Stoudenmire and Schwab [2016] E. Stoudenmire and D. J. Schwab, Supervised learning with tensor networks, in Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett (Curran Associates, Inc., 2016) pp. 4799–4807.
- Dilip et al. [2022] R. Dilip, Y.-J. Liu, A. Smith, and F. Pollmann, Data compression for quantum machine learning, Physical Review Research 4, 043007 (2022).
- Ashhab [2022] S. Ashhab, Quantum state preparation protocol for encoding classical data into the amplitudes of a quantum information processing register’s wave function, Physical Review Research 4, 013091 (2022).
- Note [6] With a set of quantum states that form a complete basis set in a Hilbert space, any quantum state in this space can be written as a weighted summation of the basis states.
- Note [7] As the quantum analog of a classical bit, a qubit represents a two-level quantum system such as a quantum spin. If the number of levels is higher than two, such quantum systems are often referred as “qudits”.
- Note [8] The Pauli operators (, , and ) are three operators whose coefficients are given by three matrices known as Pauli matrices. They are applied to describe the interactions, operations, and algebras of quantum spins. A frequently-used complete and orthogonal set of spin states is the eigenstates of one of the Pauli operators.
- Kerenidis et al. [2019] I. Kerenidis, J. Landman, A. Luongo, and A. Prakash, q-means: A quantum algorithm for unsupervised machine learning, in Advances in Neural Information Processing Systems, Vol. 32, edited by H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Curran Associates, Inc., 2019).
- Wiebe et al. [2015] N. Wiebe, A. Kapoor, and K. M. Svore, Quantum nearest-neighbor algorithms for machine learning, Quantum Information and Computation 15, 318 (2015).
- Dang et al. [2018] Y. Dang, N. Jiang, H. Hu, Z. Ji, and W. Zhang, Image classification based on quantum k-nearest-neighbor algorithm, Quantum Information Processing 17, 239 (2018).
- Rebentrost et al. [2014] P. Rebentrost, M. Mohseni, and S. Lloyd, Quantum support vector machine for big data classification, Physical Review Letters 113, 130503 (2014).
- Li and Ran [2022] W.-M. Li and S.-J. Ran, Non-parametric semi-supervised learning in many-body hilbert space with rescaled logarithmic fidelity, Mathematics 10, 10.3390/math10060940 (2022).
- Zhou et al. [2008] H.-Q. Zhou, R. Orús, and G. Vidal, Ground state fidelity from tensor network representations, Physical Review Letters 100, 080601 (2008).
- Note [9] In the condensed matter physics and quantum many-body physics, quantum phases are defined to distinguish the states of quantum matter that possess intrinsically different properties (such as symmetries; one may refer to Sachdev S. Physics World 1999;12:33). Quantum phases are akin to the classical phases such as solids, liquids, and gases. In the paradigm of Landau and Ginzburg (see, e.g., a review article in Hohenberg P and Krekhov A. Physics Reports 2015;572:1–42), different phases of matter are separated by the phase transitions that generally exhibit certain singular properties. A phase transition can occur by changing the physical parameters, such as temperature for the solid-liquid transition of water, and the magnetic fields for the phase transitions of quantum magnets.
- Yang et al. [2021] Y. Yang, Z.-Z. Sun, S.-J. Ran, and G. Su, Visualizing quantum phases and identifying quantum phase transitions by nonlinear dimensional reduction, Physical Review B 103, 075106 (2021).
- Hinton and Roweis [2003] G. E. Hinton and S. T. Roweis, Stochastic neighbor embedding, in Advances in Neural Information Processing Systems 15, edited by S. Becker, S. Thrun, and K. Obermayer (MIT Press, 2003) pp. 857–864.
- Note [10] In the Landau-Ginzburg paradigm, one way to identify quantum phases is to look at the corresponding order parameters. For instance, one may calculate the uniform magnetization to identify the ferromagnetic phase (where all spins are pointed in the same direction) for quantum magnets. Thus, such schemes for phase identification require the prior knowledge on which order parameter to look at. Developing the schemes with no need of such prior knowledge is an important topic to study quantum phases.
- Horn [2001a] D. Horn, Clustering via hilbert space, Physica A: Statistical Mechanics and its Applications 302, 70 (2001a), proc. Int. Workshop on Frontiers in the Physics of Complex Systems.
- Shi et al. [2022] X. Shi, Y. Shang, and C. Guo, Clustering using matrix product states, Physical Review A 105, 052424 (2022).
- Cortes and Vapnik [1995] C. Cortes and V. Vapnik, Support-vector networks, Machine Learning 20, 273 (1995).
- Han et al. [2018] Z.-Y. Han, J. Wang, H. Fan, L. Wang, and P. Zhang, Unsupervised generative modeling using matrix product states, Physical Review X 8, 031012 (2018).
- Torabian and Krems [2023] E. Torabian and R. V. Krems, Compositional optimization of quantum circuits for quantum kernels of support vector machines (2023), arXiv:2203.13848 [quant-ph] .
- Note [11] Schrödinger equation is one of the most fundamental equations in quantum physics. It is a partial differential equation of multiple variables for the time-dependent problems, or eigenvalue equation for static problems. The complexity of solving Schrödinger equation in general increases exponentially with the size of quantum system.
- Horn [2001b] D. Horn, Clustering via hilbert space, Physica A: Statistical Mechanics and its Applications 302, 70 (2001b), proc. Int. Workshop on Frontiers in the Physics of Complex Systems.
- Weinstein and Horn [2009] M. Weinstein and D. Horn, Dynamic quantum clustering: A method for visual exploration of structures in data, Physical Review E 80, 066117 (2009).
- Pronchik and Williams [2003] J. N. Pronchik and B. W. Williams, Exactly solvable quantum mechanical potentials: An alternative approach, Journal of Chemical Education 80, 918 (2003).
- Sehanobish et al. [2020] A. Sehanobish, H. H. Corzo, O. Kara, and D. van Dijk, Learning potentials of quantum systems using deep neural networks (2020), arXiv:2006.13297 [cs.LG] .
- Hong et al. [2021] R. Hong, P.-F. Zhou, B. Xi, J. Hu, A.-C. Ji, and S.-J. Ran, Predicting quantum potentials by deep neural network and metropolis sampling, SciPost Physics Core 4, 022 (2021).
- Stoudenmire [2018] E. M. Stoudenmire, Learning relevant features of data with multi-scale tensor networks, Quantum Science and Technology 3, 034003 (2018).
- Liu et al. [2019] D. Liu, S.-J. Ran, P. Wittek, C. Peng, R. B. García, G. Su, and M. Lewenstein, Machine learning by unitary tensor network of hierarchical tree structure, New Journal of Physics 21, 073059 (2019).
- Cheng et al. [2021] S. Cheng, L. Wang, and P. Zhang, Supervised learning with projected entangled pair states, Physical Review B 103, 125117 (2021).
- Liu et al. [2021a] Y. Liu, W.-J. Li, X. Zhang, M. Lewenstein, G. Su, and S.-J. Ran, Entanglement-based feature extraction by tensor network machine learning, Frontiers in Applied Mathematics and Statistics 7, 10.3389/fams.2021.716044 (2021a).
- Bai et al. [2022] S.-C. Bai, Y.-C. Tang, and S.-J. Ran, Unsupervised recognition of informative features via tensor network machine learning and quantum entanglement variations, Chinese Physics Letters 39, 100701 (2022).
- Wang et al. [2021b] K. Wang, L. Xiao, W. Yi, S.-J. Ran, and P. Xue, Experimental realization of a quantum image classifier via tensor-network-based machine learning, Photonics Research 9, 2332 (2021b).
- Ran et al. [2020b] S.-J. Ran, Z.-Z. Sun, S.-M. Fei, G. Su, and M. Lewenstein, Tensor network compressed sensing with unsupervised machine learning, Physical Review Research 2, 033293 (2020b).
- Sun et al. [2020c] Z.-Z. Sun, S.-J. Ran, and G. Su, Tangent-space gradient optimization of tensor network for machine learning, Physical Review E 102, 012152 (2020c).
- Wang et al. [2020b] J. Wang, C. Roberts, G. Vidal, and S. Leichenauer, Anomaly detection with tensor networks (2020b), arXiv:2006.02516 [cs.LG] .
- Hong et al. [2022] R. Hong, Y.-X. Xiao, J. Hu, A.-C. Ji, and S.-J. Ran, Functional tensor network solving many-body schrödinger equation, Physical Review B 105, 165116 (2022).
- Hao et al. [2022] T. Hao, X. Huang, C. Jia, and C. Peng, A quantum-inspired tensor network algorithm for constrained combinatorial optimization problems, Frontiers in Physics 10, 10.3389/fphy.2022.906590 (2022).
- Liu et al. [2023] J.-G. Liu, X. Gao, M. Cain, M. D. Lukin, and S.-T. Wang, Computing solution space properties of combinatorial optimization problems via generic tensor networks, SIAM Journal on Scientific Computing 45, A1239 (2023).
- Lopez-Piqueres et al. [2023] J. Lopez-Piqueres, J. Chen, and A. Perdomo-Ortiz, Symmetric tensor networks for generative modeling and constrained combinatorial optimization (2023), arXiv:2211.09121 [quant-ph] .
- [120] http://yann.lecun.com/exdb/mnist.
- Banchi et al. [2021] L. Banchi, J. Pereira, and S. Pirandola, Generalization in quantum machine learning: A quantum information standpoint, PRX Quantum 2, 040321 (2021).
- Strashko and Stoudenmire [2022] A. Strashko and E. M. Stoudenmire, Generalization and overfitting in matrix product state machine learning architectures (2022), arXiv:2208.04372 [cs.LG] .
- Convy et al. [2022] I. Convy, W. Huggins, H. Liao, and K. B. Whaley, Mutual information scaling for tensor network machine learning, Machine Learning: Science and Technology 3, 015017 (2022).
- Gao et al. [2022] X. Gao, E. R. Anschuetz, S.-T. Wang, J. I. Cirac, and M. D. Lukin, Enhancing generative models via quantum correlations, Physical Review X 12, 021037 (2022).
- Liao et al. [2023] H. Liao, I. Convy, Z. Yang, and K. B. Whaley, Decohering tensor network quantum machine learning models, Quantum Machine Intelligence 5, 7 (2023).
- Schirmer et al. [2001] S. G. Schirmer, H. Fu, and A. I. Solomon, Complete controllability of quantum systems, Physical Review A 63, 063410 (2001).
- Deng et al. [2017] D.-L. Deng, X. Li, and S. Das Sarma, Quantum entanglement in neural network states, Physical Review X 7, 021021 (2017).
- Jia et al. [2020] Z.-A. Jia, L. Wei, Y.-C. Wu, G.-C. Guo, and G.-P. Guo, Entanglement area law for shallow and deep quantum neural network states, New Journal of Physics 22, 053022 (2020).
- Larocca et al. [2023] M. Larocca, N. Ju, D. García-Martín, P. J. Coles, and M. Cerezo, Theory of overparametrization in quantum neural networks, Nature Computational Science 3, 542 (2023).
- Larocca et al. [2022] M. Larocca, P. Czarnik, K. Sharma, G. Muraleedharan, P. J. Coles, and M. Cerezo, Diagnosing barren plateaus with tools from quantum optimal control, Quantum 6, 824 (2022).
- McClean et al. [2018] J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush, and H. Neven, Barren plateaus in quantum neural network training landscapes, Nature Communications 9, 4812 (2018).
- Verstraete et al. [2004] F. Verstraete, J. J. García-Ripoll, and J. I. Cirac, Matrix product density operators: Simulation of finite-temperature and dissipative systems, Physical Review Letters 93, 207204 (2004).
- Zwolak and Vidal [2004] M. Zwolak and G. Vidal, Mixed-state dynamics in one-dimensional quantum lattice systems: A time-dependent superoperator renormalization algorithm, Physical Review Letters 93, 207205 (2004).
- Bañuls et al. [2009] M.-C. Bañuls, M. B. Hastings, F. Verstraete, and J. I. Cirac, Matrix product states for dynamical simulation of infinite chains, Physical Review Letters 102, 240603 (2009).
- Ran et al. [2012] S.-J. Ran, W. Li, B. Xi, Z. Zhang, and G. Su, Optimized decimation of tensor networks with super-orthogonalization for two-dimensional quantum lattice models, Physical Review B 86, 134429 (2012).
- Czarnik et al. [2012] P. Czarnik, L. Cincio, and J. Dziarmaga, Projected entangled pair states at finite temperature: Imaginary time evolution with ancillas, Physical Review B 86, 245101 (2012).
- Hastings and Mahajan [2015] M. B. Hastings and R. Mahajan, Connecting entanglement in time and space: Improving the folding algorithm, Physical Review A 91, 032306 (2015).
- Kshetrimayum et al. [2017] A. Kshetrimayum, H. Weimer, and R. Orús, A simple tensor network algorithm for two-dimensional steady states, Nature Communications 8, 1291 (2017).
- Huggins et al. [2019] W. Huggins, P. Patil, B. Mitchell, K. B. Whaley, and E. M. Stoudenmire, Towards quantum machine learning with tensor networks, Quantum Science and Technology 4, 024001 (2019).
- Note [12] A quantum gate is a specific operation on quantum state, and thus can be given by a quantum operator. When considering the quantum computation in practice, the quantum gates realizable on different quantum platforms (such as super-conducting circuits, ultra-cold atoms, and single photons) are different.
- Shor [1999] P. W. Shor, Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer, SIAM Review 41, 303 (1999).
- Grover [1997] L. K. Grover, Quantum mechanics helps in searching for a needle in a haystack, Physical Review Letters 79, 325 (1997).
- Ran [2020] S.-J. Ran, Encoding of matrix product states into quantum circuits of one- and two-qubit gates, Physical Review A 101, 032310 (2020).
- Cerezo et al. [2021] M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan, L. Cincio, and P. J. Coles, Variational quantum algorithms, Nature Reviews Physics 3, 625 (2021).
- Liu et al. [2020] Y. Liu, D. Wang, S. Xue, A. Huang, X. Fu, X. Qiang, P. Xu, H.-L. Huang, M. Deng, C. Guo, X. Yang, and J. Wu, Variational quantum circuits for quantum state tomography, Physical Review A 101, 052316 (2020).
- Zhou et al. [2021] P.-F. Zhou, R. Hong, and S.-J. Ran, Automatically differentiable quantum circuit for many-qubit state preparation, Physical Review A 104, 042601 (2021).
- Peruzzo et al. [2014] A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nature Communications 5, 4213 (2014).
- Tilly et al. [2022] J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth, and J. Tennyson, The variational quantum eigensolver: A review of methods and best practices, Physics Reports 986, 1 (2022).
- McClean et al. [2016] J. R. McClean, J. Romero, R. Babbush, and A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New Journal of Physics 18, 023023 (2016).
- Markov and Shi [2008] I. L. Markov and Y. Shi, Simulating quantum computation by contracting tensor networks, SIAM Journal on Computing 38, 963 (2008).
- Huang et al. [2021a] C. Huang, F. Zhang, M. Newman, X. Ni, D. Ding, J. Cai, X. Gao, T. Wang, F. Wu, G. Zhang, et al., Efficient parallelization of tensor network contraction for simulating quantum computation, Nature Computational Science 1, 578 (2021a).
- Haghshenas et al. [2022] R. Haghshenas, J. Gray, A. C. Potter, and G. K.-L. Chan, Variational power of quantum circuit tensor networks, Physical Review X 12, 011047 (2022).
- Guo et al. [2021] C. Guo, Y. Zhao, and H.-L. Huang, Verifying random quantum circuits with arbitrary geometry using tensor network states algorithm, Physical Review Letters 126, 070502 (2021).
- Vincent et al. [2022] T. Vincent, L. J. O’Riordan, M. Andrenkov, J. Brown, N. Killoran, H. Qi, and I. Dhand, Jet: Fast quantum circuit simulations with parallel task-based tensor-network contraction, Quantum 6, 709 (2022).
- Pan and Zhang [2022] F. Pan and P. Zhang, Simulation of quantum circuits using the big-batch tensor network method, Physical Review Letters 128, 030501 (2022).
- Lykov et al. [2022] D. Lykov, R. Schutski, A. Galda, V. Vinokur, and Y. Alexeev, Tensor network quantum simulator with step-dependent parallelization, in 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) (2022) pp. 582–593.
- Preskill [2018] J. Preskill, Quantum computing in the NISQ era and beyond, Quantum 2, 79 (2018).
- Arute et al. [2019] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis, Quantum supremacy using a programmable superconducting processor, Nature 574, 505 (2019).
- Guo et al. [2019] C. Guo, Y. Liu, M. Xiong, S. Xue, X. Fu, A. Huang, X. Qiang, P. Xu, J. Liu, S. Zheng, H.-L. Huang, M. Deng, D. Poletti, W.-S. Bao, and J. Wu, General-purpose quantum circuit simulator with projected entangled-pair states and the quantum supremacy frontier, Physical Review Letters 123, 190501 (2019).
- Liu et al. [2021b] Y. A. Liu, X. L. Liu, F. N. Li, H. Fu, Y. Yang, J. Song, P. Zhao, Z. Wang, D. Peng, H. Chen, C. Guo, H. Huang, W. Wu, and D. Chen, Closing the “quantum supremacy” gap: Achieving real-time simulation of a random quantum circuit using a new sunway supercomputer, in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC ’21 (Association for Computing Machinery, New York, NY, USA, 2021).
- Gray and Kourtis [2021] J. Gray and S. Kourtis, Hyper-optimized tensor network contraction, Quantum 5, 410 (2021).
- Pan et al. [2022] F. Pan, K. Chen, and P. Zhang, Solving the sampling problem of the sycamore quantum circuits, Physical Review Letters 129, 090502 (2022).
- Benedetti et al. [2019] M. Benedetti, E. Lloyd, S. Sack, and M. Fiorentini, Parameterized quantum circuits as machine learning models, Quantum Science and Technology 4, 043001 (2019).
- Lin et al. [2021] S.-H. Lin, R. Dilip, A. G. Green, A. Smith, and F. Pollmann, Real- and imaginary-time evolution with compressed quantum circuits, PRX Quantum 2, 010342 (2021).
- Shirakawa et al. [2021] T. Shirakawa, H. Ueda, and S. Yunoki, Automatic quantum circuit encoding of a given arbitrary quantum state (2021), arXiv:2112.14524 [quant-ph] .
- Dov et al. [2022] M. B. Dov, D. Shnaiderov, A. Makmal, and E. G. D. Torre, Approximate encoding of quantum states using shallow circuits (2022), arXiv:2207.00028 [quant-ph] .
- Rudolph et al. [2022] M. S. Rudolph, J. Chen, J. Miller, A. Acharya, and A. Perdomo-Ortiz, Decomposition of matrix product states into shallow quantum circuits (2022), arXiv:2209.00595 [quant-ph] .
- Chong et al. [2017] F. T. Chong, D. Franklin, and M. Martonosi, Programming languages and compiler design for realistic quantum hardware, Nature 549, 180 (2017).
- Chen et al. [2020] S. Y.-C. Chen, C.-M. Huang, C.-W. Hsing, and Y.-J. Kao, Hybrid quantum-classical classifier based on tensor network and variational quantum circuit (2020), arXiv:2011.14651 [quant-ph] .
- Huang et al. [2021b] R. Huang, X. Tan, and Q. Xu, Variational quantum tensor networks classifiers, Neurocomputing 452, 89 (2021b).
- Kardashin et al. [2021] A. Kardashin, A. Uvarov, and J. Biamonte, Quantum machine learning tensor network states, Frontiers in Physics 8, 10.3389/fphy.2020.586374 (2021).
- Araz and Spannowsky [2022] J. Y. Araz and M. Spannowsky, Classical versus quantum: Comparing tensor-network-based quantum circuits on large hadron collider data, Physical Review A 106, 062423 (2022).
- Wall et al. [2021] M. L. Wall, M. R. Abernathy, and G. Quiroz, Generative machine learning with tensor networks: Benchmarks on near-term quantum computers, Physical Review Research 3, 023010 (2021).
- Lazzarin et al. [2022] M. Lazzarin, D. E. Galli, and E. Prati, Multi-class quantum classifiers with tensor network circuits for quantum phase recognition, Physics Letters A 434, 128056 (2022).
- Note [13] Quantum computing is expected to possess higher parallelism over classical computing. One operation on an entangled quantum state can manage to process all the exponentially-many coefficients, even this operation might be just on one qubit or a local part of the state. In comparison, such parallelism cannot be gained if the state has no entanglement (i.e., a product state). This is one reason for regarding entanglement as the source for the superior power of quantum computing.
- Nishino [1995] T. Nishino, Density matrix renormalization group method for 2D classical models, Journal of the Physical Society of Japan 64, 3598 (1995).
- Levin and Nave [2007] M. Levin and C. P. Nave, Tensor renormalization group approach to two-dimensional classical lattice models, Physical Review Letters 99, 120601 (2007).
- Evenbly and Vidal [2015] G. Evenbly and G. Vidal, Tensor network renormalization, Physical Review Letters 115, 180405 (2015).
- Chen et al. [2018a] J. Chen, S. Cheng, H. Xie, L. Wang, and T. Xiang, Equivalence of restricted boltzmann machines and tensor network states, Physical Review B 97, 085104 (2018a).
- Cheng et al. [2018b] S. Cheng, J. Chen, and L. Wang, Information perspective to probabilistic modeling: Boltzmann machines versus born machines, Entropy 20, 583 (2018b).
- Zheng et al. [2019] Y. Zheng, H. He, N. Regnault, and B. A. Bernevig, Restricted boltzmann machines and matrix product states of one-dimensional translationally invariant stabilizer codes, Physical Review B 99, 155129 (2019).
- Li et al. [2021] S. Li, F. Pan, P. Zhou, and P. Zhang, Boltzmann machines as two-dimensional tensor networks, Physical Review B 104, 075154 (2021).
- Glasser et al. [2018] I. Glasser, N. Pancotti, M. August, I. D. Rodriguez, and J. I. Cirac, Neural-network quantum states, string-bond states, and chiral topological states, Physical Review X 8, 011006 (2018).
- Medina et al. [2021] R. Medina, R. Vasseur, and M. Serbyn, Entanglement transitions from restricted boltzmann machines, Physical Review B 104, 104205 (2021).
- Wang et al. [2023] M. Wang, Y. Pan, Z. Xu, X. Yang, G. Li, and A. Cichocki, Tensor networks meet neural networks: A survey and future perspectives (2023), arXiv:2302.09019 [cs.LG] .
- Zhao et al. [2016] Q. Zhao, G. Zhou, S. Xie, L. Zhang, and A. Cichocki, Tensor ring decomposition (2016), arXiv:1606.05535 [cs.NA] .
- Chen et al. [2019] C. Chen, K. Batselier, C.-Y. Ko, and N. Wong, A support tensor train machine, in 2019 International Joint Conference on Neural Networks (IJCNN) (2019) pp. 1–8.
- Chen et al. [2022] C. Chen, K. Batselier, W. Yu, and N. Wong, Kernelized support tensor train machines, Pattern Recognition 122, 108337 (2022).
- Qiu et al. [2022] Y. Qiu, G. Zhou, Z. Huang, Q. Zhao, and S. Xie, Efficient tensor robust pca under hybrid model of tucker and tensor train, IEEE Signal Processing Letters 29, 627 (2022).
- Yang et al. [2017] Y. Yang, D. Krompass, and V. Tresp, Tensor-train recurrent neural networks for video classification, in Proceedings of the 34th International Conference on Machine Learning, Proceedings of Machine Learning Research, Vol. 70, edited by D. Precup and Y. W. Teh (Proceedings of Machine Learning Research, 2017) pp. 3891–3900.
- Chen et al. [2018b] Z. Chen, K. Batselier, J. A. K. Suykens, and N. Wong, Parallelized tensor train learning of polynomial classifiers, IEEE Transactions on Neural Networks and Learning Systems 29, 4621 (2018b).
- Wang et al. [2018] W. Wang, Y. Sun, B. Eriksson, W. Wang, and V. Aggarwal, Wide compression: tensor ring nets, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2018).
- Su et al. [2020] J. Su, W. Byeon, J. Kossaifi, F. Huang, J. Kautz, and A. Anandkumar, Convolutional tensor-train lstm for spatio-temporal learning, in Advances in Neural Information Processing Systems, Vol. 33, edited by H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin (Curran Associates, Inc., 2020) pp. 13714–13726.
- Meng et al. [2023] Y.-M. Meng, J. Zhang, P. Zhang, C. Gao, and S.-J. Ran, Residual matrix product state for machine learning, SciPost Physics 14, 142 (2023).
- Wu et al. [2023] D. Wu, R. Rossi, F. Vicentini, and G. Carleo, From tensor network quantum states to tensorial recurrent neural networks (2023), arXiv:2206.12363 [quant-ph] .
- Novikov et al. [2015] A. Novikov, D. Podoprikhin, A. Osokin, and D. P. Vetrov, Tensorizing neural networks, in Advances in Neural Information Processing Systems, Vol. 28, edited by C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett (Curran Associates, Inc., 2015).
- Hayashi et al. [2019] K. Hayashi, T. Yamaguchi, Y. Sugawara, and S.-i. Maeda, Exploring unexplored tensor network decompositions for convolutional neural networks, in Advances in Neural Information Processing Systems, Vol. 32, edited by H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Curran Associates, Inc., 2019).
- Hawkins and Zhang [2021] C. Hawkins and Z. Zhang, Bayesian tensorized neural networks with automatic rank selection, Neurocomputing 453, 172 (2021).
- Liu and Ng [2022] Y. Liu and M. K. Ng, Deep neural network compression by tucker decomposition with nonlinear response, Knowledge-Based Systems 241, 108171 (2022).
- Brown et al. [2020] T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever, and D. Amodei, Language models are few-shot learners, in Advances in Neural Information Processing Systems, Vol. 33, edited by H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin (Curran Associates, Inc., 2020) pp. 1877–1901.