Systematic characterization of nanoscale $h$-BN quantum sensor spots created by helium-ion microscopy

We prepare thin $h$-BN flakes by cleaving $h$-BN bulk crystals with Scotch tape and transferring them onto a silicon substrate. A 100 nm thick Au wire (width 4 $\mu$m) is fabricated on a silicon substrate with a 285 nm thick oxide film using photolithography, and the $h$-BN flakes are stamped on top of it using the bubble-free method [32]. Figure 2(a) is an optical micrograph of a typical fabricated device. The $h$-BN flake is large enough compared to the Au wire to have areas of adhesion to both Au and SiO₂. An atomic force microscope (AFM) is used to measure the $h$-BN flake thickness $t$. Figure 2(b) shows a profile corresponding to the white dashed line in Fig. 2(a). A few steps due to the $h$-BN flake and the Au wire (Au film) are observed. We estimate the $h$-BN flake thickness of the device shown in Fig. 2(a) to be $t=47$ nm. Similarly, we fabricate devices of $h$-BN flakes with $t=9$ nm and $t=256$ nm.

We use an Orion Plus HIM (Carl Zeiss Microscopy LLC, Peabody, MA, USA) with a helium ion beam of nominal width 0.3 nm and create $V_{\mathrm{B}}^{-}$ spots on the $h$-BN flakes on the fabricated Au wire devices. HIM is a technique to irradiate a target object with a focused beam of helium ions for processing and imaging with high spatial resolution [33]. The irradiation by helium ions, which are light, is reasonable for creating small $V_{\mathrm{B}}^{-}$ spots due to less surface scattering than electron irradiation and less damage on the material structure than heavy-atom irradiation [28].

First, we precisely determine the position of the $h$-BN flake on the Au film by observing the secondary electrons emitted from the device using HIM. Then, the target positions at the $h$-BN flakes are irradiated with helium ions as designed in square-shaped spots of 100 nm on each side at an acceleration voltage of 30 keV. Thus, each spot consists of many $V_{\mathrm{B}}^{-}$ defects. The 30 keV voltage was a value used previously for the $V_{\mathrm{B}}^{-}$ defect creation with HIM [29] and conventional ion irradiation [26]. The focused helium ion beam is discretely raster scanned with an interval of $3.2$ nm so that the average helium ion dose in the spot is $d_{\mathrm{He}}~{}(\mathrm{cm^{-2}})$. Each $h$-BN flake is irradiated at multiple positions in contact with Au and SiO₂ at $d_{\mathrm{He}}=$ 10¹⁴, 10¹⁵, 10¹⁶, and 10¹⁷ cm^-2, as shown in the right panel of Fig. 2(a) (see also Table 1). Only for the device with $t=9$ nm, we use $d_{\mathrm{He}}=10^{15}$, $10^{16}$, and $10^{17}$ $\mathrm{cm^{-2}}$.

We utilize a home-built confocal microscope system [34] to characterize the created $V_{\mathrm{B}}^{-}$ spots. The PL of $V_{\mathrm{B}}^{-}$ defects occurs in the wavelength range of 750–1000 nm [17], and it can be detected using a bandpass filter and a single photon counting module while irradiating a green laser. The laser wavelength is 515–532 nm for Sec. IV.5 and 532 nm otherwise. The laser power is 0.7 mW in ODMR and spin relaxation time measurements. It is sufficiently weaker than the typical power (on Au, 7.6 mW and on SiO₂, far stronger laser power is needed to saturate) at which the PL from $V_{\mathrm{B}}^{-}$ defects saturates in our confocal system. Only in Sec. IV.5, the laser power is set to 3.0 mW to increase the signal intensity.

Figure 2(c) displays an example of the PL intensity mapping of a fabricated device with $t=256$ nm and $d_{\mathrm{He}}=10^{15}~{}\mathrm{cm^{-2}}$. Bright spots correspond to the created $V_{\mathrm{B}}^{-}$ spots. The spots surrounded by the yellow box in Fig. 2(c) are 100 nm square size irradiated spots. The PL intensity of the spots is more prominent on Au than on SiO₂.

To perform ODMR, we apply microwaves (MW) and a static magnetic field to the devices. The MW is irradiated from a 50 $\mu$m-diameter copper wire beside the Au wire, as shown in the right panel of Fig. 2(a). This configuration allows a strong and uniform MW irradiation to the $V_{\mathrm{B}}^{-}$ spots. We examine spots with different doses $d_{\mathrm{He}}$ made on $h$-BN of different thicknesses $t$ (see Table 1). They are located along the same copper wire, as shown in the right panel of Fig. 2(a). Thus, the influence of MW amplitude variation on the sensitivity evaluation is minimized. The static magnetic field is applied using a coil. The direction of the coil’s magnetic field is perpendicular to the surface of the $h$-BN flake and parallel to the quantization axis of $V_{\mathrm{B}}^{-}$, and its maximum intensity is 12 mT. We measure spin relaxation time by pulsing MW and the laser, as described in Sec. IV.3.

We discuss the ODMR results obtained on the $V_{\mathrm{B}}^{-}$ spots on the device with a flake thickness $t=47$ nm, which is a suitable thickness for $h$-BN flakes in magnetic imaging applications [29]. We estimate the shot-noise-limited static magnetic field sensitivity $\eta$ through ODMR measurements under a sufficient bias field ($B_{z}\gg E/\gamma_{e}$), using the following expression [40, 41],

The increase in the contrast $C$ and PL intensity $I$ and the decrease in $\Delta\nu$ directly contribute to the increase in sensitivity.

Figure 4(a) shows the ODMR spectra for the $V_{\mathrm{B}}^{-}$ spots on Au with various doses $d_{\mathrm{He}}$. We note that $C$ decreases as the dose increases. We obtain $C=12.7$, 12.2, and 9.2 for $d_{\mathrm{He}}=10^{15}$, $10^{16}$, and $10^{17}~{}\mathrm{cm^{-2}}$, respectively, as shown in Fig. 4(b). The decrease in $C$ with increasing $d_{\mathrm{He}}$ is also observed for different $t$, which is also the case for the $h$-BN flakes on SiO₂. The degradation is likely caused by suppression of spin lifetime or by increased photoluminescence from non-$V_{\mathrm{B}}^{-}$ defects due to large $d_{\mathrm{He}}$. Amorphous defects in the $h$-BN lattice created by He ion irradiation have been reported to affect the luminescence intensity [28], which may be related to the present observation.

In contrast to $C$, $I$ increases monotonically with $d_{\mathrm{He}}$ as shown in Fig. 4(b). We obtain $I=2\times 10^{2}$ kcps, $1.1\times 10^{3}$ kcps, and $1.3\times 10^{3}$ kcps for $d_{\mathrm{He}}=10^{15}~{}\mathrm{cm^{-2}}$, $10^{16}~{}\mathrm{cm^{-2}}$, and $10^{17}~{}\mathrm{cm^{-2}}$, respectively. The estimated background $I_{\mathrm{b}}$ is sufficiently weak $<20~{}\mathrm{kcps}$ compared to the $V_{\mathrm{B}}^{-}$ signal [see Sec. IV.5]. Therefore, the number of $V_{\mathrm{B}}^{-}$ defects increases with the amount of dose. In this way, there is a clear trade-off between $C$ and $I$ in the dose range we investigate. Nevertheless, the increase of $I$ is not proportional to $d_{\mathrm{He}}$; the intensity is increased 5.4 times from $d_{\mathrm{He}}=10^{15}$ to $10^{16}~{}\mathrm{cm^{-2}}$, while it is only 1.1 times from $d_{\mathrm{He}}=10^{16}$ to $10^{17}~{}\mathrm{cm^{-2}}$. The aforementioned amorphous defects may have prevented the formation of $V_{\mathrm{B}}^{-}$ [28].

The linewidth $\Delta\nu$ is almost insensitive to $d_{\mathrm{He}}$, as shown in Fig. 4(a); only a 5 variation in $\Delta\nu$ ($136$–$143~{}\mathrm{MHz}$) is detected within the investigated $d_{\mathrm{He}}$. This implies that the nuclear spin primarily determines $\Delta\nu$. Since the resonance is broadened by huge (several hundred MHz) level splitting due to nuclear spins [17, 18, 19, 26], the influence of the other factors is negligibly small. Further investigation of the ODMR spectra for the isotope-controlled $h$-BN [42, 43, 44], where nuclear spins have less impact than conventional ones, might enable us to observe the dose dependence of linewidths.

We estimate the sensitivity $\eta$ using Eq. (5), as shown in Fig. 4(c). It is obtained to be 61.9 $\mathrm{\mu T/\sqrt{Hz}}$, 30.2 $\mathrm{\mu T/\sqrt{Hz}}$, and 38.2 $\mathrm{\mu T/\sqrt{Hz}}$ for $d_{\mathrm{He}}=10^{15}~{}\mathrm{cm^{-2}}$, 10${}^{16}~{}\mathrm{cm^{-2}}$, and $10^{17}~{}\mathrm{cm^{-2}}$, respectively. In Ref. [29], the sensitivity of $73.6~{}\mathrm{\mu T/\sqrt{Hz}}$ is obtained for the spots on Au in the $h$-BN flake with $t=66~{}\mathrm{nm}$ irradiated with $d_{\mathrm{He}}=10^{15}~{}\mathrm{cm^{-2}}$, being consistent with the present observation (61.9 $\mathrm{\mu T/\sqrt{Hz}}$) obtained for the similar condition. We get the best sensitivity, the minimum value of $\eta$, of $30.2~{}\mathrm{\mu T/\sqrt{Hz}}$ for the spots on Au with $d_{\mathrm{He}}=10^{16}~{}\mathrm{cm^{-2}}$. The $V_{\mathrm{B}}^{-}$ density estimated by the SRIM simulation is $6.1\times 10^{16}$ in the single spot. The sensitivity is 2.5 times better than before [29]. It is an advantage of HIM that a dose as high as $10^{16}~{}\mathrm{cm^{-2}}$ can be realized with local ion irradiation in a reasonable time and cost.

Figure 4(c) also shows the sensitivity of the $V_{\mathrm{B}}^{-}$ spots on SiO₂. While the MW intensity is expected to differ significantly between on a metal (Au) and on an insulator (SiO₂), the contrast of the spots on SiO₂ is maintained at around $71$–$83\%$ of that on Au (not shown here). In contrast, $I$ on SiO₂ is only about $1$–$3\%$ of that on Au, as discussed later in Sec. IV.5. As a result, $\eta$ is approximately an order of magnitude worse than the optimal sensitivity obtained on Au [Fig. 4(c)].

Figure 4(d) shows the $d_{\text{He}}$ dependence of the strain $E$ obtained for the spots on the device with $t=47$ nm. We notice two facts. First, increasing $d_{\mathrm{He}}$ leads to an increase in strain. For example, the strains of the spots on Au are obtained as 53 MHz and 66 MHz for $d_{\mathrm{He}}=10^{15}~{}\mathrm{cm^{-2}}$ and $10^{17}~{}\mathrm{cm^{-2}}$, respectively. Similarly, we get $E$ on SiO₂ as 58 MHz and 64 MHz for $d_{\mathrm{He}}=10^{16}~{}\mathrm{cm^{-2}}$ and $10^{17}~{}\mathrm{cm^{-2}}$, respectively. Second, for a given $d_{\mathrm{He}}$, the spots on Au exhibit $3$–$10\%$ larger $E$ than those on SiO₂. This observation might indicate the substrate-dependent damage to the $h$-BN flakes. We will consider these results with simulation in Sec. IV.4.

In Ref. [25], the dose dependence of nitrogen irradiation at an accelerating voltage of 30 keV to the 10–100 nm thick $h$-BN flakes on a silicon substrate was investigated. They observed that strain $E$ increases from about 60 to 80 MHz as the dose increases from $10^{13}$ to $10^{15}~{}\mathrm{cm^{-2}}$. In contrast, $E$ is as small as 60–65 MHz for the dose of $10^{17}~{}\mathrm{cm^{-2}}$ in our study. The difference may be mainly due to the difference in the ion mass. The nitrogen ion is about seven times heavier than the helium ion, leading to more considerable irradiation damage in the $h$-BN flakes.

The large error bars in Fig. 4(d) are due to the double-Lorentzian fit of the ODMR spectra near zero fields in determining strain $E$. The double-Lorentzian shape is insufficient to reproduce the experimentally observed ODMR spectra, so the fitting precision needs to be more satisfactory. A more appropriate analytical expression for zero-field ODMR spectra, such as discussed before [45], will enhance the estimation precision of the sensor parameters.

We measure the spin relaxation time $T_{1}$ using the pulse protocol depicted in Fig. 5(a) inset. The spin state population is estimated from the PL intensity at the first 200 ns of the readout laser pulse. Figure 5(a) shows the results for the spots irradiated with $d_{\mathrm{He}}=10^{17}~{}\mathrm{cm^{-2}}$ at the device with $t=47$ nm. The vertical axis is the normalized PL intensity $I_{w}$ so that $I_{w}=1$ at $\tau=0$ ns and $I_{w}=0$ when $\tau$ is sufficiently long. Their behaviors are well explained by Eq. (4). Remarkably, the PL intensity decays faster in the spots on Au (red, $T_{1}=7.7~{}\mathrm{\mu s}$) than those on SiO₂ (blue, $T_{1}=14.7~{}\mathrm{\mu s}$). These values are typical for $T_{1}$ of $V_{\mathrm{B}}^{-}$ centers [46, 21, 27].

We also investigate the $d_{\mathrm{He}}$ dependence of $T_{1}$, as presented in Fig. 5(b). We notice two trends. First, $T_{1}$ becomes smaller for larger $d_{\mathrm{He}}$. This observation agrees with previous studies [25, 39], which discussed that the $T_{1}$ degradation is caused by lattice damage during irradiation. For the spots on Au, changing $d_{\mathrm{He}}$ from $10^{15}~{}\mathrm{cm^{-2}}$ to $10^{16}~{}\mathrm{cm^{-2}}$ results in a 27$\%$ degradation, and changing from $10^{16}$ to $10^{17}~{}\mathrm{cm^{-2}}$ leads to a 35$\%$ degradation. For the spots on SiO₂, changing $d_{\mathrm{He}}$ from $10^{16}~{}\mathrm{cm^{-2}}$ to $10^{17}~{}\mathrm{cm^{-2}}$ results in an 11$\%$ degradation. Clearly, the degradation is more pronounced for the spots on Au than on SiO₂. Second, for a given $d_{\mathrm{He}}$, the spots on SiO₂ have a 1.4–1.9 times longer $T_{1}$ than those on Au.

Figure 5(c) shows the spin relaxation of the spots on the device with a thicker $h$-BN of $t=256$ nm with $d_{\mathrm{He}}=10^{17}~{}\mathrm{cm^{-2}}$. In contrast to the case with $t=47$ nm shown in Fig. 5(a), the decays for the spots on Au and on SiO₂ are almost identical.

The above results suggest that irradiation damage depends on the substrate and $h$-BN thickness. This insight is further investigated by the Monte Carlo simulations next.

We run a Monte Carlo simulation package, Stopping and Range of Ions in Matter [31] (SRIM), where the collision events and the resultant vacancy distribution created by ion irradiation are calculated. SRIM treats atomic collisions as classical two-body ones, including the atomic interactions and the cascade effect where one scattered atom scatters another. Since the ion irradiation spot size of HIM is extremely small, the spreading effect of ions randomly colliding in the target material should be carefully treated in estimating the actual $V_{\mathrm{B}}^{-}$ spot size.

Figure 6(a) shows the simulation configuration, where helium ions are directed perpendicular to the $h$-BN flake from left to right and enter it perpendicularly from the incident position. There, $R$ and $D$ indicate the distance from the incident axis and the depth from the surface, respectively. The flake is attached to a sufficiently thick Au or SiO₂ film. The backscattering of ions at the substrate film plays an important role in the defect creation. We set the acceleration voltage to 30 keV and the $h$-BN, SiO₂, and Au densities at 2.3 g/cm³ [47], 2.1 g/cm³ [48], and 19.3 g/cm³. We consider $V_{\mathrm{B}}^{-}$ positions to be those of the removed boron atoms. We analyze the results of irradiating each device with a total of 10⁴ helium ions.

The top panel of Fig. 6(b) shows the histogram of the density of the created $V_{\mathrm{B}}^{-}$ defects per unit length as a function of $R$ for the device with $t=47$ nm. In the range $R<12$ nm [indicated by the vertical dot-dash line in Fig. 6(b)], the $V_{\mathrm{B}}^{-}$ defect density distribution is nearly the same for the $h$-BN flakes on Au and SiO₂. In contrast, for $R>12$ nm, more $V_{\mathrm{B}}^{-}$ defects tend to be created for the flake on Au than on SiO₂. In total, the $V_{\mathrm{B}}^{-}$ defects are created 2.0 times more on the former than on the latter, which means that the total damage is higher for the flake on Au. Au has a higher density than SiO₂, so backscattering is more significant, leading to increased irradiation damage. In Secs. IV.2 and  IV.3, we discussed larger $E$ and shorter $T_{1}$ for devices on Au than on SiO₂. This is consistent with our simulation that lattice damage depends on the substrate film.

The bottom panel of Fig. 6(b) shows the normalized cumulative distribution as a function of $R$. For the $h$-BN ($t=47$ nm) on Au, three-fourths (75%) of all $V_{\mathrm{B}}^{-}$ defects are created scattered over an area up to $R~{}\sim 76$ nm, as indicated by the horizontal dashed line in the figure. Such a spreading of the $V_{\mathrm{B}}^{-}$ defects degrades the localization of the sensor. In contrast, on SiO₂, the same amount of $V_{\mathrm{B}}^{-}$ defects is concentrated only in an $R<6$ nm area. Using the SiO₂ substrate with less backscattering would help create a $V_{\mathrm{B}}^{-}$ spot as small as a few nm.

Figure 6(c) shows the depth ($D$) dependence of the defect creation for a thick $h$-BN flake ($t=1~{}\mathrm{\mu m}$). Almost all of $V_{\mathrm{B}}^{-}$ defects are created shallower than $D=256$ nm in a thick $h$-BN flake, as indicated by a vertical dashed line in the bottom panel of Fig. 6(c). This means that the backscattering from the substrate (Au or SiO₂) is almost negligible in an $h$-BN flake thicker than this. The difference in the defect creation between Au and SiO₂ in a 256 nm thick $h$-BN flake is only 1% (data not shown). It is also interesting to focus on a small $D$ region. The normalized cumulative distribution from the surface is only 7% at depth $D=47$ nm. Thus, for the thin $h$-BN flake with $t=47$ nm, most $V_{\mathrm{B}}^{-}$ defects are produced by ions that have undergone backscattering.

The above observations can explain several experimental findings discussed in Secs. IV.2 and  IV.3. Au tends to backscatter ions more than SiO₂, so a thin $h$-BN flake on Au is more subject to backscattering damage than one on SiO₂. This agrees with a larger strain $E$ for $t=47$ nm in the Au case than in the SiO₂ case, shown in Fig. 4(d) for a given $d_{\mathrm{He}}$. We can also claim that the backscattering effect is responsible for the shorter spin relaxation time $T_{1}$ of the $t=47$ nm flake on Au than on SiO₂, as shown in Fig. 5(a). In sharp contrast, $T_{1}$ is almost the same on Au and SiO₂ in a thick $h$-BN flake ($t=256$ nm) [see Fig. 5(c)], which is concordant with the calculation that the fraction of $V_{\mathrm{B}}^{-}$ defects created by backscattering is reduced for thicker flakes. Thus, the SRIM results nicely illustrate the experimental results.

We evaluate the PL intensity at the irradiated spot for various conditions. For this investigation only, we set the laser power to 3.0 mW, our maximum available power, to enhance the signal. Note that we do not treat the result of the spots of the device with $t=47$ nm and $d_{\mathrm{He}}=10^{14}~{}\mathrm{cm^{-2}}$ and of the device with $t=9$ nm on SiO₂, as they do not provide a sufficient luminescence signal from the analysis. As mentioned in Sec. III, the overall PL intensity $I$ includes background fluorescence other than $V_{\mathrm{B}}^{-}$. We separate the spot luminescence $I_{\text{s}}$ from the background $I_{\text{b}}$ to focus only on the increase in luminescence due to ion irradiation.

We separate $I_{\mathrm{s}}$ from $I_{\text{b}}$ in the following way. Figure 7(a) shows a typical PL mapping as an $XY$ plane at a $V_{\mathrm{B}}^{-}$ spot on the $h$-BN flake. The spot shape can be fitted using a two-dimensional Gaussian distribution with a peak contribution of $I_{\mathrm{peak}}$, including an offset of $I_{\mathrm{b}}$. Figures 7(b) and (c) show the cross sections of the PL intensity across the peak along the $X$ and $Y$ axes, respectively. The markers represent the experimental data, and the lines represent the fitting result. The dashed line corresponds to $I_{\mathrm{b}}$. Then, we find $I_{\mathrm{s}}$ as $I_{\mathrm{peak}}-I_{\mathrm{b}}$.

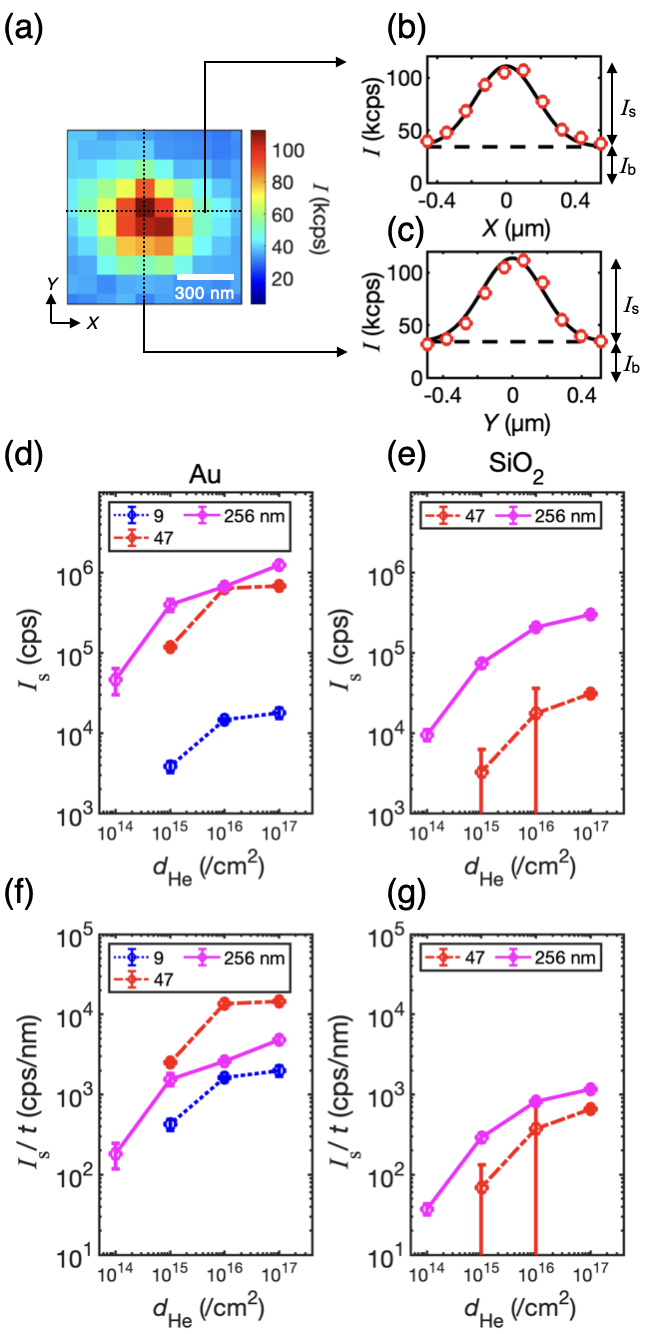
Figures 7(d) and (e) show the dose dependence of $I_{\mathrm{s}}$ for the spots on Au and SiO₂, respectively. $I_{\mathrm{s}}$ shows a monotonic increase in $d_{\mathrm{He}}$ for all devices with $t=9$, 47, and 256 nm. The rise in $I_{\mathrm{s}}$ becomes smaller for higher $d_{\mathrm{He}}$. It corresponds to a decrease in $V_{\mathrm{B}}^{-}$ defect creation efficiency at high doses and agrees with the discussion given for Fig. 4(b) in Sec. IV.1. It is known that amorphization of substrates and $h$-BN crystals occurs at helium doses of $10^{17}$ cm^-3 with an acceleration voltage of 30 keV [49, 50], and such defects may prevent $V_{\mathrm{B}}^{-}$ defect creation.

Next, we compare $I_{s}$ of the spots on Au and on SiO₂ in Figs. 7(d) and (e), respectively. For the spots with $t=47~{}$nm and $d_{\mathrm{He}}=10^{17}~{}\mathrm{cm^{-2}}$, $I_{s}$ is about 22 times larger on Au than on SiO₂. The enhancement is peculiar because the simulation results in Sec. IV.4 naively predict that the $V_{\mathrm{B}}^{-}$ defect creation efficiency on Au is about two times larger than on SiO₂. This marked enhancement is due to the luminescence enhancement on Au. In a previous study [27], for an $h$-BN flake with $t\sim 50$ nm, the luminescence on Au is 10–15 times stronger than on SiO₂. Thus, it is reasonable that $I_{s}$ increases about 20 times more on Au than on SiO₂.

In contrast, the $I_{s}$ is only 2–3 times larger on Au than on SiO₂ for the device with $t=256~{}$nm. This agrees with the fact that the luminescence enhancement on Au is suppressed at an $h$-BN as thick as 200 nm [27]. Also, as discussed in Sec. IV.4, a thick flake has no significant enhancement due to backscattering from the substrate in the $V_{\mathrm{B}}^{-}$ defect creation.

Finally, in Figs. 7(f) and (g), we compare $I_{\mathrm{s}}$ per unit flake thickness, i.e., $I_{\mathrm{s}}/t$. In the devices on Au, the value is maximized for $t=47~{}$nm, being 1.6–5.4 times higher than for $t=256$ nm and 5.9–8.4 times higher than for $t=9$ nm. This result is attributed to the composite effects of the backscattering [Sec. IV.4] and the $t$-dependent luminescence enhancement on Au [27]. In the devices on SiO₂, in contrast, $I_{\mathrm{s}}/t$ is bigger for $t=256$ nm than for $t=47$ nm. This is consistent with the fact that the depth at which most boron vacancies are created is $D=150$–250 nm for an acceleration voltage of 30 keV, as shown in the top panel of Fig. 6(c). When the $h$-BN is very thin on SiO₂, the He ion goes through without defect creation.

We now summarize the results obtained so far and provide guidelines for creating $V_{\mathrm{B}}^{-}$ spots using HIM.

First, we discuss the choice of the substrate. The advantage of selecting Au is that, even at a low $d_{\mathrm{He}}$, the effective dose increases due to significant backscattering for an $h$-BN flake with a thickness well below 256 nm. Additionally, Au significantly enhances the PL intensity, which is beneficial for high magnetic-field sensitivity. The optimum dose that maximizes sensitivity in the conditions investigated in this study is about $10^{16}~{}\mathrm{cm^{-2}}$ (Table 2). The optimal condition could be further investigated with different spot sizes and acceleration voltages.

On the other hand, the advantage of SiO₂ is that SiO₂ causes less backscattering than Au, and a well-localized spot can be created. The spot size is expected to be smaller than 10 nm for devices with a thickness of 47 nm [see Fig. 6(b)]. The optimum dose for this purpose is $10^{17}~{}\mathrm{cm^{-2}}$, which gives a sensitivity of $\sim 250~{}\mathrm{\mu T/\sqrt{Hz}}$ [Fig. 4(c)]. Further fine-tuning of dose and verification at higher doses may yield even better sensitivity. In principle, high localization and sensitivity can be obtained simultaneously by irradiating $h$-BN flakes on SiO₂ with helium ions to create $V_{\mathrm{B}}^{-}$ spots and then stamping them on Au.

Second, we comment on the choice of flake thickness $t$. Consider the case where flakes are sufficiently thin (say, $t\ll 256$ nm) and irradiated at a given $d_{\mathrm{He}}$; as shown in Fig. 6(c), in that case, the thicker the flake, the more the $V_{\mathrm{B}}^{-}$ defects are created. On the other hand, as the thickness increases, the spot size increases due to collision processes inside the flake and the backscattering at the substrate film (Au or SiO₂). Fortunately, if we use an $h$-BN flake on Au, the luminescence enhancement is substantial at $t\sim 50$ nm, so there is no need to increase the thickness of the flakes any further.