Syracuse Maps as Non-singular Power-Bounded Transformations and Their Inverse Maps
Abstract.
We prove that the dynamical system , where is a finite measure equivalent to the counting measure, is power-bounded in if and only if there exists one cycle of the map and for any , there exists such that is in some cycle of the map . This result has immediate implications for the Collatz Conjecture, and we use it to motivate the study of number theoretic properties of the inverse image for , where denotes the Collatz map here. We study similar properties for the related Syracuse maps, comparing them to the Collatz map. We also analyze some structural properties of the inverse image in relation to asymptotic density of the set .
2020 Mathematics Subject Classification:
Primary 11B75, Secondary 37A40, 37A441. Introduction
Many mathematicians have investigated the Collatz Map through a variety of means from number theory to dynamical systems. For a compendium of prior work on the subject, see [7]. However, this paper seeks to investigate a new route of analyzing this notorious map by generalizing the method introduced by the first author in [1] to a larger collection of maps, as well as to elucidate the structure of the pre-image trees of some maps with respect to this process. Mathematicians have also studied several density results related to the Collatz Map. Both Terras [12] and Everett [3] were able to show independently that for almost every , there exists such that , with Korec proving a stronger asymptotic density result, with for [4]. Tao obtained results pertaining to logarithmic density [10]. Since this topic deals with the positive integers, we shall consider not to contain . First, define the truncated Collatz map:
Definition 1.
The Collatz map is a function so
| (1) |
The Collatz Conjecture states that is the only cycle of this map, and that the trajectories of the map are bounded. We focus on the latter of these two requirements, which, put rigorously, says that for any there exists such that is part of a cycle. Next, consider a broader class of maps as presented in [9]:
Definition 2.
Let a Syracuse-type map be a function of the form
| (2) |
where and , and
While the Collatz Map is often referred to as the Syracuse map, we distinguish these general cases as Syracuse-type maps or simply Syracuse maps for brevity. A simple sub-class of these maps often called maps, which are the same as the Collatz map except with some value replacing the , has often been the focus of study. It is known that several of these maps have cycles, and that some have multiple cycles ([7]).
2. Ergodic Characterization of the General Syracuse Map
2.1. Extending the Hopf Decomposition:
While it is not completely necessary to use the Hopf Decomposition for the primary result of the next section, it is helpful in providing motivation. Colloquially, the Hopf decomposition provides that, in a non-singular system, the ambient space may be separated into sets conservative and dissipative with respect to the map (for a full proof and rigorous statement, see [5]). In the case of the Collatz system, any unbounded trajectory must be in the dissipative part, while any cycle must be in the conservative part. In fact, this may be sharpened further, and an extended version of this decomposition is given in [1] for the Collatz map. It may also be expanded to more general maps on the natural numbers.
Theorem 1.
Consider a non-singular dynamical system . There exists a partition of into sets such that:
-
(1)
The restriction of to is conservative. The set is -absorbing, and is the at-most-countable union of cycles .
-
(2)
The set is equal to .
-
(3)
The set is the complement of in , .
-
(4)
Any and all unbounded trajectories of lie in
Proof.
: The Hopf Decomposition provides a partition of into sets and , so that the restriction of to is conservative and is -absorbing. Since is countable, also is, so it can contain at most countable many cycles. This proves (1). Let . Let . Then, . Therefore, , and (2) and (3) are proven. Finally, given any , a bounded trajectory means that there exists so , so either or . Given an unbounded trajectory of the point , the set is wandering, and for any natural number . Thus, and (4) is proven. ∎
This characterization sets aside the unbounded trajectories of a map in a set . Showing that this set is empty would prove half of the Collatz conjecture. This leads to the following characterization that is equivalent to such a case. Furthermore, showing that is exactly would prove the entire conjecture.
2.2. Dynamical System Characterization:
Proving that is empty is essentially the same problem as proving the trajectories bounded, thus it is important to introduce some equivalent criteria for such a case. To do so, consider the following definition.
Definition 3.
: Let be a non-singular dynamical system. It is said to be power bounded in (or often simply just power bounded) if there exists some such that for all sets and natural numbers , .
Using this structure from the study of dynamics, the first author presented the following characterization of the Collatz map:
Theorem 2.
Let be the Collatz dynamical system with the counting measure . The following are equivalent:
-
(1)
There exists a finite measure equivalent to for which the dynamical system is power bounded in .
-
(2)
The set is empty.
-
(3)
The trajectories of each point are bounded.
This characterization may be extended to nearly all maps. Of course, the Collatz map and other similar maps have cycles that define the conjecture surrounding them. It is necessary for these maps to have at least one cycle to use such a characterization, because otherwise the set cannot be empty in any case. Given this caveat, the next theorem follows.
Theorem 3.
Let be a dynamical system where is a finite measure equivalent to the counting measure. Then, it is power-bounded in if and only if there exists at least one cycle of the map and for any , there exists a non-negative integer such that is in some cycle of the map .
Proof.
) Consider the power-bounded system . By contradiction, let there exist some so is never in a cycle. Then, for all , , . Let . Further, since the measure is finite, , implying that as . Given any , we may take some large such that . Hence, , contradicting that the system is power bounded since was arbitrary.
) Let this property hold. Since the space is countable, there are at most countable many cycles, and every point is in a pre-image of a cycle. Let the cycles be the sets . First consider . The cycle must be of finite length, N, so we construct a measure on . Define a function , which will have a measure value at each specified point, and set the measure of any to be the sum of the measures of the points in . Let for any , and let so that . Next, there are at most countably many points in . The infinite case implies the finite case, so we consider this case. Enumerate these points as . Set , so that . Next, consider , which does not contain nor any other point with a defined measure since such a case would generate a cycle. It again may be enumerated as , since the set is at most countably infinite. Set so that and so . Repeat inductively over the pre-images generated by this set, and set all points not in to have measure zero.
The process above gives that . Repeat this inductively again over the , and we may generate a new measure by the countable sum of measures. Let , so and is a finite measure. Further, every point in is in one of the , so every point has nonzero measure under . Next, we need to show that the measure allows our point transformation to be power bounded. By construction, for any set such that . For a set intersecting the cycle , separating gives for all . Therefore, . The measure is finite and power-bounded in , as well as equivalent to the counting measure, as desired.
∎
Remark 1: Given the previous result, it is helpful to note which Syracuse maps have cycles and thus can use this characterization. For example, consider a map
| (3) |
where is an odd number. It is easy to see that , and if , there exists a cycle . The Collatz map falls into this category. It is also known that cycles exist in the case of , and [2].
3. Chain Structure in The Collatz Map
Looking at the Collatz and generalized Collatz maps in terms of a power-bounded system as above leads naturally to examining the inverse map. The action of the Collatz map is rather erratic when looking in the forward direction, but in the backward direction, some patterns begin to arise, specifically when classifying values as nodes modulo 3. However, these patterns don’t necessarily extend to general maps, allowing for classification of these maps.
3.1. The Collatz Map:
While the map may seem unpredictable at first, looking at values modulo 3 presents some regularity. A simple check shows that , , and . For shorthand, we designate three sets.
Definition 4.
A value is said to be in if .
The pre-image of a node in is again in , the pre-image of a node in is in , and the pre-image of a node in includes one node either in or and another in . The latter behavior is the most interesting, and may be characterized in a more lucid way, using a simple lemma.
Lemma 4.
Any node in may be written as where , , and is not a multiple of or .
Proof.
For arbitrary , it may be written as be definition, and thus as . Using the Fundamental Theorem of Arithmetic, has the desired representation . ∎
Under this representation, . In particular, we may characterize a family of nodes by either the image or part of the pre-image, where , , and this repeats until . Define this as a family structure, when such a repeating form occurs.
In this final case, the node is even and its image is a node. The pre-image of the node is again a node, starting the process again. Connecting these families forms a chain. This chain may extend in the other direction as well. In the case that is an node, its pre-image is in , and so it takes the form following the conditions of the lemma as well. It has been useful to distinguish the nodes of the form as “chain head nodes,” although they are on equal footing of importance with the nodes of the form .

3.2. More General Maps:
Many of the more general maps with similar forms to the Collatz Map have extremely different structures and properties, for example, that many currently are not known to have a cycle. Consider a sub-class of these maps, where
| (4) |
where is an odd integer and is taken to be an integer so and is relatively prime to . In this case, the idea of a family structure includes some repeating form over a number of nodes. For example, if . We then have the following.
Theorem 5.
A map has a chain structure precisely when or .
Proof.
This relies on a couple building blocks of concepts that led to the chain structure in the Collatz map. First, the family structure gives a node of the form (where is neither a multiple of or ) so that . This requires that be odd, and so
| (5) |
Hence, and . Since is an integer, is, and since , . Note that these calculations also show that elements in the class of have two pre-images. These are, in fact, the only nodes with pre-images.
This case where gives a further sub-class of maps with the family structure. Next, we most consider the connection of families to create chains. Using the previous notation, let be the largest positive integer so divides . We would require that
| (6) |
Such a condition would connect two families, since would then have a representation .
The above equation says that
| (7) |
Since is odd, this occurs exactly when
| (8) |
which reduces to the trivial
| (9) |
We thus have that the families connect for this form of map whenever they occur. ∎
Remark 2: We may extend further to the case of
| (10) |
where and , and , as proposed in [9] and [8]. In this case, since , when is an integer, . These families may occur in one such class modulo , or in several depending on this condition. Future results using the chain structure on the Collatz map may be generalized to such a class of maps.
4. The Set and Previous Density Results
The properties of the set are of interest, as the Collatz Conjecture is equivalent to the statement . The set was introduced by R. Terras in [11], where it was also shown to have density 1. The works of Korec generalized this set to for in [4], which also has density 1, and further generalizations follow in Lagarias [6], Everett [3], and Tao [10].
However, these density results do not have immediate implications to the structure of , the elements of with unbounded trajectories, or , since and could contain elements which have unbounded trajectories as long as they have some lesser iterated image.
Proposition 6.
Assume that . Then,
-
•
1) There exists for any .
-
•
2) Assume has density , and that there are finitely many cycles . Let satisfy for all . Then has density .
-
•
2) can be written as a countable disjoint union of sets of the form where each is in . Furthermore, each is invariant under .
Proof.
(1) Let be nonempty. By the well-ordering of the natural numbers, there exists some minimum element . Consider that for any and in particular . Fix some . Then, Take large enough such that , and then .
(2) Since has density , has density . So it suffices to show that . If has bounded trajectories, then by definition for some we have for some . By taking more iterates, we have .
(3) We clearly have which is a countable union since is countable. Since is invariant under and implies , we can discard some elements in the above union to yield a disjoint union. By definition, is the smallest set that contains all preimages of all images of under so is invariant.
∎
Remark 3: With these assumptions, we would obtain stronger density results for the likes of functions previously analyzed. In addition, while this set is not as well-understood as , Theorem 1 shows that it has invariance under the forward and reverse Collatz map, and . Similarly, if any number has bounded trajectories, then so does and so do the values in the set . Such invariance properties are not immediate for : If for some and is even, then it is not immediate that , or if any iterate is less than . If , then does not imply . This motivates the study of the structure of , assuming it is non-empty.
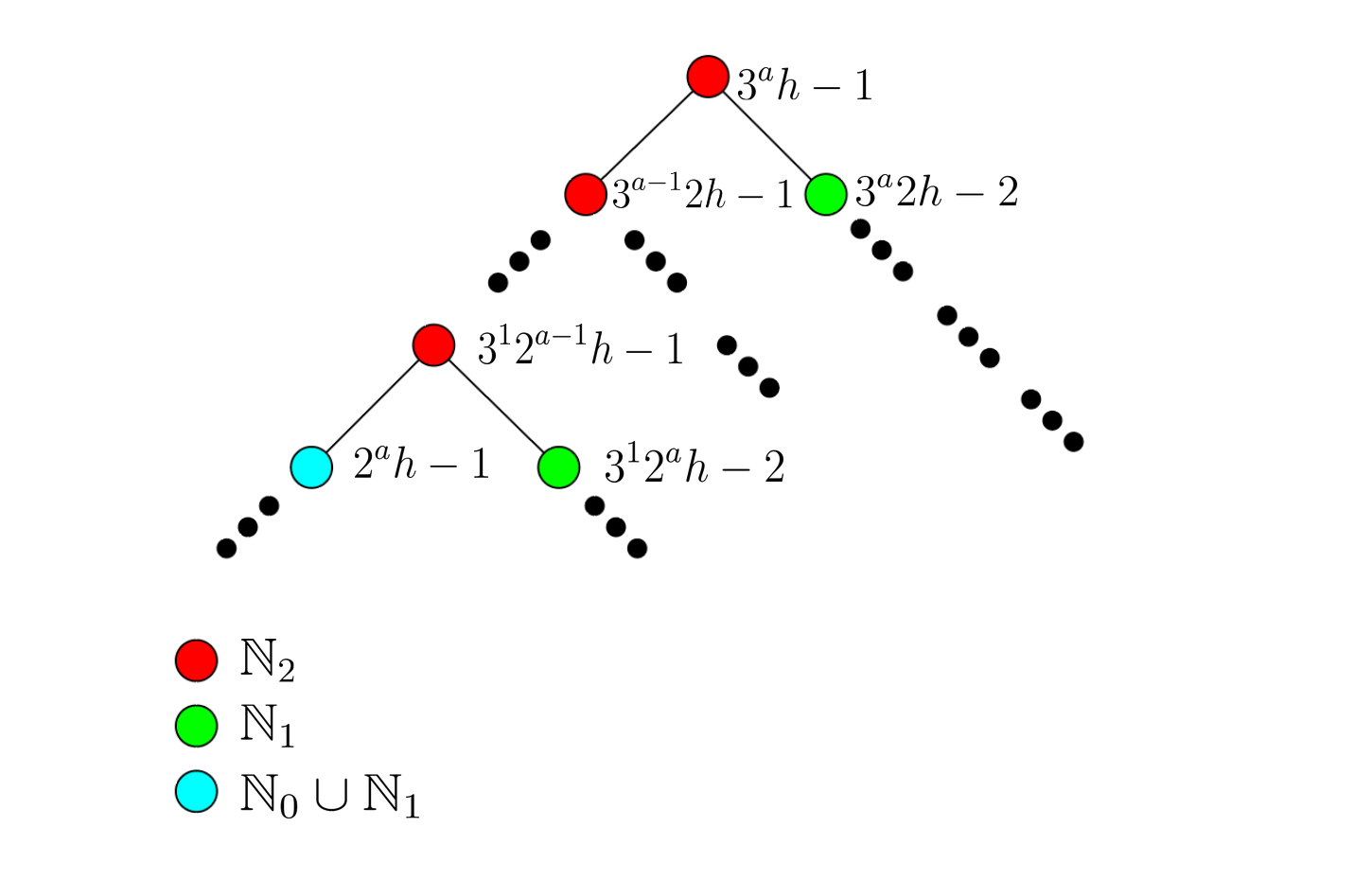
Part 3 of the above proposition gives a way to organize in relatively nice, invariant chunks which generate . Following the family and chain structures introduced previously, the values in and how they behave under determine the structure of the sets and hence . Given that the preimages of expand under the action exactly times before reaching a non- node, we then focus on this preimage level.
Definition 5.
We refer to the nodes in as the triangle generated by the node and the nodes as the -th level preimages.
For example, the triangle generated by is just the first levels of the tree generated by , i.e . By a quick computation, one can see that the only possible elements of the triangle which are not in are iterates of the action (specifically, the nodes ). For brevity, let us consider the two possible actions of the inverse map . Call the the left action, and the action the right action. Thus, the iterates of left actions are on the leftmost branch of the triangle (see Figure 1). This leads to the following claim:
Claim: For all in a triangle generated by , we can find such that , if does not lie on the left branch of the triangle.
This statement has been verified for several different values of and . In particular, we have verified this statement for all possible combinations of and , through the code in the appendix.
The numerical data suggests that this claim is true, which would give a more precise characterization of the elements of .
5. Code Appendix
References
- [1] Idris Assani. Collatz map as a power bounded nonsingular transformation. https://arxiv.org/abs/2208.11675, 2022.
- [2] R. E. Crandall. On the “” problem. Mathematics of Computation, 32(144):1281–1292, 1978.
- [3] CJ Everett. Iteration of the number-theoretic function. The Ultimate Challenge: The 3x+ 1 Problem, page 225, 2010.
- [4] Ivan Korec. A density estimate for the problem. Mathematica Slovaca, 44(1):85–89, 1994.
- [5] Ulrich Krengel. Ergodic Theorems. De Gruyter, 2011.
- [6] Jeffrey C. Lagarias. The 3x + 1 problem and its generalizations. The American Mathematical Monthly, 92(1):3–23, 1985.
- [7] Jeffrey C. Lagarias. The 3x+1 Problem: An Overview. https://arxiv.org/abs/2111.02635, 2021.
- [8] Keith R. Matthews and Robert N. Buttsworth. On some Markov matrices arising from the generalized Collatz mapping. Acta. Arithmetica, 55:43–57, 1990.
- [9] Keith R. Matthews and Anthony M Watts. A generalization of Hasse’s generalization of the Syracuse algorithm. Acta. Arithmetica, 43:167–175, 1984.
- [10] Terence Tao. Almost all orbits of the collatz map attain almost bounded values. https://arxiv.org/abs/1909.03562, 2019.
- [11] Riho Terras. A stopping time problem on the positive integers. Acta Arithmetica, 30(3):241–252, 1976.
- [12] Riho Terras. On the existence of a density. Acta Arithmetica, XXXV:85–89, 1979.