Synaptic-Like Plasticity in 2D Nanofluidic Memristor from Competitive Bicationic Transport
Abstract
Synaptic plasticity, the dynamic tuning of signal transmission strength between neurons, serves as a fundamental basis for memory and learning in biological organisms. This adaptive nature of synapses is considered one of the key features contributing to the superior energy efficiency of the brain. In this study, we utilize molecular dynamics simulations to demonstrate synaptic-like plasticity in a subnanoporous 2D membrane. We show that a train of voltage spikes dynamically modifies the membrane’s ionic permeability in a process involving competitive bicationic transport. This process is shown to be repeatable after a given resting period. Due to a combination of sub-nm pore size and the atomic thinness of the membrane, this system exhibits energy dissipation of 0.1–100 aJ per voltage spike, which is several orders of magnitude lower than 0.1–10 fJ per spike in the human synapse. We reveal the underlying physical mechanisms at molecular detail and investigate the local energetics underlying this apparent synaptic-like behavior.
Synapses are junctions that enable chemo-electrical signaling between neurons. In a typical synapse, the signal transmission strength is dynamically modulated in response to previous neural activity, a feature referred to as synaptic plasticity Abbott and Nelson (2000); Martin et al. (2000). This adaptive alteration of synaptic strength plays a fundamental role in memory and learning functions in living organisms. Moreover, it enables biological neural networks to concurrently perform both processing and storage of information in a sparse manner, a feature believed to be central to their superior energy efficiency. Inspired by these biological functionalities, artificial electrical elements with synaptic-like plasticity have been studied extensively Huh et al. (2020); Marković et al. (2020); Sebastian et al. (2020); Noy et al. (2023); Chen et al. (2023); Lee et al. (2021), aimed at building analog artificial neural networks with substantially enhanced energy efficiency compared to emulations based on the von Neumann computing architecture.
Memristors Chua (1971) comprise an area of extensive research due to their potential promise as artificial synaptic elements for neuromorphic computing. Physically, a memristor is an electrical conductor capable of modulating its conductivity in response to previous voltage inputs and maintaining the modulated state without a continuous source of power. This internal gating enables memristor networks to perform information processing and storage simultaneously. Over the past decade, solid-state neuromorphic chips featuring memristor networks have been demonstrated to perform analog machine learning tasks at a fraction of the energy cost of their von Neumann counterparts Duan et al. (2024); Sebastian et al. (2020); Ning et al. (2023); Le Gallo et al. (2023). More recently, there has been a spike of interest in nanofluidic memristors to directly mimic biological neural networks Bu et al. (2019); Sheng et al. (2017); Zhang et al. (2019); Robin et al. (2021); Xiong et al. (2023); Robin et al. (2023); Emmerich et al. (2024); Paulo et al. (2023); Shi et al. (2023); Noh and Smolyanitsky (2024a); Zhou et al. (2024); Ramirez et al. (2024a, b), with two recent works notably reporting long-term memory effects along with basic Hebbian learning Robin et al. (2023)), as well as operating voltage comparable to that of biological synapses and yielding sub-picojoule energy consumption per spike Xiong et al. (2023). In nanofluidic memristors, aqueous ions serve as the charge carriers instead of electrons, in resemblance to the human brain. One noteworthy difference between electrons and ions as charge carriers is the rich diversity of the latter, which can coexist within a given system. In particular, the competitive interplay between the ionic species leads to interesting phenomena, including ion sieving Fang et al. (2019a) and memristive ion transport Noh and Smolyanitsky (2024a). It is well known that biological systems readily harness the diversity of ion species for their functions, as most notably exemplified by the generation of action potentials in neurons Bean (2007). Therefore, exploring ways to harness ionic diversity in artificial nanofluidic systems to achieve neuromorphic functions may represent a crucial research direction in nanofluidics.
Among fluidic ion conductors, nanoporous 2D membranes represent a class of materials with high energy efficiency of ion transport. The primary reason for this efficiency is the atomic thinness, which, combined with sub-nm pore dimensions, enables relatively low, highly localized and ion-selective permeation barriers, as described earlier Smolyanitsky et al. (2018); Fang et al. (2019a, b); Hassani et al. (2021). Unsurprisingly, this class of materials has been considered for a range of applications, including water desalination Liu et al. (2016); Cohen-Tanugi and Grossman (2012); Yang et al. (2019); Noh and Aluru (2021), molecular separation Liu et al. (2016); Zhu et al. (2018); Xu et al. (2022), and osmotic energy harvesting Feng et al. (2016); Safaei and Wang (2022). Combined with high permeation selectivity and the prospect of high-density pore array fabrication Moreno et al. (2018); Choi et al. (2018); Zhong et al. (2019), subnanoporous 2D membranes appear to be excellent candidates for artificial synaptic devices. Achieving reliable memory functionality, however, is neither trivial, nor necessarily intuitive. In this study, we demonstrate synaptic-like plasticity of aqueous ion transport through a sub-nanoporous 2D membrane. We demonstrate that it arises from the adsorption/desorption and transport of two cation species with markedly different ion-pore affinities. Finally, We provide a comprehensive molecular-level insight into the underlying mechanisms.
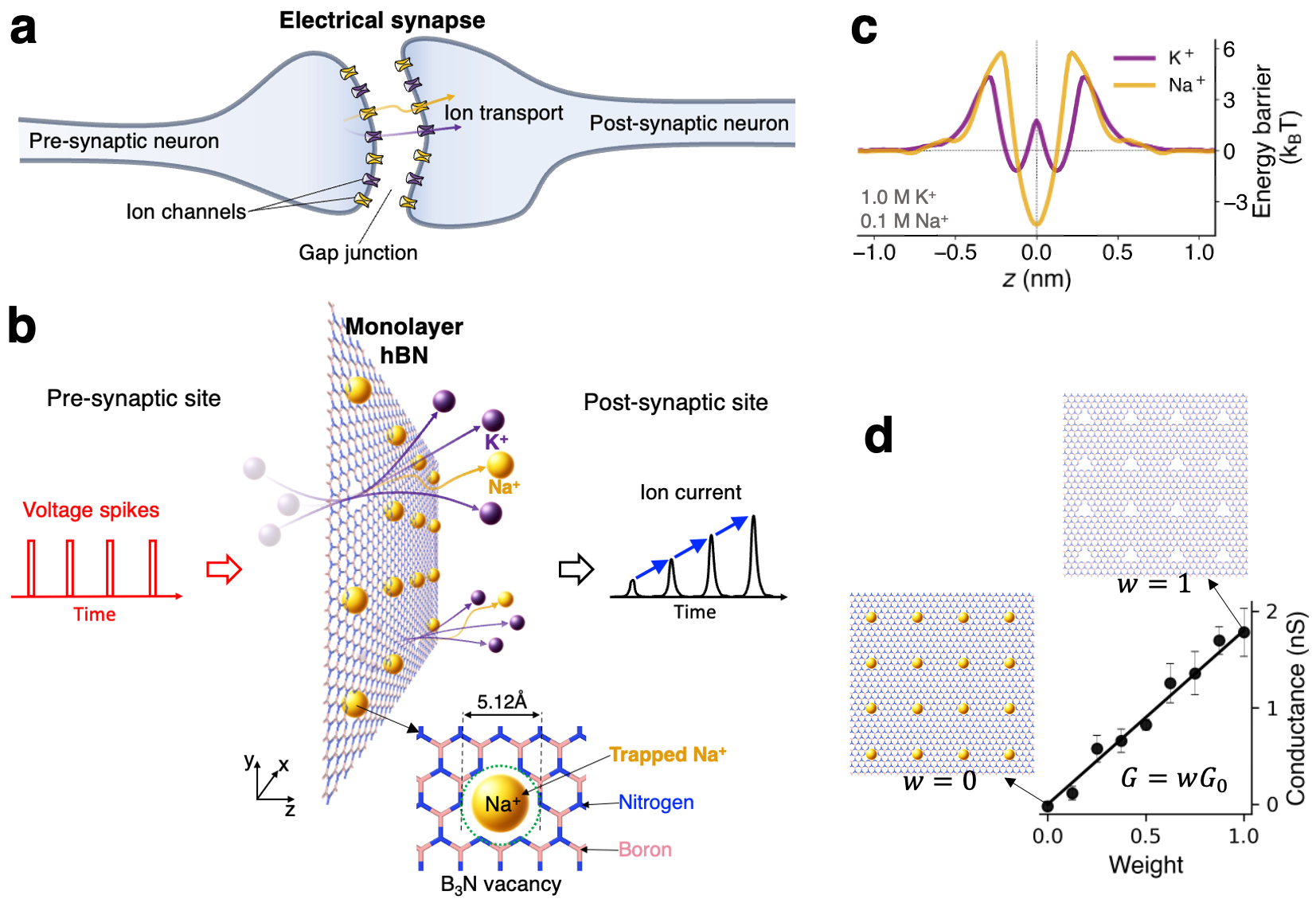
We used all-atom molecular dynamics (MD) simulations to investigate dynamic ion transport across a 2D porous membrane under a sequence of rectangular voltage pulses. Fig. 1a shows a sketch of ion transport in a biological electrical synapse, where ions are transported between the ion channels across the gap junction between the pre-synaptic neuron and the post-synaptic neuron. The plasticity of such synapses typically arises from the dynamic changes in conductance of the voltage-gated channels, as well as the gap region Curti and O’Brien (2016); Harris (2001). In this study, we considered a sub-nanoporous 2D membrane mimicking a simplified artificial synapse. Fig. 1b illustrates bicationic (Na+ and K+) ion transport through an array of sub-nanometer pores hosted by a 2D membrane. In this case, the membrane material is a hexagonal boron nitride (hBN) monolayer with a total of 16 regularly spaced B3N triangular multivacancy pores within an area of approximately 7 nm 7 nm. The B3N pore is a defect commonly found in monolayer hBN Park et al. (2021) and its effects on wettability Kumar Verma and Govind Rajan (2022), water slippage Seal and Govind Rajan (2021), as well as ion trapping and mechanosensitive ion transport Noh and Smolyanitsky (2024b) have been studied. The membrane is suspended in the middle of a simulation box and immersed in a binary mixture of water-dissociated 1.0 M KCl and 0.1 M NaCl, unless the concentrations are stated otherwise. Dynamic transport response in this system is initiated by a sequence of rectangular electric field pulses externally applied in the -direction, as shown in Fig. 1b. Further details on the simulation procedures can be found in the Methods section.
The permeation properties of B3N vacancies in hBN are worth introducing first. These electrically neutral sub-nm pores feature dipolar electrostatics with negatively charged dipole components located at the edge nitrogen atoms, enabling selective transport. More specifically, anions are outright rejected, while K+ ions permeate relatively rapidly and Na+ ions hardly permeate as they become stably trapped in the pores Noh and Smolyanitsky (2024b). Fig. 1c shows the corresponding free energy landscapes in the form of potentials of mean force (PMF) along the transport coordinate () for both ion species. For Na+, the energy profile features a barrier of at ( is the Boltzmann constant and K is the system temperature). The K+ ions, however, experience a much shallower energy well, -deep, resulting in relatively weak trapping of K+ ions. As described earlier Smolyanitsky et al. (2018); Fang et al. (2019a, b), the rate of ion transport through these barrier-limited pores is of the Arrhenius type, i.e., , where is the rate-setting peak-to-peak free energy barrier. Unsurprisingly, given an energy barrier difference of , the rate of K+ permeation is nearly two orders of magnitude higher than that of Na+ in a single-salt scenario. Following from the same argument, Na+ ions spend significantly more time trapped inside the pores, compared to K+, which overall is similar to 18-crown-6 ether pores in graphene, except the ion-pore affinity is reversed for the same cation pair Smolyanitsky et al. (2018); Fang et al. (2019a). Given that a pore of this size becomes impermeable when a cation is trapped inside, the number of available conductive paths is the total number of pores unoccupied by Na+. The effective membrane conductance for a salt mixture thus can be written as a simple linearly weighted function proposed earlier Noh and Smolyanitsky (2024a), directly evaluated in Fig. 1d:
| (1) |
where is the conductance of a membrane completely deoccupied by Na+. The corresponding weight is the time-dependent fraction of empty pores: , where is the number of pores “plugged” by Na+ and is the total number of pores in the array.
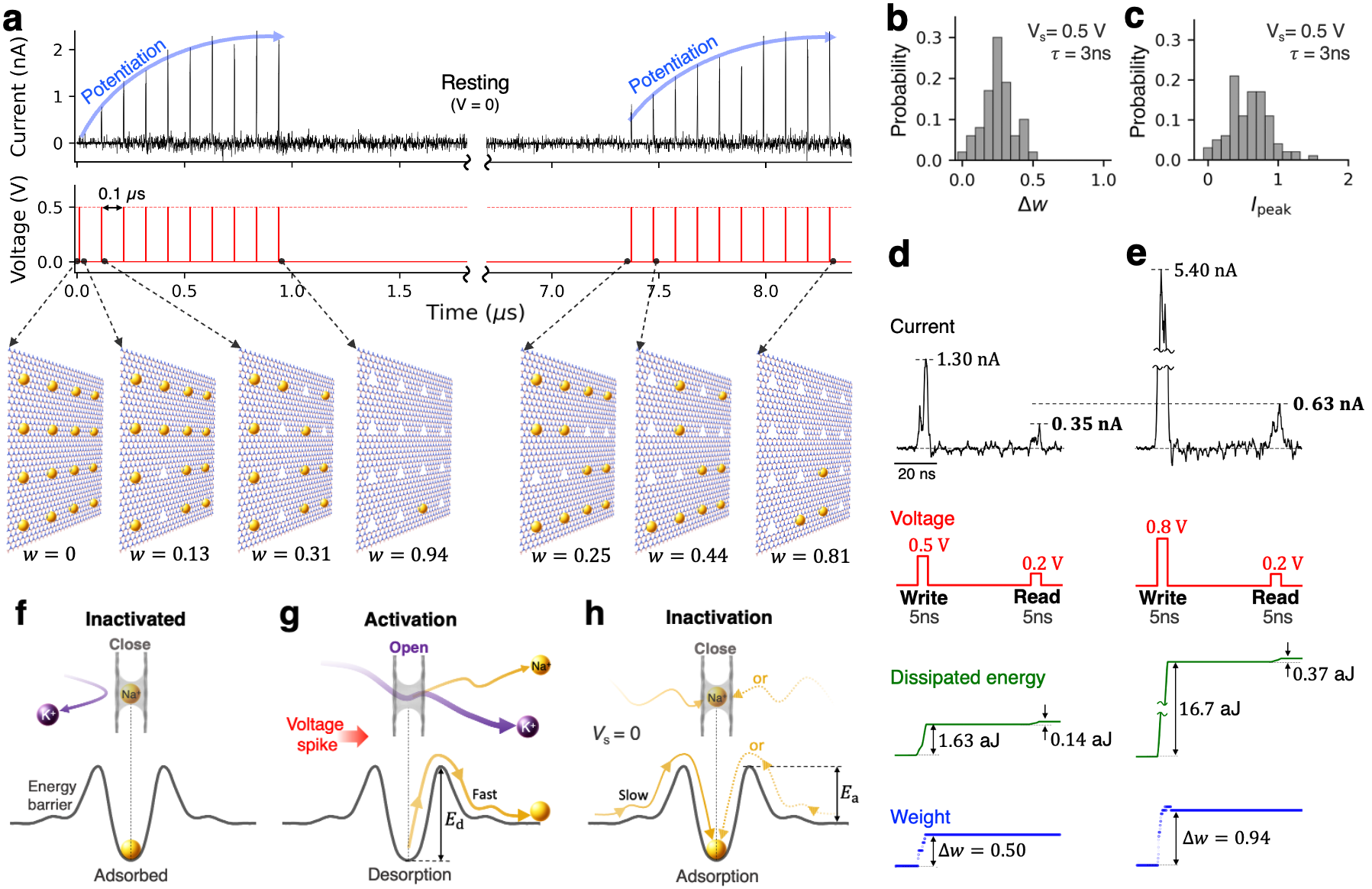
Shown in Fig. 2 are the results for synaptic-like plasticity exhibited by the aqueous ion transport through an array of B3N vacancies in an 2D hBN monolayer under a pulsed bias. In the context of this work, plasticity refers to the dynamic alteration of the membrane’s ionic permeability in response to voltage bias history. We first applied ten 3-ns-long, 0.5V voltage pulses with an interval of 0.1 s (results obtained for different intervals can be found in the supplementary Fig. 1). Before the first voltage pulse, none of the pores were activated i.e., all 16 pores were occupied by the trapped Na+ ions. The pore activation dynamics as a function of subsequent voltage pulses is shown in Fig. 2a, with the first pulse activating two pores and second pulse activating three more pores, corresponding to and , respectively–and so forth. At a finite temperature, the individual increments are of course stochastic and thus the analytical discussions provided later in the text correspond to the statistically significant values, i.e., those obtainable from repeated identical pulse trains applied to a system initially at . The distributions of weight change and peak current () resulting from a 3-ns-long 0.5V pulse are shown in Figs. 2b and c, respectively. The corresponding average weight change is 0.256 with a standard deviation of 0.108 for a membrane featuring 16 pores. This type of stochasticity introduces a degree of inherent randomness, which results in natural diversity in conductance switching. In principle, intrinsic stochasticity is commonly found in solid-state memristors Duan et al. (2024) and the human brain Marković et al. (2020). Specifically for the presented system, the degree of randomness should decrease with increasing array size. As successive voltage pulses are applied, these spikes expectedly exhibit an increasing trend with a clear asymptote corresponding to the maximum weight (at the end of the first 10-pulse sequence, the value of increased to 0.94, corresponding to only one trapped Na+ ion). The information about the prior history of voltage pulses is stored in the form of cumulatively added deoccupancy of Na+. This gradual potentiation of ion permeability arises due to the competitive transport between K+ and Na+, and thus the potentiation effects do not take place with a monocationic electrolyte (see Supplementary Fig. 2). As expected for a system symmetric with respect to the membrame, the potentiation occurs regardless of bias reversal, resulting in bidirectional memristive behavior described in Supplementary Fig. 3. Once the pulse train stops, the system undergoes resting, during which the Na+ ions are slowly re-trapped, volatilizing the previously gained memory. After approximately 6 s of rest, 11 additional Na+ ions are re-trapped, leaving only four pores empty and corresponding to . After that, the system underwent another learning cycle with the same sequence of voltage pulses, exhibiting ion current potentiation similar to that observed in the first cycle, except with a different initial value of . As demonstrated, the conductance state of the device is switchable by voltage pulses a few nanoseconds in duration, resulting in a switching resolution at the scale of order 0.1 GHz. The relaxation time of a few microseconds, on the other hand, corresponds to the effective memory retention time, tunable by the local association barriers, as well as the ion concentrations, as discussed in greater detail further in the text. These timing ranges may therefore be of specific interest for implementing devices that aim to combine GHz-scale state switching with MHz-scale state retention.
Given the discussion above, the high-magnitude component of the bias pulse can be viewed as the write operation performed on a membrane, while a measurement of the ion current during the lower-magnitude pulse is the read operation aimed at probing the membrane’s ionic permeability. For writing, we used 5-ns-long pulses of relatively high magnitude (0.5 V and higher), which enable rapid removal of some of the Na+ ions from the pores. For reading, pulses of lower magnitude (0.2 V) were used, allowing to merely probe the membrane permeability in its Na+-occupancy state without modifying the latter. Figs. 2d and 2e show the corresponding results for write-pulses of 0.5 V and 0.8 V, followed by a read-pulse after 50 ns. As expected, permeability potentiation is stronger with a write-pulse of higher magnitude: and for 0.5 V and 0.8 V pulse, respectively. The corresponding dissipated energy expenditure is quite low. We define the energy dissipated in a given pulse as , where is the ion current and is the pulse height, integrated for the pulse duration . As shown in Figs. 2g and 2g, the energy dissipation per voltage spike in this 2D nanofluidic memristor is on the attojoule scale, attributed to the relatively low ion currents and the nanosecond-scale pulse. These energy estimates are several orders of magnitude lower than those of human synapses, which have an energy expenditure of roughly 0.1-10 fJ per synaptic event Lee et al. (2021); Noy et al. (2023); Laughlin et al. (1998). Note that the attojoule-scale dissipation estimate given above should only be viewed as an idealized lower bound. In a more realistic scenario, especially given the current state-of-the art fabrication techniques, parasitic effects in the form of ion current leakage and other sources would certainly increase dissipative losses. At the same time, this lower bound may serve as a suitable objective in terms of device design and fabrication.
The main mechanism underlying the simple potentiating-forgetting cycle described above is dynamic adsorption/desorption of Na+ ions by the pores, with inactivated and activated states of pores as sketched in Figs. 2f and 2g, respectively. When a write-pulse is applied, a significant probability of Na+ desorption arises, as set by the write-pulse voltage peak and the desorption barrier (see Fig. 2g for the definition). Upon forgetting, adsorption occurs with a considerably lower probability, as set by the adsorption barrier (see Fig. 2g) and the low concentration of Na+ ions. In particular, to achieve low memory volatility (i.e., in the form of a long forgetting time in Fig. 2a), a combination of relatively high and sufficiently low Na+ concentration is essential, because the corresponding adsorption rate that describes the spontaneous “forgetting” process is , where is the sodium concentration.
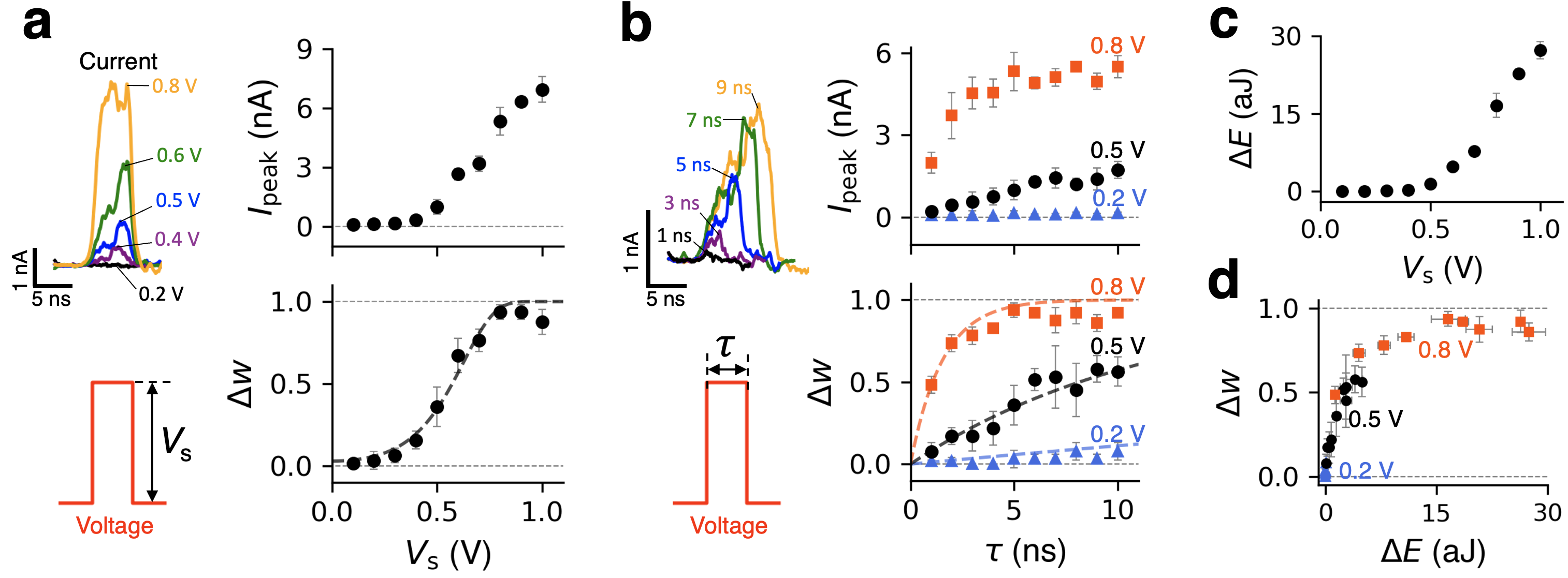
A simple analytical model describing the entire process presented above is possible. For an individual pore, the effective desorption rate in the presence of external bias is given by , where is the attempt frequency associated with thermal fluctuations, is the bias-induced local shift of the ion’s electrostatic potential, and is the electric charge of the ion. As mentioned earlier, the concentration-dependent adsorption rate is (see Fig. 2g for the definition of ), where is the concentration of Na+ ions and is a suitable transmission coefficient, such that is the corresponding adsorption attempt frequency. In general, is bias-dependent, but we posit that the dependence here is considerably weaker than for desorption. For a pore array, let us consider the system state determined by the number of Na+ ions trapped in the pores as a function of time, in response to a voltage pulse. We note that despite the fact that the ability to observe time delays in the form of ion currents requires at least two cation species with markedly different ion-pore affinities Noh and Smolyanitsky (2024a), the time-delayed state dynamics itself can be described in a single-cation scenario. The number of trapped Na+ ions satisfies a simple differential equation: . For a constant bias (e.g., during a rectangular voltage pulse), the analytical solution is then , where is the initial state. The corresponding weight is then given by , where is the initial weight. Given that is an exponential function of the external bias, two distinct processes are possible, depending on the relative strengths of and .
As shown earlier, the system “learns” from a train of “writing” pulses when during each pulse and the interval between the pulses is insufficiently long for significant memory loss to occur. A necessary requirement here is that the bias magnitude is sufficiently high for a pulse lasting only a few nanoseconds to remove a considerable number of sodium ions from the pores. The learning process is then cumulative, i.e., the state after the -th pulse remembers the sum of changes caused by the previous pulses, until all pores are deoccupied by Na+. After -th pulse of duration :
| (2) |
where and is the weight before and after the pulse, respectively. At , , and assuming no appreciable re-adsorption between the equation pulses, the difference equation above yields a geometric series , asymptotically convergent to unity, in accord with the results in Fig. 2a. Of potential interest, for a train of voltage pulses of constant magnitude and duration, the increments are statistically numerically unique. In principle, this suggests the possibility of implicitly “encoding” information about the number of pulses that preceded a given unsaturated value of in the case of large pore arrays. The ’s sensitivity to the bias magnitude is worth considering in greater detail. Shown in Fig. 3a are the results of simulated potentiation by a single 5-ns-long voltage pulse of height , applied to a membrane initially fully inactivated (). Both the current spike height and are marked by a threshold in the amount of V, consistent with the definition of . Sensitive dependence on the pulse duration at a fixed (see 0.5 V and 0.8 V cases in Fig. 3b) above the threshold is also shown in Fig. 3b, causing the corresponding current peak and to increase rapidly when increases. In addition, there is reasonable agreement between given by Eq. 2 and the simulated data (see the dashed curves in Fig. 3a and 3b). Note that the resulting energy expenditure for various values of shown in Fig. 3c exhibits a rapid increase above the threshold. In particular, Fig. 3d shows that energy consumption increases nonlinearly with the weight increment, naturally following the corresponding rapid increase in (compare the top panels in Figs. 3a and 3c).
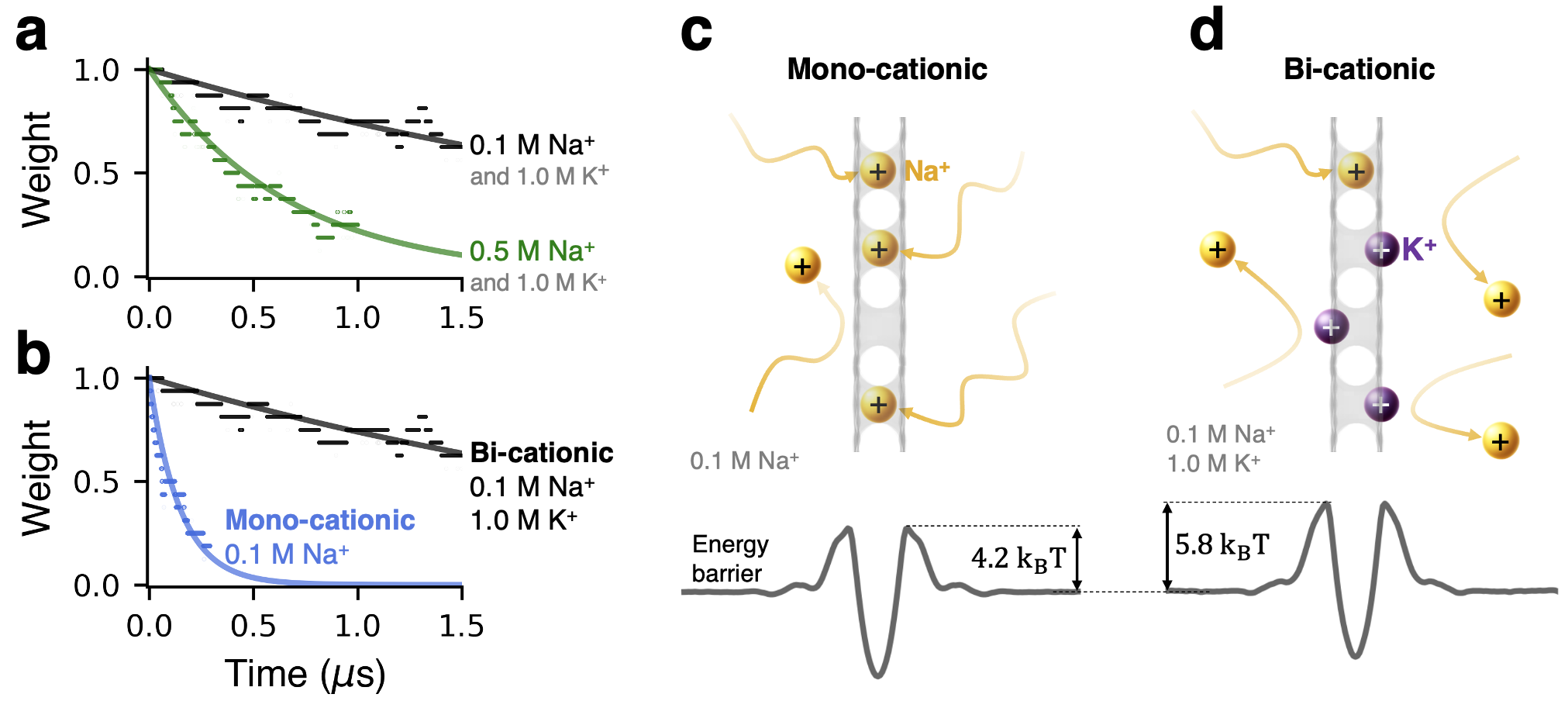
The second important process that can occur is the loss of memory in the longer-term absence of external bias, which manifests as spontaneous gradual decrease in . The unbiased dynamics is described identically to Eq. 2, except now and are more comparable:
| (3) |
where is the state prior to the start of memory loss and is the elapsed time. The decay rate is a sensitive function of via , consistent with the results in Fig. 4a, which shows spontaneous decay of at several concentrations of NaCl. The final state of the membrane is also concentration-dependent, because regardless of , at Eq. 3 yields , where is a constant – also consistent with the results in Fig. 4a. An important factor affecting the forgetting process omitted in the discussion above is the presence of K+ ions, which are expected to interfere with Na+-pore binding. As shown in Fig. 4b, the presence of K+ ions indeed slows down the rate of decay (also see Supplementary section S2). The effects of potassium are in fact deeper than the level of interference captured by our analytical model. Shown in Figs. 4c and 4d is the effect of K+ on the barrier heights, because K+ ions contribute short-range steric and longer-range electrostatic cation-cation repulsion through their presence in the direct vicinity of the pores and near the membrane surfaces, respectively. These observations suggest that the concentration of the main conducting ion species can also be used as a tuning parameter for controlling the system dynamics. The possible influence of spurious defects essentially guaranteed to be present in realistic post-fabricaton hBN membranes is worth noting briefly. Smaller defects (e.g., in the form of single-atom or B2N vacancies), are expected to be entirely impermeable to K+ and Na+ ions, because the B3N vacancy is essentially the smallest permeable pore for these cation species. At the same time, smaller cations, such as Li+ and protons, may still be able to permeate through smaller defects. Larger multivacancies, on the other hand, are not expected to trap ions and thus the transport contributions from those pores would likely manifest as baseline leakage current. Although fabrication of large uniform arrays of B3N vacancies indeed remains a challenge, a new fabrication method reported recently shows significant promise in achieving increased control over pore size and shape distribution in an array of multivacancies Byrne et al. (2024); Byrne and Allen (2024).
To summarize, we have demonstrated synaptic-like plasticity of aqueous ion transport through a sub-nanoporous 2D membrane made of a monolayer hBN featuring an array of B3N vacancies in a binary aquous salt. The ion conductance of this nanofluidic memristor can be dynamically modulated by few-nanoseconds-long transmembrane voltage pulses, resulting in a switching speed of approximately 0.1 GHz. The resulting energy dissipation per voltage spike is very low, roughly 0.1—100 aJ per spike, which is several orders of magnitude lower than that of the human brain, 0.1—10 fJ per spike. Notably, this synaptic-like plasticity arises from the dynamic interplay between two cationic species (Na+ and K+), exemplifying an illustrative approach to leveraging ionic diversity for achieving neuromorphic functionality. The conductive state of the membrane is shown to be governed by the adsorption/desorption dynamics of Na+ trapped in the pores, while K+ ions permeate through the empty pores. We derived a set of illustrative analytical expressions associated with the apparent synaptic-like potentiation and memory volatility. Further experimentation is needed to demonstrate the predicted behaviors for various subnanoporous 2D membranes, as well as ionic permeants. It is our hope to stimulate further work aimed at a better understanding of the effects of ionic diversity, including at the system level, i.e., in the case of interconnected nanofluidic memristive elements.
Methods
For the MD simulations of ion transport, we used a rectangular box with dimension nm nm nm, periodic in all directions. The subnanoporous hBN monolayer was placed in the -plane at with the pore array consisted of 16 triangular B3N vacancies. To prevent the membrane from drifting, its edge atoms were tethered to their initial positions by spring restraints. The system was filled with aqueous salt mixtures consisting of explicitly simulated K+, Na+, and Cl- ions. As the system was periodic in all directions, the time- and ensemble-averaged salt concentration on each side of the membrane was identical under zero bias. The membrane was simulated using parameters developed earlier Govind Rajan et al. (2018) within the OPLS-AA forcefield framework Jorgensen et al. (1996). The partial charges of the nitrogen atoms at the edges of B3N vacancies were set at of their bulk values (obtained earlier from quantum-chemical calculations Govind Rajan et al. (2018)), ensuring electrical neutrality of the membrane. Explicitly simulated water molecules were simulated using the TIP4P model Jorgensen et al. (1983). All of the non-bonded interactions were simulated using the OPLS-AA forcefield framework Jorgensen et al. (1996). A particle-particle–particle-mesh scheme was used to simulate the electrostatic interactions. A 1.2 nm cut-off radius was used for all short-range interactions, including short-range Coulomb interactions and the Lennard-Jones interactions. To initialize the conductive weight of the membrane to zero in all of our simulations, we placed Na+ ions inside the B3N vacancies. The system first underwent static energy minimization and then dynamics relaxation in the NPT ensemble at K and bar, using a 1 fs time step, with the Parrinello-Rahman barostat modifying simulation box dimensions only in the -direction. Relaxed systems underwent ion transport simulations under rectangular pulses of external electric field applied in the -direction, using a 2 fs time step. The corresponding pulse magnitudes were calculated as the electric field magnitude, multiplied by . To obtain the ion currents, we first calculated the cumulative ionic fluxes as a function of time . The flux data was recorded every 10 ps, corresponding to a 100 GHz sampling rate. The raw data were then filtered using a Chebyshev low-pass digital filter with a 200 MHz cutoff frequency. Finally, time-derivatives of the filtered flux data were obtained using an 8th-order central difference method, yielding the time-dependent ionic current , where is the filtered cumulative flux and is the ionic charge. Further details can be found in the supplementary materials of our previous work Noh and Smolyanitsky (2024a). The PMF data were obtained using the Weighted Histogram Analysis Method Hub et al. (2010) applied to a total of 60 umbrella samples of the ion’s position along the -coordinate incremented by 0.05 nm; each umbrella sample was obtained from a 20-ns-long simulation. All MD simulations were performed using GPU-accelerated GROMACS Abraham et al. (2015); Páll et al. (2020) and the molecular visualization tasks were carried using the OVITO software Stukowski (2009).
Acknowledgments
A substantial portion of the simulations was conducted using the GPU-accelerated high-performance computing facilities at the National Institute of Standards and Technology. We thank Frances Allen for numerous illuminating discussions regarding fabrication of multivacancy arrays in 2D materials. Yechan Noh’s work on subdiffusive transport characterization was supported by National Science Foundation (NSF) under Award No. 2110924. Use of computational resources was supported by NSF under ACCESS program, Award No. NNT230006.
References
- Abbott and Nelson (2000) L. F. Abbott and S. B. Nelson, Nat. Neurosci. 3, 1178 (2000).
- Martin et al. (2000) S. J. Martin, P. D. Grimwood, and R. G. Morris, Annu. Rev. Neurosci. 23, 649 (2000).
- Huh et al. (2020) W. Huh, D. Lee, and C.-H. Lee, Adv. Mater. 32, 2002092 (2020).
- Marković et al. (2020) D. Marković, A. Mizrahi, D. Querlioz, and J. Grollier, Nat. Rev. Phys. 2, 499 (2020).
- Sebastian et al. (2020) A. Sebastian, M. Le Gallo, R. Khaddam-Aljameh, and E. Eleftheriou, Nat. Nanotechnol. 15, 529 (2020).
- Noy et al. (2023) A. Noy, Z. Li, and S. B. Darling, Nano Today 53, 102043 (2023).
- Chen et al. (2023) S. Chen, T. Zhang, S. Tappertzhofen, Y. Yang, and I. Valov, Adv. Mater. 35, 2301924 (2023).
- Lee et al. (2021) Y. Lee, H.-L. Park, Y. Kim, and T.-W. Lee, Joule 5, 794 (2021).
- Chua (1971) L. Chua, IEEE Trans. Circuits Syst. 18, 507 (1971).
- Duan et al. (2024) X. Duan, Z. Cao, K. Gao, W. Yan, S. Sun, G. Zhou, Z. Wu, F. Ren, and B. Sun, Adv. Mater. p. 2310704 (2024).
- Ning et al. (2023) H. Ning, Z. Yu, Q. Zhang, H. Wen, B. Gao, Y. Mao, Y. Li, Y. Zhou, Y. Zhou, J. Chen, et al., Nat. Nanotechnol. 18, 493 (2023).
- Le Gallo et al. (2023) M. Le Gallo, R. Khaddam-Aljameh, M. Stanisavljevic, A. Vasilopoulos, B. Kersting, M. Dazzi, G. Karunaratne, M. Brändli, A. Singh, S. M. Mueller, et al., Nat. Electron. 6, 680 (2023).
- Bu et al. (2019) Y. Bu, Z. Ahmed, and L. Yobas, Analyst 144, 7168 (2019).
- Sheng et al. (2017) Q. Sheng, Y. Xie, J. Li, X. Wang, and J. Xue, Chem. Commun. 53, 6125 (2017).
- Zhang et al. (2019) P. Zhang, M. Xia, F. Zhuge, Y. Zhou, Z. Wang, B. Dong, Y. Fu, K. Yang, Y. Li, Y. He, et al., Nano Lett. 19, 4279 (2019).
- Robin et al. (2021) P. Robin, N. Kavokine, and L. Bocquet, Science 373, 687 (2021).
- Xiong et al. (2023) T. Xiong, C. Li, X. He, B. Xie, J. Zong, Y. Jiang, W. Ma, F. Wu, J. Fei, P. Yu, et al., Science 379, 156 (2023).
- Robin et al. (2023) P. Robin, T. Emmerich, A. Ismail, A. Niguès, Y. You, G.-H. Nam, A. Keerthi, A. Siria, A. Geim, B. Radha, et al., Science 379, 161 (2023).
- Emmerich et al. (2024) T. Emmerich, Y. Teng, N. Ronceray, E. Lopriore, R. Chiesa, A. Chernev, V. Artemov, M. Di Ventra, A. Kis, and A. Radenovic, Nat. Electron. 7, 271 (2024).
- Paulo et al. (2023) G. Paulo, K. Sun, G. Di Muccio, A. Gubbiotti, B. Morozzo della Rocca, J. Geng, G. Maglia, M. Chinappi, and A. Giacomello, Nat. Commun. 14, 8390 (2023).
- Shi et al. (2023) D. Shi, W. Wang, Y. Liang, L. Duan, G. Du, and Y. Xie, Nano Lett. 23, 11662 (2023).
- Noh and Smolyanitsky (2024a) Y. Noh and A. Smolyanitsky, J. Phys. Chem. Lett. 15, 665 (2024a).
- Zhou et al. (2024) X. Zhou, Y. Zong, Y. Wang, M. Sun, D. Shi, W. Wang, G. Du, and Y. Xie, Natl. Sci. Rev. 11, nwad216 (2024).
- Ramirez et al. (2024a) P. Ramirez, S. Portillo, J. Cervera, J. Bisquert, and S. Mafe, Phys. Rev. E 109, 044803 (2024a).
- Ramirez et al. (2024b) P. Ramirez, S. Portillo, J. Cervera, S. Nasir, M. Ali, W. Ensinger, and S. Mafe, J. Chem. Phys. 160 (2024b).
- Fang et al. (2019a) A. Fang, K. Kroenlein, D. Riccardi, and A. Smolyanitsky, Nat. Mater. 18, 76 (2019a).
- Bean (2007) B. P. Bean, Nat. Rev. Neurosci. 8, 451 (2007).
- Smolyanitsky et al. (2018) A. Smolyanitsky, E. Paulechka, and K. Kroenlein, ACS Nano 12, 6677 (2018), ISSN 1936-0851.
- Fang et al. (2019b) A. Fang, K. Kroenlein, and A. Smolyanitsky, J. Phys. Chem. C 123, 3588 (2019b), ISSN 1932-7447.
- Hassani et al. (2021) N. Hassani, M. Ghorbani-Asl, B. Radha, M. Drndic, A. V. Krasheninnikov, and M. Neek-Amal, J. Phys. Chem. C 125, 25055 (2021).
- Liu et al. (2016) G. Liu, W. Jin, and N. Xu, Angew. Chem. Int. Ed. 55, 13384 (2016).
- Cohen-Tanugi and Grossman (2012) D. Cohen-Tanugi and J. C. Grossman, Nano Lett. 12, 3602 (2012).
- Yang et al. (2019) Y. Yang, X. Yang, L. Liang, Y. Gao, H. Cheng, X. Li, M. Zou, R. Ma, Q. Yuan, and X. Duan, Science 364, 1057 (2019).
- Noh and Aluru (2021) Y. Noh and N. Aluru, Nano Lett. 22, 419 (2021).
- Zhu et al. (2018) J. Zhu, J. Hou, A. Uliana, Y. Zhang, M. Tian, and B. Van der Bruggen, J. Mater. Chem. A 6, 3773 (2018).
- Xu et al. (2022) L.-H. Xu, S.-H. Li, H. Mao, Y. Li, A.-S. Zhang, S. Wang, W.-M. Liu, J. Lv, T. Wang, W.-W. Cai, et al., Science 378, 308 (2022).
- Feng et al. (2016) J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis, and A. Radenovic, Nature 536, 197 (2016).
- Safaei and Wang (2022) J. Safaei and G. Wang, Nano Res. Energy 1, e9120008 (2022).
- Moreno et al. (2018) C. Moreno, M. Vilas-Varela, B. Kretz, A. Garcia-Lekue, M. V. Costache, M. Paradinas, M. Panighel, G. Ceballos, S. O. Valenzuela, D. Peña, et al., Science 360, 199 (2018).
- Choi et al. (2018) K. Choi, A. Droudian, R. M. Wyss, K.-P. Schlichting, and H. G. Park, Sci. Adv. 4, eaau0476 (2018).
- Zhong et al. (2019) Y. Zhong, B. Cheng, C. Park, A. Ray, S. Brown, F. Mujid, J.-U. Lee, H. Zhou, J. Suh, K.-H. Lee, et al., Science 366, 1379 (2019).
- Curti and O’Brien (2016) S. Curti and J. O’Brien, BMC Cell Biol. 17, 13 (2016).
- Harris (2001) A. L. Harris, Q. Rev. Biophys. 34, 325 (2001).
- Park et al. (2021) H. Park, Y. Wen, S. X. Li, W. Choi, G.-D. Lee, M. Strano, and J. H. Warner, Small 17, 2100693 (2021).
- Kumar Verma and Govind Rajan (2022) A. Kumar Verma and A. Govind Rajan, Langmuir 38, 9210 (2022).
- Seal and Govind Rajan (2021) A. Seal and A. Govind Rajan, Nano Lett. 21, 8008 (2021).
- Noh and Smolyanitsky (2024b) Y. Noh and A. Smolyanitsky (2024b), submitted for publication.
- Laughlin et al. (1998) S. B. Laughlin, R. R. de Ruyter van Steveninck, and J. C. Anderson, Nat. Neurosci. 1, 36 (1998).
- Byrne et al. (2024) D. O. Byrne, J. Ciston, and F. I. Allen, Microsc. Microanal. p. ozae064 (2024), eprint https://academic.oup.com/mam/advance-article-pdf/doi/10.1093/mam/ozae064/58599876/ozae064.pdf, URL https://doi.org/10.1093/mam/ozae064.
- Byrne and Allen (2024) D. O. Byrne and F. I. Allen, Atomic engineering of triangular nanopores in monolayer hBN: A decoupled seeding and growth approach (2024), eprint 2408.09355, URL https://arxiv.org/abs/2408.09355.
- Govind Rajan et al. (2018) A. Govind Rajan, M. S. Strano, and D. Blankschtein, J. Phys. Chem. Lett. 9, 1584 (2018).
- Jorgensen et al. (1996) W. L. Jorgensen, D. S. Maxwell, and J. Tirado-Rives, J. Am. Chem. Soc. 118, 11225 (1996).
- Jorgensen et al. (1983) W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein, J. Chem. Phys. 79, 926 (1983).
- Hub et al. (2010) J. S. Hub, B. L. de Groot, and D. van der Spoel, J. Chem. Theory Comput. 6, 3713 (2010), ISSN 1549-9618.
- Abraham et al. (2015) M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess, and E. Lindahl, SoftwareX 1, 19 (2015).
- Páll et al. (2020) S. Páll, A. Zhmurov, P. Bauer, M. Abraham, M. Lundborg, A. Gray, B. Hess, and E. Lindahl, J. Chem. Phys. 153 (2020).
- Stukowski (2009) A. Stukowski, Modell. Simul. Mater. Sci. Eng. 18, 015012 (2009).