Symmetry breaking fluctuations split the porphyrin bands
Abstract
Porphyrins offer a malleable and cost-efficient platform to sculpt bioinspired technologies with tunable charge transfer, energy conversion, and photocatalytic properties. Yet, despite decades of research, the physical mechanisms that determine their electronic spectra remain elusive. Even for metal-free porphyrins, no consensus exists on the origin of the splitting of their -bands, an energetic region critical in photosynthesis. We leverage our recent statistical treatment of molecular motions in the condensed phase to predict their linear absorption spectra. By bridging exact quantum-dynamical expressions with atomistic simulations, our theory is the first to capture the spectra of representative porphyrins in solution: porphine, tetraphenylporphyrin, and tetraphenylporpholactone. Our work reveals that -band splitting arises from extreme timescale separation of nuclear motions that turn symmetry-forbidden transitions bright. We exploit these insights to propose and confirm how chemical modifications tune the optical properties of porphyrins, demonstrating the potential for developing design principles to tailor their optoelectronic behavior.
Porphyrins are ubiquitous in biology and chemistry and play crucial roles in, for example, oxygen transport and storage in blood, charge transfer in cellular respiration, and photosynthesis in plantsMERCER-SMITH and Mauzerall (1984); Amanullah et al. (2022). Their synthetic tunabilityTanaka and Osuka (2015) make porphyrins ideal in advancing bioinspired charge and energy transport and storage technologiesMathew et al. (2014); Swierk et al. (2015); Zhang et al. (2023); Kumagai et al. (2014), especially as they offer a convenient chemical scaffold that can be functionalized with substituentsNing et al. (2020); Roy et al. (2022a), paired with transition metalsMoisanu et al. (2023), or wreathed together in polymer chainsGotfredsen et al. (2022); Kosugi et al. (2023); Magnera et al. (2023); Chen et al. (2024) to tailor and exploit their optoelectronic properties. Numerous studies have turned to sophisticated multidimensional spectroscopies to disentangle the palette of spectral features generated by porphyrin and porphyrin-like systemsNiedringhaus et al. (2018); Policht, Niedringhaus, and Ogilvie (2018); Song et al. (2019); Arsenault et al. (2018); Jana et al. (2023); Zhao et al. (2023); Petropoulos et al. (2024). Yet, predicting and interpreting even the linear electronic spectra of small porphyrin monomers remains challenging as their photophysics continues to elude a conclusive microscopic interpretation.
In photosynthesis, energy transfer between carotenoids and porphyrin-based chlorophyll bands facilitate photoprotectionMa et al. (2003); Holt et al. (2005); Ruban et al. (2007); Polívka and Frank (2010); Bode et al. (2009); Son et al. (2020). These bands in free-base porphyrins present four peaks corresponding to two distinct electronic transitions, in contrast to their metalloporphyrin counterparts which present only two peaks. The widely accepted group-theoretic description of porphyrin spectraGouterman, Wagnière, and Snyder (1963) interprets these transitions as having mutually orthogonal transition dipoles in the plane of the tetrapyrrole ring: the lower-energy half of the bands () denoted as the band and the higher-energy half () denoted as the band, with transition dipoles aligned parallel and orthogonal to the central proton axis, respectively. Yet, even the pioneering work of GoutermanGouterman (1961); Gouterman, Wagnière, and Snyder (1963), which explained the competition of intensities and center frequencies of the Soret and bands in metalloporphyrins, does not explain why the band peaks split from two to four upon removal of the metal center. Crucially, the microscopic mechanism underlying this spectral splitting continues to spark disagreementGouterman (1961); Roy et al. (2022b); Yu, Baskin, and Zewail (2002); Schalk et al. (2008); He et al. (2012); Kullmann et al. (2012). Indeed, this doubling (four peaks instead of two) of the bands has been variously ascribed to a Condon-allowed vibronic progressionGouterman (1961); Yu, Baskin, and Zewail (2002), where the transition dipole is assumed to be insensitive to nuclear motions, or non-Condon effects via symmetry-breaking nuclear motions that tune the brightness, or selection rules, of transitionsRoy et al. (2022b); Neville and Schuurman (2024). Given this controversy, it is not surprising that this critical problem in porphyrin photophysics has been the subject of intense theoretical focus.
Yet, state-of-the-art theoretical spectroscopy tools can only tackle isolated aspects of this question. For example, one can capture non-Condon effects under the microscopic harmonic approximation using the Franck-Condon Herzberg-Teller (FCHT) methodSantoro et al. (2008) but only in the gas phase and for fairly small and rigid molecules Zuehlsdorff et al. (2019); address non-Condon fluctuations with atomistic anharmonicities in the condensed phase but only in the static limit (Ensemble)Bergsma et al. (1984); or treat the dynamics and atomistic anharmonicities in the condensed phase but only in the Condon limit (2nd order cumulant)Mukamel (1985); Zuehlsdorff et al. (2019). Thus, a more general approach is required.
This impasse has led to seemingly contradictory explanations of the physical origin of the bands. One of the dominant interpretationsYu, Baskin, and Zewail (2002) assigns the first two peaks (1.9-2.2 eV) of the tetraphenylporphyrin (TPP) band (see, for example, the experimental spectrum of TPP in in Fig. 1) as the 0-0 and 0-1 features in the vibronic progression of the S1 () electronic transition, and the latter two (2.2-2.5 eV) as the 0-0 and 0-1 vibronic progression of the S2 () transition. However, recent studies have used FCHT-type arguments to assign the bands of porphine to mixed Condon-allowed (first and third peaks) and non-Condon-enabled electronic transitions (second and fourth)Santoro et al. (2008); Roy et al. (2022b). Yet, these interpretations do not provide a fully predictive theory of the lineshape that unambiguously captures the splitting and broadening of spectral peaks. Hence, it is crucial to employ a theoretical framework that can capture both dynamical vibronic progressions and the non-Condon fluctuations that tune transition brightness as molecules vibrate and jostle in solution.
We bridge this theoretical gap by leveraging our recent theory of non-Condon fluctuations that offers a quantum dynamical means to process the output of classical molecular dynamics (MD) simulations and electronic structure theory to predict linear optical spectra in the condensed phase Wiethorn et al. (2023). Our theory predicts the optical response of solvated chromophores while faithfully incorporating their anharmonic atomistic interactions, arbitrarily strong non-Condon effects (nuclear motion-induced variations of the transition dipoles), and significant environmental coupling. Our expressions encode the chemical details that determine optical spectra through spectral densities that quantify how nuclear motions modulate the energy gap, the transition dipole, and their correlations. Crucially, one can directly calculate these spectral densities from atomistic simulations of a material, offering a direct route to identifying and interpreting the optical response. This ultimately allows us to resolve the long-standing controversy over the physical origin of the band splitting of porphyrins by quantifying the influence of the following processes:
-
1.
Vibronic features on Condon-allowed transitions.
-
2.
Static and dynamic non-Condon fluctuations.
-
3.
Energy transfer between and bands.
Our work is the first to accurately reproduce and explain the spectral splitting and intensity distribution of the bands of representative porphyrins: porphine, TPP, and tetraphenylporpholactone (TPPL). Our analysis reveals that the -band splitting arises from extreme timescale separation between the slow torsions of the pendant phenyls (in TPP and TPPL) and collective solvent motions and the fast tetrapyrrole ring vibrations that modulate the transition dipole, making this splitting a primarily non-Condon feature. We further introduce a perturbative treatment of excited-state energy transfer to confirm that this splitting is robust to energy flow across the bands.
Our theory of non-Condon spectroscopy exploits the idea that the macroscopic number of nuclear motions that modulate the energy gap and transition dipole in the condensed phase are likely to cause Gaussian fluctuations. This enables us to write an effective Gaussian model for which we have derived exact closed-form expressions for the optical response function Wiethorn et al. (2023) that can be parameterized directly from MD simulations (see Methods Section LABEL:Methods_Sec:Theory-GNCT-nature). In contrast to previous works, our Gaussian non-Condon theory (GNCT) does not resort to fitting parameters that restrict its predictive power and can lead to ill-converging spectra when strongly anharmonic nuclear motions render harmonic approximations inapplicable (see FCHT prediction in Fig. 5(c). In addition, it enables us to isolate contributions to the absorption spectrum, , arising from transition dipole fluctuations that are static and dynamic relative to electronic dephasing times,
| (1) |
Here, is the linear absorption coefficientMukamel (1995) centered at where as and are shifted by the average transition energy between the ground () and excited () state. Below, we describe the physical meaning of the two components in Eq. (1) within the pure-dephasing limit (i.e., in the absence of energy transfer), and discuss analogous expressions we derive and employ to capture the influence of excited-state energy flow on the spectrum in Sec. IV of the supplementary information (SI).
Our GNCT predicts that the average transition dipole, , determines the magnitude of the static non-Condon contribution to the spectrum,
| (2) |
Here, arises from the average effect of nuclear motions that break the symmetry of a molecule. When dominates the spectrum, it captures non-Condon disorder while accounting for the energy gap dynamics, which encode vibronic progressions. When is insensitive to nuclear configurations, it can be replaced by the transition dipole at any nuclear configuration, recovering the celebrated second-order cumulant within the Condon approximation, Zuehlsdorff et al. (2019); Mukamel (1985) (see Methods A for the full expression). The energy gap spectral density, Mukamel (1995), encodes the dynamical energy gap fluctuations () that control the lineshape of and its ability to exhibit distinct vibronic progressions or its related asymmetry.
Our GNCT quantifies how dynamic non-Condon fluctuations impact the spectrum via and ,
| (3) |
Just as encodes how energy gap fluctuations control the prominence of vibronic progressions in , here, two new spectral densities, and , encode how nuclear motions cause dynamic transition dipole fluctuations () and determine and . quantifies how nuclear motions modulate the brightness of transitions while measures how nuclear motions jointly tune the energy gap and transition brightness. Together, Eqs. (2) and (3) determine the optical spectrum arising from static and dynamic transition dipole modulations. Our GNCT thus reveals that dynamic non-Condon effects arise from the convolution (denoted by ) of the energy gap lineshape, , with the contributions arising from the transition dipole fluctuations.
Because our theory provides a transparent protocol to parameterize Eqs. (2) and (3) using atomistic simulations, we can assign spectral signals to specific nuclear motions and assess their effect on both energy gap and transition dipole fluctuations. We now show how our GNCT, unlike previous theories, recapitulates the condensed phase spectra of porphyrins and uncovers the mechanism leading to the splitting of their bands as a function of their chemical structure.
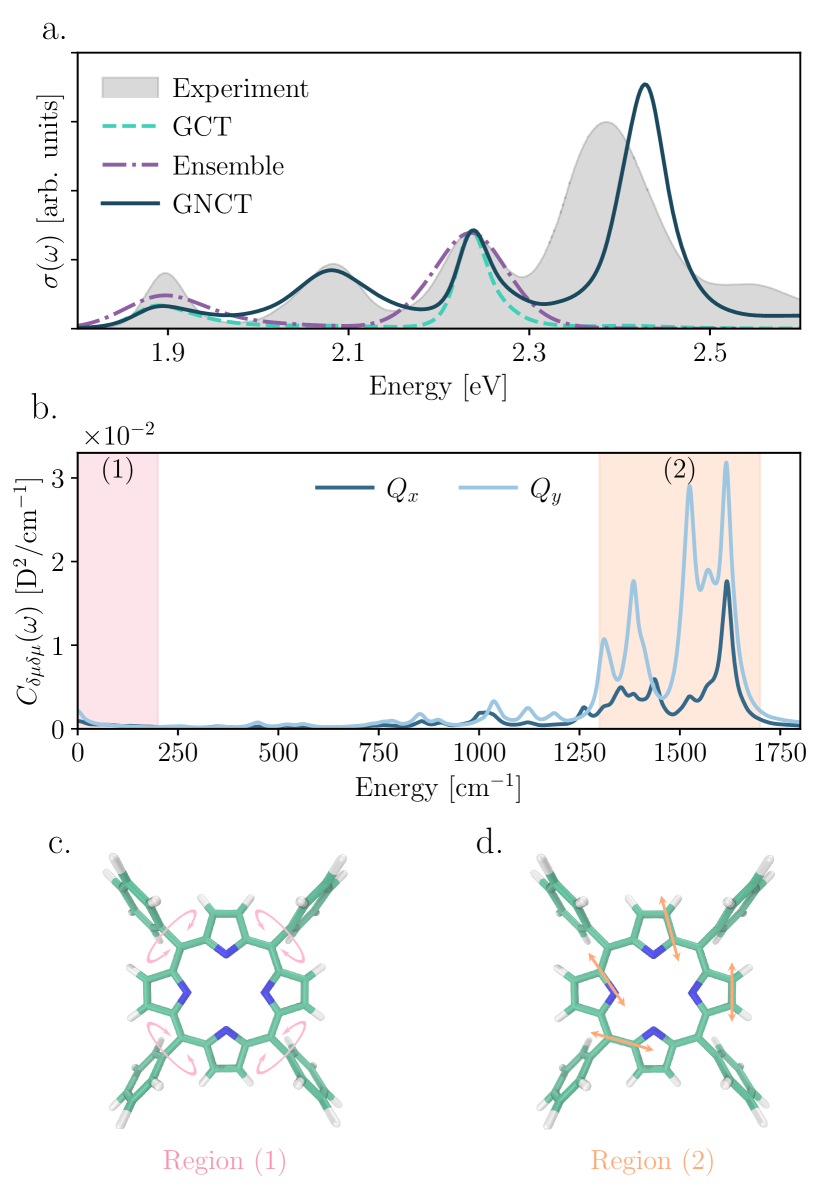
We first ask if the observed peak splitting arises purely from Condon-allowed vibronic progressions. The second-order cumulant method in the Condon limit (to which we refer henceforth as “GCT” for Gaussian Condon theory) successfully captures vibronic progressionsMukamel (1985); Loco et al. (2018); Zuehlsdorff et al. (2019), and is analogous to in our GNCT (Eq. (2)) in the Condon limit (i.e., ). Figure 1 shows that the predicted GCT spectrum (teal) only recovers the first () and third () peaks, revealing that the -band splitting does not arise from a Condon-allowed vibronic progression and non-Condon effects must be considered.
Since Condon-allowed transitions do not cause the peak splitting, we turn to static non-Condon effects. The ensemble methodBergsma et al. (1984), widely used to predict condensed phase spectraZuehlsdorff et al. (2021), treats non-Condon fluctuations under the approximation that nuclear motions are slower than electronic dephasing times, thereby capturing the static limit of both non-Condon and energy gap fluctuations. However, similar to the GCT, Fig. 1 shows that the ensemble method (purple) can capture only the first () and third () peaks. Hence, the splitting does not arise solely from static non-Condon effects.
To incorporate both static and dynamic non-Condon fluctuations, we turn to our GNCT. Figure 1 illustrates that our GNCT (dark green) is the only method that correctly reproduces the four peaks of the TPP bands, their relative intensities, and even their linewidths. Thus, peak splitting in the TPP bands appears to arise from dynamic non-Condon fluctuations.
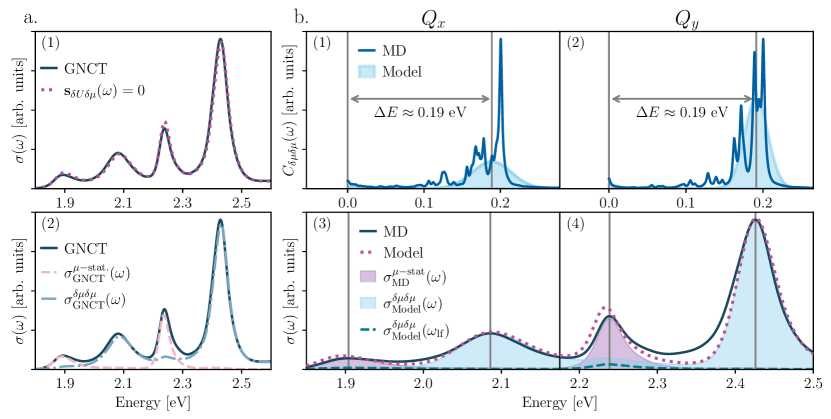
We are now poised to interrogate the microscopic mechanism leading to band splitting. First, Fig. 2(a.1) shows that excluding (dotted) causes only negligible changes to the intensity distribution of the spectrum (see also SI Fig. S1), demonstrating that the joint modulation of transition dipoles and energy gaps by nuclear motions does not participate in splitting the TPP bands. Further, Fig. 2(a.2) shows that zeroing the purely dynamical non-Condon contribution, , causes the second and fourth peaks in the TPP spectrum to disappear (pink-dashed). Since this is tantamount to neglecting the full dynamical non-Condon contribution, , one can assign the second () and fourth () peaks in TPP to purely dynamical non-Condon effects. In contrast, zeroing the static non-Condon component, , decimates the first () and third () peaks (blue-dashed), revealing these as largely static non-Condon contributions. This suggests that peak splitting in TPP arises from a static-dynamic divide in the nuclear motion-induced modulation of the selection rules. However, the persistence of small components in the first and third peaks upon neglecting motivates a more microscopic interrogation of .
To uncover the origin of the persistent splitting in the surviving dynamical non-Condon contribution to the GNCT lineshape, , we analyze the transition dipole spectral density that determines its behavior, (see Fig. 1(b)). and display complex structure with a small contribution at low frequency ( cm-1) and a region of considerable spectral weight centered around . Restricted normal mode analyses in the gas phase enable us to assign the high-frequency region of the spectral density (region 2 in Fig. 1(b)) to inner-ring C-C and C-N vibrations (see SI Sec. II). The low-frequency contribution below cm-1 arises from collective solvent motions in solution and torsional motions of the phenyl substituents with timescales cm-1 (see SI Sec. III). But to what extent does the structure of these spectral densities matter and how does this apparent timescale separation in nuclear motions contribute to the splitting of the -bands?
To address the first question, we replace the MD-derived transition dipole spectral densities () with model counterparts composed of low- and high-frequency contributions, . For , we employ an often adopted Debye form,Weiss (2012) and subsume the high-frequency intramolecular vibrations into a Gaussian envelope for (see Methods Sec. LABEL:Methods_Sec:Model-system-spectral-densities-GNCT-nature). Figure 2(b.1)-(b.2) illustrate the MD-based (line) and our simplified (shaded) for the and bands, with their corresponding absorption spectra in (b.3)-(b.4). Our simplified spectral densities faithfully reproduce the splitting of the -bands (dashed-peach), agreeing semi-quantitatively with the MD-based spectrum (solid), indicating that the detailed structure of the MD-derived spectral density is not essential to recover the TPP band splitting and validates our use of these models in our investigation of timescale separation.
We now assess the influence of timescale-separated fluctuations in . By turning off the high-frequency Gaussian envelopes in , one observes that the second () and fourth () peaks vanish in Fig. 2(b.3) and (b.4), leaving only the small contributions to the first () and third () peaks (green-dashed), which we had largely assigned as static non-Condon contributions. What is more, the energy difference between split band peaks (0.19 eV) in Fig. 2(b.3)-(b.4) matches the energetic split between the low- versus high-frequency components of the simplified non-Condon spectral densities in Fig. 2(b.1)-(b.2). A consistent picture emerges: the first () and third () peaks arise from static () and slow (collective solvent motions and phenyl torsions) non-Condon contributions, while second () and fourth () peaks arise from the fast modulation of the transition dipoles arising from intra-tetrapyrrole ring vibrations, revealing that the extreme timescale separation of the nuclear motions that modulate the transition dipole, and thus the optical selection rules, offers the mechanism that splits the TPP bands.
While our GNCT addresses the pure dephasing limit where no energy transfer occurs between excited states, TPP is known to undergo internal conversion as energy flows from the to the bandYu, Baskin, and Zewail (2002). Hence, we developed a framework to quantify the impact of energy flow on the spectrum (see SI Sec. IV) by treating the driver of energy flow as a perturbation. We tailor an excited state transformationMedders et al. (2017) to move into the frame where states have spatially orthogonal transition dipoles, consistent with the traditional interpretation of porphyrin photophysics (see SI Sec. IVB). We find that including energy flow across the bands has a marginal effect on the computed spectrum (Fig. S10), indicating that our timescale separation mechanism for band splitting remains valid even in the presence of internal conversion.
Besides offering mechanistic insights, our GNCT yields design principles to tune optoelectronic properties. Specifically, the spectral splitting mechanism in porphyrins suggests that one can balance the contributions of and via simple chemical changes. For instance, we hypothesize that one can suppress the first and third peaks of the porphyrin bands by removing the meso-phenyls or replacing them with bulky chemical moieties. In contrast, asymmetrically modifying the tetrapyrrole ring by hydrating one of the pyrroles to form a chlorin or substituting a functional group into the ring can be expected to: (1) change the intensity distribution across the band by modulating via steric or electron conjugation effects that tune the rotation of the pendant phenyls; and (2) modify the individual / lineshapes by tuning the energy gap spectral density which determines the prominence of vibronic progressions in . To assess the validity of our design hypotheses, we turn to porphine and TPPL. These molecules offer an ideal testing ground since replacing the pendant phenyls in TPP with hydrogens yields porphine, whereas TPPL retains TPP’s phenyls but replaces an external (-periphery) on one pyrrole orthogonal () to the proton axis () with a lactone.
We begin by leveraging the transition dipole spectral densities, , to analyze the effect of the chemical modifications required to transform TPP to porphine and TPPL. We employ the non-Condon factorWiethorn et al. (2023), , to quantify how these changes tune the balance between static and dynamic non-Condon effects, with an increase (decrease) in indicating that dynamical (static) non-Condon effects become more significant. Figure 3 shows and for porphine (a) and TPPL (b). In porphine, the absence of phenyl torsions that drive low-frequency transition dipole fluctuations in TPP leads to spectral densities with no low-frequency weight, and an increase in and by factors of 1.51 and 1.65, respectively, indicating that the optoelectronic properties of porphine depend more strongly on dynamic non-Condon fluctuations. In TPPL, these spectral densities exhibit significant low-frequency spectral weight from the phenyl torsions, albeit with greater intensity than in TPP. In contrast to TPP, one also observes enhanced intensity centering at 1000 emerging from dynamic modulations of the transition dipoles by the C-O stretch. Moreover, the enhanced low-frequency motions lead to a reduction in and by factors of 2.42 and 2.79, respectively, indicating that static non-Condon effects are increasingly significant to the optoelectronic properties of TPPL as compared to TPP.
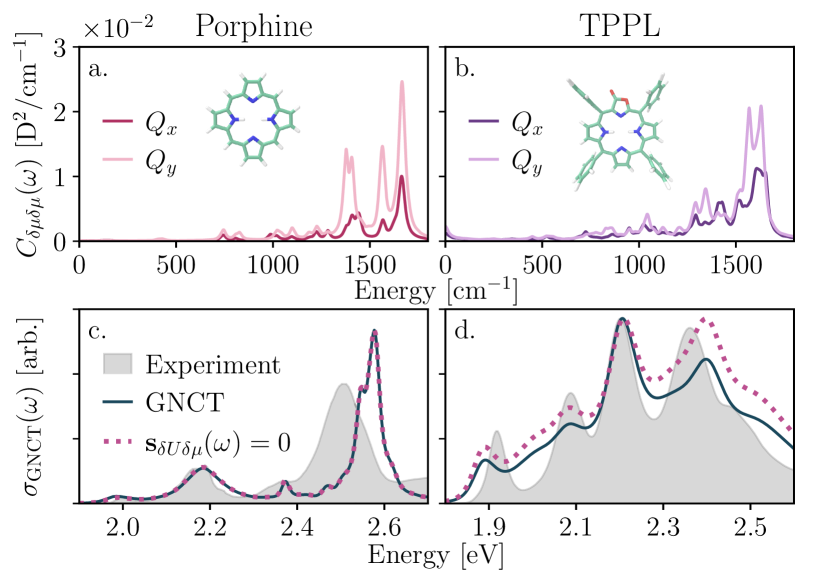
We now turn to the optical spectra in Fig. 3(c) and (d). In porphine and TPPL (as in TPP), setting (dotted) reveals that captures the dynamic contribution to the band splitting (see also SI Sec. I). Hence, we analyze the resulting spectra through the lens of static and dynamic non-Condon contributions. Figure 3(c) shows the porphine spectrum and confirms our hypothesis that removing the phenyl groups reduces both the low-frequency dynamical and static contributions arising from non-Condon fluctuations, leading to suppressed first and third peaks in the porphyrin bands. TPPL is more complex. Figure 3(d) reveals that the TPPL bands contain three features that are absent in porphine and TPP: (1) spectral intensity is greatest at the third peak rather than the fourth; (2) a vibronic shoulder now emerges from the fourth peak and; (3) the energetic separation of cm-1 between second (dynamic-) and third (static-) peaks deviates from the former cm-1 splitting between subsequent peaks. Two of these changes align with our hypotheses: the shift in spectral intensity across the bands from the lactone-induced change to the static-dynamic balance of non-Condon effects, and the larger vibronic progression from the lactone-induced modification of the high-frequency component of the energy gap spectral density that shifts peak prominence. However, the modified splitting between the second and third peaks is surprising, motivating a closer inspection of our hypotheses.
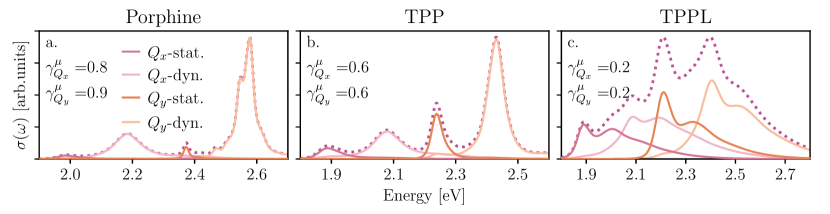
Hypothesis (1) centers on the balance between and . Figure 4 decomposes our GNCT prediction for the and bands of porphine, TPP, and TPPL, illustrating the relative contributions of (red and orange) and (pink and peach) to the individual bands (dotted) as a function of the non-Condon factors. This figure shows that the contribution is negligible in porphine, becomes significant in TPP, and reaches commensurate values with the dynamic contribution in TPPL, thus aligning with our hypothesis that the phenyl groups continue to emphasize the first and third peaks relative to the second and fourth. Figure 4 further reveals the true complexity of the TPPL spectrum as all four contributions overlap significantly, with each displaying a prominent lactone-induced vibronic progression. This is in stark contrast to the four unimodal peaks that lack energy gap-derived vibronic structure underlying the bands of porphine and TPP. This observation also confirms hypothesis (2) as it reveals that the asymmetric lactone functionalization of the inner ring induces vibronic progressions that can redistribute spectral weight.
Yet, it seems that a contradiction lingers in our analysis. Figure 3(d) shows that the third peak in the experimental TPPL spectrum carries greater intensity than the fourth peak, which one may naively ascribe to a greater static non-Condon contribution in the band based on our current analysis. However, Fig. 4(c) shows the opposite is true: the dynamical non-Condon peak is predicted to be greater. This seeming contradiction is a result of considering the static and dynamic non-Condon peaks separately. Fortuitously, the peak separation in the vibronic progression of the dynamic non-Condon feature (light pink solid line) is nearly identical to the peak separation between dynamic ( eV) and static ( eV) in the full spectrum. As a result, the overlapping dynamic satellite peak (vibronic progression) supplies spectral weight to the static non-Condon peak at eV, causing it to appear to dominate over that of the dynamic at eV in the total spectrum. This analysis thus demonstrates how the interplay between Condon-allowed vibronic progressions and symmetry-forbidden transitions control the TPPL -band intensity distribution. Yet, despite our GNCT’s success in predicting the relative peak heights, it appears to overestimate the prominence of a lactone-induced vibronic progression for the static peak that is absent in the experimental spectrum (consider the eV gap between first and second peaks in Fig. 3(d)). Since energy gap spectral densities encode vibronic progressions, an analysis of ought to reveal why our GNCT predicts this spurious effect in the TPPL band.
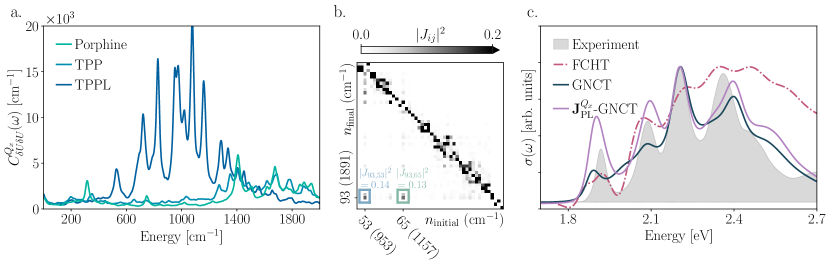
Figure 5(a) compares for porphine, TPP, and TPPL (see SI Figs. S2(a), S3(a), and S4(a) for of porphine, TPP, and TPPL). This figure shows that, while for porphine and TPP are similar, the spectral density of TPPL shows a greater weight, especially in the region between 600–1400 cm-1, which roughly corresponds to internal-ring C-O stretching around 1000 cm-1. Because the lactone group contains a carbonyl, one might expect that the vibration of this C=O should modulate the energy gap, leading to a peak near . Yet, this peak is conspicuously absent from the TPPL spectral density, while porphine and TPP display greater spectral weight in this region. This is suspect and can indicate a violation of Gaussian statistics. Indeed, employing the Kullback-Leibler divergence between each MD-derived energy gap distribution and their corresponding normal distributions of identical mean and variance (denoted as ) to quantify the extent of non-Gaussian behavior, we find that the TPPL energy gap is more non-Gaussian than both its counterpart and the energy gaps for porphine and TPP (see SI Sec. V and Figure S9). This suggests the need for a closer interrogation of the energy gap.
Since the only change between TPP and TPPL is the lactone substitution, which largely affects high-frequency intramolecular vibrations, one can interrogate the source of non-Gaussian behavior via a microscopic harmonic analysis of the nuclear motions that modulate the energy gap for an isolated propholactone ring (see Sec. SVI of the SI). This analysis reveals that the normal modes on the ground electronic surface mix to yield those on the excited state. Figure 5(b) illustrates this by visualizing the Duschinsky rotation, ,Duschinsky (1937) of the normal modes upon photoexcitation. The extent to which the Duschinsky matrix displays non-diagonal entries quantifies the amount of mode mixing, which causes non-Gaussian behavior and masks high-frequency vibrational coupling as lower-frequency weight in the spectral density.Zuehlsdorff et al. (2019) Although the Duschinsky matrix is diagonally dominant, indicating that mode mixing is an overall weak effect (see SI Fig. S11), Fig. 5(b) shows a region of the Duschinsky matrix for the band of porpholactone that reveals non-negligible mode mixing between ground state (horizontal-axis) and excited state (vertical-axis) normal modes with frequencies cm-1.
Does the spurious vibronic progression predicted by our GNCT for the TPPL band arise from mode mixing-induced non-Gaussianity? To answer this question, we correct the energy gap contribution in our GNCT, in Eqs. (2) and (3), with an energy gap contribution that incorporates mode mixing (see SI Sec. VI). Specifically, we calculate the exact response function for the microscopically harmonic model of the porpholactone ring and add the effect of the collective solvent motions and phenyl torsions in solvated TPPL by extracting the broadening one would obtain from fitting a Debye contribution to the low-frequency portion of our atomistically derived spectral density. Figure 5(c) shows the resulting spectrum (-GNCT) compared to the predicted TPPL bands from our GNCT result and the FCHT which yields an unphysical negative absorption feature at eV. Here, we confirm that by accounting for microscopically harmonic mode mixing corrections in the TPPL band, our GNCT (purple line) now accurately captures the splitting of both and bands of TPPL, resolving all four peaks and agreeing well with the experimental lineshape. Thus, our results for porphine and TPPL confirm our hypothesis that our theory’s mechanistic insights enable us to tailor and optimize the optical properties of a molecular system by manipulating nuclear motions that induce statistical transition dipole fluctuations with characteristic timescales.
In summary, we have leveraged our GNCT to successfully simulate, reproduce, and analyze, for the first time, the condensed phase -band spectra of representative porphyrins: TPP, its parent porphine without phenyl substituents, and the lactone-substituted TPPL. The band region plays a key role in the fundamental energy and charge transfer steps in photosynthesis Amanullah et al. (2022); Ma et al. (2003); Holt et al. (2005); Ruban et al. (2007); Polívka and Frank (2010); Bode et al. (2009); Son et al. (2020), highlighting the importance of our analysis, which enabled us to settle the long-standing debate over the physical origin of the splitting of the bands observed for metal-free porphyrins. We showed that peak-splitting arises from extreme timescale separation in the nuclear motions that modulate selection rules: low-frequency phenyl torsions and high-frequency inner-ring vibrations. The insights we uncovered can be expected to shed light on the dynamical mechanisms at play in metal-substituted porphyrins that often appear in natural and artificial light-harvesting complexes and photo- and electro-catalysis. Such timescale-separated transition dipole fluctuations are also likely crucial in understanding the linewidths and relative intensities between the and transitions in the optical spectra of metallo-porphyrins even if the respective bands do not appear to split.
We further demonstrated that our theory can reveal design principles to tune porphyrin optoelectronic behavior. To this end, we exploited the atomistic detail of our GNCT to selectively suppress slow transition dipole fluctuations and tune fast fluctuations of the transition dipoles and energy gap via chemical modifications. By simulating the bands of porphine, we proved that severing the pendant phenyls on TPP almost entirely eliminates the low-frequency nuclear motions leading to the systematic suppression of the first and third peaks in the band region, in agreement with our theory-led hypothesis. In turn, we also confirmed that substituting the most distant carbons in one of the pyrrole groups in the tetrapyrrole ring indeed shifted the peak height ratios of the second and fourth peaks by tuning the fast transition dipole fluctuations and caused a vibronic progression-induced asymmetry of all peaks, especially those corresponding to the transition, through the enhancement of energy gap modulations from fast intra-ring motions.
Our results constitute an exciting breakthrough that opens the door to elucidating the physical mechanisms that produce the versatile optoelectronic properties of the large porphyrin family and beyond. With the promising properties that porphyrins offer as chemically tunable scaffolds to guide energy and charge transfer for energy conversion, catalysis, and even electrochemistry, the ability to employ theory to design chemical structures that exhibit desired functionality is essential. By offering a simple and reliable framework to simulate and interpret the spectral features of chromophores that transcend the standard approximations (e.g., harmonic motions, lack of appreciable non-Condon fluctuations, lack of disorder or thermal effects), our theory sets the stage to provide novel insight, disentangle the interplay between thermally accessible molecular motions and spectral lineshapes, and establish robust design principles for next-generation bioinspired charge and energy transfer technologies in terms of tuning material optoelectronic properties as a function of composite chemical structure.
Acknowledgements.
T. J. Z. acknowledges start-up funding provided by Oregon State University. A. M. C. and Z. R. W. were supported by an Early Career Award in the CPIMS program in the Chemical Sciences, Geosciences, and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy under Award DE-SC0024154. A. M. C. and Z. R. W. thank Josef Michl, David Jonas, Niels Damrauer, Ralph Jimenez and Yuezhi Mao for helpful conversations. Z. R. W. thanks Jo Kurian, Leo Romanetz and Rory McClish for insightful discussions. We collectively thank Tom Sayer and Nanako Shitara for comments on the manuscript.I Data availability
The data, input files for MD calculations, excitation energy and transition dipole fluctuations, and input files for generating spectra needed to reproduce our results can be accessed under the following persistent URI: https://doi.org/10.5281/zenodo.13975838. All molecular spectra systems were calculated using the open-source MolSpeckPy code freely available on GitHub (https://github.com/tjz21/Spectroscopy_python_code).
References
- MERCER-SMITH and Mauzerall (1984) J. A. MERCER-SMITH and D. C. Mauzerall, “Photochemistry of porphyrins: a model for the origin of photosynthesis,” Photochemistry and photobiology 39, 397–405 (1984).
- Amanullah et al. (2022) S. Amanullah, C. Ghosh, S. G. Dey, and A. Dey, Fundamentals of Porphyrin Chemistry (John Wiley & Sons, Ltd, 2022).
- Tanaka and Osuka (2015) T. Tanaka and A. Osuka, “Conjugated porphyrin arrays: synthesis, properties and applications for functional materials,” Chemical Society Reviews 44, 943–969 (2015).
- Mathew et al. (2014) S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin, and M. Grätzel, “Dye-sensitized solar cells with 13% efficiency achieved through the molecular engineering of porphyrin sensitizers,” Nat. Chem. 6, 242–247 (2014).
- Swierk et al. (2015) J. R. Swierk, D. D. Méndez-Hernández, N. S. McCool, P. Liddell, Y. Terazono, I. Pahk, J. J. Tomlin, N. V. Oster, T. A. Moore, A. L. Moore, et al., “Metal-free organic sensitizers for use in water-splitting dye-sensitized photoelectrochemical cells,” Proc. Natl. Acad. Sci. 112, 1681–1686 (2015).
- Zhang et al. (2023) Y. Zhang, C. Pan, G. Bian, J. Xu, Y. Dong, Y. Zhang, Y. Lou, W. Liu, and Y. Zhu, “H2o2 generation from o2 and h2o on a near-infrared absorbing porphyrin supramolecular photocatalyst,” Nat. Energy 8, 361–371 (2023).
- Kumagai et al. (2014) T. Kumagai, F. Hanke, S. Gawinkowski, J. Sharp, K. Kotsis, J. Waluk, M. Persson, and L. Grill, “Controlling intramolecular hydrogen transfer in a porphycene molecule with single atoms or molecules located nearby,” Nature Chemistry 6, 41–46 (2014).
- Ning et al. (2020) Y. Ning, Y.-W. Liu, Z.-S. Yang, Y. Yao, L. Kang, J. L. Sessler, and J.-L. Zhang, “Split and use: structural isomers for diagnosis and therapy,” J. Am. Chem. Soc. 142, 6761–6768 (2020).
- Roy et al. (2022a) P. P. Roy, S. Kundu, J. Valdiviezo, G. Bullard, J. T. Fletcher, R. Liu, S.-J. Yang, P. Zhang, D. N. Beratan, M. J. Therien, et al., “Synthetic control of exciton dynamics in bioinspired cofacial porphyrin dimers,” J. Am. Chem. Soc. 144, 6298–6310 (2022a).
- Moisanu et al. (2023) C. M. Moisanu, R. M. Jacobberger, L. P. Skala, C. L. Stern, M. R. Wasielewski, and W. R. Dichtel, “Crystalline arrays of copper porphyrin qubits based on ion-paired frameworks,” J. Am. Chem. Soc. 145, 18447–18454 (2023).
- Gotfredsen et al. (2022) H. Gotfredsen, J.-R. Deng, J. M. Van Raden, M. Righetto, J. Hergenhahn, M. Clarke, A. Bellamy-Carter, J. Hart, J. O’Shea, T. D. Claridge, et al., “Bending a photonic wire into a ring,” Nat. Chem. 14, 1436–1442 (2022).
- Kosugi et al. (2023) K. Kosugi, C. Akatsuka, H. Iwami, M. Kondo, and S. Masaoka, “Iron-complex-based supramolecular framework catalyst for visible-light-driven co2 reduction,” J. Am. Chem. Soc. 145, 10451–10457 (2023).
- Magnera et al. (2023) T. F. Magnera, P. I. Dron, J. P. Bozzone, M. Jovanovic, I. Rončević, E. Tortorici, W. Bu, E. M. Miller, C. T. Rogers, and J. Michl, “Porphene and porphite as porphyrin analogs of graphene and graphite,” Nat. Commun. 14, 6308 (2023).
- Chen et al. (2024) Q. Chen, A. Lodi, H. Zhang, A. Gee, H. I. Wang, F. Kong, M. Clarke, M. Edmondson, J. Hart, J. N. O’Shea, et al., “Porphyrin-fused graphene nanoribbons,” Nat. Chem. 16, 1133–1140 (2024).
- Niedringhaus et al. (2018) A. Niedringhaus, V. R. Policht, R. Sechrist, A. Konar, P. D. Laible, D. F. Bocian, D. Holten, C. Kirmaier, and J. P. Ogilvie, “Primary processes in the bacterial reaction center probed by two-dimensional electronic spectroscopy,” Proc. Natl. Acad. Sci. 115, 3563–3568 (2018).
- Policht, Niedringhaus, and Ogilvie (2018) V. R. Policht, A. Niedringhaus, and J. P. Ogilvie, “Characterization of vibrational coherence in monomeric bacteriochlorophyll a by two-dimensional electronic spectroscopy,” J. Phys. Chem. Lett. 9, 6631–6637 (2018).
- Song et al. (2019) Y. Song, A. Schubert, E. Maret, R. K. Burdick, B. D. Dunietz, E. Geva, and J. P. Ogilvie, “Vibronic structure of photosynthetic pigments probed by polarized two-dimensional electronic spectroscopy and ab initio calculations,” Chem. Sci. 10, 8143–8153 (2019).
- Arsenault et al. (2018) E. A. Arsenault, Y. Yusuke, M. Iwai, K. K. Niyogi, and G. R. Fleming, “The role of vibronic qy-qx states in green light absorption of light-harvesting complex ii,” Nat. Commun. 9, 6011 (2018).
- Jana et al. (2023) S. Jana, T. N. Do, P. J. Nowakowski, M. F. Khyasudeen, D. V. Le, I. J. Y. Lim, S. Prasad, J. Zhang, and H. S. Tan, “Measuring the ultrafast correlation dynamics of a multilevel system using the center line slope analysis in two-dimensional electronic spectroscopy,” J. Phys. Chem. B 127, 7309–7322 (2023).
- Zhao et al. (2023) Y. Zhao, K. Jiang, C. Li, Y. Liu, G. Zhu, M. Pizzochero, E. Kaxiras, D. Guan, Y. Li, H. Zheng, et al., “Quantum nanomagnets in on-surface metal-free porphyrin chains,” Nat. Chem. 15, 53–60 (2023).
- Petropoulos et al. (2024) V. Petropoulos, P. S. Rukin, F. Quintela, M. Russo, L. Moretti, A. Moore, T. Moore, D. Gust, D. Prezzi, G. D. Scholes, et al., “Vibronic coupling drives the ultrafast internal conversion in a functionalized free-base porphyrin,” J. Phys. Chem. Lett. 15, 4461–4467 (2024).
- Ma et al. (2003) Y.-Z. Ma, N. E. Holt, X.-P. Li, K. K. Niyogi, and G. R. Fleming, “Evidence for direct carotenoid involvement in the regulation of photosynthetic light harvesting,” Proc. Natl. Acad. Sci. 15, 4377–4382 (2003).
- Holt et al. (2005) N. E. Holt, D. Zigmantas, L. Valkunas, X.-P. Li, K. K. Niyogi, and G. R. Flemming, “Carotenoid cation formation and the regulation of photosynthetic light harvesting,” Science 307, 433–436 (2005).
- Ruban et al. (2007) A. V. Ruban, R. Berera, C. Ilioaia, I. H. V. Stokkum, J. T. Kennis, A. A. Pascal, H. V. Amerongen, B. Robert, P. Horton, and R. V. Grondelle, “Identification of a mechanism of photoprotective energy dissipation in higher plants,” Nature 450, 575–578 (2007).
- Polívka and Frank (2010) T. Polívka and H. A. Frank, “Molecular factors controlling photosynthetic light harvesting by carotenoids,” Accounts of Chemical Research 43, 1125–1134 (2010).
- Bode et al. (2009) S. Bode, C. C. Quentmeier, P.-N. Liao, N. Hafi, T. Barros, L. Wilk, F. Bittner, and P. J. Walla, “On the regulation of photosynthesis by excitonic interactions between carotenoids and chlorophylls,” Proc. Natl. Acad. Sci. 106, 12311–12316 (2009).
- Son et al. (2020) M. Son, A. Pinnola, S. C. Gordon, R. Bassi, and G. S. Schlau-Cohen, “Observation of dissipative chlorophyll-to-carotenoid energy transfer in light-harvesting complex ii in membrane nanodiscs,” Nat. Commun. 11 (2020).
- Gouterman, Wagnière, and Snyder (1963) M. Gouterman, G. H. Wagnière, and L. C. Snyder, “Spectra of porphyrins: Part ii. four orbital model,” J. Mol. Spectrosc. 11, 108–127 (1963).
- Gouterman (1961) M. Gouterman, “Spectra of porphyrins,” J. Mol. Spectrosc. 6, 138–163 (1961).
- Roy et al. (2022b) P. P. Roy, S. Kundu, N. Makri, and G. R. Fleming, “Interference between franck–condon and herzberg–teller terms in the condensed-phase molecular spectra of metal-based tetrapyrrole derivatives,” J. Phys. Chem. Lett. 13, 7413–7419 (2022b).
- Yu, Baskin, and Zewail (2002) H.-Z. Yu, J. S. Baskin, and A. H. Zewail, “Ultrafast dynamics of porphyrins in the condensed phase: I. free base tetraphenylporphyrin,” J. Phys. Chem. A 106, 9837–9844 (2002).
- Schalk et al. (2008) O. Schalk, H. Brands, T. S. Balaban, and A.-N. Unterreiner, “Near-infrared excitation of the q band in free base and zinc tetratolyl-porphyrins,” J. Phys. Chem. A 112, 1719–1729 (2008).
- He et al. (2012) R. He, H. Li, W. Shen, Q. Yang, and M. Li, “Vibronic fine-structure in the s0→ s1 absorption spectrum of zinc porphyrin: A franck–condon simulation incorporating herzberg–teller theory and the duschinsky effect,” J. Mol. Spectrosc. 275, 61–70 (2012).
- Kullmann et al. (2012) M. Kullmann, A. Hipke, P. Nuernberger, T. Bruhn, D. C. Götz, M. Sekita, D. M. Guldi, G. Bringmann, and T. Brixner, “Ultrafast exciton dynamics after soret-or q-band excitation of a directly , -linked bisporphyrin,” Phys. Chem. Chem. Phys. 14, 8038–8050 (2012).
- Neville and Schuurman (2024) S. P. Neville and M. S. Schuurman, “Calculation of quasi-diabatic states within the dft/mrci (2) framework: The qd-dft/mrci (2) method,” J. Chem. Phys. 160 (2024).
- Santoro et al. (2008) F. Santoro, A. Lami, R. Improta, J. Bloino, and V. Barone, “Effective method for the computation of optical spectra of large molecules at finite temperature including the duschinsky and herzberg-teller effect: The qx band of porphyrin as a case study,” J. Chem. Phys. 128, 224311 (2008).
- Zuehlsdorff et al. (2019) T. J. Zuehlsdorff, A. Montoya-Castillo, J. A. Napoli, T. E. Markland, and C. M. Isborn, “Optical spectra in the condensed phase: Capturing anharmonic and vibronic features using dynamic and static approaches,” J. Chem. Phys 151, 074111 (2019).
- Bergsma et al. (1984) J. P. Bergsma, P. H. Berens, K. R. Wilson, D. R. Fredkin, and E. J. Heller, “Electronic spectra from molecular dynamics: a simple approach,” J. Phys. Chem. 88, 612–619 (1984).
- Mukamel (1985) S. Mukamel, “Fluorescence and absorption of large anharmonic molecules-spectroscopy without eigenstates,” J. Phys. Chem. 89, 1077–1087 (1985).
- Wiethorn et al. (2023) Z. Wiethorn, K. Hunter, T. J. Zuehlsdorff, and A. Montoya-Castillo, “Beyond the condon limit: Condensed phase optical spectra from atomistic simulations,” J. Chem. Phys 159, 244114 (2023).
- Mukamel (1995) S. Mukamel, Principles of Nonlinear Optical Spectroscopy (Oxford University Press, New York, 1995).
- Loco et al. (2018) D. Loco, S. Jurinovich, L. Cupellini, M. F. Menger, and B. Mennucci, “The modeling of the absorption lineshape for embedded molecules through a polarizable qm/mm approach,” Photochem. Photobiol. Sci. 17, 552–560 (2018).
- Zuehlsdorff et al. (2021) T. J. Zuehlsdorff, S. V. Shedge, S.-Y. Lu, H. Hong, V. P. Aguirre, L. Shi, and C. M. Isborn, “Vibronic and environmental effects in simulations of optical spectroscopy,” Annu. Rev. Phys. Chem. 72, 165–188 (2021).
- Weiss (2012) U. Weiss, Quantum dissipative systems (World Scientific, 2012).
- Medders et al. (2017) G. R. Medders, E. C. Alguire, A. Jain, and J. E. Subotnik, “Ultrafast electronic relaxation through a conical intersection: Nonadiabatic dynamics disentangled through an oscillator strength-based diabatization framework,” J. Phys. Chem. A 121, 1425–1434 (2017).
- Duschinsky (1937) F. Duschinsky, “The importance of the electron spectrum in multi atomic molecules. concerning the franck-condon principle,” Acta Physicochim. URSS 7, 551–566 (1937).
- Bader and Berne (1994) J. S. Bader and B. Berne, “Quantum and classical relaxation rates from classical simulations,” J. Chem. Phys. 100, 8359–8366 (1994).
- Egorov, Everitt, and Skinner (1999) S. A. Egorov, K. F. Everitt, and J. L. Skinner, “Quantum Dynamics and Vibrational Relaxation,” J. Phys. Chem. A 103, 9494–9499 (1999).
- Kim and Rossky (2002) H. Kim and P. J. Rossky, “Evaluation of Quantum Correlation Functions from Classical Data,” J. Phys. Chem. B 106, 8240 (2002).
- Craig and Manolopoulos (2004) I. R. Craig and D. E. Manolopoulos, “Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics,” J. Chem. Phys. 121, 3368–3373 (2004).