Symmetries and Cluster Synchronization in Multilayer Networks

Multilayer networks have different types of nodes interacting through different types of connections [12, 13]. Previously defined subclasses of multilayer networks include multiplex [32, 33, 34] and multidimensional [35, 36] networks. In a multiplex network, the same set of agents exists in all layers; for example, in a social system, each node is a person, each layer represents opinion on a topic, and links capture how social interactions influence a person’s opinion on each topic. In a multidimensional network, different kinds of links connect the same set of nodes, all of the same type. For a deeper discussion of particular multilayer networks and how to reconcile each case with the general definition of a multilayer network, see [12, 13]. Sometimes the term ‘multilayer network’ has been used in the literature to indicate generic networks formed of different types of nodes and/or connections. For example, in [31] a ‘multilayer network’ has connections of different types but nodes all of the same type. Here we consider the most general situation for which both nodes and connections can be of different types, with the case of Ref. [31] remaining a special case of multilayer network.

Reference [37] introduced a mathematical model for the time evolution of a multiplex network. Following previous studies of synchronization in different instances of multilayer networks [8, 15, 37, 16, 31], next we provide a general set of equations that describe the dynamics of a multilayer network. First we define the sets of nodes and of connections (or interactions) of a multilayer network. The nodes are arranged in sets $\{X^{\alpha},\alpha=1,\ldots,M\}$, where each individual set corresponds to a given layer of the multilayer network. The uncoupled dynamics of all the $N^{\alpha}$ nodes in layer $X^{\alpha}$ is the same: $\dot{\bf x}_{i}^{\alpha}={\bf F}^{\alpha}({\bf x}_{i}^{\alpha})$, $i=1,\ldots,N^{\alpha}$, ${\bf x}^{\alpha}\in\mathbb{R}^{n^{\alpha}}$. The multilayer network has a total number of nodes equal to $N=\sum_{\alpha}N^{\alpha}$. The set of connections correspond to either intra-layer interactions that connect nodes in the same layer or inter-layer interactions that connect nodes in different layers. The intra-layer interactions inside layer $\alpha$ are described by an adjacency matrix $A^{\alpha\alpha}$, to which is associated a nonlinear coupling function ${\bf H}^{\alpha\alpha}:\mathbb{R}^{n^{\alpha}}\mapsto\mathbb{R}^{n^{\alpha}}$ and a coupling strength $\sigma^{\alpha\alpha}$. The inter-layer interactions from layer $\beta$ to layer $\alpha$ are described by an $N^{\alpha}\times N^{\beta}$ adjacency matrix $A^{\alpha\beta}$, to which is associated a nonlinear coupling function ${\bf H}^{\alpha\beta}:\mathbb{R}^{n^{\alpha}}\mapsto\mathbb{R}^{n^{\beta}}$ and a coupling strength $\sigma^{\alpha\beta}$. We assume throughout that all the couplings are undirected: $A^{\alpha\beta,\lambda}={A^{\beta\alpha,\lambda}}^{T}$, $\alpha,\beta=1,...,M$.

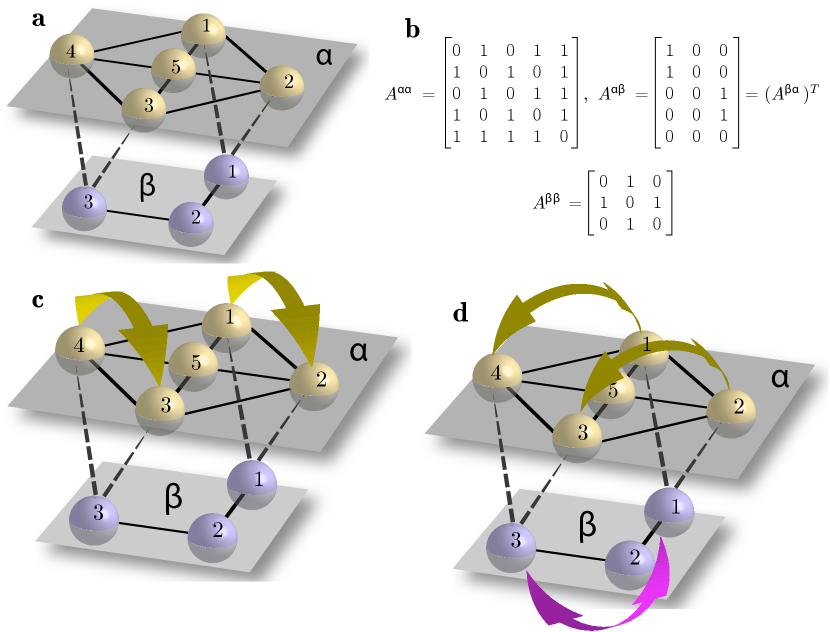
We show an example of a multilayer network in Fig. 1a. This network has two layers, labeled $\alpha$ and $\beta$, with intra-connectivity described by the matrices $A^{\alpha\alpha}$ and $A^{\beta\beta}$ and inter-connectivity described by the matrix $A^{\alpha\beta}=(A^{\beta\alpha})^{T}$, all shown in b. Fig. 1c shows an independent layer symmetry. This symmetry involves only nodes in layer $\alpha$; we can swap $\alpha$ nodes $1$ with $2$ and $\alpha$ nodes $3$ with $4$ without affecting layer $\beta$. Fig. 1d shows a dependent layer symmetry. This symmetry requires swapping nodes in both layer $\alpha$ and $\beta$; when we swap $\alpha$ nodes $2$ with $3$ and $\alpha$ nodes $1$ with $4$, we must also swap $\beta$ nodes $1$ and $3$. Note that as dependent layer symmetries involve swapping nodes of different types, they are a characteristic feature of multilayer networks with different types of nodes.

The dynamics of node $i$ in layer $\alpha$ of the multilayer network is governed by the following set of differential equations,

$$\dot{\bf x}_{i}^{\alpha}={\bf F}^{\alpha}({\bf x}_{i}^{\alpha})+\underbrace{\sigma^{\alpha\alpha}\sum_{j=1}^{N^{\alpha}}A^{\alpha\alpha}_{ij}{\bf H}^{\alpha\alpha}({\bf x}_{j}^{\alpha})}_{\text{intra-layer couplings}}+\underbrace{\sum_{\beta\neq\alpha}\sigma^{\alpha\beta}\sum_{j=1}^{N^{\beta}}A^{\alpha\beta}_{ij}{\bf H}^{\alpha\beta}({\bf x}_{j}^{\beta})}_{\text{inter-layer couplings}},$$

(1)

$i=1,...,N^{\alpha}$, $\alpha=1,...,M$. The underlying assumption here is that functions that are labeled differently are different functions. By this we mean ${\bf F}^{\alpha}(x)\neq{\bf F}^{\beta}(x)$, for $\beta\neq\alpha$.

Next we introduce a vectorial notation. We combine the dynamical variables from each layer into a vector of vectors ${\bf x}^{\alpha}=[{\bf x}^{\alpha}_{1},{\bf x}^{\alpha}_{2},...,{\bf x}^{\alpha}_{N^{\alpha}}]$ (here and after, the comma stands for vertical stacking of vector and the square brackets stand for vector concatenation). Likewise, we can define,

$${\bf F}^{\alpha}({\bf x}^{\alpha})=[{\bf F}^{\alpha}({\bf x}^{\alpha}_{1}),{\bf F}^{\alpha}({\bf x}^{\alpha}_{2}),...,{\bf F}^{\alpha}({\bf x}^{\alpha}_{N^{\alpha}})],$$

(2)

$${\bf H}^{\alpha\alpha}({\bf x}^{\alpha})=[{\bf H}^{\alpha\alpha}({\bf x}^{\alpha}_{1}),{\bf H}^{\alpha\alpha}({\bf x}^{\alpha}_{2}),...,{\bf H}^{\alpha\alpha}({\bf x}^{\alpha}_{N^{\alpha}})],$$

(3)

$${\bf H}^{\alpha\beta}({\bf x}^{\beta})=[{\bf H}^{\alpha\beta}({\bf x}^{\beta}_{1}),{\bf H}^{\alpha\beta}({\bf x}^{\beta}_{2}),...,{\bf H}^{\alpha\beta}({\bf x}^{\beta}_{N^{\beta}})].$$

(4)

This notation suppresses the summations over the nodes in each layer. We obtain the set (one for each layer) of vector equations

$$\dot{\bf x}^{\alpha}={\bf F}^{\alpha}({\bf x}^{\alpha})+\sigma^{\alpha\alpha}A^{\alpha\alpha}{\bf H}^{\alpha\alpha}({\bf x}^{\alpha})+\sum_{\beta\neq\alpha}\sigma^{\alpha\beta}A^{\alpha\beta}{\bf H}^{\alpha\beta}({\bf x}^{\beta}),\quad\alpha=1,...,M.$$

(5)

Two nodes $i$ and $j$ are synchronized if ${\bf x}_{i}(t)={\bf x}_{j}(t)\,\forall t$. Synchronous motions define invariant manifolds of Eqs. (5), i.e., ${\bf x}_{i}={\bf x}_{j}\Rightarrow\dot{\bf x}_{i}=\dot{\bf x}_{j}$. In order to study cluster synchronization, we will look for symmetries in the multilayer network; these are the node permutations that leave system (5) unchanged. The group of symmetries of the multilayer network is the set of permutations of the nodes that do not change Eqs. (5) for $\alpha=1,...,M$. Below we explain how to find this group of symmetries in arbitrary multilayer networks, and we investigate the relations between intralayer and interlayer connections in order to preserve certain symmetries properties.

Symmetries of complex networks have received recent attention from the scientific community. These symmetries influence network structural [28], spectral [38], and dynamical properties [39], including cluster synchronization [20, 21]. However, symmetries of multilayer networks have not been studied.

Here we define the group of symmetries of general multilayer networks with both nodes of different types and connections of different types. Although we will eventually use computational methods to find the symmetry group of a particular network, it is best to understand what types of structures are imposed on the symmetry group of a multilayered network in general. The study of the symmetry group provides insight into the results of the numerical calculations and into whether what we find is general or just a property of the particular network we are analyzing. Next we develop some of the mathematical properties of the final permutation group structure of the multilayer systems. As we will see, the interplay between the symmetries in each layer with the symmetries in other layers is subtle and leads to interesting structures in the final group of the whole network.

We first show that the multilayer structure imposes a block diagonal form on the permutations of the whole group. Since each layer of the network contains a different kind of node, symmetries are not allowed to move nodes from different layers. As a result, the symmetry group ${\mathcal{G}}$ of the multilayer network is represented by block diagonal permutation matrices, i. e., each $g\in{\mathcal{G}}$ is of the form,

$$g=\begin{pmatrix}g_{\alpha}&0&0&\ldots\\ 0&g_{\beta}&0&\ldots\\ 0&0&g_{\gamma}&\ldots\\ \vdots&\vdots&\vdots&\ddots\end{pmatrix},$$

(6)

where $g_{\alpha}$ is a permutation matrix for layer $\alpha$, $g_{\beta}$ is a permutation matrix for layer $\beta$, and so on. In this section we show that the symmetries of the group ${\mathcal{G}}$ of the multilayer network are formed of the symmetries of the single-layers (i.e., $g_{\alpha}\in{\mathcal{G}}^{\alpha}$, $g_{\beta}\in{\mathcal{G}}^{\beta}$, …) that are compatible with each other, where compatibility is determined by the inter-layer couplings. This means that if we perform a permutation on layer $\alpha$, we must perform a permutation on each other layer (which in some cases may be the identity permutation) by leaving the structure of the overall network unaltered. As a result, compatibility links permutations from the groups of symmetries of each layer, so that we preserve the symmetry of the whole multilayer network. The major question we want to answer here is: how does compatibility relate permutations from different layers?

Let us consider a multilayer system with two layers $\alpha$ and $\beta$. Eq. (5) becomes,

$$\begin{array}[]{rcl}\dot{\bf x}^{\alpha}&=&{\bf F}^{\alpha}({\bf x}^{\alpha})+\sigma^{\alpha\alpha}A^{\alpha\alpha}{\bf H}^{\alpha\alpha}({\bf x}^{\alpha})+\sigma^{\alpha\beta}A^{\alpha\beta}{\bf H}^{\alpha\beta}({\bf x}^{\beta})\\ \dot{\bf x}^{\beta}&=&{\bf F}^{\beta}({\bf x}^{\beta})+\sigma^{\beta\beta}A^{\beta\beta}{\bf H}^{\beta\beta}({\bf x}^{\beta})+\sigma^{\beta\alpha}A^{\beta\alpha}{\bf H}^{\beta\alpha}({\bf x}^{\alpha}).\end{array}$$

(7)

In Methods, we show that we can determine the symmetry group of a multilayer network with $M>2$ layers, multiple edge types inside each layer and in between layers. Consider two permutations $g\in{\mathcal{G}}^{\alpha}$ and $h\in{\mathcal{G}}^{\beta}$. We know from Eq. (6) that a symmetry of this multilayer network is in the form

$$\begin{pmatrix}g&0\\ 0&h\end{pmatrix},$$

(8)

so, which $g$’s and $h$’s are compatible? For the answer, we consider the inter-layer couplings terms,

$$\sigma^{\alpha\beta}A^{\alpha\beta}{\bf H}^{\alpha\beta}({\boldsymbol{x}}^{\beta})\qquad\mbox{and}\qquad\sigma^{\beta\alpha}A^{\beta\alpha}{\bf H}^{\beta\alpha}({\boldsymbol{x}}^{\alpha}).$$

(9)

We say that symmetry-related nodes must be flow invariant. That is, the symmetries must guarantee that synchronized nodes have equal dynamical variables when we include inter-layer coupling.

Application of the two permutations to the equations of the multilayer network results in

$$\begin{array}[]{rcl}g{(\dot{\bf x}^{\alpha})}&=&{\bf F}^{\alpha}(g{\bf x}^{\alpha})+\sigma^{\alpha\alpha}A^{\alpha\alpha}{\bf H}^{\alpha\alpha}(g{\bf x}^{\alpha})+\sigma^{\alpha\beta}gA^{\alpha\beta}{\bf H}^{\alpha\beta}({\bf x}^{\beta})\\ h(\dot{{\bf x}}^{\beta})&=&{\bf F}^{\beta}(h{\bf x}^{\beta})+\sigma^{\beta\beta}A^{\beta\beta}{\bf H}^{\beta\beta}(h{\bf x}^{\beta})+\sigma^{\beta\alpha}hA^{\beta\alpha}{\bf H}^{\beta\alpha}({\bf x}^{\alpha}),\end{array}$$

(10)

where the $g$ and $h$ permutations can be taken into the arguments of ${\bf F}^{\alpha},{\bf H}^{\alpha\alpha}$ and ${\bf F}^{\beta},{\bf H}^{\beta\beta}$, respectively since the functions operate sequentially on their vector arguments and we have used the properties that $g$ commutes with $A^{\alpha\alpha}$ and $h$ commutes with $A^{\beta\beta}$.

To achieve flow invariance, we need $g$ and $h$ to act on ${\mathbf{x}}^{\alpha}$ and ${\mathbf{x}}^{\beta}$, respectively, in the arguments of the interlayer coupling terms ${\bf H}^{\alpha\beta}$ and ${\bf H}^{\beta\alpha}$. Note that this does not require commutability ($gA^{\alpha\beta}=A^{\alpha\beta}g$) since we want to ‘exchange’ $g$ for $h$ and vice-versa (as the interlayer coupling matrices are generally not square, we do not expect commmutability). More generally, conjugacy relations are the requirements for symmetry compatibility, i.e.,

$$gA^{\alpha\beta}=A^{\alpha\beta}h\qquad\mbox{and}\qquad hA^{\beta\alpha}=A^{\beta\alpha}g;$$

(11)

The permutations that fulfill the conjugacy relations (11) are defined by the following sets,

$$\mathcal{H}^{\alpha}=\{g\in\mathcal{G}^{\alpha}|gA^{\alpha\beta}=A^{\alpha\beta}h\ \mbox{ and }hA^{\beta\alpha}=A^{\beta\alpha}g\mbox{ for some }\ h\in\mathcal{G}^{\beta}\}$$

(12)

and

$$\mathcal{H}^{\beta}=\{h\in\mathcal{G}^{\beta}|hA^{\beta\alpha}=A^{\beta\alpha}g\ \mbox{ and }gA^{\alpha\beta}=A^{\alpha\beta}h\mbox{ for some }\ g\in\mathcal{G}^{\alpha}\}.$$

(13)

An element $g\in\mathcal{H}^{\alpha}$ is represented by an $N^{\alpha}\times N^{\alpha}$ matrix and an element $h\in\mathcal{H}^{\beta}$ is represented by an $N^{\beta}\times N^{\beta}$ matrix. It is important to note that in general the matrix $A^{\alpha\beta}\in\mathbb{R}^{N^{\alpha}\times N^{\beta}}$ will have nontrivial left and right null spaces. As a result, we may find more than one $g$ that satisfies $gA^{\alpha\beta}=A^{\alpha\beta}h$ for a given $h$ and vice versa.

In the Methods (Formal Proofs) we first prove that $\mathcal{H}^{\alpha}$ is a subgroup of $\mathcal{G}^{\alpha}$ and $\mathcal{H}^{\beta}$ is a subgroup of $\mathcal{G}^{\beta}$. Then we show that for the case of undirected networks we only need either one of the following relationships to prove that $\mathcal{H}^{\alpha}$ and $\mathcal{H}^{\beta}$ are subgroups,

$$gA^{\alpha\beta}=A^{\alpha\beta}h\qquad\mbox{or}\qquad hA^{\beta\alpha}=A^{\beta\alpha}g.$$

(14)

We can now find the group of symmetries of the multilayer network $\mathcal{G}$ from the subgroups $\mathcal{H}^{\alpha}$ and $\mathcal{H}^{\beta}$. First, recall that the permutations of $\mathcal{G}$ have block structure of Eq. (8). While we use all permutations $g\in\mathcal{H}^{\alpha}$ and $h\in\mathcal{H}^{\beta}$ to construct $\mathcal{G}$, we can only pair the permutations that satisfy the conjugacy relation in Eq. (11) (or the simpler version in Eq. (14)).

We define an equivalence relation $\sim$ between the elements of $\mathcal{H}^{\alpha}$: $g\sim g^{\prime}$ if $gA^{\alpha\beta}=g^{\prime}A^{\alpha\beta}$. Analogously, $h\sim h^{\prime}$ if $hA^{\beta\alpha}=h^{\prime}A^{\beta\alpha}$. One can verify that $\sim$ is an equivalence relation as it is reflexive, symmetric, and transitive. We also see that if $g\sim g^{\prime}$ and $g$ and $h$ are conjugate, then so are $g^{\prime}$ and $h$, indicating that $\sim$ defines a partition of each subgroup $\mathcal{H}^{\alpha}$ and $\mathcal{H}^{\beta}$ into disjoint subsets (called equivalence classes) $\mathcal{K}^{\alpha}_{i}$ and $\mathcal{K}^{\beta}_{i}$, $i=1,...,K$, respectively. Each subset $\mathcal{K}^{\alpha}_{i}$ contains all the permutations $g$ such that $gA^{\alpha\beta}$ is equal to a given matrix $M_{i}$; correspondingly, each subset $\mathcal{K}^{\beta}_{i}$ contains all the permutations $h$ such that $hA^{\beta\alpha}$ is equal to the matrix $M_{i}^{T}$. We can then construct the group of symmetries of the multilayer network $\mathcal{G}$ as follows,

$$\mathcal{G}=\left\{\begin{pmatrix}g&0\\ 0&h\end{pmatrix}|g\in\mathcal{K}^{\alpha}_{i}\mbox{ and }h\in\mathcal{K}^{\beta}_{i},\mbox{ for }i=1,...,K\right\}$$

(15)

Although the sets $\mathcal{K}^{\alpha}_{i}$ and $\mathcal{K}^{\beta}_{i}$ have a one-to-one correspondence, the elements of each do not and often differ in number, as shown in Methods for the example multilayer network in Fig. 1.

Next, we present properties of the equivalence classes $\mathcal{K}^{\alpha}_{i}$, which then leads to the definition of Independent Layer Symmetries (ILS). Let $\mathcal{K}^{\alpha}_{1}$ be the equivalence class containing the identity. We can prove that $\mathcal{K}^{\alpha}_{1}$ is a normal subgroup of $\mathcal{H}^{\alpha}$. Moreover, we can prove that all the $\mathcal{K}^{\alpha}_{i}$, $i\neq 1$, are left and right cosets of $\mathcal{K}^{\alpha}_{1}$. Formal proofs for each statement are included in Methods (Formal Proofs.)

The structure of the equivalence classes $\mathcal{K}^{\alpha}_{i}$ gives insight into the symmetries; this facilitates the calculations of the classes themselves and of the $T$ matrices for each layer (see Methods for the structure of the $T$ matrix). In particular the subgroups $\mathcal{K}^{\alpha}_{1}$, $\mathcal{K}^{\beta}_{1}$, … identify a special set of symmetries we will refer to as Independent Layer Symmetries. The following general relationship between the symmetry operations from $\mathcal{K}^{\alpha}_{1}$, $\mathcal{K}^{\beta}_{1}$,… and the layer structures clarifies why we refer to the elements of $\mathcal{K}^{\alpha}_{1}$, $\mathcal{K}^{\beta}_{1}$,… as Independent Layer Symmetries. Given any $g\in\mathcal{K}^{\alpha}_{1}$, then for each $h\in\mathcal{K}^{\beta}_{1}$,

$$gA^{\alpha\beta}=A^{\alpha\beta}h=A^{\alpha\beta},$$

(16)

since the equivalence class subgroups are both associated with the identity operation. This means that the symmetry operations from the equivalence class subgroups do not affect the interlayer coupling and, hence, those operations (permutations) in one layer do not affect the types of allowed dynamics in the other layer(s). In particular, the loss of a symmetry associated with the ILS subgroup in the dynamics, i.e. a symmetry-breaking bifurcation, will not alter the possible clusters in other layers, provided no symmetries in the other cosets ($\mathcal{K}^{\alpha}_{i},i\neq 1$) are also broken. We will show simple examples of this in the Methods Section and when presenting the experiment. Note that the stability of the clusters is a different issue, which will receive separate consideration.

To conclude, the ILS clusters are determined by the interplay between the intralayer couplings in each layer and the interlayer couplings between layers. In what follows we will refer to symmetries that are not ILS, i.e. they involve simultaneously swapping nodes in different layers as Dependent Layer Symmetries (DLS).

From knowledge of the group of symmetries of the multilayer network, the nodes in each layer $\alpha$ can be partitioned into $L^{\alpha}$ orbital clusters, $\mathcal{C}^{\alpha}_{1},\mathcal{C}^{\alpha}_{2},...,\mathcal{C}^{\alpha}_{L^{\alpha}}$. Inside each layer, symmetries map into each other only nodes in the same orbital cluster.

In Table 1 we apply the techniques described in this section to compute the symmetries of several multilayer networks from datasets in the literature. For each network dataset, we include information on the number of layers $M$, the number of nodes in each layer $N^{\alpha},\alpha=1,...M$ (the number of nodes $\mathcal{N}$ in all layers for multiplex networks), the number of edges $E$, the order of the automorphism group $|\mathcal{G}|$, and the cardinality of the largest orbital cluster $\max(|\mathcal{C}_{k}|)$. The main underlying assumption is that nodes are homogeneous inside each layer but nodes in different layers are not, so that nodes inside each layer can be symmetric, but nodes from different layers cannot. While we understand this is an oversimplification, available datasets do not typically include information on the attributes of the individual nodes, and as a result, our symmetry analysis is solely based on the multilayer network structure [37] and not on the specific node attributes. An extensive description of each one of the datasets is included in the Supplementary Note 1 and in the Supplementary Table 1. From Table 1 we see that several real multilayer networks possess very large numbers of symmetries.

In Supplementary Note 2 we study the emergence of symmetries in artificially generated multilayer networks, where each layer is a Scale Free (SF) network and nodes from different layers are randomly matched to one another to obtain a multiplex network. We see that these networks typically do not display symmetries, except for the case that the power-law degree distribution exponents of the networks in each layer are low across the layers. It is interesting that some of the real multilayer networks we have analyzed display many more symmetries than these model multilayer networks. This observation motivated us to design a generating algorithm to construct multilayer networks with prescribed number of symmetries, which is presented in Supplementary Note 3.

In what follows we study stability of the cluster-synchronous solution for a general multilayer network described by Eqs. (1). Given an orbital partition, we define the ${L^{\alpha}}\times{L^{\alpha}}$ intralayer quotient matrix $Q^{\alpha\alpha}$ such that for each pair of $\alpha$-clusters ($\mathcal{C}^{\alpha}_{u},\mathcal{C}^{\alpha}_{v}$),

$$Q^{\alpha\alpha}_{uv}=\sum_{j\in\mathcal{C}^{\alpha}_{v}}A^{\alpha\alpha}_{ij},\qquad i\in\mathcal{C}^{\alpha}_{u},\quad u,v=1,2,\dots L^{\alpha}.$$

(17)

Analogously, we define the ${L^{\alpha}}\times{L^{\beta}}$ interlayer quotient matrix $Q^{\alpha\beta}$ such that for each pair of clusters, the first cluster ${\mathcal{C}}^{\alpha}_{u}$ from layer $\alpha$ and the second cluster ${\mathcal{C}}^{\beta}_{v}$ from layer $\beta$,

$$Q^{\alpha\beta}_{uv}=\sum_{j\in\mathcal{C}^{\beta}_{v}}A^{\alpha\beta}_{ij},\qquad i\in\mathcal{C}^{\alpha}_{u},\quad u=1,2,\dots L^{\alpha},v=1,2,\dots L^{\beta}.$$

(18)

We can thus write the equations for the time evolution of the quotient multilayer network,

$$\dot{\bf q}_{u}^{\alpha}={\bf F}^{\alpha}({\bf q}_{u}^{\alpha})+{\sigma^{\alpha\alpha}\sum_{v=1}^{L^{\alpha}}Q^{\alpha\alpha}_{uv}{\bf H}^{\alpha\alpha}({\bf q}_{v}^{\alpha})}+{\sum_{\beta\neq\alpha}\sigma^{\alpha\beta}\sum_{v=1}^{L^{\beta}}Q^{\alpha\beta}_{uv}{\bf H}^{\alpha\beta}({\bf q}_{v}^{\beta})},$$

(19)

$\alpha=1,...,M$, $u=1,...,L^{\alpha}$. Note that Eqs. (19) provides a mapping for each layer $\alpha$ from the node coordinates $\{{\bf x}_{i}^{\alpha}\}$, $i=1,...,N^{\alpha}$ to the quotient coordinates $\{{\bf q}_{u}^{\alpha}\}$, $u=1,...,L^{\alpha}$, where ${\bf x}_{i}^{\alpha}(t)\equiv{\bf q}_{u}^{\alpha}(t)$ if $i\in\mathcal{C}_{u}^{\alpha}$.

We now linearize (1) about (19),

$$\delta\dot{{\bf x}}_{i}^{\alpha}=DF^{\alpha}({\bf q}_{u}^{\alpha})\delta{{\bf x}}_{i}^{\alpha}+{\sum_{\beta}\sigma^{\alpha\beta}\sum_{j=1}^{N^{\beta}}A^{\alpha\beta}_{ij}DH^{\alpha\beta}({\bf q}_{v}^{\beta})\delta{\bf x}_{j}^{\beta}},\qquad i=1,...,N^{\alpha},$$

(20)

where again ${\bf q}_{v}^{\beta}$ is the time evolution of the quotient network node $v$ that node $j\in{\mathcal{C}}_{v}^{\beta}$ maps to. Also note that in the above equation the summation in $\beta$ runs over both intra-layer connections and inter-layer connections.

For each layer $\alpha$, the above set of equations, can be written in vectorial form, by stacking together all the individual perturbations applied to the vectors inside each layer, e.g., $\delta{\bf x}^{\alpha}=[\delta{\bf x}_{1}^{\alpha},\delta{\bf x}_{2}^{\alpha},...,\delta{\bf x}_{N^{\alpha}}^{\alpha}]$,

$$\delta\dot{\bf x}^{\alpha}=\left(\sum_{u=1}^{L^{\alpha}}E_{u}^{\alpha}\otimes DF^{\alpha}({\bf q}_{u}^{\alpha})\right)\delta{\bf x}^{\alpha}+\sum_{\beta}\left(\sigma^{\alpha\beta}(A^{\alpha\beta}\otimes I_{n^{\alpha}})\sum_{u=1}^{L^{\beta}}\left(E^{\beta}_{u}\otimes DH^{\alpha\beta}({\bf q}_{u}^{\beta})\right)\right)\delta{\bf x}^{\beta},$$

(21)

$\alpha=1,...,M,$ where each indicator matrix $E_{u}^{\alpha}$ has dimension $N^{\alpha}$ and is such that its diagonal entries are equal to one if node $i$ of layer $\alpha$ is in cluster ${\mathcal{C}_{u}^{\alpha}}$ and are equal to zero otherwise.

We then stack all the layers one above the other to form the vector $\delta{\bf x}=[\delta{\bf x}^{\alpha},\delta{\bf x}^{\beta},\dots]$, and we rewrite (21) as

$$\begin{split}\delta\dot{\bf x}=&\left(\begin{bmatrix}\sum_{u}E_{u}^{\alpha}\otimes DF^{\alpha}({\bf q}_{u}^{\alpha})&0&\cdots\\ 0&\sum_{u}E_{u}^{\beta}\otimes DF^{\beta}({\bf q}_{u}^{\beta})&\cdots\\ \vdots&\vdots&\ddots\end{bmatrix}\right.\\ \ +&\left.\begin{bmatrix}\sum_{u}A^{\alpha\alpha}E^{\alpha}_{u}\otimes D\hat{H}^{\alpha\alpha}({\bf q}_{u}^{\alpha})&\sum_{u}A^{\alpha\beta}E^{\beta}_{u}\otimes D\hat{H}^{\alpha\beta}({\bf q}_{u}^{\beta})&\cdots\\ \sum_{u}A^{\beta\alpha}E^{\alpha}_{u}\otimes D\hat{H}^{\beta\alpha}({\bf q}_{u}^{\beta})&\sum_{u}A^{\beta\beta}E^{\beta}_{u}\otimes D\hat{H}^{\beta\beta}({\bf q}_{u}^{\beta})&\cdots\\ \vdots&\vdots&\ddots\end{bmatrix}\right)\delta{\bf x},\end{split}$$

(22)

where $D\hat{H}^{\alpha\beta}=\sigma^{\alpha\beta}DH^{\alpha\beta}$.

We are looking for a transformation that applied to Eq. (22), leaves the first terms on the right hand side of (22) unchanged and decouples the second terms in independent blocks, independent of the $DF$ and the $DH$ terms as they vary in time.

From knowledge of the group of symmetries of the multilayer network $\mathcal{G}$, we can compute the irreducible representations (IRRs) of $\mathcal{G}$. For each layer $\alpha$ we can define an orthonormal transformation $T^{\alpha}$ to the IRR coordinate system (see [20]). We can then construct the following block diagonal orthonormal matrix,

$$T=\bigoplus_{\alpha}T^{\alpha},$$

(23)

that maps the entire multilayer network to the IRR coordinate system.

A formal proof of the above particular structure of the matrix $T$ can be found in Methods (Properties of the Equivalence Classes and structure of the matrix $T$). Intuitively, the matrix $T$ has a block diagonal structure, where each block corresponds to a layer, because only nodes from the same layer can be swapped by a symmetry.

Consider now the $N$-dimensional supra-adjacency matrix,

$$A=\begin{bmatrix}A^{\alpha\alpha}&A^{\alpha\beta}&\cdots\\ A^{\beta\alpha}&A^{\beta\beta}&\cdots\\ \vdots&\vdots&\ddots\end{bmatrix}.$$

(24)

The transformed $N\times N$ block diagonal matrix $B=TAT^{-1}$ is a direct sum $\oplus_{r=1}^{R}I_{d_{r}}\otimes\hat{B}_{r}$, where $\hat{B}_{r}$ is a (generally complex) $p_{r}\times p_{r}$ matrix with $p_{r}$ the multiplicity of the $r$th IRR in the permutation representation, $R$ the number of IRRs present and $d_{r}$ the dimension of the $r$th IRR, so that $\sum_{r}d_{r}p_{r}=N$. The matrix $T$ contains information on which perturbations affecting different clusters get mapped to different IRRs [24]. There is one representation (labeled $r=1$) which we call trivial and has dimension $d_{1}=\sum_{\alpha}L^{\alpha}$. All perturbations parallel to the synchronization manifold get mapped to this representation. Hence, the trivial representation is associated with all the clusters $\mathcal{C}^{1}_{1},...,\mathcal{C}^{1}_{L^{1}},\mathcal{C}^{2}_{1},...,\mathcal{C}^{2}_{L^{2}},...$ However, it is possible that other IRR representations are only associated with some of the clusters (not all of them).

We can now define the $\sum_{\alpha}N^{\alpha}n^{\alpha}$-dimensional orthonormal matrix ${\tilde{T}}=\bigoplus_{\alpha}T^{\alpha}\otimes I_{n_{\alpha}}$. Next, we will use the matrix $\tilde{T}$ to block-diagonalize Eq. (21). Applying the transformation $\text{\boldmath$\eta$}={\tilde{T}}\delta{\bf x}$ to (22) we obtain,

$$\begin{split}\dot{\text{\boldmath$\eta$}}=&\left(\begin{bmatrix}\sum_{u}J_{u}^{\alpha}\otimes DF^{\alpha}({\bf q}_{u}^{\alpha})&0&\cdots\\ 0&\sum_{u}J_{u}^{\beta}\otimes DF^{\beta}({\bf q}_{u}^{\beta})&\cdots\\ \vdots&\vdots&\ddots\end{bmatrix}\right.\\ \ +&\left.\begin{bmatrix}\sum_{u}B^{\alpha\alpha}J^{\alpha}_{u}\otimes D\hat{H}^{\alpha\alpha}({\bf q}_{u}^{\alpha})&\sum_{u}B^{\alpha\beta}J^{\beta}_{u}\otimes D\hat{H}^{\alpha\beta}({\bf q}_{u}^{\beta})&\cdots\\ \sum_{u}B^{\beta\alpha}J^{\alpha}_{u}\otimes D\hat{H}^{\beta\alpha}({\bf q}_{u}^{\beta})&\sum_{u}B^{\beta\beta}J^{\beta}_{u}\otimes D\hat{H}^{\beta\beta}({\bf q}_{u}^{\beta})&\cdots\\ \vdots&\vdots&\ddots\end{bmatrix}\right)\text{\boldmath$\eta$},\end{split}$$

(25)

where each transformed indicator matrix $J_{u}^{\alpha}=T^{\alpha}E_{u}^{\alpha}{T^{\alpha}}^{T}$ and each block $B^{\alpha\beta}={T^{\alpha}}A^{\alpha\beta}{T^{\beta}}^{T}.$

The advantage of (25) over (22) lies in the block-diagonal structure of the matrix $B=\oplus_{r=1}^{R}I_{d_{r}}\otimes\hat{B}_{r}$. The block $\hat{B}_{1}$ is associated with motion along the synchronization manifold. The blocks $\hat{B}_{2},...,\hat{B}_{R}$ describe the dynamics transverse to the synchronization manifold. As a result, we have decoupled the dynamics along the synchronous manifold from that transverse to it [20]. Moreover, each transverse block $r=2,..,R$ is associated with either an individual cluster or a subset of intertwined clusters [20]. Thus the problem of studying the behavior of a perturbation away from the synchronous solution is typically reduced into many smaller problems, which can be analyzed independently one from the other.

Next we discuss how Dependent and Independent Layer Symmetries affect the stability analysis. We recall that the matrix $B=TAT^{-1}$ can be written as a direct sum of blocks $\oplus_{r=1}^{R}I_{d_{r}}\otimes\hat{B}_{r}$. As each row of the matrix $T$ is associated to a specific cluster [47], each one of the blocks $\hat{B}_{r}$ corresponds to a set of clusters which are identified by the rows of the matrix $T$. The trivial representation ($r=1$) is associated with all the clusters $\mathcal{C}^{1}_{1},...,\mathcal{C}^{1}_{L^{1}},\mathcal{C}^{2}_{1},...,\mathcal{C}^{2}_{L^{2}},...$ The corresponding rows of the matrix $T$ are the eigenvectors associated to the eigenvalue 1 of the trivial representation; these have nonzero components all of the same sign. Now we look at the remaining ‘transverse’ blocks of the matrix $B$ ($r>1$). The corresponding rows of the matrix $T$ are such that the sums of their entries is equal zero and are called symmetry breakings: each row, in fact, describes how a cluster, generated by a symmetry, may break into smaller ones. The transverse blocks can be divided into ILS blocks if the corresponding symmetry breakings are all from the same layer and DLS blocks if the corresponding symmetry breakings are from different layers. We can then write $T=[T_{\text{ SYNC}}^{T},T_{\text{ ILS}}^{T},T_{\text{DLS}}^{T}]^{T}$ and the transformed vector $\text{\boldmath$\eta$}=[\text{\boldmath$\eta$}_{\text{SYNC}}^{T},\text{\boldmath$\eta$}_{\text{ILS}}^{T},\text{\boldmath$\eta$}_{\text{DLS}}^{T}]^{T}$.

The ILS blocks are symmetry breakings generated by the ILS subgroup. From our definition of the ILS subgroup, each $\mathcal{K}_{1}^{\alpha}$ is a normal subgroup of $\mathcal{H}^{\alpha}$. Clifford theorem [48] states that each IRR of $\mathcal{H}^{\alpha}$, when restricted on $\mathcal{K}_{1}^{\alpha}$, is either itself an IRR of $\mathcal{K}_{1}^{\alpha}$ or breaks up into a direct sum of IRRs of $\mathcal{K}_{1}^{\alpha}$ of the same dimension. The rows of the change of coordinates $T_{\text{ILS}}^{\alpha}$ (for layer $\alpha$) to the IRR of $\mathcal{K}_{1}^{\alpha}$, which are associated with the symmetry breaking perturbations of the ILS, are generated by the eigenvectors associated to the eigenvalue 1 of the projectors on the IRRs of $\mathcal{K}_{1}^{\alpha}$. These rows generate invariant subspaces of minimal dimension, and must therefore be rows of $T^{\alpha}$.

We now consider for simplicity the case of a network with two layers, labeled $\alpha$ and $\beta$. In general, the transverse IRRs associated with the ILS subgroup in layer $\alpha$ will have structure,

$$\dot{\text{\boldmath$\eta$}}_{{\text{ILS}}}=\Bigl{[}\sum_{u}J_{u}^{\alpha}\otimes DF^{\alpha}({\bf q}_{u}^{\alpha})+\sum_{u}B^{\alpha\alpha}J^{\alpha}_{u}\otimes D\hat{H}^{\alpha\alpha}({\bf q}_{u}^{\alpha})\Bigr{]}\text{\boldmath$\eta$}_{{\text{ILS}}}.$$

(26)

Note the perturbation $\text{\boldmath$\eta$}_{{\text{ILS}}}$ is independent of the dynamics on the $\beta$ layer, i.e., of both $DF^{\beta}({\bf q}_{u}^{\beta})$ and $D\hat{H}^{\beta\beta}({\bf q}_{u}^{\beta})$. This indicates that the stability of ILS symmetries can be studied through a specific class of the Master Stability Function, which is the same as for single-layer networks [20]. The transverse IRRs associated with the ILS subgroup in layer $\beta$ will have an analogous structure as (26). On the other hand, the remaining transverse IRRs will have structure,

$$\begin{split}\dot{\text{\boldmath$\eta$}}_{{\text{DLS}}}=&\left(\begin{bmatrix}\sum_{u}J_{u}^{\alpha}\otimes DF^{\alpha}({\bf q}_{u}^{\alpha})&0\\ 0&\sum_{u}J_{u}^{\beta}\otimes DF^{\beta}({\bf q}_{u}^{\beta})\end{bmatrix}\right.\\ \ +&\left.\begin{bmatrix}\sum_{u}B^{\alpha\alpha}J^{\alpha}_{u}\otimes D\hat{H}^{\alpha\alpha}({\bf q}_{u}^{\alpha})&\sum_{u}B^{\alpha\beta}J^{\beta}_{u}\otimes D\hat{H}^{\alpha\beta}({\bf q}_{u}^{\beta})\\ \sum_{u}B^{\beta\alpha}J^{\alpha}_{u}\otimes D\hat{H}^{\beta\alpha}({\bf q}_{u}^{\beta})&\sum_{u}B^{\beta\beta}J^{\beta}_{u}\otimes D\hat{H}^{\beta\beta}({\bf q}_{u}^{\beta})\\ \end{bmatrix}\right)\text{\boldmath$\eta$}_{{\text{DLS}}}.\end{split}$$

(27)

Note that the perturbations $\text{\boldmath$\eta$}_{{\text{DLS}}}$ depend on the dynamics of the systems in both layers $\alpha$ and $\beta$, through the mixed blocks appearing in Eq. (27). The structure of Eq. (27) is substantially different than that of Eq. (26), which may lead to dramatic effects in terms of stability.

Consider now the multilalyer network in Fig. 1. The matrix $T$ is equal to

$$T=\left[\begin{array}[]{cccccccc}0.5&0.5&0.5&0.5&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&\frac{1}{\sqrt{2}}&0&\frac{1}{\sqrt{2}}\\ 0&0&0&0&0&0&1&0\\ \hline\cr 0.5&-0.5&0.5&-0.5&0&0&0&0\\ 0.5&-0.5&-0.5&0.5&0&0&0&0\\ \hline\cr 0.5&0.5&-0.5&-0.5&0&0&0&0\\ 0&0&0&0&0&\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\end{array}\right]\begin{array}[]{l}\left.\begin{array}[]{l}\\ \\ \\ \\ \end{array}\right\}\text{SYNC}\\ \left.\begin{array}[]{l}\\ \\ \end{array}\right\}\text{ILS breakings}\\ \left.\begin{array}[]{l}\\ \\ \end{array}\right\}\text{DLS breakings}\end{array}$$

(28)

The matrix $B=TAT^{T}$ is equal to:

$$B=\left[\begin{array}[]{cccc|cc|cc}2&2&\sqrt{2}&0&0&0&0&0\\ 2&0&0&0&0&0&0&0\\ \sqrt{2}&0&0&\sqrt{2}&0&0&0&0\\ 0&0&\sqrt{2}&0&0&0&0&0\\ \hline\cr 0&0&0&0&-2&0&0&0\\ 0&0&0&0&0&0&0&0\\ \hline\cr 0&0&0&0&0&0&0&\sqrt{2}\\ 0&0&0&0&0&0&\sqrt{2}&0\\ \end{array}\right]\begin{array}[]{l}\left.\begin{array}[]{l}\\ \\ \\ \\ \end{array}\right\}\text{SYNC block}\\ \left.\begin{array}[]{l}\\ \\ \end{array}\right\}\text{ILS blocks}\\ \left.\begin{array}[]{l}\\ \\ \end{array}\right\}\text{DLS block}\end{array}$$

(29)

As can be seen, the matrix $B$ is the direct sum of one SYNC block, two independent ILS blocks (corresponding to breakings in the $\alpha$ layer which are independent of the $\beta$ layer), and one DLS block (corresponding to breakings in the $\alpha$ layer and in the $\beta$ layer which are dependent on each other.) The transverse ILS and DLS blocks describe linear (local) stability of clusters, when the dynamics is linearized about the quotient network time evolution. In what follows we will pay particular attention to stability of DLS blocks, which are a specific feature of multilayer networks.

To provide analytical insight, we first consider a two-layer network described by the following discrete-time dynamics,

$$\begin{array}[]{rcl}{\bf{x}^{\alpha}}^{k+1}&=&\mbox{rem}(c^{\alpha}{\bf{x}^{\alpha}}^{k}+\sigma A^{\alpha\alpha}{\bf{x}^{\alpha}}^{k}+\sigma A^{\alpha\beta}{\bf{x}^{\beta}}^{k})\\ {\bf{x}^{\beta}}^{k+1}&=&\mbox{rem}(c^{\beta}{\bf{x}^{\beta}}^{k}+\sigma A^{\beta\beta}{\bf{x}^{\beta}}^{k}+\sigma A^{\beta\alpha}{\bf{x}^{\alpha}}^{k}),\end{array}$$

(30)

where the vectorial function $\mbox{rem}({\bf{x}})$ returns a vector whose entries are the remainder of the integer division of the entries of the vector ${\bf{x}}$ by the scalar $1$ and $c^{\alpha}$ and $c^{\beta}$ are tunable layer-specific scalar parameters.

Stability is described by the following set of equations,

$$\begin{array}[]{rcl}\delta{\bf{x}^{\alpha}}^{k+1}&=&c^{\alpha}{\delta\bf{x}^{\alpha}}^{k}+\sigma A^{\alpha\alpha}{\delta\bf{x}^{\alpha}}^{k}+\sigma A^{\alpha\beta}{\delta\bf{x}^{\beta}}^{k}\\ \delta{\bf{x}^{\beta}}^{k+1}&=&c^{\beta}{\delta\bf{x}^{\beta}}^{k}+\sigma A^{\beta\beta}{\delta\bf{x}^{\beta}}^{k}+\sigma A^{\beta\alpha}{\delta\bf{x}^{\alpha}}^{k}.\end{array}$$

(31)

We now consider a generic DLS block of the form $\begin{pmatrix}a&b\\ b&a\end{pmatrix}$ ($a=0$ and $b=\sqrt{2}$ in the DLS block of Eq. (29)), to which corresponds a perturbation of the form,

$${\text{\boldmath$\eta$}}_{{\text{DLS}}}^{k+1}=\left(\begin{matrix}c^{\alpha}+\sigma a&\sigma b\\ \sigma b&c^{\beta}+\sigma a\\ \end{matrix}\right)\text{\boldmath$\eta$}_{{\text{DLS}}}^{k},$$

(32)

with $c^{\alpha}\neq c^{\beta}$ and the case $c^{\alpha}=c^{\beta}$ corresponding to an ILS perturbation. The eigenvalues have the following expression,

$$\rho^{\pm}=\bar{c}+a\sigma\pm(b^{2}\sigma^{2}+\delta_{c}^{2})^{1/2},$$

(33)

where $\bar{c}=(c^{\beta}+c^{\alpha})/2$ is the average layer-specific parameter and $\delta_{c}=(c^{\beta}-c^{\alpha})/2$ measures how different are the systems in the two layers (with $\delta_{c}=0$ corresponding to the case of an ILS.) From this equation we see the larger (smaller) eigenvalue is an increasing (decreasing) function of $\delta_{c}$, and it follows that the best condition in terms of stability is achieved for $\delta_{c}=0$. We thus conclude that DLS perturbations are more difficult to stabilize than ILS perturbations.

We present here a conjecture expanding on the above conclusion: that DLS clusters are generally more difficult to stabilize compared to the case in which the systems in different layers are of the same type. We base this on the following reasoning. Consider an ideal situation in which at first the parameters of the systems in the different layers are identical and then they are increasingly perturbed to take on different values in different layers. The Gershgorin circle’s theorem states that each eigenvalue of a matrix lies within at least one of the Gershgorin discs centered at the entries on the main diagonal and having radius equal to the sum of the off diagonal entries. As perturbing the individual system’s parameters corresponds to varying the centers of the Gershgorin discs (but not the radius), we can expect the eigenvalues to become increasingly spread out as the systems are made increasingly different from one another, resulting in reduced stability.

The particular network in Fig. 1 has one transverse irreducible representation (DLS) in the form of Eq. (32), with $a=0$ and $b=\sqrt{2}$, corresponding to simultaneous loss of synchronization between nodes $(1,3)$ in the $\beta$ layer and between the pairs of nodes $(1,2)$ and $(3,4)$ in the $\alpha$ layer. For this multilayer network, we consider the dynamics of Eq. (30) and study the effects of changing the parameters $c^{\alpha}$ and $c^{\beta}$ on stability. For the maps described by Eq. (30), as well as in the following for other kind of systems, we measure the pairwise synchronization error, defined as,

$$E^{\alpha}_{ij}=<\|{\bf{x}}^{\alpha}_{i}-{\bf{x}}^{\alpha}_{j}\|>,$$

(34)

between nodes $i$ and $j$ in layer $\alpha=1,...,M$, where the symbol $<...>$ indicates a temporal average, computed after the transient has elapsed.

Panel a of Fig. 2 shows $E_{13}^{\alpha}$ and $E_{13}^{\beta}$ vs the parameter $\delta_{c}$. $\delta_{c}=0$ corresponds to identical systems in the two layers, increasing values of $\delta_{c}$ indicate the systems in the two layers are increasingly different. Synchronization is simultaneously lost in both layers for $\delta_{c}\gtrapprox 0.35$. Panel b is a plot of the eigenvalues $\rho^{+}$ and $\rho^{-}$ in Eq. (33) as a function of $\delta_{c}$, which shows that $\rho^{+}$ ($\rho^{-}$) increases (decreases) with $\delta_{c}$. Loss of stability occurs when either one of the two eigenvalues is either larger than $1$ or smaller than $-1$. It is thus expected that stability may be lost for increasing values of $\delta_{c}$, i.e., as the systems in the two layers become increasingly different. From Panel b of Fig. 2 we see that $\rho^{+}$ grows larger than $1$ for $\delta_{c}\gtrapprox 0.35$.

We then consider the case of Eqs. (1) with $M=2$ layers, $A^{\alpha\alpha},A^{\beta\beta},A^{\alpha\beta}=(A^{\beta\alpha})^{T}$ corresponding to the multilayer network in Fig. 1, $n^{\alpha}=n^{\beta}=2$, ${\bf x}^{\alpha}=[{x}^{\alpha},{y}^{\alpha}]$, ${\bf x}^{\beta}=[{x}^{\beta},{y}^{\beta}]$,

$${\bf F}^{\alpha}({\bf x}^{\alpha})=\left[\begin{array}[]{c}y^{\alpha}\\ -x^{\alpha}-0.2y^{\alpha}[(x^{\alpha})^{2}-c^{\alpha}]\end{array}\right],\quad\quad{\bf F}^{\beta}({\bf x}^{\beta})=\left[\begin{array}[]{c}y^{\beta}\\ -x^{\beta}-0.2y^{\beta}[(x^{\beta})^{2}-c^{\beta}]\end{array}\right],$$

(35)

which both correspond to the dynamics of the Van der Pol oscillator, with layer-dependent parameters $c^{\alpha}$ and $c^{\beta}$. Moreover, we set

$${\bf H}^{\alpha\beta}({\bf x})=\begin{pmatrix}-1&0\\ 0&0\end{pmatrix}{\bf x},$$

(36)

for all pairs $\alpha,\beta=1,2$ and $\sigma^{\alpha\beta}=0.15$ for all pairs $\alpha,\beta=1,2$. We set the layer-dependent parameters $c^{\alpha}=(1+\delta_{c})$ and $c^{\beta}=(1-\delta_{c})$, so that $\delta_{c}=0$ corresponds to identical systems in the two layers and increasing values of $\delta_{c}$ indicate the systems in the two layers are increasingly different. We then numerically investigate stability of the DLS as the parameter $\delta_{c}$ is increased. This can be seen in panel c of Fig. 2, which shows that synchronization between oscillators $1$ and $3$ from the $\alpha$ layer and synchronization between oscillators $1$ and $3$ from the $\beta$ layer is simultaneously lost for $\delta_{c}\gtrapprox 0.4$. Panel d of Fig. 2 shows the numerically computed Maximum Lyapunov exponent of the DLS block (27). We also note that throughout the whole $\delta_{c}$ interval considered, neither nodes $1$ and $2$, nor nodes $1$ and $4$ from the $\alpha$ layer ever synchronize (not shown). Overall, Fig. 2 shows that increased heterogeneity between the nodes in the two layers, can lead to loss of DLS stability. Further numerical evidence of this is presented for the cases of the Lorenz oscillator and of the Roessler oscillator in Supplementary Note 4. Supplementary Note 5 investigates how varying the intra-layer and inter-layer coupling strengths affects CS stability.

We apply the techniques from the previous sections on an experimental testbed circuit. We implement three different kinds of electronic oscillators, using widely available, affordable components that can be assembled on breadboards. Simplicity, low-cost, ease of fabrication and availability of a large volume of previous studies make electronic circuits an ideal testbed for multilayer network studies [31]. The circuit is composed of three different kinds/layers of nodes: one linear resonator, which we call the “jumper”, two FitzHugh-Nagumo (FHN) oscillators, and four Colpitts oscillators. The jumper is a linear resonator (i.e., without input, its oscillations damp to zero) with two-dimensional governing equations; the FHN is a relaxational nonlinear oscillator with two-dimensional governing equations [49]; the Colpitts is a sinusoidal nonlinear oscillator with three-dimensional governing equations [50]. All three kinds of nodes have similar uncoupled frequencies. A full schematic of the experimental circuit is included in Figure 3. Figure 3 also states the measured parameter values of each component.

Figure 4 shows a simplified multilayer schematic of the circuit with the jumper as the $\alpha$ layer, the FHNs as the $\beta$ layer, and the Colpitts as the $\gamma$ layer. We couple the different oscillators in three ways. On the Colpitts layer, we induce inductive coupling through mutual inductance, red in Fig.  4. Between the Colpitts layer and the FHN layer we introduce resistive coupling; this couples each FHN circuit with two Colpitts, blue in Fig.  4. Between the FHN and jumper layer, we induce inductive coupling between each FHN and an inductor in the jumper, orange in Fig.  4.

As shown in the above schematic and equations, we can describe the system with three layers composed as follows. Layer $\alpha$ includes the jumper alone, layer $\beta$ includes 2 FHNs and the intra-layer connections, with $\mathcal{G}^{\beta}=\{(),(1,2)\}$ and layer $\gamma$ includes 4 Colpitts and one intra-layer connection that connects nodes 1 with 2, and nodes 3 with 4. The group of symmetries of this layer is

$$\mathcal{G}^{\gamma}=\{(),(1,2),(3,4),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}.$$

(37)

We have the inter-layer connections:

$$A^{\alpha\beta}=\begin{bmatrix}1&1\end{bmatrix}=(A^{\beta\alpha})^{T},\qquad A^{\beta\gamma}=\begin{bmatrix}1&1&0&0\\ 0&0&1&1\end{bmatrix}=(A^{\gamma\beta})^{T}.$$

(38)

All the permutations in the groups $\mathcal{G}^{\alpha},\ \mathcal{G}^{\beta},\ \mathcal{G}^{\gamma}$ are compatible, then $\mathcal{H}^{\alpha}=\mathcal{G}^{\alpha}$, $\mathcal{H}^{\beta}=\mathcal{G}^{\beta}$, $\mathcal{H}^{\gamma}=\mathcal{G}^{\gamma}.$