Symmetric generalized Heckman models

Helton Saulo, Roberto Vila and Shayane S. Cordeiro
Department of Statistics, Universidade de Brasília, Brasília, Brazil

Abstract

The sample selection bias problem arises when a variable of interest is correlated with a latent variable, and involves situations in which the response variable had part of its observations censored. Heckman, (1976) proposed a sample selection model based on the bivariate normal distribution that fits both the variable of interest and the latent variable. Recently, this assumption of normality has been relaxed by more flexible models such as the Student- $t$ distribution (Marchenko and Genton,, 2012; Lachos et al.,, 2021). The aim of this work is to propose generalized Heckman sample selection models based on symmetric distributions (Fang et al.,, 1990). This is a new class of sample selection models, in which variables are added to the dispersion and correlation parameters. A Monte Carlo simulation study is performed to assess the behavior of the parameter estimation method. Two real data sets are analyzed to illustrate the proposed approach.

Keywords. Generalized Heckman models $\cdot$ Symmetric distributions $\cdot$ Variable dispersion $\cdot$ Variable correlation.

1 Introduction

It is common in the areas of economics, statistics, sociology, among others, that in the sampling process there is a relationship between a variable of interest and a latent variable, in which the former is observable only in a subset of the population under study. This problem is called sample selection bias and was studied by Heckman, (1976). The author proposed a sample selection model by joint modeling the variable of interest and the latent variable. The classical Heckman sample selection (classical Heckman-normal model) model received several criticisms, due to the need to assume bivariate normality and the difficulty in estimating the parameters using the maximum likelihood (ML) method, which led to the introduction of an alternative estimation method known as the two-step method; see Heckman, (1979). Some studies on Heckman models have been done by Nelson, (1984), Paarsch, (1984), Manning et al., (1987), Stolzenberg and Relles, (1990) and Leung and Yu, (1996). These works suggested that the Heckman sample selection model can reduce or eliminate selection bias when the assumptions hold, but deviation from normality assumption may distort the results.

The normality assumption of the classical Heckman-normal model (Heckman,, 1976) has been relaxed by more flexible models such as the Student- $t$ distribution (Marchenko and Genton,, 2012; Ding,, 2014; Lachos et al.,, 2021), the skew-normal distribution (Ogundimu and Hutton,, 2016) and the Birnbaum-Saunders distribution (Bastos and Barreto-Souza,, 2021). Moreover, the classical Heckman-normal model assumes that the dispersion and correlation (sample selection bias parameter) are constant, which may not be adequate. In this context, the present work aims to propose generalized Heckman sample selection models based on symmetric distributions (Fang et al.,, 1990). In the proposed model, covariates are added to the dispersion and correlation parameters, then we have covariates explaining possible heteroscedasticity and sample selection bias, respectively. Our proposed methodology can be seen as a generalization of the generalized Heckman-normal model with varying sample selection bias and dispersion parameters proposed by Bastos et al., (2021) and the Heckman-Student- $t$ model proposed by Marchenko and Genton, (2012). We demonstrate that the proposed symmetric generalized Heckman model outperforms the generalized Heckman-normal and Heckman-Student- $t$ models in terms of model fitting, making it a practical and useful model for modelling data with sample selection bias.

The rest of this work proceeds as follows. In Section 2, we briefly describe the bivariate symmetric distributions. We then introduce the symmetric generalized Heckman models. In this section, we also describe the maximum likelihood (ML) estimation of the model parameters. In Section 3, we derive the generalized Heckman-Student- $t$ model, which is a special case of the symmetric generalized Heckman models. In Section 4, we carry out a Monte Carlo simulation study for evaluating the performance of the estimators. In Section 5, we apply the generalized Heckman-Student- $t$ to two real data sets to demonstrate the usefulness of the proposed model, and finally in Section 6, we provide some concluding remarks.

2 Symmetric generalized Heckman models

Let $\bm{Y}=(Y_{1},Y_{2})^{\top}$ be a random vector following a bivariate symmetric (BSY) distribution (Fang et al.,, 1990) with location (mean) vector $\bm{\mu}=(\mu_{1},\mu_{2})^{\top}$ , covariance matrix

\displaystyle\bm{\Sigma}=\begin{pmatrix}\sigma_{1}^{2}&\rho\sigma_{1}\sigma_{2}\\ \rho\sigma_{1}\sigma_{2}&\sigma_{2}^{2}\end{pmatrix},

(2.1)

and density generator $g_{c}$ , with $\mu_{i}\in\mathbb{R}$ , $\sigma_{i}>0$ , for $i=1,2$ . We use the notation $\bm{Y}\sim{\rm BSY}(\bm{\mu},\bm{\Sigma},g_{c})$ . Then, the probability density function (PDF) of $\bm{Y}\sim{\rm BSY}(\bm{\mu},\bm{\Sigma},g_{c})$ is given by

f_{\bm{Y}}(\bm{y};\bm{\mu},\bm{\Sigma},g_{c})=\frac{1}{|\bm{\Sigma}|^{1/2}{Z_{g_{c}}}}\,g_{c}\left((\bm{y}-\bm{\mu})^{\top}\bm{\Sigma}^{-1}(\bm{y}-\bm{\mu})\right),\quad\bm{y}\in\mathbb{R}^{2},

(2.2)

where $|\bm{\Sigma}|=\sigma_{1}^{2}\sigma_{2}^{2}(1-\rho^{2})$ and $Z_{g_{c}}$ is a normalization constant so that $f_{\bm{Y}}$ is a PDF, that is,

\displaystyle Z_{g_{c}}=\int_{\mathbb{R}^{2}}\frac{1}{|\bm{\Sigma}|^{1/2}}\,g_{c}\left((\bm{y}-\bm{\mu})^{\top}\bm{\Sigma}^{-1}(\bm{y}-\bm{\mu})\right)\,{\rm d}\bm{y}=\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}u.

The density generator $g_{c}$ in (2.2) leads to different bivariate symmetric distributions, which may contain an extra parameter (or extra parameter vector).

We propose a generalization of the classical Heckman-normal model (Heckman,, 1976) by considering independent errors terms following a BSY distribution with regression structures for the sample selection bias ( $0<\rho<1$ ) and dispersion ( $\sigma>0$ ) parameters:

\displaystyle{Y^{*}_{i}\choose U^{*}_{i}}\sim\text{BSY}\Biggl{(}\bm{\mu}={\mu_{1i}\choose\mu_{2i}},\bm{\Sigma}=\begin{pmatrix}\sigma_{i}^{2}&\rho_{i}\sigma_{i}\\ \rho_{i}\sigma_{i}&1\end{pmatrix},g_{c}\Biggr{)},\quad i=1,\ldots,n.

(2.3)

In the above equation $\mu_{1i},\mu_{2i},\sigma_{i}$ and $\rho_{i}$ are are the mean, dispersion and correlation parameters, respectively, with the following regression structure $g_{1}(\mu_{1i})=\bm{x}_{i}^{\top}\bm{\beta}$ , $g_{2}(\mu_{2i})=\bm{w}_{i}^{\top}\bm{\gamma}$ , $h_{1}(\sigma_{i})=\bm{z}_{i}^{\top}\bm{\lambda}$ and $h_{2}(\rho_{i})=\bm{v}_{i}^{\top}\bm{\kappa}$ , where $\bm{\beta}=(\beta_{1},\ldots,\beta_{k})^{\top}\in\mathbb{R}^{k}$ , $\bm{\gamma}=(\gamma_{1},\ldots,\gamma_{l})^{\top}\in\mathbb{R}^{l}$ , $\bm{\lambda}=(\lambda_{1},\ldots,\lambda_{p})^{\top}\in\mathbb{R}^{p}$ and $\bm{\kappa}=(\kappa_{1},\ldots,\kappa_{q})^{\top}\in\mathbb{R}^{q}$ are vectors of regression coefficients, ${\bm{x_{i}}}=(x_{i1},\ldots,x_{ik})^{\top}$ , ${\bm{w_{i}}}=(w_{i1},\ldots,w_{il})^{\top}$ , ${\bm{z_{i}}}=(z_{i1},\ldots,z_{ip})^{\top}$ and ${\bm{v_{i}}}=(v_{i1},\ldots,v_{iq})^{\top}$ are the values of $k$ , $l$ , $p$ and $q$ covariates, and $k+l+p+q<n$ . The links $g_{1}(\cdot),g_{2}(\cdot),h_{1}(\cdot)$ and $h_{2}(\cdot)$ are strictly monotone and twice differentiable. The link functions $g_{1}:\mathbb{R}\rightarrow\mathbb{R}$ , $g_{2}:\mathbb{R}\rightarrow\mathbb{R}$ , $h_{1}:\mathbb{R}^{+}\rightarrow\mathbb{R}$ and $h_{2}:[-1,1]\rightarrow\mathbb{R}$ must be strictly monotone, and at least twice differentiable, with $g_{1}^{-1}(\cdot)$ , $g_{2}^{-1}(\cdot)$ , $h_{1}^{-1}(\cdot)$ , and $h_{2}^{-1}(\cdot)$ being the inverse functions of $g_{1}(\cdot)$ , $g_{2}(\cdot)$ , $h_{1}(\cdot)$ , and $h_{2}(\cdot)$ , respectively. For $g_{1}(\cdot)$ and $g_{2}(\cdot)$ the most common choice is the identity link, whereas for $h_{1}(\cdot)$ and $h_{2}(\cdot)$ the most common choices are logarithm and arctanh (inverse hyperbolic tangent) links, respectively.

We can agglutinate the information from $U_{i}^{*}$ in the following indicator function $U_{i}=\mathds{1}_{\{U_{i}^{*}>0\}}$ .

Let $Y_{i}=Y_{i}^{*}U_{i}$ be the observed outcome, for $i=1,\ldots,n$ . Only $n_{1}$ out of $n$ observations $Y_{i}^{*}$ for which $U_{i}^{*}>0$ are observed. This model is known as “Type 2 tobit model” in the econometrics literature. Notice that $U_{i}\sim{\rm Bernoulli}(\mathbb{P}(U_{i}^{*}>0))$ . By using law of total probability, for $\bm{\theta}=(\bm{\beta}^{\top},\bm{\gamma}^{\top},\sigma,\rho)^{\top}$ , the random variable $Y_{i}$ has distribution function

	$\displaystyle F_{Y_{i}}(y_{i};\bm{\theta})$	$\displaystyle=\mathbb{P}(Y_{i}\leq y_{i}\|U_{i}^{}>0)\mathbb{P}(U_{i}^{}>0)+\mathbb{P}(Y_{i}\leq y_{i}\|U_{i}^{}>0)\mathbb{P}(U_{i}^{}\leq 0)$
		$\displaystyle=\begin{cases}\mathbb{P}(Y_{i}^{}\leq y_{i}\|U_{i}^{}>0)\mathbb{P}(U_{i}^{}>0),&\text{if}\,y_{i}<0,\\[5.69046pt] \mathbb{P}(Y_{i}^{}\leq y_{i}\|U_{i}^{}>0)\mathbb{P}(U_{i}^{}>0)+\mathbb{P}(U_{i}^{*}\leq 0),&\text{if}\,y_{i}\geq 0.\end{cases}$

The function $F_{Y_{i}}$ has only one jump, at $y_{i}=0$ , and $\mathbb{P}(Y_{i}=0)=\mathbb{P}(U_{i}^{*}\leq 0)$ . Therefore, $Y_{i}$ is a random variable that is neither discrete nor absolutely continuous, but a mixture of the two types. In other words,

\displaystyle F_{Y_{i}}(y_{i};\bm{\theta})=\mathbb{P}(U_{i}^{*}\leq 0)F_{\rm d}(y_{i})+\mathbb{P}(U_{i}^{*}>0)F_{\rm ac}(y_{i}),

where $F_{\rm d}(y_{i})=\mathds{1}_{[0,+\infty)}(y_{i})$ and $F_{\rm ac}(y_{i})=\mathbb{P}(Y_{i}^{*}\leq y_{i}|U_{i}^{*}>0)$ . Hence, the PDF of $Y_{i}$ is given by

$\displaystyle f_{Y_{i}}(y_{i};\bm{\theta})$	$\displaystyle=\mathbb{P}(U_{i}^{}\leq 0)\delta_{0}(y_{i})+\mathbb{P}(U_{i}^{}>0)f_{Y_{i}^{}\|U_{i}^{}>0}(y_{i};\bm{\theta})$
	$\displaystyle=(\mathbb{P}(U_{i}^{}\leq 0))^{1-u_{i}}(\mathbb{P}(U_{i}^{}>0))^{u_{i}}(f_{Y_{i}^{}\|U_{i}^{}>0}(y_{i};\bm{\theta}))^{u_{i}}$	(2.4)
	$\displaystyle=\mathbb{P}(U_{i}=u_{i})(f_{Y_{i}^{}\|U_{i}^{}>0}(y_{i};\bm{\theta}))^{u_{i}},\quad u_{i}=0,1,$

wherein $\mathbb{P}(U_{i}=0)=1-\mathbb{P}(U_{i}=1)=\mathbb{P}(U_{i}^{*}\leq 0)$ for $i=1,\ldots,n$ , and $\delta_{0}$ is the Dirac delta function. That is, the density of $Y_{i}$ is composed of a discrete component described by the probit model $\mathbb{P}(U_{i}=u_{i})=(\mathbb{P}(U_{i}^{*}\leq 0))^{1-u_{i}}(\mathbb{P}(U_{i}^{*}>0))^{u_{i}}$ , for $u_{i}=0,1$ , and a continuous part given by the conditional PDF $f_{Y_{i}^{*}|U_{i}^{*}>0}(y_{i};\bm{\theta})$ .

2.1 Finding the conditional density of ${Y}^{}_{i}$ , given that ${U}^{}_{i}>0$

In the context of sample selection models, the interest lies in finding the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ given that $({Y}^{*}_{i},{U}^{*}_{i})^{\top}$ follows the BSY distribution (2.3); see Theorem 2.5.

Before stating and proving the main result (Theorem 2.5) of this section, throughout the paper we will adopt the following notations:

\displaystyle G_{i}(x)={\displaystyle\int_{-x}^{\infty}}{f_{Z_{2i}|Z_{1i}}\Big{(}w_{i}\,\Big{|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}}\,{\rm d}w_{i}

(2.5)

and

\displaystyle H_{i}(x)=\int_{-x}^{\infty}f_{\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}}(u_{i})\,{\rm d}u_{i},

(2.6)

where

\displaystyle Z_{1i}=RDV_{1i}\quad\text{and}\quad Z_{2i}=R\sqrt[\ ]{1-D^{2}}V_{2i}

(2.7)

have the joint PDF $f_{Z_{1i},Z_{2i}}$ and $f_{X}$ denotes the PDF corresponding to a random variable $X$ . Here, the random variables $V_{1i}$ , $V_{2i}$ , $R$ , and $D$ are mutually independent and $\mathbb{P}(V_{ki}=-1)=\mathbb{P}(V_{ki}=1)=1/2$ , $k=1,2$ . The random variable $D$ in (2.7) is positive and has PDF

\displaystyle f_{D}(d)={2\over\pi\sqrt[\ ]{1-d^{2}}},\quad d\in(0,1).

The random variable $R$ in (2.7) is positive and is called the generator of the random vector $(Y_{i}^{*},U_{i}^{*})^{\top}$ . Moreover, $R$ has PDF given by

\displaystyle f_{R}(r)={2rg_{c}(r^{2})\over\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}},\quad r>0,

where $g_{c}$ is the density generator in (2.2).

Proposition 2.1.

Let us denote $S=RD$ and $T=R\sqrt[\ ]{1-D^{2}}$ .

The PDFs of $S$ and $T$ are given by

\displaystyle f_{S}(v)=f_{T}(v)={\int_{v}^{\infty}{4g_{c}(w^{2})\over\sqrt[\ ]{1-{v^{2}\over w^{2}}}}\,{\rm d}w\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}\,,\quad v>0.

(2.8)

The PDFs of $Z_{1i}$ and $Z_{2i}$ are

\displaystyle f_{Z_{1i}}(z)=f_{Z_{2i}}(z)={\int_{z}^{\infty}{2g_{c}(w^{2})\over\sqrt[\ ]{1-{z^{2}\over w^{2}}}}\,{\rm d}w\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}\,,\quad-\infty<z<\infty.

Proof.

Using the known formula for the PDF of product of two random variables $X$ and $Y$ :

\displaystyle f_{XY}(u)=\int_{-\infty}^{\infty}{1\over|x|}\,f_{X,Y}\Big{(}x,{u\over x}\Big{)}\,{\rm d}x

the proof of (2.8) follows.

The proof of second item follows by combining the law of total probability with (2.8). ∎

Proposition 2.2.

The random vector $(Z_{1i},Z_{2i})^{\top}$ is jointly symmetric about $(0,0)$ . That is, $f_{Z_{1i},Z_{2i}}(x,y)=f_{Z_{1i},Z_{2i}}(x,-y)=f_{Z_{1i},Z_{2i}}(-x,y)=f_{Z_{1i},Z_{2i}}(-x,-y)$ .

Proof.

Let $S=RD$ and $T=R\sqrt[\ ]{1-D^{2}}$ . Since $R$ and $D$ are mutually independent, by using change of variables (Jacobian Method), the joint density of $S$ and $T$ is

\displaystyle f_{S,T}(s,t)={4g_{c}(s^{2}+t^{2})\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}},\quad s,t>0.

(2.9)

Moreover, since $V_{1i}\stackrel{{\scriptstyle d}}{{=}}V_{2i}\sim{\rm Bernoulli}(1/2)$ are mutually independent, by law of total probability we get

F_{Z_{1i},Z_{2i}}(x,y)={1\over 4}\,\big{\{}F_{S,T}(x,y)\mathds{1}_{[0,\infty)\times[0,\infty)}(x,y)+\mathbb{P}(S\geqslant-x,T\geqslant-y)\mathds{1}_{(-\infty,0)\times(-\infty,0)}(x,y)\\[5.69046pt] +\mathbb{P}(S\leqslant x,T\geqslant-y)\mathds{1}_{(0,\infty)\times(-\infty,0)}(x,y)+\mathbb{P}(S\geqslant-x,T\leqslant y)\mathds{1}_{(-\infty,0)\times(0,\infty)}(x,y)\big{\}},

(2.10)

where $F_{X,Y}(\cdot,\cdot)$ denotes the (joint) distribution function of $(X,Y)^{\top}$ . Using the following well-known identity:

\displaystyle\mathbb{P}(a_{1}<X\leqslant b_{1},a_{2}<Y\leqslant b_{2})=F_{X,Y}(b_{1},b_{2})-F_{X,Y}(b_{1},a_{2})-F_{X,Y}(a_{1},b_{2})+F_{X,Y}(a_{1},a_{2}),

we have

	$\displaystyle\mathbb{P}(S\geqslant-x,T\geqslant-y)=F_{S,T}(\infty,\infty)-F_{S,T}(\infty,-y)-F_{S,T}(-x,\infty)+F_{S,T}(-x,-y),\ x<0,y<0;$
	$\displaystyle\mathbb{P}(S\leqslant x,T\geqslant-y)=F_{S,T}(x,\infty)-F_{S,T}(x,-y)-F_{S,T}(0,\infty)+F_{S,T}(0,-y),\quad x>0,y<0;$
	$\displaystyle\mathbb{P}(S\geqslant-x,T\leqslant y)=F_{S,T}(\infty,y)-F_{S,T}(\infty,0)-F_{S,T}(-x,y)+F_{S,T}(-x,0),\quad x<0,y>0.$

By replacing the last three identities in (2.10) and then by differentiating $F_{Z_{1i},Z_{2i}}(x,y)$ with respect to $x$ and $y$ , we obtain

	$\displaystyle f_{Z_{1i},Z_{2i}}(x,y)$	$\displaystyle={1\over 4}\,\big{\{}f_{S,T}(x,y)\mathds{1}_{(0,\infty)\times(0,\infty)}(x,y)+f_{S,T}(-x,-y)\mathds{1}_{(-\infty,0)\times(-\infty,0)}(x,y)$
		$\displaystyle\quad+f_{S,T}(x,-y)\mathds{1}_{(0,\infty)\times(-\infty,0)}(x,y)+f_{S,T}(-x,y)\mathds{1}_{(-\infty,0)\times(0,\infty)}(x,y)\big{\}}$
		$\displaystyle={1\over 4}\,f_{S,T}(x,y)\mathds{1}_{\mathbb{R}\setminus\{0\}\times\mathbb{R}\setminus\{0\}}(x,y)={g_{c}(x^{2}+y^{2})\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}\mathds{1}_{\mathbb{R}\setminus\{0\}\times\mathbb{R}\setminus\{0\}}(x,y),$

where in the last line we used the Equation (2.9). Note that the function $f_{Z_{1i},Z_{2i}}$ above is not defined on the abscise or ordinate axes (neither at the origin), but this is not relevant because these events have a null probability measure. Therefore, we can say that

\displaystyle f_{Z_{1i},Z_{2i}}(x,y)={g_{c}(x^{2}+y^{2})\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}},\quad-\infty<x,y<\infty.

(2.11)

From (2.11) it is clear that the vector $(Z_{1i},Z_{2i})^{\top}$ is jointly symmetric about $(0,0)$ . ∎

Proposition 2.3.

The marginal PDFs of $Z_{1i}$ and $Z_{1i}$ , denoted by $f_{1i}$ and $f_{2i}$ , respectively, are given by

	$\displaystyle f_{{1i}}(x)={\int_{-\infty}^{\infty}g_{c}(x^{2}+y^{2})\,{\rm d}y\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}=f_{Z_{1i}}(x),\quad-\infty<x<\infty,$
	$\displaystyle f_{{2i}}(y)={\int_{-\infty}^{\infty}g_{c}(x^{2}+y^{2})\,{\rm d}x\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}=f_{Z_{2i}}(y),\quad-\infty<y<\infty,$

where $f_{Z_{1i}}$ and $f_{Z_{1i}}$ are given in Proposition 2.1.

2.

The random vector $(Z_{1i},Z_{2i})^{\top}$ is marginally symmetric about $(0,0)$ . That is, $f_{{1i}}(x)=f_{{1i}}(-x)$ and $f_{{2i}}(y)=f_{{2i}}(-y)$ .

Proof.

The proof of first item is immediate from the joint density of $(Z_{1i},Z_{2i})$ , given in (2.11), and by Proposition 2.1. The proof of the second item follows from the first one. ∎

Proposition 2.4.

The function $G_{i}$ in (2.5) satisfies the following identity:

\displaystyle G_{i}(x)=1-G_{i}(-x)={\displaystyle\int_{-\infty}^{x}}{f_{Z_{2i}|Z_{1i}}\Big{(}w_{i}\,\Big{|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}}\,{\rm d}w_{i}.

That is, $G_{i}$ is the conditional CDF of $Z_{2i}$ , given that $Z_{1i}=(y_{i}-\mu_{1i})/\sigma_{i}$ . Consequently, $G_{i}$ is a distribution symmetric about $0$ .

Proof.

The proof immediately follows by applying Proposition 2.2. ∎

We now proceed to establish the main result of this section.

Theorem 2.5.

If $({Y}^{*}_{i},{U}^{*}_{i})^{\top}\sim{\rm BSY}(\bm{\mu},\bm{\Sigma},g_{c})$ then the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ is given by

\displaystyle f_{{Y}_{i}^{*}|{U}_{i}^{*}>0}(y_{i};\bm{\theta})={1\over\sigma_{i}}\,f_{Z_{1i}}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,{G_{i}\Big{(}{1\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,\mu_{2i}+{\rho_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})\Big{)}\over H_{i}(\mu_{2i})},

(2.12)

where $G_{i}$ , $H_{i}$ and $Z_{1i}$ are given in Proposition 2.4, (2.6) and (2.7), respectively.

As a by-product of the proof we get that $\mathbb{P}(U_{i}^{*}>0)=H_{i}(\mu_{2i})$ .

Proof.

Since the random vector $(Y_{i}^{*},U_{i}^{*})^{\top}$ follows the BSY distribution (2.3), this one admits the stochastic representation (Abdous,, 2005)

\displaystyle\begin{array}[]{llcc}&Y_{i}^{*}=\sigma_{i}Z_{1i}+\mu_{1i},\\[11.38092pt] &U_{i}^{*}=\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}+\mu_{2i},\end{array}

(2.15)

where $Z_{1i}$ and $Z_{2i}$ are as in (2.7). If $Y_{i}^{*}=y_{i}$ then $Z_{1i}=(y_{i}-\mu_{1i})/\sigma_{i}$ . So, the conditional distribution of $U_{i}^{*}$ , given that $Y_{i}^{*}=y_{i}$ is the same as the distribution of

\displaystyle\rho_{i}\,\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}+\mu_{2i}\ \Big{|}\ Y_{i}^{*}=y_{i}.

Consequently, the PDF of $U_{i}^{*}$ given that $Y_{i}^{*}=y_{i}$ is given by

\displaystyle f_{U_{i}^{*}|Y_{i}^{*}}(u_{i}|y_{i})=\dfrac{f_{Z_{1i},\,Z_{2i}}\Big{(}{y_{i}-\mu_{1i}\over\sigma_{i}},{1\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,(u_{i}-\mu_{2i})-{\rho_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})\Big{)}}{\sqrt[\ ]{1-\rho_{i}^{2}}\,f_{Z_{1i}}({y_{i}-\mu_{1i}\over\sigma_{i}})}.

(2.16)

Further,

\displaystyle f_{Y_{i}^{*}}(y_{i})={1\over\sigma_{i}}\,f_{Z_{1i}}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}.

(2.17)

By using the identity

f_{{Y}_{i}^{*}|{U}_{i}^{*}>0}(y_{i};\bm{\theta})=f_{Y_{i}^{*}}(y_{i})\,\dfrac{\int_{0}^{\infty}f_{U_{i}^{*}|Y_{i}^{*}}(u_{i}|y_{i})\,{\rm d}u_{i}}{\mathbb{P}(U_{i}^{*}>0)}=f_{Y_{i}^{*}}(y_{i})\,\dfrac{\int_{0}^{\infty}f_{U_{i}^{*}|Y_{i}^{*}}(u_{i}|y_{i})\,{\rm d}u_{i}}{\int_{0}^{\infty}f_{U_{i}^{*}}(u_{i})\,{\rm d}u_{i}},

and by employing identities (2.16) and (2.17), we get

	$\displaystyle f_{{Y}_{i}^{}\|{U}_{i}^{}>0}(y_{i};\bm{\theta})$	$\displaystyle={1\over\sigma_{i}}\,f_{Z_{1i}}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,\dfrac{\displaystyle\int_{0}^{\infty}\frac{f_{Z_{1i},\,Z_{2i}}\Big{(}{y_{i}-\mu_{1i}\over\sigma_{i}},{1\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,(u_{i}-\mu_{2i})-{\rho_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})\Big{)}}{\sqrt[\ ]{1-\rho_{i}^{2}}\,f_{Z_{1i}}({y_{i}-\mu_{1i}\over\sigma_{i}})}\,{\rm d}u_{i}}{\displaystyle\int_{-\mu_{2i}}^{\infty}f_{\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}}(u_{i})\,{\rm d}u_{i}}$
		$\displaystyle={1\over\sigma_{i}}\,f_{Z_{1i}}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,\dfrac{{\displaystyle\int_{-{1\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,\mu_{2i}-{\rho_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})}^{\infty}}{f_{Z_{2i}\|Z_{1i}}(w_{i}\|{y_{i}-\mu_{1i}\over\sigma_{i}})}\,{\rm d}w_{i}}{\displaystyle\int_{-\mu_{2i}}^{\infty}f_{\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}}(u_{i})\,{\rm d}u_{i}},$

where in the last line a change of variables was used. Finally, by using the notations of $G_{i}$ and $H_{i}$ given in (2.5) and (2.6), respectively, from the above identity and from Proposition 2.4 the proof follows. ∎

Corollary 2.6 (Gaussian density generator).

If $({Y}^{*}_{i},{U}^{*}_{i})^{\top}\sim{\rm BSY}(\bm{\mu},\bm{\Sigma},g_{c})$ , where $g_{c}(x)=\exp(-x/2)$ is the density generator of the bivariate normal distribution, then the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ is given by

\displaystyle f_{{Y}_{i}^{*}|{U}_{i}^{*}>0}(y_{i};\bm{\theta})={1\over\sigma_{i}}\,\phi\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,{\Phi\Big{(}{1\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,\mu_{2i}+{\rho_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})\Big{)}\over\Phi(\mu_{2i})},

wherein $\phi$ and $\Phi$ denote the PDF and CDF of the standard normal distribution, respectively.

Proof.

If $({Y}^{*}_{i},{U}^{*}_{i})^{\top}$ follows the bivariate normal distribution then there exist independent standard normal random variables $Z_{1i}$ and $Z_{2i}$ such that a stochastic representation of type (2.15) is satisfied. Therefore, $Z_{2i}|Z_{1i}=z$ and $\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}$ are distributed according to the standard normal distribution. Hence, $G_{i}$ and $H_{i}$ , given in Proposition 2.4 and Item (2.6), respectively, are written as:

\displaystyle G_{i}(x)={\displaystyle\int_{-\infty}^{x}}{f_{Z_{2i}|Z_{1i}}\Big{(}w_{i}\,\Big{|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}}\,{\rm d}w_{i}=\mathbb{P}\Big{(}Z_{2i}\leqslant-x\,\Big{|}\,Z_{1i}={y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}=\Phi(x)

and

\displaystyle H_{i}(x)=\int_{-x}^{\infty}f_{\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}}(u_{i})\,{\rm d}u_{i}=\mathbb{P}\big{(}\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}>-x\big{)}=\Phi(x).

Applying Theorem 2.5 the proof concludes. ∎

Remark 2.7.

It is well-known that, if $(X_{1},X_{2})^{\top}$ is distributed from a bivariate Student- $t$ distribution, notation $(X_{1},X_{2})^{\top}\sim t_{\nu}(\bm{\mu},\bm{\Sigma})$ , where $\bm{\mu}=(\mu_{1},\mu_{2})\in\mathbb{R}^{2}$ and $\bm{\Sigma}$ is as in (2.1), then both the marginal and the conditional distributions of $X_{2}$ given $X_{1}$ are also univariate Student’s $t$ distributions: $X_{1}\sim t_{\nu}(\mu_{1},\sigma_{1})$ and

\displaystyle X_{2}|X_{1}=x_{1}\sim t_{\nu+1}\biggl{(}\mu_{2}+\rho\sigma_{2}\Big{(}{x_{1}-\mu_{1}\over\sigma_{1}}\Big{)},{\nu+({x_{1}-\mu_{1}\over\sigma_{1}})^{2}\over\nu+1}\,\sigma_{2}^{2}(1-\rho^{2})\biggr{)}.

The above statement is equivalent to

\displaystyle\sqrt[\ ]{\nu+1\over(\nu+r^{2})(1-\rho^{2})}\,\Big{(}{X_{2}-\mu_{2}\over\sigma_{2}}-\rho r\Big{)}\,\bigg{|}{X_{1}-\mu_{1}\over\sigma_{1}}=r\sim t_{\nu+1}(0,1)\equiv t_{\nu+1}.

Corollary 2.8 (Student- $t$ density generator).

If $({Y}^{*}_{i},{U}^{*}_{i})^{\top}\sim{\rm BSY}(\bm{\mu},\bm{\Sigma},g_{c})$ , where $g_{c}(x)=(1+x/\nu)^{-(\nu+2)/2}$ is the density generator of the bivariate Student- $t$ distribution with $\nu$ degrees of freedom, then the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ is given by

\displaystyle f_{{Y}_{i}^{*}|{U}_{i}^{*}>0}(y_{i};\bm{\theta})={1\over\sigma_{i}}\,f_{\nu}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,{F_{\nu+1}\Big{(}\sqrt[\ ]{{\nu+1\over\nu+({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}}}\ \big{[}{1\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,\mu_{2i}+{\rho_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})\big{]}\Big{)}\over F_{\nu}(\mu_{2i})},

wherein $f_{\nu}$ and $F_{\nu}$ denote the PDF and CDF of a classic Student- $t$ distribution with $\nu$ degrees of freedom, respectively.

Proof.

It is well-known that the vector $({Y}^{*}_{i},{U}^{*}_{i})^{\top}$ following a bivariate Student- $t$ distribution has the stochastic representation; see Subsection 9.2.6, p. 354 of Balakrishnan and Lai, (2009):

\displaystyle\begin{array}[]{llcc}&Y_{i}^{*}=\sigma_{i}Z_{1i}+\mu_{1i},\\[11.38092pt] &U_{i}^{*}=\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}+\mu_{2i},\end{array}

(2.20)

where $Z_{1i}=\sqrt[\ ]{\nu}\widetilde{Z}_{1i}/\sqrt[\ ]{Q}$ and $Z_{2i}=\sqrt[\ ]{\nu}\widetilde{Z}_{2i}/\sqrt[\ ]{Q}$ are Student- $t$ random variables, wherein $Q\sim\chi^{2}_{\nu}$ (chi-square with $\nu$ degrees of freedom) is independent of $\widetilde{Z}_{1i}$ and $\rho_{i}\widetilde{Z}_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,\widetilde{Z}_{2i}$ , and $\widetilde{Z}_{1i}\stackrel{{\scriptstyle d}}{{=}}\widetilde{Z}_{2i}\sim N(0,1)$ are independent.

When $({Y}^{*}_{i}-\mu_{1i})/\sigma_{i}=r$ , from Remark 2.7 we have

\displaystyle\sqrt[\ ]{\nu+1\over(\nu+r^{2})(1-\rho_{i}^{2})}\,({U}^{*}_{i}-\mu_{2i}-\rho_{i}r)\,\bigg{|}{Y_{i}^{*}-\mu_{1i}\over\sigma_{i}}=r\sim t_{\nu+1}.

Hence,

\displaystyle F_{\nu+1}(w)=\mathbb{P}\left(\sqrt[\ ]{{\nu+1\over(\nu+r^{2})(1-\rho_{i}^{2})}}\,({U}^{*}_{i}-\mu_{2i}-\rho_{i}r)\leqslant w\,\Bigg{|}\,{{Y}^{*}_{i}-\mu_{1i}\over\sigma_{i}}=r\right),\quad-\infty<w<\infty.

By using the representation (2.20), a simple algebraic manipulation shows that the right-hand of the above probability is

\displaystyle=\mathbb{P}\left(Z_{2i}\leqslant{w\over\sqrt[\ ]{{\nu+1\over\nu+r^{2}}}}\,\Bigg{|}\,Z_{1i}=r\right).

Setting $w=-\sqrt[\ ]{{(\nu+1)/(\nu+r^{2})}}x$ and $r={(y_{i}-\mu_{1i})/\sigma_{i}}$ we obtain

\displaystyle\mathbb{P}\Big{(}Z_{2i}\leqslant-x\,\Big{|}\,Z_{1i}={y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}=F_{\nu+1}\left(\sqrt[\ ]{{\nu+1\over\nu+({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}}}\ x\right).

Therefore, the function $G_{i}$ , given in Proposition 2.4, is

	$\displaystyle G_{i}(x)={\displaystyle\int_{-\infty}^{x}}{f_{Z_{2i}\|Z_{1i}}\Big{(}w_{i}\,\Big{\|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}}\,{\rm d}w_{i}$	$\displaystyle=\mathbb{P}\Big{(}Z_{2i}\leqslant-x\,\Big{\|}\,Z_{1i}={y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}$
		$\displaystyle=F_{\nu+1}\left(\sqrt[\ ]{{\nu+1\over\nu+({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}}}\ x\right).$

On the other hand, note that $\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}=\sqrt[\ ]{\nu}(\rho_{i}\widetilde{Z}_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,\widetilde{Z}_{2i})/\sqrt[\ ]{Q}$ is distributed according to the a Student- $t$ distribution with $\nu$ degrees of freedom because $\rho_{i}\widetilde{Z}_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,\widetilde{Z}_{2i}\sim N(0,1)$ . Then

\displaystyle H_{i}(x)=\int_{-x}^{\infty}f_{\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}}(u_{i})\,{\rm d}u_{i}=\mathbb{P}\big{(}\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}>-x\big{)}=F_{\nu}(x).

Applying Theorem 2.5 the proof follows. ∎

Given the density generator $g_{c}$ we can directly determine the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ as follows.

Corollary 2.9.

If $({Y}^{*}_{i},{U}^{*}_{i})^{\top}\sim{\rm BSY}(\bm{\mu},\bm{\Sigma},g_{c})$ then the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ is given by

\displaystyle f_{{Y}_{i}^{*}|{U}_{i}^{*}>0}(y_{i};\bm{\theta})={\rho_{i}\sqrt[\ ]{1-\rho_{i}^{2}}\over\sigma_{i}}\,{{{\int_{-\infty}^{z_{i}}g_{c}(({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}+w_{i}^{2})\,{\rm d}w_{i}}}\over\int_{-\mu_{2i}}^{\infty}\big{\{}\int_{-\infty}^{\infty}{g_{c}\big{(}({x\over\rho_{i}})^{2}+\big{(}{u_{i}-x\over\sqrt[\ ]{1-\rho_{i}^{2}}}\big{)}^{2}\big{)}}\,{\rm d}x\big{\}}\,{\rm d}u_{i}},

where $z_{i}=\mu_{2i}/\sqrt[\ ]{1-\rho_{i}^{2}}+{\rho_{i}}\,({y_{i}-\mu_{1i}\over\sigma_{i}})/\sqrt[\ ]{1-\rho_{i}^{2}}$ .

Proof.

By using the known formula for the PDF of sum of two random variables $X$ and $Y$ :

\displaystyle f_{X+Y}(z)=\int_{-\infty}^{\infty}f_{X,Y}(x,z-x)\,{\rm d}x,

we have that $H_{i}$ , defined in (2.6), can be written as

\displaystyle H_{i}(x)={1\over\rho_{i}\sqrt[\ ]{1-\rho_{i}^{2}}}{\int_{-x}^{\infty}\big{\{}\int_{-\infty}^{\infty}{g_{c}\big{(}({\zeta\over\rho_{i}})^{2}+\big{(}{u_{i}-\zeta\over\sqrt[\ ]{1-\rho_{i}^{2}}}\big{)}^{2}\big{)}}\,{\rm d}\zeta\big{\}}\,{\rm d}u_{i}\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}.

Proposition 2.3 provides

\displaystyle f_{Z_{1i}}\Big{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\Big{)}={\int_{-\infty}^{\infty}g_{c}(({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}+y^{2})\,{\rm d}y\over\pi\int_{0}^{\infty}g_{c}(u)\,{\rm d}{u}}.

(2.21)

By combining Proposition 2.4, Equations (2.11) and (2.21), we have

\displaystyle G_{i}(x)={\int_{-\infty}^{x}{f_{Z_{1i},Z_{2i}}({y_{i}-\mu_{1i}\over\sigma_{i}},w_{i})}\,{\rm d}w_{i}\over f_{Z_{1i}}({y_{i}-\mu_{1i}\over\sigma_{i}})}={\int_{-\infty}^{x}g_{c}(({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}+w_{i}^{2})\,{\rm d}w_{i}\over{\int_{-\infty}^{\infty}g_{c}(({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}+y^{2})\,{\rm d}y}}.

Substituting the above formulas of $H_{i}$ , $f_{Z_{1i}}$ and $G_{i}$ into Theorem 2.5, we complete the proof. ∎

2.2 Maximum likelihood estimation

By combining Equation (2) with Theorem 2.5, the following formula for the PDF of $Y_{i}$ is valid:

\displaystyle f_{Y_{i}}(y_{i};\bm{\theta})

\displaystyle=(1-H_{i}(\mu_{2i}))^{1-u_{i}}(H_{i}(\mu_{2i}))^{u_{i}}\Biggl{[}{1\over\sigma_{i}}\,f_{Z_{1i}}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,{G_{i}\big{(}\tau_{i}+\alpha_{i}({y_{i}-\mu_{1i}\over\sigma_{i}})\big{)}\over H_{i}(\mu_{2i})}\Biggr{]}^{u_{i}},

where $\alpha_{i}=\rho_{i}/\sqrt[\ ]{1-\rho_{i}^{2}}$ , $\tau_{i}=\mu_{2i}/\sqrt[\ ]{1-\rho_{i}^{2}}$ , $u_{i}=1$ if $u_{i}^{*}>0$ and $u_{i}=0$ otherwise, $g_{1}(\mu_{1i})=\bm{x}_{i}^{\top}\bm{\beta}$ , $g_{2}(\mu_{2i})=\bm{w}_{i}^{\top}\bm{\gamma}$ , $h_{1}(\sigma_{i})=\bm{z}_{i}^{\top}\bm{\lambda}$ and $h_{2}(\rho_{i})=\bm{v}_{i}^{\top}\bm{\kappa}$ .

The log-likelihood of the symmetric generalized Heckman model for $\bm{\theta}=(\bm{\beta}^{\top},\bm{\gamma}^{\top},\bm{\lambda}^{\top},\bm{\kappa}^{\top})^{\top}$ is given by

$\displaystyle\ell(\bm{\theta})$	$\displaystyle=\sum_{i=1}^{n}\log f_{Y_{i}}(y_{i};\bm{\theta})$
	$\displaystyle=\sum_{i=1}^{n}u_{i}\biggl{[}-\log(\sigma_{i})+\log f_{Z_{1i}}\left(\frac{y_{i}-\mu_{1i}}{\sigma_{i}}\right)+\log{G_{i}\left(\tau_{i}+\alpha_{i}\left(\frac{y_{i}-\mu_{1i}}{\sigma_{i}}\right)\right)}\biggr{]}$
	$\displaystyle+\sum_{i=1}^{n}(1-u_{i})\log(1-H_{i}(\mu_{2i})).$	(2.22)

To obtain the ML estimate of $\bm{\theta}$ , we maximize the log-likelihood function (2.2) by equating the score vector $\dot{\ell}(\bm{\theta})$ to zero, providing the likelihood equations. They are solved by means of an iterative procedure for non-linear optimization, such as the Broyden-Fletcher-Goldfarb-Shanno (BFGS) quasi-Newton method.

The likelihood equations are given by

	$\displaystyle 0={\partial\ell(\bm{\theta})\over\partial\beta_{j}}$	$\displaystyle=\sum_{i=1}^{n}{u_{i}\over\sigma_{i}}\Biggl{[}-{f^{\prime}_{Z_{1i}}(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})\over f_{Z_{1i}}(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})}-\frac{\alpha_{i}f_{Z_{2i}\|Z_{1i}}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\,\big{\|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\big{)}}{G_{i}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\big{)}}\Biggr{]}{\partial\mu_{1i}\over\partial\beta_{j}};$
	$\displaystyle 0={\partial\ell(\bm{\theta})\over\partial\gamma_{r}}$	$\displaystyle=\sum_{i=1}^{n}\left[{u_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,{f_{Z_{2i}\|Z_{1i}}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\,\big{\|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\big{)}\over G_{i}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\big{)}}+{f_{\rho_{i}Z_{1i}+\sqrt[\ ]{1-\rho_{i}^{2}}\,Z_{2i}}(-\mu_{2i})\over 1-H_{i}(\mu_{2i})}\right]{\partial\mu_{2i}\over\partial\gamma_{r}};$
	$\displaystyle 0={\partial\ell(\bm{\theta})\over\partial\lambda_{s}}$	$\displaystyle=\sum_{i=1}^{n}{u_{i}\over\sigma_{i}}\Biggl{[}-1-{(y_{i}-\mu_{1i})\over\sigma_{i}}\,{f^{\prime}_{Z_{1i}}(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})\over f_{Z_{1i}}(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})}-\alpha_{i}\,\frac{(y_{i}-\mu_{1i})}{\sigma_{i}}\,\frac{f_{Z_{2i}\|Z_{1i}}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\,\big{\|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\big{)}}{G_{i}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\big{)}}\Biggr{]}{\partial\sigma_{i}\over\partial\lambda_{s}};$
	$\displaystyle 0={\partial\ell(\bm{\theta})\over\partial\kappa_{m}}$	$\displaystyle=\sum_{i=1}^{n}{u_{i}\over\sqrt[\ ]{1-\rho_{i}^{2}}}\,\Biggl{[}{({y_{i}-\mu_{1i}\over\sigma_{i}})\over 1-\rho_{i}^{2}}-\mu_{2i}\rho_{i}\Biggr{]}\frac{f_{Z_{2i}\|Z_{1i}}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\,\big{\|}\,{y_{i}-\mu_{1i}\over\sigma_{i}}\big{)}}{G_{i}\big{(}\alpha_{i}\,(\frac{y_{i}-\mu_{1i}}{\sigma_{i}})+\tau_{i}\big{)}}\,{\partial\rho_{i}\over\partial\kappa_{m}};$

where

	$\displaystyle{\partial\mu_{1i}\over\partial\beta_{j}}$	$\displaystyle={x_{ij}\over g_{1}^{\prime}(\mu_{1i})},\quad j=1,\ldots,k;\ i=1,\ldots,n;$
	$\displaystyle{\partial\mu_{2i}\over\partial\gamma_{r}}$	$\displaystyle={w_{ir}\over g_{2}^{\prime}(\mu_{2i})},\quad r=1,\ldots,l;\ i=1,\ldots,n;$
	$\displaystyle{\partial\sigma_{i}\over\partial\lambda_{s}}$	$\displaystyle={z_{is}\over h_{1}^{\prime}(\sigma_{i})},\quad s=1,\ldots,p;\ i=1,\ldots,n;$
	$\displaystyle{\partial\rho_{i}\over\partial\kappa_{m}}$	$\displaystyle={v_{im}\over h_{2}^{\prime}(\rho_{i})},\quad m=1,\ldots,q;\ i=1,\ldots,n.$

3 Generalized Heckman-Student- $t$ model

The generalized Heckman-normal model proposed by Bastos et al., (2021) is a special case of (2.3) when the underlying distribution is bivariate normal. In this work, we focus on the generalized Heckman- $t$ model, which is based on the bivariate Student- $t$ (B $t$ ) distribution. This distribution is a good alternative in the symmetric family of distributions because it possesses has heavier tails than the bivariate normal distribution. From (2.2), if $\bm{Y}=(Y_{1},Y_{2})^{\top}$ follows a B $t$ distribution, then the associated PDF is given by

\displaystyle f(\bm{y};\bm{\mu};\bm{\Sigma},\nu)={\frac{1}{|\bm{\Sigma}|^{1/2}Z_{g_{c}}}}\left\{1+\frac{(\bm{y}-\bm{\mu})^{\top}\bm{\Sigma}^{-1}(\bm{y}-\bm{\mu})}{\nu}\right\}^{-(\nu+2)/2},

(3.1)

where $\nu$ is the number of degrees of freedom. Here, the density generator of the B $t$ distribution is given by $g_{c}(x)=(1+x/\nu)^{-(\nu+2)/2}$ , $|\bm{\Sigma}|=\sigma_{i}^{2}(1-\rho_{i}^{2})$ and $Z_{g_{c}}=[\nu\pi\Gamma(\nu/2)]/\Gamma((\nu+2)/2)$ is a normalization constant. Therefore, if $({Y}^{*}_{i},{U}^{*}_{i})$ follow a B $t$ distribution, then, by Corollary 2.8, the PDF of ${Y}^{*}_{i}|{U}^{*}_{i}>0$ is written as

\displaystyle f_{{Y}_{i}^{*}|{U}_{i}^{*}>0}(y_{i};\mu_{1i},\sigma^{2}_{i},\alpha_{i},\tau_{i},\nu)={1\over\sigma_{i}}\,f_{\nu}\biggl{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\biggr{)}\,\frac{F_{\nu+1}\Big{(}\sqrt[\ ]{{\nu+1\over\nu+({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}}}\ \big{(}\tau_{i}+\alpha_{i}({y_{i}-\mu_{1i}\over\sigma_{i}})\big{)}\Big{)}}{F_{\nu}\big{(}\tau_{i}/\sqrt[\ ]{1+\alpha_{i}^{2}}\,\big{)}},

where $f_{\nu}$ and $F_{\nu}$ are the PDF and CDF, respectively, of a univariate Student- $t$ distribution with $\nu$ degrees of freedom, $\alpha_{i}=\rho_{i}/\sqrt[\ ]{1-\rho_{i}^{2}}$ and $\tau_{i}=\mu_{2i}/\sqrt[\ ]{1-\rho_{i}^{2}}$ . The log-likelihood for $\bm{\theta}=(\bm{\beta}^{\top},\bm{\gamma}^{\top},\bm{\lambda}^{\top},\bm{\kappa}^{\top},\nu)^{\top}$ is given by

$\displaystyle\ell(\bm{\theta})$	$\displaystyle=\sum_{i=1}^{n}\log f_{Y_{i}}(y_{i};\bm{\theta})$
	$\displaystyle=\sum_{i=1}^{n}\log\left\{(F_{\nu}(-\mu_{2i}))^{1-u_{i}}(F_{\nu}(\mu_{2i}))^{u_{i}}(f_{{Y}_{i}^{}\|{U}_{i}^{}>0}(y_{i};\mu_{1i},\sigma^{2}_{i},\alpha_{i},\tau_{i},\nu))^{u_{i}}\right\}$
	$\displaystyle=\sum_{i=1}^{n}u_{i}\left[-\log(\sigma_{i})+\log f_{\nu}\left(\frac{y_{i}-\mu_{1i}}{\sigma_{i}}\right)+\log F_{\nu+1}\left(\sqrt[\ ]{{\nu+1\over\nu+({y_{i}-\mu_{1i}\over\sigma_{i}})^{2}}}\ \big{(}\tau_{i}+\alpha_{i}\big{(}{y_{i}-\mu_{1i}\over\sigma_{i}}\big{)}\big{)}\right)\right]$
	$\displaystyle+\sum_{i=1}^{n}(1-u_{i})\log F_{\nu}(-\mu_{2i}),$	(3.2)

where $u_{i}=1$ if $u_{i}^{*}>0$ and $u_{i}=0$ otherwise, $\mu_{1i}$ , $\mu_{2i}$ , $\sigma_{i}$ and $\rho_{i}$ are as in (2.3). The ML estimate of $\bm{\theta}$ is obtained by maximizing the log-likelihood function (3), that is, by equating the score vector $\dot{\ell}(\bm{\theta})$ (given in Subsection 2.2) to zero, providing the likelihood equations. They are solved using an iterative procedure for non-linear optimization, such as the BFGS quasi-Newton method.

4 Monte Carlo simulation

In this section, we carry out Monte Carlo simulation studies to evaluate the performance of the ML estimators under the symmetric generalized Heckman model. We focus on the generalized Heckman- $t$ model and consider three different set of true parameter value, which leads to scenarios covering moderate to high censoring percentages. The studies consider simulated data generated from each scenario according to

\mu_{1i}=\beta_{1}+\beta_{2}x_{1i}+\beta_{3}x_{2i},

(4.1)

\mu_{2i}=\gamma_{1}+\gamma_{2}x_{1i}+\gamma_{3}x_{2i}+\gamma_{4}x_{3i},

(4.2)

\log\sigma_{i}=\lambda_{1}+\lambda_{2}x_{1i},

(4.3)

\text{arctanh}\,\rho_{i}=\kappa_{1}+\kappa_{2}x_{1i},

(4.4)

for $i=1,\ldots,n$ , $x_{1i}$ , $x_{2i}$ and $x_{3i}$ are covariates obtained from a normal distribution in the interval (0,1). Moreover, the simulation scenarios consider sample size $n\in\{500,1000,2000\}$ and $\nu=4$ , with $\text{NREP}=1000$ Monte Carlo replicates for each sample size. In the structure presented in (4.1) - (4.4), $\mu_{1i}$ is the primary interest equation, while $\mu_{2i}$ represents the selection equation. The R software has been used to do all numerical calculations; see R Core Team, (2022).

The performance of the ML estimators are evaluated through the bias and mean squared error (MSE), computed from the Monte Carlo replicas as

\widehat{\textrm{Bias}}(\widehat{\theta})=\frac{1}{\text{NREP}}\sum_{i=1}^{\text{NREP}}\widehat{\theta}^{(i)}-\theta\quad\text{and}\quad\widehat{\mathrm{MSE}}(\widehat{\theta})=\frac{1}{\text{NREP}}\sum_{i=1}^{\text{NREP}}(\widehat{\theta}^{(i)}-\theta)^{2},

(4.5)

where $\theta$ and $\widehat{\theta}^{(i)}$ are the true parameter value and its respective $i$ -th ML estimate, and NREP is the number of Monte Carlo replicas.

We consider the following sets of true parameter values for the regression structure in (4.1)-(4.4):

•

Scenario 1) $\bm{\beta}=(1.1,0.7,0.1)^{\top}$ , $\bm{\gamma}=(0.9,0.5,1.1,0.6)^{\top}$ , and $\bm{\lambda}=(-0.4,0.7)^{\top}$ and $\bm{\kappa}=(0.3,0.5)^{\top}$ .
•

Scenario 2) $\bm{\beta}=(1.0,0.7,1.1)^{\top}$ , $\bm{\gamma}=(0.9,0.5,1.1,0.6)^{\top}$ , $\bm{\lambda}=(-0.2,1.2)^{\top}$ , and $\bm{\kappa}=(0.7,0.3)^{\top}$ or $\bm{\kappa}=(-0.7,0.3)^{\top}$ .
•

Scenario 3) $\bm{\beta}=(1.1,0.7,0.1)^{\top}$ , $\bm{\gamma}=(0,0.5,1.1,0.6)^{\top}$ , $\bm{\lambda}=(-0.4,1.2)^{\top}$ , and $\bm{\kappa}=(-0.3,-0.3)^{\top}$ (moderate correlation) or $\bm{\kappa}=(-0.7,-0.7)^{\top}$ (strong correlation).

To keep the censoring proportion around 50%, in Scenario 1 a threshold greater than zero was used, so $U_{i}^{*}>a$ . According to Bastos et al., (2021), in general the value of $a$ is zero, as any other value would be absorbed by the intercept, so considering another value does not cause problems for the model. In Scenario 2, the dispersion and correlation parameters were changed and the censoring proportion was maintained around 30%. In Scenario 3, the censoring rate around 50% was obtained by changing the parameters of the selection equation $\mu_{2i}$ .

The ML estimation results for the Scenarios 1), 2) and 3) are presented in Tables 1-3, respectively, wherein the bias and MSE are all reported. As the ML estimators are consistent and asymptotically normally distributed, we expect the bias and MSE to approach zero as $n$ grows. Moreover, we expect that the performances of the estimates deteriorate as the censoring proportion (%) grows. A look at the results in Tables 1-3 allows us to conclude that, as the sample size increases, the bias and MSE both decrease, as expected. In addition, the performances of the estimates decrease when the censoring proportion increases.

Table 1: Bias and MSE for the indicated ML estimates of the generalized Heckman-

t

model parameters (Scenario 1).

			Generalized Heckman- $t$			Generalized Heckman- $t$
Parameters	n	Censoring	Bias	MSE	Censoring	Bias	MSE
$\beta_{1}$ 1.1	500	30.8878	0.0034	0.0053	54.0284	0.0082	0.0148
	1000	30.9352	0.0019	0.0025	53.421	0.0016	0.0060
	2000	31.0035	0.0021	0.0011	52.8706	0.0058	0.0030
$\beta_{2}$ 0.7	500	30.8878	0.0037	0.0014	54.0284	0.0060	0.0034
	1000	30.9352	0.0020	0.0007	53.421	0.0033	0.0013
	2000	31.0035	0.0016	0.0003	52.8706	0.0020	0.0005
$\beta_{3}$ 0.1	500	30.8878	0.0009	0.002	54.0284	-0.0014	0.0045
	1000	30.9352	-0.0003	0.0008	53.421	0.0003	0.0017
	2000	31.0035	0.0008	0.0004	52.8706	-0.0022	0.0008
$\gamma_{1}$ 0.9	500	30.8878	0.0163	0.0137	54.0284	-1.0167	1.0443
	1000	30.9352	0.0055	0.0065	53.421	-1.0095	1.0246
	2000	31.0035	-0.0008	0.0032	52.8706	-0.9981	0.9980
$\gamma_{2}$ 0.5	500	30.8878	0.0066	0.0091	54.0284	0.0071	0.0077
	1000	30.9352	0.0064	0.0044	53.421	0.0026	0.0039
	2000	31.0035	0.0025	0.0021	52.8706	0.0021	0.0019
$\gamma_{3}$ 1.1	500	30.8878	0.0177	0.0194	54.0284	0.0131	0.0170
	1000	30.9352	0.0081	0.0085	53.421	0.0090	0.0074
	2000	31.0035	0.0032	0.0041	52.8706	0.0044	0.0038
$\gamma_{4}$ 0.6	500	30.8878	0.0091	0.0110	54.0284	0.0076	0.0089
	1000	30.9352	0.0081	0.0085	53.421	0.0043	0.0045
	2000	31.0035	0.0028	0.0026	52.8706	0.0020	0.0020
$\kappa_{1}$ 0.3	500	30.8878	0.0139	0.0564	54.0284	0.0034	0.0467
	1000	30.9352	0.0048	0.0048	53.421	0.0080	0.0207
	2000	31.0035	-0.0005	0.0102	52.8706	-0.0029	0.0097
$\kappa_{2}$ 0.5	500	30.8878	0.0589	0.0554	54.0284	0.0416	0.0383
	1000	30.9352	0.0054	0.0225	53.421	0.0202	0.0157
	2000	31.0035	0.0120	0.0083	52.8706	0.0136	0.0064
$\lambda_{1}$ -0.4	500	30.8878	0.0011	0.0049	54.0284	-0.0029	0.0075
	1000	30.9352	0.0210	0.018	53.421	0.0009	0.0035
	2000	31.0035	0.0018	0.0011	52.8706	-0.0014	0.0018
$\lambda_{2}$ 0.7	500	30.8878	0.0017	0.0031	54.0284	0.0037	0.0046
	1000	30.9352	0.0006	0.0023	53.421	0.0026	0.0021
	2000	31.0035	0.0007	0.0007	52.8706	0.0006	0.0010
$\nu$ 4	500	30.8878	0.3633	2.3387	54.0284	0.6463	8.4442
	1000	30.9352	0.1506	0.5565	53.421	0.2221	0.8141
	2000	31.0035	0.0833	0.2377	52.8706	0.0820	0.3078

Table 2: Bias and MSE for the indicated ML estimates of the generalized Heckman-

t

model parameters (Scenario 2).

n	Parameters	Censoring	Bias	MSE	Parameters	Censoring	Bias	MSE
			Generalized Heckman- $t$				Generalized Heckman- $t$
500	$\beta_{1}$ 1.0	31.017	0.0048	0.0045	$\beta_{1}$ 1.0	30.9268	0.0052	0.0039
1000		30.9395	0.0031	0.0022		30.8644	-0.0002	0.0016
2000		30.9098	0.0013	0.0009		30.9734	0.0005	0.0009
500	$\beta_{2}$ 0.7	31.017	0.0013	0.0009	$\beta_{2}$ 0.7	30.9268	0.0045	0.0008
1000		30.9395	-0.0002	0.0046		30.8644	0.0010	0.0003
2000		30.9098	0.0002	0.0001		30.9734	0.0006	0.0001
500	$\beta_{3}$ 1.1	31.017	-0.001	0.0011	$\beta_{3}$ 1.1	30.9268	0.0001	0.0007
1000		30.9395	0.0015	0.0008		30.8644	0.0009	0.0003
2000		30.9098	-0.0007	0.0002		30.9734	0.0003	0.0001
500	$\gamma_{1}$ 0.9	31.017	0.0071	0.0141	$\gamma_{1}$ 0.9	30.9268	0.0108	0.0153
1000		30.9395	0.0165	0.0814		30.8644	0.0205	0.0555
2000		30.9098	0.0036	0.0031		30.9734	0.0027	0.0034
500	$\gamma_{2}$ 0.5	31.017	0.0072	0.0090	$\gamma_{2}$ 0.5	30.9268	0.0111	0.0096
1000		30.9395	0.0076	0.0101		30.8644	0.0115	0.0270
2000		30.9098	-0.0005	0.0020		30.9734	0.0016	0.0035
500	$\gamma_{3}$ 1.1	31.017	0.013 0	0.0180	$\gamma_{3}$ 1.1	30.9268	0.0143	0.0175
1000		30.9395	0.0151	0.0254		30.8644	0.0170	0.0450
2000		30.9098	0.0020	0.0041		30.9734	0.0028	0.0051
500	$\gamma_{4}$ 0.6	31.017	0.0067	0.0102	$\gamma_{4}$ 0.6	30.9268	-0.0003	0.0094
1000		30.9395	0.0064	0.0195		30.8644	0.0077	0.0139
2000		30.9098	0.001	0.0023		30.9734	0.0023	0.0024
500	$\kappa_{1}$ 0.7	31.017	0.0299	0.0560	$\kappa_{1}$ -0.7	30.9268	-0.0449	0.0662
1000		30.9395	0.0197	0.0628		30.8644	-0.0198	0.033
2000		30.9098	0.0031	0.0089		30.9734	-0.0058	0.0218
500	$\kappa_{2}$ 0.3	31.017	0.052	0.0702	$\kappa_{2}$ 0.3	30.9268	0.0363	0.067
1000		30.9395	0.0197	0.0576		30.8644	0.0141	0.0632
2000		30.9098	0.0097	0.0097		30.9734	0.0108	0.0345
500	$\lambda_{1}$ -0.2	31.017	0.0004	0.0053	$\lambda_{1}$ -0.2	30.9268	0.0043	0.0054
1000		30.9395	-0.0018	0.0041		30.8644	-0.0031	0.0039
2000		30.9098	0.0019	0.0012		30.9734	-0.0004	0.0013
500	$\lambda_{2}$ 1.2	31.017	0.0032	0.0038	$\lambda_{2}$ 1.2	30.9268	0.0096	0.0035
1000		30.9395	0.0018	0.0020		30.8644	0.0058	0.0016
2000		30.9098	-0.0001	0.0007		30.9734	0.0024	0.0010
500	$\nu$ 4	31.017	0.4404	2.3837	$\nu$ 4	30.9268	0.5096	17.9132
1000		30.9395	0.1418	0.6321		30.8644	0.1619	0.6922
2000		30.9098	0.1234	0.2899		30.9734	0.0789	0.2731

Table 3: Bias and MSE for the indicated ML estimates of the generalized Heckman-

t

model parameters (Scenario 3).

n	Parameters	Censoring	Bias	MSE	Parameters	Censoring	Bias	MSE
			Generalized Heckman- $t$				Generalized Heckman- $t$
500	$\beta_{1}$ 1.1	49.8604	-0.0037	0.0094	$\beta_{1}$ 1.1	49.9824	-0.0109	0.0072
1000		49.9469	-0.0008	0.0035		49.9075	-0.0049	0.003
2000		50.0265	-0.0012	0.0017		49.925	-0.0046	0.0011
500	$\beta_{2}$ 0.7	49.8604	-0.0025	0.0016	$\beta_{2}$ 0.7	49.9824	-0.0057	0.0014
1000		49.9469	-0.0006	0.0005		49.9075	-0.0026	0.0005
2000		50.0265	-0.0009	0.0002		49.925	-0.0025	0.0002
500	$\beta_{3}$ 0.1	49.8604	0.0001	0.0014	$\beta_{3}$ 0.1	49.9824	0.0017	0.0011
1000		49.9469	¡0.0001	0.0005		49.9075	0.0004	0.0004
2000		50.0265	0.0005	0.0002		49.925	-0.0002	0.0002
500	$\gamma_{1}$ 0	49.8604	0.0025	0.0065	$\gamma_{1}$ 0	49.9824	0.0012	0.0063
1000		49.9469	0.0036	0.003		49.9075	0.0029	0.004
2000		50.0265	-0.0023	0.0015		49.925	0.0022	0.0014
500	$\gamma_{2}$ 0.5	49.8604	0.0067	0.0078	$\gamma_{2}$ 0.5	49.9824	0.0051	0.0071
1000		49.9469	0.0061	0.0035		49.9075	0.0036	0.0051
2000		50.0265	0.0009	0.0019		49.925	0.0003	0.0015
500	$\gamma_{3}$ 1.1	49.8604	0.009	0.0161	$\gamma_{3}$ 1.1	49.9824	0.0095	0.0155
1000		49.9469	0.0047	0.008		49.9075	0.0116	0.0185
2000		50.0265	0.0024	0.0037		49.925	0.0046	0.0035
500	$\gamma_{4}$ 0.6	49.8604	0.0010	0.0091	$\gamma_{4}$ 0.6	49.9824	0.0048	0.0083
1000		49.9469	0.0014	0.0042		49.9075	0.0056	0.0086
2000		50.0265	-0.001	0.0023		49.925	0.0038	0.002
500	$\kappa_{1}$ -0.3	49.8604	-0.0105	0.04	$\kappa_{1}$ -0.7	49.9824	-0.0166	0.0437
1000		49.9469	-0.0107	0.0173		49.9075	-0.0061	0.0183
2000		50.0265	-0.0015	0.0085		49.925	-0.0034	0.0078
500	$\kappa_{2}$ -0.3	49.8604	-0.0302	0.0394	$\kappa_{2}$ -0.7	49.9824	-0.0831	0.0609
1000		49.9469	-0.0189	0.0163		49.9075	-0.0317	0.0195
2000		50.0265	-0.0053	0.007		49.925	-0.0214	0.0086
500	$\lambda_{1}$ -0.4	49.8604	0.0032	0.0067	$\lambda_{1}$ -0.4	49.9824	-0.0041	0.0072
1000		49.9469	-0.0003	0.0035		49.9075	-0.006	0.0034
2000		50.0265	0.0005	0.0016		49.925	-0.0033	0.0018
500	$\lambda_{2}$ 1.2	49.8604	0.0062	0.004	$\lambda_{2}$ 1.2	49.9824	0.0039	0.0038
1000		49.9469	0.0057	0.0019		49.9075	0.0029	0.0018
2000		50.0265	0.0026	0.0009		49.925	0.0016	0.0008
500	$\nu$ 4	49.8604	0.5755	3.9653	$\nu$ 4	49.9824	0.546	8.083
1000		49.9469	0.2316	0.8686		49.9075	0.1677	0.793
2000		50.0265	0.1139	0.3197		49.925	0.0841	0.4107

5 Application to real data

In this section, two real data sets, corresponding to outpatient expense and investments in education, are analyzed. The outpatient expense data data set has already been analyzed in the literature by Heckman models Marchenko and Genton, (2012), whereas the education investment data is new and is analyzed for the first time here.

5.1 Outpatient expense

In this subsection, a real data set corresponding to outpatient expense from the 2001 Medical Expenditure Panel Survey (MEPS) is used to illustrate the proposed methodology. This data set has information about the cost and provision of outpatient services, and is the most complete coverage about health insurance in the United States, according to the Agency for Healthcare Research and Quality (AHRQ).

The MEPS data set contains information collected from 3328 individuals between 21 and 64 years. The variable of interest is the expenditure on medical services in the logarithm scale ( $Y_{i}^{*}=lnambx$ ), while the latent variable ( $U_{i}^{*}=dambexp$ ) is the willingness of the individual to spend; $U_{i}=\mathds{1}_{\{U_{i}^{*}>0\}}$ corresponds the decision of the individual to spend. It was verified that 526 (15.8%) of the outpatient costs are identified as zero (censored). The covariates considered in the are: $age$ is the age measured in tens of years; $fem$ is a dummy variable that assumed value 1 for women and 0 for men; $educ$ is the years of education; $blhisp$ is a dummy variable for ethnicity (1 for black or Hispanic and 0 if non-black and non-Hispanic); $totcr$ is the total number of chronic diseases; $ins$ is the insurance status; and $revenue$ denotes the individual income.

Table 4 reports descriptive statistics of the observed medical expenditures, including the minimum, mean, median, maximum, standard deviation (SD), coefficient of variation (CV), coefficient of skewness (CS) and coefficient of (excess) kurtosis (CK) values. From this table, we note the following: the mean is almost equal to the median; a very small negative skewness value; and a very small kurtosis value. The symmetric nature of the data is confirmed by the histogram shown in Figure Figure 1(a). The boxplot shown in Figure 1(b) indicates some potential outliers. Therefore, we observe that a symmetric distribution is a reasonable assumption, more specifically a Student- $t$ model, since since we have to accommodate outliers.

Table 4: Summary statistics for the medical expenditure data.

minimum	Mean	Median	maximum	SD	CV	CS	CK	$n$
0.693	6.557	6.659	10.819	1.406	21.434%	-0.315	0.006	2801

Refer to caption — Figure 1: Histogram (a) and boxplots (b) for the medical expenditure data.

We then analyze the medical expenditure data using the generalized Heckman- $t$ model, expressed as

lnambx=\beta_{0}+\beta_{1}\,age_{i}+\beta_{2}\,fem_{i}+\beta_{3}\,educ_{i}+\beta_{4}\,blhisp_{i}+\beta_{5}\,totchr_{i}+\beta_{6}\,ins_{i},

(5.1)

dambexp=\gamma_{0}+\gamma_{1}\,age_{i}+\gamma_{2}\,fem_{i}+\gamma_{3}\,educ_{i}+\gamma_{4}\,blhisp_{i}+\gamma_{5}\,totchr_{i}+\gamma_{6}\,ins_{i}+\gamma_{7}\,income_{i},

(5.2)

\log\sigma_{i}=\lambda_{0}+\lambda_{1}\,age_{i}+\lambda_{2}\,totchr_{i}+\lambda_{3}\,ins_{i},

(5.3)

\text{arctanh}\,\rho_{i}=\kappa_{0}+\kappa_{1}\,fem_{i}+\kappa_{2}\,totchr_{i}.

(5.4)

We initially compare the adjustments of the generalized Heckman- $t$ (GH $t$ ) model, in terms of Akaike (AIC) and Bayesian information (BIC), with the adjustments of the classical Heckman-normal (CHN) (Heckman,, 1976) and generalized Heckman-normal (GHN) (Bastos et al.,, 2021) models; see Table 5. The AIC and BIC values reveal that the GH $t$ model provides the best adjustment, followed by the GHN model.

Table 5: AIC and BIC of the indicated Heckman models.

	CHN	GHN	GH $t$
AIC	11706.44	11660.29	11635.05
BIC	11810.31	11794.71	11775.59

Table 6 presents the estimation results of the GHN and GH $t$ models. From this table, we observe the following results: the explanatory variables $totchr$ and $ins$ that model the dispersion are significant, in both models, indicating the presence of heteroscedasticity in the data. The explanatory variable $age$ is only significant in the GHN model. For the correlation term, the covariates $fem$ and $totchr$ are significant for both models, which indicates the presence of selection bias in the data.

In the outcome equation, when we look at both models, $age$ , $fem$ , $blhisp$ and $totchr$ are significant at the 5% level, and $educ$ is not significant. The explanatory variable $ins$ is significant at the 5% and 10% levels in the GHN and GH $t$ models, respectively; see Table 6. We can interpret the estimated coefficients in terms of the effect on the expenditure on medical services; see Weisberg, (2014, p.82). For example, a 1-year increase in $age$ rises by $(\exp(0.1838)-1)\times 100=20.18\%$ and $(\exp(0.1895)-1)\times 100=20.86\%$ the expected value of the expenditure on medical services according to the GHN and GH $t$ , respectively. Moreover, a 1-unit increase in $totchr$ rises by $(\exp(0.4306)-1)\times 100=53.82\%$ and $(\exp(0.4464)-1)\times 100=56.27\%$ the expected value of the response according to the GHN and GH $t$ models, respectively.

In the case of the selection equation, we observe that, for both models, the explanatory variables $age$ , $fem$ , $educ$ , $blhisp$ , $totchr$ and $ins$ are significant at the 5% level and $revenue$ is significant at the 10% level; see Table 6. The interpretation is made in terms of odds ratio, which is obtained by exponentiating the estimated explanatory variable coefficient. For example, for the GH $t$ case, the odds ratio for $age$ is $\exp(0.0930)=1.0975$ , suggesting that each additional year of age raises the likelihood of an individual having expenditures on medical services by $((1.0975-1)\times 100)=9.75\%$ .

Table 6: Estimation results of the GHN and GH

t

models.

Probit selection equation
Variables	Estimates		Std. Error		$t$ Value		$p$ -value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$(Intercept)$	-0.5903	-0.6406	0.1867	0.2014	-3.1620	-3.1800	<0.001	<0.001
$age$	0.0863	0.0930	0.0264	0.0288	3.2610	3.2230	<0.001	<0.001
$fem$	0.6299	0.7087	0.0597	0.0681	1.0543	1.0395	<0.001	<0.001
$educ$	0.0569	0.0590	0.0114	0.0122	4.9830	4.8110	<0.001	<0.001
$blhisp$	-0.3368	-0.3726	0.0596	0.0647	-5.6430	-5.7590	<0.001	<0.001
$totchr$	0.7585	0.8728	0.0686	0.0858	1.1043	1.0168	<0.001	<0.001
$ins$	0.1727	0.1863	0.0611	0.0665	2.8240	2.7990	<0.001	<0.001
$revenue$	0.0022	0.0025	0.0012	0.0013	1.8380	1.8750	0.0661	0.0610
Outcome equation
Variables	Estimates		Std. Error		$t$ Value		$p$ -value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$(Intercept)$	5.7041	5.6078	0.1930	0.1912	2.9553	2.9316	<0.001	<0.001
$age$	0.1838	0.1895	0.0234	0.0230	7.8460	8.2350	<0.001	<0.001
$fem$	0.2498	0.2555	0.0587	0.0580	4.2530	4.4000	<0.001	<0.001
$educ$	0.0013	0.0062	0.0101	0.0100	0.1290	0.6240	0.8970	0.5329
$blhisp$	-0.1283	-0.1344	0.0577	0.0569	-2.2210	-2.3630	0.0264	0.0182
$totchr$	0.4306	0.4464	0.0305	0.0297	1.4115	1.5002	<0.001	<0.001
$ins$	-0.1027	-0.0976	0.0513	0.0501	-2.000	-1.9470	0.0456	0.0516
Dispersion
Variables	Estimates		Std. Error		$t$ Value		$p$ -value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$Intercept)$	0.5081	0.4172	0.0573	0.0643	8.8550	6.4820	<0.001	<0.001
$age$	-0.0249	-0.0209	0.0125	0.0136	-1.9870	-1.5360	0.0469	0.1246
$totchr$	-0.1046	-0.1118	0.0191	0.0208	-5.4760	-5.3720	<0.001	<0.001
$ins$	-0.1070	-0.1117	0.0277	0.0303	-3.8630	-3.6810	<0.001	<0.001
Correlation
Variables	Estimates		Std. Error		$t$ Value		$p$ -value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$Intercept$	-0.6475	-0.6051	0.1143	0.1118	-5.666	-5.413	<0.001	<0.001
$fem$	-0.4040	-0.4220	0.1356	0.1489	-2.978	-2.835	<0.001	<0.001
$totchr$	-0.4379	-0.4999	0.1862	0.2102	-2.351	-2.378	0.0187	0.0174
$\nu$	-	12.3230	-	2.7570	-	4.4690	-	<0.001

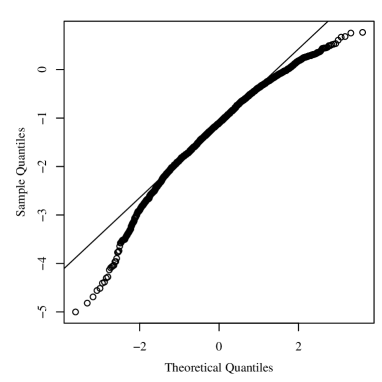
Figure 2 displays the quantile versus quantile (QQ) plots of the martingale-type (MT) residuals for the GHN and GH $t$ models. This residual is given by

{r}_{{i}}^{\text{MT}}=\textrm{sign}(r^{{}_{\textrm{\tiny M}_{i}}})\sqrt[\ ]{-2\left(r^{{}_{\textrm{\tiny M}_{i}}}+u_{i}\log(u_{i}-r^{{}_{\textrm{\tiny M}_{i}}})\right)},\quad i=1,\dots,n.

(5.5)

where $r^{{}_{\textrm{\tiny M}_{i}}}=u_{i}+\log(\widehat{S}(t_{i}))$ , $\widehat{S}(t_{i})$ is the fitted survival function, and $u_{i}=0$ or $1$ indicating that case $i$ is censored or not, respectively; see Therneau et al., (1990). The MT residual is asymptotically standard normal, if the model is correctly specified whatever the specification of the model is. From Figure 2, we see clearly that the GH $t$ model provides better fit than GHN model.

5.2 Investments in education

In this subsection, data on education investments are used to illustrate the proposed methodology. We consider the investments made by municipalities of two Brazilian states: Sao Paulo (SP) and Minas Gerais (MG). This data set was obtained from the Brazilian National Fund for Educational Development (FNDE) website¹¹1Filtered data are available at https://repositorio.shinyapps.io/plataforma_de_dados_municipais., which is a federal agency under the Ministry of Education. The origin of these investments comes from the Fund for the Maintenance and Development of Basic Education and the Valorization of Education Professionals (FUNDEB). The resources are distributed to 27 federative units (26 states plus the Federal District), according to the number of students enrolled in their basic education network. This rule is established for the previous year’s school census data, e.g., 2018 resources were based on 2017 student numbers. This method helps to better distribute resources across the country, as it takes into account the size of education networks.

The variable of interest is education investments with 1503 observations, of which 102 (7%) correspond to unobserved investment values identified as zero investment. The explanatory variables considered in the study were: $revenue$ ³³3http://www.ipeadata.gov.br/Default.aspx. represents per capita revenue collected by the municipality; $gnp$ ³³3http://www.ipeadata.gov.br/Default.aspx. is the Gross National Product of the municipality; $distribute$ ²²2https://dados.gov.br/dataset/sistema-arrecadacao. is a dummy variable indicating if the municipality receives resources from the Financial Compensation for Exploration of Mineral Resources (CFEM); this resource must be destined to investments in the areas of health, education and infrastructure for the community; $sp$ is an indicator variable for state ( $sp$ receives value 1); $enrollment$ ⁴⁴4https://www.gov.br/inep/pt-br/areas-de-atuacao/pesquisas-estatisticas-e-indicadores/censo-escolar. is the school census enrollment numbers.

As in the previous study, the response variable, investment in education, is in the logarithm scale $Y_{i}^{*}=lninvest$ . The latent variable ( $U_{i}^{*}=dinvest$ ) denotes the willingness of the $i$ th municipality to invest education; $U_{i}=\mathds{1}_{\{U_{i}^{*}>0\}}$ corresponds to the decision or not of the $i$ th municipality to invest in education.

³³footnotetext: https://www.ibge.gov.br/estatisticas/sociais/populacao/9103-estimativas-de-populacao.html?=&t=resultados.

The descriptive statistics for the investments in education are reported in Table 7. From this table, we note the following: the mean is almost equal to the median; a very small negative skewness value, and a high kurtosis value. The symmetric nature of the data is confirmed by the histogram shown in Figure Figure 3(a). The boxplot shown in Figure 3(b) indicates potential outliers. Therefore, we observe that a Student- $t$ model is a reasonable assumption.

Table 7: Summary statistics for the education investment data.

minimum	Mean	Median	maximum	SD	CV	CS	CK	$n$
4.271	12.212	12.575	18.511	1.903	15.587%	-0.5864	3.70	1401

We then analyze the education investment data using the GH $t$ model, expressed as

dinvest=\beta_{0}+\beta_{1}\,revenue_{i}+\beta_{2}\,sp_{i}+\beta_{3}\,enrollment_{i},

(5.6)

lninvest=\gamma_{0}+\gamma_{1}\,revenue_{i}+\gamma_{2}\,sp_{i}+\gamma_{3}\,enrollment_{i}+\gamma_{4}\,gnp_{i},

(5.7)

\log\sigma_{i}=\lambda_{0}+\lambda_{1}\,revenue_{i}+\lambda_{2}\,sp_{i},

(5.8)

\text{arctanh}\,\rho_{i}=\kappa_{0}+\kappa_{1}\,revenue_{i}+\kappa_{2}\,distribute_{i}.

(5.9)

Table 8 reports the AIC and BIC of the CHN, GHN and GH $t$ models. From Table 8, we observe that the GH $t$ model provides better adjustment than other models based on the values of AIC and BIC.

Table 8: AIC and BIC of the indicated Heckman models.

	CHN	GHN	GH $t$
AIC	8269.058	5873.579	5719.590
BIC	8306.147	5953.055	5804.365

Table 9 presents the estimation results of the GHN and GH $t$ models. From this table, we note that the explanatory variables $revenue$ and $sp$ associated with the dispersion are significant, in both models, suggesting the presence of heteroscedasticity. For the explanatory variables related to the correlation parameter, $revenue$ is significant at the 5% and 10% levels in the GHN and GH $t$ models, respectively, while $distribute$ is significant at the 10% and 5% levels in the GHN and GH $t$ models, respectively. Therefore, there is evidence of the presence of sample selection bias in the data.

From Table 9, we observe that in the outcome equation $revenue$ , $sp$ , $enrollment$ and $gnp$ are significant, according to the GHN and GH $t$ models. Note that increasing $revenue$ by one unit is associated with $(\exp(-0.2683)-1)\times 100=-23.53\%$ and $(\exp(-0.2167)-1)\times 100=-19.48\%$ decrease in the average investment in education according to the GHN and GH $t$ models, respectively. Note also that when the municipality is located in the state of Sao Paulo ( $sp$ ), the average investment in education increases by $(\exp(1.0714)-1)\times 100=191.95\%$ and $(\exp(1.0063)-1)\times 100=173.55\%$ , according to the GHN and GH $t$ models, respectively. These results show that the municipalities of the state of Sao Paulo invest much more in education than the municipalities of the state of Minas Gerais.

In the selection equation, we observe that the explanatory variables $revenue$ , $sp$ and $enrollment$ are significant in the GH $t$ model. On the other hand, $revenue$ and $sp$ are not significant in the GHN model; see Table 9. We observe that, for the GH $t$ case, the odds ratio for $sp$ is $\exp(0.3674)=1.4439$ , that is, the likelihood of a municipality to spend on medical services increases by $((1.4439-1)\times 100)=44.39\%$ when the municipality is located in the state of Sao Paulo

Table 9: Estimation results of the GHN and GH

t

models.

Probit selection equation
Variables	Estimate		Std. Error		t Value		p-Value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$(intercept)$	1.0523	1.4222	0.1013	0.0955	10.3870	14.8880	<0.01	<0.001
$revenue$	-0.0058	-0.0530	0.0223	0.0164	-0.2630	-3.2330	0.7920	<0.001
$sp$	0.1065	0.3674	0.0990	0.1032	1.0750	3.5600	0.2820	<0.001
$enrollment$	0.0311	0.0537	0.0032	0.0026	9.6380	20.6150	<0.001	<0.001
Outcome equation
Variables	Estimate		Std. Error		t Value		p-Value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$(intercept)$	12.4789	12.4058	0.1252	0.1208	99.6480	102.6960	<0.001	<0.001
$revenue$	-0.2683	-0.2167	0.0332	0.0274	-8.0640	-7.9030	<0.001	<0.001
$sp$	1.0714	1.0063	0.1003	0.0881	10.6810	11.4190	<0.001	<0.001
$enrollment$	0.0031	0.0226	0.0005	0.0025	5.6670	8.8410	<0.001	<0.001
$gnp$	0.0202	0.0151	0.0023	0.0005	8.4630	27.4250	<0.001	<0.001
Dispersion
Variables	Estimate		Std. Error		t Value		p-Value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$(intercept)$	0.5921	0.2947	0.0503	0.0623	11.7560	4.7250	<0.001	<0.001
$revenue$	0.0382	0.0546	0.0130	0.0146	2.9330	3.7180	<0.001	<0.001
$sp$	-0.3142	-0.4745	0.0416	0.0534	-7.5470	-8.8800	<0.001	<0.001
Correlation
Variables	Estimate		Std. Error		t Value		p-Value
Variables	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$	GHN	GH $t$
$(intercept)$	-3.7263	-6.7669	0.5463	0.9682	-6.8210	-6.9890	<0.001	<0.001
$revenue$	0.1686	0.2274	0.0839	0.1161	2.0080	-6.9890	0.0448	0.0500
$distribute$	0.8298	3.1118	0.4411	0.6867	1.8810	1.9580	0.0602	<0.001
$\nu$	-	3.6240	-	0.4320	-	8.3900	-	<0.001

Figure 4 displays the QQ plots of the MT residuals. This figure indicates that the MT residuals in the GH $t$ model shows better agreement with the reference distribution.

6 Concluding Remarks

In this paper, a class of Heckman sample selection models were proposed based symmetric distributions. In such models, covariates were added to the dispersion and correlation parameters, allowing the accommodation of heteroscedasticity and a varying sample selection bias, respectively. A Monte Carlo simulation study has showed good results of the parameter estimation method. We have considered high/low censoring rates and the presence of strong/weak correlation. We have applied the proposed model along with some other two existing models to two data sets corresponding to outpatient expense and investments in education. The applications favored the use of the proposed generalized Heckman- $t$ model over the classical Heckman-normal and generalized Heckman-normal models. As part of future research, it will be of interest to propose sample selection models based on skew-symmetric distributions. Furthermore, the behavior of the Wald, score, likelihood ratio and gradient tests can be investigated. Work on these problems is currently in progress and we hope to report these findings in future.

References

Abdous, (2005) Abdous, B., F. A.-L. G. K. (2005). Extreme behaviour for bivariate elliptical distributions. The Canadian Journal of Statistics, 33:317–334.
Balakrishnan and Lai, (2009) Balakrishnan, N. and Lai, C. D. (2009). Continuous Bivariate Distributions. Springer-Verlag, New York, NY.
Bastos and Barreto-Souza, (2021) Bastos, F. S. and Barreto-Souza, W. (2021). Birnbaum-Saunders sample selection model. Journal of Applied Statistics, 48:1896–1916.
Bastos et al., (2021) Bastos, F. S., Barreto-Souza, W., and Genton, M. G. (2021). A generalized heckman model with varying sample election bias and dispersion parameters. Statistica Sinica.
Ding, (2014) Ding, P. (2014). Bayesian robust inference of sample selection using selection-t models. Journal of Multivariate Analysis, pages 124:451–464.
Fang et al., (1990) Fang, K. T., Kotz, S., and Ng, K. W. (1990). Symmetric Multivariate and Related Distributions. Chapman and Hall, London, UK.
Heckman, (1976) Heckman, J. J. (1976). The common structure of statistical models of truncation, sample selection and limited dependent variables and a simple estimator for such models. Annals of Economic and Social Measurement, 5:475–492.
Heckman, (1979) Heckman, J. J. (1979). Sample selection bias as a specification error. Econometrica, 47:153–161.
Lachos et al., (2021) Lachos, V. H., Prates, M. O., and Dey, D. K. (2021). Heckman selection-t model: Parameter estimation via the em-algorithm. Journal of Multivariate Analysis, 184:104737.
Leung and Yu, (1996) Leung, S. F. and Yu, S. (1996). On the choice between sample selection and twopart models. Journal of Econometrics, pages 72:197–229.
Manning et al., (1987) Manning, W., Duan, N., and Rogers, W. (1987). Monte carlo evidence on the choice between sample selection and two-part models. Journal of Econometrics, pages 35:59 –82.
Marchenko and Genton, (2012) Marchenko, Y. V. and Genton, M. G. (2012). A heckman selection-t model. Journal of the American Statistical Association, 107:304–317.
Nelson, (1984) Nelson, F. D. (1984). Eciency of the two-step estimator for models with endogenous sample selection. pages 24:181 – 196.
Ogundimu and Hutton, (2016) Ogundimu, E. O. and Hutton, J. L. (2016). A sample selection model with skew-normal distribution. Scandinavian Journal of Statistics, pages 43:172–190.
Paarsch, (1984) Paarsch, H. J. (1984). A monte carlo comparison of estimators for censored regression models. pages 24:197–213.
R Core Team, (2022) R Core Team (2022). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
Stolzenberg and Relles, (1990) Stolzenberg, R. M. and Relles, D. A. (1990). heory testing in a world of constrained research design: The significance of heckman’s censored sampling bias correction for nonexperimental research. Sociological Methods & Research, pages 18:395–415.
Therneau et al., (1990) Therneau, T., Grambsch, P., and Fleming, T. (1990). Martingale-based residuals for survival models. Biometrika, 77:147–160.
Weisberg, (2014) Weisberg, S. (2014). Applied Linear Regression. John Wiley & Sons, Hoboken, New Jersey, fourth edition edition.

$\displaystyle f_{Y_{i}}(y_{i};\bm{\theta})$	$\displaystyle=\mathbb{P}(U_{i}^{}\leq 0)\delta_{0}(y_{i})+\mathbb{P}(U_{i}^{}>0)f_{Y_{i}^{}\|U_{i}^{}>0}(y_{i};\bm{\theta})$
	$\displaystyle=(\mathbb{P}(U_{i}^{}\leq 0))^{1-u_{i}}(\mathbb{P}(U_{i}^{}>0))^{u_{i}}(f_{Y_{i}^{}\|U_{i}^{}>0}(y_{i};\bm{\theta}))^{u_{i}}$	(2.4)
	$\displaystyle=\mathbb{P}(U_{i}=u_{i})(f_{Y_{i}^{}\|U_{i}^{}>0}(y_{i};\bm{\theta}))^{u_{i}},\quad u_{i}=0,1,$

Symmetric generalized Heckman models

Abstract

1 Introduction

2 Symmetric generalized Heckman models

2.1 Finding the conditional density of Yi∗{Y}^{*}_{i}, given that Ui∗>0{U}^{*}_{i}>0

Proposition 2.1.

Proof.

Proposition 2.2.

Proof.

Proposition 2.3.

Proof.

Proposition 2.4.

Proof.

Theorem 2.5.

Proof.

Corollary 2.6 (Gaussian density generator).

Proof.

Remark 2.7.

Corollary 2.8 (Student-tt density generator).

Proof.

Corollary 2.9.

Proof.

2.2 Maximum likelihood estimation

3 Generalized Heckman-Student-tt model

4 Monte Carlo simulation

5 Application to real data

5.1 Outpatient expense

5.2 Investments in education

6 Concluding Remarks

References

2.1 Finding the conditional density of ${Y}^{}_{i}$ , given that ${U}^{}_{i}>0$

Corollary 2.8 (Student- $t$ density generator).

3 Generalized Heckman-Student- $t$ model