Sun Yat-sen University
Switchable Self-attention Module
Abstract
Attention mechanism has gained great success in vision recognition. Many works are devoted to improving the effectiveness of attention mechanism, which finely design the structure of the attention operator. These works need lots of experiments to pick out the optimal settings when scenarios change, which consumes a lot of time and computational resources. In addition, a neural network often contains many network layers, and most studies often use the same attention module to enhance different network layers, which hinders the further improvement of the performance of the self-attention mechanism. To address the above problems, we propose a self-attention module SEM. Based on the input information of the attention module and alternative attention operators, SEM can automatically decide to select and integrate attention operators to compute attention maps. The effectiveness of SEM is demonstrated by extensive experiments on widely used benchmark datasets and popular self-attention networks.
Keywords:
Attention Mechanism Excitation Switchable.1 Introduction
Attention is a recognition mechanism which is capable of ignoring non-essential information and selectively focusing on a small subset of information [1]. Attention is widely used in sentences [9, 11, 25], images [12, 34, 31, 27], and videos [21, 33, 19] to relieve the pressure of neural networks to learn massive amounts of information. Especially in vision recognition, some operators [10, 29, 24] imitating attention mechanism serve as effective feature enhancement components in convolutional neural networks(CNNs), enabling deep neural networks to effectively identify important information in images. Such modular and pluggable operators of neural networks are called attention modules [10, 29, 23, 28], which facilitate the development of vision recognition.
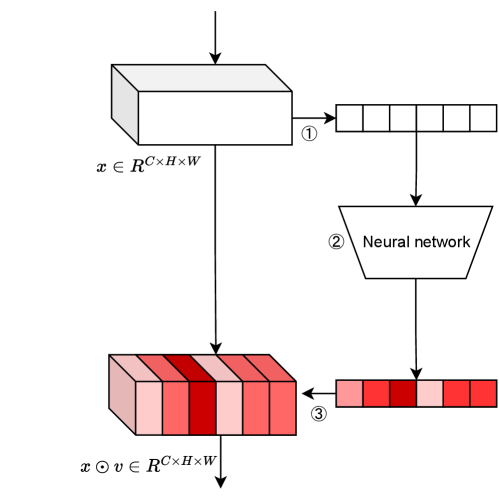
Specifically, most of the existing attention modules mainly consist of three parts [29, 13]. As shown in Fig. 1, \raisebox{-.9pt}{1}⃝ is the squeeze module, in which we get global information embeddings from input feature maps. \raisebox{-.9pt}{2}⃝ is the excitation module, where the global information embeddings is passed through the excitation operator to extract the attention maps. Finally, in stage \raisebox{-.9pt}{3}⃝ named as recalibration, the attention maps are used to the layers and adjust the feature.
\raisebox{-.9pt}{2}⃝ is a core part of attention modules. Researchers have proposed many methods to optimize the excitation operator [10, 24, 29, 13, 26]. For example, SENet [10] uses a fully connected network(FC) to fully capture channel-wise dependencies, which adaptively recalibrates channel-wise feature responses by explicitly modelling interdependencies between channels; ECA [26] is a local crosschannel interaction strategy without dimensionality reduction, which can be efficiently implemented via an 1D convolutional neural network(CNN); IEBN [20] is an attention-based BN that recalibrates the information of each channel by a simple linear transformation named instance enhance(IE). Despite their great successes, existing practices often employ the same kind of attention modules in all layers of an entire CNN with suboptimal performance. These approaches ignore two important things. On the one hand, CNN is a layered feature extractor often containing many network layers, and usually the attention modules of these network layers all use the same kind of excitation operators. On the other hand, for different scenarios (inputs, datasets and tasks, etc.), the size of the inputs and the type of datasets are different and we can only select a suitable attention module based on exploratory experiments.
However, based on our exploratory experiments, we find that it is necessary to select appropriate excitation operators for different network layers and scenarios, and combining different excitation operators can improve the effectiveness of attention modules. On CIFAR100, we randomly select excitation operators for different network layers. The experimental results are shown in Fig. 2. Through multiple groups of random repeated experiments, we dig out that attention modules of different network layers may require different excitation operators. In addition, we randomly reorganize the excitation operators of different network layers in pairs, and get that a combination of excitation operators can improve the performance of attention modules, which is better than randomly selecting a simple operator. Therefore, when we use attention modules to enhance the capability of the feature maps of CNNs, ideally we need to adjust the type of excitation operators according to the network layers and scenarios, instead of using the same kind of attention modules all the way. However, choosing the appropriate excitation operator for different network layers and scenarios requires a lot of cost and time.

In order to solve the above problems, we propose a switchable excitation module (SEM), which can automatically decide to select and integrate attention operators to compute the attention maps, realizing the combination of different excitation operators in different network layers. The contributions of this paper can be summarized as follows:
-
•
We find that different network layers and scenarios require different excitation operators.
-
•
In response to the above findings, we propose a switchable excitation module (SEM). SEM can select appropriate and integrate excitation operators for different network layers and scenarios to improve the excitation module.
-
•
The extensive experiments of SEM show that our method can achieve the state-of-the-art results on several popular benchmarks.
2 Related Works
Attention Mechanism in CNNs. CNNs with attention mechanism are widely used in a variety of vision tasks. In recent years, Zhu et al. [36] has explored the neuro-evolution application to the automatic design of CNN topologies, developing a novel solution based on Artificial Bee Colony. Gao et al.[6] proposes a novel CRF layer for graph convolutional neural networks to encourage similar nodes to have similar hidden features. Besides these works, many reseachers try to extend the attention mechanisms to specific tasks, e.g. point cloud classification [30, 15], image super-resolution [35], object detection [3, 14], semantic segmentation [32, 4], face recognition [31], person re-identification [18], action recognition [28], image generation [8, 34], and 3D vision [30].
Excitation Module of Attention Mechanism.There are many works to improve the capability of excitation module. SENet [10] adaptively recalibrates channel-wise feature responses by explicitly modelling interdependencies between channels, which makes use of fully connected networks. LightNL [7] squeezes the transformation operations and incorporating compact features. ECA [26] can be efficiently implemented via 1D convolution. IEBN [20] recalibrates the information of each channel by a simple linear transformation. CAP [2] effectively captures subtle changes via sub-pixel gradients which cognizes subcategories by introducing a simple formulation of context-aware attention via learning where to look when pooling features across an image. Unlike these studies that focus on improving the performance of certain aspects of excitation operators, SEM can automatically decide to select and integrate attention operators to compute the attention maps, realizing the combination of different excitation operators in different network layers.
3 Methodology
In this section, we formally introduce SEM. We first introduce the general structure of the SEM. Later, we introduce the details of decision module and switching module which are specific of SEM.
Input: A feature map ; A learnable transformation ; A set of excitation operators EO.
Output: The attention map .
3.1 An Overview of SEM

As shown in Fig. 3, SEM mainly improves the excitation module of attention modules, and its specific structure can be divided into two submodules: decision module and switching module. The feature map of the current network layer is defined as , and the calculation process of the attention value of is as follows. First, a global average pooling denoted as GAP() is applied to extract global information from features in the squeeze module as shown in Eq.(1).
| (1) |
where is the global information embedding. Then, we use as the input of decision module and switching module respectively.
A decision network is designed in the decision module to generate a decision vector for selecting excitation operators. Based on the decision vector , we design the switching module to select and integrate excitation operators. The switching module includes a set of excitation operators EO. The size of EO is defined as , and is the element of EO, representing the alternative excitation operator. The switching module designs the strategy to calculate the attention feature map based on .
Then, through the attention feature map , we calculate the feature map by integrating the attention information through Eq.(2).
| (2) |
where is dot product. We explain the details of each module below.
3.2 Decision Module
In order to automatically select the appropriate excitation operators for different network layers and scenarios, we design a decision module, which can generate decision weight for selecting excitation operators.
We take the global information embedding as the input, which enables the decision module to adaptively generate different decision weights according to different inputs. In addition, the decision module for each network layer is separate so that the decision module can distinguish different network layers. To make use of the information aggregated in the squeeze operation to identify the importance of different operatos, we follow it with which aims to fully capture decision information from channel-wise dependencies. To fulfil this objective, the function must meet two criteria: first, it must be flexible (in particular, it must be capable of learning a nonlinear interaction between channels) and second, it must learn a non-mutually-exclusive relationship since we would like to ensure that multiple excitation operator are allowed to be em phasised opposed to one-hot activation. To meet these criteria, we opt to employ a simple gating mechanism with a sigmoid activation:
| (3) |
where is the Sigmoid function. is the decision function. We use the fully connected network to define , is the weight of the fully connected network. Each value of decision vector represents the importance of the corresponding excitation operator. Through , the decision module makes soft decisions instead of selecting a single excitation operator. This design enables the excitation module to obtain an attention map that integrates all excitation operator information according to the importance of different excitation operators.
3.3 Switching Module
Based on the decision vector , we design the switching mechanism to select and integrate excitation operators. In the experimental exploration of this paper, we set the value of to 3, and set FC, CNN and IE as alternative excitation operators to explore the structure of the switching module.
Fully Connected Neural Networks. We use the excitation operator of SENet [10] as the full connected neural network. SENet is a classic fully connected network based attention module, which parameterises the gating mechanism by forming a bottleneck with two fully connected layers around the non-linearity to limit model complexity and aid generalisation. We opt to employ SENet as shown in Eq.(4).
| (4) |
where refers to the ReLU function, and . is the reduction ratio.
Convolutional Neural Networks. CNNs have the characteristics of few parameters and simple network structure, which can be well used to extract image features. There are many studies [26, 5, 22] using CNNs as the excitation operator of the attention module. We choose a simple-yet-effective attention module ECA [26] as the excitation operator of the CNN type. ECA only involves a handful of parameters while determining clear performance gain, which is a method to adaptively select kernel size of 1D convolution, coverage of local cross-channel interaction. We consider a standard convolution with the kernel , where is the kernel size and are the channel size. Given tensors , as the input and output feature maps, we denote , as the feature tensors of pixel () corresponding to and respectively. Then, the standard convolution can be formulated as:
| (5) |
where , represents the kernel weights with regard to the indices of the kernel position ().
The value of is canculate based on the value of [26].
| (6) |
where indicates the nearest odd number of . We set and to 2 and 1 throughout all the experiments, respectively.
Instance Enhance. In addition to FC and CNNs, we also consider the application of linear relationships in attention modules. We refer to the structure of IEBN [20] and define a pair of learnable parameters , scale and shift the global information embedding to restore the representation power. We define this structure as Instance Enhance (IE). The structure of IE is very simple and it is calculated as follows [20]:
| (7) |
Specially, the parameters , are initialized by constant 0 and -1 espectively.
Switching Operator. We use to adjust the proportion of each operator in EO, and combine the results of each operator in the form of dot product to get the final attention feature map .
| (8) |
where is the sigmoid function, is the weight of each excitation operator.
| Model | CIFAR10 | CIFAR100 |
|---|---|---|
| ResNet164 | 93.23 | 74.33 |
| ResNet164+SE | 94.32 | 75.28 |
| ResNet164+CBAM | 92.67 | 74.54 |
| ResNet164+SRM | 94.58 | 76.11 |
| ResNet164+ECA | 94.51 | 75.39 |
| ResNet164+IE | 94.44 | 75.92 |
| ResNet164+SEM(ours) | 94.95( 1.72) | 76.76( 2.43) |
4 Experiments
Dataset and Implementation Details. We evaluate our SEM on both CIFAR10 and CIFAR100 [16], which have 50k train images and 10k test images of size 32 by 32 but has 10 and 100 classes respectively. We also use normalization and standard data augmentation including random cropping and horizontal flipping during training. SGD optimizer with a momentum of 0.9 and a weight decay of is applied in our experiments. We train all of models using one Nvidia RTX 3080 GPU and uniformly set the epoch number to 164.
Image Classification. We compare our SEM with several popular attention methods using ResNet-164 on CIFAR10 and CIFAR100, including SENet [10], CBAM [29], SRM [17], ECA [26], and IE [20]. The evaluation metric is Top-1 accuracy(in %). The results are given in Table 1, where we can see that our SEM achieves 1.72% and 2.43% gains in Top-1 accuracy on CIFAR10 and CIFAR100 respectively.
| Model | CIFAR10 | CIFAR100 |
|---|---|---|
| ResNet47 | 93.54 | 72.56 |
| ResNet47+SEM(ours) | 93.6( 0.06) | 73.09( 0.53) |
| ResNet164 | 93.23 | 74.33 |
| ResNet164+SEM(ours) | 94.95( 1.72) | 76.76( 2.43) |
| ResNet272 | 93.99 | 74.08 |
| ResNet272+SEM(ours) | 95.21( 1.22) | 77.61( 3.53) |
| ResNet362 | 93.45 | 70.41 |
| ResNet362+SEM(ours) | 95.45( 2.00) | 77.72( 7.31) |
Depth of Backbone Models. Using ResNet47, ResNet164, ResNet272, and ResNet362 as backbone models, we compare our SEM with ResNet to dig out the effectiveness of the depth of backnone models. As shown in Table 2, SEM can improve the performance of backbone models of each depth by 0.06% to 7.31%. Besides, we can learn from the experiment results that as the depth increasing, the performances of ResNet is not promoted consistently. This phenomenon may be related to the gradient dispersion of deep neural networks. However, the performances of SEM is consistent of the increasing of the depth, which means that our SEM can enhance the backbone models.
5 Ablation Study
The Size of EO. We discuss the size of EO to examine whether it is necessary to integrate excitation operators. The experiment results is displayed in Table 3, showing that integrating excitation operators is effective. Although the performance of each operator is different, when the size of EO increases, the performance of SEM consistently increases. This experiment shows that the size of EO is positively related to the performance of SEM, and the switching strategy we proposed is stable and effective.
| The Size of EO | Module | CIFAR-10 | CIFAR-100 |
| N=1 | FC | 94.32 | 75.28 |
| CNN | 94.51 | 75.39 | |
| IE | 94.44 | 75.92 | |
| N=2 | FC, CNN | 94.92 | 76.37 |
| FC, IE | 94.80 | 76.52 | |
| CNN, IE | 94.81 | 76.48 | |
| N=3 | FC, CNN, IE | 94.95 | 76.76 |
Removal of Decision Module. We further verify the effectiveness of decision module. We experiment without decision weight which means that in Eq.(8), is set as 1. The results is 94.72% and 76.29% on CIFAR10 and CIFAR100 respectively, which is 0.23% and 0.47% lower than SEM respectively in terms of Top-1 accuracy. These results verify that is effective and our decision module has good recognition ability for various excitation operators.
Activation Funtion. We explore the effects of different activation functions on Eq.(8). According to the experiment results in Table 4, Eq.(8) is sensitive on the choice of activation functions, and Sigmoid is the optimal activation function. In particular, linear activation functions Relu and LeakyRelu are not suitable for Eq.(8), while the nonlinear activation functions Tanh and Sigmoid perform relatively well, indicating that the symmetric activation function is more suitable for SEM.
| Activation Function | CIFAR-100 |
|---|---|
| Tanh | 70.11 |
| ReLU | 38.98 |
| LeakyReLU | 39.32 |
| Sigmoid | 76.76 |
Without Data Augment. To verify the ability of SEM to reduce overfitting, We train the models without data augment to reduce the influence of regularization from data augment. As shown in Table 5, SEM achieves lower testing error than ResNet164 and SENet. To some extent, the switchable structure of SEM may have regularization effect.
| Model | CIFAR-10 | CIFAR-100 |
|---|---|---|
| ResNet164 | 87.18 | 60.82 |
| SENet | 88.24 | 62.87 |
| SEM | 89.58 | 67.27 |
6 Conclusion
In this paper, we focus on learning effective channel attention for deep CNNs with switchable mechanism. To this end, we propose an switchable excitation module (SEM), which can automatically decide to select and integrate attention operators to compute attention maps. Experimental results demonstrate our SEM is an plug-and-play block to improve the performance of deep CNN architectures and may have regularization effect. Moreover, our SEM have stable performance on backbone networks of various depths. In future, we will apply our SEM to more CNN architectures and tasks to further investigate incorporation of SEM with self-attention modules.
References
- [1] Anderson, J.R.: Cognitive psychology and its implications. Macmillan (2005)
- [2] Behera, A., Wharton, Z., Hewage, P.R., Bera, A.: Context-aware attentional pooling (cap) for fine-grained visual classification. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 35, pp. 929–937 (2021)
- [3] Dai, J., Qi, H., Xiong, Y., Li, Y., Zhang, G., Hu, H., Wei, Y.: Deformable convolutional networks. In: Proceedings of the IEEE international conference on computer vision. pp. 764–773 (2017)
- [4] Fu, J., Liu, J., Tian, H., Li, Y., Bao, Y., Fang, Z., Lu, H.: Dual attention network for scene segmentation. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [5] Fu, J., Zheng, H., Mei, T.: Look closer to see better: Recurrent attention convolutional neural network for fine-grained image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 4438–4446 (2017)
- [6] Gao, H., Pei, J., Huang, H.: Conditional random field enhanced graph convolutional neural networks. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. pp. 276–284 (2019)
- [7] Gao, Z., Xie, J., Wang, Q., Li, P.: Global second-order pooling convolutional networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 3024–3033 (2019)
- [8] Gregor, K., Danihelka, I., Graves, A., Rezende, D., Wierstra, D.: Draw: A recurrent neural network for image generation. In: International conference on machine learning. pp. 1462–1471. PMLR (2015)
- [9] He, W., Huang, Z., Liang, M., Liang, S., Yang, H.: Blending pruning criteria for convolutional neural networks. In: International Conference on Artificial Neural Networks. pp. 3–15. Springer (2021)
- [10] Hu, J., Shen, L., Sun, G.: Squeeze-and-excitation networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 7132–7141 (2018)
- [11] Huang, Z., Liang, S., Liang, M., He, W., Yang, H.: Efficient attention network: Accelerate attention by searching where to plug. arXiv preprint arXiv:2011.14058 (2020)
- [12] Huang, Z., Liang, S., Liang, M., He, W., Yang, H., Lin, L.: The lottery ticket hypothesis for self-attention in convolutional neural network. arXiv preprint arXiv:2207.07858 (2022)
- [13] Huang, Z., Liang, S., Liang, M., Yang, H.: Dianet: Dense-and-implicit attention network. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 34, pp. 4206–4214 (2020)
- [14] Huang, Z., Shao, W., Wang, X., Lin, L., Luo, P.: Convolution-weight-distribution assumption: Rethinking the criteria of channel pruning. arXiv preprint arXiv:2004.11627 (2020)
- [15] Huang, Z., Shao, W., Wang, X., Lin, L., Luo, P.: Rethinking the pruning criteria for convolutional neural network. Advances in Neural Information Processing Systems 34, 16305–16318 (2021)
- [16] Krizhevsky, A., Hinton, G., et al.: Learning multiple layers of features from tiny images (2009)
- [17] Lee, H., Kim, H.E., Nam, H.: Srm: A style-based recalibration module for convolutional neural networks. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 1854–1862 (2019)
- [18] Li, W., Zhu, X., Gong, S.: Harmonious attention network for person re-identification. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 2285–2294 (2018)
- [19] Li, X., Song, J., Gao, L., Liu, X., Huang, W., He, X., Gan, C.: Beyond rnns: Positional self-attention with co-attention for video question answering. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 33, pp. 8658–8665 (2019)
- [20] Liang, S., Huang, Z., Liang, M., Yang, H.: Instance enhancement batch normalization: An adaptive regulator of batch noise. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 34, pp. 4819–4827 (2020)
- [21] Ma, Y.F., Lu, L., Zhang, H.J., Li, M.: A user attention model for video summarization. In: Proceedings of the tenth ACM international conference on Multimedia. pp. 533–542 (2002)
- [22] Pan, X., Ge, C., Lu, R., Song, S., Chen, G., Huang, Z., Huang, G.: On the integration of self-attention and convolution. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 815–825 (2022)
- [23] Park, J., Woo, S., Lee, J.Y., Kweon, I.S.: Bam: Bottleneck attention module. arXiv preprint arXiv:1807.06514 (2018)
- [24] Qin, Z., Zhang, P., Wu, F., Li, X.: Fcanet: Frequency channel attention networks. In: Proceedings of the IEEE/CVF international conference on computer vision. pp. 783–792 (2021)
- [25] Wang, P., Li, J., Hou, J.: S2san: A sentence-to-sentence attention network for sentiment analysis of online reviews. Decision Support Systems 149, 113603 (2021)
- [26] Wang, Q., Wu, B., Zhu, P., Li, P., Hu, Q.: Eca-net: Efficient channel attention for deep convolutional neural networks. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [27] Wang, Q., Wu, T., Zheng, H., Guo, G.: Hierarchical pyramid diverse attention networks for face recognition. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. pp. 8326–8335 (2020)
- [28] Wang, X., Girshick, R., Gupta, A., He, K.: Non-local neural networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 7794–7803 (2018)
- [29] Woo, S., Park, J., Lee, J.Y., Kweon, I.S.: Cbam: Convolutional block attention module. In: Proceedings of the European conference on computer vision (ECCV). pp. 3–19 (2018)
- [30] Xie, S., Liu, S., Chen, Z., Tu, Z.: Attentional shapecontextnet for point cloud recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 4606–4615 (2018)
- [31] Yang, J., Ren, P., Zhang, D., Chen, D., Wen, F., Li, H., Hua, G.: Neural aggregation network for video face recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 4362–4371 (2017)
- [32] Yuan, Y., Huang, L., Guo, J., Zhang, C., Chen, X., Wang, J.: Ocnet: Object context network for scene parsing. arXiv preprint arXiv:1809.00916 (2018)
- [33] Zhai, Y., Shah, M.: Visual attention detection in video sequences using spatiotemporal cues. In: Proceedings of the 14th ACM international conference on Multimedia. pp. 815–824 (2006)
- [34] Zhang, H., Goodfellow, I., Metaxas, D., Odena, A.: Self-attention generative adversarial networks. In: International conference on machine learning. pp. 7354–7363. PMLR (2019)
- [35] Zhang, Y., Li, K., Li, K., Wang, L., Zhong, B., Fu, Y.: Image super-resolution using very deep residual channel attention networks. In: Proceedings of the European conference on computer vision (ECCV). pp. 286–301 (2018)
- [36] Zhu, W., Yeh, W., Chen, J., Chen, D., Lin, Y.: Evolutionary convolutional neural networks using abc. In: ICMLC 2019: International Conference on Machine Learning and Computing (2019)