Swimming Euglena respond to confinement with
a behavioral change enabling effective crawling

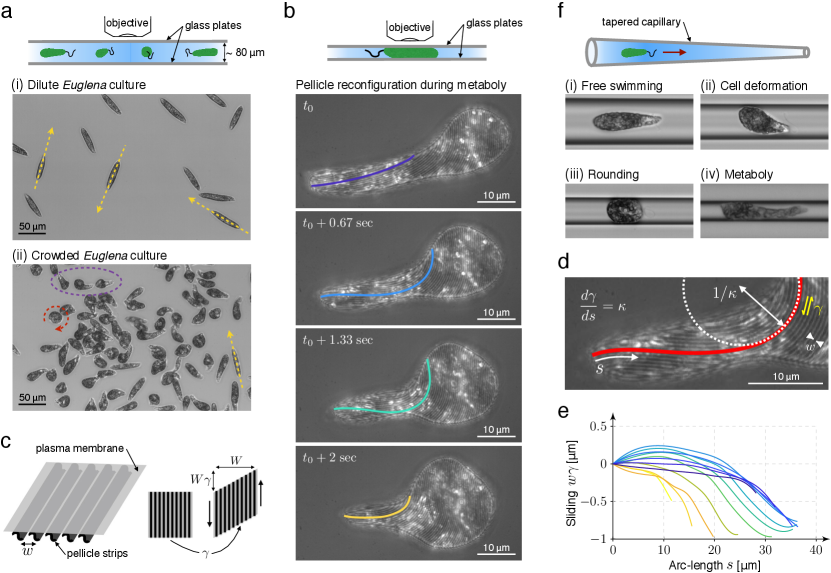
To investigate the role of confinement in the behavior of euglenids and their motility, we examined cultures of Euglena gracilis, a prototypical photosynthetic species exhibiting metaboly, at various degrees of crowding (Fig. 1a and Supplementary Movie S1). In dilute cultures, cells exhibited fast swimming in the posterior-to-anterior direction powered by an anterior flagellum, cruising at $\sim$ 68 $\upmu\text{m/s}$. During flagellar swimming, cells maintained a fixed cigar shape $\sim$ 50 $\upmu\text{m}$ long and with a maximum diameter of $\sim$ 9 $\upmu\text{m}$. Cells performed sharp turns as previously described.¹⁵ In crowded cultures, presumably triggered by mechanosensation at the cell envelope and/or at the flagella,¹ cells exhibited a variety of behaviors in addition to fast swimming, including rounding, bulging, and large amplitude periodic cell deformations. Rounding was often associated with cell spinning, whereas metaboly did not seem to have a significant effect in locomotion.

We also triggered metaboly by confining cells between two glass plates separated along one side by a spacer to produce a wedge-shaped fluid chamber. Cells in the narrower regions of the chamber (with a typical gap of $\sim$ 5 $\upmu\text{m}$) systematically developed large amplitude periodic shape changes. Using brightfield reflected light microscopy (Supplementary Methods), we were able to record simultaneously and continuously in time the shape changes and the reconfigurations of the pellicle envelope in the plane of the glass plate (Fig. 1b and Supplementary Movies S2 and S3). The pellicle is composed of interlocking narrow and long proteinaceous strips, often arranged helically and spanning from the anterior to the posterior ends of the cell. These strips lie beneath the plasma membrane and are subtended by systems of microtubules.² Previous observations in another species (Euglena fusca) showed that cell deformations were accompanied by sliding between adjacent pellicular strips, which kept constant their length and width,^{1, 5, 16} similarly to how flagellar shape depends on microtubule sliding in the axoneme.¹⁷ Inter-strip active sliding results in local deformation of the cell envelope, a simple shear along the direction of the strips (Fig. 1c), which when coordinated in space and time can explain the shape dynamics during metaboly.^{7, 18}

Our continuous observations were consistent with this sliding model; strip width remained nearly constant ($\sim$ 560 nm), and in agreement with a simple shear local deformation of the pellicle, the total cell area remained nearly constant during shape transformations (Supplementary Methods). To further examine the shape-morphing mechanism, we developed a theoretical model linking strip curvature on a planar surface, as in Fig. 1(b), and differential sliding along this strip, Fig. 1(d) and Supplementary Note 1. It allowed us to quantify over time the sliding displacement along selected strips, Fig. 1(e), finding net sliding inter-strip displacements of about one micron during the shape excursion in Fig. 1(b). By comparing sliding displacements at different instants, we estimated sliding velocities of up to $\sim$ 1 $\upmu\text{m/s}$, compatible with those of molecular motors along microtubules.¹⁹ Besides confirming the pellicle strip sliding model, these observations showed that cell volume was nearly constant during metaboly (Supplementary Methods). Interestingly, cells performing metaboly confined between two parallel plates exhibited directed motion in the anterior-to-posterior direction at speeds ranging between 0.08 and 0.2 body lengths per cycle (Supplementary Movies S2 and S3).

To mimic the more realistic situation of multidimensional confinement while having a high degree of experimental control, we drove swimming cells towards tapered glass capillaries with diameter ranging between 300 $\upmu$m and 6 $\upmu$m with slopes always smaller than 0.006 in the region of interest, Fig. 1(f) and Supplementary Fig. 2. When the diameter of the capillary was significantly larger than the cell diameter, cells exhibited fast swimming. As cells moved towards the narrow end of the capillary, they collided with the wall and started developing the behaviors described in the crowded cultures, including bulging and rounding, Supplementary Movie S4. By rounding, some cells were able to switch their orientation in the capillary, Supplementary Movies S4 and S5. Most cells eventually developed characteristic highly coordinated and periodic peristaltic body deformations consisting of a bulge moving in the posterior-to-anterior direction followed by a recovery phase during which the bulge at the posterior end reappears at the expense of that at the anterior end, Fig. 1(f)iv and Supplementary Movie S4. Thus, similarly to culture crowding, confinement provided by the capillary triggered changes in cell behavior, which now seemed to acquire a function: cell rounding to turn and metaboly to crawl.

Close examination of cells performing metaboly in the capillary showed that during their gait, the bulge moving in the posterior-to-anterior direction transiently contacted the capillary wall propelling the cell in the anterior-to-posterior direction, opposite to that of flagellar swimming, Fig. 2(a)i and Supplementary Movie S6. The kinematics of the gait were highly non-reciprocal, and thus in principle compatible with self-propulsion in the non-inertial limit of our experiments.²⁰ Since cells could switch direction in the capillary, we observed cells crawling by metaboly away from and towards its narrower end. As a result, we were able to examine the features of this mode of locomotion at varying degrees of confinement. To ease understanding of pellicle kinematics, we arranged images in the figures and movies so that cells crawl from left to right. At higher confinement, cells adapted their gait by developing a broader bulge, which remained in contact with the wall during a larger fraction of the gait, Fig. 2(a)ii and Supplementary Movie S6. However, the essential features of the crawling mechanism remained the same.

Kymographs of cells crawling showed the high regularity of the gait and its adaptation to increasing confinement, Fig. 2(b). They also revealed that the net cell displacement was the result of a power phase, when the bulge travels towards the anterior end, and a recovery phase with backward cell motion. Remarkably, cells were able to crawl up to very high degrees of confinement, despite the little space available for shape transformations. Cells crawled fastest, at about 2.5 $\upmu$m/s (0.4 body lengths per cycle), at intermediate degrees of confinement, where the bulge established sustained contact with the capillary walls and there was sufficient space for significant shape excursions, Fig. 2(c). The period of the gait, however, was largely independent of confinement, Fig. 2(d). Interestingly, the very small crawling velocities we recorded for weakly confined cells (Fig. 2(a) and largest diameter in Fig. 2(c)), which represent a transition between crawling and swimming, are in agreement with a theoretical study examining the complementary situation of swimmers undergoing large shape changes near walls under weaker capillary confinement.²¹

We then wondered if flagellar locomotion of fixed-shape cells would be effective in this situation. Confined cells propelled by flagella would have to overcome a frictional force against the capillary walls and a hydraulic resistance. We theoretically estimated that such cells would move 10 to 20 times slower than those crawling by metaboly, Supplementary Note 3. These estimations were consistent with observations of stuck cells beating their flagella, Supplementary Movie S8. Thus, by developing metaboly under confinement, cells switched from ineffective flagellar propulsion to a highly robust crawling mode of locomotion.

To propel their body forward during migration in a low Reynolds number limit, Euglena cells must exert self-equilibrated forces on their environment, here, the walls and the fluid within the capillary. To experimentally characterize the physical interaction between cells and their environment, we drove cells not exhibiting deformations into narrow sections of capillaries by applying a known pressure difference while recording cell velocity, contact area, and motion of suspended beads, Supplementary Movie S7. These observations established that confined cells acted as hydraulic plugs and characterized the friction between cells and the wall as viscous and confinement-dependent, Supplementary Note 2.

We attempted to understand force transmission during crawling by metaboly in the light of a prevalent model of animal cells crawling in narrow spaces. According to this model, non-adherent confined cells generate propulsive forces through retrograde actin flows and unspecific friction with the confining wall. This propulsive force is balanced by a resistive hydrodynamic force required to displace the water column in the capillary, ^{22, 23, 24, 25, 26} unless water transport is sufficiently fast across the cell.²⁷ This framework has explained why a large hydraulic resistance relative to the wall friction stalls cell motion and results in fast retrograde flow, whereas vanishing hydraulic resistance leads to fast cell motion and minimal sliding between the polarized actin cytoskeleton relative to the wall. Transposing this model to Euglena cells crawling by metaboly, the backward motion of the pellicle bulge would be the analog of retrograde actin flow of animal cells, Fig. 3(a).

To test this analogy, we developed an idealized theoretical model of the power phase of the gait consistent with the shape-morphing principle of the pellicle of euglenids,^{7, 18} Fig. 3(b). In this model, a bulge establishes contact with a capillary of radius $r$ over a length $\ell_{c}$, and moves backwards at speed $c<0$ in the reference frame of the cell, which otherwise is a cylinder of radius $r_{0}$. The strips in the contact region form an angle $\theta^{*}$ with the cell axis satisfying $\cos\theta^{*}=r_{0}/r$. To weigh the relative importance of hydraulic and frictional resistance, we introduced the non-dimensional quantity $\xi=\mu_{\rm wall}\ell_{c}/(\alpha r)$, where $\mu_{\rm wall}$ is the wall-cell friction coefficient and $\alpha$ is a hydraulic resistance coefficient, Supplementary Note 4.

We first considered the limit of vanishing hydrodynamic resistance relative to wall friction, expressed as $\xi\rightarrow+\infty$. In this situation, the cell velocity $v=-(1-\cos\theta^{*})\,c$ was obtained from the kinematics of the propagating bulge by requiring no slippage between the pellicle and the wall, Fig. 3(c)i and Supplementary Movie S9. This expression is consistent with the very small cell velocities at extreme confinement, where $r\approx r_{0}$ or $\cos\theta^{*}\approx 1$, Fig. 2(c). To examine the effect of cell motion on the fluid inside the capillary in this no-slip scenario, we evaluated with our model the induced water flow rate $Q$ in either side of the bulge, which we assumed to act as a hydraulic plug. Strikingly, we found that as cells crawl without sliding in a given direction, they pump water in the opposite direction at a flow rate given by $Q=\pi r^{2}(1-\cos\theta^{*})\cos\theta^{*}c$. This counterintuitive hydraulic behavior results from the peristaltic shape changes of metaboly, and fundamentally differs from that of non-adherent polarized animal cells, which move like piston-like fixed-shape squirmers.^{24, 28} We then reasoned that, if crawling Euglena cells in this limit were pumping fluid backwards, then hydraulic resistance could in fact act as a propulsive force.

To test theoretically this idea, we placed ourselves in the opposite limit of vanishing wall friction relative to hydraulic resistance, $\xi\rightarrow 0$, and computed cell velocity by requiring zero induced flow rate as the bulge moves backwards. We found that in this scenario the pellicle slides relative to the wall. Furthermore, instead of stalling under high hydraulic resistance like polarized animal cells,²⁴ peristaltic Euglena cells actually move at a faster speed $v=-\left(1-\cos^{2}\theta^{*}\right)\,c$, Fig. 3(c)iii and Supplementary Movie S9. In an intermediate regime, in which propulsion is governed by the balance of finite wall friction and hydrodynamic resistance, our model predicted that cells are propelled by hydraulic resistance and dragged by wall friction, opposite to polarized animal cells, Supplementary Note 4. In summary, despite seeming similarities between the crawling modes of Euglena cells and of non-adherent polarized animal cells, our model highlighted fundamental differences associated with the large shape modulations of the former, and portrayed metaboly as a highly robust and adaptable mode of locomotion capable of using both frictional and hydraulic forces for propulsion depending on the mechanical nature of confinement. Furthermore, the fastest crawling cells in our experiments moved about 20 times faster than the fastest reported non-adherent polarized animal cells.²⁶

One of the most striking predictions of this model is that confined Euglena cells, which act as hydraulic plugs, can move in a capillary without inducing any flow rate thanks to the shape deformations of metaboly. Supporting this prediction, we observed crawling cells accomplishing significant displacements next to stuck immobile cells, Fig. 3(d) and Supplementary Movie S10. In the absence of stuck cells, we visualized the flow generated by crawling cells tracking the motion of suspended micron-sized beads, Fig. 3(e) and Supplementary Movie S11. We found that beads in the vicinity of cells underwent rapid motions revealing local flows induced by shape changes and flagellar beating. These bead velocities, however, exhibited rapid decay away from the cell body, where they were consistent with Brownian motion in a quiescent fluid. Thus, in the light of our model, cells in our capillary experiments were close to the limit of high hydraulic resistance, which acted as the propulsive force. In agreement with this notion, we observed significant pellicle sliding in cells crawling and turning in a capillary, Fig. 3(f) and Supplementary Movies S5 and S12. By contrast and showing the robustness of metaboly, our model suggests that cells between glass plates, where hydraulic confinement is very low, crawled by exploiting frictional propulsion, Fig. 1(b) and Supplementary Movies S2 and S3.

Our previous observations have established that Euglena cells develop highly concerted shape deformations to crawl under confinement, and that cells can adapt their gait to varying degrees of confinement between plates or in a capillary. We then tried to understand whether this complex adaptive behavior necessarily required a dedicated mechanosensing and mechanotransduction machinery or if, instead, the active pellicle could mechanically self-adapt its dynamics to a changing environment. To test this second possibility, we developed a theoretical and computational model of crawling in confinement by metaboly, which included the biological activity leading to strip sliding, the pellicle mechanics, and the interaction with the environment, Supplementary Note 5.

Despite similarities, the actuation mechanism and molecular players involved in metaboly are far less understood than those behind the much faster flagellar beating.¹⁷ On the basis of calcium precipitation assays and reactivation of metaboly in detergent-extracted cell models, inter-strip sliding is thought to depend on molecular motors distinct from flagellar dyneins and associated to microtubules positioned along pellicular strips, which are locally and dynamically activated by the release/sequestration of cytoplasmic calcium from narrow subpellicular channels of endoplasmic reticulum.^{6, 29} In our model, we assumed that the space-time activation pattern driving cell deformations was unaffected by varying confinement, consistent with the confinement-independent period of metaboly, Fig. 2(d). We modeled the pellicle as an extended motor system, and its activation as a space-time modulation of the sliding velocity between adjacent strips in the absence of force, $v_{\textrm{motor}}^{0}(s,t)$ where $s$ is arc-length along the strips and $t$ is time, Fig. 4(a)i,ii. Forces between adjacent strips in the sliding direction can affect the velocity of the motor system. We considered an affine relation between the force experienced by the motor system, $\tau$, and the actual sliding velocity, $v_{\textrm{motor}}$, Fig. 4(a)iii.^{30, 31} To determine the a priori unknown force distribution $\tau(s,t)$ acting on the extended motor system, we accounted for the pellicle elasticity and for its mechanical interaction with the environment, i.e. the cellular pressure to maintain cell volume constant, hydraulic forces required to push the water column, and contact/frictional forces against the capillary, Fig. 4(a)iv. We designed the activity pattern, Fig. 4(a)ii, to match the typical shape dynamics of metaboly at low confinement.⁷ To solve the highly nonlinear equations governing the active mechanics of the deformable pellicle under confinement, we developed a spline-based finite element computational method.

In the absence of confinement, this model rapidly reached a limit cycle (or gait) within a few periods, exhibiting the characteristic peristaltic cell deformations of metaboly, Supplementary Movie S13. As confinement incrementally constrained the shape excursions, we observed that the model self-adapted by developing a new limit cycle consistent with the imposed confinement, Fig. 4(b), which led to cell migration in the presence of frictional wall coupling and/or hydraulic resistance, see Fig. 4(c,d) for the limits of high hydraulic resistance and high friction. Remarkably, the computational model reproduced all the features of confined crawling by metaboly reported in Fig. 2, including the kinematics of the gait under confinement, Fig. 4(b,c), and the non-monotonic relation between capillary diameter and cell velocity, Fig. 4(d), which we attributed to a tradeoff between the ability to develop large shape excursions at low confinement and the sustained contact of the bulge running along a longer cell at high confinement. In agreement with the theoretical model in Fig. 3(c), the computational model also predicted faster motion in the limit of high fluid resistance, in which the maximum velocity agreed quantitatively with our experiments. Taken together, these results support a view of the pellicle of euglenids as an elastic and extended motor system that, once biologically activated, can mechanically self-adjust to the degree of confinement to produce an effective gait.

We have thus established that, in analogy with the mesenchymal-to-amoeboid transition of animal cells ²⁶ or the amoeboid-to-flagellar transition of Naegleria gruberi,³² Euglena gracilis develop a transition between flagellar and metaboly modes of locomotion triggered by confinement. Biophysically, the peristaltic movement of Euglena during metaboly provides a new and remarkably robust mechanism of fast cell crawling. It is unclear, however, whether Euglena take advantage of this capability in natural conditions, where they predominantly swim in the water column. How and why Euglena cells retained an active pellicle, a vestige of a phagotrophic ancestry, and developed the ability to operate this machine in a non-reciprocal manner compatible with effective crawling is intriguing, as further emphasized by our examination of confined metaboly in a primary osmotrophic and a phagotrophic species of euglenids (Supplementary Note 6). From an engineering point of view, the ability of the pellicle to mechanically self-adapt and maintain the locomotory function under different geometric and mechanical conditions represents a remarkable instance of mechanical or embodied intelligence,^{33, 34} a design principle in bio-inspired robotics by which part of the burden involved in controlling complex behaviors is outsourced to the mechanical compliance of the materials and mechanisms that build the device.