Survey of hyperfine structure measurements in alkali atoms
Abstract
The spectroscopic hyperfine constants for all the alkali atoms are reported. For atoms from lithium to cesium, only the long lived atomic isotopes are examined. For francium, the measured data for nuclear ground states of all available isotopes are listed. All results obtained since the beginning of laser investigations are presented, while for previous works the data of Arimondo et. al. Rev. Mod. Phys. 49, 31 (1977) are recalled. Global analyses based on the scaling laws and on the hyperfine anomalies are performed.
I Note
In press J. Phys. Chem. Ref. Data.
II Introduction
Atomic spectroscopy was a key element in the original development of quantum mechanics theory at the beginning of the twentieth century. Its exploratory role continued after the Second World War, when microwave sources, very stable radiofrequency generators, optical pumping, and later on lasers, entered into the laboratories. The atomic contributions to quantum electrodynamics, parity violation, and the present searches for variation of the fundamental constants and for dark matter tests are noteworthy. In this scenery, the alkali atoms and their hyperfine splittings represent an important reference because of their rather simple energy level structure and their relatively easy laboratory exploration. Furthermore, they offer an opportunity to verify new experimental tools for a direct comparison within a wide research community. Very precise hyperfine constants of the alkalis are required for a large variety of atomic physics and quantum simulation experiments. More accurate hyperfine structure measurements have also revitalized their use in studies and tests of nuclear physics and fundamental symmetries in nature. Formidable progress achieved by atomic physics calculations supporting and also stimulating research on the above advanced topics has refined its tools on the alkali hyperfine data.
A complete collection of hyperfine constants for alkali atoms was published by Arimondo, Inguscio, and Violino (1977) at the time when laser sources introduced high-resolution atomic spectroscopy. Since that time, new spectroscopy tools have been developed, and technological advances have produced extremely precise atomic measurements. This progress is the motivation of the present work. The most amazing example of the combination of scientific and technological progress is the atomic fountain proposed by Zacharias in 1953, unpublished but described by Ramsey (1956). Although it does not operate for room temperature atoms, it is very successful for launching ultracold ones, as exploited for hyperfine measurements based on atomic clocks, (e.g., see Guéna et al. (2014); Ovchinnikov, Szymaniec, and Edris (2015)). Using such tool, the hyperfine ground states of rubidium and cesium are presently measured with such a precision that small variations of the fundamental constants can be tested. Recently, the use of frequency combs to perform absolute optical frequency measurements has provided alkali hyperfine values with a precision increased by a factor of up one thousand. In addition, some well assessed spectroscopy tools have been refined. For instance, in Bayram et al. (2014), the detection of delayed quantum beats at the hyperfine transition frequencies is used to determine very precise hyperfine coupling constants in several cesium excited states, for which the precision of other techniques suffers from short lifetimes. These approaches have increased the precision for a large set of hyperfine measurements.
In another class of experiments, the hyperfine constants have been determined for excited states accessible only by laser sources covering new spectral regions or by multiple laser excitations. The most spectacular example is the alkali Rydberg states investigated for hyperfine structure up to levels with principal quantum number . For completeness, here we report a third class of hyperfine measurements of pre-laser times for alkali states not recently investigated. A very interesting example of this class is the ground state hyperfine structures of lithium and sodium, for which the precise atomic-beam investigations of 1973-1974 remain the reference point. Certainly, atomic fountain experiments applied to those atoms could yield a precision comparable to that of the atomic clocks.
This work presents a complete overview of the measured hyperfine constants for the alkali atoms in ground or singly excited electronic states. It enlarges or supersedes the recent reviews of Das and Natarajan (2008); Kiran Kumar and Suryanarayana (2014); Williams, Herd, and Hawkins (2018) that report a limited data set for lighter alkalis. We also add data to the francium review of Sansonetti (2007). The main target is to provide to interested experimentalists and theoreticians the full set of hyperfine data in an easily accessible form. We have collected the hyperfine data of the stable alkali isotopes published after the review of Arimondo, Inguscio, and Violino (1977). In order to give a complete overview, our Tables include measurements already reported in that review in all cases where new and more precise values are not available. We do not examine the unstable isotopes for the alkalis from lithium up to cesium as for them very limited data were recently published. Instead we review the full spectrum of the francium nuclear ground state isotopes, because of the recent interest associated with this atom as a test of the nuclear structure owing to the large number of explored isotopes for this alkali. This review intends to cover the experimental investigations, while discussing theoretical results only briefly. However, it should be mentioned here that theoretical comparison has greatly progressed, and global analyses for a given alkali atom have produced a large set of theoretical values for the hyperfine constants.
For the experimentalists, this overview might stimulate investigations of specific atomic states for which the precision remains low. As advanced spectroscopic techniques are usually tested only on a few states, a large set of high precision data might boost the theoretical effort for global analyses.
Based on Kramida (2022) “NIST atomic energy levels and spectra bibliographic database” (NIST stands for National Institute of Standards and Technology, USA), we have examined all articles that to the best of our knowledge have been published so far. However, we have disregarded publications that do not target the hyperfine splittings. For publications by the same research group reporting subsequent measurements with increasing precision our Tables include only the most recent value.
Section II presents the experimental tools exploited to measure the hyperfine constants. At first the atomic sample is examined from vapor cells up to ultracold atomic clouds where the spatial and velocity confinement greatly increases the spectral resolution. In the following the experiments are classified within some broad categories allowing a connection to the precision reached in ground and excited states. The core part of this review is Sec. III. It is composed of Tables reporting the hyperfine constants for each alkali isotope classified on the basis of the atomic state and for a given state in chronological order. Before presenting the Tables, the basic theoretical concepts of the hyperfine interaction are briefly recalled. For each atom we discuss the main results and we mention large discrepancies, if any, between the data of a given state. For Rb and Cs atoms, where more data are available, Section IV presents scaling laws vs the quantum number of the excited states. Such scaling is applied to determine or confirm the sign of the hyperfine constants for several states. The scaling law is applied also to the states of francium isotopes for which few data are available. Hyperfine anomalies producing information on the nuclear structure are discussed, at least for the states measured with reasonable precision. A short Section concludes this review.
III Spectroscopic tools
III.1 Samples
Atomic beam (AB). In an atomic beam atoms propagate along a given direction with a small spread in the orthogonal plane, see Ramsey (1956). Usually, an exciting laser propagates perpendicularly to the beam propagation leading to a very small Doppler broadening.
Vapor cell (VC). In a glass/quartz cell the atoms are in the vapour phase and their vapour pressure and the atomic density are controlled by the cell temperature.
Magneto-optical trap (MOT). The combined action of laser cooling and magnetic field confinement produces dense atomic samples having a greatly reduced Doppler linewidth. Such samples allow to detect weak absorption features, as for highly excited states, and to perform experiments with long interaction times leading to increased precision.
Fountain (FOUNT). In a fountain, atoms from a MOT are launched vertically by radiation pressure or a moving optical lattice, see Metcalf and van der
Straten (1999). Excitation and detection take place at the same vertical position, the first one at the launching time and the second after the parabolic motion. Very high parabolic evolutions are used in order to increase the interrogation time. This approach is applied to the atomic clocks.
Optical Dipole Trap (ODT) In the experiment by Neuzner et al. (2015) a single 87Rb atom is trapped by an optical dipole trap created by a 2-D optical lattice. Cavity-enhanced state detection of the optical absorption produces a good signal-to-noise ratio even for a single atom. Light-shift correction is carefully applied.
Thermoionic diode (TD). In presence of a weak electrical discharge in a VC, the light excited atoms are ionized by electron collisions. These ions diffuse into the space charge region of the diode, compensate partially the space charge, and increase the thermionic diode current, as described in Herrmann et al. (1985)
III.2 Spectroscopic Techniques
The experimental techniques used to measure the reported hyperfine measurements are classified in the following. Several research groups have introduced a specific name for their technique. While our classification scheme is concise, detailed presentations of the techniques can be found in textbooks, such as Ramsey (1956); Kopfermann (1958); Foot (2005); Budker, Kimball, and DeMille (2008); Inguscio and Fallani (2013).
Coherent-control spectroscopy (CCS). This saturated absorption spectroscopy is based on copropagating pump and probe acting on a three-level V system. Similar to saturated absorption spectroscopy in a two-level system and to the electromagnetic-induced transparency in a level scheme, a pump laser originates an atomic coherence in a branch of the V scheme. The absorption profile of a probe laser is modified. The frequency difference between pump and probe lasers furnishes the excited state energy splitting, as in Das and Natarajan (2005)
Delayed detection (DD). The natural linewidth of a spectroscopic resonance is reduced by monitoring the atom evolution for times longer than the spontaneous emission lifetime. This refinement was combined with other techniques, such as as laser-induced fluorescence by Shimizu et al. (1987) or hyperfine quantum-beats by Deech et al. (1977); Krist et al. (1977); Yei, Sieradzan, and Havey (1993).
Double-resonance optical
pumping (DROP). A double-resonance optical excitation on a ladder three-level scheme is applied. An increased signal-to-noise ratio is obtained by detecting the population of the ground state rather than the excited state one. In the copropagating geometry, one laser excites zero velocity atoms on the lower transition and a second laser is scanned in frequency, as in Moon, Lee, and Suh (2009). In the counterpropaganting geometry, it is often combined with electomagnetic-induced transparency.
Electromagnetic induced transparency (EIT). This coupling/probe spectroscopy is based on the very narrow coherent feature produced in the absorption spectrum of three-level or ladder systems. For the scheme a very narrow linewidth is determined by the long relaxation rate of the ground state coherence. Counterpropagating lasers and one laser locked to an atomic transition are used to produce sub-Doppler resolution, as presented in Krishna et al. (2005); Wang et al. (2013, 2014a) .
Frequency comb spectroscopy (FC), The atomic absorption peaks are determined with a reference to a frequency comb. The absolute precision of the frequency readings is largely increased, see for instance Udem et al. (1999); Das et al. (2006a).
Frequency modulated laser (FML). When the exciting laser is modulated at the hyperfine splitting frequency, cross-over resonances are induced in three-level or V systems, as in Noble et al. (2006). The advantage of this technique is that only a single laser is required.
Hyperfine optical pumping and focus (HOPF). Hyperfine transitions induced by microwaves or by optical pumping change the relative populations of the hyperfine levels of the ground state. In HOPF this modification is detected by measuring the atomic beam intensity at the exit of a magnet that focuses or defocuses atoms with different magnetic quantum numbers. The focused atoms are analyzed by a mass spectrometer, as in Liberman et al. (1980).
Hyperfine quantum beats (HQB). Quantum beats are based on coherent pulsed excitation of excited hyperfine levels producing a time decay of the excited state populations modulated by the hyperfine frequency splitting. Polarized excitation and detection are required, as in Deech et al. (1977). Bellini, Bartoli, and Hänsch (1997) applied delayed pulses of a frequency comb in order to probe the coherent hyperfine superposition of excited states.
Ion detection (ION). This detection technique is very sensitive because a single ion can be detected. It is applied within different schemes, such as the resonant laser ionization (RIS), the selective electric field ionization of a Rydberg state or the thermoionic diode operation.
Laser-induced fluorescence spectroscopy (LIF). The emitted fluorescence is monitored as a function of the laser frequency. In Doppler spectroscopy, a high resolution is achieved by a careful analysis of the absorption lineshapes, as in Truong et al. (2015). In an AB with the laser propagation perpendicular to the atomic motion, the resolution is limited by the natural linewidth. By applying a sudden change to the laser phase and monitoring the atomic evolution at a later time , subnatural width resolution reaching is achieved in Shimizu et al. (1987). For short-lived atoms with low density using a fast beam and a collinear laser propagation, LIF is combined with nuclear decay to increase the signal to noise ratio as in Duong et al. (1987); Lynch et al. (2016).
Level crossing by magnetic or electric fields. An energy crossings of excited state levels vs an external parameter, either magnetic field (MLC) or electric field (ELC), is monitored, see for instance Nagourney, Happer, and Lurio (1978); Auzinsh et al. (2007). A precise determination of the applied field is required.
Maser (MA). The emission frequency of a maser operating on a hyperfine ground state transition is measured in Tetu, Fortin, and Savard (1976).
Magnetic field decoupling (MFD). Starting from an initial anisotropic Zeeman sublevel population distribution, the hyperfine constants are derived from the polarization of the fluorescent emission monitored vs an applied magnetic field decoupling the nuclear and electronic angular momenta, as presented in van Wijngaarden and Sagle (1991b).
Microwave spectroscopy (MWS). The population modifications induced by transitions between hyperfine levels, mainly in the microwaves, are detected. In order to increase the signal-to-noise ratio, MWS is combined to other techniques, such as HOPF, LIF, or selective electric field ionisation for Rydberg states as in Goy et al. (1982). The FOUNT+MWS combination applied to optical clocks leads to an extremely high precision, as in Guéna et al. (2014); Ovchinnikov, Szymaniec, and Edris (2015). A Ramsey optical interferometer is used for the potassium ground state measurement of Arias et al. (2019); Peper et al. (2019).
Optical radiofrequency or microwave double resonance (ORFDR). The radio-frequency induced transitions between excited states are detected through the modification of the LIF, either in its spectrum or in its polarization, as in Farley, Tsekeris, and Gupta (1977); Lam, Gupta, and Happer (1980). Optical pumping is applied to modify the population distribution and increase the detected signal.
Optical-optical double-resonance (OODR). A two-colour excitation via an intermediate step produces the population of excited states. The sub-Doppler resolution is obtained by operating in a MOT in Fort et al. (1995a), by applying the lasers in a counterpropagating geometry in Stalnaker et al. (2010), by a counterpropagating laser geometry selecting a single class of velocities different from zero in Lee and Moon (2015), or by using saturated absorption to lock on the first transition and excite only the atoms at zero velocity in Yang et al. (2016). Detection is based mainly on the spontaneous emission from the intermediate or final state. In presence of an optical pumping process, the population distribution perturbed by the second step excitation is monitored, as in Wang et al. (2014b).
Optical spectroscopy (OS). Doppler limited high optical resolution spectroscopy from an alkali cell as in Truong et al. (2015), or Doppler-free in a MOT as in Antoni-Micollier et al. (2017); Arias et al. (2019).
Resonant ionization spectroscopy (RIS). Atoms in specific states are ionized by multistep laser absorption, and the ions are detected. It was introduced by Andreev, Letokhov, and Mishin (1987) for measuring of the ground state hyperfine structure in francium. The resonant tuning of the intermediate step provides the spectroscopic resolution of its hyperfine structure. High resolution and sensitivity due to ion detection, are associated with this technique as in the MOT experiment by Gabbanini et al. (1999) or for exotic isotopes in an atomic beam of exotic isotopes using
the collinear laser spectroscopy as in Lynch et al. (2014). These last authors directed the ion to an alpha-decay detection station for clear identification in order to reduce isobaric and ground state contamination in their francium isotopes studies. In order to increase the frequency resolution, in recent francium accelerated atomic beam experiments Neugart et al. (2017) the excitation laser is split into two beams, co-propagating and counter-propagating with the atoms in order to increase the frequency resolution.
Saturated absorption spectroscopy (SAS). This technique is based on a pump and probe laser applied to the same transition. It produces spectra with a natural linewidth resolution. The counter-propagating geometry compensates for the Doppler broadening. Main limitations are imposed by the laser stability, as analyzed in Das and Natarajan (2008); Glaser et al. (2020) .
Stark spectroscopy (SS). Stark spectroscopy is based on the electric field shift of atomic level energies. It is used mainly for Rydberg states as in Stevens et al. (1995). Information on lower energy states may be derived by the difference in level Stark shifts.
Two-photon sub-Doppler spectroscopy (TPSDS). A single-colour two photon not-resonant excitation explores highly excited states. The sub-Doppler resolution is obtained by operating with counterpropagating beams in a VC as described by Herrmann et al. (1985); Hagel et al. (1999) or in a MOT as in Georgiades, Polzik, and Kimble (1994).
IV Hyperfine theory
The hyperfine structure Hamiltonian of an atom having a single valence electron outside the closed shells consists of the magnetic dipole , the electric quadrupole and the octupole terms
| (1) |
describes the interaction of the nuclear magnetic moment with the magnetic field generated by the electrons. For the electron angular momentum and the nuclear angular momentum , it is given by
| (2) |
where is the magnetic dipole constant and is the Planck constant.
The electric quadrupole term originates from the Coulomb interaction between the electron and a nonspherically symmetric nucleus. It is given by
| (3) |
where is the electric quadrupole moment coupling constant. This expression is valid for nuclear spins and is zero otherwise.
The octupole Hamiltonian presented in Armstrong (1971) depends on the electron and nuclear tensor operators of rank 3, requires an electron angular momentum at least equal to 3/2 and is characterised by the hyperfine constant. The explicit dependence on the atomic quantum numbers is detailed in Gerginov, Derevianko, and Tanner (2003).
Hyperfine interactions decrease rapidly for higher-lying
states. Kopfermann (1958) showed that the hyperfine constants are proportional to the expectation value of , where is the distance between the nucleus
and valence electron. For highly excited electrons, the valence electron is far from the core electrons and is well approximated by the hydrogenic result
| (4) |
where is the effective principal quantum number, is the principal quantum number, and the difference is the quantum defect. In a more refined treatment, by expressing the Schrödinger wavefunction at the nucleus position through the effective nuclear charge in the inner region where the orbit penetrates, and setting for the net charge of the ion around which the single electron moves, the modified Fermi-Segre formula for the dipolar constant of the state with angular momentum is derived in Kopfermann (1958)
| (5) |
with being the Rydberg constant, the fine structure constant, and the gyromagnetic ratio of the nuclear magnetic moment. The relativistic effects are expressed by the factor near unity for light atoms and different from unity for large numbers. The factor is the change in the electronic wave function for distributions of the nuclear charge over its volume. The factor is the change in the electron-nuclear interaction by the distribution of the magnetic moment, which is called the Breit-Weisskopf effect.
For the quadrupole coupling constant the following expression is derived in Kopfermann (1958):
| (6) |
with the charge of the electron, the vacuum permittivity, the quadrupole nuclear moment and a relativistic correction factor. From Eq. (4) for , it follows that the constant is also proportional to .
On the basis of the above expressions, where the nucleus is represented by a point charge, the following scaling is derived in Kopfermann (1958) for the magnetic dipole and magnetic quadrupole constants and associated with two different isotopes:
| , | (7) | ||||
| , | (8) |
where and represent the nuclear gyromagnetic factor and the quadrupole moment of the isotope , respectively. Deviations from these isotopic scaling laws represent the hyperfine anomalies presented in Subsection VI.2.
The dipolar and quadrupolar hfs Hamiltonians, involving the interaction of spin and orbital angular momenta with the nuclear moments, have matrix elements diagonal over the hyperfine quantum numbers, but also off-diagonal ones connecting fine-structure states with different values as presented in Arimondo, Inguscio, and Violino (1977). These off-diagonal couplings produce a mixing of the eigenstates and a shift of the energies. For fine structure states far apart in energy, a perturbation of the hyperfine constants includes the influence of the off-diagonal matrix elements, as for the Cs doublet in Johnson et al. (2004). In the opposite case, such as the 7Li doublet, the hyperfine splittings are expressed through the parameters of an effective hyperfine-splitting Hamiltonian: contact, dipolar and orbital, respectively, as derived in Lyons and Das (1970). In the first perturbation order and using the one-electron
theory, the different hyperfine constants are written as
| (9) |
These relations have been used by experimentalists for their data analysis.
Higher perturbation order corrections to the Li constants were derived in Beloy and Derevianko (2008); Puchalski and Pachucki (2009). The mixing produced by off-diagonal hyperfine interactions plays an important role in the cesium measurements for parity nonconservation, as in the experiments of Gilbert et al. (1986); Bouchiat, M.-A. and Guéna,
J. (1988), and in the theoretical analysis of Dzuba and Flambaum (2000). It is expected to be even more important in francium.
Eq. (5) predicts the following scaling law:
| (10) |
A similar one applies to on the basis of Eqs. (4) and (6).
For the 87Rb low- states, the dependence on was tested in 1976 by Belin, Holmgren, and Svanberg (1976b) using the dependence of the fine structure data. The scaling law was later verified for 85Rb high states within 2 percent by van Wijngaarden, Li, and Koh (1993). More recently, with the very high- values having been precisely derived from laser spectroscopy, the scaling was tested for the 85Rb Rydberg states between and in Li et al. (2003) and Ramos, Cardman, and Raithel (2019). The 87Rb data obtained by Li et al. (2003) were reexamined for the scaling in Mack et al. (2011). In Saßmannshausen, Merkt, and Deiglmayr (2013) the scaling law was verified for the Cs and Rydberg states in the range.
The theoretical determination of the hyperfine constants has greatly evolved within the last few years. Instead of focusing on a few atomic states, the more recent calculations target a very large number of states. While in 1999 a few hyperfine constants of different alkalis were calculated, e.g., in Safronova, Johnson, and Derevianko (1999), more recently M. Safronova and coworkers in ( Johnson et al. (2008); Safronova and Safronova (2008, 2011); Auzinsh et al. (2007)) have produced a global derivation of the constants for 7Li, 39K, 87Rb, and 133Cs. Later, the hyperfine data for all the K isotopes were carefully examined by Singh, Nandy, and Sahoo (2012), for Rb and Cs by Grunefeld, Roberts, and Ginges (2019), for Cs by Tang, Lou, and Shi (2019), and for Fr by Sahoo et al. (2015); Lou et al. (2019); Grunefeld, Roberts, and Ginges (2019). The global analysis by Singh, Nandy, and Sahoo (2012) has derived precise values for the nuclear quadrupole moments of the potassium isotopes demonstrating a good internal consistency of the hyperfine data. The development led by Marianna Safronova to provide both experimental and theoretical energy level information for a large variety of atoms is a welcome addition to the data compilation. It is currently available online, see Barakhshan et al. (2022).
The hyperfine interaction and the weak interaction that gives rise to parity-nonconservation (PNC) in atoms both happen because the electron density overlaps with the nucleus. From a particle physics point of view, the exchange of the boson carries the weak interaction with its PNC. Atomic PNC interest comes from its unique possibility to test the standard model at low energy. The structure of the nucleus is key to the details of nuclear-spin-independent PNC, where the electron axial-vector-current interacts with the nucleon vector-current. The nuclear-spin-dependent PNC, where the nucleon axial-vector-current interacts with the electron vector-current also depends on nuclear structure and is primarily due to the nuclear anapole moment. As noted by Flambaum and Khriplovich (1985) and confirmed by Bouchiat and Piketty (1991); Johnson, Safronova, and Safronova (2003) the hyperfine interaction leads to the nuclear spin dependence of the matrix element in the atomic PNC. Cs measurements by Wood et al. (1997) reached enough sensitivity to measure the anapole moment in the nuclear-spin-dependent part of the PNC interaction. A new generation of atomic parity violation experiments is underway, e.g. Gwinner and Orozco (2022). These experiments are made with francium atoms. The PNC effects in Fr with respect to Cs are estimated to be 18 times larger for the nuclear-spin-independent and 11 times larger for the nuclear-spin-dependent part.
The determination of the parity-conserving quantities in both high precision experiments and ab initio calculations, such as transition matrix elements, lifetimes, polarizabilities, and hyperfine constants, is essential for PNC studies. The hyperfine constants test in quantitative ways the quality of the electronic wavefunction near the nucleus. This unique combination between theory and experiment has greatly favored the heaviest alkali atoms and has stimulated a large search effort for the hyperfine structures in their isotopes as presented in Safronova et al. (2018).
V Measured hyperfine constants
In the following, we present several Tables for the measured and constants of the alkali atoms. In a few cases, we derive the constant from the measured hyperfine splitting reported by the authors using the formula for the hyperfine energies given by Kopfermann (1958). In each Table, the atomic states are listed in order of increasing , then of increasing , increasing , and finally chronologically. Two columns report the acronyms determining the atomic sample and the spectroscopic technique applied in the measurement. The reference to the original publication is in the last column. The spectroscopic technique column reports the “From” notation for the data taken from Arimondo, Inguscio, and Violino (1977), for which a critical examination or a weighted averaging over several measurements was performed, leading to a recommended value. When the hyperfine value reported in that reference remains the only one available, or its error bar is smaller than later measurements, the original work is directly quoted in the Table. Within the Table’s column the entry "" denotes that the authors have assumed the quadrupole constant equal to zero.
A few techniques, such as the HQB, are not able to resolve the sign of the constants for the explored state. On the basis of the above scaling laws applied to different atoms within Section VI.1, we have produced a dependable sign assignment for most states. If the sign was not identified, the absolute value is reported.
The measurement uncertainties are reported in the text and Tables in parentheses after the value, in units of the last decimal place of the value. For example, 153.3(11) means 153.3 1.1. Most authors specify their uncertainty on the level of one standard deviation. If a different convention is used, it is mentioned in the text.
For each atomic species, we mention in the text the states where a very high precision is obtained or where a disagreement between the measured values exists. When several () measurements are associated with a single state, the Tables include a weighted average, w.a., representing a reference for further work. We follow the procedure of the Particle Data Group in Zyla et al. (2020) in the Introduction, Sec. 5.2.2, Unconstrained averaging, to find the weighted error (w.e.). We calculate it first based on the individual errors (), w.e. We also calculate the reduced -squared with degrees of freedom, to test the size of the weighted error. If is greater than unity by more than one standard deviation , then we increase the w.e. of the w.a. by the factor , so that the weighted enhanced error (w.e.e.) is w.e.e.= w.e..
We report in the table either the w.a. with its weighted error or the enhanced error (w.e.e.), which we explicitly state.
Such averaging is not performed when the precision of one measurement is greater than all the remaining ones, which is then denoted by “Recommended” in the Table’s last column. The last column contains a “See text” statement, if one or more values are not included into the w.a..
A different way of averaging developed by Rukhin (2009, 2019) evaluates the clustering of the data and assigns individual hidden uncertainties to the measurements from different groups. These uncertainties are then added in quadrature to the stated uncertainties. Weighted averages and weighted errors calculated by this cluster maximum likelihood estimator (CMLE) are not always identical to the values reported in our Tables. For completeness, whenever a Table recommended value includes a w.e.e. derived from the analysis, we have used the CMLE method to calculate the corresponding w.a.CMLE weighted average and w.e.e.CMLE weighted enhanced error. The comparison between the recommended values obtained by these two approaches shows that in almost all the
28 cases the weighted average of the two analyses
agrees within two times the w.e.e.. There are only two cases with a greater difference, associated with a large value as an indicator of an anomalous scatter of the data. The interested reader can find results and plots in the Supplementary Information (SI) of this review, reference Allegrini, Arimondo, and Orozco (2022).
V.1 Lithium
Data for this atom are reported in Table LABEL:Table:Li. As for all alkalis, several spectroscopic investigations are stimulated by the interest in laser cooling, but only a few experiments are performed in a MOT. The recent 6Li MOT experiments by Wu et al. (2018); Li et al. (2020); Rui et al. (2021) at Shanghai may open a new trend. For the ground state of both lithium isotopes, the "old” atomic beam measurements based on MWS report the highest precision, not reached by the several ones based on laser spectroscopy. Otto et al. (2002) performed measurements for a few high- states of 7Li, as well as for other alkalis.
For the 6,7Li 2 state measurements by Umfer, Windholz, and Musso (1992), the error bar is derived on the basis of Eqs. (9) from the off-diagonal constants presented in the following. For the value of the 3 state of both isotopes measured by Lien et al. (2011), we estimated the error bar not reported by the authors.
A wide experimental effort concentrates on the state of both isotopes. Instead, the state of 6Li remains with the data obtained before laser spectroscopy. For 7Li, three experimental investigations of this doublet, by Orth, Ackermann, and Otten (1975), Nagourney, Happer, and Lurio (1978) and Umfer, Windholz, and Musso (1992),
consider the contribution of the off-diagonal hyperfine couplings linked to the small fine-structure splitting. Orth, Ackermann, and Otten (1975) include in their analysis the previous level crossing data by Brog, Eck, and Wieder (1967). The analysis by Nagourney, Happer, and Lurio (1978) combines their own data and the previous ones. Umfer, Windholz, and Musso (1992) acquired enough data for their own analysis. Orth, Ackermann, and Otten (1975) using Eqs. (9) and their measured MHz found , , . Nagourney, Happer, and Lurio (1978) reported , , , and Umfer, Windholz, and Musso (1992) obtained , , (all in MHz). For the same doublet, Beloy and Derevianko (2008) performed an accurate evaluation of the off-diagonal hyperfine couplings. They produced corrections to the measured dipole constant in the accurately measured by Orth, Ackermann, and Otten (1975), Walls et al. (2003), and Das and Natarajan (2008). For this last one, the 27.0 kHz correction should be compared to the author’s original 3 kHz experimental uncertainty.
A disagreement exceeding the error bars exists for the 3 7Li hyperfine constant measured in Stevens et al. (1995), compared to those of Bushaw et al. (2003); Lien et al. (2011). We do not include that measurement in the w.a.
The discrepancy for the 7Li constants between the previous values byBudick et al. (1966); Isler, Marcus, and Novick (1969) and the Nagourney, Happer, and Lurio (1978) ones remains unexplained as pointed out by these authors. Therefore, instead of the recommended value from Arimondo, Inguscio, and Violino (1977), we consider all the previous measurements. The correction is applied to the statistical error. An analysis of the off-diagonal elements was performed by Nagourney, Happer, and Lurio (1978) for the 7Li doublet, leading to , , .
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 6Li | |||||
| 2 | AB | MWS | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | ION | Lorenzen and Niemax (1982) | ||
| " | AB | LIF | Windholz et al. (1990) | ||
| " | AB | LIF | Walls et al. (2003) | ||
| " | AB | FML | Noble et al. (2006) | ||
| " | AB | LIF+FC | Sansonetti et al. (2011) | ||
| " | MOT | LIF | Wu et al. (2018); Li et al. (2020) | ||
| " | - | - | Recommended | ||
| 2 | VC | ORFDR | Orth et al. (1974) | ||
| " | VC | MLC | Nagourney, Happer, and Lurio (1978) | ||
| " | AB | LIF | Windholz et al. (1990) | ||
| " | AB | LIF | Walls et al. (2003) | ||
| " | AB | FML | Noble et al. (2006) | ||
| " | AB | LIF | Das and Natarajan (2008) | ||
| " | AB | LIF+FC | Sansonetti et al. (2011) | ||
| " | MOT | LIF | Li et al. (2020); Rui et al. (2021) | ||
| " | MOT | LIF+DD | Li et al. (2021) | ||
| " | - | - | w.a. | ||
| 2 | AB | ORFDR | Orth et al. (1974) | ||
| 3 | VC | ION | Vadla, Obrebski, and Niemax (1987) | ||
| " | AB | TPSDS+RIS | Bushaw et al. (2003) | ||
| " | AB | RIS | Ewald et al. (2004) | ||
| " | AB | LIF | Lien et al. (2011) | ||
| " | AB | RIS | Nörtershäuser et al. (2011) | ||
| " | - | - | w.a. | ||
| 3 | VC | MLC | Nagourney, Happer, and Lurio (1978) | ||
| 3 | VC | MLC | Isler, Marcus, and Novick (1969) | ||
| 4 | AB | LIF | Kowalski et al. (1978) | ||
| " | VC | ION | Lorenzen and Niemax (1982) | ||
| " | AB | LIF | DeGraffenreid and Sansonetti (2003) | ||
| " | - | - | w.a. | ||
| 7Li | |||||
| 2 | AB | MWS | Beckmann, Böklen, and Elke (1974) | ||
| " | VC | ION | Lorenzen and Niemax (1982) | ||
| " | AB | LIF | Windholz et al. (1990) | ||
| " | AB | LIF | Walls et al. (2003) | ||
| " | AB | MFL | Noble et al. (2006) | ||
| " | AB | LIF+FCS | Sansonetti et al. (2011) | ||
| " | AB | LIF | Huang et al. (2013) | ||
| " | - | - | Recommended | ||
| 2 | AB | ORFDR | Orth et al. (1974) | ||
| " | AB | LIF | Windholz et al. (1990) | ||
| " | AB | MLC | Umfer, Windholz, and Musso (1992) | ||
| " | AB | LIF | Walls et al. (2003) | ||
| " | AB | FML | Noble et al. (2006) | ||
| " | AB | LIF | Das and Natarajan (2008) | ||
| " | VC | SAS | Singh, Muanzuala, and Natarajan (2010) | ||
| " | AB | LIF+FCS | Sansonetti et al. (2011) | ||
| " | AB | LIF | Huang et al. (2013) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 2 | AB | ORFDR | Orth, Ackermann, and Otten (1975) | ||
| " | VC | MLC | Nagourney, Happer, and Lurio (1978) | ||
| " | AB | LIF+DD | Shimizu et al. (1987) | ||
| " | AB | LIF | Windholz et al. (1990) | ||
| " | AB | HQB | Carlsson and Sturesson (1989) | ||
| " | AB | MLC | Umfer, Windholz, and Musso (1992) | ||
| " | - | - | w.a. | ||
| 3 | VC | ION | Vadla, Obrebski, and Niemax (1987) | ||
| " | AB | SS | Stevens et al. (1995) | ||
| " | AB | TPSDS+RIS | Bushaw et al. (2003) | ||
| " | AB | RIS | Ewald et al. (2004) | ||
| " | AB | LIF | Lien et al. (2011) . | ||
| " | AB | RIS | Nörtershäuser et al. (2011) | ||
| " | AB | SAS | Kumar and Natarajan (2017) | ||
| " | - | - | See text. w.a. | ||
| 3 | VC | MLC | Budick et al. (1966) | ||
| " | VC | MLC | Nagourney, Happer, and Lurio (1978) | ||
| " | - | - | Recommended | ||
| 3 | VC | MLC | Budick et al. (1966) | ||
| " | VC | MLC | Isler, Marcus, and Novick (1969) | ||
| " | VC | MLC | Nagourney, Happer, and Lurio (1978) | ||
| " | - | - | w.a. (w.e.e.) | ||
| 3 | AB | TPSDS | Burghardt, Hoffmann, and Meisel (1988) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 3 | AB | TPSDS | Burghardt, Hoffmann, and Meisel (1988) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 4 | AB | LIF | Kowalski et al. (1978) | ||
| " | VC | ION | Lorenzen and Niemax (1982) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | AB | LIF | DeGraffenreid and Sansonetti (2003) | ||
| " | - | - | w.a. | ||
| 4 | VC | MLC | Isler, Marcus, and Novick (1969) | ||
| 6 | VC | TPSDS | Otto et al. (2002) | ||
| 7 | " | " | " |
V.2 Sodium
The sodium results of Table LABEL:Table:Na are emblematic of the progress achieved in hyperfine constant measurements. In chronological order, the two-photon sub-Doppler spectroscopy was applied in 1978 to probe the excited states, by Biraben and Beroff (1978) and Burghardt et al. (1978), extended by this last research group to the states in Burghardt, Hoffmann, and Meisel (1988). In 1989, Kasevich et al. (1989) published the first hyperfine ground state determination in an atomic fountain with 1 mHz precision, close to the previous best atomic beam value of Table LABEL:Table:Na, opening the road to further amazing improvements in fountain atomic clocks. Zhu, Oates, and Hall (1993) performed the first hyperfine constant measurement in a MOT exploring the states with a relative precision among the best ones for excited states. In the same year, Yei, Sieradzan, and Havey (1993) performed subnatural linewidth measurements of hyperfine coupling constants using the delayed detection in polarization quantum beat spectroscopy. In 2003, the excitation of ultracold atoms in a MOT on the electric quadrupole transition allowed Bhattacharya, Haimberger, and Bigelow (2003) to perform high resolution spectroscopy of the 4 level. Das and Natarajan (2006b) introduced the CCS approach for the first excited state, 3. However, no competitive new data for the ground state are available.
The 3 states have been examined by several authors, with an increasing precision and a good agreement among the different results.
For the 4 states of Biraben and Beroff (1978) and for the 7, 8 and 9
ones of Jiang, Jönsson, and Lundberg (1982), the sign has been determined here from the scaling law. In sodium, there is not enough data for a global analysis. For the large majority of excited states above the ones, no new data have been published after 1982.
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 3 | AB | MWS | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | SAS | Pescht, Gerhardt, and Matthias (1977) | ||
| " | FOUNT | RIS | Kasevich et al. (1989) | ||
| " | - | - | Recommended | ||
| 3 | VC | SAS | Pescht, Gerhardt, and Matthias (1977) | ||
| " | AB | LIF | Griffith et al. (1977) | ||
| " | AB | LIF | Umfer, Windholz, and Musso (1992) | ||
| " | AB | HQB | Carlsson et al. (1992) | ||
| " | AB | LIF | van Wijngaarden and Li (1994) | ||
| " | AB | LIF | Scherf et al. (1996) | ||
| " | VC | SAS | Das and Natarajan (2008) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 3 | AB | HQB | Krist et al. (1977) | ||
| " | AB | HQB | Carlsson and Sturesson (1989) | ||
| " | AB | LIF | Umfer, Windholz, and Musso (1992) | ||
| " | VC | HQB+DD | Yei, Sieradzan, and Havey (1993) | ||
| " | AB | LIF | van Wijngaarden and Li (1994) | ||
| " | AB | LIF | Scherf et al. (1996) | ||
| " | AB | HQB | Volz et al. (1996) | ||
| " | AB | LIF | Gangrsky et al. (1998) | ||
| " | VC | CCS | Das et al. (2006b) | ||
| " | - | - | w.a.(w.e.e.); w.a. | ||
| 3 | AB | TPSDS | Burghardt, Hoffmann, and Meisel (1988) | ||
| 3 | " | " | " | ||
| 4 | VC | TPSDS+LIF | Arqueros (1988) | ||
| 4 | VC | ORFDR | Grundevik and Lundberg (1978) | ||
| " | MOT | OODR+RIS | Bhattacharya, Haimberger, and Bigelow (2003) | ||
| " | - | - | w.a. | ||
| 4 | VC | LC+ORFDR | From Arimondo, Inguscio, and Violino (1977) | ||
| 4 | VC | TPSDS | Biraben and Beroff (1978) | ||
| " | AB | TPSDS | Burghardt et al. (1978) | ||
| " | - | - | Recommended | ||
| 4 | VC | TPSDS | Biraben and Beroff (1978) | ||
| " | AB | TPSDS | Burghardt et al. (1978) | ||
| " | - | - | Recommended | ||
| 5 | VC | ORFDR | Tsekeris, Liao, and Gupta (1976) | ||
| " | MOT | TPSDS+RIS | Marcassa et al. (1998) | ||
| " | - | - | w.a. | ||
| 5 | VC | ORFDR | Grundevik and Lundberg (1978) | ||
| " | MOT | SAS | Zhu, Oates, and Hall (1993) | ||
| " | - | - | Recommended | ||
| 5 | AB | HQB | Grundevik et al. (1979) | ||
| " | MOT | SAS | Zhu, Oates, and Hall (1993) | ||
| " | - | - | Recommended | ||
| 6 | VC | ORFDR | Lundberg, Mårtensson, and Svanberg (1977) | ||
| " | AB | SS | Hawkins et al. (1977) | ||
| " | - | - | Recommended | ||
| 6 | AB | HQB | Grundevik et al. (1979) | ||
| 7 | AB | ORFDR | Lundberg, Mårtensson, and Svanberg (1977) | ||
| " | AB | SS | Hawkins et al. (1977) | ||
| " | - | - | Recommended | ||
| 7 | VC | QBS | Jiang, Jönsson, and Lundberg (1982) | ||
| 8 | VC | ORFDR | Lundberg, Mårtensson, and Svanberg (1977) | ||
| 8 | VC | QBS | Jiang, Jönsson, and Lundberg (1982) | ||
| 9 | " | " | " |
V.3 Potassium
Our previous Li and Na remarks on the ground state values do not apply to the 39K ground state, as shown in Table LABEL:Table:K. For this atom, several recent measurements exist, with the frequency comb spectral resolution applied to determine the absolute transition frequencies, and from them, the fine and hyperfine splittings. A high precision is achieved, usually with a good agreement among data from different research groups, e. g. for several states with measurements performed over a long time span. Otto et al. (2002) explored the states of the 39 and 41 isotopes up to using two-photon sub-Doppler spectroscopy.
The spatial dependence of the HQB polarized fluorescence intensity in a given magnetic field was used by Głódź and Kraińska-Miszczak (1985a) to derive for the first time the signs of the constants in the states of 39K. For other states, the investigations by Belin et al. (1975b), Sieradzan et al. (1997)and Głódź and Kraińska-Miszczak (1985b) produced only the absolute sign of the and constants. Their signs are determined here on the basis of the scaling laws.
V.3.1
The ground 4 state was measured in three MOT experiments by Antoni-Micollier et al. (2017); Arias et al. (2019); Peper et al. (2019). Peper et al. (2019) obtained a value close to the old atomic beam experiments with a difference in the 10 Hz range. Arias et al. (2019) claimed that their small discrepancy with the previous AB measurement can be accounted for by the Hz quadratic Zeeman shift of the bias field and by the differential ac Stark shift in the optical dipole trap. The Table LABEL:Table:K value takes into account such shift. Antoni-Micollier et al. (2017) reported an all-optical measurement of the hyperfine splitting with a low statistical uncertainty, but there were uncontrolled systematical errors in their work, according to Peper et al. (2019).
A large disagreement exists between the measured values of the 4 states, some of them having been reported with high precision. The data are centred around two separate values 27.78(4) and 28.849(5) MHz with a separation larger than the reported precision. The lower values are by Bendali, Duong, and Vialle (1981); Touchard et al. (1982); Duong (1982); Papuga et al. (2014), (all of them with low precision) and by Falke et al. (2006) with higher precision. The greater values were obtained in an AB magnetic resonance experiment by Buck and Rabi (1957) with a low precision and in two recent measurements by the Bangalore research group Banerjee, Das, and Natarajan (2004); Das and Natarajan (2008) used the accurate CCS technique. The for the full data set leads to a very large error bar. Light shifts corrections, an important issue for several recent publications, were taken into account by the Bangalore group. They stated, "we do not have a satisfactory explanation for such a large discrepancy”. Such a discrepancy does not exist for the 4 values determined at the same time by Falke et al. (2006) and Das and Natarajan (2008). Falke et al. (2006) compared their 6,7Li optical transition values to those by Banerjee, Das, and Natarajan (2004) and attributed the discrepancies to systematic errors in the laser calibration, more precisely to phase shifts in the wavelength (not frequency) comparison of the atomic excitation lasers. In Das and Natarajan (2008), the driving frequency of an acousto-optical modulator gives a direct measurement of the hyperfine interval and the calibration issue should have been resolved. For the discrepancies in those optical frequencies, Brown et al. (2013) pointed out the important role of quantum interference and light polarization effects. For the 4 state the Table LABEL:Table:K reports a w.a. excluding the Banerjee, Das, and Natarajan (2004); Das and Natarajan (2008) values.
For the 6 state, the value referred to Thompson et al. (1983) in the Table LABEL:Table:K was derived from their hyperfine splitting in Stalnaker et al. (2017).
V.3.2
The 7 values by Thompson et al. (1983) and by Otto et al. (2002) have a large disagreement. The first value is not consistent with the scaling law applied to the states of this isotope. The Otto et al. (2002) value is the “Recommended” one.
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 39K | |||||
| 3 | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | VC | HQB+DD | Sieradzan et al. (1997) | ||
| " | - | - | Recommended | ||
| 3 | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | VC | HQB+DD | Sieradzan et al. (1997) | ||
| " | - | - | Recommended | ||
| 4 | AB | MWS | From Arimondo, Inguscio, and Violino (1977) | ||
| " | AB | LIF | Touchard et al. (1982) | ||
| " | AB | MWS | Duong et al. (1993) | ||
| " | AB | LIF | Papuga et al. (2014) | ||
| " | MOT | MWS | Arias et al. (2019) | ||
| " | MOT | MWS | Peper et al. (2019) | ||
| " | AB | RIS | Koszorús et al. (2019) | ||
| " | - | - | Recommended | ||
| 4 | AB | MWS | Buck and Rabi (1957) | ||
| " | AB | FML | Bendali, Duong, and Vialle (1981); Duong (1982) | ||
| " | AB | LIF | Touchard et al. (1982) | ||
| " | VC | SAS | Banerjee, Das, and Natarajan (2004) | ||
| " | AB | LIF+FC | Falke et al. (2006) | ||
| " | VC | CCS | Das and Natarajan (2008) | ||
| " | AB | LIF | Papuga et al. (2014) | ||
| " | - | - | See Text. w.a.(w.e.e.) | ||
| 4 | AB | LIF+FC | Falke et al. (2006) | ||
| " | VC | CCS | Das and Natarajan (2008) | ||
| " | - | - | w.a. | ||
| 5 | VC | ORFDR | Gupta et al. (1973) | ||
| 5 | VC | ORFDR | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | SAS | Halloran et al. (2009) | ||
| " | - | - | w.a. | ||
| 5 | VC | MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| 5 | VC | ORFDR | Belin et al. (1975b) | ||
| 5 | " | " | " | ||
| 6 | VC | ORFDR | Gupta et al. (1973) | ||
| " | TD | TPSDS | Thompson et al. (1983) | ||
| " | VC | TPSDS | Kiran Kumar and Suryanarayana (2011) | ||
| " | VC | OODR+FC | Stalnaker et al. (2017) | ||
| " | - | - | w.a. | ||
| 6 | VC | ORFDR | Belin et al. (1975b) | ||
| 6 | VC | MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| 6 | VC | HQB+MFD | Głódź and Kraińska-Miszczak (1985a) | ||
| 6 | " | " | " | ||
| 7 | VC | ORFDR+MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| " | TD | TPSDS | Thompson et al. (1983) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 7 | VC | ORFDR | Belin et al. (1975b) | ||
| 7 | " | " | " | ||
| 8 | " | " | " | ||
| " | VC | TPSDS | Thompson et al. (1983) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 9 | TPSDS | " | Otto et al. (2002) | ||
| 10 | VC | MLC | Belin et al. (1975a) also | ||
| in Arimondo, Inguscio, and Violino (1977) | |||||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 11 | VC | TPSDS | Otto et al. (2002) | ||
| 12 | " | " | " | ||
| 13 | " | " | " | ||
| 14 | " | " | " | ||
| 40K | |||||
| 3 | VC | HQB+DD | Sieradzan et al. (1997) | ||
| 3 | " | " | " | ||
| 4 | AB | MWS | From Arimondo, Inguscio, and Violino (1977) | ||
| 4 | AB | FML | Bendali, Duong, and Vialle (1981) | ||
| " | AB | LIF+FC | Falke et al. (2006) | ||
| " | - | - | Recommended | ||
| 4 | VC | MLC | Ney et al. (1968) | ||
| " | AB | FML | Bendali, Duong, and Vialle (1981) | ||
| " | AB | LIF+FC | Falke et al. (2006) | ||
| " | - | - | Recommended | ||
| 5 | VC | SAS | Behrle, Koschorreck, and Köhl (2011) | ||
| 5 | VC | MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| 41K | |||||
| 3 | VC | HQB+DD | Sieradzan et al. (1997) | ||
| 3 | " | " | " | ||
| 4 | AB | MWS | From Arimondo, Inguscio, and Violino (1977) | ||
| " | AB | LIF | Touchard et al. (1982) | ||
| " | - | - | Recommended | ||
| 4 | VC | FML | Bendali, Duong, and Vialle (1981) | ||
| " | AB | LIF | Touchard et al. (1982) | ||
| " | AB | LIF+FC | Falke et al. (2006) | ||
| " | - | - | Recommended | ||
| 4 | VC | MFD | Ney (1969) | ||
| " | VC | MFD | Kraińska-Miszczak (1981) | ||
| " | VC | HQB | Sieradzan, Kulatunga, and Havey (1995) | ||
| " | AB | LIF+FC | Falke et al. (2006) | ||
| " | - | - | w.a. | ||
| 5 | VC | ORFDR | Gupta et al. (1973) | ||
| 5 | VC | MLC | Ney (1969) | ||
| 5 | VC | MLC | Ney (1969) | ||
| 6 | VC | ORFDR | Gupta et al. (1973) | ||
| " | VC | TPSDS | Kiran Kumar and Suryanarayana (2011), also | ||
| in Kiran Kumar et al. (2014) | |||||
| " | - | - | Recommended | ||
| 6 | VC | HQB | Głódź and Kraińska-Miszczak (1985b) | ||
| 7 | TD | TPSDS | Thompson et al. (1983) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 8 | TD | TPSDS | Thompson et al. (1983) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 9 | VC | TPSDS | Otto et al. (2002) | ||
| 10 | " | " | " | ||
| 11 | " | " | " |
V.4 Rubidium
The long list of recent spectroscopic data for this atom is the result of the laser cooling research in worldwide spread laboratories. For both the 85 and 87 isotopes, the ultracold atomic samples have produced very precise measurements of several hyperfine splittings, in particular for the ground state and the Rydberg ones from =26 to =46. Note that 87Rb has 50 neutrons, the exact magic number that makes it a closed shell.
Entries with very high precision and good agreement are presented in the Tables LABEL:Table:85Rb and LABEL:Table:87Rb for 85Rb and 87Rb, respectively. The Tables report the weighted average of the two published measured values for the 87Rb 6 state by Nyakang’o et al. (2020), while for the 85,87Rb 5, and 6 states, the reported average was communicated by Shiner et al. (2007). The error bars of the hyperfine constants for both isotopes measured by Orson et al. (2021) and the measurements with a 30 KHz precision of McLaughlin et al. (2022) were communicated privately by M. Lindsay. For the constants of the 57 and 58 states measured by Meschede (1987) for the 87Rb the missing error bar is assumed equal to the 85Rb ones.
For () states the investigations by Svanberg and Tsekeris (1975), van Wijngaarden, Li, and Koh (1993) and by Głódź and Kraińska-Miszczak (1987, 1990, 1991); Kraińska-Miszczak (1994) produced only the relative signs of the and constants. Their signs are determined here on the basis of the scaling laws presented in Fig. 3 of Sec. VI.1.
For the 85 isotope in Table LABEL:Table:85Rb, the ground state hyperfine measurement in a maser by Tetu, Fortin, and Savard (1976) agrees with and supersedes the atomic beam MWS results reported in Arimondo, Inguscio, and Violino (1977). The following Table entries based on saturated absorption spectroscopy by Barwood, Gill, and Rowley (1991); Shiner et al. (2007) or atomic beam laser spectroscopy by Duong et al. (1993) have a lower precision. They are superseded by the clock measurements in an optical fountain by Wang et al. (2019). The 87Rb fountain progress was summarized in 2012 by the International Committee for Weights and Measures with their recommended Table LABEL:Table:87Rb value. Later observations by Guéna et al. (2014); Ovchinnikov, Szymaniec, and Edris (2015) improved its precision.
Data for the level of both isotopes are classified in two groups. The first one includes Barwood, Gill, and Rowley (1991), and Maric, McFerran, and Luiten (2008) while the second one includes the optical spectroscopy determination by Beacham and Andrew (1971) recommended in Arimondo, Inguscio, and Violino (1977), the Banerjee, Das, and Natarajan (2004) and Das and Natarajan (2006a) data from the Bangalore research team, and the Rupasinghe et al. (2022) value. The agreement of the results within each group is good. However, the first group compared to the second one derives the 85Rb constant lower by 0.146(13) MHz, and the 87Rb value higher by 2 202(33) MHz. The data of both groups lead to peculiar values for the hyperfine anomaly. The higher measured values for 87Rb are closer to the theoretical predictions by Safronova and Safronova (2011) of 408.53 MHz and by Grunefeld, Roberts, and Ginges (2019) of 410.06 MHz. The only theoretical prediction for 85Rb by Pal et al. (2007) of 119.192 MHz is off by a few MHz above both group results. The search for similar systematic errors as discussed for the case of the 39K 4 state combined with the present restricted data set does not resolve the discrepancy. For this state the weighted average entry in both Tables LABEL:Table:85Rb and LABEL:Table:87Rb is reported with a large error bar determined from the approach.
For the 85Rb 5 state, excellent agreement exists for the value. This is not the case for the constant, where the SAS measurement by Barwood, Gill, and Rowley (1991) considered as a reference point increases greatly the and as a consequence the error bar. An agreement within less than 30 kHz is reached for most data of the 87Rb 5 state. An excellent relative precision of was reached by two separate measurements on the 87Rb isotope by Ye et al. (1996); Das and Natarajan (2008). In Table 6, the Ye et al. (1996) data reexamined by Gerginov, Tanner, and Johnson (2009) bring evidence of the octupole contribution to the Rb hyperfine interactions.
Another example of large discrepancies is found for the 85Rb state. The 39.470(32) MHz SAS+FC measurement by Glaser et al. (2020) presents a difference exceeding the error bar, compared to the values reported by by Shiner et al. (2007) based on the same SAS+FC technique, and also the ORFDR measurement by Feiertag and zu Putlitz (1973) and the OODR-EIT measurement by Nyakang’o et al. (2020). Our derivation of the hyperfine splitting from the measured optical frequencies of Glaser et al. (2020) leads to the 39.11(22) MHz value in good agreement with other ones. Therefore, the Glaser et al. (2020) entry is not included in the weighted average.
In contrast, the Glaser
et al. (2020) data for both isotopes are in very good agreement with the earlier radiofrequency and level-crossing data. For that state in 85Rb, the value derived by Zhang et al. (2017) on the basis of saturated absorption and EIT measurements is close to those of other references. However, that experiment produced a constant with a large deviation from other values, probably because the hyperfine lines were not well resolved. Both their and values are not included into the w.a..
The state of both isotopes has received a wide attention because of the large probability for the two-photon excitation from the ground state. Precision at the level is reached in the 87 isotope and at the level in the 85 one, limited by the 2 kHz resolution of the frequency comb in Krishna et al. (2005); Chui et al. (2005); Barmes, Witte, and Eikema (2013); Morzyński et al. (2013). However, in both isotopes the EIT results by Krishna et al. (2005) are lower than the other ones by kHz, while their claimed precision is kHz precision. The presence of light shifts originated by the intense control laser producing the EIT signal was not tested. The weighted average are performed excluding the Krishna et al. (2005) values.
For the states, the optical spectra recorded by Stoicheff and Weinberger (1979) produce hyperfine constants in good agreement with more recent ones, but only for the 85 isotope. Their data for the 87 isotope are very far off and not included in the w.a..
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 4 | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | VC | OODR | Moon, Lee, and Suh (2009) | ||
| " | - | - | Recommended | ||
| 4 | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | MOT | OODR | Sinclair et al. (1994) | ||
| " | VC | OODR+EIT | Wang et al. (2014b) | ||
| " | VC | OODR+FC | Lee and Moon (2015) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 5 | AB | MA | Tetu, Fortin, and Savard (1976) | ||
| " | VC | SAS | Barwood, Gill, and Rowley (1991) | ||
| " | AB | LIF | Duong et al. (1993) | ||
| " | VC | SAS+FC | Shiner et al. (2007) | ||
| " | FOUNT | MWS | Wang et al. (2019) | ||
| " | - | - | Recommended | ||
| 5 | VC | OS | Beacham and Andrew (1971) | ||
| " | VC | SAS | Barwood, Gill, and Rowley (1991) | ||
| " | VC | SAS | Banerjee, Das, and Natarajan (2004) | ||
| " | VC | SAS | Das and Natarajan (2006a) | ||
| " | MOT | LIF+FC | Maric, McFerran, and Luiten (2008) | ||
| " | VC | SAS | Rupasinghe et al. (2022) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 5 | VC | ORFDR | From Arimondo, Inguscio, and Violino (1977) | ||
| " | AB | LIF | Thibault et al. (1981b) | ||
| " | VC | SAS | Barwood, Gill, and Rowley (1991) | ||
| " | VC | SAS | Rapol, Krishna, and Natarajan (2003) | ||
| " | VC | SAS | Banerjee, Das, and Natarajan (2003) | ||
| " | VC | SAS | Das and Natarajan (2008) | ||
| " | - | - | w.a.; w.a.(w.e.e.). | ||
| 5 | VC | TPSDS | Nez et al. (1993) | ||
| " | MOT | OODR+RIS | Gabbanini et al. (1999) | ||
| " | - | - | Recommended | ||
| 5 | VC | TPSDS | Nez et al. (1993) | ||
| " | VC | TPSDS | Grove et al. (1995) | ||
| " | MOT | OODR+RIS | Gabbanini et al. (1999) | ||
| " | VC | EIT | Yang, Wang, and Wang (2017) | ||
| " | - | - | Recommended | ||
| 6 | VC | FML | Pérez Galván et al. (2007) also | ||
| . | in Pérez Galván, Zhao, and Orozco (2008) | ||||
| " | VC | TPSDS | Orson et al. (2021) | ||
| " | VC | TPSDS | McLaughlin et al. (2022) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 6 | VC | ORFDR | Feiertag and zu Putlitz (1973) | ||
| " | VC | SAS+FC | Shiner et al. (2007) | ||
| " | VC | SAS+FC | Glaser et al. (2020) | ||
| " | - | - | See text. w.a. | ||
| 6 | VC | ORFDR+MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | SAS | Zhang et al. (2017) | ||
| " | VC | SAS+FC | Glaser et al. (2020) | ||
| " | - | - | See text. w.a. | ||
| 6 | VC | MLC | Hogervorst and Svanberg (1975) | ||
| " | VC | HQB | van Wijngaarden, Bonin, and Happer (1986) | ||
| " | - | - | w.a. | ||
| 6 | VC | OODR | Brandenberger and Lindley (2015) | ||
| 7 | MOT | TPSDS | Snadden et al. (1996) | ||
| " | MOT | OODR | Gomez et al. (2004) | ||
| " | VC | EIT | Krishna et al. (2005) | ||
| " | VC | TPSDS+FC | Chui et al. (2005) | ||
| " | " | " | Barmes, Witte, and Eikema (2013) | ||
| " | " | " | Morzyński et al. (2013, 2014) | ||
| " | " | " | Morgenweg, Barmes, and Eikema (2014) | ||
| " | - | - | See text. w.a. | ||
| 7 | VC | ORFDR | Feiertag and zu Putlitz (1973) | ||
| 7 | " | " | Bucka, Kopfermann, and Minor (1961) | ||
| 7 | VC | MLC | Hogervorst and Svanberg (1975) | ||
| " | VC | HQB | van Wijngaarden and Sagle (1991a) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 7 | VC | MLC | Hogervorst and Svanberg (1975) | ||
| 8 | VC | ORFDR | Gupta et al. (1973) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 8 | VC | ORFDR | zu Putlitz and Venkataramu (1968) | ||
| 8 | VC | MLC | Hogervorst and Svanberg (1975) | ||
| " | VC | HQB | van Wijngaarden, Li, and Koh (1993) | ||
| " | - | - | w.a. (w.e.e.); w.a. | ||
| 8 | VC | MLC | Hogervorst and Svanberg (1975) | ||
| 9 | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 9 | VC | HQB | Kraińska-Miszczak (1994) | ||
| 10 | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 10 | VC | HQB | Głódź and Kraińska-Miszczak (1993) | ||
| 11 | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 11 | VC | HQB | Głódź and Kraińska-Miszczak (1993) | ||
| 12 | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| 13 | " | " | " | ||
| 28 | MOT | MWS | Li et al. (2003) | ||
| 29 | " | " | " | ||
| 30 | " | " | " | ||
| 31 | " | " | " | ||
| 32 | " | " | " | ||
| 33 | " | " | " | ||
| 43 | MOT | MWS | Ramos, Cardman, and Raithel (2019) | ||
| 44 | " | " | " | ||
| 45 | " | " | " | ||
| 46 | " | " | " | ||
| 50 | AB | MWS | Meschede (1987) | ||
| 51 | " | " | " | ||
| 52 | " | " | " | ||
| 53 | " | " | " | ||
| 54 | " | " | " | ||
| 55 | " | " | " | ||
| 56 | " | " | " | ||
| 57 | " | " | " | ||
| 58 | " | " | " | ||
| 59 | " | " | " |
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 4 | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | VC | OODR | Moon, Lee, and Suh (2009) | ||
| " | - | - | Recommended | ||
| 4 | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | VC | SAS+FC | Lee, Moon, and Suh (2007, 2015) | ||
| " | VC | OODR+EIT | Wang et al. (2014b) | ||
| " | VC | OODR+FC | Lee and Moon (2015) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 5 | VC | SAS | Barwood, Gill, and Rowley (1991) | ||
| " | AB | LIF | Duong et al. (1993) | ||
| " | - | - | CCTF (2012) | ||
| " | VC | SAS+FC | Shiner et al. (2007) | ||
| " | MOT | FOUNT | Guéna et al. (2014) | ||
| " | MOT | FOUNT | Ovchinnikov, Szymaniec, and Edris (2015) | ||
| " | - | - | w.a. | ||
| 5 | VC | OS | Beacham and Andrew (1971) | ||
| " | VC | SAS | Barwood, Gill, and Rowley (1991) | ||
| " | VC | SAS | Banerjee, Das, and Natarajan (2004) | ||
| " | VC | SAS | Das and Natarajan (2006a) | ||
| " | MOT | LIF+FC | Maric, McFerran, and Luiten (2008) | ||
| " | ODT | OS | Neuzner et al. (2015) | ||
| " | VC | SAS | Rupasinghe et al. (2022) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 5 | VC | SAS | Thibault et al. (1981b) | ||
| " | VC | SAS | Barwood, Gill, and Rowley (1991) | ||
| " | MOT | SAS | Ye et al. (1996) | ||
| " | MOT | SAS | Gerginov, Tanner, and Johnson (2009) | ||
| " | VC | SAS | Das and Natarajan (2008) | ||
| " | VC | SAS | Chang et al. (2017) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 5 | VC | TPSDS | Nez et al. (1993) | ||
| " | MOT | OODR+RIS | Gabbanini et al. (1999) | ||
| " | - | - | Recommended | ||
| 5 | VC | TPSDS | Nez et al. (1993) | ||
| " | MOT | OODR | Grove et al. (1995) | ||
| " | MOT | OODR+RIS | Gabbanini et al. (1999) | ||
| " | - | - | Recommended | ||
| 6 | VC | FML | Pérez Galván et al. (2007) also | ||
| in Pérez Galván, Zhao, and Orozco (2008) | |||||
| VC | TPSDS | Orson et al. (2021) | |||
| " | " | " | McLaughlin et al. (2022) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 6 | VC | ORFDR | Feiertag and zu Putlitz (1973) | ||
| " | VC | SAS+FC | Shiner et al. (2007) | ||
| " | VC | OODR+EIT | Nyakang’o et al. (2020) | ||
| " | VC | SAS+FC | Glaser et al. (2020) | ||
| " | - | - | See text. w.a. | ||
| 6 | VC | ORFDR | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | SAS+FC | Glaser et al. (2020) | ||
| " | - | - | w.a.(w.e.e. for ) | ||
| 6 | VC | MLC | Svanberg and Tsekeris (1975) | ||
| 6 | VC | ORFDR+MLC | Hogervorst and Svanberg (1975) | ||
| " | VC | OODR | Brandenberger and Lindley (2015) | ||
| " | - | - | Recommended | ||
| 7 | MOT | TPSDS | Snadden et al. (1996) | ||
| " | VC | EIT | Krishna et al. (2005) | ||
| " | MOT | TPSDS+FC | Marian et al. (2005) | ||
| " | VC | " | Chui et al. (2005) | ||
| " | VC | " | Barmes, Witte, and Eikema (2013) | ||
| " | VC | " | Morzyński et al. (2013) also | ||
| in Morzyński et al. (2014) | |||||
| " | VC | " | Morgenweg, Barmes, and Eikema (2014) | ||
| " | - | - | See text. w.a. | ||
| 7 | VC | ORFDR | Feiertag and zu Putlitz (1973) | ||
| 7 | VC | ORFDR+MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| 7 | VC | MLC | Svanberg and Tsekeris (1975) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 7 | VC | ORFDR+MLC | Hogervorst and Svanberg (1975) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 8 | VC | ORFDR | Tsekeris and Gupta (1975) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 8 | VC | ORFDR | Tsekeris, Farley, and Gupta (1975) | ||
| 8 | VC | ORFDR+MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| 8 | VC | MLC+ORFDR | Belin, Holmgren, and Svanberg (1976b) | ||
| 8 | VC | ORFDR+MLC | Hogervorst and Svanberg (1975) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 9 | VC | ORFDR | Tsekeris and Gupta (1975) | ||
| " | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 9 | VC | ORFDR | Belin, Holmgren, and Svanberg (1976b) | ||
| 9 | VC | MLC+ORFDR | Belin, Holmgren, and Svanberg (1976b) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 9 | VC | MLC+ORFDR | Belin, Holmgren, and Svanberg (1976b) | ||
| " | VC | HQB | Głódź and Kraińska-Miszczak (1990) | ||
| " | - | - | Recommended | ||
| 10 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| " | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 10 | VC | ORFDR | Belin, Holmgren, and Svanberg (1976b) | ||
| 10 | VC | HQB | Głódź and Kraińska-Miszczak (1991) | ||
| 10 | " | " | Głódź and Kraińska-Miszczak (1987) | ||
| 11 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| " | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 11 | VC | HQB | Głódź and Kraińska-Miszczak (1991) | ||
| 11 | " | " | Głódź and Kraińska-Miszczak (1989) | ||
| 12 | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| 12 | VC | HQB | Głódź and Kraińska-Miszczak (1991) | ||
| 12 | " | " | Głódź and Kraińska-Miszczak (1989) | ||
| 13 | TD | TPSDS | Stoicheff and Weinberger (1979) | ||
| 13 | VC | HQB | Głódź and Kraińska-Miszczak (1989) | ||
| 20 | VC | EIT | Tauschinsky et al. (2013) | ||
| 21 | " | " | " | ||
| 22 | " | " | " | ||
| 23 | " | " | " | ||
| 24 | " | " | " | ||
| 28 | MOT | MWS | Li et al. (2003) | ||
| 29 | " | " | " | ||
| 30 | " | " | " | ||
| 31 | " | " | " | ||
| 32 | " | " | " | ||
| 33 | " | " | " | ||
| 50 | AB | MWS | Meschede (1987) | ||
| 51 | " | " | " | ||
| 52 | " | " | " | ||
| 53 | " | " | " | ||
| 54 | " | " | " | ||
| 55 | " | " | " | ||
| 56 | " | " | " | ||
| 57 | " | " | " | ||
| 58 | " | " | " | ||
| 59 | " | " | " |
V.5 Cesium
Considering the large set of measured values that cover up Rydberg states with high numbers, cesium is a favourite atom for hyperfine spectroscopy. In addition. there is a good (or very good) agreement for the large majority of states.
The use of frequency combs in order to perform absolute optical frequency measurements produces very precise values for the explored states. For instance, the constant was reported with a precision in Arimondo, Inguscio, and Violino (1977), while it reached in Gerginov et al. (2006). A similar spectacular improvement is associated with the 8 state, object of several investigations owing to its large two-photon excitation probability.
The nuclear magnetic octupole dipole moment was measured for the first time in the state by Gerginov, Derevianko, and Tanner (2003) with the value of kHz, and remeasured as kHz by Das and Natarajan (2008), as shown in Table 6. The first reference reaches a higher precision, but leads to a constant in poor agreement with the values by the second reference and by Tanner and Wieman (1988). For the 6 state, the octupole moment was recently measured by Chen et al. (2018) with the value of kHz, much larger than the above value for the state.
Off-diagonal elements between 6 and 6 levels derived theoretically in Johnson et al. (2004) at the level of Hz, are negligible even at the high precision level of the 6 state hyperfine data.
For several high , with , states, the investigations by Svanberg and Belin (1974); Belin, Holmgren, and Svanberg (1976a), Deech et al. (1977); Nakayama, Kelly, and Series (1981), Sagle and van
Wijngaarden (1991), Głódź and Kraińska-Miszczak (1987, 1990, 1991) produced only the absolute value of the constant. Their signs are determined here on the basis of the scaling laws. All values for those states were assumed equal zero.
The inversion of the hyperfine states is basically due to core-polarization and electron-correlation effects induced by the valence electron, as initially pointed out by Fredriksson, Lundberg, and Svanberg (1980) and carefully examined recently in Auzinsh et al. (2007); Grunefeld, Roberts, and Ginges (2019); Tang, Lou, and Shi (2019).
The 6 coefficient corresponding to the ground state hyperfine splitting is not listed in the Table LABEL:Table:Cs because it is related, as the 2298.157943 MHz frequency, to the Bureau International des Poids et Mesures definition of the second.
For the 6 state, the Table LABEL:Table:Cs reports the value by Kortyna, Masluk, and Bragdon (2006), because the remeasured value in Kortyna et al. (2011) using a different method is less precise. The and values measured by Cheng et al. (2017) are not included into the calculation of the weighted average because their fit does not reproduce all the measured hyperfine frequencies within the reported error bar.
For the 7 state, several values were measured with good overall agreement. This is not the case for the values, where large discrepancies are reported. The small values of the hyperfine constants limit the frequency resolution. Three experiments Lee et al. (2011); Wang et al. (2020b, 2021) measured a restricted number of hyperfine splittings with a limited agreement of their frequency. Stalnaker et al. (2010) reported a full high-resolution spectrum and a careful study of systematic errors. Having observed
a dependence of the value on the applied magnetic field, they increase the error bar of their measurement in order to cover both negative and positive values. Their and values are recommended in Table LABEL:Table:Cs.
For the 8 state, the and values examined by Arimondo, Inguscio, and Violino (1977) were based on early ORFDR investigations by Barbey and Geneux (1962); Bucka and von
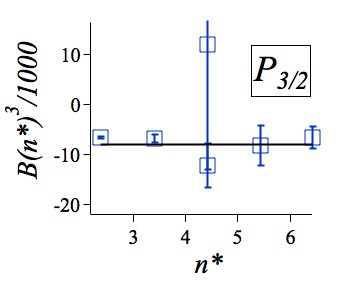
Oppen (1962); Faist, Geneux, and Koide (1964), all suffering from radiofrequency shifts as discussed in this last reference. All of them are reported in Table LABEL:Table:Cs. Arimondo, Inguscio, and Violino (1977) recommended the Faist, Geneux, and Koide (1964) values, where the shift corrections were included. That value and the one by Bayram et al. (2014) agree at 0.15 MHz level. Table LABEL:Table:Cs reports the w.a. of Faist, Geneux, and Koide (1964) and Bayram et al. (2014) with correction. The values by Faist, Geneux, and Koide (1964) and Bayram et al. (2014) are identical except for their sign. Bayram et al. (2014) defended their positive value on the basis of their earlier Na 3 hyperfine constants by Yei, Sieradzan, and Havey (1993) using a similar technique and agreeing with the best other measurements as in Table LABEL:Table:Na. A negative value is confirmed by the scaling law of Fig. 1. Despite weighted average being -0.12(5), Table LABEL:Table:Cs recommends the value of Faist, Geneux, and Koide (1964).
For the measured constant of 9, the high reported precision of Jin et al. (2013) leads to an anomalously large contribution to . When that value is excluded from the w.a., the error bar is greatly reduced. It is worth noting that the 8 and 7 values presented by the same authors with a similar precision match very well those by other authors. The 9 recommended value is the
Morgenweg, Barmes, and Eikema (2014) measurement having a precision.
The 9 and 10 values by Rydberg and Svanberg (1972) are corrected for the value in Arimondo, Inguscio, and Violino (1977). Rydberg and Svanberg (1972) derive the 10 value on the basis of the average measured ratio in the lower levels.
We have received privately from J. Deiglmayr the values for the states with between 43 and 81 measured by Saßmannshausen, Merkt, and Deiglmayr (2013).
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 5 | AB | LIF | Fredriksson, Lundberg, and Svanberg (1980) | ||
| " | VC | HQB | Ryschka and Marek (1981) | ||
| " | VC | HQB+DD | Yei et al. (1998) | ||
| " | - | - | Recommended | ||
| 5 | AB | LIF | Fredriksson, Lundberg, and Svanberg (1980) | ||
| " | VC | ORFDR | Lam, Gupta, and Happer (1980) | ||
| " | VC | HQB+DD | Yei et al. (1998) | ||
| " | - | - | Recommended | ||
| 5 | VC | ORFDR | Svanberg, Tsekeris, and Happer (1973) | ||
| 5 | " | " | " | ||
| 6 | VC | ORFDR | Abele (1975a) | ||
| " | AB | ORFDR | Coc et al. (1987) | ||
| " | AB | LIF | Rafac and Tanner (1997) | ||
| " | VC | SAS+FCS | Udem et al. (1999) | ||
| " | VC | SAS | Das et al. (2006a) | ||
| " | VC | SAS | Das and Natarajan (2006b) | ||
| " | AB | LIF +FC | Gerginov et al. (2006) | ||
| " | VC | OS | Truong et al. (2015) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 6 | AB | HOPF | Thibault et al. (1981a) | ||
| " | AB | LIF | Tanner and Wieman (1988) | ||
| " | AB | LIF | Gerginov, Derevianko, and Tanner (2003) | ||
| " | VC | CCS | Das and Natarajan (2005) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 6 | VC | TPSDS | Tai, Happer, and Gupta (1975) | ||
| " | VC | TPSDS | Ohtsuka et al. (2005) | ||
| " | VC | OODR | Kortyna, Masluk, and Bragdon (2006) | ||
| " | VC | OODR | Cheng et al. (2017) | ||
| " | VC | TPSDS | Chen et al. (2018) | ||
| " | - | - | See text. Recommended | ||
| 6 | MOT | TPSDS | Georgiades, Polzik, and Kimble (1994) | ||
| " | VC | TPSDS | Ohtsuka et al. (2005) | ||
| " | VC | OODR | Kortyna, Masluk, and Bragdon (2006) | ||
| " | VC | OODR | Wang et al. (2020a) | ||
| " | VC | TPSDS | Herd, Cook, and Williams (2021) | ||
| " | - | - | Recommended | ||
| 7 | AB | LIF | Gilbert, Watts, and Wieman (1983) | ||
| " | VC | OODR | Yang et al. (2016); Ren et al. (2016) | ||
| " | MOT | TPSDS | Tian et al. (2019) | ||
| " | VC | OODR+EIT | He et al. (2020) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 7 | VC | ORFDR | Feiertag, Sahm, and zu Putlitz (1972) | ||
| " | VC | SAS | Gerhardt et al. (1978) | ||
| " | VC | SAS | Williams, Herd, and Hawkins (2018) | ||
| " | - | - | w.a. | ||
| 7 | VC | VR | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | VC | SAS | Williams, Herd, and Hawkins (2018) | ||
| " | - | - | w.a. | ||
| 7 | AB | OODR | Kortyna, Fiore, and Farrar (2008) | ||
| " | VC | OODR+FC | Stalnaker et al. (2010) | ||
| " | VC | TPSDS | Lee et al. (2011) | ||
| " | VC | TPSDS | Kiran Kumar, Sankari, and Suryanarayana (2013) | ||
| " | VC | OODR+FC | Jin et al. (2013) | ||
| " | VC | TPSDS | Wang et al. (2021) | ||
| " | - | - | w.a. | ||
| 7 | VC | ELC | Auzinsh et al. (2007) | ||
| " | VC | OODR+FC | Stalnaker et al. (2010) | ||
| " | VC | TPSDS | Lee et al. (2011) | ||
| " | VC | OODR+EIT | Wang et al. (2020b) | ||
| " | VC. | TPSDS | Wang et al. (2021) | ||
| " | - | - | See text. Recommended. | ||
| 8 | VC | LOF | Campani et al. (1978) | ||
| " | TD | TPSDS | Herrmann et al. (1985) | ||
| " | MOT | OODR | Fort et al. (1995a) | ||
| " | VC | TPSDS | Fort et al. (1995b) | ||
| " | VC | FC+QBS | Bellini, Bartoli, and Hänsch (1997) | ||
| " | VC | TPSDS | Hagel et al. (1999) | ||
| " | VC | TPSDS+FC | Fendel et al. (2007) | ||
| " | VC | OODR+FC | Stalnaker et al. (2010) | ||
| " | VC | SAS | Wu et al. (2013) | ||
| " | VC | OODR+EIT | Wang et al. (2013, 2014a) | ||
| " | VC | OODR+FC | Jin et al. (2013) | ||
| " | - | - | w.a. | ||
| 8 | VC | ORFDR+MFD | Tai, Gupta, and Happer (1973) | ||
| " | VC | SAS | Cataliotti et al. (1996) | ||
| " | - | - | w.a. | ||
| 8 | VC | ORFDR | Barbey and Geneux (1962) | ||
| " | VC | ORFDR | Bucka and von Oppen (1962) | ||
| " | VC | ORFDR | Faist, Geneux, and Koide (1964) | ||
| VC | ORFDR | Abele (1975b) | |||
| " | VC | HQB+DD | Bayram et al. (2014) | ||
| " | - | - | See text. w.a.(w.e.e.); Recommended. | ||
| 8 | VC | MLC+HQB | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | VC | MFD | van Wijngaarden and Sagle (1991b) | ||
| " | VC | HQB | Sagle and van Wijngaarden (1991) | ||
| " | - | - | Recommended | ||
| 8 | VC | ORFDR+MLC | From Arimondo, Inguscio, and Violino (1977) | ||
| 9 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| " | VC | OODR+FC | Stalnaker et al. (2010) | ||
| " | VC | TPSDS | Kiran Kumar and Suryanarayana (2012) | ||
| " | VC | OODR+FC | Jin et al. (2013) | ||
| " | VC | TPSDS+FC | Morgenweg, Barmes, and Eikema (2014) | ||
| " | - | - | Recommended | ||
| 9 | VC | ORFDR | Tsekeris, Farley, and Gupta (1975) | ||
| 9 | VC | MLC | Rydberg and Svanberg (1972) | ||
| 9 | VC | MLC+HQB | From Arimondo, Inguscio, and Violino (1977) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | VC | HQB | Sagle and van Wijngaarden (1991) | ||
| " | - | - | w.a. | ||
| 9 | VC | ELC | Auzinsh et al. (2007) | ||
| 10 | VC | ORFDR | Tsekeris et al. (1974) | ||
| 10 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| 10 | VC | MLC | Rydberg and Svanberg (1972) | ||
| 10 | VC | MLC | Svanberg and Tsekeris (1975) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | VC | HQB | Sagle and van Wijngaarden (1991) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | w.a. | ||
| 10 | VC | ELC | Auzinsh et al. (2007) | ||
| 11 | VC | ORFDR | Tsekeris et al. (1974) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | VC | OODR+EIT | He et al. (2012) | ||
| " | - | - | w.a. (w.e.e.) | ||
| 11 | VC | ORFDR | Belin and Svanberg (1974) | ||
| 11 | VC | MLC | Svanberg and Belin (1974) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | VC | TPSDS+FC | Quirk et al. (2022) | ||
| " | - | - | Recommended | ||
| 11 | VC | ORFDR | Svanberg and Belin (1974) | ||
| " | VC | TPSDS+FC | Quirk et al. (2022) | ||
| " | - | - | w.a. | ||
| 12 | VC | ORFDR | Tsekeris and Gupta (1975) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | VC | TPSDS+FC | Quirk et al. (2022) | ||
| " | - | - | Recommemded | ||
| 12 | VC | ORFDR | Belin, Holmgren, and Svanberg (1976a) | ||
| 12 | VC | MLC | Svanberg and Belin (1974) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | - | - | Recommended | ||
| 12 | VC | ORFDR | Svanberg and Belin (1974) | ||
| 13 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | VC | TPSDS+FC | Quirk et al. (2022) | ||
| " | - | - | Recommended | ||
| 13 | VC | ORFDR | Belin, Holmgren, and Svanberg (1976a) | ||
| 13 | VC | MLC | Svanberg and Belin (1974) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | - | - | Recommemded | ||
| 13 | VC | ORFDR | Svanberg and Belin (1974) | ||
| 14 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| " | VC | TPSDS | Otto et al. (2002) | ||
| " | - | - | Recommended | ||
| 14 | VC | MLC | Belin, Holmgren, and Svanberg (1976a) | ||
| " | VC | HQB | Deech et al. (1977) | ||
| " | - | - | Recommended | ||
| 15 | "VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| 15 | VC | MLC | Belin, Holmgren, and Svanberg (1976a) | ||
| " | VC | HQB | Nakayama, Kelly, and Series (1981) | ||
| " | - | - | Recommended | ||
| 16 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| 16 | VC | MLC | Belin, Holmgren, and Svanberg (1976a) | ||
| " | VC | HQB | Nakayama, Kelly, and Series (1981) | ||
| " | - | - | Recommended | ||
| 17 | VC | ORFDR | Farley, Tsekeris, and Gupta (1977) | ||
| 17 | VC | MLC | Belin, Holmgren, and Svanberg (1976a) | ||
| 18 | " | " | " | ||
| 23 | AB | OODR+MWS | Raimond et al. (1981), also in Goy et al. (1982) | ||
| 23 | " | " | " | ||
| 25 | " | " | " | ||
| 25 | " | " | " | ||
| 26 | " | " | " | ||
| 26 | " | " | " | ||
| 28 | " | " | " | ||
| 28 | " | " | " | ||
| 45 | MOT | MWS | Saßmannshausen, Merkt, and Deiglmayr (2013) | ||
| 49 | " | " | " | ||
| 59 | " | " | " | ||
| 67 | " | " | " | ||
| 68 | " | " | " | ||
| 72 | " | " | " | ||
| 81 | " | " | " | ||
| 90 | " | " | " | ||
| 66 | " | " | " | ||
| 66 | " | " | " |
V.6 Francium
In the 1980-87 years, the Orsay group at the ISOLDE atomic beam facility in CERN measured several hyperfine constants of different Fr isotopes reported in Liberman et al. (1980); Coc et al. (1985, 1987); Duong et al. (1987). Francium spectroscopy has reached a higher precision level with the preparation of a cold atom MOT in 1996-97 by Simsarian et al. (1996); Lu et al. (1997). Two years later, the important information on the nuclear structure associated with the hyperfine structure pointed out by Grossman et al. (1999) has triggered a new interest leading to several more recent experimental investigations.
Table LABEL:Table:Fr reports all results for the Fr nuclear ground state configuration, avoiding duplicates when the same value was published more than once. The Table does not include the francium data published by Voss et al. (2013), where systematic errors are unaccounted, since updates and corrections of these measurements were presented by Voss et al. (2015); see Table I of that paper. Table LABEL:Table:Fr evidences that a very large set of isotopes was investigated, all of them targeted at the nuclear structure exploration. The agreement between different hyperfine values is not exceptional, in several cases the differences being greater than the error bars. Because for most isotopes the explored energy levels are limited in number, usually only the lower levels for each series, global analyses are not efficient. A partial spectroscopic information is associated with the series in the 210 and 212 isotopes composed by three explored states, with both and hyperfine values missed out in the second isotope. The inconsistency in Gomez et al. (2008) between the number in Table 1 and that reported in the text and the abstract, is resolved by using the number reported in the text and the abstract as checked against the original data by one of us (LAO).
| State | Sample | Technique | Ref. | ||
|---|---|---|---|---|---|
| 202gFr | |||||
| 7 | AB | LIF | Flanagan et al. (2013), also in Lynch et al. (2014) | ||
| 203gFr | |||||
| 7 | AB | RIS | Lynch et al. (2014) | ||
| " | AB | LIF | Wilkins et al. (2017) | ||
| " | - | - | w.a. | ||
| 8 | " | " | Wilkins et al. (2017) | ||
| 204gFr | |||||
| 7 | AB | RIS | Lynch et al. (2014) | ||
| " | AB | LIF | Voss et al. (2015) | ||
| " | - | - | w.a. (w.e.e) | ||
| 7 | " | " | Voss et al. (2015) | ||
| 205gFr | |||||
| 7 | AB | LIF | Voss et al. (2013, 2015) | ||
| " | AB | RIS | Lynch et al. (2014) | ||
| " | - | - | Recommended | ||
| 7 | AB | LIF | Voss et al. (2015) | ||
| 206gFr | |||||
| 7 | " | " | Voss et al. (2015) | ||
| " | AB | RIS | Lynch et al. (2016) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 7 | MOT | FML | Zhang et al. (2015) | ||
| 7 | AB | LIF | Voss et al. (2015) | ||
| 8 | AB | LIF | Lynch et al. (2016) | ||
| 207gFr | |||||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Lynch et al. (2014) | ||
| " | AB | LIF | Wilkins et al. (2017) | ||
| " | - | - | w.a. | ||
| 7 | MOT | FML | Zhang et al. (2015) | ||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| 8 | AB | LIF | Wilkins et al. (2017) | ||
| 208gFr | |||||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Voss et al. (2015) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 7 | MOT | FML | Grossman et al. (1999) | ||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Voss et al. (2015) | ||
| " | - | - | w.a. | ||
| 209gFr | |||||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | - | - | w.a. | ||
| 7 | MOT | FML | Grossman et al. (1999) | ||
| " | MOT | FML | Zhang et al. (2015) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | - | - | w.a. | ||
| 7 | MOT | LIF | Agustsson et al. (2017) | ||
| 210gFr | |||||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Coc et al. (1987) | ||
| " | MOT | FML | Grossman et al. (1999) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | - | - | w.a. | ||
| 7 | MOT | OODR | Grossman et al. (2000) | ||
| 7 | " | " | " | ||
| 8 | MOT | TCSDS | Simsarian et al. (1999) | ||
| 9 | MOT | TCSDS | Gomez et al. (2008) | ||
| 211gFr | |||||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | AB | RIS | Lynch et al. (2014) | ||
| " | - | - | w.a. | ||
| 7 | MOT | FML | Grossman et al. (1999) | ||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | - | - | w.a. | ||
| 212gFr | |||||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Coc et al. (1987) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | MOT | FML | Grossman et al. (1999) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | LIF | Coc et al. (1985) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | - | - | w.a.(w.e.e.); w.a. | ||
| 8 | AB | LIF | Duong et al. (1987) | ||
| 8 | AB | " | " | ||
| 8 | AB | LIF | Arnold et al. (1990) | ||
| 8 | AB | " | " | ||
| 9 | AB | " | " | ||
| 9 | AB | " | " | ||
| 10 | AB | " | " | ||
| 11 | AB | " | " | ||
| 213gFr | |||||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Coc et al. (1987) | ||
| " | MOT | FML | Zhang et al. (2015) | ||
| " | - | - | Recommended | ||
| 7 | AB | HOPF | Liberman et al. (1980) | ||
| " | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | - | - | w.a. | ||
| 8 | AB | LIF | Duong et al. (1987) | ||
| 214gFr | |||||
| 7 | AB | RIS | Farooq-Smith et al. (2016a, b) | ||
| 219gFr | |||||
| 7 | AB | RIS | Budinčević et al. (2014) | ||
| " | AB | RIS | de Groote et al. (2015) | ||
| " | - | - | Recommended | ||
| 8 | " | " | de Groote et al. (2015) | ||
| 220gFr | |||||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | AB | RIS | Lynch et al. (2014) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | AB | HOPF | Coc et al. (1987) | ||
| " | - | - | w.a. | ||
| 8 | AB | LIF | Duong et al. (1987) | ||
| 221gFr | |||||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | AB | HOPF | Andreev, Letokhov, and Mishin (1986) | ||
| " | AB | HOPF | Coc et al. (1987) | ||
| " | AB | LIF | Duong et al. (1987) | ||
| " | AB | RIS | Lynch et al. (2014) | ||
| " | AB | RIS | de Groote et al. (2015) | ||
| " | - | - | w.a.(w.e.e.) | ||
| 7 | AB | HOPF | Coc et al. (1987) | ||
| " | MOT | LIF | Lu et al. (1997) | ||
| " | MOT | FML | Zhang et al. (2015) | ||
| " | - | - | w.a. | ||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | AB | HOPF | Coc et al. (1987) | ||
| " | MOT | LIF | Lu et al. (1997) | ||
| " | - | - | w.a. | ||
| 8 | AB | LIF | Duong et al. (1987) | ||
| " | AB | RIS | de Groote et al. (2015) | ||
| " | - | - | w.a.; w.a.(w.e.e.) | ||
| 222gFr | |||||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| 7 | " | " | " | ||
| 223gFr | |||||
| 7 | " | " | " | ||
| 7 | " | " | " | ||
| 224gFr | |||||
| 7 | " | " | " | ||
| 7 | " | " | " | ||
| 225gFr | |||||
| 7 | " | " | " | ||
| " | AB | HOPF | Coc et al. (1987) | ||
| " | - | - | Recommended | ||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | AB | HOPF | Coc et al. (1987) | ||
| " | - | - | w.a. | ||
| 226gFr | |||||
| 7 | AB | HOPF | Coc et al. (1985) | ||
| " | " | Duong et al. (1986) | |||
| " | - | - | w.a. | ||
| 7 | " | " | Coc et al. (1985) | ||
| 227gFr | |||||
| 7 | " | " | " | ||
| 7 | " | " | " | ||
| 228gFr | |||||
| 7 | " | " | " | ||
| 7 | " | " | " | ||
| 229gFr | |||||
| 7 | AB | RIS | Budinčević et al. (2014) | ||
| 231gFr | |||||
| 7 | " | " | " |
VI Data analysis
VI.1 Quantum number scaling law
The present level of high precision for the theoretical computations leads to agreement with selected experimental results up to 0.1 percent, also for high quantum numbers. Even at that precision level, semi-empirical laws, such as the scaling ones, remain useful for verifying or predicting data, or confirming the presence of perturbations for specific atomic states.
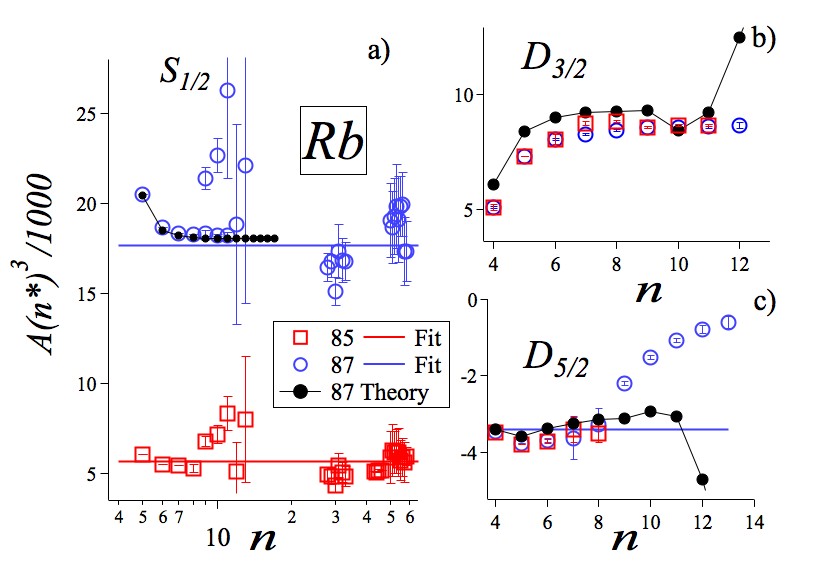
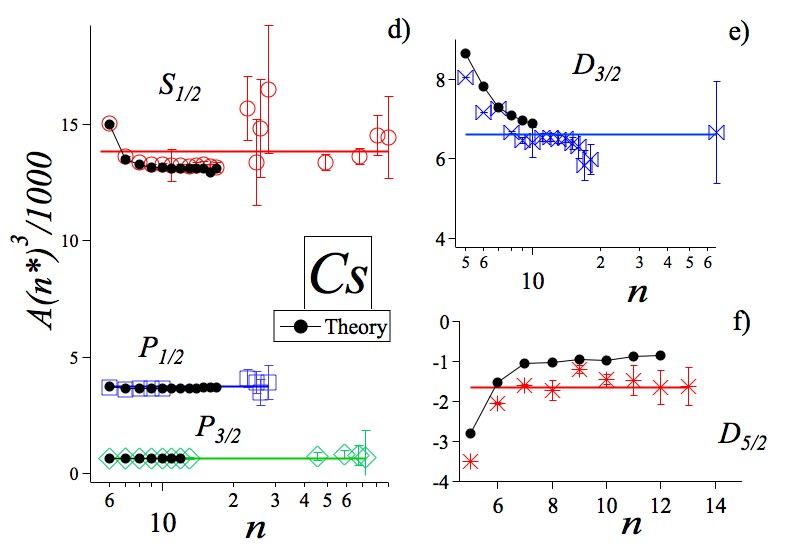
We have tested the scaling laws of Eq. (10) for and similar one of , for the overall , and states of potassium, rubidium, cesium and francium, using the quantum defect parameters from Lorenzen and Niemax (1983); Li et al. (2003); Lorenzen and Niemax (1984); Simsarian et al. (1999); Peper et al. (2019). As examples, we report in Fig. 2 the dipole constant results for both Rb isotopes, in (a) for states, and in (b), (c) for the ones. Panel (d) of that figure reports the data for the and states of Cs, and for the ones. The 87Rb data by Stoicheff and Weinberger (1979) with large error bars are not plotted. Note that the values are plotted vs. enhancing the deviations from the scaling law. The validity of the scaling law is tested by the horizontal lines derived from data fits. For the states in (b) and (c), the 85Rb data have been scaled to the 87Rb ones by supposing the validity of the scaling of Eq. (7), leading to a precise superposition of the two isotope values. Similar results are obtained for all the states and the states of .
For the states, the 87Rb theoretical results by Grunefeld, Roberts, and Ginges (2019) reproduce very closely the experimental values for all quantum numbers, as shown by the black dots in the (a) panel of the figure. The scaling law was tested theoretically for the , and Rb states in the log/log plot of Safronova and Safronova (2011). In panels (b) and (c) of Fig. 2, the black dots depict those theoretical predictions for the states. For the values up to , the differences between theoretical and experimental results are small. For higher values, the differences are significant, because of the limitation in the computer codes at that time. A good agreement with experimental data exists for the Grunefeld, Roberts, and Ginges (2019) predictions of the Cs and states, as shown in (d). For Cs, there are additional theoretical results for the states by Tang, Lou, and Shi (2019), for by Auzinsh et al. (2007), and for by Tang, Lou, and Shi (2019). For the states, the data by Auzinsh et al. (2007) cannot be distinguished on the figure scale. In addition, they cover a short range of values.
In most cases, the scaling law is verified in both experimental and theoretical data, and its validity is used to assign the sign of the values reported in the Tables of the previous Section. For the Cs and states in a large range of values, the horizontal fits are good. The scaling validity applies to the high- states, as for the and data of Saßmannshausen, Merkt, and Deiglmayr (2013) as seen in panel (d). For the 87Rb and Cs states, the scaling does not apply precisely to low- values because of additional contributions to in Eq. (5). In contrast, the 85Rb values satisfy the scaling. The low- difference between the two isotopes produces the deviation from the scaling, linked to the hyperfine anomalies discussed in the following subsection. For the low- states, large deviations from the scaling lead to lower values in Rb and higher ones in Cs for both experimental and theoretical data. These deviations are equivalent for the two Rb isotopes. They originate from the pair-correlation and core-polarization, as explained in Auzinsh et al. (2007); Tang, Lou, and Shi (2019).
We have verified the validity of the scaling law also for the constants. Fig. 3 reports the constants of both Rb isotopes for the and states. The continuous horizontal lines indicate that the scaling law is valid for the 87Rb constants of both states. For the 85Rb isotope, deviations appear in Fig 3(b) for the states at intermediate values. The
theoretical predictions by Safronova and Safronova (2011) denoted by black dots indicate a good agreement between the theory and experiments. The scaling applies also to the Cs states. For the Rb and Cs states, a definitive conclusion cannot be reached owing to the limited number of data. For the states, the 85Rb data are precisely scaled to the 87Rb ones by assuming the validity of the quadrupole moment dependence of Eq. (8), with the values of Raghavan (1989). This proportionality applies also to the data, where the scaling is valid.
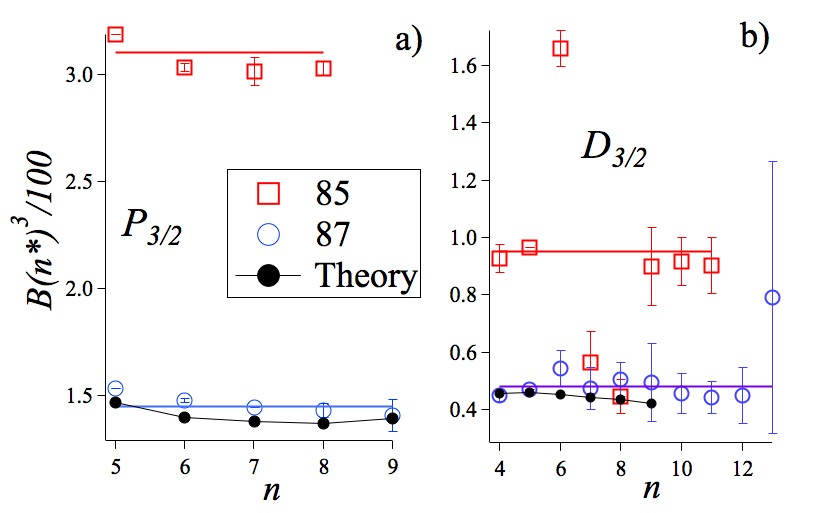
Since the data for each Fr isotope are very limited in number, the application of the quantum number scaling law is not very efficient. Neverthless, its validity test is useful to verify the present level of knowledge. The law is also useful for the experimental determination of the hyperfine constants in states not yet explored. While the francium effective quantum numbers may be derived from the quantum defects of Arnold et al. (1990); Simsarian et al. (1999); Huang and Sun (2010), we rely on those of Simsarian et al. (1999) based on the full spectrum of the francium absorption lines compiled by Sansonetti (2007). The francium Table evidences that hyperfine sequences are available only for the states of the 210 and 212 isotopes, each sequence limited to three entries. Fig. 4 presents those experimental results in a plot. The dipole constant for the 211 isotope 7 state is also plotted. The dots joined by continuous lines represent the theoretical data for 210Fr by Sahoo et al. (2015), for 211Fr by Grunefeld, Roberts, and Ginges (2019), and for 212Fr by Lou et al. (2019). On the figure scale, equivalent results are obtained using the quantum defect numbers of all the above references. For the experimental and theoretical data on the 210,212Fr isotopes, the deviations from the scaling law for the lowest number are similar to those presented for the Rb and Cs low- and states in Fig. 2. Such deviation from the scaling law does not appear in the 211Fr theoretical data by Grunefeld, Roberts, and Ginges (2019), while their prediction for the Cs and Rb states match very closely the experimental data as shown in Fig. 2. An acquisition of more experimental data is required in order to progress with this exploration. The program highlighted by Grunefeld, Roberts, and Ginges (2019) and by Roberts and Ginges (2020) focuses on the importance of having more hyperfine splitting information for higher excited levels to better understand not only the Fr atom, but the properties of the different nuclear isotopes.
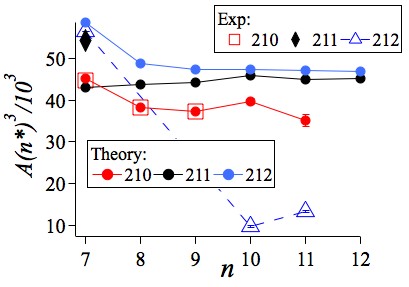
VI.2 Anomalies
The hyperfine anomalies, first introduced by Bohr and Weisskopf (1950), are defined as the deviations from Eq. (7) produced by the finite size of the nucleus. As a measure of the finite structure influence on the dipole constants of isotopes 1 and 2, following Persson (2013) the expression for the hyperfine anomaly is:
| (11) |
where are the hyperfine magnetic dipole constant and the nuclear gyromagnetic ratio, respectively, of the isotopes. For a point-like nucleus, the hyperfine anomaly is null.
The article of Persson (2013) represents the most recent review of the atomic anomalies. Those of the Fr states are examined in Zhang et al. (2015). Recent theoretical studies of Fr anomalies can be found in Konovalova et al. (2018); Konovalova, Demidov, and Kozlov (2020); Roberts and Ginges (2020).
Anomalies can be derived from measured constants and accurate values of the nuclear -ratio. This is the case for light alkali atoms with their precise values in the gas phase determined in the sixties and seventies, as discussed in Arimondo, Inguscio, and Violino (1977). Anomalies for those atoms are reported in Table 9, derived from the weighted mean values and variances of the dipole constants reported in the Tables of the previous Section. Only anomalies with a value significantly different from zero are presented in Table 9. For the state of the Rb isotopes, where a very large discrepancy between the measured values was noted in subsection V, the value is missed because none reasonable anomaly is associated to the different set of data. The Rb values of Table 9 are in good agreement with those derived by Pérez Galván et al. (2007); Pérez Galván, Zhao, and Orozco (2008); Wang et al. (2014b) for and states. For the Rydberg states, enormous anomalies are obtained, percent, a quite surprising result, because the interaction of a Rydberg electron with the nucleus should be comparable to that of low orbitals. The fairly constant anomaly for all the states of the Rb isotopes was pointed out by Pérez Galván et al. (2007). For Rb states the situation is not well defined, with the the value reflecting the discording results associated to this state, and for the states the quadrupole interaction playing an important role. The constant value of the anomaly applies also to the K isotopes.
| Element | Isotope 1 | Isotope 2 | State | |
|---|---|---|---|---|
| Li | 6 | 7 | 2 | 0.0068067(8) |
| 2 | -0.1734(2) | |||
| 2 | -0.155(8) | |||
| K | 39 | 40 | 4 | 0.467(2) |
| 4 | 3.90(13) | |||
| K | 39 | 41 | 4 | -0.22937(13) |
| 4 | 3.9(3) | |||
| Rb | 85 | 87 | 5 | 0.35141(2) |
| 6 | 0.361(19) | |||
| 7 | 0.342(3) | |||
| 5 | 0.55(8) | |||
| 5 | 0.168(5) | |||
| 6 | 0.31(7) | |||
| 6 | 0.46(5) | |||
| 4 | 0.60(15) | |||
| 5 | 0.279(6) | |||
| 5 | 0.44(5) |
The francium case is different, because the list of isotope data is quite long and therefore, interesting information about the nuclear structures could be derived from the anomaly determinations. However, for francium an important element is missing in Eq. (11) because a direct measurement of the nuclear gyromagnetic ratio is available only for 211Fr in Stone (2005). For the remaining isotopes, the ratios are derived by assuming a zero anomaly: see Raghavan (1989). In the recent theoretical studies of Fr anomalies by Konovalova et al. (2018); Roberts and Ginges (2020); Konovalova, Demidov, and Kozlov (2020), the information on the nuclear structure is replaced by derivations of the radial nuclear structure and of the nuclear radius. In order to obtain the anomalies without relying on such theoretical analyses, Grossman et al. (1999), following Persson (1998), concentrated their attention on the and states. The electron probes the nucleus with a more uniform radial dependence of the interaction than does the electron. They introduced the following ratio of their hyperfine constants:
| (12) |
as a probe of the nuclear magnetization distribution. Since both states are spin-1/2, these ratios are independent of quadrupole effects that complicate the extraction of the nuclear structure information. For several francium isotopes, the ratio is presented in Fig 5. Notice the staggered isotope behaviour of vs. the even/odd isotope number. Such behavior evidences the different radial distributions of the nuclear magnetization for the even/odd number of neutrons. The ratios of the hyperfine constants of the and states, as well as those of the and ones, do not exhibit such a clear staggered dependence as the ratio plotted in the figure. We have tested the presence of a staggered dependence also for the Rb isotopes using the 85 and 87 data in Table LABEL:Table:85Rb,LABEL:Table:87Rb, and the 82 isotope ones from Zhao et al. (1999). This limited data set appears to confirm the staggered behavior.
The ratio of the hyperfine constants of the and states has been proposed in Konovalova, Demidov, and Kozlov (2020) as an additional test of the nuclear structure, even if the nuclear quadrupole coupling is important for the latter state. This ratio calculated from the francium Table LABEL:Table:Fr data does not exhibit a clear dependence on the isotope number.
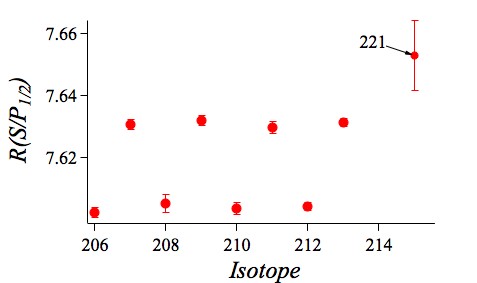
VII Conclusions
The previously published experimental values for the stable isotopes of the light alkali atoms and for all the nuclear-ground-configuration francium isotopes have been compiled. The Tables report the most accurate data obtained before 1977 and all those published after that time. For each measured hyperfine constant we present a recommended value. A critical examination of the most interesting cases, or of the most discording ones, is presented. For the discording cases we have calculated a weighted enhanced error
following the procedure of the Particle Data Group in Zyla et al. (2020). For those cases a comparison of our data analysis to the cluster maximum likelihood estimator introduced by Rukhin (2009, 2019), is presented in the supplementary information (SI) of this review Allegrini, Arimondo, and Orozco (2022). We encourage future reviewers of larges sets of data to look into these more recent methods, that are currently gaining adepts in the community, but are not followed by those in charge of the recent redefinition of the fundamental constants of physics and chemistry Tiesinga et al. (2021).
The experimental interest in measuring hyperfine constants is renewed in the recent years. Today, the laser sources required to excite energy levels not easily assessed at the optical pumping time are available on the market. Those sources and the associated atomic species can be important for quantum simulation and computational investigations. As in the past, the quest for higher precision spectroscopic measurement could represent an additional step for refining the experimental tools required in those areas.
Instead of concentrating the attention on a specific atomic state, the recent global theoretical analyses cover all the atomic states of a single species, possibly of all the isotopes. For this global approach, precise experimental data are required for a large set of states, stimulating the hyperfine data search in several directions.
Spectroscopic investigations of alkali atoms are also associated with the theoretical progress on the electron-nucleus hyperfine coupling. The hyperfine coupling being an important probe of the nuclear structure, the Grossman et al. (1999) francium research has introduced the ratio of the and state hyperfine couplings as a new tool for studying nuclear properties. This has stimulated a large theoretical effort, but it has pointed out the need for more precise experimental data. The application of this ratio to lighter alkalis could be an interesting exploration direction.
The electron-nucleus interaction contains a term characterized by the nuclear magnetic octupole moment. In recent years three different measures of that moment are reported for 133Cs by Gerginov, Derevianko, and Tanner (2003), for 87Rb in the experimental data of Ye et al. (1996) reexamined by Gerginov, Tanner, and Johnson (2009), and more recently for the 133Cs state by Chen et al. (2018). The parity violation search in alkali atoms may also find new life. Up to now, the most accurate data on the atomic parity-non-conserving interaction was derived from the transition in cesium by Wood et al. (1997). To obtain
a more accurate value of the nuclear weak charge producing the parity-violating Hamiltonian, it would be desirable to consider other candidates. Gwinner and Orozco (2022) with their collaborators are pursuing its measurement in the transition in a variety of Fr isotopes, while Aoki et al. (2017) have proposed to search for that violation operating on the electric quadrupole transition in 210Fr. It is expected that advances in the understanding of hyperfine interactions will continue to illuminate atomic parity nonconversion and vice versa.
As a final expectation, in the near future, a few totally new entries will be added to the above Tables, counterbalanced by several refined entries.
VIII Acknowledgments
The authors are grateful to Marianna Safronova for a guide through the recent progress in the theoretical analyses of the hyperfine structures and a careful reading of the manuscript, and to Roberto Calabrese for hints on the francium spectroscopy. The authors are grateful and indebted to the referee for ample comments that have made this a much better review and for providing the algorithm of the CMLE approach. Hassan Jawahery, Peter J. Mohr and William D. Phillips have helped elucidate the evaluation of the errors to report recommended values. The authors acknowledge Wang-Yau Cheng, Pierre Dubé, Johannes Deiglmayr, Randy J. Knize, Mark Lindsay, Frederic Merkt, Dieter Meschede, Priyanka Rupasinghe and Sun Svanberg for communicating data of various atomic states. The very kind help of the librarians Armelle Michetti and Odile Richaud in Grenoble, and Massimiliano Bertelli in Pisa is also acknowledged.
References
- Abele (1975a) Abele, J., “Bestimmung der -faktoren in den zuständen -62p3/2 und - 82p3/2 von 133Cs,” Zeitschrift für Physik A 274, 179–184 (1975a).
- Abele (1975b) Abele, J., “Untersuchung der hyperfeinstruktur des -zustandes von133Cs im starken magnetfeld mit der optischen doppelresonanzmethode,” Zeitschrift für Physik A 274, 185–190 (1975b).
- Agustsson et al. (2017) Agustsson, S., Bianchi, G., Calabrese, R., Corradi, L., Dainelli, A., Khanbekyan, A., Marinelli, C., Mariotti, E., Marmugi, L., Mazzocca, G., Moi, L., Ricci, L., Stiaccini, L., and Tomassetti, L., “Observation of 7p 7d optical transitions in 209 and 210 francium isotopes,” Opt. Lett. 42, 3682–3685 (2017).
- Allegrini, Arimondo, and Orozco (2022) Allegrini, M., Arimondo, E., and Orozco, L. A., “Supplementary information: Survey of hyperfine structure measurements in alkali atoms,” J. Phys. Chem. Ref. Data ??, ?? (2022).
- Andreev, Letokhov, and Mishin (1986) Andreev, S. V., Letokhov, V. S., and Mishin, V. I., “Laser resonant photoionization detection of traces of the radioactive isotope in a sample,” Sov. Phys. JEPT Lett. 43, 736–740 (1986).
- Andreev, Letokhov, and Mishin (1987) Andreev, S. V., Letokhov, V. S., and Mishin, V. I., “Laser resonance photoionization spectroscopy of Rydberg levels in Fr,” Phys. Rev. Lett. 59, 1274–1276 (1987).
- Antoni-Micollier et al. (2017) Antoni-Micollier, L., Barrett, B., Chichet, L., Condon, G., Battelier, B., Landragin, A., and Bouyer, P., “Generation of high-purity low-temperature samples of 39K for applications in metrology,” Phys. Rev. A 96, 023608 (2017).
- Aoki et al. (2017) Aoki, T., Torii, Y., Sahoo, B., Das, B., Harada, K., Hayamizu, T., Sakamoto, K., Kawamura, H., Inoue, T., Uchiyama, A., Ito, S., Yoshioka, R., Tanaka, K., Itoh, M., Hatakeyama, A., and Sakemi, Y., “Parity-nonconserving interaction-induced light shifts in the transition of the ultracold 210Fr atoms to probe new physics beyond the standard model,” Applied Physics B: Lasers and Optics 123 (2017), 10.1007/s00340-017-6673-3.
- Arias et al. (2019) Arias, A., Lochead, G., Wintermantel, T. M., Helmrich, S., and Whitlock, S., “Realization of a Rydberg-dressed Ramsey interferometer and electrometer,” Phys. Rev. Lett. 122, 053601 (2019).
- Arimondo, Inguscio, and Violino (1977) Arimondo, E., Inguscio, M., and Violino, P., “Experimental determinations of the hyperfine structure in the alkali atoms,” Rev. Mod. Phys. 49, 31–75 (1977).
- Armstrong (1971) Armstrong, J. L., Theory of the Hyperfine Structure of Free Atoms, 1st ed. (Wiley-Interscienc, New York, 1971).
- Arnold et al. (1990) Arnold, E., Borchers, W., Duong, H. T., Juncar, P., Lerme, J., Lievens, P., Neu, W., Neugart, R., Pellarin, M., Pinard, J., Vialle, J. L., and Wendt, K. (ISOLDE Collaboration), “Optical laser spectroscopy and hyperfine structure investigation of the , , , and excited levels in francium,” Journal of Physics B: Atomic, Molecular and Optical Physics 23, 3511–3520 (1990).
- Arqueros (1988) Arqueros, F., “Doppler-free two-photon spectroscopy of the 4 state of Na,” Optics Communications 67, 341–342 (1988).
- Auzinsh et al. (2007) Auzinsh, M., Bluss, K., Ferber, R., Gahbauer, F., Jarmola, A., Safronova, M. S., Safronova, U. I., and Tamanis, M., “Level-crossing spectroscopy of the 7, 9, and states of and validation of relativistic many-body calculations of the polarizabilities and hyperfine constants,” Phys. Rev. A 75, 022502 (2007).
- Banerjee, Das, and Natarajan (2003) Banerjee, A., Das, D., and Natarajan, V., “Precise frequency measurements of atomic transitions by use of a Rb-stabilized resonator,” Opt. Lett. 28, 1579–1581 (2003).
- Banerjee, Das, and Natarajan (2004) Banerjee, A., Das, D., and Natarajan, V., “Absolute frequency measurements of the lines in 39K, 85Rb, and 87Rb with 0.1 ppb uncertainty,” Europhysics Letters 65, 172–178 (2004).
- Barakhshan et al. (2022) Barakhshan, P., Marrs, A., Bhosale, A., Arora, B., Eigenmann, R., and Safronova, M. S., “Portal for High-Precision Atomic Data and Computation (version 2.0) ,” University of Delaware, Newark, DE, USA. (2022).
- Barbey and Geneux (1962) Barbey, P. and Geneux, E., “Structure hyperfine de l’état du césium 133,” Helv. Phys. Acta 35, 561–562 (1962).
- Barmes, Witte, and Eikema (2013) Barmes, I., Witte, S., and Eikema, K. S. E., “High-precision spectroscopy with counterpropagating femtosecond pulses,” Phys. Rev. Lett. 111, 023007 (2013).
- Barwood, Gill, and Rowley (1991) Barwood, G. P., Gill, P., and Rowley, W. R. C., “Frequency measurements on optically narrowed Rb-stabilised laser diodes at 780 nm and 795 nm,” Applied Physics B 53, 142–147 (1991).
- Bayram et al. (2014) Bayram, S. B., Arndt, P., Popov, O. I., Güney, C., Boyle, W. P., Havey, M. D., and McFarland, J., “Quantum beat spectroscopy: Stimulated emission probe of hyperfine quantum beats in the atomic Cs level,” Phys. Rev. A 90, 062510 (2014).
- Beacham and Andrew (1971) Beacham, J. R. and Andrew, K. L., “Optical study of the hyperfine structure of the rubidium resonance lines,” J. Opt. Soc. Am. 61, 231–235 (1971).
- Beckmann, Böklen, and Elke (1974) Beckmann, A., Böklen, K. D., and Elke, D., “Precision measurements of the nuclear magnetic dipole moments of 6Li, 7Li, 23Na, 39K and 41K,” Zeitschrift für Physik 270, 173–186 (1974).
- Behrle, Koschorreck, and Köhl (2011) Behrle, A., Koschorreck, M., and Köhl, M., “Isotope shift and hyperfine splitting of the transition in potassium,” Phys. Rev. A 83, 052507 (2011).
- Belin et al. (1975a) Belin, G., Holmgren, L., Lindgren, I., and Svanberg, S., “Hyperfine Interaction in Excited Alkali Atoms,” in Summary of Contributions. Seventh Annual Conference (Laboratoire de Spectrometrie Physique. Université Grenoble, 1975) p. 13.
- Belin et al. (1975b) Belin, G., Holmgren, L., Lindgren, I., and Svanberg, S., “Hyperfine interaction, Zeeman and Stark effects for excited states in potassium,” Physica Scripta 12, 287–294 (1975b).
- Belin, Holmgren, and Svanberg (1976a) Belin, G., Holmgren, L., and Svanberg, S., “Hyperfine interaction, Zeeman and Stark effects for excited states in cesium,” Physica Scripta 14, 39–47 (1976a).
- Belin, Holmgren, and Svanberg (1976b) Belin, G., Holmgren, L., and Svanberg, S., “Hyperfine interaction, Zeeman and Stark effects for excited states in rubidium,” Physica Scripta 13, 351–362 (1976b).
- Belin and Svanberg (1974) Belin, G. and Svanberg, S., “Laser spectroscopy investigation of the hyperfine structure of highly excited 2 states in alkali atoms,” Physics Letters A 47, 5–6 (1974).
- Bellini, Bartoli, and Hänsch (1997) Bellini, M., Bartoli, A., and Hänsch, T. W., “Two-photon fourier spectroscopy with femtosecond light pulses,” Opt. Lett. 22, 540–542 (1997).
- Beloy and Derevianko (2008) Beloy, K. and Derevianko, A., “Second-order effects on the hyperfine structure of states of alkali-metal atoms,” Phys. Rev. A 78, 032519 (2008).
- Bendali, Duong, and Vialle (1981) Bendali, N., Duong, H. T., and Vialle, J. L., “High-resolution laser spectroscopy on the and lines of 39,40,41K using RF modulated laser light,” Journal of Physics B: Atomic and Molecular Physics 14, 4231–4240 (1981).
- Bhattacharya, Haimberger, and Bigelow (2003) Bhattacharya, M., Haimberger, C., and Bigelow, N. P., “Forbidden transitions in a magneto-optical trap,” Phys. Rev. Lett. 91, 213004 (2003).
- Biraben and Beroff (1978) Biraben, F. and Beroff, K., “Hyperfine interaction in the 4 and the 4 levels of sodium,” Physics Letters A 65, 209–212 (1978).
- Bohr and Weisskopf (1950) Bohr, A. and Weisskopf, V. F., “The influence of nuclear structure on the hyperfine structure of heavy elements,” Phys. Rev. 77, 94–98 (1950).
- Bouchiat and Piketty (1991) Bouchiat, C. and Piketty, C., “Nuclear spin dependent parity violating electron-nucleus interaction in heavy atoms. the anapole moment and the perturbation of the hadronic vector neutral current by the hyperfine interaction,” Physics Letters B 269, 195–200 (1991).
- Bouchiat, M.-A. and Guéna, J. (1988) Bouchiat, M.-A., and Guéna, J.,, “The e2 6s-7s amplitude in cesium and its importance in a precise calibration of epv1,” J. Phys. France 49, 2037–2044 (1988).
- Brandenberger and Lindley (2015) Brandenberger, J. R. and Lindley, R. E., “Hyperfine structure in the and states of 87Rb and 85Rb,” Phys. Rev. A 91, 062505 (2015).
- Brog, Eck, and Wieder (1967) Brog, K. C., Eck, T. G., and Wieder, H., “Fine and Hyperfine Structure of the Term of and ,” Phys. Rev. 153, 91–103 (1967).
- Brown et al. (2013) Brown, R. C., Wu, S.-J., Porto, J. V., Sansonetti, C. J., Simien, C. E., Brewer, S. M., Tan, J. N., and Gillaspy, J. D., “Quantum interference and light polarization effects in unresolvable atomic lines: Application to a precise measurement of the 6,7Li lines,” Phys. Rev. A 87, 032504 (2013).
- Buck and Rabi (1957) Buck, P. and Rabi, I. I., “Hyperfine Structure of in the State,” Phys. Rev. 107, 1291–1294 (1957).
- Bucka, Kopfermann, and Minor (1961) Bucka, H., Kopfermann, H., and Minor, A., “Präzisionsmessung der Hyperfeinstruktur des Terms des Rb I-Spektrums,” Zeitschrift für Physik 161, 123–131 (1961).
- Bucka and von Oppen (1962) Bucka, H. and von Oppen, G., “Hyperfeinstruktur und Lebensdauer des -Terms im Cs I-Spektrum,” Ann. Phys. 456, 119–120 (1962).
- Budick et al. (1966) Budick, B., Bucka, H., Goshen, R. J., Landman, A., and Novick, R., “Fine and hyperfine structure of the term in lithium,” Phys. Rev. 147, 1–5 (1966).
- Budinčević et al. (2014) Budinčević, I., Billowes, J., Bissell, M. L., Cocolios, T. E., de Groote, R. P., De Schepper, S., Fedosseev, V. N., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Lynch, K. M., Marsh, B. A., Neyens, G., Procter, T. J., Rossel, R. E., Rothe, S., Strashnov, I., Stroke, H. H., and Wendt, K. D. A., “Laser spectroscopy of francium isotopes at the borders of the region of reflection asymmetry,” Phys. Rev. C 90, 014317 (2014).
- Budker, Kimball, and DeMille (2008) Budker, D., Kimball, D., and DeMille, D., Atomic physics (Oxford University Press, 2008).
- Burghardt et al. (1978) Burghardt, B., Dubke, M., Jitschin, W., and Meisel, G., “Sub-natural linewidth laser spectroscopy of Doppler-free two-photon resonances,” Physics Letters A 69, 93–96 (1978).
- Burghardt, Hoffmann, and Meisel (1988) Burghardt, B., Hoffmann, B., and Meisel, G., “The 3 states of 23Na and 7Li: determination of unresolved hyperfine splittings and radiative lifetimes,” Zeitschrift für Physik D Atoms, Molecules and Clusters 8, 109–118 (1988).
- Bushaw et al. (2003) Bushaw, B. A., Nörtershäuser, W., Ewald, G., Dax, A., and Drake, G. W. F., “Hyperfine splitting, isotope shift, and level energy of the states of ,” Phys. Rev. Lett. 91, 043004 (2003).
- Campani et al. (1978) Campani, E., Degan, G., Gorini, G., and Polacco, E., “Measurement of the hyperfine splitting in cesium,” Optics Communications 24, 203–206 (1978).
- Carlsson et al. (1992) Carlsson, J., Jönsson, P., Sturesson, L., and Froese Fischer, C., “Multi-configuration Hartree-Fock calculations and time-resolved laser spectroscopy studies of hyperfine structure constants in sodium,” Physica Scripta 46, 394–398 (1992).
- Carlsson and Sturesson (1989) Carlsson, J. and Sturesson, L., “Accurate time-resolved laser spectroscopy on lithium atoms,” Zeitschrift für Physik D Atoms, Molecules and Clusters 14, 281–287 (1989).
- Cataliotti et al. (1996) Cataliotti, F. S., Fort, C., Pavone, F. S., and Inguscio, M., “Doppler-free excitation of the weak cesium transition at 389 nm,” Zeitschrift für Physik D Atoms, Molecules and Clusters 38, 31–33 (1996).
- CCTF (2012) CCTF,, Consultative Committee for Time and Frequency, Recommendation CCTF 1 (2012). Report of the 19th meeting (13-14 September 2012) to the International Committee for Weights and Measures (BIPM, Sèvres, 2012) p. 59.
- Chang et al. (2017) Chang, H., Myneni, K., Smith, D. D., and Liaghati-Mobarhan, H. R., “High-precision, accurate optical frequency reference using a Fabry-Perot diode laser,” Review of Scientific Instruments 88, 063101 (2017).
- Chen et al. (2018) Chen, T.-J., Chen, J.-E., Yu, H.-H., Liu, T.-W., Hsiao, Y.-F., Chen, Y.-C., Chang, M.-S., and Cheng, W.-Y., “Absolute frequency of cesium hyperfine transition with a precision to nuclear magnetic octupole interaction,” Opt. Lett. 43, 1954–1957 (2018).
- Cheng et al. (2017) Cheng, W.-Y., Chen, T.-J., Lin, C.-W., Chen, B.-W., Yang, Y.-P., and Hsu, H. Y., “Robust sub-millihertz-level offset locking for transferring optical frequency accuracy and for atomic two-photon spectroscopy,” Opt. Express 25, 2752–2762 (2017).
- Chui et al. (2005) Chui, H.-C., Ko, M.-S., Liu, Y.-W., Shy, J.-T., Peng, J.-L., and Ahn, H., “Absolute frequency measurement of rubidium 5S–7S two-photon transitions with a femtosecond laser comb,” Opt. Lett. 30, 842–844 (2005).
- Coc et al. (1987) Coc, A., Thibault, C., Touchard, F., Duong, H., Juncar, P., Liberman, S., Pinard, J., Carre, M., Lerme, J., Vialle, J., Büttgenbach, S., Mueller, A., and Pesnelle, A. (ISOLDE Collaboration), “Isotope shifts, spins and hyperfine structures of 118,146Cs and of some francium isotopes,” Nuclear Physics A 468, 1–10 (1987).
- Coc et al. (1985) Coc, A., Thibault, C., Touchard, F., Duong, H., Juncar, P., Liberman, S., Pinard, J., Lermé, J., Vialle, J., Büttgenbach, S., Mueller, A., and Pesnelle, A. (ISOLDE Collaboration), “Hyperfine structures and isotope shifts of 207-213,220-228Fr; Possible evidence of octupolar deformation,” Physics Letters B 163, 66–70 (1985).
- Das et al. (2006a) Das, D., Banerjee, A., Barthwal, S., and Natarajan, V., “A rubidium-stabilized ring-cavity resonator for optical frequency metrology: precise measurement of the line in 133Cs,” The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics 38, 545–552 (2006a).
- Das and Natarajan (2005) Das, D. and Natarajan, V., “Hyperfine spectroscopy on the state of 133Cs using coherent control,” Europhysics Letters (EPL) 72, 740–746 (2005).
- Das and Natarajan (2006a) Das, D. and Natarajan, V., “Precise measurement of hyperfine structure in the state of Rb,” The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics 37, 313–317 (2006a).
- Das and Natarajan (2006b) Das, D. and Natarajan, V., “Precise measurement of hyperfine structure in the state of 133Cs,” Journal of Physics B: Atomic, Molecular and Optical Physics 39, 2013–2019 (2006b).
- Das and Natarajan (2008) Das, D. and Natarajan, V., “High-precision measurement of hyperfine structure in the D lines of alkali atoms,” Journal of Physics B: Atomic, Molecular and Optical Physics 41, 035001 (2008).
- Das et al. (2006b) Das, D., Pandey, K., Wasan, A., and Natarajan, V., “Resolving closely spaced hyperfine levels in the 3state of 23Na,” Journal of Physics B: Atomic, Molecular and Optical Physics 39, 3111–3119 (2006b).
- de Groote et al. (2015) de Groote, R. P., Budinčević, I., Billowes, J., Bissell, M. L., Cocolios, T. E., Farooq-Smith, G. J., Fedosseev, V. N., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Li, R., Lynch, K. M., Marsh, B. A., Neyens, G., Rossel, R. E., Rothe, S., Stroke, H. H., Wendt, K. D. A., Wilkins, S. G., and Yang, X., “Use of a continuous wave laser and Pockels cell for sensitive high-resolution collinear resonance ionization spectroscopy,” Phys. Rev. Lett. 115, 132501 (2015).
- Deech et al. (1977) Deech, J. S., Luypaert, R., Pendrill, L. R., and Series, G. W., “Lifetimes, depopulation cross sections and hyperfine structures of some Rydberg S and D states of 133Cs,” Journal of Physics B: Atomic and Molecular Physics 10, L137–L141 (1977).
- DeGraffenreid and Sansonetti (2003) DeGraffenreid, W. and Sansonetti, C. J., “ transition of atomic lithium by Doppler-free two-photon spectroscopy,” Phys. Rev. A 67, 012509 (2003).
- Duong (1982) Duong, H.-T., “Hyperfine structure and isotope shifts of by rf modulated laser light,” Nuclear Instruments and Methods in Physics Research 202, 341–342 (1982).
- Duong et al. (1993) Duong, H.-T., Ekström, C., Gustafsson, M., Inamura, T. T., Juncar, P., Lievens, P., Lindgren, I., Matsuki, S., Murayama, T., Neugart, R., Nilsson, T., Nomura, T., Pellarin, M., Penselin, S., Persson, J., Pinard, J., Ragnarsson, I., Redi, O., Stroke, H. H., and Vialle, J. L. (ISOLDE Collaboration), “Atomic beam magnetic resonance apparatus for systematic measurement of hyperfine structure anomalies (Bohr-Weisskopf effect),” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 325, 465–474 (1993).
- Duong et al. (1987) Duong, H.-T., Juncar, P., Liberman, S., Mueller, A. C., Neugart, R., Otten, E. W., Peuse, B., Pinard, J., Stroke, H. H., Thibault, C., Touchard, F., Vialle, J. L., and Wendt, K. (ISOLDE Collaboration), “First observation of the blue optical lines of francium,” Europhysics Letters (EPL) 3, 175–182 (1987).
- Duong et al. (1986) Duong, H. T., Liberman, S., Pinard, J., Coc, A., Thibault, C., Touchard, F., Carré, M., Lermé, J., Vialle, J. L., Juncar, P., Büttgenbach, S., and Pesnelle, A. (ISOLDE Collaboration), “Accurate determination of ground state hyperfine structures of some radioactive alkali isotopes by r. f. magnetic resonance and laser optical pumping,” J. Phys. France 47, 1903–1908 (1986).
- Dzuba and Flambaum (2000) Dzuba, V. A. and Flambaum, V. V., “Off-diagonal hyperfine interaction and parity nonconservation in cesium,” Phys. Rev. A 62, 052101 (2000).
- Ewald et al. (2004) Ewald, G., Nörtershäuser, W., Dax, A., Götte, S., Kirchner, R., Kluge, H.-J., Kühl, T., Sanchez, R., Wojtaszek, A., Bushaw, B. A., Drake, G. W. F., Yan, Z.-C., and Zimmermann, C., “Nuclear charge radii of determined by laser spectroscopy,” Phys. Rev. Lett. 93, 113002 (2004).
- Faist, Geneux, and Koide (1964) Faist, A., Geneux, E., and Koide, S., “Frequency shift in magnetic transitions between hyperfine levels of states of Cs133,” Journal of the Physical Society of Japan 19, 2299–2305 (1964).
- Falke et al. (2006) Falke, S., Tiemann, E., Lisdat, C., Schnatz, H., and Grosche, G., “Transition frequencies of the lines of , , and measured with a femtosecond laser frequency comb,” Phys. Rev. A 74, 032503 (2006).
- Farley, Tsekeris, and Gupta (1977) Farley, J., Tsekeris, P., and Gupta, R., “Hyperfine-structure measurements in the Rydberg and states of rubidium and cesium,” Phys. Rev. A 15, 1530–1536 (1977).
- Farooq-Smith et al. (2016a) Farooq-Smith, G. J., Cocolios, T. E., Billowes, J., Bissell, M. L., Budinčević, I., Day Goodacre, T., de Groote, R. P., Fedosseev, V. N., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Li, R., Lynch, K. M., Marsh, B. A., Neyens, G., Rossel, R. E., Rothe, S., Stroke, H. H., Wendt, K. D. A., Wilkins, S. G., and Yang, X. F., “Laser and decay spectroscopy of the short-lived isotope in the vicinity of the shell closure,” Phys. Rev. C 94, 054305 (2016a).
- Farooq-Smith et al. (2016b) Farooq-Smith, G. J., Cocolios, T. E., Billowes, J., Bissell, M. L., Budinčević, I., Day Goodacre, T., de Groote, R. P., Fedosseev, V. N., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Li, R., Lynch, K. M., Marsh, B. A., Neyens, G., Rossel, R. E., Rothe, S., Stroke, H. H., Wendt, K. D. A., Wilkins, S. G., and Yang, X. F., “Publisher’s note: Laser and decay spectroscopy of the short-lived isotope in the vicinity of the shell closure [Phys. Rev. C 94, 054305 (2016)],” Phys. Rev. C 94, 059903 (2016b).
- Feiertag and zu Putlitz (1973) Feiertag, D. and zu Putlitz, G., “Hyperfine structure, factors and lifetimes of excited states of Rb,” Zeitschrift für Physik A 261, 1–12 (1973).
- Feiertag, Sahm, and zu Putlitz (1972) Feiertag, D., Sahm, A., and zu Putlitz, G., “Core polarization of the 133Cs atom by the 7p electron,” Zeitschrift für Physik A Hadrons and nuclei 255, 93–96 (1972).
- Fendel et al. (2007) Fendel, P., Bergeson, S. D., Udem, T., and Hänsch, T. W., “Two-photon frequency comb spectroscopy of the transition in cesium,” Opt. Lett. 32, 701–703 (2007).
- Flambaum and Khriplovich (1985) Flambaum, V. V. and Khriplovich, I. B., “New bounds on the electric dipole moment of the electron and on T-odd electron-nucleon coupling,” Sov. Phys. - JETP (Engl. Transl.) 62, 872 (1985).
- Flanagan et al. (2013) Flanagan, K. T., Lynch, K. M., Billowes, J., Bissell, M. L., Budinčević, I., Cocolios, T. E., de Groote, R. P., De Schepper, S., Fedosseev, V. N., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Marsh, B. A., Neyens, G., Procter, T. J., Rossel, R. E., Rothe, S., Strashnov, I., Stroke, H. H., and Wendt, K. D. A., “Collinear resonance ionization spectroscopy of neutron-deficient francium isotopes,” Phys. Rev. Lett. 111, 212501 (2013).
- Foot (2005) Foot, C. J., Atomic Physics (Oxford University Press, 2005).
- Fort et al. (1995a) Fort, C., Cataliotti, F. S., Raspollini, P., Tino, G. M., and Inguscio, M., “Optical double-resonance spectroscopy of trapped Cs atoms: hyperfine structure of the 8s and 6d excited states,” Zeitschrift für Physik D Atoms, Molecules and Clusters 34, 91–95 (1995a).
- Fort et al. (1995b) Fort, C., Inguscio, M., Raspollini, P., Baldes, F., and Sasso, A., “Doppler-free two-color spectroscopy of the cesium transition using semiconductor diode lasers,” Appl. Phys. B 61, 462–471 (1995b).
- Fredriksson, Lundberg, and Svanberg (1980) Fredriksson, K., Lundberg, H., and Svanberg, S., “Fine- and hyperfine-structure investigation in the series of cesium,” Phys. Rev. A 21, 241–247 (1980).
- Gabbanini et al. (1999) Gabbanini, C., Ceccherini, F., Gozzini, S., and Lucchesini, A., “Resonance-enhanced ionization spectroscopy of laser-cooled rubidium atoms,” Measurement Science and Technology 10, 772–776 (1999).
- Gangrsky et al. (1998) Gangrsky, Y. P., Karaivanov, D. V., Marinova, K. P., Markov, B. N., Melnikova, L. M., Mishinsky, G. V., Zemlyanoi, S. G., and Zhemenik, V. I., “Hyperfine splitting and isotope shift in the atomic line of 22,23Na and the quadrupole moment of 22Na,” The European Physical Journal A - Hadrons and Nuclei 3, 313–318 (1998).
- Georgiades, Polzik, and Kimble (1994) Georgiades, N. P., Polzik, E. S., and Kimble, H. J., “Two-photon spectroscopy of the → transition of trapped atomic cesium,” Opt. Lett. 19, 1474–1476 (1994).
- Gerginov et al. (2006) Gerginov, V., Calkins, K., Tanner, C. E., McFerran, J. J., Diddams, S., Bartels, A., and Hollberg, L., “Optical frequency measurements of transitions in and their impact on the fine-structure constant,” Phys. Rev. A 73, 032504 (2006).
- Gerginov, Derevianko, and Tanner (2003) Gerginov, V., Derevianko, A., and Tanner, C. E., “Observation of the nuclear magnetic octupole moment of ,” Phys. Rev. Lett. 91, 072501 (2003).
- Gerginov, Tanner, and Johnson (2009) Gerginov, V., Tanner, C. E., and Johnson, W. R., “Observation of the nuclear magnetic octupole moment of 87Rb from spectroscopic measurements of hyperfine intervals,” Canadian Journal of Physics 87, 101–104 (2009).
- Gerhardt et al. (1978) Gerhardt, H., Matthias, E., Schneider, F., and Timmermann, A., “Isotope shifts and hyperfine structure of the 6s-7p transitions in the cesium isotopes 133, 135, and 137,” Zeitschrift für Physik A Atoms and Nuclei 288, 327–333 (1978).
- Gilbert et al. (1986) Gilbert, S. L., Masterson, B. P., Noecker, M. C., and Wieman, C. E., “Precision measurement of the off-diagonal hyperfine interaction,” Phys. Rev. A 34, 3509–3512 (1986).
- Gilbert, Watts, and Wieman (1983) Gilbert, S. L., Watts, R. N., and Wieman, C. E., “Hyperfine-structure measurement of the state of cesium,” Phys. Rev. A 27, 581–582 (1983).
- Glaser et al. (2020) Glaser, C., Karlewski, F., Kluge, J., Grimmel, J., Kaiser, M., Günther, A., Hattermann, H., Krutzik, M., and Fortágh, J., “Absolute frequency measurement of rubidium transitions,” Phys. Rev. A 102, 012804 (2020).
- Głódź and Kraińska-Miszczak (1985a) Głódź, M. and Kraińska-Miszczak, M., “Hyperfine interaction constants and lifetime of the 6 and 6 states of 39K measured by the quantum beam method,” Journal of Physics B: Atomic and Molecular Physics 18, 1515–1522 (1985a).
- Głódź and Kraińska-Miszczak (1985b) Głódź, M. and Kraińska-Miszczak, M., “Lifetime and hyperfine structure constants of the 6 state in 41K,” Physics Letters A 110, 203–205 (1985b).
- Głódź and Kraińska-Miszczak (1987) Głódź, M. and Kraińska-Miszczak, M., “Magnetic-dipole and electric-quadrupole interaction constants in the state of 87Rb,” Journal of Physics B: Atomic and Molecular Physics 20, L541–L545 (1987).
- Głódź and Kraińska-Miszczak (1989) Głódź, M. and Kraińska-Miszczak, M., “Measurements of magnetic-dipole and electric-quadrupole interaction constants of the 11, 12 and 13 states in 87Rb by the quantum-beat method,” Journal of Physics B: Atomic, Molecular and Optical Physics 22, 3109–3117 (1989).
- Głódź and Kraińska-Miszczak (1990) Głódź, M. and Kraińska-Miszczak, M., “Magnetic-dipole and electric-quadrupole interaction constants and lifetime of the 9 state in Rb-87,” Acta Phys. Pol. 78, 317–322 (1990).
- Głódź and Kraińska-Miszczak (1991) Głódź, M. and Kraińska-Miszczak, M., “Hyperfine interaction constants of the 10, 11 and 12 states in 87Rb measured by the quantum beat method,” Physics Letters A 160, 85–89 (1991).
- Głódź and Kraińska-Miszczak (1993) Głódź, M. and Kraińska-Miszczak, M., “Hyperfine structure constants in the 10 and 11 states of 85Rb,” Acta Phys. Pol. 83, 161–165 (1993).
- Gomez et al. (2004) Gomez, E., Aubin, S., Orozco, L. A., and Sprouse, G. D., “Lifetime and hyperfine splitting measurements on the 7 and 6 levels in rubidium,” J. Opt. Soc. Am. B 21, 2058–2067 (2004).
- Gomez et al. (2008) Gomez, E., Aubin, S., Orozco, L. A., Sprouse, G. D., Iskrenova-Tchoukova, E., and Safronova, M. S., “Nuclear magnetic moment of : A combined theoretical and experimental approach,” Phys. Rev. Lett. 100, 172502 (2008).
- Goy et al. (1982) Goy, P., Raimond, J. M., Vitrant, G., and Haroche, S., “Millimeter-wave spectroscopy in cesium Rydberg states. Quantum defects, fine- and hyperfine-structure measurements,” Phys. Rev. A 26, 2733–2742 (1982).
- Griffith et al. (1977) Griffith, J. A. R., Isaak, G. R., New, R., Ralls, M. P., and van Zyl, C. P., “Optical heterodyne spectroscopy using tunable dye lasers: hyperfine structure of sodium,” Journal of Physics B: Atomic and Molecular Physics 10, L91–L95 (1977).
- Grossman et al. (2000) Grossman, J. M., Fliller III, R. P., Mehlstäubler, T. E., Orozco, L. A., Pearson, M. R., Sprouse, G. D., and Zhao, W. Z., “Energies and hyperfine splittings of the levels of atomic francium,” Phys. Rev. A 62, 052507 (2000).
- Grossman et al. (1999) Grossman, J. S., Orozco, L. A., Pearson, M. R., Simsarian, J. E., Sprouse, G. D., and Zhao, W. Z., “Hyperfine anomaly measurements in francium isotopes and the radial distribution of neutrons,” Phys. Rev. Lett. 83, 935–938 (1999).
- Grove et al. (1995) Grove, T. T., Sanchez-Villicana, V., Duncan, B. C., Maleki, S., and Gould, P. L., “Two-photon two-color diode laser spectroscopy of the Rb 5 state,” Physica Scripta 52, 271–276 (1995).
- Grundevik and Lundberg (1978) Grundevik, P. and Lundberg, H., “Measurement of the hyperfine structure splitting for the 4 and 5 states of sodium using radio-frequency spectroscopy,” Zeitschrift für Physik A Atoms and Nuclei 285, 231–233 (1978).
- Grundevik et al. (1979) Grundevik, P., Lundberg, H., Martensson, A. M., Nystrom, K., and Svanberg, S., “Hyperfine-structure study in the P sequence of 23Na using quantum-beam spectroscopy,” Journal of Physics B: Atomic and Molecular Physics 12, 2645–2654 (1979).
- Grunefeld, Roberts, and Ginges (2019) Grunefeld, S. J., Roberts, B. M., and Ginges, J. S. M., “Correlation trends in the hyperfine structure for Rb, Cs, and Fr, and high-accuracy predictions for hyperfine constants,” Phys. Rev. A 100, 042506 (2019).
- Guéna et al. (2014) Guéna, J., Abgrall, M., Clairon, A., and Bize, S., “Contributing to TAI with a secondary representation of the SI second,” Metrologia 51, 108–120 (2014).
- Gupta et al. (1973) Gupta, R., Happer, W., Lam, L. K., and Svanberg, S., “Hyperfine-structure measurements of excited states of the stable isotopes of potassium, rubidium, and cesium by cascade radio-frequency spectroscopy,” Phys. Rev. A 8, 2792–2810 (1973).
- Gwinner and Orozco (2022) Gwinner, G. and Orozco, L. A., “Studies of the weak interaction in atomic systems: towards measurements of atomic parity non-conservation in francium,” Quantum Science and Technology 7, 024001 (2022).
- Hagel et al. (1999) Hagel, G., Nesi, C., Jozefowski, L., Schwob, C., Nez, F., and Biraben, F., “Accurate measurement of the frequency of the 6S-8S two-photon transitions in cesium,” Optics Communications 160, 1–4 (1999).
- Halloran et al. (2009) Halloran, L., Fostner, S., Paradis, E., and Behr, J., “Specific mass shift of potassium state,” Optics Communications 282, 554–557 (2009).
- Hawkins et al. (1977) Hawkins, R. T., Hill, W. T., Kowalski, F. V., Schawlow, A. L., and Svanberg, S., “Stark-effect study of excited states in sodium using two-photon spectroscopy,” Phys. Rev. A 15, 967–974 (1977).
- He et al. (2020) He, Y.-H., Fan, J.-B., Hao, L.-P., Jiao, Y.-C., and Zhao, J.-M., “Precise measurement of hyperfine structure of cesium excited state,” Applied Sciences 10 (2020), 10.3390/app10020525.
- He et al. (2012) He, Z.-S., Tsai, J.-H., Lee, M.-T., Chang, Y.-Y., Tsai, C.-C., and Whang, T.-J., “Determination of the cesium hyperfine magnetic coupling constant using electromagnetically induced transparency,” Journal of the Physical Society of Japan 81, 124302 (2012).
- Herd, Cook, and Williams (2021) Herd, M. T., Cook, E. C., and Williams, W. D., “Absolute frequency measurement of the level of neutral using two-photon spectroscopy,” Phys. Rev. A 104, 042812 (2021).
- Herrmann et al. (1985) Herrmann, P., Hoffnagle, J., Pedroni, A., Schlumpf, N., and Weis, A., “Doppler-free spectroscopy of the 8 state of Cs,” Optics Communications 56, 22–24 (1985).
- Hogervorst and Svanberg (1975) Hogervorst, W. and Svanberg, S., “Stark effect investigation of states in 85Rb and 133Cs using level crossing spectroscopy with a CW dye laser,” Physica Scripta 12, 67–74 (1975).
- Huang and Sun (2010) Huang, S.-H. and Sun, Q.-F., “Calculation of the Rydberg energy levels for francium atom,” Physics Research International 2010, 203497 (2010).
- Huang et al. (2013) Huang, Y.-C., Luo, W.-J., Kuo, Y.-T., and Wang, L.-B., “Precision measurement of hyperfine intervals in the lines of atomic 7Li,” Journal of Physics B: Atomic, Molecular and Optical Physics 46, 075004 (2013).
- Inguscio and Fallani (2013) Inguscio, M. and Fallani, L., Atomic Physics: Precise Measurements and Ultracold Matter (Oxford University Press, 2013).
- Isler, Marcus, and Novick (1969) Isler, R. C., Marcus, S., and Novick, R., “Hyperfine structure of the and states of lithium and lifetime of the state,” Phys. Rev. 187, 76–84 (1969).
- Jiang, Jönsson, and Lundberg (1982) Jiang, Z.-K., Jönsson, G., and Lundberg, H., “Hyperfine-structure study of the 7, 8 and 9 states in using quantum-beat spectroscopy,” Physica Scripta 26, 459–461 (1982).
- Jin et al. (2013) Jin, L., Zhang, Y.-C., Xiang, S.-S., Wang, L.-R., Ma, J., Zhao, Y.-T., Xiao, L.-T., and Jia, S.-T., “Experimental measurement of the absolute frequencies and hyperfine coupling constants of 133Cs using a femtosecond optical frequency comb,” Chinese Physics Letters 30, 103201 (2013).
- Johnson et al. (2004) Johnson, W. R., Ho, H. C., Tanner, C. E., and Derevianko, A., “Off-diagonal hyperfine interaction between the and levels in ,” Phys. Rev. A 70, 014501 (2004).
- Johnson, Safronova, and Safronova (2003) Johnson, W. R., Safronova, M. S., and Safronova, U. I., “Combined effect of coherent exchange and the hyperfine interaction in the atomic parity-nonconserving interaction,” Phys. Rev. A 67, 062106 (2003).
- Johnson et al. (2008) Johnson, W. R., Safronova, U. I., Derevianko, A., and Safronova, M. S., “Relativistic many-body calculation of energies, lifetimes, hyperfine constants, and polarizabilities in ,” Phys. Rev. A 77, 022510 (2008).
- Kasevich et al. (1989) Kasevich, M. A., Riis, E., Chu, S., and DeVoe, R. G., “rf spectroscopy in an atomic fountain,” Phys. Rev. Lett. 63, 612–615 (1989).
- Kiran Kumar et al. (2014) Kiran Kumar, P. V., Nisheeth, B., Sankari, M., and Suryanarayana, M. V., “Precision measurement of the hyperfine structure of 8d2D3/2 state of 133Cs by the radio-frequency phase modulation technique,” Optics Communications 320, 77–83 (2014).
- Kiran Kumar, Sankari, and Suryanarayana (2013) Kiran Kumar, P. V., Sankari, M., and Suryanarayana, M. V., “Hyperfine structure of the level in cesium measured by Doppler-free two-photon spectroscopy,” Phys. Rev. A 87, 012503 (2013).
- Kiran Kumar and Suryanarayana (2011) Kiran Kumar, P. V. and Suryanarayana, M. V., “Isotope shift and hyperfine structure measurements of 4s2S 6s2S1/2 two-photon transition of potassium isotopes,” Journal of Physics B: Atomic, Molecular and Optical Physics 44, 055003 (2011).
- Kiran Kumar and Suryanarayana (2012) Kiran Kumar, P. V. and Suryanarayana, M. V., “Measurement of the hyperfine splitting of the 9S1/2 level in Cesium by Doppler-free two-photon spectroscopy,” Optics Communications 285, 1838–1842 (2012).
- Kiran Kumar and Suryanarayana (2014) Kiran Kumar, P. V. and Suryanarayana, M. V., “Precision two-photon spectroscopy of alkali elements,” Pramana 83, 189–219 (2014).
- Konovalova, Demidov, and Kozlov (2020) Konovalova, E. A., Demidov, Y. A., and Kozlov, M. G., “Calculation of the hyperfine magnetic anomaly in many-electron atoms,” Optics and Spectroscopy 128, 1530–1536 (2020).
- Konovalova et al. (2018) Konovalova, E. A., Demidov, Y. A., Kozlov, M. G., and Barzakh, A. E., “Calculation of francium hyperfine anomaly,” Atoms 6, 39 (2018).
- Kopfermann (1958) Kopfermann, H., Nuclear Moments (Academic, New York, 1958).
- Kortyna, Fiore, and Farrar (2008) Kortyna, A., Fiore, V., and Farrar, J., “Measurement of the cesium hyperfine coupling constants in a thermal beam using two-photon fluorescence spectroscopy,” Phys. Rev. A 77, 062505 (2008).
- Kortyna, Masluk, and Bragdon (2006) Kortyna, A., Masluk, N. A., and Bragdon, T., “Measurement of the hyperfine structure of cesium using resonant two-photon sub-Doppler spectroscopy,” Phys. Rev. A 74, 022503 (2006).
- Kortyna et al. (2011) Kortyna, A., Tinsman, C., Grab, J., Safronova, M. S., and Safronova, U. I., “Experimental and theoretical study of the polarizability of cesium,” Phys. Rev. A 83, 042511 (2011).
- Koszorús et al. (2019) Koszorús, A., Yang, X. F., Billowes, J., Binnersley, C. L., Bissell, M. L., Cocolios, T. E., Farooq-Smith, G. J., de Groote, R. P., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Geldhof, S., Gins, W., Kanellakopoulos, A., Lynch, K. M., Neyens, G., Stroke, H. H., Vernon, A. R., Wendt, K. D. A., and Wilkins, S. G., “Precision measurements of the charge radii of potassium isotopes,” Phys. Rev. C 100, 034304 (2019).
- Kowalski et al. (1978) Kowalski, J., Neumann, R., Suhr, H., Winkler, K., and zu Putlitz, G., “Two-photon intracavity dye laser spectroscopy of the 4 and 3 term in 6,7Li,” Zeitschrift für Physik A Atoms and Nuclei 287, 247–253 (1978).
- Kraińska-Miszczak (1981) Kraińska-Miszczak, M., “Decoupling in the state and D2 fluorescence of alkali metal atoms,” Optics Communications 38, 255–258 (1981).
- Kraińska-Miszczak (1994) Kraińska-Miszczak, M., “Hyperfine interaction constants in the 9 state of 85Rb measured by the quantum beat method,” Acta Phys. Pol. 86, 343–347 (1994).
- Kramida (2022) Kramida, A., “NIST atomic energy levels and spectra bibliographic database,” (2022), https://doi.org/10.1016/0030-4018(94)90278-X.
- Krishna et al. (2005) Krishna, A., Pandey, K., Wasan, A., and Natarajan, V., “High-resolution hyperfine spectroscopy of excited states using electromagnetically induced transparency,” Europhysics Letters 72, 221–227 (2005).
- Krist et al. (1977) Krist, T., Kuske, P., Gaupp, A., Wittmann, W., and Andrä, H., “Improved 23Na I 3 HFS measurement beyond the natural linewidth by beam laser quantum beats,” Physics Letters A 61, 94–96 (1977).
- Kumar and Natarajan (2017) Kumar, P. and Natarajan, V., “Precise measurement of hyperfine structure in the 3S1/2 state of 7Li,” Scientific Reports 7, 13204 (2017).
- Lam, Gupta, and Happer (1980) Lam, L. K., Gupta, R., and Happer, W., “Hyperfine-structure measurements in the first excited levels of potassium, rubidium, and cesium by cascade-fluorescence spectroscopy,” Phys. Rev. A 21, 1225–1234 (1980).
- Lee and Moon (2015) Lee, W.-K. and Moon, H. S., “Measurement of absolute frequencies and hyperfine structure constants of and levels of and using an optical frequency comb,” Phys. Rev. A 92, 012501 (2015).
- Lee, Moon, and Suh (2007) Lee, W.-K., Moon, H. S., and Suh, H. S., “Measurement of the absolute energy level and hyperfine structure of the 87Rb state,” Opt. Lett. 32, 2810–2812 (2007).
- Lee, Moon, and Suh (2015) Lee, W.-K., Moon, H. S., and Suh, H. S., “Measurement of the absolute energy level and hyperfine structure of the 87Rb 4 state: erratum,” Opt. Lett. 40, 2111–2111 (2015).
- Lee et al. (2011) Lee, Y.-C., Chang, Y.-H., Chang, Y.-Y., Chen, Y.-Y., Tsai, C.-C., and Chui, H.-C., “Hyperfine coupling constants of cesium 7 states using two-photon spectroscopy,” Applied Physics B 105, 391–397 (2011).
- Li et al. (2020) Li, R., Wu, Y.-L., Rui, Y., Li, B., Jiang, Y.-Y., Ma, L.-S., and Wu, H.-B., “Absolute Frequency Measurement of Lines with khz-Level Uncertainty,” Phys. Rev. Lett. 124, 063002 (2020).
- Li et al. (2021) Li, R., Wu, Y.-L., Rui, Y., and Wu, H.-B., “Observation of subnatural-linewidth spectra in cold atoms,” Phys. Rev. A 103, 032823 (2021).
- Li et al. (2003) Li, W.-H., Mourachko, I., Noel, M. W., and Gallagher, T. F., “Millimeter-wave spectroscopy of cold Rb Rydberg atoms in a magneto-optical trap: Quantum defects of the , , and series,” Phys. Rev. A 67, 052502 (2003).
- Liberman et al. (1980) Liberman, S., Pinard, J., Duong, H. T., Juncar, P., Pillet, P., Vialle, J.-L., Jacquinot, P., Touchard, F., Büttgenbach, S., Thibault, C., de Saint-Simon, M., Klapisch, R., Pesnelle, A., and Huber, G., “Laser optical spectroscopy on francium resonance line,” Phys. Rev. A 22, 2732–2737 (1980).
- Lien et al. (2011) Lien, Y.-H., Lo, K.-J., Chen, H.-C., Chen, J.-R., Tian, J.-Y., Shy, J.-T., and Liu, Y.-W., “Absolute frequencies of the 6,7Li 2 transitions,” Phys. Rev. A 84, 042511 (2011).
- Lorenzen and Niemax (1982) Lorenzen, C. J. and Niemax, K., “Level isotope shifts of ,” Journal of Physics B: Atomic and Molecular Physics 15, L139–L145 (1982).
- Lorenzen and Niemax (1983) Lorenzen, C.-J. and Niemax, K., “Quantum Defects of the Levels in 39K I and 85Rb I,” Physica Scripta 27, 300–305 (1983).
- Lorenzen and Niemax (1984) Lorenzen, C. J. and Niemax, K., “Precise quantum defects of , and Levels in Cs I,” Zeitschrift für Physik A Atoms and Nuclei 315, 127–133 (1984).
- Lou et al. (2019) Lou, B.-Q., Li, F., Wan, P.-Y., Wang, L.-M., and Tang, Y.-B., “Ab initio calculation of hyperfine-structure constant of Fr and evaluation of magnetic dipole moments of Fr isotopes,” Acta Phys. Sin. 68, 093101 (2019).
- Lu et al. (1997) Lu, Z.-T., Corwin, K. L., Vogel, K. R., Wieman, C. E., Dinneen, T. P., Maddi, J., and Gould, H., “Efficient collection of 221Fr into a vapor cell magneto-optical trap,” Phys. Rev. Lett. 79, 994–997 (1997).
- Lundberg, Mårtensson, and Svanberg (1977) Lundberg, H., Mårtensson, A. M., and Svanberg, S., “Hyperfine structure in the sequence of sodium states,” Journal of Physics B: Atomic and Molecular Physics 10, 1971–1978 (1977).
- Lynch et al. (2014) Lynch, K. M., Billowes, J., Bissell, M. L., Budinčević, I., Cocolios, T. E., de Groote, R. P., De Schepper, S., Fedosseev, V. N., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Marsh, B. A., Neyens, G., Procter, T. J., Rossel, R. E., Rothe, S., Strashnov, I., Stroke, H. H., and Wendt, K. D. A., “Decay-assisted laser spectroscopy of neutron-deficient francium,” Phys. Rev. X 4, 011055 (2014).
- Lynch et al. (2016) Lynch, K. M., Cocolios, T. E., Billowes, J., Bissell, M. L., Budinčević, I., Day Goodacre, T., de Groote, R. P., Farooq-Smith, G. J., Fedosseev, V. N., Flanagan, K. T., Franchoo, S., Garcia Ruiz, R. F., Heylen, H., Li, R., Marsh, B. A., Neyens, G., Rossel, R. E., Rothe, S., Stroke, H. H., Wendt, K. D. A., Wilkins, S. G., and Yang, X., “Combined high-resolution laser spectroscopy and nuclear decay spectroscopy for the study of the low-lying states in , , and ,” Phys. Rev. C 93, 014319 (2016).
- Lyons and Das (1970) Lyons, J. D. and Das, T. P., “Theoretical analysis of level crossing in a atomic state,” Phys. Rev. A 2, 2250–2259 (1970).
- Mack et al. (2011) Mack, M., Karlewski, F., Hattermann, H., Höckh, S., Jessen, F., Cano, D., and Fortágh, J., “Measurement of absolute transition frequencies of to and Rydberg states by means of electromagnetically induced transparency,” Phys. Rev. A 83, 052515 (2011).
- Marcassa et al. (1998) Marcassa, L., Muniz, S., Telles, G., Zilio, S., and Bagnato, V., “Measurement of Na 5 hyperfine splitting by ionization using a sample of cold atoms,” Optics Communications 155, 38–42 (1998).
- Marian et al. (2005) Marian, A., Stowe, M. C., Felinto, D., and Ye, J., “Direct frequency comb measurements of absolute optical frequencies and population transfer dynamics,” Phys. Rev. Lett. 95, 023001 (2005).
- Maric, McFerran, and Luiten (2008) Maric, M., McFerran, J. J., and Luiten, A. N., “Frequency-comb spectroscopy of the line in laser-cooled rubidium,” Phys. Rev. A 77, 032502 (2008).
- McLaughlin et al. (2022) McLaughlin, C., Ayachitula, R., Lindsay, M., and Knize, R., “Hyperfine splittings and isotope shift of the Rb - two-photon transition,” Bulletin of the American Physical Society 53rd Annual Meeting of the APS Division of Atomic, Molecular and Optical Physics, Abstract: N01.00124 (2022).
- Meschede (1987) Meschede, D., “Centimeter-wave spectroscopy of highly excited rubidium atoms,” J. Opt. Soc. Am. B 4, 413–419 (1987).
- Metcalf and van der Straten (1999) Metcalf, H. J. and van der Straten, P., Laser Cooling and Trapping of Neutral Atoms (Springer-Verlag, New York, 1999).
- Moon, Lee, and Suh (2009) Moon, H. S., Lee, W.-K., and Suh, H. S., “Hyperfine-structure-constant determination and absolute-frequency measurement of the Rb state,” Phys. Rev. A 79, 062503 (2009).
- Morgenweg, Barmes, and Eikema (2014) Morgenweg, J., Barmes, I., and Eikema, K. S. E., “Ramsey-comb spectroscopy with intense ultrashort laser pulses,” Nature Physics 10, 30–33 (2014).
- Morzyński et al. (2013) Morzyński, P., Wcisło, P., Ablewski, P., Gartman, R., Gawlik, W., Masłowski, P., Nagórny, B., Ozimek, F., Radzewicz, C., Witkowski, M., Ciuryło, R., and Zawada, M., “Absolute frequency measurement of rubidium two-photon transitions,” Opt. Lett. 38, 4581–4584 (2013).
- Morzyński et al. (2014) Morzyński, P., Wcisło, P., Ablewski, P., Gartman, R., Gawlik, W., Masłowski, P., Nagórny, B., Ozimek, F., Radzewicz, C., Witkowski, M., Ciuryło, R., and Zawada, M., “Line shape measurements of rubidium two-photon transition,” Journal of Physics: Conference Series 548, 012023 (2014).
- Nagourney, Happer, and Lurio (1978) Nagourney, W., Happer, W., and Lurio, A., “Level-crossing study of the hyperfine structure of lithium,” Phys. Rev. A 17, 1394–1407 (1978).
- Nakayama, Kelly, and Series (1981) Nakayama, S., Kelly, F. M., and Series, G. W., “Hyperfine structures, lifetimes and collisional cross sections of some Rydberg states of 133Cs,” Journal of Physics B: Atomic and Molecular Physics 14, 835–838 (1981).
- Neugart et al. (2017) Neugart, R., Billowes, J., Bissell, M. L., Blaum, K., Cheal, B., Flanagan, K. T., Neyens, G., Nörtershäuser, W., and Yordanov, D. T., “Collinear laser spectroscopy at ISOLDE: new methods and highlights,” Journal of Physics G: Nuclear and Particle Physics 44, 064002 (2017).
- Neuzner et al. (2015) Neuzner, A., Körber, M., Dürr, S., Rempe, G., and Ritter, S., “Breakdown of atomic hyperfine coupling in a deep optical-dipole trap,” Phys. Rev. A 92, 053842 (2015).
- Ney (1969) Ney, J., “Hyperfeinstrukturuntersuchung der 4 und 5-Terme im K I-Spektrum durch Resonanzstreuung von Licht zur Bestimmung der Kernquadrupolmomente von K39 und K41,” Zeitschrift für Physik A 223, 126–138 (1969).
- Ney et al. (1968) Ney, J., Repnow, R., Bucka, H., and Svanberg, S., “Untersuchung des 4 und 5-terms des KI-spektrums durch resonanzstreuung von licht zur bestimmung des kernquadrupolmoments von K40,” Zeitschrift für Physik A 213, 192–201 (1968).
- Nez et al. (1993) Nez, F., Biraben, F., Felder, R., and Millerioux, Y., “Optical frequency determination of the hyperfine components of the 5-5 two-photon transitions in rubidium,” Optics Communications 102, 432–438 (1993).
- Noble et al. (2006) Noble, G. A., Schultz, B. E., Ming, H., and van Wijngaarden, W. A., “Isotope shifts and fine structures of lines and determination of the relative nuclear charge radius,” Phys. Rev. A 74, 012502 (2006).
- Nörtershäuser et al. (2011) Nörtershäuser, W., Sánchez, R., Ewald, G., Dax, A., Behr, J., Bricault, P., Bushaw, B. A., Dilling, J., Dombsky, M., Drake, G. W. F., Götte, S., Kluge, H.-J., Kühl, T., Lassen, J., Levy, C. D. P., Pachucki, K., Pearson, M., Puchalski, M., Wojtaszek, A., Yan, Z.-C., and Zimmermann, C., “Isotope-shift measurements of stable and short-lived lithium isotopes for nuclear-charge-radii determination,” Phys. Rev. A 83, 012516 (2011).
- Nyakang’o et al. (2020) Nyakang’o, E. O., Shylla, D., Natarajan, V., and Pandey, K., “Hyperfine measurement of the 6P1/2 state in 87Rb using double resonance on blue and IR transition,” Journal of Physics B: Atomic, Molecular and Optical Physics 53, 095001 (2020).
- Ohtsuka et al. (2005) Ohtsuka, T., Nishimiya, N., Fukuda, T., and Suzuki, M., “Doppler-Free Two-Photon Spectroscopy of 6 Transition in Cesium,” Journal of the Physical Society of Japan 74, 2487–2491 (2005).
- Orson et al. (2021) Orson, S. T., McLaughlin, C. D., Lindsay, M. D., and Knize, R. J., “Absolute hyperfine energy levels and isotope shift of Rb 5S–6S two-photon transition,” Journal of Physics B: Atomic, Molecular and Optical Physics 54, 175001 (2021).
- Orth, Ackermann, and Otten (1975) Orth, H., Ackermann, H., and Otten, E. W., “Fine and hyperfine structure of the 22P term of 7Li; determination of the nuclear quadrupole moment,” Zeitschrift für Physik A Atoms and Nuclei 273, 221–232 (1975).
- Orth et al. (1974) Orth, H., Veil, R., Ackermann, H., and Otten, E. W., “Fine and hyperfine structure of the 2 term of 6Li and 7Li; determination of the 7Li quadrupole moment,” in Abstracts of Contributed Papers to the Fourth International Conference on Atomic Physics, edited by J. Kowalski and H. G. Weber (1974) p. 93.
- Otto et al. (2002) Otto, P., Gamperling, M., Hofacker, M., Meyer, T., Pagliari, V., Stifter, A., Krauss, M., and Hüttner, W., “Level magnetizabilities of the alkaline metal atoms,” Chemical Physics 282, 289–304 (2002).
- Ovchinnikov, Szymaniec, and Edris (2015) Ovchinnikov, Y. B., Szymaniec, K., and Edris, S., “Measurement of rubidium ground-state hyperfine transition frequency using atomic fountains,” Metrologia 52, 595–599 (2015).
- Pal et al. (2007) Pal, R., Safronova, M. S., Johnson, W. R., Derevianko, A., and Porsev, S. G., “Relativistic coupled-cluster single-double method applied to alkali-metal atoms,” Phys. Rev. A 75, 042515 (2007).
- Papuga et al. (2014) Papuga, J., Bissell, M. L., Kreim, K., Barbieri, C., Blaum, K., De Rydt, M., Duguet, T., Garcia Ruiz, R. F., Heylen, H., Kowalska, M., Neugart, R., Neyens, G., Nörtershäuser, W., Rajabali, M. M., Sánchez, R., Smirnova, N., Somà, V., and Yordanov, D. T., “Shell structure of potassium isotopes deduced from their magnetic moments,” Phys. Rev. C 90, 034321 (2014).
- Peper et al. (2019) Peper, M., Helmrich, F., Butscher, J., Agner, J. A., Schmutz, H., Merkt, F., and Deiglmayr, J., “Precision measurement of the ionization energy and quantum defects of I,” Phys. Rev. A 100, 012501 (2019).
- Pérez Galván et al. (2007) Pérez Galván, A., Zhao, Y., Orozco, L., Gómez, E., Lange, A., Baumer, F., and Sprouse, G., “Comparison of hyperfine anomalies in the and levels of 85Rb and 87Rb,” Physics Letters B 655, 114–118 (2007).
- Pérez Galván, Zhao, and Orozco (2008) Pérez Galván, A., Zhao, Y., and Orozco, L. A., “Measurement of the hyperfine splitting of the level in rubidium,” Phys. Rev. A 78, 012502 (2008).
- Persson (1998) Persson, J. R., “Extraction of hyperfine anomalies without precise values of the nuclear magnetic dipole moment,” The European Physical Journal A - Hadrons and Nuclei 2, 3–4 (1998).
- Persson (2013) Persson, J. R., “Table of hyperfine anomaly in atomic systems,” Atomic Data and Nuclear Data Tables 99, 62–68 (2013).
- Pescht, Gerhardt, and Matthias (1977) Pescht, K., Gerhardt, H., and Matthias, E., “Isotope shift and HFS of lines in Na-22 and 23 measured by saturation spectroscopy,” Zeitschrift für Physik A Atoms and Nuclei 281, 199–204 (1977).
- Puchalski and Pachucki (2009) Puchalski, M. and Pachucki, K., “Fine and hyperfine splitting of the state in Li and ,” Phys. Rev. A 79, 032510 (2009).
- Quirk et al. (2022) Quirk, J. A., Damitz, A., Tanner, C. E., and Elliott, D. S., “Measurement of the hyperfine coupling constants and absolute energies of the , and levels in atomic cesium,” Phys. Rev. A 105, 022819 (2022).
- Rafac and Tanner (1997) Rafac, R. J. and Tanner, C. E., “Measurement of the state hyperfine structure,” Phys. Rev. A 56, 1027–1030 (1997).
- Raghavan (1989) Raghavan, P., “Table of nuclear moments,” Atomic Data and Nuclear Data Tables 42, 189–291 (1989).
- Raimond et al. (1981) Raimond, J. M., Goy, P., Vitrant, G., and Haroche, S., “Millimeter-wave spectroscopy of cesium Rydberg states and possible applications to frequency metrology,” J. Phys. Colloques 42, 37–43 (1981).
- Ramos, Cardman, and Raithel (2019) Ramos, A., Cardman, R., and Raithel, G., “Measurement of the hyperfine coupling constant for Rydberg states of ,” Phys. Rev. A 100, 062515 (2019).
- Ramsey (1956) Ramsey, N. F., Molecular Beams (Oxford University Press, New York, 1956).
- Rapol, Krishna, and Natarajan (2003) Rapol, U. D., Krishna, A., and Natarajan, V., “Precise measurement of hyperfine structure in the 5 state of 85Rb,” The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics 23, 185–188 (2003).
- Ren et al. (2016) Ren, Y.-N., Yang, B.-D., Wang, J., Yang, G., and Wang, J.-M., “Measurement of the magnetic dipole hyperfine constant of cesium 7S1/2 state,” Act. Phys. Sin. 65, 073103 (2016).
- Roberts and Ginges (2020) Roberts, B. M. and Ginges, J. S. M., “Nuclear magnetic moments of francium-207–213 from precision hyperfine comparisons,” Phys. Rev. Lett. 125, 063002 (2020).
- Rui et al. (2021) Rui, Y., Wu, Y.-L., Li, R., and Wu, H.-B., “Precise absolute frequency measurement of three-electron Li6 atom D-line transitions,” Scientia Sinica 51, 074209 (2021).
- Rukhin (2009) Rukhin, A. L., “Weighted means statistics in interlaboratory studies,” Metrologia 46, 323–331 (2009).
- Rukhin (2019) Rukhin, A. L., “Homogeneous data clusters in interlaboratory studies,” Metrologia 56, 035002 (2019).
- Rupasinghe et al. (2022) Rupasinghe, P., Wee, F., Bullock, T., and Liu, J.-X., “Measurement of hyperfine constants and the isotope shift of rubidium 5P1/2 excited-state using saturated absorption spectroscopy,” ArXiv 2208.04244 (2022).
- Rydberg and Svanberg (1972) Rydberg, S. and Svanberg, S., “Investigation of the level sequence in the Cs I spectrum by level crossing spectroscopy,” Physica Scripta 5, 209–212 (1972).
- Ryschka and Marek (1981) Ryschka, M. and Marek, J., “Observation of quantum beats in superradiance on the transition in cesium vapours,” Physics Letters A 86, 98–100 (1981).
- Safronova et al. (2018) Safronova, M. S., Budker, D., DeMille, D., Kimball, D. F. J., Derevianko, A., and Clark, C. W., “Search for new physics with atoms and molecules,” Rev. Mod. Phys. 90, 025008 (2018).
- Safronova, Johnson, and Derevianko (1999) Safronova, M. S., Johnson, W. R., and Derevianko, A., “Relativistic many-body calculations of energy levels, hyperfine constants, electric-dipole matrix elements, and static polarizabilities for alkali-metal atoms,” Phys. Rev. A 60, 4476–4487 (1999).
- Safronova and Safronova (2011) Safronova, M. S. and Safronova, U. I., “Critically evaluated theoretical energies, lifetimes, hyperfine constants, and multipole polarizabilities in ,” Phys. Rev. A 83, 052508 (2011).
- Safronova and Safronova (2008) Safronova, U. I. and Safronova, M. S., “High-accuracy calculation of energies, lifetimes, hyperfine constants, multipole polarizabilities, and blackbody radiation shift in ,” Phys. Rev. A 78, 052504 (2008).
- Sagle and van Wijngaarden (1991) Sagle, J. and van Wijngaarden, W. A., “Excited state hyperfine structures in 133Cs using quantum beat spectroscopy,” Canadian Journal of Physics 69, 808–812 (1991).
- Sahoo et al. (2015) Sahoo, B. K., Nandy, D. K., Das, B. P., and Sakemi, Y., “Correlation trends in the hyperfine structures of ,” Phys. Rev. A 91, 042507 (2015).
- Sansonetti et al. (2011) Sansonetti, C. J., Simien, C. E., Gillaspy, J. D., Tan, J. N., Brewer, S. M., Brown, R. C., Wu, S.-J., and Porto, J. V., “Absolute transition frequencies and quantum interference in a frequency comb based measurement of the lines,” Phys. Rev. Lett. 107, 023001 (2011).
- Sansonetti (2007) Sansonetti, J. E., “Spectroscopic data for neutral francium (Fr I),” Journal of Physical and Chemical Reference Data 36, 497–507 (2007).
- Saßmannshausen, Merkt, and Deiglmayr (2013) Saßmannshausen, H., Merkt, F., and Deiglmayr, J., “High-resolution spectroscopy of Rydberg states in an ultracold cesium gas,” Phys. Rev. A 87, 032519 (2013).
- Scherf et al. (1996) Scherf, W., Khait, O., Jäger, H., and Windholz, L., “Re-measurement of the transition frequencies, fine structure splitting and isotope shift of the resonance lines of lithium, sodium and potassium,” Zeitschrift für Physik D Atoms, Molecules and Clusters 36, 31–33 (1996).
- Shimizu et al. (1987) Shimizu, F., Shimizu, K., Gomi, Y.-i., and Takuma, H., “Direct observation of hyperfine splittings of the 2 state by subnatural linewidth spectroscopy,” Phys. Rev. A 35, 3149–3151 (1987).
- Shiner et al. (2007) Shiner, A. D., Madej, A. A., Dubé, P., and Bernard, J. E., “Absolute optical frequency measurement of saturated absorption lines in Rb near 422 nm,” Applied Physics B 89, 595–601 (2007).
- Sieradzan, Kulatunga, and Havey (1995) Sieradzan, A., Kulatunga, P., and Havey, M., “Hyperfine-structure measurements in the 4p state of using polarization quantum-beat spectroscopy,” Phys. Rev. A 52, 4447–4450 (1995).
- Sieradzan et al. (1997) Sieradzan, A., Stoleru, R., Yei, W., and Havey, M. D., “Measurement of hyperfine coupling constants in the levels of , , and by polarization quantum-beat spectroscopy,” Phys. Rev. A 55, 3475–3483 (1997).
- Simsarian et al. (1996) Simsarian, J. E., Ghosh, A., Gwinner, G., Orozco, L. A., Sprouse, G. D., and Voytas, P. A., “Magneto-Optic Trapping of 210Fr,” Phys. Rev. Lett. 76, 3522–3525 (1996).
- Simsarian et al. (1999) Simsarian, J. E., Zhao, W. Z., Orozco, L. A., and Sprouse, G. D., “Two-photon spectroscopy of the francium level,” Phys. Rev. A 59, 195–199 (1999).
- Sinclair et al. (1994) Sinclair, A., McDonald, B., Riis, E., and Duxbury, G., “Double resonance spectroscopy of laser-cooled Rb atoms,” Optics Communications 106, 207–212 (1994).
- Singh, Muanzuala, and Natarajan (2010) Singh, A. K., Muanzuala, L., and Natarajan, V., “Precise measurement of hyperfine structure in the state of using saturated-absorption spectroscopy,” Phys. Rev. A 82, 042504 (2010).
- Singh, Nandy, and Sahoo (2012) Singh, Y., Nandy, D. K., and Sahoo, B. K., “Reexamination of nuclear quadrupole moments in 39-41K isotopes,” Phys. Rev. A 86, 032509 (2012).
- Snadden et al. (1996) Snadden, M., Bell, A., Riis, E., and Ferguson, A., “Two-photon spectroscopy of laser-cooled Rb using a mode-locked laser,” Optics Communications 125, 70–76 (1996).
- Stalnaker et al. (2017) Stalnaker, J. E., Ayer, H. M. G., Baron, J. H., Nuñez, A., and Rowan, M. E., “Measurement of the transition frequency in atomic potassium via direct frequency-comb spectroscopy,” Phys. Rev. A 96, 012504 (2017).
- Stalnaker et al. (2010) Stalnaker, J. E., Mbele, V., Gerginov, V., Fortier, T. M., Diddams, S. A., Hollberg, L., and Tanner, C. E., “Femtosecond frequency comb measurement of absolute frequencies and hyperfine coupling constants in cesium vapor,” Phys. Rev. A 81, 043840 (2010).
- Stevens et al. (1995) Stevens, G. D., Iu, C.-H., Williams, S., Bergeman, T., and Metcalf, H., “Hyperfine splitting of the 3 2S state of measured using Stark spectroscopy of Rydberg states,” Phys. Rev. A 51, 2866–2869 (1995).
- Stoicheff and Weinberger (1979) Stoicheff, B. P. and Weinberger, E., “Doppler-free two-photon absorption spectrum of rubidium,” Canadian Journal of Physics 57, 2143–2154 (1979).
- Stone (2005) Stone, N. J., “Table of nuclear magnetic dipole and electric quadrupole moments,” Atomic Data and Nuclear Data Tables 90, 75–176 (2005).
- Svanberg and Belin (1974) Svanberg, S. and Belin, G., “Determination of hyperfine structure and factors in the sequences of states in alkali atoms using a tunable dye laser,” Journal of Physics B: Atomic and Molecular Physics 7, L82–L86 (1974).
- Svanberg and Tsekeris (1975) Svanberg, S. and Tsekeris, P., “Hyperfine-structure investigation of highly excited levels in and using a cw tunable dye laser in a two-step excitation scheme,” Phys. Rev. A 11, 1125–1137 (1975).
- Svanberg, Tsekeris, and Happer (1973) Svanberg, S., Tsekeris, P., and Happer, W., “Hyperfine-structure studies of highly excited and levels in alkali atoms using a cw tunable dye laser,” Phys. Rev. Lett. 30, 817–820 (1973).
- Tai, Gupta, and Happer (1973) Tai, C., Gupta, R., and Happer, W., “Hyperfine structure of the state of ,” Phys. Rev. A 8, 1661–1665 (1973).
- Tai, Happer, and Gupta (1975) Tai, C., Happer, W., and Gupta, R., “Hyperfine structure and lifetime measurements of the second-excited states of rubidium and cesium by cascade fluorescence spectroscopy,” Phys. Rev. A 12, 736–747 (1975).
- Tang, Lou, and Shi (2019) Tang, Y.-B., Lou, B.-Q., and Shi, T.-Y., “Ab initio studies of electron correlation effects in magnetic dipolar hyperfine interaction of Cs,” Journal of Physics B: Atomic, Molecular and Optical Physics 52, 055002 (2019).
- Tanner and Wieman (1988) Tanner, C. E. and Wieman, C., “Precision measurement of the hyperfine structure of the 6 state,” Phys. Rev. A 38, 1616–1617 (1988).
- Tauschinsky et al. (2013) Tauschinsky, A., Newell, R., van Linden van den Heuvell, H. B., and Spreeuw, R. J. C., “Measurement of 87Rb Rydberg-state hyperfine splitting in a room-temperature vapor cell,” Phys. Rev. A 87, 042522 (2013).
- Tetu, Fortin, and Savard (1976) Tetu, M., Fortin, R., and Savard, J.-Y., “A new determination of the Rb 85 unperturbed hyperfine transition frequency,” IEEE Transactions on Instrumentation and Measurement IM-25, 477–480 (1976).
- Thibault et al. (1981a) Thibault, C., Touchard, F., Büttgenbach, S., Klapisch, R., De Saint Simon, M., Duong, H., Jacquinot, P., Juncar, P., Liberman, S., Pillet, P., Pinard, J., Vialle, J., Pesnelle, A., and Huber, G., “Hyperfine structure and isotope shift of the line of and some of their isomers,” Nuclear Physics A 367, 1–12 (1981a).
- Thibault et al. (1981b) Thibault, C., Touchard, F., Büttgenbach, S., Klapisch, R., de Saint Simon, M., Duong, H. T., Jacquinot, P., Juncar, P., Liberman, S., Pillet, P., Pinard, J., Vialle, J. L., Pesnelle, A., and Huber, G., “Hyperfine structure and isotope shift of the line of and some of their isomers,” Phys. Rev. C 23, 2720–2729 (1981b).
- Thompson et al. (1983) Thompson, D. C., O’Sullivan, M. S., Stoicheff, B. P., and Xu, G.-X., “Doppler-free two-photon absorption spectrum of potassium,” Canadian Journal of Physics 61, 949–955 (1983).
- Tian et al. (2019) Tian, Y.-L., Yang, P.-F., Wu, W., Li, S.-K., Li, G., Zhang, P.-F., and Zhang, T.-C., “Precision measurement of cesium 6S–7S two-photon spectra with single trapped atoms,” Japanese Journal of Applied Physics 58, 042002 (2019).
- Tiesinga et al. (2021) Tiesinga, E., Mohr, P. J., Newell, D. B., and Taylor, B. N., “Codata recommended values of the fundamental physical constants: 2018,” Reviews of Modern Physics 93, 025010– (2021).
- Touchard et al. (1982) Touchard, F., Guimbal, P., Büttgenbach, S., Klapisch, R., De Saint Simon, M., Serre, J., Thibault, C., Duong, H., Juncar, P., Liberman, S., Pinard, J., and Vialle, J., “Isotope shifts and hyperfine structure of 38-47K by laser spectroscopy,” Physics Letters B 108, 169–171 (1982).
- Truong et al. (2015) Truong, G. W., Anstie, J. D., May, E. F., Stace, T. M., and Luiten, A. N., “Accurate lineshape spectroscopy and the Boltzmann constant,” Nature Communications 6, 8345 (2015).
- Tsekeris, Farley, and Gupta (1975) Tsekeris, P., Farley, J., and Gupta, R., “Measurement of the hyperfine structure of the state of and the state of ,” Phys. Rev. A 11, 2202–2203 (1975).
- Tsekeris and Gupta (1975) Tsekeris, P. and Gupta, R., “Measurement of hyperfine structure of the and states of rubidium, and state of cesium by stepwise dye-laser spectroscopy,” Phys. Rev. A 11, 455–459 (1975).
- Tsekeris et al. (1974) Tsekeris, P., Gupta, R., Happer, W., Belin, G., and Svanberg, S., “Determination of hyperfine structure of highly excited states in alkali atoms using a CW dye laser,” Physics Letters A 48, 101–102 (1974).
- Tsekeris, Liao, and Gupta (1976) Tsekeris, P., Liao, K. H., and Gupta, R., “Radiofrequency spectroscopy of the state of : Hyperfine-structure measurement,” Phys. Rev. A 13, 2309–2310 (1976).
- Udem et al. (1999) Udem, T., Reichert, J., Holzwarth, R., and Hänsch, T. W., “Absolute optical frequency measurement of the cesium line with a mode-locked laser,” Phys. Rev. Lett. 82, 3568–3571 (1999).
- Umfer, Windholz, and Musso (1992) Umfer, C., Windholz, L., and Musso, M., “Investigations of the sodium and lithium D-lines in strong magnetic fields,” Zeitschrift für Physik D Atoms, Molecules and Clusters 25, 23–29 (1992).
- Vadla, Obrebski, and Niemax (1987) Vadla, C., Obrebski, A., and Niemax, K., “Isotope shift of the 3s and 3p levels in ,” Optics Communications 63, 288–292 (1987).
- Volz et al. (1996) Volz, U., Majerus, M., Liebel, H., Schmitt, A., and Schmoranzer, H., “Precision lifetime measurements on and by beam-gas-laser spectroscopy,” Phys. Rev. Lett. 76, 2862–2865 (1996).
- Voss et al. (2015) Voss, A., Buchinger, F., Cheal, B., Crawford, J. E., Dilling, J., Kortelainen, M., Kwiatkowski, A. A., Leary, A., Levy, C. D. P., Mooshammer, F., Ojeda, M. L., Pearson, M. R., Procter, T. J., and Tamimi, W. A., “Nuclear moments and charge radii of neutron-deficient francium isotopes and isomers,” Phys. Rev. C 91, 044307 (2015).
- Voss et al. (2013) Voss, A., Pearson, M. R., Billowes, J., Buchinger, F., Cheal, B., Crawford, J. E., Kwiatkowski, A. A., Levy, C. D. P., and Shelbaya, O., “First use of high-frequency intensity modulation of narrow-linewidth laser light and its application in determination of ground-state properties,” Phys. Rev. Lett. 111, 122501 (2013).
- Walls et al. (2003) Walls, J., Ashby, R., Clarke, J. J., Lu, B., and van Wijngaarden, W. A., “Measurement of isotope shifts, fine and hyperfine structure splittings of the lithium lines,” The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics 22, 159–162 (2003).
- Wang et al. (2014a) Wang, J., Liu, H.-F., Yang, B.-D., He, J., and Wang, J.-M., “Determining the hyperfine structure constants of caesium 8S1/2 state aided by atomic coherence,” Measurement Science and Technology 25, 035501 (2014a).
- Wang et al. (2014b) Wang, J., Liu, H.-F., Yang, G., Yang, B.-D., and Wang, J.-M., “Determination of the hyperfine structure constants of the and state and the isotope hyperfine anomaly,” Phys. Rev. A 90, 052505 (2014b).
- Wang et al. (2013) Wang, J., Wang, J.-M., Liu, H.-F., Yang, B.-D., and He, J., “Measurement of hyperfine splitting and determination of hyperfine structure constant of cesium 8 state by using of ladder-type EIT,” in Photon Counting Applications IV; and Quantum Optics and Quantum Information Transfer and Processing, Vol. 8773, edited by J. Fiurásek, I. Prochazka, and R. Sobolewski, International Society for Optics and Photonics (SPIE, 2013) pp. 159 – 165.
- Wang et al. (2019) Wang, Q., Zhang, N., Guang, W., Zhang, S.-G., Wang, W.-L., Wei, R., and Wang, Y.-Z., “Precision measurements of the ground-state hyperfine splitting of using an atomic fountain clock,” Phys. Rev. A 100, 022510 (2019).
- Wang et al. (2021) Wang, S.-D., Yuan, J.-P., Wang, L.-R., Xiao, L.-T., and Jia, S.-T., “Investigation on the Cs to 7 electric quadrupole transition via monochromatic two-photon process at 767 nm,” Frontiers of Physics 16, 12502 (2021).
- Wang et al. (2020a) Wang, Z., Zhang, J., Zeng, Z., Yan, K., Zhou, H., and Yang, B., “Hyperfine energy level splitting structure measurement of the excited state 6D5/2 for cesium atom,” Laser and Optoelectronics Progress 57, 030202 (2020a).
- Wang et al. (2020b) Wang, Z.-R., Hou, X.-K., Bai, J.-D., and Wang, J.-M., “Measuring the hyperfine splitting and deriving the hyperfine interaction constants of the cesium excited state,” Applied Sciences 10 (2020b), 10.3390/app10228178.
- van Wijngaarden, Bonin, and Happer (1986) van Wijngaarden, W. A., Bonin, K. D., and Happer, W., “Observation of quantum beats in the 65 transition in ,” Phys. Rev. A 33, 77–81 (1986).
- van Wijngaarden and Li (1994) van Wijngaarden, W. A. and Li, J., “Measurement of hyperfine structure of sodium states using optical spectroscopy,” Zeitschrift für Physik D Atoms, Molecules and Clusters 32, 67–71 (1994).
- van Wijngaarden, Li, and Koh (1993) van Wijngaarden, W. A., Li, J., and Koh, J., “Hyperfine-interaction constants of the 8 state in using quantum-beat spectroscopy,” Phys. Rev. A 48, 829–831 (1993).
- van Wijngaarden and Sagle (1991a) van Wijngaarden, W. A. and Sagle, J., “Hyperfine structure of excited alkali states using quantum beat spectroscopy,” Journal of Physics B: Atomic, Molecular and Optical Physics 24, 897–903 (1991a).
- van Wijngaarden and Sagle (1991b) van Wijngaarden, W. A. and Sagle, J., “Magnetic-field decoupling of an alkali-metal excited-state hyperfine structure,” Phys. Rev. A 43, 2171–2178 (1991b).
- Wilkins et al. (2017) Wilkins, S. G., Lynch, K. M., Billowes, J., Binnersley, C. L., Bissell, M. L., Cocolios, T. E., Goodacre, T. D., de Groote, R. P., Farooq-Smith, G. J., Flanagan, K. T., Franchoo, S., Ruiz, R. F. G., Gins, W., Heylen, H., Koszorús, A., Neyens, G., Stroke, H. H., Vernon, A. R., Wendt, K. D. A., and Yang, X. F., “Quadrupole moment of ,” Phys. Rev. C 96, 034317 (2017).
- Williams, Herd, and Hawkins (2018) Williams, W. D., Herd, M. T., and Hawkins, W. B., “Spectroscopic study of the and states in cesium-133,” Laser Physics Letters 15, 095702 (2018).
- Windholz et al. (1990) Windholz, L., Jäger, H., Musso, M., and Zerza, G., “Laserspectroscopic investigations of the lithium--lines in magnetic fields,” Zeitschrift für Physik D Atoms, Molecules and Clusters 16, 41–47 (1990).
- Wood et al. (1997) Wood, C. S., Bennett, S. C., Cho, D., Masterson, B. P., Roberts, J. L., Tanner, C. E., and Wieman, C. E., “Measurement of parity nonconservation and an anapole moment in cesium,” Science 275, 1759–1763 (1997).
- Wu et al. (2013) Wu, C.-M., Liu, T.-W., Wu, M.-H., Lee, R.-K., and Cheng, W.-Y., “Absolute frequency of cesium 6S-8S 822 nm two-photon transition by a high-resolution scheme,” Opt. Lett. 38, 3186–3189 (2013).
- Wu et al. (2018) Wu, Y.-L., Li, R., Rui, Y., Jiang, H.-F., and Wu, H.-B., “Precise measurement of 6Li transition frequencies and hyperfine splitting,” Acta Physica Sinica 67, 163201 (2018).
- Yang, Wang, and Wang (2017) Yang, G., Wang, J., and Wang, J.-M., “Determination of the hyperfine coupling constants of the of atoms by using high signal-to-noise ratio electromagnetically-induced transparency spectra,” Acta Physica Sinica 66, 103201 (2017).
- Yang et al. (2016) Yang, G., Wang, J., Yang, B.-D., and Wang, J.-M., “Determination of the hyperfine coupling constant of the cesium state,” Laser Physics Letters 13, 085702 (2016).
- Ye et al. (1996) Ye, J., Swartz, S., Jungner, P., and Hall, J. L., “Hyperfine structure and absolute frequency of the 87Rb state,” Opt. Lett. 21, 1280–1282 (1996).
- Yei et al. (1998) Yei, W., Sieradzan, A., Cerasuolo, E., and Havey, M. D., “Measurement of hyperfine coupling constants of the levels in Cs using polarization quantum-beat spectroscopy,” Phys. Rev. A 57, 3419–3424 (1998).
- Yei, Sieradzan, and Havey (1993) Yei, W., Sieradzan, A., and Havey, M. D., “Delayed-detection measurement of atomic Na 3p 2 hyperfine structure using polarization quantum-beat spectroscopy,” Phys. Rev. A 48, 1909–1915 (1993).
- Zhang et al. (2015) Zhang, J., Tandecki, M., Collister, R., Aubin, S., Behr, J. A., Gomez, E., Gwinner, G., Orozco, L. A., Pearson, M. R., and Sprouse, G. D. (FrPNC Collaboration), “Hyperfine anomalies in Fr: Boundaries of the spherical single particle model,” Phys. Rev. Lett. 115, 042501 (2015).
- Zhang et al. (2017) Zhang, S.-N., Zhang, X.-G., Jiang, Z.-J., Shang, H.-S., Chang, P.-Y., Chen, J.-B., Lian, J.-Q., Tu, J.-H., and Yang, S.-Y., “Precision measurement of the hyperfine structure of the 85Rb state,” in 2017 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS) (2017) pp. 762–764.
- Zhao et al. (1999) Zhao, X., Crane, S. G., Guckert, R., and Vieira, D. J., “Hyperfine structure and isotope shift of 82Rb and transitions,” Phys. Rev. A 60, 4730–4733 (1999).
- Zhu, Oates, and Hall (1993) Zhu, M., Oates, C. W., and Hall, J. L., “Improved hyperfine measurements of the Na excited state through frequency-controlled Dopplerless spectroscopy in a Zeeman magneto-optic laser trap,” Opt. Lett. 18, 1186–1188 (1993).
- zu Putlitz and Venkataramu (1968) zu Putlitz, G. and Venkataramu, K. V., “Hyperfeinstruktur und Lebensdauer des 8-Terms von Rubidium,” Zeitschrift für Physik A Hadrons and nuclei 209, 470–473 (1968).
- Zyla et al. (2020) Zyla, P. et al. (Particle Data Group), “Review of Particle Physics,” PTEP 2020, 083C01 (2020), and 2021 update.