Surface mapping class group actions on 3-manifolds

Alina al Beaini , Lei Chen and Bena Tshishiku Alina Al Beaini
Department of Mathematics
Brown University
151 Thayer St.
Providence, RI, 02912, USA
alina

\_

\_

[email protected]. Lei Chen
Department of Mathematics
University of Maryland
4176 Campus Drive
College Park, MD 20742, USA
[email protected] Bena Tshishiku
Department of Mathematics
Brown University
151 Thayer St.
Providence, RI, 02912, USA
bena

\_

[email protected].

Abstract.

For each circle bundle $S^{1}\to X\to\Sigma_{g}$ over a surface with genus $g\geq 2$ , there is a natural surjection $\pi:\operatorname{Homeo}^{+}(X)\to\operatorname{Mod}(\Sigma_{g})$ . When $X$ is the unit tangent bundle $U\Sigma_{g}$ , it is well-known that $\pi$ splits. On the other hand $\pi$ does not split when the Euler number $e(X)$ is not divisible by the Euler characteristic $\chi(\Sigma_{g})$ by [CT23]. In this paper we show that this homomorphism does not split in many cases where $\chi(\Sigma_{g})$ divides $e(X)$ .

1. Introduction

Let $\Sigma_{g}$ be a closed oriented surface of genus $g\geq 2$ , and let $X_{g,e}$ denote the oriented $S^{1}$ -bundle over $\Sigma_{g}$ with Euler number $e$ . Let $\operatorname{Homeo}^{+}(X_{g,e})$ be the group of orientation-preserving homeomorphisms of $X_{g,e}$ that act trivially on the center of $\pi_{1}(X_{g,e})$ , and let $\operatorname{Mod}(X_{g,e}):=\pi_{0}\big{(}\operatorname{Homeo}^{+}(X_{g,e})\big{)}$ denote the mapping class group.

The (generalized) Nielsen realization problem for $X_{g,e}$ asks whether the surjective homomorphism

\operatorname{Homeo}^{+}(X_{g,e})\to\operatorname{Mod}(X_{g,e})

splits over subgroups of $\operatorname{Mod}(X_{g,e})$ . In this paper we study a closely related problem. For each $g,e$ there is a surjection $\operatorname{Mod}(X_{g,e})\to\operatorname{Mod}(\Sigma_{g})$ . Consider the composition

\pi_{g,e}:\operatorname{Homeo}^{+}(X_{g,e})\twoheadrightarrow\operatorname{Mod}(X_{g,e})\twoheadrightarrow\operatorname{Mod}(\Sigma_{g}).

Problem 1.1.

Does $\pi_{g,e}:\operatorname{Homeo}^{+}(X_{g,e})\twoheadrightarrow\operatorname{Mod}(\Sigma_{g})$ spilt?

If $e=\pm(2g-2)$ , then $X_{g,e}$ is the unit (co)tangent bundle, and $\pi_{g,e}$ does split; see [Sou10, §1]. On the other hand, if $e$ is not divisible by $2g-2$ , then the surjection $\operatorname{Mod}(X_{g,e})\to\operatorname{Mod}(\Sigma_{g})$ does not split by work of the second two authors [CT23], so $\pi_{g,e}$ also does not split in these cases. Given this, it remains to study the case when $e$ is divisible by $2g-2$ and $e\neq\pm(2g-2)$ . In these cases $\operatorname{Mod}(X_{g,e})\to\operatorname{Mod}(\Sigma_{g})$ does split [CT23], but we prove $\pi_{g,e}$ does not split in many cases.

Theorem A.

Fix a surface $\Sigma_{g}$ of genus $g$ and $e\in\mathbb{Z}$ . Assume that $g=4k-1$ where $k\geq 3$ and $k$ is not a power of $2$ , and assume that $e$ is divisible by $(2g-2)2p$ where $p$ is an odd prime dividing $k$ . Then the natural surjective homomorphism $\pi_{g,e}:\operatorname{Homeo}^{+}(X_{g,e})\to\operatorname{Mod}(\Sigma_{g})$ does not split.

For example, if $e=0$ , we find that $\pi_{g,e}:\operatorname{Homeo}^{+}(\Sigma_{g}\times S^{1})\to\operatorname{Mod}(\Sigma_{g})$ does not split when $g=11,19,23,27,35,39,43,47,\ldots$ .

Theorem A solves the Nielsen realization problem for $\operatorname{Mod}(\Sigma_{g})$ subgroups of $\operatorname{Mod}(X_{g,e})$ in the cases of the theorem. Specifically, if $e$ is divisible by $2g-2$ , then $\operatorname{Mod}(X_{g,e})\cong H^{1}(\Sigma_{g};\mathbb{Z})\rtimes\operatorname{Mod}(\Sigma_{g})$ [CT23], and every $\operatorname{Mod}(\Sigma_{g})$ subgroup of $\operatorname{Mod}(X_{g,e})$ is the image of a splitting of $\operatorname{Mod}(X_{g,e})\to\operatorname{Mod}(\Sigma_{g})$ . By Theorem A, $\operatorname{Homeo}^{+}(X_{g,e})\to\operatorname{Mod}(X_{g,e})$ does not split over any of these $\operatorname{Mod}(\Sigma_{g})$ subgroups.

Theorem A has the following topological consequence. When $2g-2$ divides $e$ , there is a “tautological” $X_{g,e}$ -bundle $E_{g,e}^{\text{taut}}\to B\operatorname{Homeo}(\Sigma_{g})$ whose monodromy

\operatorname{Mod}(\Sigma_{g})\cong\pi_{1}\big{(}B\operatorname{Homeo}(\Sigma_{g})\big{)}\to\operatorname{Mod}(X_{g,e})

splits the surjection $\operatorname{Mod}(X_{g,e})\to\operatorname{Mod}(\Sigma_{g})$ (c.f. [CT23, §1]). One can ask whether or not the bundle $E_{g,e}^{\text{taut}}\to B\operatorname{Homeo}(\Sigma_{g})$ is flat. Recall that an $X$ -bundle $E\to B$ is flat if there is a homomorphism $\rho:\pi_{1}(B)\to\operatorname{Homeo}(X)$ and an $X$ -bundle isomorphism $E\cong X\rtimes_{\rho}B$ . Such bundles are characterized by the existence of a horizontal foliation on $E$ , or, equivalently, by the property that their monodromy $\pi_{1}(B)\to\operatorname{Mod}(X)$ lifts to $\operatorname{Homeo}(X)$ . When $e=2g-2$ , the bundle $E_{g,e}^{\text{taut}}\to B\operatorname{Homeo}(\Sigma_{g})$ is flat because of the splitting of $\pi_{g,e}$ in this case. When $\pi_{g,e}$ does not split, we deduce that $E_{g,e}^{\text{taut}}\to B\operatorname{Homeo}(S_{g})$ is not flat.

Corollary 1.2.

Fix $g,e$ as in the statement of Theorem A. Then the tautological $X_{g,e}$ -bundle $E_{g,e}^{\text{taut}}\to B\operatorname{Homeo}(S_{g})$ is not flat.

Short proof sketch of Theorem A. The proof strategy is similar to an argument of Chen–Salter [CS22] that shows that $\operatorname{Homeo}^{+}(\Sigma_{g})\to\operatorname{Mod}(\Sigma_{g})$ does not split when $g\geq 2$ . Theorem A is proved by contradiction: assuming the existence of a splitting $\operatorname{Mod}(\Sigma_{g})\to\operatorname{Homeo}^{+}(X_{g,e})$ , first we obtain, by lifting, an action of the based mapping class group $\operatorname{Mod}(\Sigma_{g},*)$ on the cover $\widehat{X}_{g,e}\cong\mathbb{R}^{2}\times S^{1}$ corresponding to the center of $\pi_{1}(X_{g,e})$ . The conditions on $g$ and $e$ in Theorem A guarantee the existence of a $\mathbb{Z}/2p\mathbb{Z}$ subgroup of $\operatorname{Mod}(\Sigma_{g},*)$ for which we can show the action on $\widehat{X}_{g,e}$ has a fixed circle. Denoting a generator of $\mathbb{Z}/2p\mathbb{Z}$ by $\alpha$ , we show that $\operatorname{Mod}(\Sigma_{g},*)$ is generated by the centralizers of $\alpha^{2}$ and $\alpha^{p}$ . This shows that the entire group $\operatorname{Mod}(\Sigma_{g},*)$ acts on $\widehat{X}_{g,e}$ with a fixed circle, which contradicts the fact that the point-pushing subgroup $\pi_{1}(\Sigma_{g})<\operatorname{Mod}(\Sigma_{g},*)$ acts freely (by deck transformations) on $\widehat{X}_{g,e}$ .

Other questions. Related to the $\operatorname{Mod}(\Sigma_{g})$ action on the unit tangent bundle $U\Sigma_{g}$ , we pose the following question.

Question 1.3.

Do either of the following surjections split?

\operatorname{Diff}^{+}(U\Sigma_{g})\to\operatorname{Mod}(\Sigma_{g})\>\>\>\text{ or }\>\>\>\operatorname{Homeo}(U\Sigma_{g})\to\operatorname{Mod}(U\Sigma_{g})

If one includes orientation-reversing diffeomorphisms and mapping classes, then if $g\geq 12$ , then $\operatorname{Diff}(U\Sigma_{g})\to\operatorname{Mod}^{\pm}(\Sigma_{g})$ does not split by Souto [Sou10, Thm. 1].

Acknowledgement. The authors LC and BT are supported by NSF grants DMS2203178, DMS-2104346, and DMS-2005409.

2. Proof of Theorem A

Fix $g=4k-1$ and $e$ as in the theorem statement, and set $\Sigma=\Sigma_{g}$ and $X=X_{g,e}$ . Suppose for a contradiction that there is a homomorphism

\sigma:\operatorname{Mod}(\Sigma)\to\operatorname{Homeo}(X)

whose composition with $\pi=\pi_{g,e}:\operatorname{Homeo}(X)\to\operatorname{Mod}(\Sigma)$ is the identity.

2.1. Step 1: lifting argument

Consider the covering space $\widehat{X}=\widetilde{\Sigma}\times S^{1}$ of $X$ , where $\widetilde{\Sigma}\cong\mathbb{R}^{2}$ is the universal cover. This is the covering corresponding to the center $\zeta$ of $\pi_{1}(X)$ . Given the action of $\operatorname{Mod}(\Sigma)$ on $X$ , we consider the set of all lifts of homeomorphisms in this action to $\widehat{X}$ . This is an action of the pointed mapping class group $\operatorname{Mod}(\Sigma,*)$ on $\widehat{X}$ . To explain this, we start with the following general proposition.

Proposition 2.1.

Let $Y$ be a closed manifold. Let $\zeta<\pi_{1}(Y)$ be the center of the fundamental group, and denote $\Delta=\pi_{1}(Y)/\zeta$ . Let $\widehat{Y}\to Y$ be the covering space with $\pi_{1}(\widehat{Y})=\zeta$ . Fix a basepoint $*\in Y$ . Assume that the evaluation map

\operatorname{Homeo}(Y)\to Y,\>\>\>\>f\mapsto f(*)

induces a surjection $\pi_{1}\big{(}\operatorname{Homeo}(Y)\big{)}\twoheadrightarrow\zeta<\pi_{1}(Y)$ . Then there is a commutative diagram

(1)

whose rows are exact, where the bottom row is the (generalized) Birman exact sequence. Furthermore, this diagram is a pullback diagram.

A version of Proposition 2.1 when $Y=\Sigma_{g}$ (whose center is trivial) is used in [CS22].

We prove Proposition 2.1 after explaining how it gives the desired lifting. In our situation, the center of $\pi_{1}(X)$ is the kernel of $\pi_{1}(X)\to\pi_{1}(\Sigma)$ since $\pi_{1}(\Sigma)$ has trivial center. Thus Proposition 2.1 gives us the following diagram.

The splitting $\sigma$ defines a subgroup $\operatorname{Mod}(\Sigma)<\operatorname{Mod}(X)$ and a splitting of $p$ over this subgroup. Since the top row is a pullback of the middle row, it follows that $\widehat{p}$ splits over $\operatorname{Mod}(\Sigma,*)$ (this uses only general facts about pullbacks). Denote this splitting by

\widehat{\sigma}:\operatorname{Mod}(\Sigma,*)\to\operatorname{Homeo}(\widehat{X})^{\Delta}.

Under this splitting the point-pushing subgroup $\pi_{1}(\Sigma)$ acts by deck transformations.

Remark 2.2.

If $G<\operatorname{Mod}(\Sigma)$ and $\sigma(G)$ has a fixed point $*$ , then after choosing a lift $\widehat{*}$ of $*$ , one can lift canonically elements of $\sigma(G)$ to $\widehat{X}$ by choosing the unique lift that fixes $\widehat{*}$ . This implies that $G<\operatorname{Mod}(\Sigma)$ can be lifted to $G<\operatorname{Mod}(\Sigma,*)$ so that $\widehat{\sigma}(G)$ has a fixed point.

Proof of Proposition 2.1.

First we recall the construction of the bottom row of diagram (1). Evaluation at $*\in Y$ defines a fibration

\operatorname{Homeo}(Y,*)\to\operatorname{Homeo}(Y)\xrightarrow{\epsilon}Y.

The long exact sequence of homotopy groups gives an exact sequence

\pi_{1}\big{(}\operatorname{Homeo}(Y))\xrightarrow{\epsilon_{*}}\pi_{1}(Y)\to\operatorname{Mod}(Y,*)\to\operatorname{Mod}(Y)\to 1.

In general the image of $\epsilon_{*}$ is contained in the center of $\pi_{1}(Y)$ ; see e.g. [Hat02, §1.1, Exer. 20]. By assumption, $\epsilon_{*}$ surjects onto the center, so we obtain the short exact sequence in the bottom row of (1). The homomorphism $\pi_{1}(Y)\to\operatorname{Mod}(Y,*)$ is the so-called “point-pushing” homomorphism. It sends $\eta\in\pi_{1}(Y)$ (basepoint= $*$ ) to the time-1 map of an isotopy that pushes $*$ around $\eta$ in reverse (this follows directly from the definition of the connecting homomorphism in the long exact sequence; note that it makes sense for the reverse of $\eta$ to appear in defining this homomorphism since concatenation of paths is left-to-right, while composition of functions is right-to-left).

Next we define $\widehat{p}:\operatorname{Homeo}(\widehat{Y})^{\Delta}\to\operatorname{Mod}(Y,*)$ . Fix a point $\widehat{*}\in\widehat{Y}$ that covers the basepoint $*\in Y$ . Given $f\in\operatorname{Homeo}(\widehat{Y})^{\Delta}$ . Choose a path $[0,1]\to\widehat{Y}$ from $\widehat{*}$ to $f(\widehat{*})$ and let $\gamma_{f}$ denote the composition $[0,1]\to\widehat{Y}\to Y$ . By isotopy extension, there exists an isotopy $h_{t}:Y\to Y$ where $h_{0}=\operatorname{id}_{Y}$ and $h_{t}(*)=\gamma_{f}(t)$ for each $t\in[0,1]$ . Define

\widehat{p}(f)=[h_{1}\circ q(f)].

The map $\widehat{p}$ is well-defined. The choice of $\gamma_{f}$ is unique only up to an element of $\pi_{1}(\widehat{Y})=\zeta$ . This implies that the isotopy class $[h_{1}\circ f]$ is only well-defined up to composition by a point-pushing mapping class by an element of $\zeta$ , but such a point-push is trivial by assumption.

It is a straightforward exercise to check that $\widehat{p}$ is a homomorphism. The right square in diagram (1) commutes because $q(f)$ and $h_{1}\circ q(f)$ are isotopic by construction. It is easy to see that the left square in the diagram commutes by applying the definition of $\widehat{p}$ to deck transformations.

Finally, regarding the claim that the diagram is a pullback, we show that the map to the fibered product

\widehat{p}\times q:\operatorname{Homeo}(\widehat{Y})^{\Delta}\to\operatorname{Mod}(Y,*)\times_{\operatorname{Mod}(Y)}\operatorname{Homeo}(Y)

is an isomorphism. The codomain consists of pairs $(\phi,g)\in\operatorname{Mod}(Y,*)\times\operatorname{Homeo}(Y)$ such that $g$ is isotopic to a representative of the isotopy class $\phi$ .

We define an inverse $\iota$ to $\widehat{p}\times q$ . Given $(\phi,g)$ in the fibered product, choose an isotopy $g_{t}$ from $g$ to a homeomorphism representing $\phi$ . Lift $g_{t}$ to an isotopy $\widetilde{g}_{t}$ such that $\widetilde{g}_{1}$ fixes $\widehat{*}$ , and define $\iota(\phi,g)=\widetilde{g}_{0}$ . The reader can check that the maps $\iota$ and $\widehat{p}\times q$ are inverses. ∎

2.2. Step 2: finite group action rigidity

Recall that $g=4k-1$ and $k\geq 3$ is not a power of 2; let $p$ be an odd prime dividing $k$ . From Step 1, we have homomorphism $\widehat{\sigma}:\operatorname{Mod}(\Sigma,*)\to\operatorname{Homeo}(\widehat{X})$ that descends to a splitting $\sigma:\operatorname{Mod}(\Sigma)\to\operatorname{Homeo}(X)$ . In this section we describe the action of a particular finite subgroup of $\operatorname{Mod}(\Sigma,*)$ on $\widehat{X}$ .

Proposition 2.3.

There exists an element $\alpha\in\operatorname{Mod}(\Sigma,*)$ of order $2p$ such that the fixed sets of $\widehat{\sigma}(\alpha)$ , $\widehat{\sigma}(\alpha)^{2}$ , and $\widehat{\sigma}(\alpha)^{p}$ coincide and are equal to an embedded circle $c\subset\widehat{X}$ .

It is worth noting that the fixed set of a finite-order, orientation-preserving homeomorphism of a 3-manifold can be wildly embedded [MZ54].

In order to prove Proposition 2.3 we first construct the specific element $\alpha$ . Then we prove (Proposition 2.5) a weaker version of Proposition 2.3 with the additional assumption that the action is smooth. Finally, we combine this with a result of Pardon [Par21] and Smith theory to prove Proposition 2.3.

Construction of $\alpha$ . We obtain $\alpha$ as an element in a dihedral subgroup $D_{4k}$ of $\operatorname{Mod}(\Sigma)$ , where $D_{4k}$ denotes the dihedral group of order $8k$ . The dihedral action $D_{4k}\curvearrowright\Sigma$ we use has quotient $\Sigma/D_{4k}$ homeomorphic to $T^{2}$ and the quotient $\Sigma\to\Sigma/D_{4k}$ has a single branch point; it is determined by the homomorphism

\langle x,y\rangle=F_{2}\cong\pi_{1}(T^{2}\setminus\operatorname{pt})\to D_{4k}=\langle a,b\mid a^{4k}=b^{2}=1,bab=a^{-1}\rangle

x\mapsto a,\>\>\>\>y\mapsto b.

By Riemann–Hurwitz, the genus of $\Sigma$ is $4k-1$ . The orbifold $O=\Sigma/D_{4k}$ has fundamental group

\pi_{1}^{orb}(O)=\langle x,y,h\mid h^{2k}=1,h=[x,y]\rangle,

and there is a short exact sequence

(2)

1\to\pi_{1}(\Sigma)\to\pi_{1}^{orb}(O)\to D_{4k}\to 1.

This sequence induces a homomorphism $\pi_{1}^{orb}(O)\to\operatorname{Mod}(\Sigma,*)$ . We take $\alpha=h^{k/p}$ , where $p$ , as defined above, is an odd prime dividing $k$ , which exists by assumption. Then $\alpha$ is an element of order $2p$ in the subgroup $\langle h\rangle\cong\mathbb{Z}/2k\mathbb{Z}$ of $\pi_{1}^{orb}(O)<\operatorname{Mod}(\Sigma,*)$ .

Remark 2.4.

The argument that follows works equally well when $\Sigma/D_{4k}$ is a genus- $g$ surface and $\Sigma\to\Sigma/D_{4k}$ has a single branched point. This provides more values of $g,e$ for which the conclusion of Theorem A holds.

Smooth case. Here we prove the following proposition.

Proposition 2.5.

Fix $D_{4k}<\operatorname{Mod}(\Sigma)$ as above. Suppose that $\sigma:D_{4k}\to\operatorname{Diff}^{+}(X)$ and is a splitting of $\pi:\operatorname{Homeo}^{+}(X)\to\operatorname{Mod}(\Sigma)$ over $D_{4k}$ . Then $\widehat{\sigma}(\alpha)$ fixes a unique circle on $\widehat{X}=\mathbb{H}^{2}\times S^{1}$ . Consequently, the fixed set of $\sigma(a^{2k/p})$ is nonempty.

The last part of the statement of Proposition 2.5 follows from the preceding statement because the image of $\alpha$ under $\pi_{1}^{orb}(O)\to D_{4k}$ is $a^{2k/p}$ .

Proof of Proposition 2.5.

First we reduce to a more geometric setting. By Meeks–Scott [MS86, Thm. 2.1], the smooth(!) action $\sigma(D_{4k})\curvearrowright X$ preserves some geometric metric on $X$ . There are two possibilities for the geometry: if $e(X)=0$ , then $X$ has $\mathbb{H}^{2}\times\mathbb{R}$ -geometry, and if $e(X)\neq 0$ , then $X$ has $\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}$ -geometry. We treat these cases in parallel.

The universal cover $\widetilde{X}$ (with the induced geometric structure) is either $\mathbb{H}^{2}\times\mathbb{R}$ or $\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}$ . In either case, $\widetilde{X}$ has an isometric foliation by lines whose leaf space is isometric to $\mathbb{H}^{2}$ , and this foliation is preserved by $\operatorname{Isom}(\widetilde{X})$ , so there is a homomorphism $\operatorname{Isom}(\widetilde{X})\to\operatorname{Isom}(\mathbb{H}^{2})$ . Let $\operatorname{Isom}^{+}(\widetilde{X})<\operatorname{Isom}(\widetilde{X})$ be the group whose action on the leaves and on the leaf space are both orientation preserving. There is an exact sequence

(3)

1\to\mathbb{R}\to\operatorname{Isom}^{+}(\widetilde{X})\xrightarrow{F}\operatorname{Isom}^{+}(\mathbb{H}^{2})\to 1.

Claim 2.6.

The restriction of the sequence (3) to $\Lambda$ is a short exact sequence

1\to\zeta\to\Lambda\to\pi_{1}^{orb}(O)\to 1

where $\zeta$ is the center of $\pi_{1}(X)$ .

Proof of Claim 2.6.

Recall the map $F:\operatorname{Isom}^{+}(\widetilde{X})\to\operatorname{Isom}^{+}(\mathbb{H}^{2})$ from (3). First we identify $F(\Lambda)<\operatorname{Isom}^{+}(\mathbb{H}^{2})$ with $\pi_{1}^{orb}(O)$ . For this, it suffices to show that $F(\Lambda)$ fits into a short exact sequence

(4)

1\to\pi_{1}(\Sigma)\to F(\Lambda)\to D_{4k}\to 1,

where the “monodromy” $D_{4k}\to\operatorname{Out}^{+}\big{(}\pi_{1}(\Sigma)\big{)}\cong\operatorname{Mod}(\Sigma)$ has image the given subgroup $D_{4k}<\operatorname{Mod}(\Sigma)$ . This implies that $F(\Lambda)\cong\pi_{1}^{orb}(O)$ because $\pi_{1}^{orb}(O)$ is an extension of the same form (see (2)), and extensions of $\pi_{1}(\Sigma)$ are determined by their monodromy [Bro82, §IV.3].

To construct the extension (4), first note that the restriction of (3) to $\pi_{1}(X)$ is the short exact sequence

1\to\zeta\to\pi_{1}(X)\to\pi_{1}(\Sigma)\to 1.

The group $\pi_{1}(\Sigma)=F(\pi_{1}(X))$ is normal in $F(\Lambda)$ because $\pi_{1}(X)$ is normal in $\Lambda$ . Furthermore, the surjection $\Lambda\to F(\Lambda)$ induces a surjection $D_{4k}=\Lambda/\pi_{1}(X)\to F(\Lambda)/\pi_{1}(\Sigma)$ .

The quotient map $\widetilde{X}\to\mathbb{H}^{2}$ , which is equivariant with respect to $\Lambda\to F(\Lambda)$ descends to a map $X=\widetilde{X}/\pi_{1}(X)\to\mathbb{H}^{2}/\pi_{1}(\Sigma)=\Sigma$ that’s equivariant with respect to $D_{4k}=\Lambda/\pi_{1}(X)\to F(\Lambda)/\pi_{1}(\Sigma)$ .

Since $\sigma$ is a realization, the induced action of $\sigma(D_{4k})$ on $\Sigma$ is a realization of the $D_{4k}<\operatorname{Mod}(\Sigma)$ , and in particular the $D_{4k}$ action on $\Sigma$ is faithful. Therefore, $F(\Lambda)/\pi_{1}(\Sigma)\cong D_{4k}$ , and the monodromy of the associated extension

1\to\pi_{1}(\Sigma)\to F(\Lambda)\to D_{4k}\to 1,

is the given inclusion $D_{4k}<\operatorname{Mod}(\Sigma)$ . This concludes the proof that $F(\Lambda)$ is isomorphic to $\pi_{1}^{orb}(O)$ .

To finish the proof of Claim 2.6, it remains to show that the intersection of $\Lambda$ with $\mathbb{R}=\ker(F)$ is $\zeta$ . We do this by showing (i) $\Lambda\cap\mathbb{R}$ is the center of $\Lambda$ , and (ii) the center of $\Lambda$ is contained in $\pi_{1}(X)$ . Together with the obvious containment $\zeta<\Lambda\cap\mathbb{R}$ , (i) and (ii) imply $\Lambda\cap\mathbb{R}=\zeta$ .

(i): First note that $\Lambda\cap\mathbb{R}$ is central because $\mathbb{R}$ is central in $\operatorname{Isom}(\widetilde{X})$ . On the other hand, the center of $\Lambda$ is contained in $\Lambda\cap\mathbb{R}$ because the center of $\Lambda/(\Lambda\cap\mathbb{R})\cong\pi_{1}^{orb}(O)$ has trivial center.

(ii): To show the center of $\Lambda$ is contained in $\pi_{1}(X)$ , we show that the center of $\Lambda$ projects trivially to $D_{4k}=\Lambda/\pi_{1}(X)$ . This is true because $\Lambda\to D_{4k}$ factors through $\pi_{1}^{orb}(O)$ , which has trivial center.∎

We summarize the relation between the relevant groups in Diagram (5).

(5)

By Claim 2.6, $\Lambda/\zeta\cong\pi_{1}^{orb}(O)$ , so $\rho$ takes the form

\rho:\pi_{1}^{orb}(O)\to\operatorname{Isom}^{+}(\widetilde{X})/\zeta\cong\operatorname{Isom}(\widehat{X})

By construction, this homomorphism is the restriction of $\widehat{\sigma}:\operatorname{Mod}(\Sigma,*)\to\operatorname{Homeo}(\widehat{X})$ to $\pi_{1}^{orb}(O)$ . Since $\alpha=h^{k/p}$ , to show the fixed set of $\widehat{\sigma}(\alpha)$ is a circle, it suffices to show the same statement for $\rho(h^{k/p})$ . To prove this, we first compute $\operatorname{Isom}(\widehat{X})\cong\operatorname{Isom}^{+}(\widetilde{X})/\zeta$ .

Claim 2.7.

The group $\operatorname{Isom}^{+}(\widetilde{X})/\zeta$ is isomorphic to $\operatorname{Isom}^{+}(\mathbb{H}^{2})\times\operatorname{SO}(2)$ .

Proof of Claim 2.7.

First note that there is an extension

1\to\operatorname{SO}(2)\to\operatorname{Isom}^{+}(\widetilde{X})/\zeta\to\operatorname{Isom}^{+}(\mathbb{H}^{2})\to 1

induced from (3). This sequence is obviously split when $\widetilde{X}=\mathbb{H}^{2}\times\mathbb{R}$ since $\operatorname{Isom}^{+}(\widetilde{X})\cong\operatorname{Isom}^{+}(\mathbb{H}^{2})\times\mathbb{R}$ is a product.

Assume now that $\widetilde{X}=\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}$ , and write $e=(2g-2)n$ where $n$ is a nonzero integer. Let $K$ denote the kernel of the universal cover homomorphism $\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}\to\operatorname{PSL}_{2}(\mathbb{R})$ .

We claim that $\zeta=\frac{1}{n}K$ . To see this, note that the extension

1\to K\to\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}\to\operatorname{PSL}_{2}(\mathbb{R})\to 1

pulled back under a Fuchsian representation $\pi_{1}(\Sigma)\to\operatorname{PSL}_{2}(\mathbb{R})$ induces the extension of the unit tangent bundle group $\pi_{1}(U\Sigma)$ , which has Euler number $2-2g$ , and there is an $n$ -fold fiberwise cover $U\Sigma\to X$ , so the center of $\pi_{1}(U\Sigma)<\pi_{1}(X)$ is generated by the $n$ -the power of the generator of the center of $\pi_{1}(X)$ , i.e. $\zeta=\frac{1}{n}K$ .

The inclusion of $\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}$ in $\operatorname{Isom}\big{(}\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}\big{)}$ (given by left-multiplication) descends to a homomorphism

\operatorname{PSL}_{2}(\mathbb{R})=\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}/K\to\operatorname{Isom}\big{(}\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}\big{)}/K\twoheadrightarrow\operatorname{Isom}\big{(}\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}\big{)}/\zeta

that defines a splitting of the sequence

1\to\operatorname{SO}(2)\to\operatorname{Isom}(\widetilde{\operatorname{PSL}_{2}(\mathbb{R})})/\zeta\to\operatorname{PSL}_{2}(\mathbb{R})\to 1.\qed

The following Claim 2.8 is the last step in the proof of Proposition 2.5.

Claim 2.8.

Let $p$ be an odd prime dividing $k$ . If $e$ is divisible by $(2g-2)2p$ , then the fixed set of $\rho(h^{k/p})$ is a circle.

Before proving the claim, we explain how the factors of $\operatorname{Isom}^{+}(\mathbb{H}^{2})\times\operatorname{SO}(2)\cong\operatorname{Isom}^{+}(\widehat{X})$ act on $\widehat{X}=\widetilde{X}/\zeta$ .

Remark 2.9.

Consider the isomorphism $\operatorname{Isom}(\widehat{X})\cong\operatorname{Isom}^{+}(\mathbb{H}^{2})\times\operatorname{SO}(2)$ from Claim 2.7. In each case ( $e=0$ or $e\neq 0$ ) the action of $\operatorname{SO}(2)$ on $\widehat{X}$ covers the identity of $\mathbb{H}^{2}$ and acts freely by rotation on the circle fibers of $X\to\mathbb{H}^{2}$ . For the $\operatorname{Isom}^{+}(\mathbb{H}^{2})$ action, when $e=0$ , then $\widehat{X}\cong\mathbb{H}^{2}\times S^{1}$ is a metric product, and the action of $\operatorname{Isom}^{+}(\mathbb{H}^{2})$ is trivial on the $S^{1}$ factor and is the natural action on $\mathbb{H}^{2}$ . If $e=(2g-2)n$ is nonzero, then

\widehat{X}\cong\widetilde{\operatorname{PSL}_{2}(\mathbb{R})}/\zeta\cong\operatorname{PSL}_{2}(\mathbb{R})/(\mathbb{Z}/n\mathbb{Z}),

and with respect to this isomorphism, the action of $\operatorname{Isom}^{+}(\mathbb{H})\cong\operatorname{PSL}_{2}(\mathbb{R})$ on $\widehat{X}$ is induced from left multiplication of $\operatorname{PSL}_{2}(\mathbb{R})$ on $\operatorname{PSL}_{2}(\mathbb{R})$ . Identifying $\operatorname{PSL}_{2}(\mathbb{R})$ with the unit tangent $U\mathbb{H}^{2}$ , we can also view $\operatorname{PSL}_{2}(\mathbb{R})/(\mathbb{Z}/n\mathbb{Z})$ as the quotient of $U\mathbb{H}^{2}$ by the $\mathbb{Z}/n\mathbb{Z}$ action that covers the identity of $\mathbb{H}^{2}$ and rotates each fiber.

Proof of Claim 2.8.

Write $e=(2g-2)2pm$ for some integer $m$ .

First note that since $\rho(h)$ has finite order, the induced isometry of $\mathbb{H}^{2}$ has a unique fixed point, so $\rho(h)$ preserves a unique circle $C$ of the fibering $\widehat{X}\to\mathbb{H}^{2}$ . The same is true for $\rho(h^{k/p})$ , and we will show that $\rho(h^{k/p})$ acts trivially on $C$ .

Since $h=[x,y]$ is a commutator in $\pi_{1}^{orb}(O)$ and $\operatorname{SO}(2)$ is abelian, we find that the projection

\rho(h)\in\operatorname{Isom}^{+}(\widehat{X})\cong\operatorname{Isom}^{+}(\mathbb{H}^{2})\times\operatorname{SO}(2)\to\operatorname{SO}(2)

is trivial. Therefore, the action of $\rho(h)$ on $\widehat{X}$ factors through $\operatorname{Isom}^{+}(\mathbb{H}^{2})$ acting on $\widehat{X}$ . This action is described in Remark 2.9. If $e=0$ , since $\operatorname{Isom}^{+}(\mathbb{H}^{2})$ acts trivially on the $S^{1}$ factor of $\widehat{X}\cong\mathbb{H}^{2}\times S^{1}$ , we conclude that $\rho(h)$ acts trivially on $C$ . If $e\neq 0$ , then $\rho(h)$ acts as a a rotation by $2\pi(pm/k)$ on $C$ , so $\rho(h^{k/p})$ acts as a rotation by $2\pi m$ , which is trivial. ∎

This completes the proof of Proposition 2.5. ∎

Homeomorphism case. Here prove Proposition 2.3.

Proof of Proposition 2.3.

By Pardon [Par21, Thm. 1.1], there is a sequence of smooth $D_{4k}$ actions converging in $\operatorname{Hom}\big{(}D_{4k},\operatorname{Homeo}(X)\big{)}$ to the given action of $\sigma(D_{4k})$ on $X$ . Sufficiently close approximates also give a splitting of $\pi$ over $D_{4k}<\operatorname{Mod}(\Sigma)$ because $\operatorname{Homeo}(X)$ is locally path connected [EK71].

For each of the smooth approximations of $\sigma(D_{4k})$ , the fixed set of $a^{2k/p}$ is nonempty by Proposition 2.5. This implies that $\sigma(a^{2k/p})$ has a fixed point (a sequence of fixed points, one for each smooth action, sub-converges to a fixed point of the $\sigma(a^{2k/p})$ action). By Remark 2.2, there exists a lift of $a^{2k/p}\in D_{4k}<\operatorname{Mod}(\Sigma)$ to a finite order element $\alpha^{\prime}\in\pi_{1}^{orb}(O)<\operatorname{Mod}(\Sigma,*)$ so that $\widehat{\sigma}(\alpha^{\prime})$ has a fixed point. Since $\pi_{1}^{orb}(O)$ has a unique conjugacy class of finite subgroup of order $2p$ , the subgroups $\langle\alpha^{\prime}\rangle$ and $\langle\alpha\rangle$ are conjugate, so the fixed set of $\widehat{\sigma}(\alpha)$ is nonempty.

It remains to show the fixed set of $\widehat{\sigma}(\alpha)$ is a circle, and that this circle is the same as the fixed sets of $\widehat{\sigma}(\alpha)^{2}$ and $\widehat{\sigma}(\alpha)^{p}$ .

First we show (using Smith theory) that both $\widehat{\sigma}(\alpha)^{2}$ and $\widehat{\sigma}(\alpha)^{p}$ have fixed set a single circle (we are not yet claiming/arguing that the fixed sets of $\widehat{\sigma}(\alpha)^{2}$ and $\widehat{\sigma}(\alpha)^{p}$ are the same). To see this, we focus on $\widehat{\sigma}(\alpha)^{2}$ for concreteness. Consider the group $\Lambda_{0}$ of all lifts of powers of $\widehat{\sigma}(\alpha)^{2}$ to the universal cover $\widetilde{X}$ . This group is an extension

1\to\mathbb{Z}\to\Lambda_{0}\to\mathbb{Z}/p\mathbb{Z}\to 1,

which is central and split; hence $\Lambda_{0}\cong\mathbb{Z}\times\mathbb{Z}/p\mathbb{Z}$ . It is central because $\alpha$ acts orientation-preservingly on fibers of $X\to\Sigma$ (otherwise, the action of $\alpha$ on $\Sigma$ would reverse orientation, contrary to the construction); it splits because $\widehat{\sigma}(\alpha)$ has a fixed point. The (lifted) action of $\widehat{\sigma}(\alpha)^{2}$ on $\widetilde{X}$ has fixed set a line (i.e. embedded copy of $\mathbb{R}$ ) by Smith theory and local Smith theory [Bre12, Theorem 20.1], and this line is preserved and acted properly by $\mathbb{Z}<\Lambda_{0}$ ; thus $\widehat{\sigma}(\alpha)^{2}$ acts on $\widehat{X}$ with a circle in its fixed set. Furthermore, each component of the fixed set of $\widehat{\sigma}(\alpha)^{2}$ acting on $\widehat{X}$ corresponds to a distinct conjugacy class of order- $p$ subgroup of $\Lambda_{0}$ . Since there is only one $\mathbb{Z}/p\mathbb{Z}$ subgroup of $\Lambda_{0}$ , the fixed set of $\widehat{\sigma}(\alpha)^{2}$ is connected, i.e. a single circle. The same argument¹¹1Smith theory applies to prime-order finite cyclic group actions, so we cannot apply this argument directly to $\widehat{\sigma}(\alpha)$ . works for $\widehat{\sigma}(\alpha)^{p}$ .

Now we determine the fixed set of $\widehat{\sigma}(\alpha)$ . First observe that $\widehat{\sigma}(\alpha)$ preserves the fixed set of $\widehat{\sigma}(\alpha)^{2}$ and has a fixed point there (the fixed set of $\widehat{\sigma}(\alpha)$ is nonempty and contained in the fixed set of $\widehat{\sigma}(\alpha)^{2}$ ). The only $\mathbb{Z}/2p\mathbb{Z}$ action on the circle with a fixed point is the trivial action, so in fact the fixed sets of $\widehat{\sigma}(\alpha)$ and $\widehat{\sigma}(\alpha)^{2}$ are the same. The same argument applies to $\widehat{\sigma}(\alpha)$ and $\widehat{\sigma}(\alpha)^{p}$ . This proves Proposition 2.3. ∎

2.3. Step 3: centralizer argument

Recall that we have defined $\alpha$ as an element of order $2p$ in $\pi_{1}^{orb}(O)<\operatorname{Mod}(\Sigma,*)$ . In this step we prove that $\operatorname{Mod}(\Sigma,*)$ is generated by the centralizers of $\alpha^{2}$ and $\alpha^{p}$ .

Proposition 2.10 (centralizer property).

Let $\alpha\in\operatorname{Mod}(\Sigma,*)$ be the element of order $2p$ constructed above. Then

\operatorname{Mod}(\Sigma,*)=\langle C(\alpha^{2}),C(\alpha^{p})\rangle,

where $C(-)$ denotes the centralizer in $\operatorname{Mod}(\Sigma,*)$ .

Strategy for proving Proposition 2.10. Set $\Gamma=\langle C(\alpha^{2}),C(\alpha^{p})\rangle$ . Our method for showing $\Gamma=\operatorname{Mod}(\Sigma,*)$ , which is similar to the proof of [CS22, Thm. 1.1], is to inductively build subsurfaces

(6)

S_{0}\subset S_{1}\subset\cdots\subset S_{N}\subset\Sigma\setminus\{*\}

such that $\operatorname{Mod}(S_{n})\subset\Gamma$ for each $n$ and $S_{N}$ fills $\Sigma\setminus\{*\}$ (i.e. each boundary component of $S_{N}$ is inessential in $\Sigma\setminus\{*\}$ ). The fact that $S_{N}$ fills implies that $\operatorname{Mod}(S_{N})=\operatorname{Mod}(\Sigma,*)$ , so then $\operatorname{Mod}(\Sigma,*)\subset\Gamma$ by the last step in the inductive argument.

In order to ensure that $\operatorname{Mod}(S_{n})\subset\Gamma$ , the subsurface $S_{n}$ is obtained from $S_{n-1}$ by an operation known as subsurface stabilization. If $S\subset\Sigma$ is a subsurface and $c\subset\Sigma$ is a simple closed curve that intersects $S$ in a single arc, then the stabilization of $S$ along $c$ is the subsurface $S\cup N(c)$ , where $N(c)$ is a regular neighborhood of $c$ . It is easy to show that $\operatorname{Mod}(S\cup N(c))$ is generated by $\operatorname{Mod}(S)$ and the Dehn twist $\tau_{c}$ [CS22, Lem. 4.2], so if $\operatorname{Mod}(S)\subset\Gamma$ and $\tau_{c}\in\Gamma$ , then $\operatorname{Mod}(S\cup N(c))\subset\Gamma$ . Therefore, for the proof, it suffices to find a sequence of subsurface stabilizations along curves whose Dehn twist belongs to $\Gamma=\langle C(\alpha^{2}),C(\alpha^{p})\rangle$ .

Model for the $\alpha$ action. Our proof of Proposition 2.10 makes use of an explicit model for $\Sigma$ with its $\alpha$ action, which is pictured below in the case $k=6$ and $p=3$ (recall that $g=4k-1$ and $p$ is an odd prime dividing $k$ ).

Refer to caption — Figure 1. The model of the surface $\Sigma_{23}$ where $p=3$ .

The surface $\Sigma$ is built out of two copies of the standard action of $\mathbb{Z}/2p\mathbb{Z}$ on $S^{2}$ and one copy of a free action of $\mathbb{Z}/2p\mathbb{Z}$ on $T^{2}$ . We glue each copy of $S^{2}$ to $T^{2}$ along $k/p$ free orbits by an equivariant connected sum. In the figure, $\alpha$ acts by vertical translation. Note that the fixed points of $\alpha$ on $S^{2}$ are not pictured in the figure – they are at $\pm\infty$ along the $x$ -axis.

To derive this model, recall that $D_{4k}=\langle a,b\mid a^{4k}=1=b^{2},bab=a^{-1}\rangle$ has abelianization $D_{4k}\to(\mathbb{Z}/2\mathbb{Z})^{2}$ with kernel $\langle a^{2}\rangle\cong\mathbb{Z}/2k\mathbb{Z}$ . Then there is a sequence of regular covers

\Sigma\xrightarrow{\langle a^{2}\rangle}\Sigma/\langle a^{2}\rangle\xrightarrow{(\mathbb{Z}/2\mathbb{Z})^{2}}\Sigma/D_{4k}.

The cover $\Sigma/\langle a^{2}\rangle\to\Sigma/D_{4k}$ is unbranched and is the $\mathbb{Z}/2\mathbb{Z}$ -homology cover of $T^{2}$ (in particular, $\Sigma/\langle a^{2}\rangle$ is also a torus). The cover $\Sigma\to\Sigma/\langle a^{2}\rangle$ is branched over four points; the local monodromy around the branched points is $a^{2}$ at two of the branched points and $a^{-2}$ at the other two. Choosing branched cuts joining branched points in $a^{\pm 2}$ pairs gives a model for $\Sigma$ , and one can check that this model is equivalent to the one described above. (The spheres in Figure 1 arise from pre-images under $\Sigma\to\Sigma/\langle a^{2}\rangle$ of neighborhoods of the branch cuts.)

By Remark 2.2, since $\sigma(a^{2k/p})$ has a fixed point, the subgroup $\langle\alpha\rangle\subset\operatorname{Mod}(\Sigma,*)$ , which lifts $\langle a^{2k/p}\rangle$ , has a fixed point. The different lifts of $\langle a^{2k/p}\rangle$ to a finite subgroup of $\operatorname{Mod}(\Sigma,*)$ are in one-to-one correspondence to fixed points of $a^{2k/p}$ . Since these fixed points are permuted transitively by the action of $D_{4k}$ , the different lifts of $\langle a^{2k/p}\rangle$ are conjugate. Consequently, for the purpose of our argument, we can choose $*$ to be any one of the four fixed points of $\alpha$ and prove Proposition 2.10 for this choice, without loss of generality. (It will also be evident from the argument that a similar argument applies if $*$ is changed to another fixed point.)

Remark 2.11.

We do not known how generally the relation $\operatorname{Mod}(\Sigma,*)=\langle C(\alpha^{2}),C(\alpha^{p})\rangle$ holds. For example, it may hold for every $\mathbb{Z}/2p\mathbb{Z}$ subgroup of $\operatorname{Mod}(\Sigma,*)$ . We do not know a general (abstract) approach to this problem.

Proof of Proposition 2.10.

Symmetry breaking. In preparation for constructing a sequence of subsurface stabilizations, in this paragraph we find a suitable collection of Dehn twists that belong to $\Gamma$ . The obvious way for $\tau_{c}$ to belong to $\Gamma$ is if $c$ is preserved by either $\alpha^{2}$ or $\alpha^{p}$ . More generally, we use a process that we call symmetry breaking to show $\tau_{c}\in\Gamma$ for certain $c$ . We formulate this in the following lemma, which is similar to [CS22, Lem. 3.2].

Lemma 2.12 (Symmetry breaking).

Assume that $c,d\subset\Sigma$ are simple closed curves that intersect once and $\tau_{d}\in\Gamma$ . Suppose that either (i) $\alpha^{p}(c)$ is disjoint from $c$ and $d$ or (ii) the curves $\alpha^{2}(c),\alpha^{4}(c)\ldots,\alpha^{2p-2}(c)$ are disjoint from $d$ and the curves $c,\alpha^{2}(c),\alpha^{4}(c)\ldots,\alpha^{2p-2}(c)$ are pairwise disjoint. Then $\tau_{c}\in\Gamma$ .

Proof of Lemma 2.12.

We prove case (i) of the statement; case (ii) is similar. Since Dehn twists about disjoint curves commute,

\big{(}\tau_{c}\tau_{\alpha^{p}(c)}\big{)}\tau_{d}\big{(}\tau_{c}\tau_{\alpha^{p}(c)}\big{)}^{-1}=\tau_{c}\tau_{d}\tau_{c}^{-1}.

The left hand side of the equation is in $\Gamma$ because $\tau_{d}\in\Gamma$ by assumption and $\tau_{c}\tau_{\alpha^{p}(c)}\in\Gamma$ because the curves $c,\alpha^{p}(c)$ are permuted by $\alpha^{p}$ and are disjoint (so their twists commute), and thus $\tau_{c}\tau_{\alpha^{p}(c)}\in C(\alpha^{p})\subset\Gamma$ . Since $c$ and $d$ intersect once, the braid relation implies that $\tau_{d}\tau_{c}\tau_{d}^{-1}=\tau_{c}\tau_{d}\tau_{c}^{-1}$ also belongs to $\Gamma$ . Since $\tau_{d}\in\Gamma$ this implies that $\tau_{c}\in\Gamma$ , as desired. ∎

Remark 2.13.

When applying Lemma 2.12(i) or (ii) we refer to it as the $\alpha^{p}$ - or $\alpha^{2}$ -symmetry breaking, respectively.

Lemma 2.14.

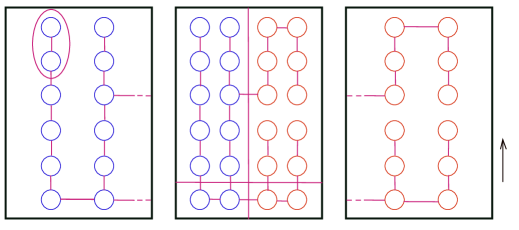
Dehn twists about the curves in Figure 2 are in $\Gamma$ .

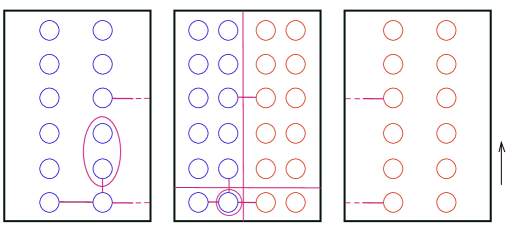
In Figure 2, we illustrate the case $k=6,p=3$ . The corresponding curves in the general case belong to $\Gamma$ by the exact same argument.

Proof of Lemma 2.14.

First observe that $\tau_{c_{1}}$ and $\tau_{c_{6}}$ are in $\Gamma$ because each is invariant under $\alpha^{p}$ . We deduce that $\tau_{c_{2}}\in\Gamma$ using $\alpha^{2}$ -symmetry breaking with $d=c_{1}$ . Each of $\tau_{c_{3}}$ and $\tau_{c_{4}}$ are in $\Gamma$ by $\alpha^{p}$ -symmetry breaking with $d=c_{2}$ . Finally, both $\tau_{c_{5}}$ and $\tau_{c_{7}}$ are in $\Gamma$ by $\alpha^{p}$ -symmetry breaking with $d=c_{3}$ . ∎

Surface stabilization sequence. We stabilize with the sequence of curves represented in Figure 3. To get the initial subsurface $S_{0}$ we can take the subsurface spanned by the chain of curves $c_{0},c_{1},\ldots,c_{4}$ . This subsurface has genus 2 and one boundary component, and these curves are Humphries generators for $S_{0}$ [FM12, Fig. 4.10]. Next we extend this chain with the curves $c_{5},\ldots,c_{4k-1}$ ; at this point the left genus-0 subsurface has been filled. Next we stabilize with $c_{4k}$ and the curves ( $c_{4k+1},c_{4k+2},\cdots,c_{8k-2}$ ) that fill the right genus-0 subsurface; there is some choice in the order of curves we stabilize, but this is not important. Finally we stabilize with the curves $c_{8k-1}$ and $c_{8k}$ that generate $\pi_{1}(T^{2})$ .

All of the twists about the curves used are in $\Gamma$ . In each case, this can be seen either directly from the statement of Lemma 2.14 or by an argument that is a small variation of its proof. Since this collection of curves fills $\Sigma$ , we have shown that $\Gamma=\operatorname{Mod}(\Sigma,*)$ . This proves Proposition 2.10. ∎

2.4. Step 4: conclusion

By Proposition 2.3, $\widehat{\sigma}(\alpha)$ , $\widehat{\sigma}(\alpha^{2})$ and $\widehat{\sigma}(\alpha^{p})$ all have the same fixed set, which is a circle $c\subset\widehat{X}$ . The centralizers $C(\alpha^{2})$ and $C(\alpha^{p})$ preserve $c$ . By Proposition 2.10, $\operatorname{Mod}(\Sigma,*)=\langle C(\alpha^{2}),C(\alpha^{p})\rangle$ , so $\widehat{\sigma}\big{(}\operatorname{Mod}(\Sigma,*)\big{)}$ preserves $c$ . This contradicts the fact that $\widehat{\sigma}(\pi_{1}(\Sigma_{g}))$ acts as the deck group, which as a properly discontinuous action does not preserve any compact set.

References

[Bre12] Glen E Bredon. Sheaf theory, volume 170. Springer Science & Business Media, 2012.
[Bro82] K. S. Brown. Cohomology of groups, volume 87 of Graduate Texts in Mathematics. Springer-Verlag, New York-Berlin, 1982.
[CS22] L. Chen and N. Salter. Global fixed points of mapping class group actions and a theorem of Markovic. J. Topol., 15(3):1311–1324, 2022.
[CT23] Lei Chen and Bena Tshishiku. Mapping class groups of circle bundles over a surface, 2023.
[EK71] R. Edwards and R. Kirby. Deformations of spaces of imbeddings. Ann. of Math. (2), 93:63–88, 1971.
[FM12] B. Farb and D. Margalit. A primer on mapping class groups, volume 49 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 2012.
[Hat02] A. Hatcher. Algebraic topology. Cambridge University Press, Cambridge, 2002.
[MS86] W. H. Meeks, III and P. Scott. Finite group actions on $3$ -manifolds. Invent. Math., 86(2):287–346, 1986.
[MZ54] D. Montgomery and L. Zippin. Examples of transformation groups. Proc. Amer. Math. Soc., 5:460–465, 1954.
[Par21] J. Pardon. Smoothing finite group actions on three-manifolds. Duke Math. J., 170(6):1043–1084, 2021.
[Sco83] P. Scott. The geometries of $3$ -manifolds. Bull. London Math. Soc., 15(5):401–487, 1983.
[Sou10] J. Souto. A remark on the action of the mapping class group on the unit tangent bundle. Ann. Fac. Sci. Toulouse Math. (6), 19(3-4):589–601, 2010.