\cfoot

Supplementary Information

Renjie Zhao Chemical Physics Program and Institute for Physical Science and Technology, University of Maryland, College Park 20742, USA. Ziyue Zou Department of Chemistry and Biochemistry, University of Maryland, College Park 20742, USA. John D. Weeks [email protected] Institute for Physical Science and Technology and Department of Chemistry and Biochemistry, University of Maryland, College Park 20742, USA. Pratyush Tiwary [email protected] Institute for Physical Science and Technology and Department of Chemistry and Biochemistry, University of Maryland, College Park 20742, USA.

Supplementary Notes

Note 1: Averaged intermolecular angles

For an arbitrary solute molecule $i$ , we have

\hat{\theta}(i)=\frac{\sum_{j}\sigma(r_{ij})\frac{1}{2}[(\pi-2\theta)\tanh\funcapply(5\theta-9.25)+\pi]}{\sum_{j}\sigma(r_{ij})},

(1)

where $\theta$ is the intermolecular angle between characteristic vectors on molecule $i$ and molecule $j$ , and $\sigma(r_{ij})$ is a switching function of intermolecular distance $r_{ij}$ . In order to eliminate the mirror image symmetry, the hyperbolic tangent switching function is implemented in Eq. 1. We then compute the mean of $\hat{\theta}(i)$ over the group of solutes to obtain the averaged intermolecular angles $\bar{\theta}_{1}$ and $\bar{\theta}_{2}$ , for which the subscripts refer to the specific intermolecular angles defined in the context of pair orientational entropy. $\mu^{2}_{\theta_{1}}$ and $\mu^{2}_{\theta_{2}}$ are computed as the second moments of the $\hat{\theta}_{1}(i)$ and $\hat{\theta}_{2}(i)$ distributions.

Note 2: Coordination number

We calculate the coordination number of urea molecules by the following continuous and differentiable expression,

c(i)=\sum_{j}\frac{1-(r_{ij}/r_{\text{c}})^{6}}{1-(r_{ij}/r_{\text{c}})^{12}},

(2)

where $r_{ij}$ is the distance between reference sites of molecules $i$ and $j$ , and $r_{\text{c}}$ is the cutoff. $N_{8+}$ , $N_{11+}$ , which are the populations of molecules with coordination numbers greater than 8 and 11, and the second moment of coordination numbers $\mu^{2}_{c}$ are derived from the $c(i)$ distribution.

Note 3: Distributions of $N_{8+}$

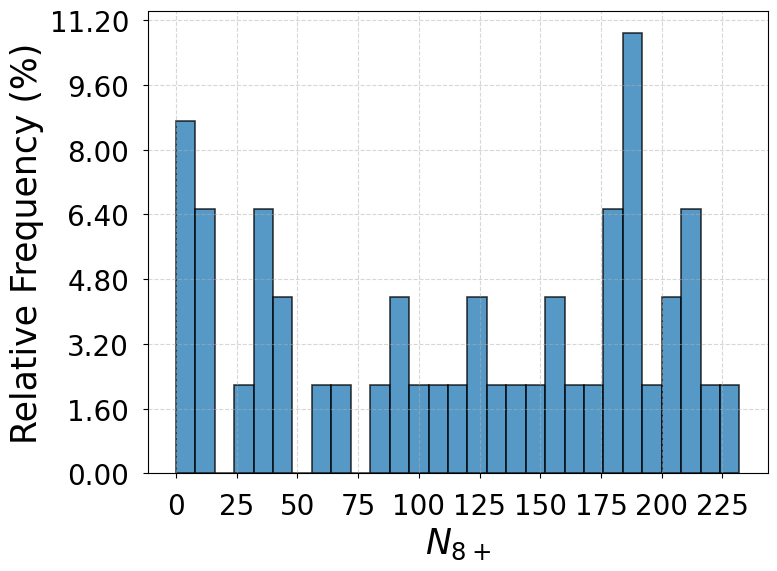
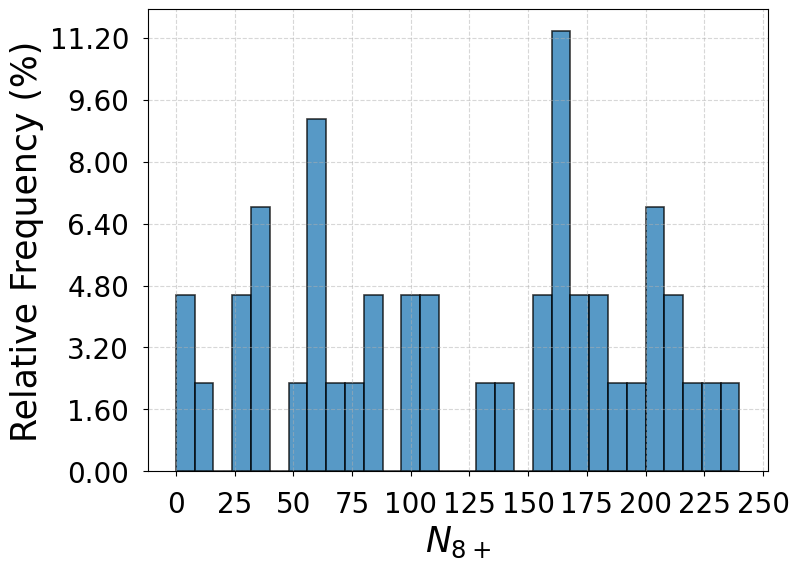
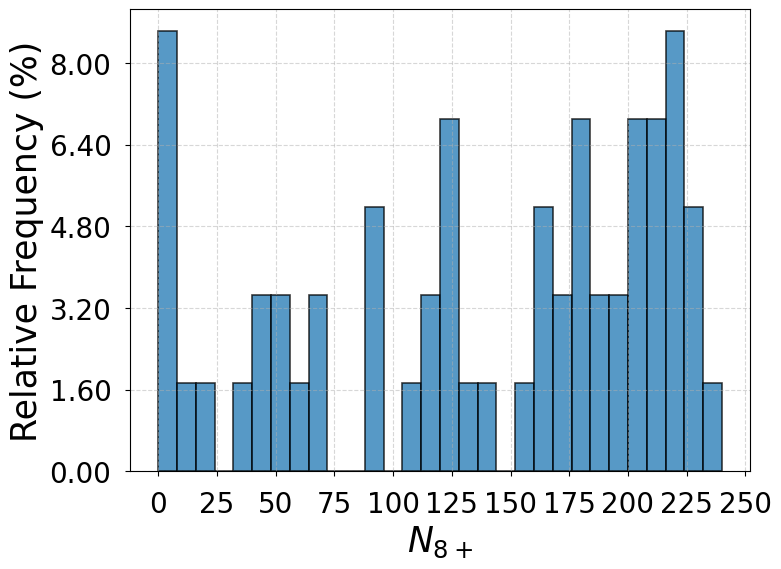
Refer to caption — Supplementary Fig. 1: Cluster size information during transitions. Distributions of $N_{8+}$ occurring with transitions between the liquid-like basin and the primary crystal basin from WTmetaD simulations performed with (a) the SS model, (b) the GT model, and (c) the full model.

In Supplementary Fig. 1 are the distributions of $N_{8+}$ when the system transitions between the liquid-like basin and the primary crystal basin for the SS model, the GT model, and the full model. Based on the criterion that the liquid-like configurations from WTmetaD simulations count toward the liquid state when their $N_{8+}$ values are within the three-sigma limits of the liquid state $N_{8+}$ distribution drawn from a 50 ns unbiased simulation and otherwise count toward the dense liquid state, the transitions between the liquid-like basin and the primary crystal basin take place directly from or to the liquid state in $8.7\%$ of the total 46 events for the SS model, $4.5\%$ of the total 44 events for the GT model, and $8.6\%$ of the total 58 events for the full model. The other transitions are mediated by the dense liquid state. The results from the three models consistently indicate a predominant two-step nucleation mechanism.

The distributions of $N_{8+}$ beyond the dense liquid state threshold ( $\sim 9.61$ ) do not necessarily take similar shapes for the three models. This is because there can exist one or multiple clusters in different configurations and $N_{8+}$ is not accurately proportional to the size of the cluster.

Supplementary Information

Supplementary Notes

Note 1: Averaged intermolecular angles

Note 2: Coordination number

Note 3: Distributions of N8+N_{8+}

Supplementary Figure

Note 3: Distributions of $N_{8+}$