Superharmonic double-well systems with zero-energy ground states: Relevance for diffusive relaxation scenarios

It is a folk wisdom, that a sequence of potentials $U_{m}(x)=(x/L)^{m}/m$, $L>0$, $m$ even, for large values of $m$, can be used as an approximation of the infinite well potential of width $2L$ with reflecting boundaries located at $x=\pm L$, c.f. dubkov ; khar ; dybiec ; dybiec0 . Actually, quite often reproduced statement reads: ”the reflecting boundary can be implemented by considering the motion in a bounding potential $\lim_{m\to\infty}U_{m}(x)$”, khar ; dybiec0 ; dybiec ). Things are however not that simple and obvious, see e.g. jph and references linetsky ; bickel ; pilipenko on the reflected Brownian motion in a bounded domain.

For computational simplicity, we prefer to use the dimensionless notation $x/L\rightarrow x$, next skip the lower index $m$, so passing to $U(x)=x^{m}/m$. The ultimate limiting case (e.g. that of the interval with conjectured reflecting boundaries) is to be supported on the interval $[-1,1]$. Potentials of the form $U(x)=\kappa_{m}x^{m}/m$, Eq. (3), with $\kappa_{m}=1,m,m^{2}$, are employed to the same end, khar ; dybiec0 ; dybiec .

We point out that one needs to observe possibly annoying boundary subtleties. Namely, at $x=\pm 1$, we have the following limiting values of $U(\pm 1)$ (point-wise limits, as $m$ grows to $\infty$)

$$U(x)={\frac{\kappa_{m}}{m}}x^{m}\Rightarrow U(\pm 1)=\left\{{\frac{1}{m}},1,m\right\}\rightarrow\{0,1,\infty\}.$$

(5)

On formal grounds, with reference to the open interval $(-1,1)$ and the complement $R\setminus[-1,1]$ of $[-1,1]$, we have the point-wise limit $U(x)\to\infty$, for all $|x|>1$, as $m\to\infty$, while the interior limit equals zero for all $|x|<1$. In addition to the emergent exterior boundary data (instead of the customary local ones for the Neumann Laplacian), we encounter significant differences in the boundary ($x=\pm 1$) properties of $m\to\infty$ limit of $U(x)$.

These in turn have an impact on the limiting properties of $\rho_{*}(x)$ (and of the prospective ground state function $\rho_{*}^{1/2}(x)$ of $\hat{H}$ ). The outcome appears not to be quite innocent as far as the domain of $\hat{H}$ is concerned. Specifically, if the Neumann Laplacian $\Delta_{\cal{N}}$ is to be spectrally approached/approximated in the $m\to\infty$ limit.

We note that, as $m\to\infty$, we arrive at $\rho_{*}(x)=0$ for all $|x|>1$, while $\rho_{*}(x)=1/2$ for all $|x|<1$. However, the pointwise limit $m\to\infty$ of $\rho_{*}(\pm 1)$ reads, respectively (in correspondence with that for $U(x)$, Eq. (5)):

$${\rho_{*}(\pm 1)}_{m\to\infty}=\left\{\frac{1}{2},\frac{1}{2e},0\right\}.$$

(6)

This implies the Dirichlet-type boundary data for $\rho_{*}^{1/2}(x)$ at boundaries $\pm 1$ of the interval $[-1,1]$. In case of $\kappa_{m}=m^{2}$ we deal with a ”canonical” form of Dirichlet boundaries, since $\rho_{*}^{1/2}(x)$ vanishes at $x=\pm 1$.

The behavior of $U(x)$ and $\rho_{*}(x)$ with the growth of $m$, we depict in Fig. 1 for the case of $U(x)=mx^{m}$. The exemplary functional forms of the inferred potential ${\cal{V}}(x)$ are shown in Fig.2. The conspicuous higher order double well structure is clearly seen.

As long as we prefer to deal with traditional Langevin-type methods of analysis, it is of some pragmatic interest to know, how reliable is an approximation of the reflected Brownian motion in $[-1,1]$ by means of the attractive Langevin driving (and thence by solutions of Eq. (1)), with force terms (e.g. drifts) coming from extremally anharmonic (steep) potential wells.

The main obstacle, we encounter here, is that a ”naive” $m=2n\rightarrow\infty$ limit is singular and cannot be safely executed on the level of diffusions proper. We note that for any finite $m$, irrespective of how large $m$ actually is, we deal with a continuous and infinitely differentiable higher order double-well potential and the smooth Boltzmann- type pdf. These properties are broken in the (formal) limit $m\to\infty$.

At this point we recall that for the Neumann Laplacian $\Delta_{\cal{N}}$ on $[-1,1]$, the boundary condition for all its eigenfunctions, bickel ; carlsaw , is imposed locally. In particular, for the ground state function we should have $\Delta_{\cal{N}}\rho_{*}^{1/2}(x)=0$ and $\nabla\rho_{*}^{1/2}(\pm 1)=0$, see e.g. also Ref. carlsaw , chap. 4.1. This formally holds true or a constant function $1/\sqrt{2}$, defined on $[-1,1]$, but can not be achieved through a controlled limiting procedure: $m\to\infty$ of $\nabla\rho_{*}(\pm 1)$.

Indeed, we know from Ref. jph that for $U(x)=x^{m}/2$, the inferred square root of the Boltzmann-type pdf $\rho_{*}^{1/2}(x)=(1/\sqrt{Z})\exp(-x^{m}/2m)$ does not reproduce the Neumann condition in the $m\to\infty$ limit. Namely, we have: $\lim_{m\to\infty}\nabla\rho_{*}^{1/2}(+1)=-1/2\sqrt{2}$.

Since, in accordance with the notation (3) we have:

$$\nabla\rho_{*}^{1/2}(x)=-{\frac{1}{2}}[\nabla U(x)]\rho_{*}^{1/2}(x)$$

(7)

where $\nabla U(x)=\kappa_{m}x^{m-1}$, we can readily complement formulas (5) and (6), by these referring to the limiting behavior of $\nabla\rho_{*}^{1/2}(\pm 1)$:

$${\nabla\rho_{*}^{1/2}(\pm 1)}_{m\to\infty}=\left\{\mp{\frac{1}{2\sqrt{2}}},\mp\infty,\mp\infty\right\}.$$

(8)

Clearly, the point-wise $m\to\infty$ limit of $\nabla\rho_{*}^{1/2}(\pm 1)$ has nothing to do with the Neumann boundary condition, which is not reproduced in this limiting regime. Conseqeuntly, $\rho_{*}^{1/2}(x)$ is not in the domain of the Neumann Laplacian $\Delta_{\cal{N}}$, in plain contradiction with popular expectations, dubkov - dybiec0 .

We can readily infer the location of (negative) minima of the potential ${\cal{V}}(x)$, c.f. Eq. (3) and Fig. 2, where

$$\mathcal{V}^{\prime}(x)=0\Longrightarrow|x_{min}|=\left[{\frac{b}{2a}}{\frac{m-2}{m-1}}\right]^{1/m}=\left[{\frac{m-2}{\kappa_{m}}}\right]^{1/m}.$$

(9)

For $\kappa_{m}=1$ we have $|x_{min}|=(m-2)^{1/m}>1$ for all $m>2$. For $\kappa_{m}=m$ we obtain $|x_{min}|=[(m-2)/m]^{1/m}<1$, and likewise for $\kappa_{m}=m^{2}$, when $|x_{min}|=[(m-2)/m^{2}]^{1/m}<1$.

We point out that $m^{1/m}>1$ and $\lim_{m\rightarrow\infty}m^{1/m}=1$, c.f. kuczma ; jph . Accordingly, in the large m limit, the minimum locations approach the interval $[-1,1]$ endpoints $\pm 1$, respectively from the interval exterior $R\setminus[-1,1]$ for $\kappa_{m}=1$, or interior of $[-1,1]\subset R$ if otherwise. This behavior is (continuously) depicted in Fig.3.

Since we are interested in the large m regime it is useful to rewrite the formula (9) as follows:

$$|x_{min}|=\exp\left\{{\frac{1}{m}}\left[\ln{\frac{m}{\kappa_{m}}}+\ln(1-{\frac{2}{m}})\right]\right\}\sim 1+\frac{\ln(m/\kappa_{m})}{m}-\frac{2}{m^{2}}+\frac{\ln^{2}(m/\kappa_{m})}{2m^{2}},$$

(10)

where $\ln(m/\kappa_{m})=\{\ln m,0,-\ln m\}$, and we have employed the series expansion $\ln(1-x)=-\sum_{n=1}^{\infty}x^{n}/n$, valid in the range $-1\leq x<1$, and here considered for $x=2/m$. In the large $m$ approximate formula (10), expansion terms up to the $m^{-2}$ order have been kept. We recall that $\kappa_{m}=\{1,m,m^{2}\}$.

We immediately realize that in the regime of large $m$, for $\kappa_{m}=1$ the dominant contribution to $|x_{min}|$, Eq. (10), comes from $1+{\frac{\ln m}{m}}$, for $\kappa_{m}=m$ from $1-1/m^{2}$, and for $\kappa_{m}=m^{2}$ from $1-{\frac{\ln m}{m}}$.

Let us denote

$$\triangle=\triangle(m)=|1-|x_{min}||$$

(11)

the distance of $|x_{\min}|$ from the nearby boundary point $\pm 1$. In passing we note that $\triangle\sim\{+{\frac{\ln m}{m}},1/m^{2},{\frac{\ln m}{m}}\}$ for $\kappa_{m}=\{1,m,m^{2}\}$ respectively.

In Fig. 4 we visualize the $m$-dependence of the signed deviation $\delta=1-x_{min}$ of $+1$ from the nearby $x_{min}>0$. For large $m$, we have $\delta\sim\{-{\frac{\ln m}{m}},1/m^{2},{\frac{\ln m}{m}}\}$. For $x_{min}>1$ the signed deviation is negative, and positive for $x_{min}<1$. Note that $\triangle=|\delta|$.

By turning back to Eq. (3), plugging there the minimum location value $|x_{min}|$, Eq. (9), we arrive at the following expression for the depth of local wells of the potential (3):

$${\cal{V}}(|x_{min}|)=-{\frac{m\kappa_{m}}{4}}|x_{min}|^{m-2}=-{\frac{m(m-2)}{4}}|x_{min}|^{-2}.$$

(12)

For sufficiently large values of $m$ (basically above $m=100$), we can pass to rough approximations

$${\cal{V}}(|x_{min}|)\sim-{\frac{m(m-2)}{4}}\sim-{\frac{m^{2}}{4}}.$$

(13)

(We note that in this approximation regime, the well depth becomes independent of the choice of $\kappa_{m}$.) This rough estimate of ${\cal{V}}(|x_{min}|)$, comes from presuming that $|x_{min}|^{-2}\to 1$.

It is instructive to have more detailed insight into the pertinent large $m$ asymptotics. We proceed by repeating basic steps in the derivation of Eq. (10):

$$|x_{min}|^{-2}=\exp\left\{-{\frac{2}{m}}\left[\ln{\frac{m}{\kappa_{m}}}+\ln(1-{\frac{2}{m}})\right]\right\}\sim 1-\frac{2\ln(m/\kappa_{m})}{m}+\frac{4}{m^{2}}+\frac{2\ln^{2}(m/\kappa_{m})}{2m^{2}}.$$

(14)

For large $m$, the dominant contributions read: for $\kappa=1$ we have $1-2{\frac{\ln m}{m}}$, for $\kappa_{m}=m$ we get $1+2/m^{2}$, and for $\kappa_{m}=m^{2}$ we have $1+2{\frac{\ln m}{m}}$. This outcome lends support to our approximation (13) of the well depth.

We recall that for sufficiently large values of $m$, local minimum locations $x_{min}$ are close to $\pm 1$, and in the interval of the size $2\vartriangle$ in the vicinity of $\pm 1$, we encounter rapid (albeit smooth, e.g. continuous and continuously differentiable) variations of ${\cal{V}}(x)$. Considering $m$ to be large, we exemplify this behavior for $\kappa_{m}=m^{2}$, within the interval $1-2\triangle<x_{min}<1$ of length $2\triangle$:

$${\cal{V}}(x_{min}-\triangle)\simeq 0\Rightarrow{\cal{V}}(x_{min})\simeq-{\frac{m(m-2)}{4}}\Rightarrow{\cal{V}}(x_{min}+\triangle)={\cal{V}}(1)={\frac{m^{2}}{2}}\left[{\frac{m^{2}}{2}}-(m-1)\right]\simeq{\frac{m^{4}-2m^{3}}{4}},$$

(15)

We have thus a ”wild” variation of ${\cal{V}}(x)$, ranging from nearly $0$, through (roughly) $-(m^{2}-2m)/4$, to (roughly as well) $+(m^{4}-2m^{3})/4$, in the interval of length $2\triangle\sim 2/m^{2}$.

For further discussion we restrict consideration to the choice of $U(x)=mx^{m}$, with all ensuing formal consequences. Essentially, we need $|x_{min}|<1$ for all $m$, an the point-wise limit of $\lim_{m\to\infty}U(\pm 1)=\infty$. Since $\rho_{*}^{1/2}(\pm 1)_{m\to\infty}=0$, we are tempted to explore an approximation of our higher degree double-well potential function, by means of a sequence of rectangular double well systems, with adjustable (internal) barrier heights and widths, bas .

We anticipate the existence of an affinity between ${\cal{V}}(x)$, as $m$ grows to $\infty$, and a properly tuned rectangular double-well potential, cf. Refs. bas ; blinder ; lopez ; jelic . That is supported by an experimentation with the dedicated Mathematica 12 routine, blinder , created to address the rectangular double-well spectral problem. Fine tuning options concerning the overall depth (large) of the well and the middle barrier size parameters (width and height) allow for a controlled manipulation. Its explicit outcome were lowest eigenvalues and eigenfunctions (up to eight) of the corresponding energy operator $\hat{H}_{well}$, see e.g. blinder .

Numerical tests confirmed that the ground state eigenvalue, which is equal (or in the least nearly equal) to the height of the barrier, is in existence if the proper width/height balance is set. The corresponding ground state eigenfunction is ”flat” (practically constant) in the area of the barrier plateau (local maximum area). This sets a background for a subsequent discussion.

We depart from the ”canonical” qualitative picture of the ammonia molecule, as visualized in terms of the rectangular double well, bas , chap. 4.5. We adopt the original notation of Ref. bas to the graphical description given below, in Figs 6 and 7, see also blinder . One must keep in mind different (D=1 versus D=1/2) scalings of the Laplacian in the employed versions of the rectangular well energy operator.

From the start, we implement the energy scale ”renormalization” of the rectangular double-well energy operator. The original non-negative potential bas ; blinder ; lopez ; jelic is shifted down along the energy axis, by the value of its local maximum (barrier height), from the original minimum value $0$ (well bottom) of the rectangular potential. This in turn enables and effective fitting of the higher order double-well potential to the rectangular double-well potential contour.

The fitting procedure, graphically outlined in Figs. 6 and 7, looks promising but is somewhat deceptive. To justify its usefulness, we must first check under what circumstances the rectangular well spectral problem does admit the bottom (ground state) eigenvalue zero. In contrast to the higher order double-well $\hat{H}$, Eqs. (1) to (3), where the zero energy ground state is introduced as a matter of principle, its existence is obviously not the generic property in the rectangular double-well setting. Accordingly, the proposed approximation methodology might seem bound to fail.

Fortunately, we can demonstrate that potentially disparate two-well settings (higher order versus rectangular one), actually coalesce if we look comparatively at the higher $m$ data (say $m\geq 80$) and set them in correspondence with these belonging to the rectangular well system. To this end, let us employ the rectangular double-well lore of Ref. blinder . Temporarily, the notation will at some points differ from this adopted by us in Section III.A.

Following Ref. blinder , we consider the potential $V_{rect}(x)=V(x)=\infty$ for $x<0$ and $x>\pi$, while we assign a constant positive value $V(x)=V_{0}$ for $(\pi-a)/2\leq x\leq(\pi+a)/2$, where $0<a<\pi$, and demand $V(x)=0$ elswhere. This defines a rectangular double well profile immersed in the infinite well. The double well is set on the interval $[0,\pi]$, its bottom is located at the energy value zero, while the barrier with height $V_{0}$ has the width $a$, and separates two symmetrical wells extending over the intervals $[0,(\pi-a)/2]$ and $[(\pi+a)/2,\pi]$.

As far as the ground state function and the bottom eigenvalue of $\hat{H}_{rect}=-{\frac{1}{2}}\Delta+V(x)$ is concerned, we have in hands two steering parameters $a$ and $V_{0}$, which can be fine-tuned. In passing, we notice the presence of the $1/2$ factor preceding the Laplacian, and recall that the interval of interest is $[0,\pi]$ instead of $[-1,1]$. This needs to be accounted for, when we shall pass to the spectral comparisons between $\hat{H}_{rect}$ and $\hat{H}$ of Eqs. (1)-(3).

In view of the standard infinite well enclosure, all (piece-wise connected) eigenfunctions are presumed to obey the Dirichlet boundary data: $\psi(0)=0=\psi(\pi)$. We are interested in the ground state function, hence our focus is on even eigensolutions $\psi(x)=\psi(\pi-x)$ of $\hat{H}_{rect}\psi=E\psi$.

In the two local well areas we have $V_{0}(x)=0$ , hence respective even solutions have the self-defining form, blinder ; bas :

$$\psi_{L}(x)=\alpha\sin(kx),\,\,\,0\leq x\leq(\pi-a)/2$$

(16)

and

$$\psi_{R}(x)=\alpha\sin[k(x-\pi)],\,\,\,(\pi-a)/2\leq x\leq\pi$$

(17)

where subscripts $L$ and $R$ refer to the left or right well, respectively. Within the wells we have:

$$-{\frac{1}{2}}{\frac{\Delta\psi(x)}{\psi(x)}}={\frac{k^{2}}{2}}=E.$$

(18)

On the other hand, within the barrier region, the proper form of the even eigenfunction is:

$$\psi_{barrier}(x)=\beta\cosh[{\cal{K}}(x-\pi/2)],\,\,\,(\pi-a)/2\leq x\leq(\pi+a)/2.$$

(19)

Since the total energy is preserved throughout the well and equal $E$, Eq. (18), along the barrier we have:

$$\left[-{\frac{1}{2}}\Delta+V(x)\right]\psi(x)=\left[{\frac{{\cal{K}}^{2}}{2}}+V_{0}\right]\psi(x)=E\psi(x).$$

(20)

Accordingly, for $E\geq V_{0}$, we have

$${\cal{K}}=\sqrt{2V_{0}-k^{2}}=\sqrt{2(V_{0}-E)}.$$

(21)

The connection formulas at the barrier boundaries, may be conveniently expressed as continuity conditions for logartithmic derivatives. For example at $x=(\pi-a)/2$ we require:

$$\nabla\ln\psi_{well}([\pi\mp a]/2)=\nabla\ln\psi_{barrier}([\pi\mp a]/2),$$

(22)

which results in the transcendental equations (for even states):

$$k\cot[k(\pi-a)/2]=-\sqrt{2V_{0}-k^{2}}\tanh[(a/2)\sqrt{2V_{0}-k^{2}}].$$

(23)

We point out, that the regime of $V_{0}\leq E$ may be achieved a formal substitution ${\cal{K}}\rightarrow i{\cal{K}}$, where $i$ is an imaginary unit. This would transform $\cosh({\cal{K}}(x-\pi/2)$ into $\cos({\cal{K}}(x-\pi/2)$, in parallel with the replacement of $V_{0}-E\geq 0$ by $E-V_{0}\geq 0$ in Eq. (21).

The transition point between two spectral regimes $E\leq V_{0}$ and $V_{0}\leq E$ follows from the demand:

$$2V_{0}-k^{2}=0\Longrightarrow k\cot[k(\pi-a)/2]=0$$

(24)

which implies $k=\sqrt{2V_{0}}$ and $E=k^{2}/2=V_{0}$.

The condition (24) sets a relationship between $a$ and $V_{0}$, showing for which pairs ${a,V_{0}}$, the spectral (non-negative) ground state eigenvalue $E=V_{0}$ is admissible. We have:

$$a=a(V_{0})=\pi\left(1-{\frac{1}{\sqrt{2V_{0}}}}\right)$$

(25)

or, equivalently:

$$V_{0}=V_{0}(a)={\frac{\pi^{2}}{2(\pi-a)^{2}}}$$

(26)

which we depict in Fig. 8.

We note that the condition (22) requires ${\cal{K}}=0$, and in agreement with Eq. (19) identifies $\psi_{barrier}(x)=\beta$ to be constant along the barrier ”plateau”. Given $a$, we have in hands the corresponding barrier height $V_{0}=V_{0}(a)$, Eq. (26). Since $k=\sqrt{2V_{0}}$, we have also in hands an explicit functional form for the left and right well eigenfunction ”tails” $\psi_{L}(x)$ and $\psi_{R}(x)$, c.f. Eqs. (16), (17). We point out the validity of the Dirichlet boundary conditions at $0$ and $\pi$. Moreover, the continuity conditions (22) for logarithmic derivatives at the barrier endpoints, do not need nor necessarily imply the Neumann condition (e.g. the vanishing of derivatives at these points).

Coming back to the comparative (higher order well versus rectangular well) ”eigenvalue zero” issue, let us notice that plugging ${\cal{K}}=0$ in Eq. (20), we need to ”renormalize” the energy scale by subtracting $V_{0}$:

$$\left\{-{\frac{1}{2}}\Delta+[V(x)-V_{0}]\right\}\psi(x)=0.$$

(27)

to pass to the ”eigen-energy zero” regime of the rectangular well problem. This is properly reflected in Figs. 6 to 8. We note, that to maintain the link with the potential (3) for all $m$, we need to allow $V_{0}$ to escape to $\infty$, with $m\to\infty$. This may be considered as a motivaton for invoking the phrase ”additive energy renormalization”, in connection with the $V_{0}$ - subtraction in Eq. (27).

Remark: Let us mention that the zero energy association with the unstable equilibrium of the potential profile, has been discussed for standard quartic double well. A transition value of the well steering parameter has been identified, turbiner ; turbiner1 ; jph , as a sharp divide point between two spectral regimes: nonnegative and that comprising a finite number of negative eigenvalues (near the local minima standard WKB methods give reliable spectral outcomes for the ”normal” double-well system, blinder ; lopez ; jelic ).

Since some of the defining parameters in the rectangular double-well and in the higher order (superharmonic) double-well differ, we need to analyze means of the removal of this obstacle in our subsequent analysis.

First we shall comparatively address the width/height balance of the barrier in the rectangular case, with its analog (approximate width and the elevation of the ”plateau” above the potential minima, c.f. Fig. 7) in the higher order case. To this end, we need to resolve the $[0,\pi]$ of Fig. 8, versus $[-1,1]$ of Figs. 6 and 7, interval size discrepancy.

We note that it is $U(x)=(x/L)^{m}$, which in the large $m$ regime gives rise to the well with the support on the interval $[-L,L]$ of length $2L$. Setting $L=1$ we recover $[-1,1]$, while $L=\pi/2$ gives rise to $[-\pi/2,\pi/2]$.

These support intervals are examples of centered boxes with the center location $x_{c}=0$. An arbitrarily relocated (shifted) box of length $2L$, if centered around any $x_{c}\in R$ has a support $[x_{c}-L,x_{c}+L]$. Hence, choosing $x_{c}=L$, we pass to the supporting interval $[0,2L]$, which upon the adjustment $L=1\rightarrow L=\pi/2$ leads to the required $[0,\pi]$.

The rectangular well width-height/depth, $a$-$V_{0}$ balance, as depicted in Figs. 7 and 8, is to be compared with the corresponding data of the superharmonic double-well system (1)-(3). To this end, we must recompute the potential (3) minima (their bottom is set at $-V_{0}$ in Figs. 6 to 8), identify the location of $x_{0}$, and next evaluate $4\triangle$, to get the width identifier $a=\pi-4\triangle$. The computation must be accomplished by rescaling everywhere the variable $x$ to the form $x/L$, where $L=\pi/2$. The outcome is presented in the comparative Fig. 9.

To analyze spectral affinities between ${\hat{H}}$ of Eqs. (10-(3) and the rectangular double well Hamiltonian (c.f. Eq. (27)), additional precautions need to be observed. The original numerical evaluation of up to eight eigenvalues and eigenfunctions involves what we have identified as $\hat{H}_{rect}=-{\frac{1}{2}}\Delta+V(x)$, with the detailed definition of the rectangular double-well potential given in Section III.B.

To compare these results with the $[-1,1]$, $D=1$ setting of $\hat{H}$, as visualized in Figs. (6) and (7), all numerically obtained data (we have employed Mathematica 12 routines, blinder ) must ultimately be converted from the original $[0,\pi]$, $D=1/2$ framework to the superharmonic one.

We show how our procedure works, by means of the exemplary data set in Table I. We emphasize that the spectral solution is sought for $\hat{H}_{well}$, and from the outset we are interested in the nonnegative spectrum, including the bottom eigenvalue $E=V_{0}$, or a close neraby candidate value (this computation is quite sensitive to a proper choice of $a$ and $V_{0}$, and basically much more than first four decimal digits are needed to get the exact result (this is untenable within Mathematica routines, hence some flexibility must be admitted).

Once a spectral solution of $\hat{H}_{rect}$ is numerically retrieved, we must compensate the extra factor $D=1/2$ preceding the Laplacian, by considering $2\hat{H}_{rect}$. This amounts to the doubling of all computed eigenvalues.

To enable a comparison with the superharmonic case, we need one more correction, actually a conversion of obtained spectral data to the $[-1,1]$ regime. This may be accomplished by means of a factor $\pi^{2}/4$. In view of the energy doubling, mentioned before, an overall conversion factor reads $2\times(\pi^{2}/4)=\pi^{2}/2$.

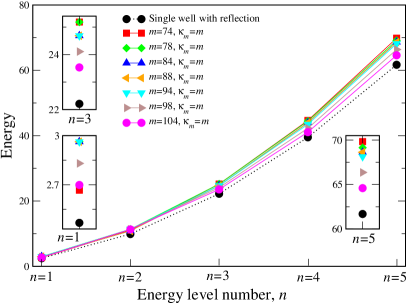
In below, in Table II we reproduce five lowest positive eigenvalues $E_{n}(m),i=1,2,3,4,5$ of the ”renormalized” rectangular double well energy operators

$$\hat{H}_{ren}=-\Delta+2[V(x)-V_{0}],$$

(28)

while set on [-1,1], provided $V(x)$ is the best approximate fit to $m=74,78,84,88,94$ superharmonic potential ${\cal{V}}(x)$, $\kappa_{m}=m^{2}$. These numerical outcomes are set in comparison with positive eigenvalues of the Neumann operator $-\Delta_{\cal{N}}$ on $[-1,1]$, $E_{n}=(\pi^{2}/4)n^{2}$.

We point out that $E_{n}(m)$ outcomes of Mathematica 12 routines, blinder , for the rectangular double-well, Table II, originally refer to the interval $[0,\pi]$, the diffusion coefficient $D=1/2$ and the barrier height $V_{0}(m)$. The reproduced data follow from the $(\pi^{2}/2)[E_{n}(m)-V_{0}(m)]$ conversion recipe, where the data-converting coefficient $\pi^{2}/2$ adjusts the original rectangular well data to the $[-1,1]$, $D=1$ setting. See e.g. a complementary Fig. 11.

Remark 1: Since we have invoked the standard Neumann well notion, let us briefly comment on this, jph , linetsky -pilipenko . We use the term Neumann Laplacian for the standard Laplacian, while restricted to the interval on $R$ and subject to reflecting (e.g. Neumann) boundary conditions. In this case, any solution of the diffusion equation

$$\partial_{t}\Psi(x,t)=\Delta_{\cal{N}}\Psi(x,t)$$

(29)

while restricted to $[-L,L]\subset R$, $L>0$ of length $2L$, needs to respect the boundary data

$$(\partial_{x}\Psi)(-L,t)=0=(\partial_{x}\Psi)(+L,t)$$

(30)

for all $t\geq 0$. The solution of the Neumann spectral problem $-\Delta_{\cal{N}}\psi(x)=E\psi(x)$ comprises eigenfunctions $\{1/\sqrt{2L},(1/\sqrt{L})\,\cos[(n\pi/2L)(x+L);\,n=1,2,3,...\}$ and eigenvalues $\{E_{0}=0,E_{1}=(\pi/2L)^{2},...,E_{n}=n^{2}E_{1};\,n=1,2,3,...\}$. The choice of $L=1$ maps the problem to the interval $[-1,1]$.

Remark 2: One should realize that more familiar Dirichlet spectral problem $-\Delta_{\cal{D}}\psi(x)=E\psi(x)$, in the interval $[-L,L]$, typically involves the boundary conditions $\psi(-L)=0=\psi(L)$. As a consequence the spectrum is strictly positive, with $\{E_{n}=n^{2}(\pi/2L)^{2};\,n=1,2,...\}$, while the eigenfunctions have the form $(1/\sqrt{L})\,\{\sin[(n\pi/2L)(x+L)];\,n=1,2,3,...\}$.

We take advantage of the existence of the dedicated Mathematica routine, blinder , which has been tailored to yield an ”exact solution for rectangular double-well potential”. Actually, up to eight lowest eigenvalues and eigenfunctions of the operator $\hat{H}_{rect}=-{\frac{1}{2}}\Delta+V(x)$ , can be numerically retrieved, with a moderate accuracy, whose efficiency testing is possible due to (i) fine-tuning options of the barrier width-height balance, and (ii) the presumed validity of Eqs. (25) and (26).