Superfluid vacuum theory and deformed dispersion relations

One can describe quantum liquid by a condensate wavefunction $\Psi$ obeying a nonlinear wave equation, which can be chosen to have a minimal $U(1)$-symmetric form: $i\partial_{t}\Psi=\left[-\frac{\hbar}{2m}\nabla^{2}+V_{\text{ext}}(\textbf{x},t)-F(|\Psi|^{2})\right]\Psi$, where $m$ is the mass of a constituent particle, $F(\rho)$ is a differentiable function on a positive semi-axis $\rho$, and $V_{\text{ext}}(\textbf{x},t)$ is an external potential representing a trapping potential or container (we shall neglect it in what follows). The condensate wavefunction must be normalized: $\int_{\cal V}|\Psi|^{2}d{\cal V}=\int_{\cal V}\rho\,d{\cal V}={\cal M}>0$, where ${\cal M}$ and ${\cal V}$ are the total mass and volume of the liquid.

SVT assumes that physical vacuum is described by a similar equation, while photon-like excitations are analogous to acoustic waves in superfluid which propagate with the velocity $c_{s}\propto\sqrt{p^{\prime}(\rho)}$, where prime denotes a derivative. The correspondence principle requires that in low-momenta limit, SVT must recover Einstein’s theory of relativity. One of postulates of the latter implies that the speed of photon-like excitations of vacuum should not depend on density, at least in a leading order with respect to $\hbar$. At low momenta, $c_{s}$ tends to $c_{0}\approx c$, where $c=2.9979\times 10^{10}$ $\text{cm}\,\text{s}^{-1}$ is historically called the speed of light in vacuum. As shown in Ref. z11appb, , this results in the following equation $\rho|F^{\prime}(\rho)|=mc_{s}^{2}/\hbar\approx\text{const}(\rho)$, where $\text{const}(\rho)$ is a function which does not dependent on density. The solution of this differential equation is a logarithmic function: $F(\rho)=b\ln{(\rho/\bar{\rho})}$, where $b$ and $\bar{\rho}$ are real parameters. The wave equation thus becomes

This introduces a model with logarithmic nonlinearity as a further development and generalization of the non-perturbative theory of quantum gravity with non-exact Lorentz symmetry. It tremendously facilitates analytical studies that the ground state solution for positive values of $b$ was known, though for purposes other than ours, since the works of Rosen and Bialynicki-Birula and Mycielski.ros68 ; bb76 In Cartesian coordinates, it is a Gaussian wave packet modulated by the de Broglie plane wave; in a rotationally symmetric 3D case, it is a Gaussian function of a radius-vector.

A theory of superfluid vacuum can be formulated in different ways. The first way is to treat vacuum effects as a small perturbation of a Lorentz-covariant theory.z10gc ; z11pla The second, more recent, approach is to consider particle-like excitations within the framework of a post-relativistic superfluid vacuum theory where spacetime is an induced phenomenon, as discussed above. Correspondingly, dispersion relations turn out to be different in each approach. For the former approach, the relations were derived in Sec. 4 of Ref. z10gc, , therefore, we do not consider them here; we just mention that their energy has a non-polynomial dependence on momentum. This alerts us that a perturbative series cannot provide a full description of vacuum, therefore the latter requires non-perturbative treatment.

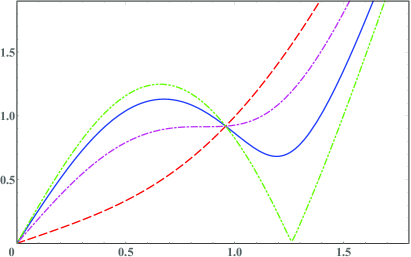
The dispersion relations for the second approach can be introduced by analogy with conventional superfluids. In superfluid ⁴He, energy as a function of momentum has a distinct shape, usually dubbed the Landau “roton” form. As the excitation’s momentum increases, this energy grows from zero, until it reaches a local maximum (called the maxon peak), which is crucial for suppressing dissipative fluctuations.z12eb Then it dives down to a local minimum (called the “roton” minimum, for historical reasons), and eventually it starts growing again, all the way to a border of a theory’s applicability domain, akin to a solid curve in Fig. 1a. In the regime of small momenta, the dispersion relation is approximately linear with respect to momentum, which is a behaviour typical for relativistic particles.

We thus assume that the physical vacuum has a similar energy spectrum of excitations - with its own values of parameters of course. It also means that one can use the relativistic approach (with perhaps some tweaking by adding additional fields) for a large range of energies - until momentum reaches a value corresponding to the maxon peak, which can be rather large, up to a Planck scale. These intermediate models can still provide valuable understanding about various fundamental phenomena, such as the mass generation mechanism and non-zero extent of particles.z11appb ; az11 ; dz11 ; dmz15 However, conceptually new physics steps in near and above the maxon threshold; vacuum Cherenkov radiation and luminal boom being examples thereof.z11pla

An analytical example of a dispersion relation, which has a Landau form and correct proportions for local extrema, is given by the formula:

where $D_{+}(k)$ is a Dawson function, $\aleph=\sqrt{\pi}/2+1/(\text{e}\,\text{erf}(1))\approx 1.32$, $p_{a}=2\hbar/a$ is de Broglie momentum corresponding to the length scale $a=\hbar/\sqrt{2m|b|}$, and $M_{a}=p_{a}^{2}/2E_{a}\propto m$. Here, $p_{a}$, $E_{a}$ and $M_{a}$ set the momentum, energy and mass scales of the theory, whereas the parameter $\eta$ controls local extrema of the dispersion curve: one can check that $E_{p}$ acquires the Landau form, cf. a solid curve in Fig. 1a, only if $11.43<\eta<25.98$.

Furthermore, Fig. 1b displays the excitations’ velocity $c_{p}\equiv\sqrt{dE_{p}/dp}$ divided by its low-momentum value $c_{0}=\lim\limits_{p\to 0}c_{p}$. As in Fig. 1a, it is the solid curve which is of interest to us. One can see that at small momenta, its behaviour follows the relativistic pattern, but becomes a rather nontrivial as $p$ grows. Initially it decreases with increasing $p$, which corresponds to a photon’s slow-down and thus it can be interpreted as a photon acquiring the effective mass $\mu$ – when expanded in Taylor series at small $p$, Eq. (2) expectantly yields a deformed-relativistic dispersion:

where $c_{0}=(p_{a}/2M_{a})\sqrt{\eta\,(1-\aleph/2)}$, $A_{4}=(p_{a}/c_{0})^{2}(\aleph-8/3+2/\eta)/(2-\aleph)$, $A_{6}=(p_{a}/c_{0})^{2}(8/5-\aleph/2)/(2-\aleph)$, and ${\cal O}[k^{n}]$ denotes terms of order $k^{n}$ and above.

Note that this effective mass generation mechanism is different from the gap mechanism in conventional quantum condensed matter such as superconductors: it is a post-relativistic effect and it happens before one reaches any of the local extrema. Since $c_{0}\approx c$, the following experimental constraint applies to our parameters: $aM_{a}/\sqrt{\eta}=(\hbar/c_{0})\sqrt{1-\aleph/2}\approx 2.04\times 10^{-38}\,\text{g}\,\text{cm}$, whereas $A_{6}$ does not explicitly depend on $\eta$.

A series (3) converges only at $p<p_{a}$: in the vicinity of local extrema $p\sim p_{a}$, not to mention at $p\to\infty$, a formula changes drastically, which reaffirms necessity of non-perturbative treatment. As momentum grows, energy reaches first the maxon peak which marks the beginning of a region in which $c_{p}^{2}$ becomes negative thus indicating absence of any classical propagation. Starting from that region, classical 4D spacetime is no longer a robust description, and the definition of a particle can no longer be based on irreducible representations of a Poincarè group. This region extends until object’s momentum approaches a value corresponding to the “roton” minimum, after which the maximum attainable velocity can eventually go above $c_{0}$. This is where the luminal boom occurs, which is the vacuum analogue of sonic boom in air.z11pla Beyond that value, breakdown of the quantum liquid occurs: a moving object or observer no longer experiences vacuum condensate nor induced spacetime.