Superconductivity on ScH3 and YH3 hydrides: Effects of applied pressure in combination with electron- and hole-doping on the electron-phonon coupling properties
Abstract
The implementation of electron- and hole-doping, in conjunction to applied pressure, is analyzed as a mechanism to induce or enhance the superconducting state on fcc YH3 and ScH3. In particular, the evolution of their structural, electronic, and lattice dynamical properties, as well as the electron-phonon coupling and superconducting critical temperature () is presented and discussed, as a function of the electron- and hole-doping content as well as applied pressure. The study was performed within the density functional perturbation theory, taking into account the effects of zero-point energy through the quasi-harmonic approximation, while the doping was implemented by means of the construction of the Sc1-xMxH3 (M=Ca,Ti) and Y1-xMxH3 (M=Sr,Zr) solid solutions modeled with the virtual crystal approximation (VCA). We found that the ScH3 and YH3 hydrides shown a significant improvement of their electron-phonon coupling properties under hole-doping (M=Ca,Sr) and at pressure values close to dynamical instabilities. Instead, by electron-doping (M=Ti,Zr), the systems do not improve such properties, whatever value of applied pressure is considered. Then, as a result, rapidly increases as a function of on the hole-doping region, reaching its maximum value of K and K at for Sc1-xCaxH3 at GPa and Y1-xSrxH3 at GPa respectively, with , while for both, electron- and hole-doping, decreases as a function of the applied pressure, mainly due to phonon hardening. By the thorough analysis of the electron-phonon properties as a function of doping and pressure, we can conclude that the tuning of the lattice dynamics is a promising path for improving the superconductivity on both systems.
pacs:
33.15.TaI Introduction
Materials with a high-superconducting critical temperature () are of great interest since at ambient conditions could have many technological applications. The theoretical breakthrough and progress for reaching high- superconductivity came after the Ashcroft[1] pioneering idea, suggesting that hydrogen-rich materials could be promising candidates for high- superconductivity. After that, several theoretical predictions have been proposed and performed on the crystal structure, at high pressure, of stoichiometric and hydrogen-rich materials, for which their electronic structure, lattice dynamics, and electron-phonon (el-ph) coupling properties have been calculated[2, 3, 4, 5]. As a result of those predictions, several metal hydrides were proposed as conventional-superconductor candidates with a near room-temperature[6, 7, 8]. The experimental breakthrough came with the discovery of phonon-mediated superconductivity on H3S, with a of K under pressures as high as GPa[9, 10]. Some years latter, high- superconductivity measurements were reported in other compounds, all of them at high applied pressure values, like LaH10 with in the range of - K[11, 12] at GPa, and more recently, YH9 with K at GPa[13] and YH6 giving K at GPa[14], as well as a top reported value of K in a carbonaceous sulfur-hydride at GPa[15].
As a result of the available theoretical and experimental reports, it has been determined that the tendency for superconductivity depends upon the species used to build up the metal hydride (together with hydrogen), a high density of states at the Fermi level, and that the resulting hydride compound must have a large electron-phonon coupling related to the hydrogen atoms. In particular, some of the highest values have being obtained from hydrides constructed with elements that belong to the alkaline family as well as the scandium group (first group of the transition metals) [5]. Regarding this group, from calculations on YHn, the was estimated around - K at an applied pressure of GPa for [7, 5]; while for , was on the range of - K at GPa[5]; and for , lower values (around - K) at GPa were reported [16]. For this family, only the YH9 and YH6 have been studied experimentally, as already mentioned. For the ScHn family, in the range of - K was predicted for different members, with and , for an applied pressure above GPa[17, 5]. All the already mentioned metal hydrides can be considered as chemically precompressed phases relative to pure hydrogen, where high pressure is necessary for metallization[1].
With respect to ScH3 and YH3 (metal-hydrides with low hydrogen content), they have hcp structures at ambient pressure, and are driven to fcc (cubic NaCl (B1) structure) (see Fig.1) phase under applied pressure. For YH3, Raman [18] and infrared [19] studies found that the cubic structure can exist at approximately GPa, and is clearly stabilized around GPa. It has been suggested that another intermediate phase [20] or a coexisting hcp-cubic phase [21] could also appear in the – GPa pressure range. It has been shown experimentally that YH3 can be stabilized in the fcc phase at ambient pressure by substituting Y for 10 Li (Li0.1Y0.9H3)[22, 23]. Recently, J. Purans et al.[24] and Kong et al.[14] reported the syntheses of this metal-hydride with a pure metallic fcc phase at a broad pressure interval, GPa. For lower applied pressure values, between and GPa, they found it to be a semi-metal with a distorted fcc crystal structure. Similarly, for ScH3, Raman and infrared[25] studies observed an hcp-intermediate-cubic phase at GPa. Theoretically, Kong et al.[26] reported the hcp-cubic phase transition at GPa, while Pakornchote et al.[27] found the cubic phase to be energetically more stable at slightly lower pressure of GPa. For these metal-hydrides, YH3 and ScH3, Kim et al.[28, 5] performed first principles calculations and found that the fcc structure is dynamically stable on both of them at a pressure of GPa, with an estimated around and K, respectively, with a rapid decreased of as the pressure is incremented, in agreement with the experimental report of Kong et al.[14] where superconductivity where not found above K for metallic fcc structure.
Besides applied pressure, doping is another mechanism for metallization of metal hydrides, in order to induce or increase superconductivity by the improvement of some properties, like the electronic density of states at the Fermi level () or the el-ph coupling. For example, the substitution of Li by Be, Mg, or Ca in LiH was studied by Zhang et al.[29]. In that work, the dopant acts as a donor which delivers electrons to the system, obtaining a -doped material with a K for an electron content as high as 2.06, calculated at ambient pressure. Another work on that direction was performed by Olea-Amezcua et al.[30]. There the authors showed the metallization of alkali-metal hydrides LiH, NaH, and KH by doping with alkaline-earth metals Be, Mg, and Ca, respectively, and analyzed the superconducting properties as a function of metal content. The maximum estimated values were K for Li0.95Be0.05H, K for Na0.8Mg0.2H, and even K for K0.55Ca0.45H, without applied pressure. More recently, Villa-Cortés et al. [31] studied the structural, electronic, and lattice dynamical properties, as well as the electron-phonon coupling and superconducting critical temperature () of ScH2 and YH2 metal hydrides solid solutions, as a function of the electron- and hole-doping content, in absence of applied pressure. They found that for electron-doping content , increases rapidly, reaching its maximum value of the entire range at the Sc0.05Ti0.95H2 and Y0.2Zr0.8H2 solid solutions. These results show that such scheme to induce metallization and superconductivity on metal-hydrides works as an alternative to the applied-pressure approach. So, in this paper we implement it, in addition to applied pressure, in order to study the ScH3 and YH3 compounds in the fcc structure (NaCl (B1) phase), which is reported to present superconductivity, as discussed previously. Under this approach we are able to trace down the evolution of the structural, electronic, and lattice dynamical properties, as well as the el-ph coupling and , as a function of metal content, by inducing holes (-doped) and electrons (-doped), as well as applied pressure, of the proposed systems. Such approach is done by the construction of solid solutions with the metal atom of the hydride: Sc1-xMxH3 (M=Ca,Ti) and Y1-xMxH3 (=Sr,Zr) within the Density Functional Theory (DFT)[32], using the virtual crystal approximation (VCA)[33], which has been successfully applied on the study of doped superconductors [34, 35, 36, 37, 30].
The paper is organized as follows. The computational details of our method are presented in Section II. In Section III.A we present our results related to the structural properties; while in Section III.B the electronic structure analysis is shown. The lattice dynamics are discussed in Section III.C; and the electron-phonon and superconducting properties, as well as , are shown in Section III.D. Last, our conclusions are presented in Section IV.
II Computational details
The calculations of the structural, electronic, lattice dynamics and el-ph coupling properties were carried out within the framework of Density Functional Theory (DFT)[32] and Density Functional Perturbation Theory (DFPT) [38, 39], both implemented in the QUANTUM ESPRESSO suit code [38]. The calculations were performed with a -point mesh, and a Ry cutoff for the plane-wave basis, while the Perdew-Burke-Ernzerhof (PBE) functional [40] was employed to take into account the exchange and correlation contributions.
Fourier interpolation of dynamical matrices, calculated on a -point mesh, were used to determine the complete phonon spectra of the studied systems. Corrections due to quantum fluctuations at zero temperature, zero-point energy (ZPE) effects, are estimated through the quasi-harmonic approximation (QHA)[41, 30]. Within this approximation, the phonon contribution to the ground-state energy is taken into account and then a equation of state for each concentration can be constructed. Thus, the electronic structure, lattice dynamics, and el-ph properties, calculated for the fcc (B1) crystal structure at different applied pressure values, incorporate the ZPE correction.
Included on the el-ph calculations, the phonon linewidths of the phonon mode were also obtained, which are given by[42, 43]
| (1) |
where are the matrix elements of the electron-phonon interaction (calculated over a denser -point mesh), and are one-electron band energies, with band index , and vectors , respectively, while is the phonon frequency for mode at wave-vector .
With the knowledge of and , the isotropic Eliashberg spectral function, , can be described as
| (2) |
where is the electronic density of states (per atom and spin) at , and a sum over a denser Fourier interpolated -point mesh of was required. In addition, the average electron-phonon coupling constant , which quantifies the coupling strength as well as the Allen-Dynes characteristic phonon frequency [44], are related to the Eliashberg function as
| (3) |
| (4) |
Regarding , it was estimated for each case by solving numerically the isotropic Migdal-Eliashberg gap equations[45, 46, 47], using the respective for each content at its specific applied pressure value, and treating the Coulomb pseudopotential as an adjusted parameter.
Furthermore, we used the formalism of Rainer and Culleto for the calculation of the differential isotope effect coefficient [48, 49], , to gain more insight into the coupling and how a specific phonon-frequency interval contributes to . is defined as
| (5) |
where is given by
| (6) |
and the functional derivative respect to the Eliashberg function is expressed as [46, 47, 50, 49]
| (7) |
with corresponding to the breaking parameter that becomes zero at . Finally, the isotope effect coefficient, , in a specific frequency interval is given by
| (8) |
III Results and discussion
III.1 Structural properties
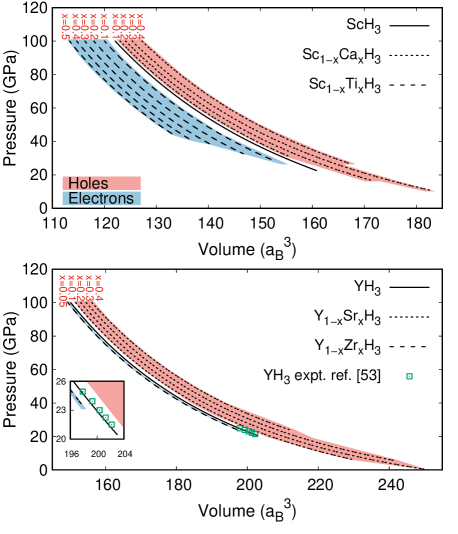
We performed structural optimizations of the fcc (cubic NaCl (B1)) structure ( space group) with a primitive cell of four atoms (one metal and three hydrogen) for the two Sc1-xMxH3 (M=Ca, Ti) and Y1-xMxH3 (M=Sr, Zr) solid solutions at different values of metal M content . For both systems, the equations of state were constructed from the minimum pressure, at which each system becomes stable at the cubic structure, to 100 GPa as maximum pressure value.
For Sc1-xMxH3, the equation of state was determined for concentrations up to of electron(hole) doping, while for Y1-xMxH3, the range was for concentrations up to of electron(hole) doping. Electron- and hole-doping thresholds and the minimum pressures where the systems are stable were determined through dynamical instabilities, observed as imaginary frequencies in the phonon dispersion for larger contents and smaller pressure values. Phonon instabilities in metal hydrides induced by alloying have been reported previously in literature [51, 52, 30], where such dynamical behavior have been related to an increase of the heat of formation, meaning that the solid solutions become less stable.
In Fig. 2, we show the evolution of the equation of state of each metal content . For both systems, Sc1-xMxH3 and Y1-xMxH3, increasing the electron content leads to a monotonous reduction of the volume, at a given pressure, as well as an increment in the minimum stable pressure value. For hole doping, the volume tendency is opposite, while the minimum stable pressure values are not following any specific trend. This behavior indicates a strengthening of the chemical bonding as the electron-content is increased, given by the increment of Zr- and Ti-content, suggesting a hardening of phonon frequencies. Similarly, as the hole-content grows, by the increase of Sr- and Ca-content, the chemical bonding gets weaker, implying a softening of the phonon frequencies. A complete set of structural parameters, that is, the equilibrium volume (), bulk modulus (), and its pressure derivative () are given in Tab. 1 (Appendix A), for both systems, of all M content () values studied. It is worth noting that our YH3 results are in excellent agreement with the experimental data reported by Machida et al.[53].
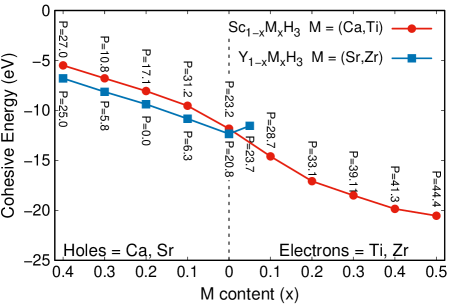
In Fig.3 we show the calculated cohesive energy () of the two systems, within their respective electron and hole stability-range at their corresponding minimum pressure threshold. This quantity is used to characterize the stability of alloys and solid solutions, and is given by the following:
| (9) |
where is the total energy of the N1-xMxH3 solid solution at content , while , , and are the calculated total energies of the isolated atoms N = Y, Sc; M = Sr, Zr, Ca, Ti; and hydrogen, respectively. In general, for the two solid solutions, the hole-doped systems are less stable than their corresponding pristine systems () (the larger the absolute value, the more stable the system is), nevertheless, they are still in the stability range (negative ). For the case of electron-doped regime, while Y1-xZrxH3 follows the same observed tendency than the hole-doped systems, we found that Sc1-xTixH3 is more stable than the pristine one, indicating the possibility to synthesize experimentally such solid solutions.
With the optimized lattice parameters and the corresponding equation of state for each system, at different content for their electron- and hole-doping regions, we proceeded to calculate their electronic and lattice dynamical properties for different applied pressure values at each . Furthermore, we are presenting results obtained by the ZPE scheme. While the ZPE effects on the electronic properties are hardly visible, comparing with the static scheme, on the lattice dynamical ones, there is a noticeable softening as a general effect. This tendency comes mainly from the unit cell expansion as the ZPE contribution to the energy is taken into account.
III.2 Electronic properties

The evolution of the electronic band structure and the density of states at the Fermi level, , is analyzed in order to evaluate the effects of electron- and hole-content and pressure on the electronic properties of the solid-solutions.
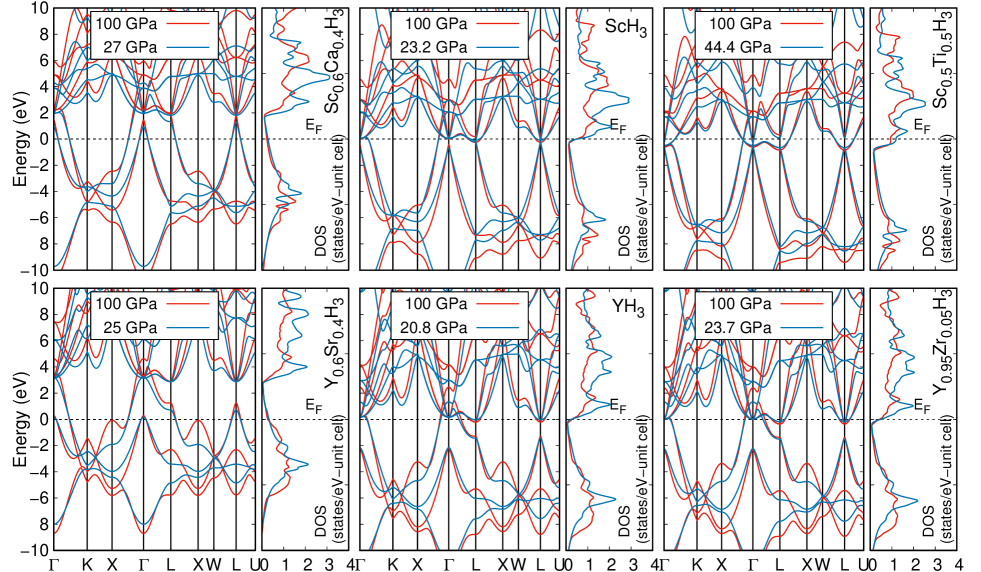
In Fig. 4 we show the band structure for Sc1-xMxH3 and Y1-xMxH3 of the pristine system and of their corresponding threshold electron- (Ti, Zr) and hole- (Ca, Sr) doping content, each of them at the minimum pressure (where the system is dynamically stable) and the maximum pressure considered ( GPa).
It can be seen that the main pressure effect on the band structure, independent of the electron- or hole-content, is a slight increase of the bandwidth. That is, the low-energy bands are push to even lower energy, and the high-energy ones to higher values, while keeping almost unaffected the bands around the Fermi level (). The band structure of the pristine ScH3 shows a threefold degenerate state on the L-point (giving place to one hole-like and two electron-like bands) and a twofold degenerate state on the -point (electron-like bands), both located at . In comparison, the pristine YH3 compound shows a twofold state on the L-point, also at the Fermi level, while the twofold state on the -point is located just above . As the electron content is increased for ScH3 (by Ti), the degeneracy at the L-point breaks, giving place to a new twofold state that continue to move far away from , rising as an electron-like band and a hole-like band. Instead, at -point the twofold state is intact, moving as a whole to lower energy values, indicating that electronic topological transitions (ETT) take place. In the case of electron-doping for YH3 (by Zr), the degenerate states at L- and -points are maintained, while they undergo a minor shift to lower energies. Regarding the hole-content increase on both systems, SH3 by Ca and YH3 by Sr, its essential effect is the shift of the band structure to higher energies, without noticeable changes on the degenerate states discussed before.
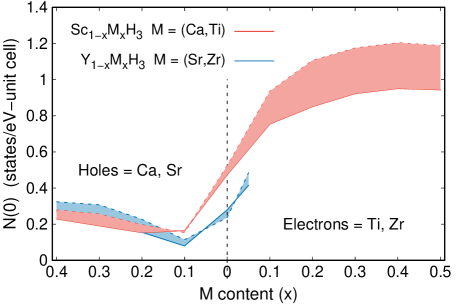
Analyzing the evolution of , as a function of M content () for the minimum and maximum pressure values of both systems, Sc1-xMxH3 and Y1-xMxH3 (see Fig. 5), it can be observed that, in general, reduces at on the hole-doping regime, and in a more drastic way for the ScH3 case. As the hole-content increases, starts to rise slowly, getting close to its value at for the YH3 system. For the electron doping regime, while YH3 undergoes a minor increase, mainly by the threshold limit on the Zr-content, of ScH3 grows rapidly, doubling its pristine value at . As increases even more, the grow ratio slows considerably, tending to saturate. As the applied pressure raises, shows an small reduction, which is due to the expand of the bandwidth discussed previously.
III.3 Lattice dynamics
The phonon dispersion is presented on Fig. 6, including their respective phonon linewidth and the phonon density of states (PHDOS), for Sc1-xMxH3 and Y1-xMxH3 at the pristine () and the threshold electron- (Ti,Zr) and hole- (Ca,Sr) contents. In general, for both systems, the optical branches soften slightly as the hole-content increases, while they are shifted to higher frequencies as the electron-content rises. In particular for the high-frequency optical branches, while they shift almost on a rigid way above the frequencies of the pristine systems for the electron-doping case, on the hole-doping solid-solutions they show, in addition to the softening, a small renormalization in the and optical branches at . While the mid-frequency region shows subtle renormalizations at - and L-point for electron-content regime, they are stronger for the same high-symmetry points, in addition to the X-point, for hole-content systems. Regarding the acoustic branches, they remain almost unchanged for electron-doping, whereas for hole-doping they lightly harden. Interestingly, the phonon linewidths (vertical lines along the phonon branches), mainly localized around at the and optical phonon branches for , remain almost unchanged for the hole-doping regime in both alloys, while for the electron-doping regime it slightly reduces in Sc1-xMxH3, and increases in Y1-xMxH3. In general, for both solid solid-solutions, independent of doping-scheme, the observed effect of applied pressure is a rigid hardening of the phonon frequencies and a lifting of phonon anomalies, that leans to instabilities at K and X-point, for the acoustic branches.
III.4 Electron-phonon and superconducting properties
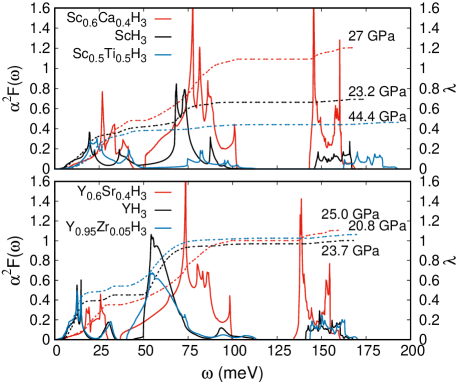
With the electronic and the lattice dynamics information, the electron-phonon spectral functions were calculated for the entire range of hole- and electron-content stable regimes in a broad pressure range. The for the threshold electron- and hole-content, as well as the pristine cases, at the minimum pressure where the systems are dynamically stable, can be seen in Fig. 7. As the electron(hole)-content increases on both systems, the high-frequency optical region of the Eliashberg function shifts to higher(lower) frequencies, while the mid-range frequency region shows an opposite behavior, and the acoustical one practically does not shift. For both systems, the weight of the spectral function is incremented as the doping goes from the electron- to the hole-content thresholds, passing through the pristine one (). Regarding the pressure effects, in general, for all different content cases (electron- and hole-doping), at both solid-solutions, the spectra shift to a higher frequency region as the pressure arises, going from the minimum dynamically stable value up to 100 GPa.
As the Eliashberg spectral function determines the electron-phonon coupling parameter (see Eq. 3), the observed shift due to both, doping and applied pressure, has an impact on as well. The evolution of the electron-phonon coupling constant as a function of frequency, , is shown in Fig.7. For the pristine () and the electron-doped Sc1-xTixH3 solid solution, it can be observed that the main contribution to comes from the acoustic region. However, for the hole-doped Sc1-xCaxH3, the main contribution comes from the mid-range frequency optical phonons. The behavior of for the Y1-xMxH3 solid solution is slightly different. In this case, both regions, the acoustic and the mid-range frequency optical ones, contribute almost at the same rate to . It is worth noting that, for both solid-solutions, the high-frequency optical phonons have marginal contribution to .
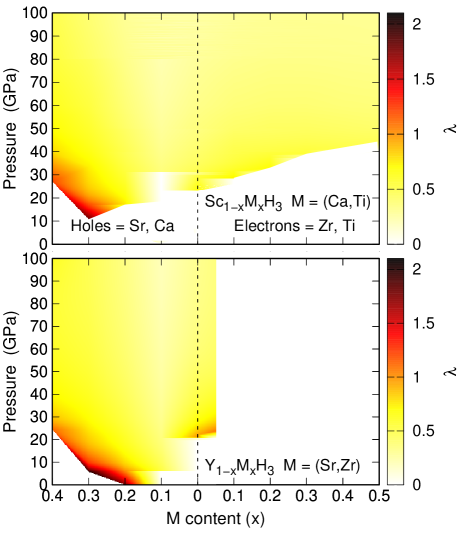
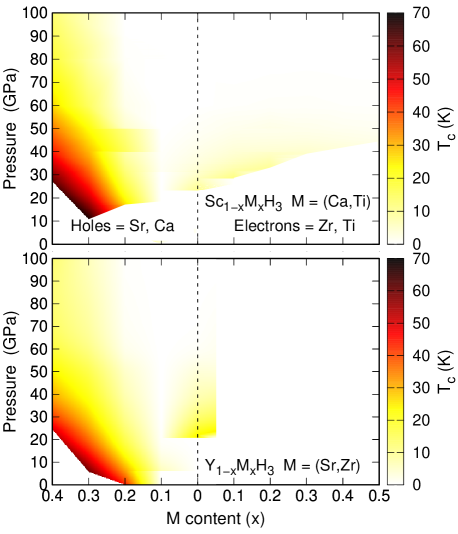
In order to analyze the behavior of as a function of pressure and electron- or hole-content for the solid-solutions, we present it as a color-map plot in Fig. 8. In general, it can be observed that for most of the scanned pressure values, on both doping schemes (electron and hole) hardly goes beyond , regardless of the solid-solution. It is worth to mention that higher values are obtained for pressure close to dynamical instabilities at each electron- or hole-threshold content. Interestingly, only for very specific combination of pressure and hole-content it is possible to reach higher values, like for Sc0.7Ca0.3H3 at GPa, and for Y0.7Sr0.3H3 at GPa. In particular for the latter solid-solution, the region of pressure and hole-content that could provide values close to is spread between and , and around to GPa on applied pressure.
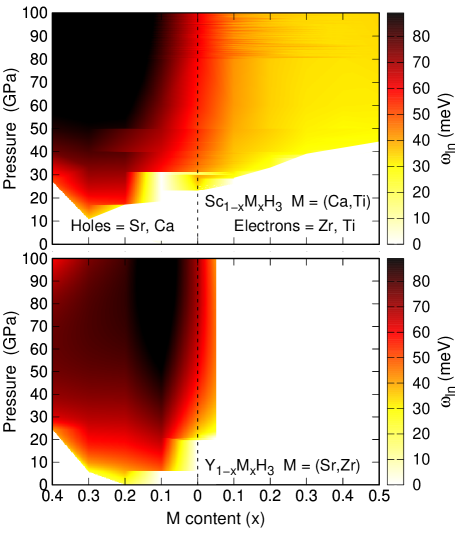
In a similar fashion as , the evolution of the Allen-Dynes characteristic phonon frequency, , as a function of pressure and electron- and hole-content is shown in Fig. 9. It can be observed a hardening as the pressure increases, specially noticeable for the hole-doping regime and more subtle for the electron-doping one, while the lower values are located at the pressure and hole-content regions where both solid-solutions present their maximum values.
The calculated electron-phonon coupling properties were used to obtain estimates for the superconducting critical temperature, , as a function of applied pressure and content for both solid solutions. The isotropic Migdal-Eliashberg gap equations where solved numerically with two different values of the Coulomb pseudopotential (): (which provides an upper limit for ) and , in order to get an idea of how strong could be affected by the variation. In general, we get the maximum at the minimum pressure values were we found dynamically stable solid solutions for each content () of both regimes, electron- and hole-doping, as can be observed in Fig. 10. Comparing doping regimes, the hole-doping one reports the highest critical temperature, with values of K and K at for Sc1-xCaxH3 and Y1-xSrxH3 respectively, with . These maximum values corresponds to the highest , the lowest , and a comparatively low (related to its corresponding electron-doping values). Such behavior shows that the tuning of the lattice dynamics is the path to enhance superconductivity in both systems. It is worth to mention that Y0.8Sr0.2H3, the only system that is dynamically stable at ambient pressure ( GPa), presents K for .
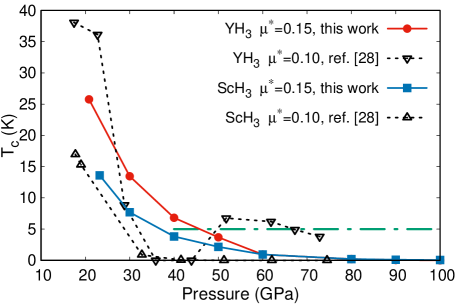
Regarding the pristine systems, we are fully aware that have not been experimental observation of superconductivity for fcc-phase YH3 and SH3 compounds. In particular, Kong et al.[14] reported no superconductivity for temperatures above K for pure-fcc metallic YH3, at pressures values going from GPa up to GPa. Then, in Fig. 11 we show our results for ScH3 and YH3, as a function of applied pressure, and from there it can be seen that for pressure values above GPa, goes below K, and gets even smaller as pressure arises, in good agreement with the experimental reports. Additionally, comparing with previous results calculated by Kim et al.[28], it can be observed that the downward tendency is reproduced on both systems.
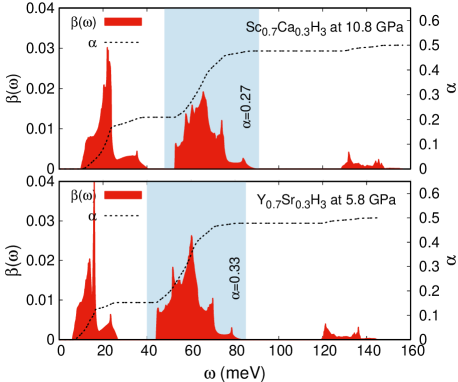
Finally, to get more insight about the contribution of the different phonon-frequency intervals to the superconductivity state, we have calculated the Rainer and Culleto differential isotope effect coefficient, (Eq. 5), and the partial isotope effect (Eq. 8), which give information on how strong can be modified due to an infinitesimal ion-mass change in a specific phonon interval.
In Fig. 12 we present and for both solid-solutions at the pressure and hole-content that presents the highest (): Sc0.7Ca0.3H3 at GPa and Y0.7Sr0.3H3 at GPa. We found to be at the acoustic interval, and for the mid-frequency region (shadow interval) for Sc0.7Ca0.3H3(Y0.7Sr0.3H3), values that contribute to the and , respectively, of the total isotope coefficient , showing the importance of the mid-frequency region to the superconducting state.
In order to get an idea of how these different phonon regions contribute to , we calculated the critical-temperature change, , when a phonon region is suppressed by means of the Bergmann and Rainer formalism[46, 47]:
| (10) |
where . Here, is the total Eliashberg function and is the one with a specific phonon region suppressed. Then, applying it to the same cases as before (the ones with the highest obtained for ) we found to be K for the acoustic region and K for the mid-frequency region for Sc0.7Ca0.3H3(Y0.7Sr0.3H3), representing the later a reduction in of when the mid-frequency region is suppressed in .
IV CONCLUSIONS
We have performed a thorough analysis of the structural, electronic, lattice dynamics, electron-phonon coupling, and superconducting properties of the metal-hydride fcc solid-solutions Sc1-xMxH3 (M=Ca,Ti) and Y1-xMxH3 (M=Sr,Zr), as a function of electron- and hole-doping content , as well as applied pressure. For both systems, while increasing the electron content leads to an increment of the minimum stable pressure in comparison to pristine systems, for hole-doping we found lower minimum stable pressure values for most of content , even finding a particular hole-doping case, Y0.8Sr0.2H3, that was dynamically stable at zero applied pressure. Although is not improved in the whole hole-doping region for both systems, and even decreasing for Sc0.9Ca0.1H3 in comparison with ScH3, at the electron-doping regime shows an important increment at for the Sc-doped hydride, almost twice the corresponding value for the pristine system. As the pressure increases, shows a reduction, which is related to the observed bandwidth expansion in both solid solutions. As for the lattice dynamics, the optical phonons soften in both systems by hole-doping, which is more pronounced for the high-frequency region than the the mid-frequency one, while the acoustic branches lightly harden. Meanwhile, for the electron-doping regime, the optical branches shift to higher values and the acoustic ones remain almost unchanged. In general, for both solid-solutions, independent of doping-scheme, the applied pressure effect is a rigid hardening of the phonon frequencies and a lifting of phonon anomalies at the acoustic branches. Regarding the electron-phonon coupling parameter, , the main contribution comes from the acoustic and mid-range optical phonon branches for both solid solutions, while the high-frequency optical ones have marginal participation. Interestingly, a remarkable improvement of is observed in the hole-doping range and for low applied pressure values, close to dynamical instabilities, while by electron-doping, the systems do not improve such property, whatever value of applied pressure is considered. In particular, the systems can reach values as high as for Sc0.7Ca0.3H3 at GPa, and for Y0.7Sr0.3H3 at GPa, which represent an improvement of and , respectively, in comparison with the highest values at their corresponding pristine systems, under applied pressure. Then, as a consequence, the maximum superconducting critical temperature, at each system, was obtained for those particular conditions of hole-doping and pressure, with values of K and K for ScH3 and YH3 doped systems, respectively, with , while a general reduction of and as the applied pressure rises, independent of electron- or hole-doping content, is mainly coming from the phonon hardening. Finally, by calculating the Rainer and Culleto differential isotope effect coefficient, we found the mid-frequency region as the most crucial phonon zone to the superconducting state. Then, due to all the above, we can conclude that the tuning of the lattice dynamics is a promising path for improving the superconductivity on both systems.
Acknowledgements.
The authors thankfully acknowledge computer resources, technical advise, and support provided by Laboratorio Nacional de Supercómputo del Sureste de México (LNS), a member of the CONACYT national laboratories. One of the authors (S. Villa-Cortés.) also acknowledges the Consejo Nacional de Ciencia y Tecnología (CONACyT, México) by the support under grant 769301.Appendix A Equation of state parameters
In Table 1 we show the equation of state parameters of the third-order Birch-Murnaghan equation[54] for both solid solutions, Sc1-xMxH3 and Y1-xMxH3, in the fcc (NaCl (B1)) structure ( space group) within the ZPE scheme.
| Sc1-xCaxH3 | |||
| () | (GPa) | ||
| 0.1 | 191.10 | 100.72 | 3.66 |
| 0.2 | 197.03 | 92.94 | 3.70 |
| 0.3 | 202.76 | 86.40 | 3.70 |
| 0.4 | 207.74 | 82.47 | 3.74 |
| ScH3 | |||
| () | (GPa) | ||
| 189.06 | 104.49 | 3.64 | |
| Sc1-xTixH3 | |||
| () | (GPa) | ||
| 0.1 | 184.52 | 106.24 | 3.69 |
| 0.2 | 180.43 | 107.47 | 3.73 |
| 0.3 | 174.96 | 116.36 | 3.68 |
| 0.4 | 170.91 | 121.80 | 3.66 |
| 0.5 | 169.66 | 116.31 | 3.77 |
| Y1-xSrxH3 | |||
| () | (GPa) | ||
| 0.1 | 245.38 | 89.43 | 3.77 |
| 0.2 | 251.58 | 79.36 | 3.77 |
| 0.3 | 258.51 | 74.04 | 3.78 |
| 0.4 | 265.01 | 70.43 | 3.77 |
| YH3 | |||
| () | (GPa) | ||
| 240.35 | 88.21 | 3.77 | |
| Y1-xZrxH3 | |||
| () | (GPa) | ||
| 0.05 | 238.20 | 89.10 | 3.79 |
References
- [1] N. W. Ashcroft. Hydrogen dominant metallic alloys: High temperature superconductors? Phys. Rev. Lett., 92:187002, May 2004.
- [2] Lijun Zhang, Yanchao Wang, Jian Lv, and Yanming Ma. Materials discovery at high pressures. Nature Reviews Materials, 2, Feb 2017.
- [3] Defang Duan, Hongyu Yu, Hui Xie, and Tian Cui. Ab initio approach and its impact on superconductivity. Journal of Superconductivity and Novel Magnetism, 32(1):53–60, Jan 2019.
- [4] K. Tanaka, J. S. Tse, and H. Liu. Electron-phonon coupling mechanisms for hydrogen-rich metals at high pressure. Phys. Rev. B, 96:100502, Sep 2017.
- [5] Tiange Bi, Niloofar Zarifi, Tyson Terpstra, and Eva Zurek. The search for superconductivity in high pressure hydrides. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering. Elsevier, 2019.
- [6] Duan Defang, Liu Yunxian, Tian Fubo, Li Da, Huang Xiaoli, Zhao Zhonglong, Yu Hongyu, Liu Bingbing, Tian Wenjing, and Cui Tian. Pressure-induced metallization of dense (h2s)2h2 with high-tc superconductivity. Scientific Reports, 4, Sept 2014.
- [7] Hanyu Liu, Ivan I. Naumov, Roald Hoffmann, N. W. Ashcroft, and Russell J. Hemley. Potential high-tc superconducting lanthanum and yttrium hydrides at high pressure. Proceedings of the National Academy of Sciences, 114(27):6990–6995, 2017.
- [8] Hui Wang, John S. Tse, Kaori Tanaka, Toshiaki Iitaka, and Yanming Ma. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proceedings of the National Academy of Sciences, 109(17):6463–6466, 2012.
- [9] A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov, and S. I. Shylin. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature, Letter, 525:73–76, Sept 2015.
- [10] Mari Einaga, Masafumi Sakata, Takahiro Ishikawa, Katsuya Shimizu, Mikhail I. Eremets, Alexander P. Drozdov, Ivan A. Troyan, Naohisa Hirao, and Yasuo Ohishi. Crystal structure of the superconducting phase of sulfur hydride. Nature Physics, 12, 2016.
- [11] A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. Balakirev, D. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz, and M. I. Eremets. Superconductivity at 250 k in lanthanum hydride under high pressures. Nature, 569:528–531, 2019.
- [12] Maddury Somayazulu, Muhtar Ahart, Ajay K. Mishra, Zachary M. Geballe, Maria Baldini, Yue Meng, Viktor V. Struzhkin, and Russell J. Hemley. Evidence for superconductivity above 260 k in lanthanum superhydride at megabar pressures. Phys. Rev. Lett., 122:027001, Jan 2019.
- [13] Elliot Snider, Nathan Dasenbrock-Gammon, Raymond McBride, Xiaoyu Wang, Noah Meyers, Keith V. Lawler, Eva Zurek, Ashkan Salamat, and Ranga P. Dias. Synthesis of yttrium superhydride superconductor with a transition temperature up to 262 k by catalytic hydrogenation at high pressures. Phys. Rev. Lett., 126:117003, Mar 2021.
- [14] Panpan Kong, Vasily S. Minkov, Mikhail A. Kuzovnikov, Alexander P. Drozdov, Stanislav P. Besedin, Shirin Mozaffari, Luis Balicas, Fedor Fedorovich Balakirev, Vitali B. Prakapenka, Stella Chariton, Dmitry A. Knyazev, Eran Greenberg, and Mikhail I. Eremets. Superconductivity up to 243 k in the yttrium-hydrogen system under high pressure. Nature Communications, 12, Aug 2021.
- [15] Elliot Snider, Nathan Dasenbrock-Gammon, Raymond McBride, Mathew Debessai, Hiranya Vindana, Kevin Vencatasamy, Keith V. Lawler, Ashkan Salamat, and Ranga P. Dias. Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature, 586:373–377, Octuber 2020.
- [16] Yinwei Li, Jian Hao, Hanyu Liu, John S. Tse, Yanchao Wang, and Yanming Ma. Pressure-stabilized superconductive yttrium hydrides. Scientific Reports, 5:9948, May 2015.
- [17] Xiaoqiu Ye, Niloofar Zarifi, E. Zurek, R. Hoffmann, and N. Ashcroft. High hydrides of scandium under pressure: Potential superconductors. Journal of Physical Chemistry C, 2018.
- [18] Tetsuji Kume, Hiroyuki Ohura, Shigeo Sasaki, Hiroyasu Shimizu, Ayako Ohmura, Akihiko Machida, Tetsu Watanuki, Katsutoshi Aoki, and Kenichi Takemura. High-pressure study of by raman and visible absorption spectroscopy. Phys. Rev. B, 76:024107, Jul 2007.
- [19] Ayako Ohmura, Akihiko Machida, Tetsu Watanuki, Katsutoshi Aoki, Satoshi Nakano, and K. Takemura. Infrared spectroscopic study of the band-gap closure in at high pressure. Phys. Rev. B, 73:104105, Mar 2006.
- [20] A. Machida, A. Ohmura, T. Watanuki, K. Aoki, and K. Takemura. Long-period stacking structures in yttrium trihydride at high pressure. Phys. Rev. B, 76:052101, Aug 2007.
- [21] T. Palasyuk and M. Tkacz. Hexagonal to cubic phase transition in yh3 under high pressure. Solid State Communications, 133(7):477–480, 2005.
- [22] Riki Kataoka, Toru Kimura, Nobuhiko Takeichi, and Atsunori Kamegawa. Stabilization of face-centered cubic high-pressure phase of reh3 (re = y, gd, dy) at ambient pressure by alkali or alkaline-earth substitution. Inorganic Chemistry, 57(8):4686–4692, 2018. PMID: 29620366.
- [23] Riki Kataoka, Toru Kimura, Kouji Sakaki, Masashi Nozaki, Toshikatsu Kojima, Kazutaka Ikeda, Toshiya Otomo, Nobuhiko Takeichi, and Atsunori Kamegawa. Facile synthesis of lih-stabilized face-centered-cubic yh3 high-pressure phase by ball milling process. Inorganic Chemistry, 58(19):13102–13107, 2019. PMID: 31502447.
- [24] J. Purans, A. P. Menushenkov, S. P. Besedin, A. A. Ivanov, V. S. Minkov, I. Pudza, A. Kuzmin, K. V. Klementiev, S. Pascarelli, O. Mathon, A. D. Rosa, T. Irifune, and Mikhail I. Eremets. Local electronic structure rearrangements and strong anharmonicity in yh3 under pressures up to 180gpa. Nature Communications, 12, March 2021.
- [25] Tetsuji Kume, Hiroyuki Ohura, Tomoo Takeichi, Ayako Ohmura, Akihiko Machida, Tetsu Watanuki, Katsutoshi Aoki, Shigeo Sasaki, Hiroyasu Shimizu, and Kenichi Takemura. High-pressure study of sch3: Raman, infrared, and visible absorption spectroscopy. Phys. Rev. B, 84:064132, Aug 2011.
- [26] Bo Kong, Zhu-Wen Zhou, De-Liang Chen, and Rong-Feng Ling-hu. Structures and phase transitions of ScH3under high pressure. Chinese Physics B, 22(5):057102, may 2013.
- [27] T Pakornchote, U Pinsook, and T Bovornratanaraks. The hcp to fcc transformation path of scandium trihydride under high pressure. Journal of Physics: Condensed Matter, 26(2):025405, dec 2013.
- [28] Duck Young Kim, Ralph H. Scheicher, Ho-kwang Mao, Tae W. Kang, and Rajeev Ahuja. General trend for pressurized superconducting hydrogen-dense materials. Proceedings of the National Academy of Sciences, 107(7):2793–2796, 2010.
- [29] J Y Zhang, L J Zhang, T Cui, Y L Niu, Y M Ma, Z He, and G T Zou. A first-principles study of electron–phonon coupling in electron-doped LiH. Journal of Physics: Condensed Matter, 19(42):425218, sep 2007.
- [30] M. A. Olea-Amezcua, O. De la Peña Seaman, and R. Heid. Superconductivity by doping in alkali-metal hydrides without applied pressure: An ab initio study. Phys. Rev. B, 99:214504, Jun 2019.
- [31] S Villa-Cortés and O De la Peña-Seaman. Electron- and hole-doping on ScH2 and YH2: effects on superconductivity without applied pressure. Journal of Physics: Condensed Matter, 33(42):425401, aug 2021.
- [32] W. Kohn and L. J. Sham. Self-consistent equations including exchange and correlation effects. Phys. Rev., 140:A1133–A1138, Nov 1965.
- [33] Lothar Nordheim. Zur elektronentheorie der metalle. i. Annalen der Physik, 401(5):607–640, 1931.
- [34] H. Rosner, A. Kitaigorodsky, and W. E. Pickett. Prediction of high superconductivity in hole-doped libc. Phys. Rev. Lett., 88:127001, Mar 2002.
- [35] Lilia Boeri, Jens Kortus, and O. K. Andersen. Three-dimensional -type superconductivity in hole-doped diamond. Phys. Rev. Lett., 93:237002, Nov 2004.
- [36] Yanfeng Ge, Fan Zhang, and Yugui Yao. First-principles demonstration of superconductivity at 280 k in hydrogen sulfide with low phosphorus substitution. Phys. Rev. B, 93:224513, Jun 2016.
- [37] O. De la Peña Seaman, R. de Coss, R. Heid, and K.-P. Bohnen. Effects of al and c doping on the electronic structure and phonon renormalization in mgb2. Phys. Rev. B, 79:134523, Apr 2009.
- [38] Paolo Giannozzi et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. Journal of Physics: Condensed Matter, 21(39):395502, 2009.
- [39] Stefano Baroni, Stefano de Gironcoli, Andrea Dal Corso, and Paolo Giannozzi. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys., 73:515–562, Jul 2001.
- [40] John P. Perdew, Kieron Burke, and Matthias Ernzerhof. Generalized gradient approximation made simple. Phys. Rev. Lett., 77:3865–3868, Oct 1996.
- [41] Stefano Baroni, Paolo Giannozzi, and Eyvaz Isaev. Density-Functional Perturbation Theory for Quasi-Harmonic Calculations. Reviews in Mineralogy and Geochemistry, 71(1):39–57, Jan 2010.
- [42] Philip B. Allen. Neutron spectroscopy of superconductors. Phys. Rev. B, 6:2577–2579, Oct 1972.
- [43] Philip B. Allen and Richard Silberglitt. Some effects of phonon dynamics on electron lifetime, mass renormalization, and superconducting transition temperature. Phys. Rev. B, 9:4733–4741, Jun 1974.
- [44] P. B. Allen and R. C. Dynes. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B, 12:905–922, Aug 1975.
- [45] G. M. Eliashberg. Interaction between electrons and lattice vibrations in a superconductor. J. Exptl. Theoret. Phys., 38:966–976, 1960.
- [46] G. Bergmann and D. Rainer. The sensitivity of the transition temperature to changes in 2f(). Zeitschrift für Physik, 263(1):59–68, 1973.
- [47] S. Villa-Cortés and R. Baquero. The thermodynamics and the inverse isotope effect of superconducting palladium hydride compounds under pressure. Journal of Physics and Chemistry of Solids, 123:371 – 377, 2018.
- [48] D. Rainer and F. J. Culetto. Theory of the isotope effect in superconducting compounds: Pdd and . Phys. Rev. B, 19:2540–2547, Mar 1979.
- [49] S. Villa-Cortés and O. De la Peña-Seaman. Effect of van hove singularity on the isotope effect and critical temperature of h3s hydride superconductor as a function of pressure. Journal of Physics and Chemistry of Solids, 161:110451, 2022.
- [50] S. Villa-Cortés and R. Baquero. On the calculation of the inverse isotope effect in pdh(d): A migdal-eliashberg theory approach. Journal of Physics and Chemistry of Solids, 119:80 – 84, 2018.
- [51] X. Q. Zeng, L. F. Cheng, J. X. Zou, W. J. Ding, H. Y. Tian, and C. Buckley. Influence of 3d transition metals on the stability and electronic structure of mgh2. Journal of Applied Physics, 111(9):093720, 2012.
- [52] Y. Song, Z. X. Guo, and R. Yang. Influence of selected alloying elements on the stability of magnesium dihydride for hydrogen storage applications: A first-principles investigation. Phys. Rev. B, 69:094205, Mar 2004.
- [53] A. Machida, A. Ohmura, T. Watanuki, T. Ikeda, K. Aoki, S. Nakano, and K. Takemura. X-ray diffraction investigation of the hexagonal–fcc structural transition in yttrium trihydride under hydrostatic pressure. Solid State Communications, 138(9):436–440, 2006.
- [54] F. D. Murnaghan. Finite deformations of an elastic solid. American Journal of Mathematics, 59(2):235–260, 1937.