Superconducting and Antiferromagnetic Properties of Dual-Phase V3Ga
Abstract
The binary compound V3Ga can exhibit two near-equilibrium phases, consisting of the A15 structure that is superconducting, and the Heusler D03 structure that is semiconducting and antiferromagnetic. Density functional theory calculations show that the two phases are closely degenerate, being separated by only 10 meV/atom. Magnetization measurements on bulk-grown samples show superconducting behavior below 14 K. These results indicate the possibility of using V3Ga for quantum technology devices utilizing both superconductivity and antiferromagnetism at the same temperature.
I Introduction

Combining superconductivity and antiferromagnetism could find useful applications in quantum spintronic devices. Superconductivity and magnetism were once thought to be mutually exclusive, as magnetic fields are efficient at closing the superconducting gap. Nevertheless, it was found that superconducting materials could contain 3 magnetic transition metal atoms and magnetic lattices as well Canfield-1998 . Following that, high- cuprate superconductors were found to have exceedingly strong magnetic exchangeRevModPhys.78.17 , while superconducting Fe-pnitides were found to have large Fe moments of several Bohr magnetonsMizuguchi ; Lumsden_2010 . Of interest here are binary vanadium compounds such as V3Al that belong to a class of simple superconductor materials with A15 crystal structure Du_2013 ; Bansil1999 ; Testardi-1997 ; Ohshima_1989 . Interestingly, V3Al was also synthesized in a non-superconducting D03 Heusler phase with antiferromagnetic (AFM) order Jamer4 . This D03 phase of V3Al was predicted to be a gapless semiconductorGao2013 ; V3AlGalanakis , and was found experimentallyJamer4 to be a G-type antiferromagnet having a Neél temperature of 600 K. One can draw the conclusion that V3Z-type compounds represent a class of hybrid materials with superconducting and magnetic properties at the same temperature, which could have applications in possible fault-tolerant quantum computers hosting Majorana modes and in other important quantum technology applications.
Another well-known compound in this family is V3Ga, which has been used in superconducting applications for many years markiewicz_1977 . This material has been known since 1956 to have remarkable low-temperature properties related to elastic constants, Knight shifts, electrical resistance, magnetic susceptibility, superconductivity and it has been investigated extensively both experimentally and theoretically (see e.g. Refs. Matthias-1956 ; Weger-1964 ; Izyumov_Kurmaev ; Testardi-1975 ; Klein-1978 ; Jarlborg-1979 ; MaterialsProj ). The critical temperature of superconducting V3Ga in the A15 phase is 14 K.
V3Ga can exist in two near-equilibrium phases, the A15 superconducting phase and the AFM D03 phase - an interesting and potentially useful result of their similar formation energies. Since the arrangement of atoms in binary V3Ga can accommodate both D03 and A15 structures, shown in Fig. 1, one must study the stability of these two phases. Density functional theory (DFT) was used here to compute the formation energies as a function of crystalline and magnetic structures. Previous theoretical calculations for the D03 structure of V3Ga by Galanakis et al. V3AlGalanakis have predicted a Heusler G-type AFM phase with a Neél temperature well above room temperature, which makes the compound attractive for applications Jamer4 ; JamerCrCoGa ; JamerPRA2017 . A recent study also reported on the similar formation energies of the two structures.He-2019 The present magnetization measurements on bulk samples show a strong Meissner effect indicating a superconducting transition temperature of 14 K.
II Experimental Details and Results
Bulk samples of V3Ga were synthesized via arc-melting using an Edmund Buehler MAM-1. The ingots were subsequently annealed at 1050∘C for 48 hours in an Argon environment to promote homogeneity and quenched in an ice bath. The composition was confirmed using energy dispersive spectroscopy (EDS) to be within 2% of the nominal composition. Magnetic measurements were performed in a Quantum Design MPMS XL-5 SQUID magnetometer in magnetic fields up to 5 T and temperatures from T = 2 to 400 K. Synchrotron X-ray diffraction was done using beamline 11-BM at the Advanced Photon Source (APS). The structure was refined using TOPAS.TOPAS Overall, the structural results determined that there was a mixed phase of both A15 and D03 of V3Ga. The Rietveld refinement analysis determined that the A15 was the predominant phase at 81% and the D03 accounted for 19% of the structural analysis (Supplemental Information).
Results of the magnetic measurements are shown in Figs. 2 and 3. In particular, Fig. 2 shows a magnetic hysteresis from the Meissner effect at low temperature, which is characteristic of flux pinning of the A15 type-II superconducting phase. The superconducting transition temperature K is deduced from the plot of the magnetization as a function of temperature as shown in the inset of Fig. 2. Dimensionless magnetic susceptibility is shown in Supplemental Information which indicates 90% superconducting volume fraction in line with expectations from the compositional analysis of the X-ray diffraction data through Rietveld refinement. The inset of Fig. 3 shows the magnetic moment as a function of applied field at = 300 K. The moment is linear up to at least H = 5 T, where the moment is only per formula unit (f.u.). This linear-in-H moment is similar to that found in the AFM D03 phase of V3AlJamer4 . A focus on the superconducting properties of the A15 phase is presented in Supplemental Information which shows an Hc2 of about 3.5 T for isothermal magnetization at 10 K. This value is significantly lower than the previously accepted value of 15 T at 10 K for the A15 V3Ga phase. Foner ; Decker The decrease in Hc2 is most likely due to the antiferromagnetic phase from the D03 component which attributes significant magnetic signal at higher field. Previous reports of off-stoichiometry A15 V3Ga Foner did not alter the Hc2 as drastically as the observed in the current system, therefore it is reasonable to attribute this significant decrease in Hc2 as due to the antiferromagnetic signal of another magnetic V3Ga phase present in the as-synthesized compound mixture. At higher temperatures there is a notable peak in the temperature dependence of the low-field (H = 500 Oe) moment at = 360 K, shown in Fig. 3. A similar feature was seen in the temperature-dependent resistivity of V3Ga at 350 KHe-2019 , however, the peak was not assigned to a magnetic transition. The similar temperature-dependent features in both the magnetization and the resistivity could arise from either a structural or a magnetic transition. A small peak in the magnetization of an AFM is generally characteristic of a Neél temperatureJamer4 , so there is a reasonable case to assign the small peak observed here in the magnetization of V3Ga to some type of magnetic transition.


| D03 | A15 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mag. st. | Mag. st. | ||||||||||||||
| LDA | AFM | 5.902 | 0.429 | -0.429 | 0.0 | 0.0 | -8.487 | FM | 4.678 | 0.089 | 0.164 | 0.112 | 0.368 | -8.572 | 0.085 |
| GGA | AFM | 6.064 | -1.314 | 1.314 | 0.0 | 0.0 | -7.600 | FM | 4.788 | 0.222 | 0.390 | 0.303 | 0.916 | -7.645 | 0.045 |
| GGA+ | AFM | 6.130 | -1.916 | 1.917 | 0.0 | 0.0 | -6.647 | AFM-III | 4.879 | 1.351 | 1.508 | 1.502 | 0.0 | -6.632 | -0.015 |
| SCAN | AFM | 6.035 | -1.848 | 1.848 | 0.0 | 0.0 | -17.486 | FM | 4.744 | 0.308 | 0.523 | 0.414 | 1.245 | -17.442 | -0.044 |
| AFM-III | 4.744 | 0.268 | 0.326 | 0.330 | 0.0 | -17.437 | - | ||||||||
III Computational Details and Results
Density Functional Theory (DFT) within the projector augmented wave (PAW) as implemented in VASP Kresse-1996 ; paw was used for the electronic structure calculations. Various approximations were considered for the exchange-correlation (XC) energy, such as the local density approximation (LDA) Perdew_LDA , the generalized gradient approximation (GGA) Perdew-1991 ; Burke-1997 ; Perdew1996 , GGA+ (with the Hubbard correction), and the strongly constrained and appropriately normed (SCAN) meta-GGA Perdew-1999 ; Tao-2003 ; Sun-2015 . We have allowed full lattice and spin relaxation. The calculations were converged to an accuracy of 10-8 eV, while a convergence criterion in the optimization for the residual forces was 10-7 eV/Å. Concerning the GGA+, the Coulomb integrals = 2.0 eV and = 0.67 eV have been used that were provided by He et al. He-2019 .
The main results are summarized in Table 1, while more details are contained in the Supplemental Materials. The general trend of correlation effects beyond GGA is to stabilize the D03 solution with respect to the A15 one. The ground state (GS) in both LDA and GGA is the ferromagnetic (FM) phase with A15 structure. When correlation effects are included, the GS becomes the AFM G-type D03 solution. Regarding the A15 solution, the effect of correlations is to stabilize an AFM-III solution He-2019 ; Supplemental with respect to FM one. Within SCAN, the FM and AFM-III solutions in the A15 structure are almost degenerate and within 5 meV/atom (FM is marginally more stable). However, GGA+ fully stabilizes the AFM-III solution. The AFM-III solution having a net zero magnetic moment is more compatible with the superconducting properties of A15 structure.

Given the observation of the dual phase in the present V3Ga samples, SCAN may exaggerate the stabilization of the D03 solution, while GGA+ gives almost degenerate A15 and D03 solutions within 15 meV/atom, a value found previously in DFT solutionsHe-2019 and is in better accord with the experiment. SCAN is also known to exaggerate the magnetic moment of transition metal atoms, which are well described within GGA isaacs2018 ; fu2018 ; ekholm2018 . In order to alleviate this problem, a modification of SCAN with deorbitalization has been suggested recently deorbit .
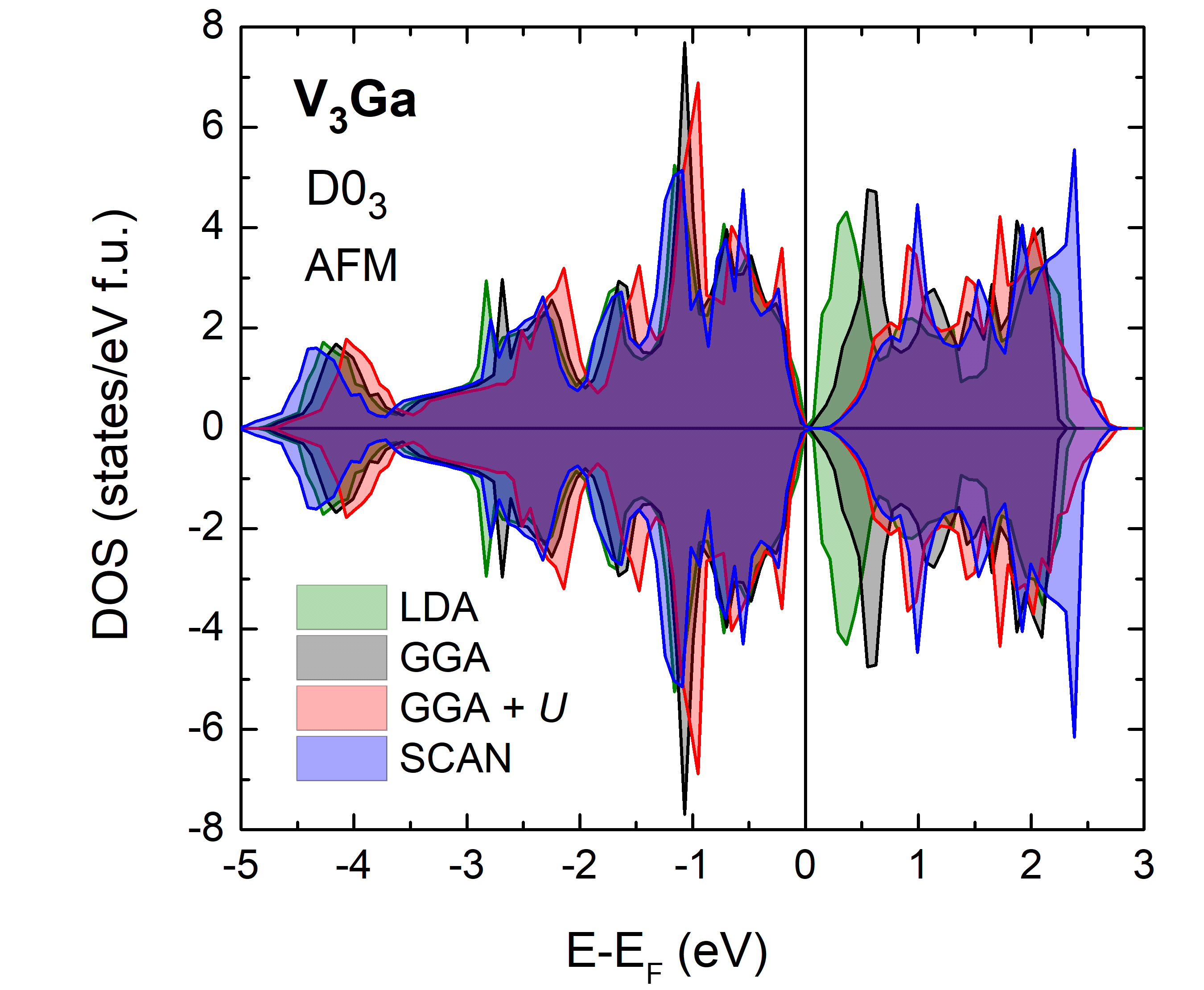
The calculated electronic structure is represented by density of states (DOS) shown in Fig. 4. LDA and GGA schemes give an almost gapless semiconductor, while the effects of correlation beyond GGA within GGA+ and SCAN lead to the opening of gap with size of about 0.2 eV. Similar gap opening has been observed by Buchelnikov et al. Buchelnikov-2019 in other Heusler alloys.
In order to estimate the magnetic transition temperature for the AFM G-type D03 phase, the GGA solution is more appropriate. Using Monte Carlo simulations with ab initio exchange integrals and Heisenberg model Supplemental , we obtain the Neél temperature K, which is somewhat higher than the peak in the experimental M(T) data at 360 K that was extracted from Fig. 3. However, the Neél temperature is found to be strongly affected by disorder. Effects of disorder on the Neél temperature are calculated by using the mean field approximation implemented in the SPR-KKR packages. Figure 5 illustrates how collapses for increasing disorder when the Ga atoms are exchanged with the nonmagnetic V atoms (those V atoms lying between the two antiferromagnetically coupled magnetic V atoms). It is seen that goes to zero with 20% exchange. Thus, a reduction of the Neél temperature to = 360 K would require only 6% of the Ga atoms exchanging for nonmagnetic V atoms. However, we note that there is a sizeable energy barrier for V-Ga exchange. Nevertheless, these results illustrate the importance of the nonmagnetic V atoms to the exchange between the other two antiferromagnetically coupled V-atoms.

IV Conclusions
We have studied the dual-phase superconducting A15 phase and the semiconducting AFM phase D03 in V3Ga. To rationalize our results, we have considered several models within DFT. We find that the effect of more accurate XC corrections within DFT is to eliminate or to weaken the total FM moment given by simpler LDA and GGA schemes in the A15 cell. This FM moment could jeopardize the A15 superconducting properties. Correlation effects also tend to stabilize the D03 solution. However, this trend could be exaggerated within SCAN. Concerning the formation energies, we believe that the most accurate results are between GGA and SCAN, therefore, we deduce that A15 and D03 phases are degenerate within an uncertainty of about 10 meV/atom. Finally, assuming that GGA gives the best description for the AFM magnetic moments of V atoms in the D03 solution, we estimated the Neél temperature to be K, but becomes lower with disorder in the atomic sublattices. Finally, the present results indicate the possibility of using V3Ga for quantum technology devices that require both superconductivity and antiferromagnetism at the same temperature.
Acknowledgements.
Use of the Advanced Photon Source at Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. The work at Northeastern University was supported by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences Grant No. DE-SC0019275 (materials discovery for QIS applications) and benefited from Northeastern University’s Advanced Scientific Computation Center and the National Energy Research Scientific Computing Center through DOE Grant No. DE-AC02-05CH11231. The work of Chelyabinsk State University was supported by RSF-Russian Science Foundation project No. 17-72-20022 (computational studies). This work was supported by NSF Grants DMR-1904446 (M.E.J) and DMR-1905662 (D.H.). V.B. acknowledges support from the NUST "MISiS" No. K2-2020-018 B.B. acknowledges support from the COST Action CA16218.References
- (1) P. C. Canfield, P. L. Gammel, and D. J. Bishop, Physics Today 51, 40 (1998).
- (2) P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys. 78, 17 (2006).
- (3) Y. Mizuguchi and Y. Takano, J. Phys. Soc. Japan 79, 102001 (2010).
- (4) M. D. Lumsden and A. D. Christianson, J. Phys: Conds. Mater. 22, 203203 (2010).
- (5) Y. Du et al., EPL (Europhys. Lett.) 103, 37011 (2013).
- (6) A. Bansil, S. Kaprzyk, P. Mijnarends, and J. Toboła, Phys. Rev. B 60, 13396 (1999).
- (7) L. R. Testardi, T. Wakiyama, and W. A. Royer, J. Appl. Phys. 48, 2055 (1977).
- (8) S. Ohshima, H. Ishida, T. Wakiyama, and K. Okuyama, Japan Soc. Appl. Phys. 28, 1362 (1989).
- (9) M. Jamer et al., Phys. Rev. B 91, 094409 (2015).
- (10) G. Gao and K. Yao, Appl. Phys. Lett. 103, 232409 (2013).
- (11) I. Galanakis, S. Tirpanci, K. \a"Ozdoğan, and E. Şaşıoğlu, Phys. Rev. B 94, 064401 (2016).
- (12) W. Markiewicz et al., IEEE Trans. Magnts. 13, 35 (1977).
- (13) B. T. Matthias, E. A. Wood, E. Corenzwit, and V. B. Bala, J. Phys. Chem. Solids 1, 188 (1956).
- (14) M. Weger, Rev. Mod. Phys. 36, 175 (1964).
- (15) Y. A. Izyumov and Z. Kurmaev, Sov. Phys. Uspekhi 17, 356 (1974).
- (16) L. R. Testardi, Rev. Mod. Phys. 47, 637 (1975).
- (17) B. M. Klein, L. L. Boyer, D. A. Papaconstantopoulos, and L. F. Mattheiss, Phys. Rev. B 18, 6411 (1978).
- (18) T. Jarlborg and P. O. Nilsson, J. Phys. C: Sol. State Phys. 12, 265 (1979).
- (19) A. Jain et al., APL Materials , 011002 (2013).
- (20) M. Jamer et al., Appl. Phys. Lett. 109, 182402 (2016).
- (21) M. E. Jamer et al., Phys. Rev. Appl. 7, 064036 (2017).
- (22) B. He et al., Phys. Stat. Sol. (RRL) 13, 1900483 (2019).
- (23) A. A. Coelho, J. Appl. Crystallogr. 51, 210 (2018).
- (24) S. Foner, E. McNiff Jr, S. Moehlecke, and A. Sweedler, Sol. State Commun 39, 773 (1981).
- (25) D. Decker and H. Laquer, J. Appl. Phys. 40, 2817 (1969).
- (26) G. Kresse and J. Furthmüller, Phys. Rev. B 54, 11169 (1996).
- (27) G. Kresse and D. Joubert, Phys. Rev. B 59, 1758 (1999).
- (28) J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981).
- (29) J. Perdew, Physica B: Conds. Mater. 172, 1 (1991).
- (30) K. Burke, J. Perdew, and M. Ernzerhof, Int. J. Quant. Chem. 61, 287 (1997).
- (31) J. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
- (32) J. P. Perdew, S. Kurth, A. c. v. Zupan, and P. Blaha, Phys. Rev. Lett. 82, 2544 (1999).
- (33) J. Tao, J. P. Perdew, V. N. Staroverov, and G. E. Scuseria, Phys. Rev. Lett. 91, 146401 (2003).
- (34) J. Sun, A. Ruzsinszky, and J. P. Perdew, Phys. Rev. Lett. 115, 036402 (2015).
- (35) M. Jamer et al., Supplemental Information (2020).
- (36) E. B. Isaacs and C. Wolverton, Phys. Rev. Mater. 2, 063801 (2018).
- (37) Y. Fu and D. J. Singh, Phys. Rev. Lett. 121, 207201 (2018).
- (38) M. Ekholm et al., Phys. Rev. B 98, 094413 (2018).
- (39) D. Mejia-Rodriguez and S. B. Trickey, Phys. Rev. B 98, 115161 (2018).
- (40) V. D. Buchelnikov et al., Phys. Rev. B 99, 014426 (2019).