Summary Statistics Knockoffs Inference with Family-wise Error Rate Control

Consider independently and identically distributed (i.i.d.) observations $\{(\textbf{x}_{i},y_{i})\in\mathbb{R}^{p}\times\mathbb{{R}}|i=1,\ldots,n\}$ from a joint distribution $f(\mathbf{X},Y)$ with $\textbf{X}=(X_{1},\ldots,X_{p})^{\mathsf{T}}$, our interest is to test hypotheses

under the joint distribution $f(\mathbf{X},Y)$, where $\textbf{X}_{-j}=(X_{1},\ldots,X_{j-1},X_{j+1},\ldots,X_{p})^{\mathsf{T}}$. Believing that the conditional distribution $Y|\mathbf{X}$ only depends upon a small subset of relevant features in X, our target is to classify each feature as relevant or not. Here, feature $X_{j}$ is said to be nonnull (or relevant to $Y$) if the corresponding assumption $H_{j}$ is not true, and null (or irrelevant to $Y$) otherwise. Let ${\mathcal{H}_{0}}\subset\{1,\dots,p\}$ denote the set of null features whose $H_{j}$’s are true and the remaining as $\mathcal{H}_{1}$. In this paper, we denote $\mathcal{R}$ as the set of rejected hypotheses and $V$ as the number of false discoveries (true $H_{j}$’s being rejected). Our target is to obtain an estimate $\mathcal{R}$ of $\mathcal{H}_{1}$ such that

is not larger than $\alpha$ ($0<\alpha<1$).

In large-scale genome-wide association studies, individual data required for knockoffs generation are generally inaccessible. Even available, computational cost can be extremely large due to the large sample size, which blocks the potential of existing individual knockoff-based methods in analyzing large-scale data. Recently, He et al., (2022) developed GhostKnockoff, which only requires $Z$-scores of Pearson’s correlations between features and the response and the (estimated) correlation matrix $\boldsymbol{\Sigma}$ of features to directly generate knockoff copies of $Z$-scores as follows.

Let $\mathbf{x}_{i}=(x_{i1},\dots,x_{ip})^{\mathsf{T}}$ and $y_{i}$ be the feature vector and the outcome of the $i$-th individual ($i=1,\ldots,n$) under the distribution $f(\mathbf{X},Y)$. Without loss of generality, we assume that both features and response are standardized with mean 0 and variance 1. To measure importance of different features, we consider $Z$-scores of Pearson’s correlations,

As shown in He et al., (2022), when the Gaussian model $\textbf{X}\sim\text{N}(\mathbf{0},\boldsymbol{\Sigma})$ is assumed to generate knockoff copies $(\mathbf{\widetilde{X}}^{1},\dots\mathbf{\widetilde{X}}^{M})$ of features following the method of Gimenez and Zou, (2019), corresponding knockoff copies of $Z$-scores $\mathbf{\widetilde{Z}}^{1},\dots\mathbf{\widetilde{Z}}^{M}$ that

satisfy

where $\mathbf{\widetilde{Z}}^{1:M}=(\widetilde{Z}^{1}_{1},\ldots,\widetilde{Z}^{1}_{p},\ldots,\widetilde{Z}^{M}_{1},\ldots,\widetilde{Z}^{M}_{p})^{\mathsf{T}}$, $\widetilde{\textbf{E}}\sim\text{N}\left(\mathbf{0},\textbf{V}\right)$,

$\mathbf{D}=\operatorname{diag}\left(s_{1},\ldots,s_{p}\right)\succeq 0$ is a diagonal matrix and $\mathbf{C}=2\mathbf{D}-\mathbf{D}\mathbf{\Sigma}^{-\mathbf{1}}\mathbf{D}$. In this article, we use the SDP construction of $\mathbf{D}=\{s_{1},\ldots,s_{p}\}$ by solving the optimization problem,

In practice, the number of knockoff copies ($M$) is determined by the target FWER level as details in Section 2.3.

With the convention that $\mathbf{\widetilde{Z}}^{0}=\textbf{Z}$, we show in Appendix B that under Gaussian model $\textbf{X}\sim\text{N}(\mathbf{0},\boldsymbol{\Sigma})$, $Z$-scores $\mathbf{\widetilde{Z}}^{0:M}=(\widetilde{Z}^{0}_{1},\ldots,\widetilde{Z}^{0}_{p},\ldots,\widetilde{Z}^{M}_{1},\ldots,\widetilde{Z}^{M}_{p})^{\mathsf{T}}$ possess the extended exchangeability property with respect to $\{H_{j}:j=1,\ldots,p\}$,

where

• •

  $\mathbf{\widetilde{Z}}^{0:M}_{swap(\boldsymbol{\sigma})}=(\widetilde{Z}^{\sigma_{1}(0)}_{1},\ldots,\widetilde{Z}^{\sigma_{p}(0)}_{p},\ldots,\widetilde{Z}^{\sigma_{1}(M)}_{1},\ldots,\widetilde{Z}^{\sigma_{p}(M)}_{p})^{\mathsf{T}}$;

• •

  $\boldsymbol{\sigma}=\{\sigma_{1},\ldots,\sigma_{p}\}$ is a family of permutations on $\{0,1,\ldots,M\}$;

• •

  $\sigma_{j}$ is any permutation on $\{0,1,\ldots,M\}$ if $H_{j}$ is true and is the identity permutation if $H_{j}$ is false ($j=1,\ldots,p$).

Given $Z$-scores and their knockoff copies $\mathbf{\widetilde{Z}}^{0},\dots\mathbf{\widetilde{Z}}^{M}$, we then compare $\widetilde{Z}_{j}^{0}$ with its knockoff copies to obtain the knockoff statistics of feature $X_{j}$ as

Here, $\kappa_{j}$ and $\tau_{j}$ are generalization of the sign and the magnitude to feature statistic $W_{j}$ in Candes et al., (2018) respectively. Similar to existing works of multiple knockoffs (Gimenez and Zou,, 2019; He et al.,, 2021, 2022), we also have $\kappa_{j}$’s corresponding to null features are independent uniform random variables as provided in Lemma 1.

Proof of Lemma 1 is provided in Appendix A, which is analogous to the proof of Lemma 3.2 in Gimenez and Zou, (2019). However, different to the work of Gimenez and Zou, (2019), our Lemma 1 directly utilizes the extended exchangeability property of $Z$-scores $\mathbf{\widetilde{Z}}^{0},\dots\mathbf{\widetilde{Z}}^{M}$.

Given knockoff statistics $\{(\kappa_{j},\tau_{j})|j=1,\ldots,p\}$ generated from (9), the next step is developing a FWER filter to reject as many $H_{j}$’s as possible such that (a) evidences against rejected $H_{j}$’s are strong and (b) the probability of rejecting at least one true $H_{j}$ (FWER) is bounded by the target level $\alpha$. Without loss of generality, we reindex all features such that $\tau_{j}$’s satisfy $\tau_{1}\geq\tau_{2}\geq\cdots\geq\tau_{p}$ as shown in Figure 1. Recalling that $\kappa_{j}$ and $\tau_{j}$ respectively measure whether the original feature $X_{j}$ is more important than its knockoff copies and the overall importance of $X_{j}$ and its knockoff copies, we can achieve (a) by including the first several $H_{j}$’s in the rejection set $\mathcal{R}$ whose $\kappa_{j}$’s are $0$ and $\tau_{j}$’s are large. In other words, we achieve (a) by letting $\mathcal{R}=\{j|\kappa_{j}=0\}\cap\{1,\ldots,T\}$ with the threshold $T$ as large as possible. However, as $T$ increases, $\mathcal{R}$ becomes larger, making it more likely to have true $H_{j}$’s in $\mathcal{R}$ and leading to violation of FWER control in (b). Thus, we propose the FWER filter (Algorithm 1) to obtain the rejection set such that (a) and (b) are achieved simultaneously.

As the threshold $T$ increases from $1$ to $p$, Algorithm 1 sequentially includes $H_{T}$ in the rejection set $\mathcal{R}$ if the corresponding $\kappa_{T}$ is zero (steps 6-7). Such a procedure terminates when the $v$-th nonzero $\kappa_{T}$’s is met or $T=p$ (step 8), where $v$ is determined by step 3 to guarantee FWER control at the level $\alpha$. The rationale underlying the selection rule (10) comes from Lemma 1, which suggests $\kappa_{j}$’s for all true $H_{j}$’s are independent uniform random variables on $\{0,1,\ldots,M\}$. That is to say, indicators $I(\kappa_{j}=0)$’s independently follow binomial distribution $\text{B}(1,1/(1+M))$ for all true $H_{j}$’s. Based on the connection of binomial distribution and negative binomial distribution, we have among all true $H_{j}$’s, the number of $\kappa_{j}$’s that equal zero before the $v$-th nonzero $\kappa_{j}$ follows negative binomial distribution $\text{NB}(v,1/(M+1))$. Given that the rejection set $\mathcal{R}=\{j|\kappa_{j}=0\}\cap\{1,\ldots,T\}$ includes $H_{j}$’s with $\kappa_{j}=0$ and $j\leq T$, if the inclusion procedure (steps 6-7) stops when we meet the $v$-th nonzero $\kappa_{j}$ among all true $H_{j}$’s, we have the number of false discoveries (or the number of zero $\kappa_{j}$’s of true $H_{j}$ in $\mathcal{R}$) follows $\text{NB}(v,1/(M+1))$. Thus, to control FWER under $\alpha$ with power as large as possible, we should select $v$ as large as possible such that (10) stands. In practice, as whether $H_{j}$’s are true or not is unknown, Algorithm 1 terminates the inclusion procedure (steps 6-7) when we meet the $v$-th nonzero $\kappa_{j}$ (as shown in Figure 1) or $T=p$, which does not violate the FWER control.

As the selection rule (10) is valid in FWER control for any target level $\alpha$ and the number of knockoff copies $M$, we can utilize it to determine $M$ for knockoff copies generation in Section 2.2. If $M$ is too small, selection rule (10) would obtain $v=0$, resulting in empty rejection set and no power. Taking such issue into account, we suggest choosing the smallest $M$ such that selection rule (10) obtains $v=1$. For example, when the target FWER level is $\alpha=0.05$, we have selection rule (10) obtains $v=0$ for $M=1,\ldots,18$ and $v=1$ for $M=19$. As a result, we use $M=19$ (which leads to $v=1$) throughout all numerical experiments with the target FWER level $\alpha=0.05$ in this article.

To generate knockoff copies of $Z$-scores $\mathbf{\widetilde{Z}}^{1},\dots\mathbf{\widetilde{Z}}^{M}$ via (5), it is crucial to sample a $pM$-dimensional random vector $\widetilde{\textbf{E}}\sim\text{N}(\mathbf{0,V})$. However, directly doing so usually requires performing Cholesky decomposition of the $pM\times pM$ matrix $\mathbf{V}$, which is computationally intensive especially when $M$ is large. For example, as the target FWER level is fixed as $\alpha=0.05$ throughout this article, we need to generate $M=19$ knockoff copies of $Z$-scores and thus need to implement Cholesky decomposition of a $19000\times 19000$ matrix when we are inferring $p=1000$ features. To circumvent such an obstacle, we propose an efficient algorithm to generate $\widetilde{\mathbf{E}}$ as detailed in the following.

Noting that the covariance matrix V can be decomposed as $\textbf{V}=\textbf{V}_{1}+\textbf{V}_{2}$ where

and

we can sample $\widetilde{\textbf{E}}\sim\text{N}(\mathbf{0,V})$ as the sum

Based on the block structure of $\textbf{V}_{1}$ and $\textbf{V}_{2}$ in (11), random vectors $\widetilde{\textbf{E}}_{1}$ and $\widetilde{\textbf{E}}_{2}$ can be efficiently generated as follows.

• $\star$

  (Generating $\widetilde{\mathbf{E}}_{1}$) Noting that $\mathbf{V}_{1}$ is a $M\times M$ block matrix with the common positive semi-definite block $\textbf{C}-\frac{M-1}{M}\textbf{D}$, we generate $\widetilde{\mathbf{E}}_{1}=((\textbf{L}\widetilde{\textbf{e}}_{1})^{\mathsf{T}},\ldots,(\textbf{L}\widetilde{\textbf{e}}_{1})^{\mathsf{T}})^{\mathsf{T}}$, where $\widetilde{\textbf{e}}_{1}\sim\text{N}(\mathbf{0},\textbf{I})$ and L is the solution of the $p\times p$ Cholesky decomposition equation,

  $$\textbf{C}-\frac{M-1}{M}\textbf{D}=\textbf{L}\textbf{L}^{\mathsf{T}}.$$

• $\star$

  (Generating $\widetilde{\mathbf{E}}_{2}$) With i.i.d. samples $\widetilde{\textbf{e}}^{1}_{2},\widetilde{\textbf{e}}^{2}_{2},\ldots,\widetilde{\textbf{e}}^{M}_{2}\sim\text{N}(\mathbf{0},\textbf{D})$, we compute $\widetilde{\mathbf{E}}_{2}=((\widetilde{\textbf{e}}^{1}_{2}-\overline{\textbf{e}}_{2})^{\mathsf{T}},(\widetilde{\textbf{e}}^{2}_{2}-\overline{\textbf{e}}_{2})^{\mathsf{T}},\ldots,(\widetilde{\textbf{e}}^{M}_{2}-\overline{\textbf{e}}_{2})^{\mathsf{T}})^{\mathsf{T}}$, where $\overline{\textbf{e}}_{2}=M^{-1}\sum_{m=1}^{M}\widetilde{\textbf{e}}^{m}_{2}$.

Details of generating knockoff copies of $Z$-scores $\mathbf{\widetilde{Z}}^{1},\dots\mathbf{\widetilde{Z}}^{M}$ are summarized in Algorithm 2. Compared with the trivial approach that relies on Cholesky decomposition of V, Algorithm 2 decreases the computational complexity from $O(M^{3}p^{3})$ to $O(p^{3})$.

To empirically evaluate the computational efficiency of our method in generating knockoff copies of $Z$-scores and performing inference, we conduct experiment to compare our method with derandomized knockoffs (where $M=1$, Ren et al.,, 2023) and the trivial approach via (5) with Cholesky decomposition of V. For different number of features $p=50,100,200$ and $500$, $200$ datasets are generated and inferred. Within each dataset, $n=1000$ i.i.d. samples $\{(\textbf{x}_{i},y_{i}):i=1,\ldots,n\}$ are generated from the linear model

where $p$-dimensional feature vector $\mathbf{X}\sim\text{N}\big{(}0,\mathbf{\Sigma}=(0.25^{|i-j|})_{p\times p}\big{)}$. With a fixed number of nonnull features $|\mathcal{H}_{1}|=10$, locations of nonnull features are randomly drawn from $\{1,\ldots,p\}$ with $\beta_{j}$’s uniformly distributed in $\{5/\sqrt{n},-5/\sqrt{n}\}$ if $j\in\mathcal{H}_{1}$ and $\beta_{j}=0$ for null features. With the target FWER level $0.05$, the hyperparameter of derandomized knockoffs are selected as the number of repetitions $M_{deran}=50$ using codes of Ren et al., (2023).

Specifically, we compare computation time of three approaches in

• (a)

  Cholesky decomposition (derandomized knockoffs: $2\mathbf{D}-\mathbf{D}\mathbf{\Sigma}^{-\mathbf{1}}\mathbf{D}$; trivial approach: V; our method: $\textbf{C}-\frac{M-1}{M}\textbf{D}$);

• (b)

  Sampling knockoff copies of $Z$-scores, including sampling $\widetilde{\textbf{E}}$ and computing $\mathbf{\widetilde{Z}}^{1:M}=\mathbf{P}\textbf{Z}+\widetilde{\textbf{E}}$ ($M_{\text{deran}}$ repetitions for derandomized knockoffs with $M=1$);

• (c)

  Inference (Algorithm 1 for both trivial approach and our method; $M_{\text{deran}}$ repetitions for derandomized knockoffs).

Here, we omit the comparison in performing precalculation of D and $\textbf{I}-\textbf{D}\boldsymbol{\Sigma}^{-1}$ because the total complexity of this step is the same for different methods. Average computational time of different approaches under different dimensions $p$ is summarized in Table 1 (CPU: Apple M2 Pro, 3.5 GHz; RAM: 16GB). Generally, our method has the least computational time. Compared to derandomized knockoffs, our method has comparable computational complexity in Cholesky decomposition and outperforms in sampling knockoff copies and inference. The reason is that $M_{\text{deran}}$ samplings of $p$-dimensional random vector and $M_{\text{deran}}$ inferences are needed in derandomized knockoffs, leading to $\Omega(M_{\text{deran}}p^{2})$ and $\Omega(M_{\text{deran}}p\log p)$ computational costs respectively. Compared to the trivial approach, our method do relieve the computational burden of Cholesky decomposition from $O(M^{3}p^{3})$ to $O(p^{3})$. As a result, the overall computational complexity of Algorithm 2 is the smallest.

To investigate how the proposed FWER filter with GhostKnockoff performs under different correlation structures with comparison to existing knockoff-based methods, we conduct experiments of $500$ randomly generated datasets under both the compound symmetry correlation structure and the $\text{AR}(1)$ correlation structure of features. For each dataset, $n=500$ observations are generated by drawing i.i.d. samples of $100$-dimensional features $\textbf{x}_{1},\ldots,\textbf{x}_{n}\sim\text{N}(0,\mathbf{\Sigma})$, where

and simulating responses $y_{1},\ldots,y_{n}$ from the linear model (12). With a fixed number of nonzero elements $|\mathcal{H}_{1}|=5$ in the parameter vector $\boldsymbol{\beta}=(\beta_{1},\ldots,\beta_{p})^{\mathsf{T}}$, locations of these nonzero elements are uniformly sampled from $\{1,\ldots,p\}$ without replacement while their values are i.i.d. uniform variables in $\{A/\sqrt{n},-A/\sqrt{n}\}$. To exhibit the complete power curve, we let the amplitude $A$ of signals range in $\{1,2,\ldots,20\}$ under compound symmetry structure and $\{1,2,\ldots,25\}$ under $\text{AR}(1)$ structure respectively.

With the correlation coefficient $\rho=0.5$ and the target FWER level $0.05$, average power of different methods over $500$ datasets under compound symmetry structure and $\text{AR}(1)$ structure is presented in Figure 2. With FWER controlled under the target level, the power of the proposed FWER filter with GhostKnockoff and derandomized knockoffs increase as the signal amplitude $A$ grows under both structures, while the procedure of Janson and Su, (2016) maintains a low power. The reason is that the procedure of Janson and Su, (2016) only makes rejection with probability $2\times 0.05=0.1$ as shown in Section 2.3, making the power bounded by $0.1$. Although the proposed FWER filter with GhostKnockoff dominates derandomized knockoffs in power under both structures, its power can only reach $1$ as $A$ grows under $\text{AR}(1)$ structure and converges to a limit smaller than 1 under the compound symmetry structure. More results under different dimensions and correlation strengths are also provided in Appendix C.1 with similar conclusions.

To further investigate how correlation strength affects the performance of the proposed FWER filter with GhostKnockoff, we generate $500$ datasets for each possible correlation strength $\rho\in\{0,0.1,\ldots,0.9\}$ under both compound symmetry and $\text{AR}(1)$ structure. With a fixed sample size $n=500$, $100$-dimensional features are sampled as i.i.d. observations $\textbf{x}_{1},\ldots,\textbf{x}_{n}\sim\text{N}(0,\mathbf{\Sigma})$ and responses $y_{1},\ldots,y_{n}$ are computed from the linear model (12). With a fixed number of nonzero elements $|\mathcal{H}_{1}|=5$ in the parameter vector $\boldsymbol{\beta}=(\beta_{1},\ldots,\beta_{p})^{\mathsf{T}}$, locations of these nonzero elements are obtained by uniformly sampling of $\{1,\ldots,p\}$ without replacement while their values are i.i.d. uniform variables in $\{A/\sqrt{n},-A/\sqrt{n}\}$. The amplitude $A$ is $6$ and $8$ under compound symmetry and $\text{AR}(1)$ structure respectively to completely show how power varies with respect to correlation strength. To avoid the power loss phenomenon when the SDP construction of $\mathbf{D}$ is used under the compound symmetry structure with $\rho\geq 0.5$ as discovered in Spector and Janson, (2022), we adopt their strategy by multiplying $\mathbf{D}$ with a perturbation factor $\gamma=0.9$.

Empirical FWER and power of the proposed FWER filter with GhostKnockoff and other existing approaches are visualized in Figure 3. Consistent with our theoretical derivation, our method can control the FWER under the target level $\alpha=0.05$. While the procedure of Janson and Su, (2016) remains powerless, both the proposed FWER filter with GhostKnockoff and knockoffs have a decreasing power as the correlation strength $\rho$ grows. The main reason is that when $\rho$ gets larger, nearby features become more similar, making it more difficult to distinguish true signals. Even though, our method still outperforms derandomized knockoffs, whose power has a sudden drop when $\rho\geq 0.5$ due to the perturbation factor $\gamma$.

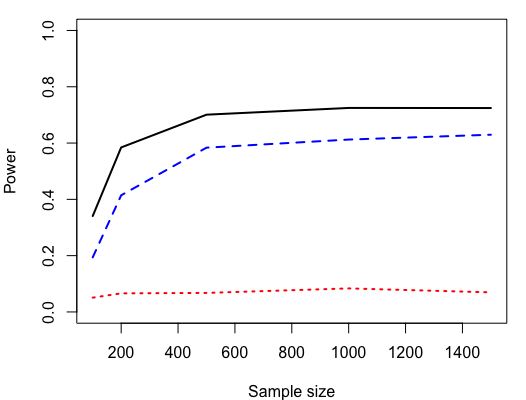
To demonstrate the empirical performance of the proposed FWER filter with GhostKnockoff under different number of nonnull features, we generate 500 datasets for each possible number of nonnull features $|\mathcal{H}_{1}|=5,6,\ldots,20$ under both compound symmetry (amplitude $A=6$) and AR(1) (amplitude $A=8$) structures with sample size $n=500$, dimension $p=200$ and correlation strength $\rho=0.25$. Empirical FWER and power of the proposed FWER filter with GhostKnockoff under different $|\mathcal{H}_{1}|$ are visualized in Figures 4, with comparison to derandomized knockoffs and the procedure of Janson and Su, (2016). Similarly, we also simulate 500 datasets for sample sizes $n=100,200,500$ and $1000$ under both compound symmetry (amplitude $A=6$) and AR(1) (amplitude $A=8$) structures with $p=200$, $|\mathcal{H}_{1}|=5$ and $\rho=0.25$. Empirical FWER and power of the proposed FWER filter with GhostKnockoff and existing methods under different sample sizes are shown in Figures 5.

From Figure 4, it is found that as the number of nonnull features $|\mathcal{H}_{1}|$ grows, the power of both the proposed FWER filter with GhostKnockoff and derandomized knockoffs decreases, suggesting that their ability to detect nonnull features deteriorates under dense but weak signals. As the sample size $n$ increases, the power of both methods grows to $1$ as shown in Figure 5, implying their consistency. In contrast, the procedure of Janson and Su, (2016) keeps a bounded power under $10\%$ throughout all scenarios. More results under different correlation strengths are provided in Appendix C.2 with similar conclusions.

The main reason why the power of the proposed method decreases with respect to $|\mathcal{H}_{1}|$ and increases with respect to $n$ is that the signal-to-noise ratio is of the order $\Omega(\sqrt{n/|\mathcal{H}_{1}|})$. This can be seen in the following toy example. Consider i.i.d. samples $\textbf{x}_{1},\ldots,\textbf{x}_{n}\sim\text{N}(\textbf{0},\textbf{I})$ and responses $y_{1},\ldots,y_{n}$ generated from the linear model (12), where $\beta_{1}=\ldots=\beta_{k}=A/\sqrt{n}$ and $\beta_{k+1}=\cdots=\beta_{p}=0$ for some integer $k$. In other words, we have $|\mathcal{H}_{1}|=k$. By definition (3) of $Z$-scores after standardizing both features and the response, we have $Z_{j}=\sqrt{n}\hat{\rho}_{j}$ where $\hat{\rho}_{j}$ is the empirical correlation of $X_{j}$ and $Y$. By (12), we have $\text{Var}(X_{j})=1$ ($j=1,\ldots,p$), $\text{Cov}(X_{j},Y)=\beta_{j}$ and $\text{Var}(Y)=\sum_{j=1}^{p}\beta_{j}^{2}+1$, leading to true correlations ${\rho}_{j}$ as

By the central limit theorem of correlation coefficient (Lehmann,, 1999) that

we have that as the amplitude $A$ grows, the expected mean of $Z_{j}$ for nonnull features is $\sqrt{n/k}\{1+o(1)\}$. Since the mean and asymptotic variance of $Z_{j}$ corresponding to null features remain $0$ and $1$, the signal-to-noise ratio is $\Omega(\sqrt{n/k})$. Thus, smaller $|\mathcal{H}_{1}|$ and larger sample size would both lead to larger signal-to-noise ratio and higher power.