SUDDEN CHANGE OF INTERFEROMETRIC POWER FOR X SHAPE STATES

Amplitude damping, or amplitude noise, which is used to characterize spontaneous emission, describes the energy dissipation from a quantum system. One can consider a two-qubit system where the first qubit is through this quantum channel. Then the Kraus operators for the whole system are given by[33]

where $\eta=e^{-\frac{\tau t}{2}}$, $\tau$ is the amplitude decay rate, $t$ is time. The evolution of the initial states Eq. (9) under this quantum channel can be described by

where $r(t)=\eta^{2}-1$, $s(t)=0$, $c_{1}(t)=\eta c_{1}$, $c_{2}(t)=\eta c_{2}$ and $c_{3}(t)=\eta^{2}c_{3}$. By Eq. (8), the IP of $\mathcal{E}_{a}(rho)$ is

In particular, Eq. (7) can reduce to the following simple form when $t=0$:

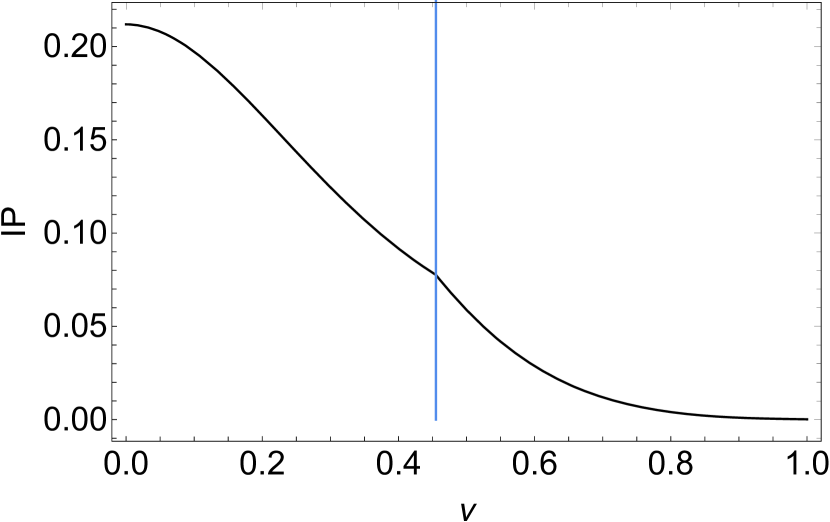
It is easy to find that $M_{11}(0)>M_{22}(0)$ (or $M_{11}(t)<M_{22}(0)$) if $|c_{1}|<|c_{2}|$ (or $|c_{1}|>|c_{2}|$), and when $t\rightarrow\infty$, $M_{11}(\infty)=M_{22}(\infty)>M_{33}(\infty)$. Hence, a sudden change of IP occurs when $|c_{3}|<\max\{|c_{1}|,|c_{2}|\}$ in the initial Bell-diagonal state $\rho$ with this kind of amplitude noisy channel. However, a sudden change of quantum discord occurs when $|c_{3}|>\max\{|c_{1}|,|c_{2}|\}$ in the initial state $\rho$ with the same noise environment. We find that the initial state satisfying the condition of a sudden change of quantum discord also exhibits a sudden change of IP, which means that the conditions of the sudden change of IP and quantum discord are not complementary. These results have been shown in Fig. 1.

Next we investigate the dynamics of IP over phase noise channel. Phase noise describes the loss of quantum information without loss of energy. The Kraus operators of phase noise for the whole system can be read as[1, 34]

where $\alpha=\frac{1}{2}(1+\sqrt{1-\gamma})$, $\gamma=e^{-\frac{\tau t}{2}}$ and $\tau$ denotes transversal decay rate. The output states from this quantum channel is

where $c_{1}(t)=\gamma c_{1}$, $c_{2}(t)=\gamma c_{2}$ and $c_{3}(t)=c_{3}$. By Eq. (8), the expression of IP of $\mathcal{E}_{p}(\rho)$ can be obtained, that is

where

One can find that the IP of $\mathcal{E}_{p}(\rho)$ can be rewritten as the following form:

where $\|C(t)\|^{2}=\mathsf{Tr}[C^{T}C]=c_{1}^{2}(t)+c_{2}^{2}(t)+c_{3}^{2}(t)$ the square Hilbert-Schmidt of $C(t)$ and $\|C(t)\|_{\infty}^{2}=\max\{c_{1}^{2}(t),c_{2}^{2}(t),c_{3}^{2}(t)\}$ the operator norm of $C(t)$.[29] If $|c_{3}|\geq\max\{|c_{1}|,|c_{2}|\}$, $\|C(t)\|_{\infty}^{2}$ will reduce to $c_{3}^{2}(t)$ since the decay rate of $\max\{|c_{1}(t)|,|c_{2}(t)|\}$ and $|c_{3}(t)|$ is different, then the IP $\mathcal{IP}(\mathcal{E}_{p}(\rho))$ decays monotonically. If $|c_{3}|<\max\{|c_{1}|,|c_{2}|\}$ and $c_{3}\neq 0$, the decay rate of IP $\mathcal{IP}(\mathcal{E}_{p}(\rho))$ sudden changes at $t_{0}=-\frac{2}{\tau}\ln\left|\frac{c_{3}}{\max\{|c_{1}|,|c_{2}|\}}\right|$. In Fig. 2, we choose three different $\{c_{i}\}$ to represent the dynamics of IP of $\rho$ under single qubit phase noise. As a result, a sudden change of IP may occur under this kind of noise environment.

As one of the important types of quantum noise, the depolarizing noise describes a process that takes a state into completely mixed state $\mathbb{1}/2$ with probability $p$ and the state being left untouched with probability $1-p$. The operation elements for depolarizing noise are shown as $\{\sqrt{1-3p/4}\mathbb{1},\sqrt{p}\sigma_{x}/2,\sqrt{p}\sigma_{y}/2,\sqrt{p}\sigma_{z}/2\}$ and the Kraus operators for the whole system are given by[1]

where $p=1-e^{-\tau t}$. The Bell-diagonal states after this noise is

where $c_{i}(t)=(1-p)c_{i}$, $i=1,2,3$. Similarly, the form of the IP of $\mathcal{E}_{d}(\rho)$ is Eq. (18) but $c_{i}(t)=(1-p)c_{i}$, $i=1,2,3$. Since the identical decay rate of $|c_{1}(t)|$, $|c_{2}(t)|$ and $|c_{3}(t)|$, $\|C(t)\|_{\infty}^{2}$ will be determined once $\{c_{i}\}$ has been chosen. Therefore, there is no sudden change of IP of $\rho$ under depolarizing noise, see Fig. 3.

The study of the dynamics quantum open system based on the Markov approximation contains the majority of physical situation but lacking the case of system-environment interactions with memory. In Ref. 35, a model describing system-environment interactions with memory without using Born-Markov approximation has been presented, and the conditions for system evolution to satisfy the complete positive trace-preserving map have been given.

The Kraus operators describing the above dynamics are given as follows:[36]

where the operators satisfy $\sum_{k}^{2}M_{k}^{\dagger}M_{k}=\mathbb{1}$, $\beta=\frac{1+\Lambda(\nu)}{2}$ and $\Lambda(\nu)=e^{-\nu}[\cos(\mu\nu)+\sin(\mu\nu)/\mu]$, $\mu=\sqrt{(4a\tau)^{2}-1}$, and $a$ is a coin-flip random variable, $\nu=\frac{t}{2\tau}$ is the dimensionless time. After the evolution of Bell-diagonal states under the independent interaction with identical colored dephasing environment, the output density matrix can be obtained as

where the operators $M_{i}$ and $M_{j}$ act on the first and second qubits, respectively. Actually, this is a completely positive trace-preserving map.

After the straightforward calculation, one can obtain that

where $c_{1}(t)=\Lambda^{2}(\nu)c_{1}$, $c_{2}(t)=\Lambda^{2}(\nu)c_{2}$ and $c_{3}(t)=c_{3}$. By Eq. (18), we get the form of the IP of $\mathcal{E}_{ic}(\rho)$. Since $\Lambda^{2}(\nu)$ is monotonically decreasing as similar as $\gamma$, the sudden change of IP for $\mathcal{E}_{ic}(\rho)$ can occur with the proper $\{c_{i}\}$, see Fig. 4.

Considering the two-qubit system coupling to a same bosonic environment, the total Hamiltonian can be written as[37]

The dynamics of Bell-diagonal states under such common dephasing bath can be expressed by the following Kraus operators:

where $\chi=\frac{\xi^{4}+1}{2}$, $\xi(t)=\exp[-\Gamma(t)]$, and $\Gamma(t)$ is the decoherence function with the form

By considering the spectral density as $J(\omega)=\frac{\omega^{s}}{\omega_{c}^{s-1}}\exp(-\frac{\omega}{\omega_{c}})$ with the cut-off frequency $\omega_{c}=1$ and the positive parameter $s=4$, we can investigate the dynamics of the Bell-diagonal states coupling to a same bosonic environment.

The matrix form of $\mathcal{E}_{cb}(\rho)$ with the initial Bell-diagonal state is as follow:

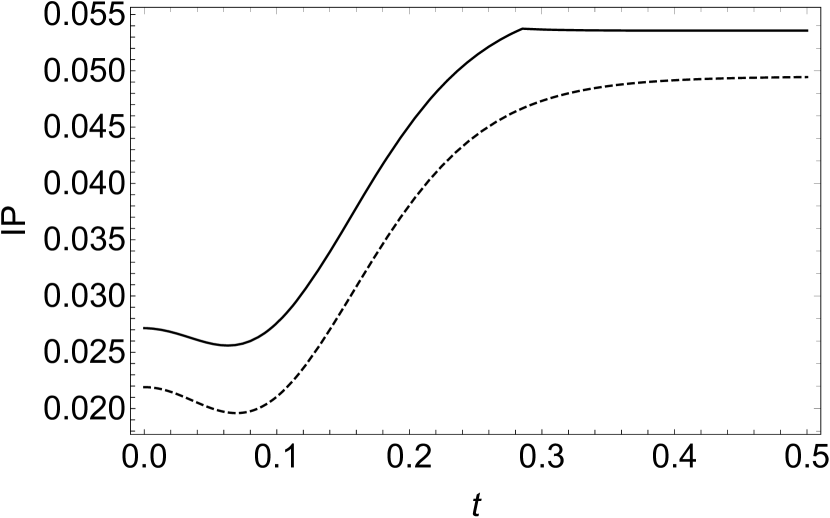
where $c_{1}(t)=[(1+\xi^{4}(t))c_{1}+(1-\xi^{4}(t))c_{2}]/2$, $c_{2}(t)=[(1-\xi^{4}(t))c_{1}+(1+\xi^{4}(t))c_{2}]/2$, and $c_{3}(t)=c_{3}$. By Eq. (18) with the proper parameter $s=4$, we find that if $c_{1}=c_{2}$, $c_{1}(t)$ and $c_{2}(t)$ will equal to $c_{1}$, then the IP of $\mathcal{E}_{cb}(\rho)$ will reduce to a constant. If $c_{1}\neq c_{2}$, the sudden change of IP happens when $c_{3}>(c_{1}+c_{2})/2$ with this kind of noise environment. We show this in Fig. 5.