Sub-Planck structures: Analogies between the Heisenberg-Weyl and SU(2) groups
Abstract
Coherent-state superpositions are of great importance for many quantum subjects, ranging from foundational to technological, e.g., from tests of collapse models to quantum metrology. Here we explore various aspects of these states, related to the connection between sub-Planck structures present in their Wigner function and their sensitivity to displacements (ultimately determining their metrological potential). We review this for the usual Heisenberg-Weyl algebra associated to a harmonic oscillator, and extend it to find analogous results for the algebra, typically associated with angular momentum. In particular, in the Heisenberg-Weyl case, we identify phase-space structures with support smaller than the Planck action in both Schrödinger-cat-state mixtures and superpositions, the latter known as compass states. However, as compared to coherent states, compass states are shown to have -enhanced sensitivity against displacements in all phase-space directions ( is the average number of quanta), whereas cat states and cat mixtures show such enhanced sensitivity only for displacements in specific directions. We then show that these same properties apply for analogous SU(2) states provided (i) coherent states are restricted to the equator of the sphere that plays the role of phase space for this group, (ii) we associate the role of the Planck action to the size of SU(2) coherent states in such a sphere, and (iii) we associate the role of with the total angular momentum.
I Introduction
The description and generation of quantum states presenting non-classical features has been a recurrent topic since the early days of quantum mechanics, attracting more and more attention as our ability to control quantum coherently optical, atomic, and solid-state systems has developed. Nonclassical properties come in many flavors such as squeezing Dodonov and Man’ko (2003); Schnabel (2017), entanglement Horodecki et al. (2009), Wigner negativity Lütkenhaus and Barnett (1995); Kenfack and Yczkowski (2004), -function divergence Richter and Vogel (2002); Hertz et al. (2020), and phase-space interference Bužek and Knight (1995); Gerry and Knight (2005); Schleich (2001), to name a few. The latter is the subject of our present work, specifically through states built as coherent-state superpositions. Such states are relevant to many areas, ranging from the foundations of quantum physics to the design and implementation of modern quantum technologies. For example, they can be used to test collapse models aimed at explaining the quantum-to-classical transition Bassi and Ghirardi (2003); Schlosshauer (2005); Abdi et al. (2016); Pino et al. (2018), but also as resources for quantum sensors with unprecedented resolution Zurek (2001); Toscano et al. (2006); Dalvit et al. (2006).
Coherent-state superpositions are especially well studied for the harmonic oscillator Gerry and Knight (2005), whose position and momentum operators form the so-called Heisenberg-Weyl (HW) algebra Weyl (1950) for a single degree of freedom, and act on an infinite-dimensional Hilbert space. Quantum mechanical states can be visualized on phase space, which is a symplectic manifold, via the Wigner quasi-probability density function Schleich (2001); Navarrete-Benlloch (2015). As the product of the uncertainties of position and momentum is bounded below by the Planck action , for quite some time phase-space features below this scale were believed not to play a physical role Berry (1979); Korsch and Berry (1981). Indeed, this is the case for Gaussian states Weedbrook et al. (2012); Cerf et al. (2007) (coherent, squeezed, thermal, etc.) and even for Schrödinger-cat states (superposition of two distinct coherent states Yurke and Stoler (1986) or other Gaussian states such as squeezed states Sanders (1989a)), which show fast oscillations in one direction of phase space, but an unlimited Gaussian profile in the orthogonal direction.
This notion was challenged by Zurek Zurek (2001), who showed that the Wigner function of chaotic systems typically develops spotty structures with features below the Planck scale, arguing that these are crucial in determining the sensitivity of the system to decoherence Zurek (2003) and to phase-space displacements Toscano et al. (2006); Dalvit et al. (2006) (ultimately determining its potential for quantum metrology). As prototypical states that show such sub-Planck features, he built the so-called compass states (one coherent state, so to speak, at the north, south, east and west corners), a superposition of four distant coherent states, which can also be understood as superpositions of two cat states. By now, there are multiple theoretical proposals for the controlled generation of these states Agarwal and Pathak (2004); Pathak and Agarwal (2005); Stobińska et al. (2011); Leghtas et al. (2013); Govia et al. (2014); Hastrup et al. (2020), apart from actual experimental implementations Ofek et al. (2016); Vlastakis et al. (2013); Praxmeyer et al. (2016); Lemos et al. (2012); Austin et al. (2010), and their properties and effects in different contexts have been well explored Jacquod et al. (2002); Wisniacki (2003); Ghosh et al. (2006); Praxmeyer et al. (2007); Scott and Caves (2008); Bhatt et al. (2008); Stobińska et al. (2008); Ghosh et al. (2009); Roy et al. (2009); Ghosh (2012); Kumari et al. (2015); Dodonov et al. (2016); Kumar and Lee (2017); Howard et al. (2019).
The concept of coherent states can be generalized to arbitrary groups Perelomov (1986, 1972). Of special interest for physics is the Lie SU(2) group Radcliffe (1971); Perelomov (1972); Gilmore (1972); Arecchi et al. (1972); Perelomov (1986), associated with generalized rotations and generated by the angular momentum operators, which satisfy the so-called algebra. This group includes spin- whereas the Lie group SO(3) is for integer-labeled rotations. The space of classical configurations corresponds in this case to the surface of a unit sphere Sanders (1989b). Superposing two coherent states pinned at antipodal points on the sphere, one generalizes the cat states first introduced for the algebra Sanders (1989b); Huang et al. (2015, 2018); Maleki and Zheltikov (2020); Davis et al. . The cat with states pinned at the sphere’s poles is the most studied one, since it corresponds to the popular entangled states known as Greenberger-Horne-Zeilinger (GHZ) Greenberger et al. (1989) or NOON Dowling (2008) states depending on the physical implementation, respectively, two-level atomic ensembles or two bosonic modes Sanders and Gerry (2014); Davis et al. . Even though the Hilbert space on which the algebra acts has finite dimension ( when considering a specific irreducible representation with fixed total angular momentum ), one can define a Wigner function that allows visualizing quantum states as quasi-probability distributions defined over the unit sphere Várilly and Gracia-Bondía (1989); Heiss and Weigert (2000); Klimov et al. (2017); Koczor et al. (2020). The Wigner function of a coherent state appears as a single lobe around the location where it is pinned, with a slight negativity and an effective support that decrease as increases Davis et al. . Cat states show an additional interference pattern along the great circle halfway between the locations of their underlaying coherent states Davis et al. (e.g., the equator for coherent states at the poles). The use of these states for quantum metrology has been analyzed in great depth Giovannetti et al. (2004); Dowling (2008); Giovannetti et al. (2011); Pezzè et al. (2018).
The goal of our present work is two-fold. First, for the algebra, we point out that the same sub-Planck structures present in compass states, are present in cat mixtures as well. Hence, it is argued that sub-Planck structures alone cannot be responsible for the remarkable sensibility of compass states against displacements in arbitrary directions of phase space, which is enhanced by with respect to that of coherent states ( is the average number of quanta in the state). Indeed, it is shown that cat states and mixtures show this enhanced sensitivity only for displacements along specific phase-space directions. These results have been discussed in previous literature Zurek (2001); Toscano et al. (2006); Kumari et al. (2015) (but without reaching some of the insights that we offer), so this part of the work is to be taken mainly as a review.
The second and main goal of our work is the generalization of these results to the SU(2) group. In particular, we show that the concept of sub-Planck structures can be extended to this case by associating the effective support of coherent states in the sphere, which scales as , with the SU(2) counterpart of the Planck action. Hence, it is shown that considering coherent-state superpositions along the equator, we can build cat states, compass states, and cat-state mixtures that show similar Wigner interference features as their HW counterparts when represented in the stereographic plane. Finally, we prove that these states have exactly the same enhanced sensitivity to displacements found for the algebra, with playing the role of .
II Sub-Planck structures in phase space
Let us start by introducing in this section the main concepts that accompany us throughout this article, including phase-space representations of quantum states, sub-Planck structures, and the metrological potential of coherent-state superpositions. We do this by means of the common example of the harmonic oscillator or algebra, defined through an annihilation operator that satisfies the canonical commutation relation . We work with dimensionless versions of position and momentum , so-called quadratures, which satisfy the uncertainty relation , where
| (1) |
defines the uncertainty of any operator Robertson (1929); Wheeler and Zurek (1983).
II.1 Sub-Planck structures:
compass state versus cat mixture
Coherent states were introduced by Schrödinger as non-spreading wave packets of the quantum harmonic oscillator Schrödinger (1935). They are defined Glauber (1963); Gerry and Knight (2005); Navarrete-Benlloch (2015) as the eigenstates of the annihilation operator , with , and are obtained from the vacuum state by acting on the displacement operator as
| (2) |
where
| (3) |
In this work we are interested in states built as superpositions of coherent states
| (4) |
The superposition of two coherent states with the same amplitude and opposite phase leads to the so-called cat state Dodonov et al. (1974); Gerry and Knight (2005), while the superposition of four coherent states along the same phase-space line is known as the quantum tetrachotomous state Shukla et al. (2019). On the other hand, superposing four coherent states with the same amplitude and maximally-spread phases we obtain the so-called compass states Zurek (2001). We provide specific examples shortly.
The Wigner function provides a useful way to visualize all these states in phase space Hillery et al. (1984); Schleich (2001); Leonhardt (2010); Navarrete-Benlloch (2015). For a generic quantum state , it can be written as the expectation value of the displaced parity operator Royer (1977)
| (5) |
where
| (6) |
is the coordinate vector in phase space and is the parity operator. Using the well-known properties
| (7a) | ||||
| (7b) | ||||
| (7c) | ||||
it is easy to find for the arbitrary coherent-state superposition (4) that
| (8) |
where the Wigner function of the operator is the complex Gaussian
| (9) | ||||
where
| (10) |
represents the locations of the coherent states in phase space and is known as the symplectic form.
The product of quadrature uncertainties has a lower limit , which is sometimes denoted by the Planck action in phase space (note that it is equal to for position and momentum with proper units). This led to the belief that phase-space structures with areas below this Planck scale either do not exist or pose no observational consequences for physical quantum states. This was challenged by Zurek Zurek (2001), who showed that compass states not only have sub-Planck structures, but play a crucial role in enhancing their sensitivity to phase-space displacements, which is related to their metrological power as we discuss later.
In order to discuss in more detail the origin of sub-Planck structures, we consider next some specific classes of coherent-state superpositions. Let us start with cat states Gerry and Knight (2005), in particular the horizontal-cat defined along the position phase-space axis (in the following we omit normalizations of states and Wigner functions to simplify the notation)
| (11) |
with . Particularizing the general Wigner function (8) to this state we obtain
| (12) |
for
| (13) |
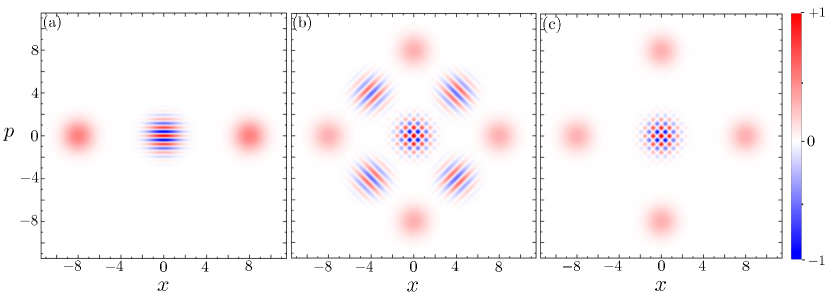
which we plot in Fig. 1(a). The figure presents two Gaussian lobes centered at positions , which correspond to the Wigner functions of the underlying coherent states . In addition, around the origin of phase space, it shows oscillations along the momentum direction with period , generated from the quantum interference between the coherent states.
We can also build vertical cat states as a superposition of two coherent states in the momentum axis, and hence just as a rotation of the horizontal cat states, that is,
| (14) |
The corresponding Wigner function has the same form as Eq. (12), but swapping and as
| (15) |
Let us consider now the superposition of horizontal and vertical cat states, leading to Zurek’s compass state Zurek (2001)
| (16) |
The corresponding Wigner function is represented in Fig. 1(b), which using Eq. (8) can be written as
| (17) |
where
| (18) |
corresponds to the Wigner functions of the four coherent states underlaying the compass state (Gaussian lobes at the north, south, east, and west positions),
| (19) |
corresponds to their interference pattern at the center of phase space, and
| (20) |
for
| (21) |
contains the interference terms generated far from the phase-space origin (cat-like interference patterns located at the northeast, northwest, southeast, and southwest positions).
Remarkably, the central chessboard-like pattern contains tiles of alternating sign (denoted by different colors in the figure) with areas proportional to , hence below the Planck scale for . These are the sub-Planck structures first identified in Zurek (2001), whose size is limited in all phase space directions. In contrast, the structures appearing in the interference pattern of the cat state of Fig. 1(a) are limited only in the vertical direction, but not in the horizontal direction, where they show a Gaussian profile.
It is interesting for our purposes to consider one more type of states, built as incoherent mixtures of the cat states introduced above
| (22) |
The corresponding Wigner function, shown in Fig. 1(c), reads
| (23) |
which is almost the same as that of the compass state, just missing the interference terms. Remarkably, this means that the same chessboard pattern with sub-Planck structures appears for the cat mixture Kumari et al. (2015). Now, since the interference structures of cat states are not considered to be sub-Planck (since they are not limited in all phase-space directions), and an incoherent mixing of two states cannot enhance their individual quantum properties, this raises legitimate doubts about up to what point the presence of sub-Planck structures in the Wigner function is enough to claim that any interesting quantum properties appear.

II.2 Sensitivity to displacements
In order to show the differences between the three types of states introduced in the preceding section, it is interesting to consider their sensitivity to phase-space displacements. In particular, given a state and its displaced version , where is an arbitrary displacement, we consider their overlap
| (24) |
where the last equality applies when the state is pure, . This quantity provides a measure Audenaert (2014) for the distinguishability of the state and its displaced version. The smaller the displacement needs to be in order to bring the overlap to zero, the more sensitive the state is said to be against displacements. This has immediate implications for quantum metrology: Imagine that a signal that we want to measure is linearly coupled to our harmonic oscillator, which then experiences a displacement proportional to the signal’s strength; the sensitivity of the oscillator to displacements is then translated into a signal resolution, such that quantum states with higher sensitivity are able to resolve weaker signals Toscano et al. (2006).
Let us consider the example of coherent states. Using (7), we easily find the overlap as
| (25) |
We see that displacements above the Planck scale are required in order to make this overlap vanish. This determines the resolution of coherent states as metrological tools. It is interesting to note that, in the case of coherent states, the sensitivity to displacements is independent of the number of quanta present in the state, . Hence, the sensitivity cannot be improved by increasing and is solely limited by the shot noise introduced by vacuum fluctuations.
Consider next cat states, in particular the horizontal cat state defined in Eq. (11). Decomposing the displacement in real and imaginary parts as
| (26) |
the overlap (24) is easily found to be
| (27) |
Here and in the following we make heavy use of the properties (7). The overlap function vanishes identically when
| (28) |
Note that the number of excitations in the cat state is for . Hence, in contrast to coherent states, the sensitivity of cat states to displacements in the momentum direction scales as , which is well beyond the Planck scale for “macroscopic” cat states with (this scaling is known as the Heisenberg limit of the sensitivity). On the other hand, for displacements in the position direction, cat states pose no advantage with respect to coherent states. This is illustrated in Fig. 2(a), where we plot the overlap as a function of the displacement.
Consider now the compass state of Eq. (16), for which we easily obtain
| (29) |
with . This overlap is shown in Fig. 2(b). The vanishing condition is now either of the following
| (30) |
As appreciated in Fig. 2(b), this is satisfied for displacements with and arbitrary phase. Hence, as compared to coherent states, a compass state with excitations (approximately equal to for ) has a -enhanced sensitivity against displacements, but now in any phase-space direction, making it much more valuable for quantum metrology than cat states Toscano et al. (2006).
There is a natural impulse to associate this property of compass states with their sign-alternating sub-Planck structures. However, only by themselves, these structures are not enough to generate such enhancement of the sensitivity to arbitrary displacements. In order to show this, consider now the cat-state mixture (22), which as mentioned above also presents the same sub-Planck structures in the center of phase space. The overlap (24) reads in this case
| (31) |
In order for this expression to vanish, the following two conditions need to be satisfied simultaneously:
| (32a) | ||||
| (32b) | ||||
Hence, the cat-state mixture also has -enhanced sensitivity against displacements, but only for those performed along the directions diagonal with respect to the axis system formed by the cat states ( in our case). This is illustrated in Fig. 2(c). Hence, in spite of also having sub-Planck structures in the Wigner function, cat-state mixture do not have the potential for metrology of compass states, for which the extra quantum coherence of the cat-state superposition plays a crucial role.
In summary, as compared to coherent states, for a given number of quanta , compass states show a -enhancement of the sensitivity against displacements in arbitrary directions in phase space. In contrast, cat states and cat-state mixtures show this sensitivity enhancement only in specific phase-space directions. Interestingly, this shows that even though the same sub-Planck scales are present in the Wigner function of cat-state mixtures and superpositions, the latter have way more potential for quantum metrology.
III Generalization to the SU(2) group
Quantum mechanics associates a Hilbert space to each physical system. In turn, one common way of characterizing Hilbert spaces is through an operator algebra. For example, in §II we considered the algebra, which acts on an infinite-dimensional Hilbert space and is typically associated to one-dimensional mechanical systems. As different systems are characterized by different algebras, from the early days of quantum mechanics there was an interest in extending results found for one algebra to different ones, or, even better, developing full generalizations when possible Perelomov (1986). This is of even more practical interest these days, since we are now able to devise experimental implementations of essentially any algebra we can think of.
In this spirit, in this section we show that the previous results found for the algebra can be extended to another of the most common algebras appearing in quantum-mechanical systems: the (2) or angular momentum algebra. This algebra involves a vector operator , the generator of rotations Cohen-Tannoudji et al. (1977); Basdevant and Dalibard (2002); Sakurai (1994), and is characterized by the commutation relations
| (33) |
where is the Levi-Cività symbol (totally antisymmetric form). The irreducible representations of this algebra can be labeled by an index that can only take integer or half-integer values, and is related to the spectrum of , the quadratic Casimir operator of the (2) algebra, which commutes with all (2) generators. Each of these representations has dimension , and is spanned by the common eigenbasis of and one projection of , say , so that
| (34) |
In the following we provide a SU(2) generalization of the various coherent-state superpositions discussed in §II, showing that even their properties related to sub-Planck structures and sensitivity against displacements can be properly adapted to this case. In order to make a connection with the preceding section, it is interesting to note that, in quantum-optical experimental implementations, the maximal eigenvalue is typically related to a number of excitations that need to be deposited in the system. For example, an (2) algebra with angular momentum can be implemented with an ensemble of indistinguishable two-level systems ( corresponding to all atoms excited) or with two bosonic modes sharing excitations (this is the so-called Schwinger representation of angular momentum, where corresponds to all excitations gathered on one of the modes, leaving the other in vacuum) Pezzè et al. (2018). We see that the -sensitivity enhancement of HW coherent-state superpositions is then replaced by a enhancement.
III.1 Preliminaries:
SU(2) coherent states and the Wigner function
Let us introduce the SU(2) coherent states Radcliffe (1971); Perelomov (1972); Gilmore (1972); Arecchi et al. (1972); Perelomov (1986). Our starting point is the SU(2) displacement operator, which admits either of the forms
| (35) |
parametrized through for convenience, with and , in which case , , and . The raising and lowering operators are
| (36) |
The SU(2) displacements correspond to rotations of angle around the axis. Throughout the article, we make use of their composition rule Perelomov (1986)
| (37) |
where
| (38a) | ||||
| (38b) | ||||
As Eq. (37) does not depend on , it is easily proven by particularizing it to the representation, where all operators correspond to matrices (Pauli matrices for the components of ).
Applying the displacement operator to the reference state , we obtain a SU(2) coherent state
| (39) |
where
| (40) |
is easily found by using the intermediate form of the displacement (35), taking into account that
| (41a) | ||||
| (41b) | ||||
where . The coherent states can be associated with the points
| (42) |
on a unit sphere, such that corresponds to the north pole. The overlap between two coherent states is
| (43) |
Hence, for the overlap between the reference state and any coherent state is approximately Gaussian as a function of ,
| (44) |
similarly to the HW coherent states. Note that with this parametrization of SU(2) coherent states in terms of , the width of the Gaussian scales as . In general, the overlap between two coherent states pinned at different points of the unit sphere decreases with as
| (45) |
where
| (46) |
for
| (47) |
Indeed, we see later that the effective support of the SU(2) coherent-state’s Wigner function (which can be defined as a quasi-probability distribution on the sphere) decreases following the corresponding scaling in .

In the next section we consider different coherent-state superpositions of the type
| (48) |
which generalize the ones studied for the algebra. Just as in that case, the Wigner function is a very useful tool for the characterization of these states Várilly and Gracia-Bondía (1989); Heiss and Weigert (2000); Klimov et al. (2017); Koczor et al. (2020). In the SU(2) case, for any state , it can be evaluated via the Stratonovich-Weyl correspondence as Davis et al. ,
| (49) |
with
| (50) |
where
| (51) |
with the Clebsch-Gordan coefficients. As for the Heisenberg-Weyl group, this Wigner function is real and bounded (but not necessarily positive, not even for coherent states in this case, although their negativity decreases with Davis et al. ). Hence, we can use it to visualize the state, by plotting it either over the surface of the unit sphere or, as we do, in the stereographic plane , where
| (52) |
Note that the origin of this plane corresponds to the north pole of the sphere, while the equator is represented as the circle of unit radius, and the south pole as a circle of infinite radius.
The Wigner function of the generic superposition (48) can be written as
| (53) |
where, using Eqs. (37) and (39), the Wigner function of the operator is easily found to be
| (54) |
with
| (55a) | ||||
| (55b) | ||||
This form is suited for numerical computation, but, for analytical purposes, sometimes alternative derivations are more convenient, as we show in the Appendix for the states that we consider in the next section.
III.2 SU(2) cat and compass states:
sub-Planck structures
Let us now consider specific coherent-state superpositions, and show how the concept of sub-Planck structures presented in §II for the algebra, also extends to the case. To this aim, we focus on coherent states distributed along the equator, that is, in Eq. (48).
Superposing two antipodal SU(2) coherent states we obtain a SU(2) cat state Sanders (1989b); Huang et al. (2015, 2018); Maleki and Zheltikov (2020); Davis et al. . Consider in particular the coherent states along the horizontal axis of the stereographic plane (as in §II, we omit normalizations in states and Wigner functions), defining the horizontal cat state
| (56) |
We derive the Wigner function of this state in the Appendix, obtaining
| (57) |
where the last term provides the interference between the underlying coherent states
| (58) |
with
| (59a) | ||||
| (59b) | ||||
while the first terms correspond to the Wigner functions of the coherent states
| (60) |
where is the Legendre polynomial Várilly and Gracia-Bondía (1989).
In Fig. 3(a) we plot this Wigner function in the stereographic plane , as explained in the preceding section. We can clearly see two lobes centered at positions , which correspond to the coherent states. Increasing has the effect of reducing the extension (effective support) of these lobes. In addition, the interference between these coherent states generates an oscillating pattern in the vertical direction, similarly to what happens for the horizontal HW cat states. The zeros of this interference pattern , occur when
| (61) |
Along the axis (), this means that the first zeros are located at for . On the other hand, in the horizontal direction for any fixed , the interference pattern simply decays as a Gaussian for , hence with a width proportional to . This is precisely the same scaling that we found for the width of the overlap between coherent states. Hence, similarly to the HW case, we see that the support of the structures appearing in the interference pattern of horizontal SU(2) cat states is limited only in the direction.
We can also define cat states along the vertical axis of the stereographic plane as
| (62) |
whose Wigner function is like the one of the horizontal cat state, but rotated by in the stereographic plane, that is,
| (63) |
Note that, similarly to Eq. (57) for , we write the Wigner function of as the sum of the Wigner function of its underlaying coherent states , plus their interference .
Given these cat states, we then define the SU(2) compass states as we already did for the HW case: the balanced superposition defined by
| (64) |
The corresponding Wigner function, which we show in Fig. 3(b), is equal to the sum of the individual Wigner functions of each cat state, plus the terms coming from the interference between these (the northwest, northeast, southeast, and southwest structures shown in the figure). We discuss the analytic form of this Wigner function in the Appendix. For our purposes here, it is interesting to note that for the interference pattern close to the origin of the stereographic plane (say ) is the sum of the interference patterns of the cat states, that is,
| (65) |
leading to the chessboardlike pattern shown in Fig. 3(b). This pattern is reminiscent of the one found for the algebra, and shows that structures limited in all directions of the stereographic plane appear in this SU(2) compass state. This alternating-sign tiles have an extension proportional to in any direction, which is a factor smaller than the extension found for coherent states. This generalizes the concept of sub-Planck structures to SU(2): structures with a support of area smaller than the support of coherent states.
From the previous discussion, it is clear that a mixture of cat states also present the same chessboard pattern. Indeed, considering the mixture,
| (66) |
the corresponding Wigner function of above cat-state mixture can be simply written as,
| (67) |
which is shown in Fig. 3(c), where the chessboard can be appreciated. In fact, just like in the case of the algebra, only the inter-cat-state interference regions are missing with respect to the Wigner function of the compass state.
In summary, we have shown that the same phase-space features found for HW cat and compass states, as well as cat-state mixtures, are found for their SU(2) counterparts in the stereographic plane, provided we restrict the underlying coherent states to the equator. Interestingly, the role of in the HW case (distance of the coherent states from the origin) is played by in the SU(2) case. Let us remark that, around the equator, the SU(2) group is contracted in the limit to the two-dimensional Euclidean group E(2) group Rowe et al. (2001), which makes the results that we are exposing in this section nontrivial. In contrast, around the poles SU(2) is contracted to the HW group (Holstein-Primakoff approximation) Arecchi et al. (1972); Rowe et al. (2001), in which case all the results of the preceding section are trivially generalized, since simply becomes an annihilation operator.

III.3 Distinguishability under SU(2) displacements
Let us now show that the SU(2) coherent-state superpositions discussed above also behave similarly to their HW counterparts regarding their sensitivity against displacements. For this, again we compute the overlap between the states and their -displaced versions, as given by Eq. (24). This overlap is easily evaluated for coherent-state superpositions by making use of the property
| (68) |
which is proven by using the composition rule (37) and the coherent-state overlap (43).
In the case of a single coherent state, we have already established in §II that, for , this overlap has an approximately Gaussian form . Hence, in the SU(2) case, the sensitivity of coherent states to displacements scales as . We then have to compare the sensitivity of coherent-state superpositions against this scaling.
Let us start with cat states. Defining , with , using Eq. (68), for the horizontal cat (56) we easily obtain
| (69) |
We show this overlap in Fig. 4(a). As long as and , Eq. (69) shows that plays no relevant role in the overlap, which vanishes for displacements
| (70) |
For large , minimum displacement that turns the cat state into an orthogonal state scales as and must occur in the vertical direction of the stereographic plane. Therefore, in this direction, as compared to coherent states, cat states show a -enhanced sensitivity to displacements. In contrast, for horizontal displacements they show no enhancement of the sensitivity compared to coherent states.
Let us now consider the compass state, for which the overlap (68) leads to
| (71) |
We show this overlap in Fig. 4(b). Similarly to the HW compass state, now the -enhanced sensitivity to displacements is independent of the displacement direction.
Finally, we calculate the overlap for the SU(2) cat-state mixture (66). The key point here is to note that, for and , the contribution of the cross terms between the cat states to the overlap, e.g., , is negligible. Then, for small displacements the overlap is the sum of overlaps of the individual cat states, that is,
| (72) |
where . The corresponding overlap is shown in Fig. 4(c), and shows the same properties as its HW counterpart: the -enhanced sensitivity is only present for displacements in the directions.
These results show that, as promised, all the features we found for HW coherent-state superpositions are exported to SU(2) coherent-state superpositions, as long as the states are restricted to the equator, where the SU(2) group contracts to the Euclidean group in two dimensions E(2) Rowe et al. (2001), as already mentioned above. In particular, we have shown that SU(2) compass states have a -enhanced sensitivity against displacements as compared to coherent states. This occurs for displacements in arbitrary directions in the stereographic plane, while cat states and mixtures show such an enhanced sensitivity only in special directions.
Note that one of the main motivations for the study of SU(2) compass states is their potential application to quantum metrology, in particular as sensors of rotations. When the rotation axis is known, cat states along that axis are known to provide the desired quantum advantage over coherent states Giovannetti et al. (2004); Dowling (2008); Giovannetti et al. (2011); Pezzè et al. (2018). In contrast, when the axis of rotation is completely unknown, it has been found that the optimal quantum rotosensor states are complicated in general Björk et al. (2015, 2015); Chryssomalakos and Hernández-Coronado (2017); Goldberg and James (2018); Martin et al. (2020), but well approximated for small angles by anticoherent states, whose so-called Majorana constellation is uniformly spread over the unit sphere Giraud et al. (2010). This has been checked so far up to , but it is believed to be true for arbitrary based on physical arguments Chryssomalakos and Hernández-Coronado (2017); Martin et al. (2020). Our compass states can be very useful for intermediate situations in which the rotation axis is bound to a given plane, but is otherwise unknown. This is because the SU(2) displacements defined in Eq. (35) effect rotations around any axis defined on the equator of the unit sphere so that by orienting the sphere appropriately, compass states will provide -enhanced sensitivity to the rotations we want to measure as compared to coherent states.
IV Conclusions and outlook
In this work we have generalized to the SU(2) group some features of coherent-state superpositions commonly studied for the HW group associated with the harmonic oscillator. Specifically, by restricting the SU(2) coherent states to the equator of the sphere that plays the role of phase space, we have shown that four-state superpositions have a Wigner function with properties similar to that of the HW compass states: A chess-board like pattern appears around the origin of the stereographic plane, which contains structures with support that scales as with respect to the effective support of coherent states. This generalizes the sub-Planck structures found in HW compass states, with the role of the number of quanta being played by the total angular momentum . Further, SU(2) cat states can also be defined as superpositions of two coherent states, which show an interference pattern with structures limited only along one direction, just as their HW counterparts. Moreover, SU(2) cat-state mixtures present the same sub-Planck structures as compass states. However, we have shown that compass states and cat-state mixtures are very different regarding their sensitivity to SU(2) displacements: As compared to coherent states, compass states have a -enhanced sensitivity against displacements in any direction, while cat states and cat-state mixtures show such enhancement only along specific directions. Again, this is exactly the same behavior found for the HW case, with playing the role of .
For there is a well known connection between the HW group and the restriction of SU(2) to the neighborhood of a pole (Holstein-Primakoff approximation) Arecchi et al. (1972). In contrast, for states around the equator, SU(2) contracts to the two-dimensional Euclidean group E(2) Rowe et al. (2001), which makes our generalizations nontrivial. Looking ahead, it is interesting to extend the notion of sub-Planck structures and the corresponding sensitivity to displacements to arbitrary groups, especially those relevant to modern experimental quantum-optical platforms such as SU(1,1) Perelomov (1986); Seyfarth et al. (2020) and higher-dimensional Lie groups including SU(3) Nemoto and Sanders (2001).
Having established these connections between the HW and SU(2) groups, there are many other routes that one can pursue. For example, in this work we have considered only superpositions of coherent states with the same amplitude. Interestingly, in the case of the HW group, superpositions of states with different amplitudes have been shown to play a role as eigenstates of the displaced-parity operator , which in turn is related to a nontrivial symmetry of the forced Harmonic oscillator Markovich and Messina (2020). Generalizing to the SU(2) case the parity operator as , it is easy to show that the coherent-state superpositions are eigenstates of the SU(2) displaced-parity operator , similarly to the HW case. It will then be interesting to extend to the SU(2) group all the results known in this context for the HW group, in particular exploring whether the latter operator is also related to a nontrivial symmetry of some SU(2) Hamiltonian. Moreover, generalized displaced-parity operators with very interesting properties have been defined for the HW group Messina and Drăgănescu (2013), whose SU(2) counterparts can also be investigated in future works.
Another clear future endeavor would concern how to generate the SU(2) compass states introduced in our work. There is already a vast literature discussing plausible schemes for the implementation of SU(2) cat states, particularly NOON and GHZ states, as mentioned in the introduction (see Omran et al. (2019); Monz et al. (2011); Wang et al. (2016); Afek et al. (2010); Zhang et al. (2018) for actual recent experimental implementations in different platforms). Perhaps some of these methods can be adapted for the generation of a superposition of the four coherent states required for compass states, which otherwise will require developing completely new proposals. As a concrete promising candidate, let us mention weak-field homodyne detection Thekkadath et al. (2020a), which so far has been used to engineer HW cat states of arbitrary amplitude Thekkadath et al. (2020b), but can be generalized for the robust preparation of compass states and should be exportable to some of the SU(2) platforms in which homodyne detection is available.
Acknowledgements.
N.A. thanks everyone at the Wilczek Quantum Center for their hospitality and the Chinese Scholarship Council for financial support. B.C.S. acknowledges the National Natural Science Foundation of China for their financial support (Grant No. 11675164). C.N.B. appreciates support from a Shanghai talent program and from the Shanghai Municipal Science and Technology Major Project (Grant No. 2019SHZDZX01).Appendix A Wigner function of SU(2) states
Let us here provide more detailed derivations of the various SU(2) Wigner functions that we have introduced in the main text. Instead of directly using the general form of Eq. (54), in some cases simpler expressions are found using the composition property of displacement operators, which we rewrite here as
| (73) |
with
| (74a) | ||||
| (74b) | ||||
and their action on the kernel Várilly and Gracia-Bondía (1989); Klimov et al. (2017):
| (75) |
where , and we have defined the spherical harmonics and the irreducible tensor operators
| (76) |
where we recall that are Clebsch-Gordan coefficients. In the following, we use these expressions to simplify the derivations of some Wigner functions.
Let us start with the Wigner function of the coherent state , which is expressed as
| (77) |
Using the composition rule (73) we can rewrite this expression as
| (78) | ||||
| (79) |
with . Inserting (75) in this expression, and taking into account that
| (80a) | ||||
| (80b) | ||||
we obtain the expression (60).
The Wigner function of the coherent state , which reads
| (81) |
is found in a similar fashion, but first we need to manipulate a bit the expression. In particular, we use the identity
| (82) |
to write
| (83) |
where in the last step we have used the composition rule (73). Inserting this expression in (81), we obtain
| (84) |
Finally, using the expression (75) for the displaced kernel and taking into account Eqs. (80), together with
| (85a) | ||||
| (85b) | ||||
we obtain expression (60) for .
Let us now consider the Wigner function of the horizontal cat state , which is expanded as
| (86) |
Using various results from the previous lines, the last term is written as
| (87) | ||||
with coming from the composition rule for the displacements. Inserting now the expression (75) for the displaced kernel, taking into account that
| (88a) | ||||
| (88b) | ||||
and considering only the real part of we obtain precisely the term of Eq. (58).
The same approach is easily applied to the vertical cat . On the other hand, for the Wigner function of the compass state we also need to evaluate cross terms between vertical and horizontal coherent states of the type
| (89) |
These cross terms can be obtained by using Eq. (54). However, numerical inspection of this expression shows that for these terms do not contribute for small , as mentioned in the main text.
References
- Dodonov and Man’ko (2003) V. V. Dodonov and V. I. Man’ko, Theory of Nonclassical States of Light (Taylor & Francis, New York, 2003).
- Schnabel (2017) R. Schnabel, “Squeezed states of light and their applications in laser interferometers,” Phys. Rep. 684, 1 (2017).
- Horodecki et al. (2009) R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki, “Quantum entanglement,” Rev. Mod. Phys. 81, 865 (2009).
- Lütkenhaus and Barnett (1995) N. Lütkenhaus and S. M. Barnett, “Nonclassical effects in phase space,” Phys. Rev. A 51, 3340 (1995).
- Kenfack and Yczkowski (2004) A. Kenfack and K. Yczkowski, “Negativity of the Wigner function as an indicator of non-classicality,” J. Opt. B 6, 396 (2004).
- Richter and Vogel (2002) T. Richter and W. Vogel, “Nonclassicality of quantum states: A hierarchy of observable conditions,” Phys. Rev. Lett. 89, 283601 (2002).
- Hertz et al. (2020) A. Hertz, N. J. Cerf, and S. De Bièvre, “Relating the entanglement and optical nonclassicality of multimode states of a bosonic quantum field,” Phys. Rev. A 102, 032413 (2020).
- Bužek and Knight (1995) V. Bužek and P. L. Knight, Quantum Interference, Superposition States of Light and Nonclassical Effects, Prog. Opt., Vol. 34 (Elsevier, Amsterdam, 1995) p. 1.
- Gerry and Knight (2005) C. Gerry and P. Knight, Introductory Quantum Optics (Cambridge University Press, Cambridge, 2005).
- Schleich (2001) W. P. Schleich, Quantum Optics in Phase Space (Wiley-VCH, Weinheim, 2001).
- Bassi and Ghirardi (2003) A. Bassi and G. C. Ghirardi, “Dynamical reduction models,” Phys. Rep. 379, 257 (2003).
- Schlosshauer (2005) M. Schlosshauer, “Decoherence, the measurement problem, and interpretations of quantum mechanics,” Rev. Mod. Phys. 76, 1267 (2005).
- Abdi et al. (2016) M. Abdi, P. Degenfeld-Schonburg, M. Sameti, C. Navarrete-Benlloch, and M. J. Hartmann, “Dissipative Optomechanical Preparation of Macroscopic Quantum Superposition States,” Phys. Rev. Lett. 116, 233604 (2016).
- Pino et al. (2018) H. Pino, J. Prat-Camps, K. Sinha, B. P. Venkatesh, and O. Romero-Isart, “On-chip quantum interference of a superconducting microsphere,” Quantum Sci. Technol. 3, 025001 (2018).
- Zurek (2001) W. H. Zurek, “Sub-Planck structure in phase space and its relevance for quantum decoherence,” Nature 412, 712 (2001).
- Toscano et al. (2006) F. Toscano, D. A. R. Dalvit, L. Davidovich, and W. H. Zurek, “Sub-Planck phase-space structures and Heisenberg-limited measurements,” Phys. Rev. A 73, 023803 (2006).
- Dalvit et al. (2006) D. A. R Dalvit, R. L. de Matos Filho, and F. Toscano, “Quantum metrology at the Heisenberg limit with ion trap motional compass states,” New J. Phys. 8, 276 (2006).
- Weyl (1950) H. Weyl, The Theory of Groups and Quantum Mechanics (Dover, New York, 1950).
- Navarrete-Benlloch (2015) C. Navarrete-Benlloch, An Introduction to the Formalism of Quantum Information with Continuous Variables (Morgan & Claypool/IOP, Bristol, 2015).
- Berry (1979) M. V. Berry, “Evolution of semiclassical quantum states in phase space,” J. Phys. A: Math. Gen. 12, 625–642 (1979).
- Korsch and Berry (1981) H. J. Korsch and M. V. Berry, “Evolution of Wigner’s phase-space density under a nonintegrable quantum map,” Physica D 3, 627 (1981).
- Weedbrook et al. (2012) C. Weedbrook, S. Pirandola, R. García-Patrón, N. J. Cerf, T. C. Ralph, J. H. Shapiro, and S. Lloyd, “Gaussian quantum information,” Rev. Mod. Phys. 84, 621–669 (2012).
- Cerf et al. (2007) N. J. Cerf, G. Leuchs, and E. S. Polzik, Quantum Information with Continuous Variables of Atoms and Light (Imperial College Press, London, 2007).
- Yurke and Stoler (1986) B. Yurke and D. Stoler, “Generating Quantum Mechanical Superpositions of Macroscopically Distinguishable States via Amplitude Dispersion,” Phys. Rev. Lett. 57, 13–16 (1986).
- Sanders (1989a) B. C. Sanders, “Superposition of two squeezed vacuum states and interference effects,” Phys. Rev. A 39, 4284–4287 (1989a).
- Zurek (2003) W. H. Zurek, “Decoherence, einselection, and the quantum origins of the classical,” Rev. Mod. Phys. 75, 715 (2003).
- Agarwal and Pathak (2004) G. S. Agarwal and P. K. Pathak, “Mesoscopic superposition of states with sub-Planck structures in phase space,” Phys. Rev. A 70, 053813 (2004).
- Pathak and Agarwal (2005) P. K. Pathak and G. S. Agarwal, “Generation of a superposition of multiple mesoscopic states of radiation in a resonant cavity,” Phys. Rev. A 71, 043823 (2005).
- Stobińska et al. (2011) M. Stobińska, A. S. Villar, and G. Leuchs, “Generation of Kerr non-Gaussian motional states of trapped ions,” Europhys. Lett. 94, 54002 (2011).
- Leghtas et al. (2013) Z. Leghtas, G. Kirchmair, B. Vlastakis, M. H. Devoret, R. J. Schoelkopf, and M. Mirrahimi, “Deterministic protocol for mapping a qubit to coherent state superpositions in a cavity,” Phys. Rev. A 87, 042315 (2013).
- Govia et al. (2014) L. C. G. Govia, E. J. Pritchett, and F. K. Wilhelm, “Generating nonclassical states from classical radiation by subtraction measurements,” New J. Phys. 16, 045011 (2014).
- Hastrup et al. (2020) J. Hastrup, J. S. Neergaard-Nielsen, and U. L. Andersen, “Deterministic generation of a four-component optical cat state,” Opt. Lett. 45, 640 (2020).
- Ofek et al. (2016) N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “Extending the lifetime of a quantum bit with error correction in superconducting circuits,” Nature 536, 441 (2016).
- Vlastakis et al. (2013) B. Vlastakis, G. Kirchmair, Z. Leghtas, S. E. Nigg, L. Frunzio, S. M. Girvin, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “Deterministically encoding quantum information using 100-photon Schrödinger cat states,” Science 342, 607 (2013).
- Praxmeyer et al. (2016) L. Praxmeyer, C.-C. Chen, P. Yang, S. D. Yang, and R. K. Lee, “Direct measurement of time-frequency analogs of sub-Planck structures,” Phys. Rev. A 93, 053835 (2016).
- Lemos et al. (2012) G. B. Lemos, R. M. Gomes, S. P. Walborn, P. H. S. Ribeiro, and F. Toscano, “Experimental observation of quantum chaos in a beam of light,” Nat. Commun. 3, 2041 (2012).
- Austin et al. (2010) D. R. Austin, T. Witting, A. S. Wyatt, and I. A. Walmsley, “Measuring sub-Planck structural analogues in chronocyclic phase space,” Opt. Commun. 283, 855 (2010).
- Jacquod et al. (2002) P. Jacquod, I. Adagideli, and C. W. J. Beenakker, “Decay of the Loschmidt Echo for Quantum States with Sub-Planck-scale Structures,” Phys. Rev. Lett. 89, 154103 (2002).
- Wisniacki (2003) D. A. Wisniacki, “Short-time decay of the loschmidt echo,” Phys. Rev. E 67, 016205 (2003).
- Ghosh et al. (2006) S. Ghosh, A. Chiruvelli, J. Banerji, and P. K. Panigrahi, “Mesoscopic superposition and sub-Planck-scale structure in molecular wave packets,” Phys. Rev. A 73, 013411 (2006).
- Praxmeyer et al. (2007) L. Praxmeyer, P. Wasylczyk, C. Radzewicz, and K. Wódkiewicz, “Time-Frequency Domain Analogues of Phase Space Sub-Planck Structures,” Phys. Rev. Lett. 98, 063901 (2007).
- Scott and Caves (2008) A. J. Scott and C. M. Caves, “Teleportation fidelity as a probe of sub-Planck phase-space structure,” Ann. Phys. (NY) 323, 2685 (2008).
- Bhatt et al. (2008) J. R. Bhatt, P. K. Panigrahi, and M. Vyas, “Entanglement-induced sub-Planck phase-space structures,” Phys. Rev. A 78, 034101 (2008).
- Stobińska et al. (2008) M. Stobińska, G. J. Milburn, and K. Wódkiewicz, “Wigner function evolution of quantum states in the presence of self-Kerr interaction,” Phys. Rev. A 78, 013810 (2008).
- Ghosh et al. (2009) S. Ghosh, U. Roy, C. Genes, and D. Vitali, “Sub-Planck-scale structures in a vibrating molecule in the presence of decoherence,” Phys. Rev. A 79, 052104 (2009).
- Roy et al. (2009) U. Roy, S. Ghosh, P. K. Panigrahi, and D. Vitali, “Sub-Planck-scale structures in the Pöschl-teller potential and their sensitivity to perturbations,” Phys. Rev. A 80, 052115 (2009).
- Ghosh (2012) S. Ghosh, “Coherent control of mesoscopic superpositions in a diatomic molecule,” Int. J. Quantum Inf. 10, 1250014 (2012).
- Kumari et al. (2015) A. Kumari, A. K. Pan, and P. K. Panigrahi, “Sub-Planck structure in a mixed state,” Eur. Phys. D 69, 248 (2015).
- Dodonov et al. (2016) V.V. Dodonov, C. Valverde, L.S. Souza, and B. Baseia, “Decoherence of odd compass states in the phase-sensitive amplifying/dissipating environment,” Ann. Phys. (NY) 371, 296 (2016).
- Kumar and Lee (2017) P. Kumar and R.-K. Lee, “Sensitivity of sub-Planck structures of mesoscopically superposed coherent states to the thermal reservoirs induced decoherence,” Opt. Commun. 394, 23 (2017).
- Howard et al. (2019) L. A. Howard, T. J. Weinhold, F. Shahandeh, J. Combes, M. R. Vanner, A. G. White, and M. Ringbauer, “Quantum Hypercube States,” Phys. Rev. Lett. 123, 020402 (2019).
- Perelomov (1986) Askold Perelomov, Generalized Coherent States and Their Applications, Theoretical and Mathematical Physics (Springer-Verlag, Berlin, 1986).
- Perelomov (1972) A. M. Perelomov, “Coherent states for arbitrary Lie group,” Commun. Math. Phys. 26, 222 (1972).
- Radcliffe (1971) J. M. Radcliffe, “Some properties of coherent spin states,” J. Phys. A: Math. Theor. 4, 313 (1971).
- Gilmore (1972) R. Gilmore, “Geometry of symmetrized states,” Ann. Phys. (NY) 74, 391 (1972).
- Arecchi et al. (1972) F. T. Arecchi, E. Courtens, R. Gilmore, and H. Thomas, “Atomic coherent states in quantum optics,” Phys. Rev. A 6, 2211 (1972).
- Sanders (1989b) B. C. Sanders, “Quantum dynamics of the nonlinear rotator and the effects of continual spin measurement,” Phys. Rev. A 40, 2417 (1989b).
- Huang et al. (2015) J. Huang, X. Qin, H. Zhong, Y. Ke, and C. Lee, “Quantum metrology with spin cat states under dissipation,” Sci. Rep. 5, 1 (2015).
- Huang et al. (2018) J. Huang, M. Zhuang, B. Lu, Y. Ke, and C. Lee, “Achieving Heisenberg-limited metrology with spin cat states via interaction-based readout,” Phys. Rev. A 98, 012129 (2018).
- Maleki and Zheltikov (2020) Y. Maleki and A. M. Zheltikov, “Spin cat-state family for Heisenberg-limit metrology,” J. Opt. Soc. Am. B 37, 1021 (2020).
- (61) J. Davis, M. Kumari, R. B. Mann, and S. Ghose, “Wigner negativity in spin- systems,” arXiv:2008.10167 .
- Greenberger et al. (1989) D. M. Greenberger, M. A. Horne, and A. Zeilinger, “Going beyond Bell’s theorem,” in Bell’s Theorem, Quantum Theory and Conceptions of the Universe, edited by M. Kafatos (Kluwer, Dordrecht, 1989) pp. 69–72.
- Dowling (2008) J. P. Dowling, “Quantum optical metrology – the lowdown on high-N00N states,” Contemp. Phys. 49, 125 (2008).
- Sanders and Gerry (2014) B. C. Sanders and C. C. Gerry, “Connection between the NOON state and a superposition of SU(2) coherent states,” Phys. Rev. A 90, 045804 (2014).
- Várilly and Gracia-Bondía (1989) J. C. Várilly and J. M. Gracia-Bondía, “The Moyal representation for spin,” Ann. Phys. (NY) 190, 107 (1989).
- Heiss and Weigert (2000) S. Heiss and S. Weigert, “Discrete Moyal-type representations for a spin,” Phys. Rev. A 63, 012105 (2000).
- Klimov et al. (2017) A. B. Klimov, J. L. Romero, and H. de Guise, “Generalized SU(2) covariant Wigner functions and some of their applications,” J. Phys. A: Math. Theor. 50, 323001 (2017).
- Koczor et al. (2020) B. Koczor, R. Zeier, and S. J. Glaser, “Continuous phase-space representations for finite-dimensional quantum states and their tomography,” Phys. Rev. A 101, 022318 (2020).
- Giovannetti et al. (2004) V. Giovannetti, S. Lloyd, and L. Maccone, “Quantum-enhanced measurements: Beating the standard quantum limit,” Science 306, 1330 (2004).
- Giovannetti et al. (2011) V. Giovannetti, S. Lloyd, and L. Maccone, “Advances in quantum metrology,” Nat. Photonics 5, 222 (2011).
- Pezzè et al. (2018) L. Pezzè, A. Smerzi, M. K. Oberthaler, R. Schmied, and P. Treutlein, “Quantum metrology with nonclassical states of atomic ensembles,” Rev. Mod. Phys. 90, 035005 (2018).
- Robertson (1929) H. P. Robertson, “The uncertainty principle,” Phys. Rev. 34, 163 (1929).
- Wheeler and Zurek (1983) J. A. Wheeler and W. H. Zurek, Quantum Theory and Measurement (Princeton University Press, Princeton, 1983).
- Schrödinger (1935) E. Schrödinger, “Die gegenwärtige Situation in der Quantenmechanik,” Naturwissenschaften 23, 807 (1935).
- Glauber (1963) R. J. Glauber, “Coherent and incoherent states of the radiation field,” Phys. Rev. 131, 2766 (1963).
- Dodonov et al. (1974) V. V. Dodonov, I. A. Malkin, and V. I. Man’ko, “Even and odd coherent states and excitations of a singular oscillator,” Physica 72, 597 (1974).
- Shukla et al. (2019) N. Shukla, N. Akhtar, and B. C. Sanders, “Quantum tetrachotomous states: Superposition of four coherent states on a line in phase space,” Phys. Rev. A 99, 063813 (2019).
- Hillery et al. (1984) M. Hillery, R. F. O’Connell, M. O. Scully, and E. P. Wigner, “Distribution functions in physics: Fundamentals,” Phys. Rep. 106, 121 (1984).
- Leonhardt (2010) U. Leonhardt, Essential Quantum Optics: From Quantum Measurements to Black Holes (Cambridge University Press, Cambridge, 2010).
- Royer (1977) A. Royer, “Wigner function as the expectation value of a parity operator,” Phys. Rev. A 15, 449 (1977).
- Audenaert (2014) K. M. R. Audenaert, “Comparisons between quantum state distinguishability measures,” Quantum Inf. Comput. 14, 31 (2014).
- Cohen-Tannoudji et al. (1977) C. Cohen-Tannoudji, B. Diu, and F. Lalöe, Quantum Mechanics,, Vol. I and II (Wiley, Paris, 1977).
- Basdevant and Dalibard (2002) J. L. Basdevant and J. Dalibard, Quantum Mechanics (Springer, Berlin, 2002).
- Sakurai (1994) J. J. Sakurai, Modern Quantum Mechanics (Addison-Wesley, Reading, 1994).
- Rowe et al. (2001) D. J. Rowe, H. de Guise, and B. C. Sanders, “Asymptotic limits of SU(2) and SU(3) Wigner functions,” J. Math. Phys. 42, 2315 (2001).
- Björk et al. (2015) G. Björk, M. Grassl, P. de la Hoz, G. Leuchs, and L. L. Sánchez-Soto, “Stars of the quantum universe: Extremal Constellations on the Poincaré sphere,” Phys. Scr. 90, 108008 (2015).
- Björk et al. (2015) G. Björk, A. B. Klimov, P. de la Hoz, M. Grassl, G. Leuchs, and L. L. Sánchez-Soto, “Extremal quantum states and their Majorana constellations,” Phys. Rev. A 92, 031801 (2015).
- Chryssomalakos and Hernández-Coronado (2017) C. Chryssomalakos and H. Hernández-Coronado, “Optimal quantum rotosensors,” Phys. Rev. A 95, 052125 (2017).
- Goldberg and James (2018) A. Z. Goldberg and D. F. V. James, “Quantum-limited Euler angle measurements using anticoherent states,” Phys. Rev. A 98, 032113 (2018).
- Martin et al. (2020) J. Martin, S. Weigert, and O. Giraud, “Optimal detection of rotations about unknown axes by coherent and anticoherent states,” Quantum 4, 285 (2020).
- Giraud et al. (2010) O. Giraud, P. Braun, and D. Braun, “Quantifying quantumness and the quest for queens of quantum,” New J. Phys. 12, 063005 (2010).
- Seyfarth et al. (2020) U. Seyfarth, A. B. Klimov, H. de Guise, G. Leuchs, and L. L. Sánchez-Soto, “Wigner function for SU(1,1),” Quantum 4, 317 (2020).
- Nemoto and Sanders (2001) K. Nemoto and B. C. Sanders, “Superpositions of SU(3) coherent states via a nonlinear evolution,” J. Phys. A: Math. Gen. 34, 2051 (2001).
- Markovich and Messina (2020) L. A. Markovich and A. Messina, “The fertile marriage between the two Glauber parity and displacement operators,” Phys. Scr. 95, 074008 (2020).
- Messina and Drăgănescu (2013) A. Messina and G. Drăgănescu, “Unitary representations of quantum superpositions of two coherent states and beyond,” Open Syst. Inf. Dyn. 20, 1340004 (2013).
- Omran et al. (2019) A. Omran, H. Levine, A. Keesling, G. Semeghini, T. T. Wang, S. Ebadi, H. Bernien, A. S. Zibrov, H. Pichler, S. Choi, J. Cui, M. Rossignolo, P. Rembold, S. Montangero, T. Calarco, M. Endres, M. Greiner, V. Vuletić, and M. D. Lukin, “Generation and manipulation of Schrödinger cat states in Rydberg atom arrays,” Science 365, 570 (2019).
- Monz et al. (2011) T. Monz, P. Schindler, J. T. Barreiro, M. Chwalla, D. Nigg, W. A. Coish, M. Harlander, W. Hänsel, M. Hennrich, and R. Blatt, “14-Qubit Entanglement: Creation and Coherence,” Phys. Rev. Lett. 106, 130506 (2011).
- Wang et al. (2016) X. L. Wang, L. K. Chen, W. Li, H.-L. Huang, C. Liu, C. Chen, Y.-H. Luo, Z.-E. Su, D. Wu, Z.-D. Li, H. Lu, Y. Hu, X. Jiang, C.-Z. Peng, L. Li, N.-L. Liu, Y. A. Chen, C. Y. Lu, and J. W. Pan, “Experimental Ten-Photon Entanglement,” Phys. Rev. Lett. 117, 210502 (2016).
- Afek et al. (2010) I. Afek, O. Ambar, and Y. Silberberg, “High-NOON states by mixing quantum and classical light,” Science 328, 879–881 (2010).
- Zhang et al. (2018) J. Zhang, M. Um, D. Lv, J. N. Zhang, L. M. Duan, and K. Kim, “Noon states of Nine Quantized Vibrations in Two Radial Modes of a Trapped ion,” Phys. Rev. Lett. 121, 160502 (2018).
- Thekkadath et al. (2020a) G. S. Thekkadath, D. S. Phillips, J. F. F. Bulmer, W. R. Clements, A. Eckstein, B. A. Bell, J. Lugani, T. A. W. Wolterink, A. Lita, S. W. Nam, T. Gerrits, C. G. Wade, and I. A. Walmsley, “Tuning between photon-number and quadrature measurements with weak-field homodyne detection,” Phys. Rev. A 101, 031801 (2020a).
- Thekkadath et al. (2020b) G. S. Thekkadath, B. A. Bell, I. A. Walmsley, and A. I. Lvovsky, “Engineering Schrödinger cat states with a photonic even-parity detector,” Quantum 4, 239 (2020b).