Sub-kilometre scale ionospheric studies at the SKA-Low site, using MWA extended baselines

Low frequency radio astronomy is under-going a rebirth, with the arrival of the next-generation instruments that will provide two orders of magnitude improvement in sensitivity and an order of magnitude improvement in frequency coverage. In particular the Low frequency Square Kilometre Array (SKA-Low) will provide an instantaneous frequency coverage of 50 to 350 MHz, a collecting area of 0.4 sq. kilometres, spread over 65km baselines in the Phase-1 and the full 1.0 sq. kilometres in Phase-2, and exciting prospects of new science. Thus it is vital that we update the radio-astronomical methods and strategies to match the potential of the radio-astronomical instruments. In this paper we focus on the challenges at the foundation of accurate direction-dependent ionospheric calibration, as these are among the most difficult obstacles to achieving the nominal SKA-Low performance.

Directional dependent (DD) calibration is vital at low frequencies, because the field of view (FoV) is intrinsically large and the propagation effects caused by inhomogeneties in the distribution of the ionospheric plasma ($\Delta{\rm I}$, measured in TECU or 10¹⁶ electrons per m²) imposes temporal and spatial phase disturbances on the incoming wavefront whose magnitude scales inversely proportional to the observing frequency ($\phi_{\rm ion}({\rm deg})=480\,\Delta{\rm I}\,\nu_{\rm GHz}^{-1}$, with $\nu_{\rm GHz}$ the observing frequency in GHz [1]).

Traditionally, with observations of smaller fields of view and at higher frequencies, these effects could largely be handled with a single station-based correction (or direction independent (DI) correction), valid for all of the field of view. Lonsdale (2005, Figure 1)[2] classified four operating regimes based on the relative sizes of the FoV (V), the ionospheric phase fluctuation disturbances (S) and the projected size of the array (A). Traditionally, with observations of smaller fields of view and at higher frequencies (V$\ll$S), these effects could largely be handled with a single correction per station valid within the FoV. This applies for both compact (A$\ll$S) and extended (A$\gg$S) arrays, which are cases 1 and 2, respectively, for which conventional self-calibration techniques are suitable.

For modern low-frequency arrays this is no longer sufficient, as the FoV is greater than the scale size of the disturbances (V$\geq$S). Case 3 is for sufficiently compact arrays such that the DD wavefront disturbances over the array can be treated as planar (i.e. linear approx.) and yield coherent apparent source position shifts varying in time and direction. When the linear approximation is no longer valid (i.e. extended array) the presence of non-planar (i.e. curvature) disturbances additionally lead to source shape deformations; this is case 4, which requires a more complex calibration algorithm, where an independent solution for each direction and station must be applied. We show here that this is an important issue even for the pathfinders such as Murchison Widefield Phase-2 Array (MWA-2), which has baselines less than 5 kilometres long.

A prime challenge with DD corrections is in the imaging of the data. The Van-Citter relationship that is the basis of all radio-interferometric imaging requires that the data in the Fourier domain has a uniform calibration applied before transforming it to the image domain. Several research groups are developing solutions for this issue, for example DDFacet[3], which takes a facetting approach, and is widely used for LOFAR LBA imaging and WSClean[4] with Image Domain Gridding[5], which uses gridding in the image domain to correct for direction-dependent effects, and is widely used for MWA imaging.

We have been looking at efficient methods to generate accurate DD-calibrations, for application in these next generation imaging tools. We have been developing a method called LEAP (Low-frequency Excision of Atmosphere in Parallel), which is discriminated from other methods by the fact that every direction can be treated as independent, and thus analysed in parallel. This compares favourably to sequential (‘peeling’) methods (e.g. SPAM[6] or RTS[7]) that correct for each source in order of strength, and simultaneous methods (e.g. SAGECal[8]) that solve for all directions with a very large solution matrix, which do not scale well to large numbers of sources or stations.

LEAP of course has its limitations; the fact that it does not perform source subtraction can elevate the noise floor, and the flux density cutoff for calibrator sources. Nevertheless, as it does not require a complete sky model (other than a catalogue of LEAP calibrator positions, which are each treated independently) and is very simple and robust, it can play an important role in providing a preliminary solution to the more sophisticated and complicated methods, and a unique role in providing the real-time direction-dependent calibration for the SKA tied-array beamforming. The latter is used to form multiple simultaneous beams within the field of view, as required in VLBI[9] and equally in pulsar studies.

Traditional MWA DD-calibration strategies, as used by GLEAM[10] for example, assume that observations fall in “Case 3”, and ignore the potential defocusing effect arising from non-linear disturbances in the wavefront above the array. The ionospheric calibration is carried out in the image domain, as a rubber sheet-type correction to the individual 2-min long scan images before mosaicing. This approach worked perfectly well for GLEAM (with a maximum MWA Phase-1 baseline of 2 km), and has had some success with GLEAM-X (with a maximum MWA Phase-2 baseline of 5 km). However, as we will show, for the increased sensitivity of SKA-Low this is going to be completely inadequate, even for this range of short baseline lengths.

The ionospheric calibration data itself provides a means to gain information on the physical nature, and spatial and temporal structure scales of the propagation media [11]. Previous MWA large-scale studies have been performed using image-based analysis [12, 13, 14], however these cannot probe the fine scale.

In this paper we use the LEAP station-based calibration data, in the visibility domain, to quantify the presence of higher order spatial and temporal phase structure over the MWA Phase-2 array imprinted in the incoming wavefront as it propagates through the ionospheric plasma irregularities, for directions within the FoV. As LEAP measures the phase variations within the baselines formed by the array, we are able to study the small scale spatial and temporal structures; that is at scales from 30m to 5km. Our particular interest is to discover at what level the planar distortions approximations breakdown, entering the calibration regime 4, as that is crucial information for the planning of the SKA-Low calibration schemes.

We used two datasets of GLEAM[10, 16] observations with the MWA Phase-2 long baseline configuration[17] at two of the lowest frequency bands, with an instantaneous bandwidth of 30 MHz for the explorations presented for this paper.

One dataset consisted of a series of interleaving 2-min long scans, centred at 88MHz and 154MHz, on December 18th, 2017, under moderate-weather conditions. The interval between observations at the same frequency was 10 minutes, spanning an hour and a half.

The other dataset includes a small number of 2-min long scans carried out on June 2018, with the strong source 3C444 (J221425-170140) near the phase centre, under a variety of weather conditions. That is, good weather on June 3^rd and poor weather on June 12^th[18]. The latter was flagged to be rejected and reobserved based on severe coherent artefacts (residual sidelobes from several strong sources caused by ionospheric distortions) that contaminated the whole of the image, following the standard GLEAM analysis.

All the observations were calibrated using LEAP, following the calibration and imaging procedure described in Section 1.1, as part of a wider-scope project to advance the effective imaging implementation (e.g. a single gridding and imaging inversion) of LEAP DD calibration along with a comparative study of ‘refocusing’ calibration in wide FoV imaging using MWA observations (Dodson et al., 2021, in prep).

However the aim of this paper is to provide answers to some of the questions about the local spatial and temporal scales of the ionospheric disturbances pertinent for the SKA, and identify the requirements for an optimum strategy for the removal of systematic errors depending on the observing frequency and under different ionospheric conditions.

Of special interest for this work are the LEAP calibration by-products, namely the measured station-based phase solutions which define the so-called ionospheric phase screens above the array, along the directions of the stronger LEAP calibrators (i.e. those with reduced thermal noise error contribution). They are a measure of the wavefront disturbances introduced by its propagation through the ionosphere. Hence, each screen conveys information of the spatial (and temporal) structure of the DD ionospheric disturbances, at scales smaller than the array size (i.e. less than 5km and potentially down to 30m). They are the main observable for the ionospheric analysis in the visibility domain followed here.

The station-based phase observables are obtained with the script discussed in LEAP-I, where casa was used to: call WSClean for phase rotation to calibrator source directions and imaging for analysis and validation, and to solve for gain solutions. As part of ICRAR bridging contributions to the SKA science processing a GPU version has been written¹¹1https://jira.skatelescope.org/browse/SP-994 that can efficiently process multiple directions in parallel. This addresses the issue of parallel reading of the data, however the processing here predated the release of that tool.

We have followed two methods of analysis of the individual ionospheric phase screens. Firstly, a regression analysis fitting, using linear and second order surfaces.

As a result we measured the planar ‘slope’ and orientation from the 1^st order 2D linear fits, along with the ‘curvature’; obtained as the quadratic mean of the three 2^nd order fits coefficients.

Also we measured the Root Mean Squared residual errors (RMSE) to the first and second-order fit (${\rm RMSE}_{1}$ and ${\rm RMSE}_{2}$ respectively), and computed the RMSE fractional improvement, defined, for a given screen, as:

Secondly, we compute the 2nd-moment structure function (hereafter Full Structure Function or SF) of the ionospheric screens ($\phi_{ion}$) over the range of (projected) baselines in the MWA array, $r$, following the approach in, for example, Van de Tol, 2009[19]:

were $\langle....\rangle$ stands for a statistical average.

The SF analysis is traditionally used to measure the scaling features of the electron density fluctuations in the ionosphere in order to understand the nature of the physical processes (e.g. turbulences) at the origin of the measured signal.

Here we use the ability of the SF as a tool to characterize complex surfaces, particularly with non-uniformly sampled and non-periodic data, using the measured phase values that form the ionospheric screens. [11, 20, 21]. Of particular interest here is the capacity to detect deviations from linearity. We calculated the SFs using the baseline phase values, deduced from the station solutions. In addition we formed the Detrended Structure Function (DSF) from the residual phase values, after subtracting the corresponding planar fits from the station solutions. This eliminates the overall dominant influence of a planar slope in the data set.

We expected D(r), in a noise-free environment, to follow:

where $C$ would be the slope of the ionospheric phase screen (i.e. change of phase per unit baseline distance), and where $\beta$ is the so-called scaling exponent, which allows us to characterize the scaling nature of the signal under investigation (in our case, the ionospheric disturbances); this value is equal to 5/3 for pure thin-screen Kolmogorov turbulence, or 2 for perfectly planar surfaces. This behaviour holds over the inertial region, which is the approximately linear regime in log-log space between the outer scale at which power is injected and the inner scale at which power is dissipated in the Kolmogorov theory of turbulence.

We also generated spatial structure functions using simulated datasets of synthetic phase surfaces base on our MWA observations, i.e ionospheric toy-models with known properties, to test the applicability of SF analysis to the characterization of ionospheric phase screens and to help with interpretation of our empirical findings in terms of ionospheric behaviour. The toy models consisted of a family of surfaces defined by 2D linear and quadratic polynomial functions with and without added noise, for a range of values for the polynomial coefficients and noise parameters, compatible with our findings from the regression analysis.

Dodson et al. (2021, in prep.) will present a complementary analysis of the ionospheric disturbances based on the comparison of pre- and post-calibration images. The latter has the capacity to additionally correct for defocusing artifacts in the image, such as changes in the source shape and residual sidelobe patterns, which arise from the small scale ionospheric disturbances.

Figure 1 showed an example of LEAP ionospheric phase screens above the MWA array in the direction of a strong LEAP calibrator, for a 2-min scan solution. For weaker sources, it is expected that the ionospheric signature will be diluted, and ultimately buried under the increasing thermal noise. The results presented here comprise the analysis of the ionospheric screens in the directions of all ($\sim$200) LEAP calibrators (with SNR$>$2, per station) within the MWA FoV in each 2-min scan, for the set of scans and the analysis described in Section 2.

Regression Analysis

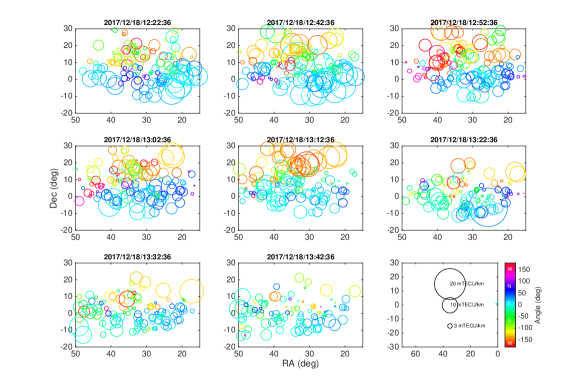
Figures 4a) and b) show the outcomes from the linear 2D regression analysis of the unwrapped station-based phase solutions in an ionospheric screen, for 8 consecutive 2-min scans, at 88 and 154 MHz, respectively. Unwrapping, that is taking into account full wraps of phase by enforcing continuity, is essential to accurately fit the phase slopes on the longer baselines. Shown are the magnitude of the ‘slope’ (circle size, mTECU/km) and the orientation angle (circle colour, degrees) of the fitted plane. The sky location of the symbols correspond to that of the LEAP calibrators across the FoV, for each scan. The FoV at 154 MHz is smaller than for 88 MHz, and each subplot is taken at a different moment in time (although all those shown have a common phase centre). Thus the station gains vary between each subplot and the selected sources vary between scans.

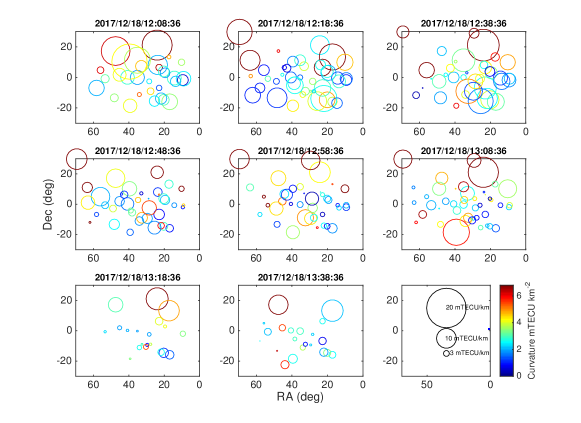
Figure 5 corresponds to the second order 2D regression analysis, showing the magnitude of the fitted curvature (circle colour, mTECU/km²) and slope (circle size with same scale as Figure 4, in mTECU/km), at 88 MHz, with SNR$>$6. Because higher SNR is required to measure the curvature, there are significantly fewer data points. Furthermore, we do not show the corresponding figure for 154 MHz; there were too few data points per scan to show the spatial correlation.

The median value for the ionospheric slope is 5$\pm$3 mTECU/km, across the $\sim$5km span of the array, for all LEAP calibrator directions, at both 88 and 154 MHz. The median value for the curvature is 3$\pm$2 mTECU/km², at both frequencies for SNR$>$6.

For each screen, the linear and second order RMSE errors from the regression analysis are combined to form the fractional $\Delta$RMSE quantity, that would show a significant improvement of one fit above the other, as expected if deviations from linearity are significant. That is, cases when the curvature signature is large enough so that its magnitude is comparable to or greater than the thermal noise contribution and results in a large fractional reduction of the RMSE.

Figure 6 shows a histogram of the fractional $\Delta$RMSE values corresponding to the screens shown in Figure 4, binned by SNR. This shows that the ionospheric curvature signature, if present, appears more significant towards the directions of strong LEAP calibrators, where the thermal noise is reduced.

Some limited insights in the temporal behaviour also come from the regression analysis. We searched the solutions from all the stronger sources for indications of significant variation on shorter time spans than the full scan length of 2min. Three of the more than 300 source directions with a SNR$>$6 per station, for all scans, at each frequency, showed significant temporal variability. Their location is marked on Figure 2. Figure 3 shows a similar plot to Figure 1 for the example with the best SNR, with solutions every 30s. Clear changes in their spatial and temporal structure are easily seen, even by visual inspection.

Structure Functions: Structure function analysis is the traditional method to infer the nature of a propagation media. We have formed the spatial structure functions of the ionospheric screens corresponding to the strongest sources in our data across the limited MWA baseline range. For the “full” SF we use the station-based phase values measured with LEAP in the direction of the source, and the values after subtracting the linear plane from the linear regression analysis, for the “detrended” SF, respectively.

The clearest example, for the direction towards the strongest source 3C444 with a point source flux of 44 Jy at 154MHz, is shown in Figure 7, for the full (solid lines) and detrended (dotted lines) SF analysis, for observations on two days with “good” (red for 154MHz and green for 88MHz) and “poor” (blue for 154MHz) weather conditions. In this case the SFs increase with baseline length with gradients of $1.8^{+0.2}_{-0.2},1.7^{+0.2}_{-0.2},1.82^{+0.04}_{-0.04}$, respectively. The noise floor is not reached until very short baselines, below a few hundred meters. The detrended SF analysis shows a rise of the residual signal over the noise at baselines greater than 0.6km, which is more clear for the “poor” weather observations and lower frequencies.

Figure 8 shows the behaviour of the spatial structure functions (left full; right detrended) for simulated 2D ionospheric screens (i.e. “toy models”) defined by ionospheric slope and curvature values comparable with the measurements from our regression analysis in the 2017 datasets (i.e. a slope of 5.1mTECU/km and curvature of 6.8mTECU/km²), to four times greater, for moderate (blue dots) and poor (yellow cross) weather, respectively; for comparison, the case for a linear screen (i.e. no curvature, and a slope double of the minimum) is shown with green squares. In addition, we tested the effect of measurement noise in the SF by adding a random noise signal with an RMSE of up to 10^o per station (i.e. $\sim$2mTECU at 88MHz) to these toy models (red circles and purple crosses for moderate and poor weather, respectively). Figure 8 (lower) shows the behaviour of the gradient of the structure functions, across the limited range of MWA baseline lengths, as a function of the added noise signals to the toy models.

Figure 9 shows a compilation of the full structure functions of the ionospheric screens towards strong (SNR$>$20) sources, for each individual 2-min measurement set and source direction (dashed lines). Also using multiple scans and directions to form the combined SF (black solid line, in bold), at 88 MHz (upper left) and 154 MHz (upper right). A histogram of the structure function gradients over the range of 0.5 to 5 km baselines is shown (lower left), along with the histogram of the ionospheric slopes (measured on the input ionospheric screens with the linear regression analysis (lower right). Figure 10 shows the detrended structure functions for the same datasets as Figure 9, at 88 MHz (left) and 154 MHz (right); here, after the contribution from a nominal planar surface is subtracted out, the detrended SF is dominated by the presence of non-linear structures in the ionospheric screens.