![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/0e16d5fa-c15f-4b43-9f24-19eb132d26cb/stun_emoji.png) STUN: Structured-Then-Unstructured Pruning
STUN: Structured-Then-Unstructured Pruning
for Scalable MoE Pruning
Abstract
Mixture-of-experts (MoEs) have been adopted for reducing inference costs by sparsely activating experts in Large language models (LLMs). Despite this reduction, the massive number of experts in MoEs still makes them expensive to serve. In this paper, we study how to address this, by pruning MoEs. Among pruning methodologies, unstructured pruning has been known to achieve the highest performance for a given pruning ratio, compared to structured pruning, since the latter imposes constraints on the sparsification structure. This is intuitive, as the solution space of unstructured pruning subsumes that of structured pruning. However, our counterintuitive finding reveals that expert pruning, a form of structured pruning, can actually precede unstructured pruning to outperform unstructured-only pruning. As existing expert pruning, requiring forward passes for experts, cannot scale for recent MoEs, we propose a scalable alternative with complexity, yet outperforming the more expensive methods. The key idea is leveraging a latent structure between experts, based on behavior similarity, such that the greedy decision of whether to prune closely captures the joint pruning effect. Ours is highly effective– For Snowflake Arctic, a 480B-sized MoE with 128 experts, our method needs only one H100 and two hours to achieve nearly no loss in performance with 40% sparsity, even in generative tasks such as GSM8K, where state-of-the-art unstructured pruning fails to. The code will be made publicly available.
STUN: Structured-Then-Unstructured Pruning
for Scalable MoE Pruning
Jaeseong Lee*, Seung-won Hwang††thanks: Work done while visiting Snowflake. Correspond to [email protected], Aurick Qiao, Daniel Campos, Zhewei Yao, Yuxiong He Snowflake AI Research, Seoul National University*
1 Introduction
Large language models (LLMs) have become the state-of-the-art for various tasks OpenAI (2023); Touvron et al. (2023); Jiang et al. (2023); Team et al. (2023); Lieber et al. (2024). However, their prohibitive inference cost is becoming a bottleneck to deployment Kaddour et al. (2023), and detrimental to the environment Strubell et al. (2019); Zeng et al. (2023).
Mixture-of-experts (MoE) presents a promising alternative, by sparsely activating a specific subset of parameters, named as experts, to reduce the inference cost. This architecture has been empirically proven effective, in training cost Fedus et al. (2022), and inference cost Du et al. (2022).
Despite the reduction in computational costs, the massive number of parameters remain unchanged, requiring significantly more GPU memory which makes serving large MoE models out of reach for many. To make matters worse, recent MoEs tend to increase the number of experts , resulting in even larger MoEs. For instance, accommodating 56B parameters of Mixtral Jiang et al. (2024) with 8 experts or 132B of DBRX Databricks (2024) with 16 experts, or 480B of Snowflake Arctic Snowflake (2024) with 128 experts, requires an ever-increasing amount of memory and thus more GPUs to host and serve.

To reduce the number of parameters, unstructured Frantar and Alistarh (2023); Sun et al. (2024), or structured pruning Ma et al. (2023) can be considered. Unstructured pruning allows weight tensors to be sparse anywhere. Structured pruning imposes a restricted pattern on sparsification, such as removing rows, entire weight tensors, or pruning experts in MoE Lu et al. (2024).
Unstructured pruning has been believed to achieve a higher pruning ratio, compared to structured pruning Chen et al. (2022), due to structural restriction.111When comparing Table 1 in Ma et al. (2023) with Table 22 in Sun et al. (2024), the BoolQ performance drops from 71.22 to 61.44, by changing to structured pruning, even allowing less pruning ratio. This seems intuitive, as the solution space of unstructured pruning is a superset of the structured counterpart with structural restrictions. Consequently, an optimal solution that violates the restriction cannot be found from structured pruning, which may result in suboptimal outcomes.
In this paper, we show that Structured-Then-UNstructured pruning (STUN) outperforms unstructured pruning in MoEs. Though it may seem counter-intuitive, we demonstrate that a well-designed structured pruning, which is our expert pruning, would retain the performance after the pruning, and also ensure the pruned network remains robust to unstructured pruning that follows.
First, we argue that MoEs, by design, are ‘robust’ to expert pruning, as MoE training is intended to maintain performance after a number of experts have been pruned. This allows us to design expert pruning to maintain performance similar before and after pruning. To support this argument, we later draw a connection between standard MoE training and targeted dropout Gomez et al. (2019), a training method designed to enhance a network’s robustness to pruning.
Second, we argue that our proposed expert-pruned network remains robust to unstructured pruning. According to Mason-Williams and Dahlqvist (2024), higher kurtosis of weights, or having many outliers in the weight distribution deviating from the normal distribution, suggests more weights can be pruned while maintaining performance, or high robustness of unstructured pruning. We argue that, unlike unstructured pruning, expert (structured) pruning does not decrease kurtosis values, thereby maintaining the network’s robustness to unstructured pruning.
However, existing expert-level pruning for MoE does not scale well over the solution space Lu et al. (2024), requiring an exhaustive combination of experts, leading to GPU calls, with , and is pruning ratio. While this was acceptable in an early MoE work with few experts, it does not scale to recent trends in MoEs with large Bai et al. (2023); Dai et al. (2024); Snowflake (2024), or even infinity He (2024).
Our distinction is drastically reducing the complexity of expert pruning to , without compromising the performance. The main intuition is leveraging a latent structure between experts, based on behavior similarity, such that the greedy decision of whether to prune closely captures the joint pruning effect.
Our contributions can be summarized as follows:
-
•
We propose STUN, the first counterintuitive solution combining structured and unstructured pruning to break the pruning ratio limits of unstructured pruning, to the best of our knowledge.
-
•
We show that a well-designed expert pruning would retain the performance after the pruning, and the pruned network remains robust to unstructured pruning.
-
•
To materialize, we design expert-level pruning method, which outperforms the previously proposed solution Lu et al. (2024).
-
•
Our structured pruning, when followed by unstructured pruning, jointly optimizes pruning to achieve a state-of-the-art compression ratio. For Snowflake Arctic, a 480B-sized MoE with 128 experts, STUN needs only 1 H100 and two hours, achieving no loss up to 40% of sparsity, even for generative tasks such as GSM8K, where state-of-the-art unstructured pruning methods fail.
-
•
Code will be publicly available.
2 Related Work
2.1 LLM Pruning
LLM pruning can be classified into unstructured and structured pruning Behnke and Heafield (2021). Unstructured pruning involves finding mask tensors to sparsify weight tensors. SparseGPT Frantar and Alistarh (2023) uses the Hessian matrix for second-order Taylor approximation, while GBLM-Pruner Das et al. (2024) and Pruner-Zero Dong et al. (2024) leverage gradients to identify mask tensors. However, as these methods demand substantial GPU memory for LLMs, we consider two recent works with higher memory efficiency and strong performance as our baselines: Wanda Sun et al. (2024) evaluates the importance of neurons in each layer by its weight multiplied by the activation value, removing those with low scores. While Wanda assumes a uniform pruning ratio across layers, OWL Yin et al. (2024) probes the optimal pruning ratio per layer, given the pruning budget.
Structured pruning, on the other hand, imposes constraints on the sparsification pattern, such as removing rows, columns, or even entire weight tensors. Early methods that involve pruning attention heads Voita et al. (2019); Shim et al. (2021); Zhang et al. (2021), rows Gong et al. (2022), entire dense layers Liang et al. (2021), or whole transformer blocks Fan et al. (2019); Li et al. (2020) fall under this category. Recent works have applied structured pruning for LLMs Ma et al. (2023); Cheng et al. (2024); Gao et al. (2024); Zhang et al. (2024); Dery et al. (2024), but without fine-tuning, these methods generally underperform compared to unstructured pruning.
Our distinction is to introduce a new class of pruning—structured-then-unstructured pruning—and demonstrate its significant advantages for MoEs, surpassing the performance of unstructured-only pruning. This approach differs from previous methods that combine structured and unstructured pruning Kurtic et al. (2022), which have not succeeded in outperforming unstructured pruning.
2.2 Expert Pruning
Early work on expert pruning was domain-specific, such as in translation MoEs, by keeping most activated experts Kim et al. (2021), or pruning based on gate statistics Koishekenov et al. (2023).
Lu et al. (2024) introduced a domain-agnostic expert pruning, searching for the best combination of experts to reduce the reconstruction loss, and quantify their criticality in output prediction.
Our distinction is eliminating the need for expensive combination enumeration, reducing the GPU calls from to .
2.3 Pruning Robustness
Robustness in post-hoc pruning is quantified by whether performance is maintained after pruning. Training methods aimed at enhancing this robustness include applying group lasso Wen et al. (2016); Behnke and Heafield (2021), L1 Han et al. (2015); Liu et al. (2017), or L0 Louizos et al. (2018) regularization to the weights, as well as learning a sparse scaling factor Huang and Wang (2018); Li et al. (2020); Gong et al. (2022). Additionally, Targeted Dropout Gomez et al. (2019) demonstrates that applying stochastic dropout to less important parts of the network can increase robustness to pruning.
Meanwhile, kurtosis of weights Mason-Williams and Dahlqvist (2024) has been used as a proxy of robustness, stating networks with higher weight kurtosis can tolerate higher unstructured pruning ratios.
Our contribution lies in connecting these findings for designing expert pruning. We argue that MoE training inherently enhances robustness to expert-level pruning, and this coarse structured pruning subsequently makes the remaining network more resilient to unstructured pruning. In section 5, we argue the former, based on the resemblance of MoE training and targeted dropout, and the latter, inspired by Mason-Williams and Dahlqvist (2024).
3 Preliminaries: MoE
As a promising alternative to large language models, which incur prohibitive inference costs, MoE employs a multitude of specialized experts. In each forward pass, MoE selectively activates specific experts conditioned on input tokens, thereby reducing the train and inference costs.
We now formally describe the behavior of an MoE. An MoE layer consists of experts , where represents the parameters of expert , and a router layer . Each expert typically follows the same MLP architecture.
First, the router layer selects which experts to sparsely activate based on the current input token, and provides the coefficients for linear combination of selected expert outputs. The coefficients and the top-k indices of experts are formulated as follows:
| (1) | |||
| (2) |
where is the learnable weight matrix for router .
Next, these coefficients are used for the linear combination of expert outputs:
| (3) |
4 Structured-Then-UNstructured Pruning (STUN)
4.1 Overview
Essentially, STUN first performs structured (expert) pruning, until the loss is negligible, then followed by unstructured pruning, such as OWL Yin et al. (2024) or Wanda Sun et al. (2024).
Our key contribution is to replace combinatorial loss with expert pruning method, by leveraging latent cluster structure among experts, based on behavioral similarity.
Specifically, we find clusters of similar experts layer by layer, yielding a total of clusters in the whole MoE, where is the pruning ratio, is the number of experts in each layer, and is the number of layers in MoE. Then we greedily prune every expert but one representative per each cluster.
Later sections show why our greedy pruning is as effective as its combinatorial counterpart, and how it effectively connects to MoE training beforehand, and unstructured pruning afterwards.
4.2 : Combinatorial Reconstruction Loss
Now we will derive our algorithm in section 4.1 formally, starting from the conventional goal of pruning– minimizing the reconstruction loss. Reconstruction loss has been employed to assess how closely the pruned model without expert set mirrors the behavior of the unpruned Lu et al. (2024). Formally, this loss is quantified by the Frobenius norm of the difference between the original output and the output of pruned layer , denoted as .
| (4) |
where is the whole input we consider. The objective of pruning is to explore all possible combinations of experts, , to determine the expert set that minimizes .
While such an exhaustive search is feasible for smaller models like Mixtral Jiang et al. (2024), which contains only 8 experts, it becomes prohibitive for recent MoEs featuring a massive number of experts.
To elaborate, deciding which experts to prune using Eq. 4 for requires forward passes according to Stirling’s approximation, where , and represents the pruning ratio.222In detail, 23951146041928082866135587776380551750 forward passes per layer at minimum, for massive MoEs with experts such as Snowflake Arctic Snowflake (2024). Our distinction is to lower the computation to , without compromising the performance– In fact, as we will elaborate later, we outperform the combinatorial objective.
4.3 Towards : Probabilistic Interpretation
As a stepping stone towards , we propose to rephrase the goal of finding to minimize as:
| (5) |
where s are the experts included in the expert set , and is the joint probability of pruning .
Section 4.2 corresponds to enumerating joint probability from all combinations, requiring different values, which is compute-intensive. When chain rule is applied, Eq. 5 can be reformulated as follows:
| (6) |
We propose a greedy optimization for Eq. 6– We decompose the multiplication of Eq. 6 and at each step , and obtain the distribution , to select that maximizes the probability. For simplicity, we will omit s from this point on.
As our goal is finding the argmax of the probabilities as in Eq. 6, estimating the rank between them is sufficient, rather than evaluating exact values. Such rank estimation can benefit from the latent structure among experts, specifically, a cluster of similar experts in MoE, enabling calculation without chain-rule multiplications in Eq. 6.
Assume we know oracle clusters, , where is the mapping from an expert to a set of similarly behaving experts identified from the latent clusters. When we have knowledge of similar experts, for example, indicating and are highly similar, we will decide not to prune if is already pruned. That is, if then should be lowered by some value , to guide the model against pruning. Moreover, should be larger, or rank higher, otherwise.
To generalize, we will cluster similar experts. Once the cluster of similar experts is finalized, we assign the value , as follows:
| (7) |
We set as a constant for simplicity. This enables the calculation of all in Eq. 6 from s, which needs only forwards in total.
Clustering the Similar Experts
Our remaining task is to obtain cluster information : One signal is pairwise behavioral similarity , from the pretrained weights at a minimal cost. Suppose two rows are similar; then , meaning tend to be selected by similar inputs, implying similar expertise. Thus, the behavioral similarity between two experts can be obtained as follows:
| (8) |
Next, we generalize pairwise similarity into clusters of experts, such that experts in each cluster are highly similar to its representative . Formally, the objective of clustering is to minimize the sum of squared errors between and experts in the cluster:
| (9) |
which is an NP-hard problem Megiddo and Supowit (1984); Dasgupta (2008); Aloise et al. (2009).
Practically, we found that the agglomerative clustering algorithm Sneath and Sokal (1973) performs well.333We tried other clustering algorithms in the Appendix. Specifically, clusters are initialized as individual experts and then iteratively merged, with a termination condition that prevents the experts within each cluster from being too dissimilar. This condition is tuned based on the desired pruning ratio.
Lastly, if we allow inference on some data, we can improve Eq. 8 with coactivation statistics , which measure the frequency with which are selected simultaneously.444We normalize by dividing it with the total coactivations in one layer. However, these coactivation statistics depend on the given data, whose distribution may differ from the test data. Therefore we combine the two as follows:
| (10) |
We recap the algorithm in the Appendix (Alg 1).
4.4 Towards : Taylor Approximation and Selective Reconstruction
1st-order Taylor Approximation
While the approach immensely reduces the cost to obtain the probability distribution, we can further reduce the number of forward passes needed by precalculating s in Eq. 7.
The key idea is approximating ’s reconstruction loss value , and assigning as some high value if the reconstruction loss is lowest. This neatly estimates the rank between s.
Though can be approximated via conventional 2nd-order reconstruction methods Hassibi and Stork (1992); Frantar and Alistarh (2023), the size of the hessian matrix increases quadratically with the number of experts, which often yields out-of-memory errors.
To address this, we propose using a 1st order Taylor approximation. To rank the reconstruction loss values, we consider approximating the reconstruction loss when replacing the output from with some specific expert in as follows:
| (11) |
As the convention of 2nd order Taylor approximation Hassibi and Stork (1992); Frantar and Alistarh (2023), we assume the parameters are near a local minimum. Thus, with a small constant , , leading to:
| (12) |
whose upper bound in the right-hand side can be minimized when , where denotes the average.
Therefore, the expert closest to within each cluster has the highest priority to be retained. We assign a large number if is the closest to from the corresponding cluster , and set it to zero otherwise. The same greedy algorithm is applied to optimize Eq. 6.
Selective Reconstruction of Experts
While letting as the expert closest to successfully minimizes , sometimes we can minimize them further, by replacing the weight of the closest expert to . However, blindly doing so is suboptimal, as there is another kind of error to consider. The decision boundaries of the next layer are accustomed to the output of , but changing the output as could result in a distribution that the model is unfamiliar with. This potential error, which we denote as , would be minimized if .
To balance these two types of errors, we selectively decide whether to reconstruct. We observe that increases if the total number of clusters in a layer decreases, as this would introduce more terms. Therefore, if the total number of clusters is below a threshold , we use to minimize . Otherwise, we set as the expert within the cluster closest to the , to minimize . The router weight reconstruction is done similarly, following its corresponding expert. The final algorithm is summarized in the Appendix (Alg 2).
5 Robustness of Structured-Then-Unstructured Pruning
In this section, we deliver the key insights into why STUN works: MoEs are inherently robust to expert pruning, and the expert-pruned MoE is robust to subsequent post-hoc unstructured pruning.
MoE Robustness to Structured (Expert) Pruning
To support this, we find a resemblance between the MoE (Eq. 3) and the targeted dropout Gomez et al. (2019). Targeted dropout achieves a higher post-hoc pruning ratio by stochastically dropping out unimportant units or weights during training. Formally, in each training step, is modified as follows:
| (13) |
where is a function that extracts only an unimportant part of a given weight , and is a stochastic mask to ensure also has a chance to be updated. Gomez et al. (2019) designed as the bottom elements sorted by their absolute values, and where is the dropout ratio. After training, the performance is better retained when is pruned.
We recognize the resemblance between the MoE (Eq. 3) and the targeted dropout (Eq. 13). If we interpret as , then resembles Eq. 3. Moreover, just as is added in Eq. 13 to ensure that is updated, MoE ensures that is updated through the stochastic nature of .
Therefore, after training, MoE is expected to be robust to pruning , which, in this context, corresponds to pruning some experts s. However, identifying is not as straightforward as in Gomez et al. (2019). In MoE training, is conditioned on each token, such that we need to marginalize token dependency, by identifying unimportant experts across a broad range of inputs. This challenge is connected to the problem of finding in Eq. 4, which minimizes the reconstruction loss.
Expert-Pruned MoE Robustness to Unstructured Pruning
Robustness to unstructured pruning can be estimated by the kurtosis of weights Mason-Williams and Dahlqvist (2024). Kurtosis is expressed as follows:
| (14) |
Suppose the weight of experts follow a zero-meaned Gaussian distribution . Unstructured pruning Sun et al. (2024); Yin et al. (2024); Das et al. (2024); Dong et al. (2024), which tends to remove near-zero weights,555The importance score of unstructured pruning typically increases as the absolute value of the weight increases. would shift the distribution closer to a bimodal symmetric distribution, whose kurtosis is minimum Darlington (1970). As a result, unstructured pruning would lower the kurtosis value, leaving less margin for further unstructured pruning.
In contrast, coarse structured pruning, such as expert pruning, is less likely to decrease the kurtosis value, since the assumption still holds for remaining experts. This implies that expert pruning preserves the robustness of unstructured pruning, unlike applying unstructured pruning with a similar pruning ratio.
6 Experiments
| model | sparsity | method | GSM8K | Avg(→) | ARC-c | ARC-e | HellaSwag | MMLU |
|---|---|---|---|---|---|---|---|---|
| Arctic | 0% | unpruned | 70.74 | 68.33 | 56.91 | 84.60 | 66.94 | 64.86 |
| 40% | STUN (w/ OWL) | 70.28 | 67.66 | 57.68 | 83.29 | 64.94 | 64.75 | |
| OWL | 63.76 | 67.35 | 56.74 | 84.13 | 65.08 | 63.47 | ||
| STUN (w/ Wanda) | 69.60 | 67.64 | 57.25 | 83.63 | 64.86 | 64.81 | ||
| Wanda | 64.59 | 67.54 | 57.00 | 84.64 | 65.19 | 63.32 | ||
| 65% | STUN (w/ OWL) | 43.97 | 62.67 | 51.54 | 80.01 | 59.91 | 59.24 | |
| OWL | 13.42 | 56.68 | 44.37 | 76.64 | 53.69 | 52.02 | ||
| Mixtral-8x7B (Instruct) | 65% | STUN (w/ OWL) | 25.09 | 60.34 | 48.12 | 78.79 | 54.05 | 60.39 |
| OWL | 1.29 | 45.20 | 24.15 | 49.79 | 49.27 | 57.60 | ||
| Mixtral-8x22B (Instruct) | 70% | STUN (w/ OWL) | 30.78 | 60.20 | 47.95 | 77.86 | 55.41 | 59.56 |
| OWL | 19.64 | 57.74 | 45.48 | 76.60 | 52.47 | 56.42 |
| model | sparsity | method | cost | ARC-c | ARC-e | BoolQ | HellaSwag | MMLU | OBQA | RTE | WinoGrande | Avg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mixtral-8x7B (Instruct) | 0% | unpruned | 62.20 | 87.04 | 88.50 | 67.59 | 68.87 | 36.60 | 72.20 | 76.87 | 69.98 | |
| 25% | Ours | 59.30 | 85.44 | 88.13 | 64.42 | 64.52 | 35.40 | 71.84 | 75.37 | 68.05 | ||
| Lu et al. (2024) | 58.19 | 84.89 | 87.34 | 65.24 | 62.47 | 35.60 | 70.04 | 75.85 | 67.45 | |||
| Mixtral-8x7B | 0% | unpruned | 57.17 | 84.01 | 85.35 | 64.88 | 67.88 | 35.00 | 70.40 | 75.93 | 67.58 | |
| 25% | Ours | 52.73 | 81.82 | 83.09 | 60.84 | 63.34 | 31.60 | 68.59 | 72.69 | 64.34 | ||
| Lu et al. (2024) | 51.62 | 81.94 | 83.64 | 61.60 | 58.72 | 33.00 | 67.87 | 75.37 | 64.22 |



In this section, we aim to address the following research questions:
-
•
RQ1: Does STUN outperform unstructured pruning alone?
-
•
RQ2: Does the expert pruning we propose outperform existing baselines?
-
•
RQ3: Does STUN favor recent MoE trends with a large number of small experts?
-
•
RQ4: Is each component of STUN essential for achieving performance gains?
-
•
RQ5: Does STUN generalize to non-MoE models as well?
6.1 Experimental Settings
We use Snowflake Arctic Snowflake (2024) as a representative large MoE, with a total of 480B parameters and 128 experts. To compare our method with previous works Lu et al. (2024), we also experiment with Mixtral Jiang et al. (2024).
Tasks and Datasets
In contrast to previous unstructured pruning studies Sun et al. (2024); Yin et al. (2024), we also evaluate on the NLG task, GSM8K Cobbe et al. (2021), where maintaining performance proves to be much more challenging (see Table 1). We further assess performance on four NLU tasks– ARC-challenge and ARC-easy Clark et al. (2018), HellaSwag Zellers et al. (2019), and MMLU Hendrycks et al. (2021). When comparing with expert pruning methods, following previous work Lu et al. (2024), we also conduct a zero-shot evaluation on BoolQ Wang et al. (2019), OpenBookQA Mihaylov et al. (2018), RTE Wang et al. (2018), WinoGrande Sakaguchi et al. (2021).
Implementation Details
We explore the values of , except for Snowflake Arctic, the largest MoE in our experiments, where we only consider , meaning no GPU calls are required for expert pruning. We evaluate methods using the lm-evaluation-harness Gao et al. (2021). Due to the model size, we use 4-bit quantization Dettmers et al. (2023) for experiments with Mixtral-8x22B and Arctic. The expert pruning ratios are set to 20%, 12.5%, and 10% for Snowflake Arctic, Mixtral-8x7B, and Mixtral-8x22B respectively. We use for selective reconstruction. More detailed implementation information is provided in the Appendix.
6.2 Experimental Results
6.2.1 RQ1: STUN Outperforms Unstructured Pruning
Table 1 describes that our proposed (STUN) significantly outperforms the unstructured pruning methods. We emphasize that we use the same unstructured pruning approach for all for fair comparison.
For example, with 40% of sparsity for the Arctic, STUN neatly retains the original GSM8K performance, while unstructured pruning results in a noticeable performance drop. This is consistent for different unstructured pruning methods, Wanda, as well. For 65% of sparsity for Mixtral-8x7B-Instruct, STUN’s GSM8K performance is nearly 20 times better than that of unstructured pruning. In the ARC-challenge, the unstructured pruning performance falls below the random-guess accuracy of 25.02 Clark et al. (2018), whereas STUN maintains a significantly higher performance, achieving twice the score.
6.2.2 RQ2: Our Expert Pruning Outperforms Existing
Table 2 shows that our proposed expert pruning method is highly effective, outperforming the previous solution. This is because we derive the latent structure from the pretrained MoE, while the previous work Lu et al. (2024) relies solely on the given calibration data. This validates our design of in section 4.
6.2.3 RQ3: STUN Favors Large Number of Small Experts
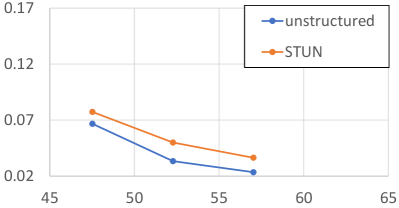
Figure 2 illustrates the trend of STUN in 3 different MoEs. The performance gap between STUN and unstructured pruning increases as the MoE has more experts with small sizes (from (c) to (a)). This is because having more experts, rather than having fewer but larger ones, provides greater flexibility to our expert pruning. Notably, MoEs with a large number of small experts are favored in recent models He (2024).
6.2.4 RQ4: Ablation
To validate our design of expert pruning in sections 4.3 and 4.4, we evaluate alternative approaches to expert-prune Mixtral-8x7B at 50% sparsity. Table 3 confirms that our design choices are valid. Our agglomerative clustering algorithm outperforms the DSatur algorithm, an alternative clustering algorithm we discuss in the Appendix. Additionally, selective reconstruction proves superior to always or never reconstructing, as shown in the last two rows. Detailed evaluation results are provided in the Appendix.
6.2.5 RQ5: STUN Outperforms Unstructured Pruning in non-MoEs
To investigate whether STUN is generalizable to non-MoE as well, we employ a state-of-the-art structured pruning algorithm for non-MoE model, namely, LLM-surgeon van der Ouderaa et al. (2024) with 5% sparsity before performing unstructured pruning, which is OWL in our case. Figure 3 illustrates that such STUN outperforms unstructured pruning.

7 Conclusion
In this paper, we proposed STUN for MoEs, which outperforms unstructured-only pruning. Although this may seem counterintuitive, we provide both theoretical and empirical evidence demonstrating why designing expert pruning before unstructured pruning is beneficial. Since existing expert pruning requires forward passes for experts, we proposed complexity, which outperforms the more expensive approaches. Our experimental results show STUN is highly effective– For 480B-sized MoE with 128 experts, STUN needs only 1 H100 and two hours, achieving nearly no loss in performance with 40% sparsity, even in generative tasks such as GSM8K, where state-of-the-art unstructured pruning fails to.
Limitation
Since our method utilizes unstructured pruning in the second stage, we share the same disadvantages with unstructured pruning, that is, it may need specialized hardware for acceleration. However, it is shown that general-purpose hardware, such as CPU, can successfully accelerate unstructure-pruned networks NeuralMagic (2021). Therefore we have the same potential as existing unstructured pruning methods– with the support from the community, our method will scale up to existing accelerators.
References
- Aloise et al. (2009) Daniel Aloise, Amit Deshpande, Pierre Hansen, and Preyas Popat. 2009. NP-hardness of Euclidean sum-of-squares clustering. Machine Learning, 75(2):245–248.
- Bai et al. (2023) Jinze Bai, Shuai Bai, Yunfei Chu, Zeyu Cui, Kai Dang, Xiaodong Deng, Yang Fan, Wenbin Ge, Yu Han, Fei Huang, Binyuan Hui, Luo Ji, Mei Li, Junyang Lin, Runji Lin, Dayiheng Liu, Gao Liu, Chengqiang Lu, Keming Lu, Jianxin Ma, Rui Men, Xingzhang Ren, Xuancheng Ren, Chuanqi Tan, Sinan Tan, Jianhong Tu, Peng Wang, Shijie Wang, Wei Wang, Shengguang Wu, Benfeng Xu, Jin Xu, An Yang, Hao Yang, Jian Yang, Shusheng Yang, Yang Yao, Bowen Yu, Hongyi Yuan, Zheng Yuan, Jianwei Zhang, Xingxuan Zhang, Yichang Zhang, Zhenru Zhang, Chang Zhou, Jingren Zhou, Xiaohuan Zhou, and Tianhang Zhu. 2023. Qwen Technical Report. Preprint, arXiv:2309.16609.
- Behnke and Heafield (2021) Maximiliana Behnke and Kenneth Heafield. 2021. Pruning Neural Machine Translation for Speed Using Group Lasso. In Proceedings of the Sixth Conference on Machine Translation, pages 1074–1086, Online. Association for Computational Linguistics.
- Brélaz (1979) Daniel Brélaz. 1979. New methods to color the vertices of a graph. Communications of The Acm, 22(4):251–256.
- Chen et al. (2022) Tianlong Chen, Xuxi Chen, Xiaolong Ma, Yanzhi Wang, and Zhangyang Wang. 2022. Coarsening the Granularity: Towards Structurally Sparse Lottery Tickets. In Proceedings of the 39th International Conference on Machine Learning, pages 3025–3039. PMLR.
- Cheng et al. (2024) Hongrong Cheng, Miao Zhang, and Javen Qinfeng Shi. 2024. MINI-LLM: Memory-Efficient Structured Pruning for Large Language Models. Preprint, arXiv:2407.11681.
- Clark et al. (2018) Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. 2018. Think you have Solved Question Answering? Try ARC, the AI2 Reasoning Challenge. Preprint, arXiv:1803.05457.
- Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. 2021. Training Verifiers to Solve Math Word Problems. Preprint, arXiv:2110.14168.
- Dai et al. (2024) Damai Dai, Chengqi Deng, Chenggang Zhao, R.x. Xu, Huazuo Gao, Deli Chen, Jiashi Li, Wangding Zeng, Xingkai Yu, Y. Wu, Zhenda Xie, Y.k. Li, Panpan Huang, Fuli Luo, Chong Ruan, Zhifang Sui, and Wenfeng Liang. 2024. DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1280–1297, Bangkok, Thailand. Association for Computational Linguistics.
- Darlington (1970) Richard B. Darlington. 1970. Is Kurtosis Really "Peakedness?". The American Statistician, 24(2):19–22.
- Das et al. (2024) Rocktim Jyoti Das, Mingjie Sun, Liqun Ma, and Zhiqiang Shen. 2024. Beyond Size: How Gradients Shape Pruning Decisions in Large Language Models. Preprint, arXiv:2311.04902.
- Dasgupta (2008) Sanjoy Dasgupta. 2008. The hardness of k-means clustering.
- Databricks (2024) Databricks. 2024. Databricks/dbrx. Databricks.
- Dery et al. (2024) Lucio Dery, Steven Kolawole, Jean-François Kagy, Virginia Smith, Graham Neubig, and Ameet Talwalkar. 2024. Everybody Prune Now: Structured Pruning of LLMs with only Forward Passes. Preprint, arXiv:2402.05406.
- Dettmers et al. (2023) Tim Dettmers, Artidoro Pagnoni, Ari Holtzman, and Luke Zettlemoyer. 2023. QLoRA: Efficient finetuning of quantized LLMs. In Thirty-Seventh Conference on Neural Information Processing Systems.
- Dong et al. (2024) Peijie Dong, Lujun Li, Zhenheng Tang, Xiang Liu, Xinglin Pan, Qiang Wang, and Xiaowen Chu. 2024. Pruner-Zero: Evolving Symbolic Pruning Metric From Scratch for Large Language Models. In Forty-First International Conference on Machine Learning.
- Du et al. (2022) Nan Du, Yanping Huang, Andrew M Dai, Simon Tong, Dmitry Lepikhin, Yuanzhong Xu, Maxim Krikun, Yanqi Zhou, Adams Wei Yu, Orhan Firat, Barret Zoph, Liam Fedus, Maarten P Bosma, Zongwei Zhou, Tao Wang, Emma Wang, Kellie Webster, Marie Pellat, Kevin Robinson, Kathleen Meier-Hellstern, Toju Duke, Lucas Dixon, Kun Zhang, Quoc Le, Yonghui Wu, Zhifeng Chen, and Claire Cui. 2022. GLaM: Efficient scaling of language models with mixture-of-experts. In Proceedings of the 39th International Conference on Machine Learning, volume 162 of Proceedings of Machine Learning Research, pages 5547–5569. PMLR.
- Fan et al. (2019) Angela Fan, Edouard Grave, and Armand Joulin. 2019. Reducing Transformer Depth on Demand with Structured Dropout. In International Conference on Learning Representations.
- Fedus et al. (2022) William Fedus, Barret Zoph, and Noam Shazeer. 2022. Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. Journal of Machine Learning Research, 23(120):1–39.
- Frantar and Alistarh (2023) Elias Frantar and Dan Alistarh. 2023. SparseGPT: Massive language models can be accurately pruned in one-shot. In Proceedings of the 40th International Conference on Machine Learning, volume 202 of Proceedings of Machine Learning Research, pages 10323–10337. PMLR.
- Gao et al. (2021) Leo Gao, Jonathan Tow, Stella Biderman, Sid Black, Anthony DiPofi, Charles Foster, Laurence Golding, Jeffrey Hsu, Kyle McDonell, Niklas Muennighoff, Jason Phang, Laria Reynolds, Eric Tang, Anish Thite, Ben Wang, Kevin Wang, and Andy Zou. 2021. A framework for few-shot language model evaluation. Zenodo.
- Gao et al. (2024) Yuan Gao, Zujing Liu, Weizhong Zhang, Bo Du, and Gui-Song Xia. 2024. Optimization-based Structural Pruning for Large Language Models without Back-Propagation. Preprint, arXiv:2406.10576.
- Gomez et al. (2019) Aidan N. Gomez, Ivan Zhang, Siddhartha Rao Kamalakara, Divyam Madaan, Kevin Swersky, Yarin Gal, and Geoffrey E. Hinton. 2019. Learning Sparse Networks Using Targeted Dropout. Preprint, arXiv:1905.13678.
- Gong et al. (2022) Hongyu Gong, Xian Li, and Dmitriy Genzel. 2022. Adaptive Sparse Transformer for Multilingual Translation. arXiv:2104.07358 [cs].
- Han et al. (2015) Song Han, Jeff Pool, John Tran, and William Dally. 2015. Learning both Weights and Connections for Efficient Neural Network. In Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc.
- Hassibi and Stork (1992) Babak Hassibi and David Stork. 1992. Second order derivatives for network pruning: Optimal Brain Surgeon. In Advances in Neural Information Processing Systems, volume 5. Morgan-Kaufmann.
- He (2024) Xu Owen He. 2024. Mixture of A Million Experts. Preprint, arXiv:2407.04153.
- Hendrycks et al. (2021) Dan Hendrycks, Collin Burns, Steven Basart, Andy Zou, Mantas Mazeika, Dawn Song, and Jacob Steinhardt. 2021. Measuring massive multitask language understanding. In International Conference on Learning Representations.
- Huang and Wang (2018) Zehao Huang and Naiyan Wang. 2018. Data-Driven Sparse Structure Selection for Deep Neural Networks. In Vittorio Ferrari, Martial Hebert, Cristian Sminchisescu, and Yair Weiss, editors, Computer Vision – ECCV 2018, volume 11220, pages 317–334. Springer International Publishing, Cham.
- Jiang et al. (2023) Albert Q. Jiang, Alexandre Sablayrolles, Arthur Mensch, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Florian Bressand, Gianna Lengyel, Guillaume Lample, Lucile Saulnier, Lélio Renard Lavaud, Marie-Anne Lachaux, Pierre Stock, Teven Le Scao, Thibaut Lavril, Thomas Wang, Timothée Lacroix, and William El Sayed. 2023. Mistral 7B. Preprint, arXiv:2310.06825.
- Jiang et al. (2024) Albert Q. Jiang, Alexandre Sablayrolles, Antoine Roux, Arthur Mensch, Blanche Savary, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Emma Bou Hanna, Florian Bressand, Gianna Lengyel, Guillaume Bour, Guillaume Lample, Lélio Renard Lavaud, Lucile Saulnier, Marie-Anne Lachaux, Pierre Stock, Sandeep Subramanian, Sophia Yang, Szymon Antoniak, Teven Le Scao, Théophile Gervet, Thibaut Lavril, Thomas Wang, Timothée Lacroix, and William El Sayed. 2024. Mixtral of Experts. Preprint, arXiv:2401.04088.
- Kaddour et al. (2023) Jean Kaddour, Joshua Harris, Maximilian Mozes, Herbie Bradley, Roberta Raileanu, and Robert McHardy. 2023. Challenges and Applications of Large Language Models. Preprint, arXiv:2307.10169.
- Kim et al. (2021) Young Jin Kim, Ammar Ahmad Awan, Alexandre Muzio, Andres Felipe Cruz Salinas, Liyang Lu, Amr Hendy, Samyam Rajbhandari, Yuxiong He, and Hany Hassan Awadalla. 2021. Scalable and Efficient MoE Training for Multitask Multilingual Models. Preprint, arXiv:2109.10465.
- Koishekenov et al. (2023) Yeskendir Koishekenov, Alexandre Berard, and Vassilina Nikoulina. 2023. Memory-efficient NLLB-200: Language-specific Expert Pruning of a Massively Multilingual Machine Translation Model. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 3567–3585, Toronto, Canada. Association for Computational Linguistics.
- Kurtic et al. (2022) Eldar Kurtic, Daniel Campos, Tuan Nguyen, Elias Frantar, Mark Kurtz, Benjamin Fineran, Michael Goin, and Dan Alistarh. 2022. The Optimal BERT Surgeon: Scalable and Accurate Second-Order Pruning for Large Language Models. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, pages 4163–4181, Abu Dhabi, United Arab Emirates. Association for Computational Linguistics.
- Li et al. (2020) Xian Li, Asa Cooper Stickland, Yuqing Tang, and Xiang Kong. 2020. Deep transformers with latent depth. In Advances in Neural Information Processing Systems, volume 33, pages 1736–1746. Curran Associates, Inc.
- Liang et al. (2021) Chen Liang, Simiao Zuo, Minshuo Chen, Haoming Jiang, Xiaodong Liu, Pengcheng He, Tuo Zhao, and Weizhu Chen. 2021. Super Tickets in Pre-Trained Language Models: From Model Compression to Improving Generalization. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 6524–6538, Online. Association for Computational Linguistics.
- Lieber et al. (2024) Opher Lieber, Barak Lenz, Hofit Bata, Gal Cohen, Jhonathan Osin, Itay Dalmedigos, Erez Safahi, Shaked Meirom, Yonatan Belinkov, Shai Shalev-Shwartz, Omri Abend, Raz Alon, Tomer Asida, Amir Bergman, Roman Glozman, Michael Gokhman, Avashalom Manevich, Nir Ratner, Noam Rozen, Erez Shwartz, Mor Zusman, and Yoav Shoham. 2024. Jamba: A Hybrid Transformer-Mamba Language Model. Preprint, arXiv:2403.19887.
- Liu et al. (2017) Zhuang Liu, Jianguo Li, Zhiqiang Shen, Gao Huang, Shoumeng Yan, and Changshui Zhang. 2017. Learning Efficient Convolutional Networks through Network Slimming. In 2017 IEEE International Conference on Computer Vision (ICCV), pages 2755–2763, Venice. IEEE.
- Louizos et al. (2018) Christos Louizos, Max Welling, and Diederik P. Kingma. 2018. Learning sparse neural networks through L_0 regularization. In International Conference on Learning Representations.
- Lu et al. (2024) Xudong Lu, Qi Liu, Yuhui Xu, Aojun Zhou, Siyuan Huang, Bo Zhang, Junchi Yan, and Hongsheng Li. 2024. Not All Experts are Equal: Efficient Expert Pruning and Skipping for Mixture-of-Experts Large Language Models. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 6159–6172.
- Ma et al. (2023) Xinyin Ma, Gongfan Fang, and Xinchao Wang. 2023. LLM-Pruner: On the structural pruning of large language models. In Thirty-Seventh Conference on Neural Information Processing Systems.
- Mason-Williams and Dahlqvist (2024) Gabryel Mason-Williams and Fredrik Dahlqvist. 2024. What makes a good prune? Maximal unstructured pruning for maximal cosine similarity. In The Twelfth International Conference on Learning Representations.
- Megiddo and Supowit (1984) Nimrod Megiddo and Kenneth J. Supowit. 1984. On the Complexity of Some Common Geometric Location Problems. SIAM Journal on Computing, 13(1):182–196.
- Mihaylov et al. (2018) Todor Mihaylov, Peter Clark, Tushar Khot, and Ashish Sabharwal. 2018. Can a Suit of Armor Conduct Electricity? A New Dataset for Open Book Question Answering. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 2381–2391, Brussels, Belgium. Association for Computational Linguistics.
- NeuralMagic (2021) NeuralMagic. 2021. Neuralmagic/deepsparse: Sparsity-aware deep learning inference runtime for CPUs. https://github.com/neuralmagic/deepsparse.
- OpenAI (2023) OpenAI. 2023. GPT-4 Technical Report. Preprint, arXiv:2303.08774.
- Raffel et al. (2020) Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. 2020. Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of Machine Learning Research, 21(140):1–67.
- Sakaguchi et al. (2021) Keisuke Sakaguchi, Ronan Le Bras, Chandra Bhagavatula, and Yejin Choi. 2021. WinoGrande: An adversarial winograd schema challenge at scale. Communications of The Acm, 64(9):99–106.
- Shim et al. (2021) Kyuhong Shim, Iksoo Choi, Wonyong Sung, and Jungwook Choi. 2021. Layer-wise Pruning of Transformer Attention Heads for Efficient Language Modeling. In 2021 18th International SoC Design Conference (ISOCC), pages 357–358.
- Sneath and Sokal (1973) Peter H. A. Sneath and Robert R. Sokal. 1973. Numerical taxonomy. The principles and practice of numerical classification.
- Snowflake (2024) Snowflake. 2024. Snowflake-Labs/snowflake-arctic. Snowflake Labs.
- Strubell et al. (2019) Emma Strubell, Ananya Ganesh, and Andrew McCallum. 2019. Energy and Policy Considerations for Deep Learning in NLP. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3645–3650, Florence, Italy. Association for Computational Linguistics.
- Sun et al. (2024) Mingjie Sun, Zhuang Liu, Anna Bair, and J Zico Kolter. 2024. A simple and effective pruning approach for large language models. In The Twelfth International Conference on Learning Representations.
- Team et al. (2023) Gemini Team, Rohan Anil, Sebastian Borgeaud, Yonghui Wu, Jean-Baptiste Alayrac, Jiahui Yu, Radu Soricut, Johan Schalkwyk, Andrew M. Dai, Anja Hauth, Katie Millican, David Silver, Slav Petrov, Melvin Johnson, Ioannis Antonoglou, Julian Schrittwieser, Amelia Glaese, Jilin Chen, Emily Pitler, Timothy Lillicrap, Angeliki Lazaridou, Orhan Firat, James Molloy, Michael Isard, Paul R. Barham, Tom Hennigan, Benjamin Lee, Fabio Viola, Malcolm Reynolds, Yuanzhong Xu, Ryan Doherty, Eli Collins, Clemens Meyer, Eliza Rutherford, Erica Moreira, Kareem Ayoub, Megha Goel, George Tucker, Enrique Piqueras, Maxim Krikun, Iain Barr, Nikolay Savinov, Ivo Danihelka, Becca Roelofs, Anaïs White, Anders Andreassen, Tamara von Glehn, Lakshman Yagati, Mehran Kazemi, Lucas Gonzalez, Misha Khalman, Jakub Sygnowski, Alexandre Frechette, Charlotte Smith, Laura Culp, Lev Proleev, Yi Luan, Xi Chen, James Lottes, Nathan Schucher, Federico Lebron, Alban Rrustemi, Natalie Clay, Phil Crone, Tomas Kocisky, Jeffrey Zhao, Bartek Perz, Dian Yu, Heidi Howard, Adam Bloniarz, Jack W. Rae, Han Lu, Laurent Sifre, Marcello Maggioni, Fred Alcober, Dan Garrette, Megan Barnes, Shantanu Thakoor, Jacob Austin, Gabriel Barth-Maron, William Wong, Rishabh Joshi, Rahma Chaabouni, Deeni Fatiha, Arun Ahuja, Ruibo Liu, Yunxuan Li, Sarah Cogan, Jeremy Chen, Chao Jia, Chenjie Gu, Qiao Zhang, Jordan Grimstad, Ale Jakse Hartman, Martin Chadwick, Gaurav Singh Tomar, Xavier Garcia, Evan Senter, Emanuel Taropa, Thanumalayan Sankaranarayana Pillai, Jacob Devlin, Michael Laskin, Diego de Las Casas, Dasha Valter, Connie Tao, Lorenzo Blanco, Adrià Puigdomènech Badia, David Reitter, Mianna Chen, Jenny Brennan, Clara Rivera, Sergey Brin, Shariq Iqbal, Gabriela Surita, Jane Labanowski, Abhi Rao, Stephanie Winkler, Emilio Parisotto, Yiming Gu, Kate Olszewska, Yujing Zhang, Ravi Addanki, Antoine Miech, Annie Louis, Laurent El Shafey, Denis Teplyashin, Geoff Brown, Elliot Catt, Nithya Attaluri, Jan Balaguer, Jackie Xiang, Pidong Wang, Zoe Ashwood, Anton Briukhov, Albert Webson, Sanjay Ganapathy, Smit Sanghavi, Ajay Kannan, Ming-Wei Chang, Axel Stjerngren, Josip Djolonga, Yuting Sun, Ankur Bapna, Matthew Aitchison, Pedram Pejman, Henryk Michalewski, Tianhe Yu, Cindy Wang, Juliette Love, Junwhan Ahn, Dawn Bloxwich, Kehang Han, Peter Humphreys, Thibault Sellam, James Bradbury, Varun Godbole, Sina Samangooei, Bogdan Damoc, Alex Kaskasoli, Sébastien M. R. Arnold, Vijay Vasudevan, Shubham Agrawal, Jason Riesa, Dmitry Lepikhin, Richard Tanburn, Srivatsan Srinivasan, Hyeontaek Lim, Sarah Hodkinson, Pranav Shyam, Johan Ferret, Steven Hand, Ankush Garg, Tom Le Paine, Jian Li, Yujia Li, Minh Giang, Alexander Neitz, Zaheer Abbas, Sarah York, Machel Reid, Elizabeth Cole, Aakanksha Chowdhery, Dipanjan Das, Dominika Rogozińska, Vitaly Nikolaev, Pablo Sprechmann, Zachary Nado, Lukas Zilka, Flavien Prost, Luheng He, Marianne Monteiro, Gaurav Mishra, Chris Welty, Josh Newlan, Dawei Jia, Miltiadis Allamanis, Clara Huiyi Hu, Raoul de Liedekerke, Justin Gilmer, Carl Saroufim, Shruti Rijhwani, Shaobo Hou, Disha Shrivastava, Anirudh Baddepudi, Alex Goldin, Adnan Ozturel, Albin Cassirer, Yunhan Xu, Daniel Sohn, Devendra Sachan, Reinald Kim Amplayo, Craig Swanson, Dessie Petrova, Shashi Narayan, Arthur Guez, Siddhartha Brahma, Jessica Landon, Miteyan Patel, Ruizhe Zhao, Kevin Villela, Luyu Wang, Wenhao Jia, Matthew Rahtz, Mai Giménez, Legg Yeung, Hanzhao Lin, James Keeling, Petko Georgiev, Diana Mincu, Boxi Wu, Salem Haykal, Rachel Saputro, Kiran Vodrahalli, James Qin, Zeynep Cankara, Abhanshu Sharma, Nick Fernando, Will Hawkins, Behnam Neyshabur, Solomon Kim, Adrian Hutter, Priyanka Agrawal, Alex Castro-Ros, George van den Driessche, Tao Wang, Fan Yang, Shuo-yiin Chang, Paul Komarek, Ross McIlroy, Mario Lučić, Guodong Zhang, Wael Farhan, Michael Sharman, Paul Natsev, Paul Michel, Yong Cheng, Yamini Bansal, Siyuan Qiao, Kris Cao, Siamak Shakeri, Christina Butterfield, Justin Chung, Paul Kishan Rubenstein, Shivani Agrawal, Arthur Mensch, Kedar Soparkar, Karel Lenc, Timothy Chung, Aedan Pope, Loren Maggiore, Jackie Kay, Priya Jhakra, Shibo Wang, Joshua Maynez, Mary Phuong, Taylor Tobin, Andrea Tacchetti, Maja Trebacz, Kevin Robinson, Yash Katariya, Sebastian Riedel, Paige Bailey, Kefan Xiao, Nimesh Ghelani, Lora Aroyo, Ambrose Slone, Neil Houlsby, Xuehan Xiong, Zhen Yang, Elena Gribovskaya, Jonas Adler, Mateo Wirth, Lisa Lee, Music Li, Thais Kagohara, Jay Pavagadhi, Sophie Bridgers, Anna Bortsova, Sanjay Ghemawat, Zafarali Ahmed, Tianqi Liu, Richard Powell, Vijay Bolina, Mariko Iinuma, Polina Zablotskaia, James Besley, Da-Woon Chung, Timothy Dozat, Ramona Comanescu, Xiance Si, Jeremy Greer, Guolong Su, Martin Polacek, Raphaël Lopez Kaufman, Simon Tokumine, Hexiang Hu, Elena Buchatskaya, Yingjie Miao, Mohamed Elhawaty, Aditya Siddhant, Nenad Tomasev, Jinwei Xing, Christina Greer, Helen Miller, Shereen Ashraf, Aurko Roy, Zizhao Zhang, Ada Ma, Angelos Filos, Milos Besta, Rory Blevins, Ted Klimenko, Chih-Kuan Yeh, Soravit Changpinyo, Jiaqi Mu, Oscar Chang, Mantas Pajarskas, Carrie Muir, Vered Cohen, Charline Le Lan, Krishna Haridasan, Amit Marathe, Steven Hansen, Sholto Douglas, Rajkumar Samuel, Mingqiu Wang, Sophia Austin, Chang Lan, Jiepu Jiang, Justin Chiu, Jaime Alonso Lorenzo, Lars Lowe Sjösund, Sébastien Cevey, Zach Gleicher, Thi Avrahami, Anudhyan Boral, Hansa Srinivasan, Vittorio Selo, Rhys May, Konstantinos Aisopos, Léonard Hussenot, Livio Baldini Soares, Kate Baumli, Michael B. Chang, Adrià Recasens, Ben Caine, Alexander Pritzel, Filip Pavetic, Fabio Pardo, Anita Gergely, Justin Frye, Vinay Ramasesh, Dan Horgan, Kartikeya Badola, Nora Kassner, Subhrajit Roy, Ethan Dyer, Víctor Campos, Alex Tomala, Yunhao Tang, Dalia El Badawy, Elspeth White, Basil Mustafa, Oran Lang, Abhishek Jindal, Sharad Vikram, Zhitao Gong, Sergi Caelles, Ross Hemsley, Gregory Thornton, Fangxiaoyu Feng, Wojciech Stokowiec, Ce Zheng, Phoebe Thacker, Çağlar Ünlü, Zhishuai Zhang, Mohammad Saleh, James Svensson, Max Bileschi, Piyush Patil, Ankesh Anand, Roman Ring, Katerina Tsihlas, Arpi Vezer, Marco Selvi, Toby Shevlane, Mikel Rodriguez, Tom Kwiatkowski, Samira Daruki, Keran Rong, Allan Dafoe, Nicholas FitzGerald, Keren Gu-Lemberg, Mina Khan, Lisa Anne Hendricks, Marie Pellat, Vladimir Feinberg, James Cobon-Kerr, Tara Sainath, Maribeth Rauh, Sayed Hadi Hashemi, Richard Ives, Yana Hasson, YaGuang Li, Eric Noland, Yuan Cao, Nathan Byrd, Le Hou, Qingze Wang, Thibault Sottiaux, Michela Paganini, Jean-Baptiste Lespiau, Alexandre Moufarek, Samer Hassan, Kaushik Shivakumar, Joost van Amersfoort, Amol Mandhane, Pratik Joshi, Anirudh Goyal, Matthew Tung, Andrew Brock, Hannah Sheahan, Vedant Misra, Cheng Li, Nemanja Rakićević, Mostafa Dehghani, Fangyu Liu, Sid Mittal, Junhyuk Oh, Seb Noury, Eren Sezener, Fantine Huot, Matthew Lamm, Nicola De Cao, Charlie Chen, Gamaleldin Elsayed, Ed Chi, Mahdis Mahdieh, Ian Tenney, Nan Hua, Ivan Petrychenko, Patrick Kane, Dylan Scandinaro, Rishub Jain, Jonathan Uesato, Romina Datta, Adam Sadovsky, Oskar Bunyan, Dominik Rabiej, Shimu Wu, John Zhang, Gautam Vasudevan, Edouard Leurent, Mahmoud Alnahlawi, Ionut Georgescu, Nan Wei, Ivy Zheng, Betty Chan, Pam G. Rabinovitch, Piotr Stanczyk, Ye Zhang, David Steiner, Subhajit Naskar, Michael Azzam, Matthew Johnson, Adam Paszke, Chung-Cheng Chiu, Jaume Sanchez Elias, Afroz Mohiuddin, Faizan Muhammad, Jin Miao, Andrew Lee, Nino Vieillard, Sahitya Potluri, Jane Park, Elnaz Davoodi, Jiageng Zhang, Jeff Stanway, Drew Garmon, Abhijit Karmarkar, Zhe Dong, Jong Lee, Aviral Kumar, Luowei Zhou, Jonathan Evens, William Isaac, Zhe Chen, Johnson Jia, Anselm Levskaya, Zhenkai Zhu, Chris Gorgolewski, Peter Grabowski, Yu Mao, Alberto Magni, Kaisheng Yao, Javier Snaider, Norman Casagrande, Paul Suganthan, Evan Palmer, Geoffrey Irving, Edward Loper, Manaal Faruqui, Isha Arkatkar, Nanxin Chen, Izhak Shafran, Michael Fink, Alfonso Castaño, Irene Giannoumis, Wooyeol Kim, Mikołaj Rybiński, Ashwin Sreevatsa, Jennifer Prendki, David Soergel, Adrian Goedeckemeyer, Willi Gierke, Mohsen Jafari, Meenu Gaba, Jeremy Wiesner, Diana Gage Wright, Yawen Wei, Harsha Vashisht, Yana Kulizhskaya, Jay Hoover, Maigo Le, Lu Li, Chimezie Iwuanyanwu, Lu Liu, Kevin Ramirez, Andrey Khorlin, Albert Cui, Tian LIN, Marin Georgiev, Marcus Wu, Ricardo Aguilar, Keith Pallo, Abhishek Chakladar, Alena Repina, Xihui Wu, Tom van der Weide, Priya Ponnapalli, Caroline Kaplan, Jiri Simsa, Shuangfeng Li, Olivier Dousse, Fan Yang, Jeff Piper, Nathan Ie, Minnie Lui, Rama Pasumarthi, Nathan Lintz, Anitha Vijayakumar, Lam Nguyen Thiet, Daniel Andor, Pedro Valenzuela, Cosmin Paduraru, Daiyi Peng, Katherine Lee, Shuyuan Zhang, Somer Greene, Duc Dung Nguyen, Paula Kurylowicz, Sarmishta Velury, Sebastian Krause, Cassidy Hardin, Lucas Dixon, Lili Janzer, Kiam Choo, Ziqiang Feng, Biao Zhang, Achintya Singhal, Tejasi Latkar, Mingyang Zhang, Quoc Le, Elena Allica Abellan, Dayou Du, Dan McKinnon, Natasha Antropova, Tolga Bolukbasi, Orgad Keller, David Reid, Daniel Finchelstein, Maria Abi Raad, Remi Crocker, Peter Hawkins, Robert Dadashi, Colin Gaffney, Sid Lall, Ken Franko, Egor Filonov, Anna Bulanova, Rémi Leblond, Vikas Yadav, Shirley Chung, Harry Askham, Luis C. Cobo, Kelvin Xu, Felix Fischer, Jun Xu, Christina Sorokin, Chris Alberti, Chu-Cheng Lin, Colin Evans, Hao Zhou, Alek Dimitriev, Hannah Forbes, Dylan Banarse, Zora Tung, Jeremiah Liu, Mark Omernick, Colton Bishop, Chintu Kumar, Rachel Sterneck, Ryan Foley, Rohan Jain, Swaroop Mishra, Jiawei Xia, Taylor Bos, Geoffrey Cideron, Ehsan Amid, Francesco Piccinno, Xingyu Wang, Praseem Banzal, Petru Gurita, Hila Noga, Premal Shah, Daniel J. Mankowitz, Alex Polozov, Nate Kushman, Victoria Krakovna, Sasha Brown, MohammadHossein Bateni, Dennis Duan, Vlad Firoiu, Meghana Thotakuri, Tom Natan, Anhad Mohananey, Matthieu Geist, Sidharth Mudgal, Sertan Girgin, Hui Li, Jiayu Ye, Ofir Roval, Reiko Tojo, Michael Kwong, James Lee-Thorp, Christopher Yew, Quan Yuan, Sumit Bagri, Danila Sinopalnikov, Sabela Ramos, John Mellor, Abhishek Sharma, Aliaksei Severyn, Jonathan Lai, Kathy Wu, Heng-Tze Cheng, David Miller, Nicolas Sonnerat, Denis Vnukov, Rory Greig, Jennifer Beattie, Emily Caveness, Libin Bai, Julian Eisenschlos, Alex Korchemniy, Tomy Tsai, Mimi Jasarevic, Weize Kong, Phuong Dao, Zeyu Zheng, Frederick Liu, Fan Yang, Rui Zhu, Mark Geller, Tian Huey Teh, Jason Sanmiya, Evgeny Gladchenko, Nejc Trdin, Andrei Sozanschi, Daniel Toyama, Evan Rosen, Sasan Tavakkol, Linting Xue, Chen Elkind, Oliver Woodman, John Carpenter, George Papamakarios, Rupert Kemp, Sushant Kafle, Tanya Grunina, Rishika Sinha, Alice Talbert, Abhimanyu Goyal, Diane Wu, Denese Owusu-Afriyie, Cosmo Du, Chloe Thornton, Jordi Pont-Tuset, Pradyumna Narayana, Jing Li, Sabaer Fatehi, John Wieting, Omar Ajmeri, Benigno Uria, Tao Zhu, Yeongil Ko, Laura Knight, Amélie Héliou, Ning Niu, Shane Gu, Chenxi Pang, Dustin Tran, Yeqing Li, Nir Levine, Ariel Stolovich, Norbert Kalb, Rebeca Santamaria-Fernandez, Sonam Goenka, Wenny Yustalim, Robin Strudel, Ali Elqursh, Balaji Lakshminarayanan, Charlie Deck, Shyam Upadhyay, Hyo Lee, Mike Dusenberry, Zonglin Li, Xuezhi Wang, Kyle Levin, Raphael Hoffmann, Dan Holtmann-Rice, Olivier Bachem, Summer Yue, Sho Arora, Eric Malmi, Daniil Mirylenka, Qijun Tan, Christy Koh, Soheil Hassas Yeganeh, Siim Põder, Steven Zheng, Francesco Pongetti, Mukarram Tariq, Yanhua Sun, Lucian Ionita, Mojtaba Seyedhosseini, Pouya Tafti, Ragha Kotikalapudi, Zhiyu Liu, Anmol Gulati, Jasmine Liu, Xinyu Ye, Bart Chrzaszcz, Lily Wang, Nikhil Sethi, Tianrun Li, Ben Brown, Shreya Singh, Wei Fan, Aaron Parisi, Joe Stanton, Chenkai Kuang, Vinod Koverkathu, Christopher A. Choquette-Choo, Yunjie Li, T. J. Lu, Abe Ittycheriah, Prakash Shroff, Pei Sun, Mani Varadarajan, Sanaz Bahargam, Rob Willoughby, David Gaddy, Ishita Dasgupta, Guillaume Desjardins, Marco Cornero, Brona Robenek, Bhavishya Mittal, Ben Albrecht, Ashish Shenoy, Fedor Moiseev, Henrik Jacobsson, Alireza Ghaffarkhah, Morgane Rivière, Alanna Walton, Clément Crepy, Alicia Parrish, Yuan Liu, Zongwei Zhou, Clement Farabet, Carey Radebaugh, Praveen Srinivasan, Claudia van der Salm, Andreas Fidjeland, Salvatore Scellato, Eri Latorre-Chimoto, Hanna Klimczak-Plucińska, David Bridson, Dario de Cesare, Tom Hudson, Piermaria Mendolicchio, Lexi Walker, Alex Morris, Ivo Penchev, Matthew Mauger, Alexey Guseynov, Alison Reid, Seth Odoom, Lucia Loher, Victor Cotruta, Madhavi Yenugula, Dominik Grewe, Anastasia Petrushkina, Tom Duerig, Antonio Sanchez, Steve Yadlowsky, Amy Shen, Amir Globerson, Adam Kurzrok, Lynette Webb, Sahil Dua, Dong Li, Preethi Lahoti, Surya Bhupatiraju, Dan Hurt, Haroon Qureshi, Ananth Agarwal, Tomer Shani, Matan Eyal, Anuj Khare, Shreyas Rammohan Belle, Lei Wang, Chetan Tekur, Mihir Sanjay Kale, Jinliang Wei, Ruoxin Sang, Brennan Saeta, Tyler Liechty, Yi Sun, Yao Zhao, Stephan Lee, Pandu Nayak, Doug Fritz, Manish Reddy Vuyyuru, John Aslanides, Nidhi Vyas, Martin Wicke, Xiao Ma, Taylan Bilal, Evgenii Eltyshev, Daniel Balle, Nina Martin, Hardie Cate, James Manyika, Keyvan Amiri, Yelin Kim, Xi Xiong, Kai Kang, Florian Luisier, Nilesh Tripuraneni, David Madras, Mandy Guo, Austin Waters, Oliver Wang, Joshua Ainslie, Jason Baldridge, Han Zhang, Garima Pruthi, Jakob Bauer, Feng Yang, Riham Mansour, Jason Gelman, Yang Xu, George Polovets, Ji Liu, Honglong Cai, Warren Chen, XiangHai Sheng, Emily Xue, Sherjil Ozair, Adams Yu, Christof Angermueller, Xiaowei Li, Weiren Wang, Julia Wiesinger, Emmanouil Koukoumidis, Yuan Tian, Anand Iyer, Madhu Gurumurthy, Mark Goldenson, Parashar Shah, M. K. Blake, Hongkun Yu, Anthony Urbanowicz, Jennimaria Palomaki, Chrisantha Fernando, Kevin Brooks, Ken Durden, Harsh Mehta, Nikola Momchev, Elahe Rahimtoroghi, Maria Georgaki, Amit Raul, Sebastian Ruder, Morgan Redshaw, Jinhyuk Lee, Komal Jalan, Dinghua Li, Ginger Perng, Blake Hechtman, Parker Schuh, Milad Nasr, Mia Chen, Kieran Milan, Vladimir Mikulik, Trevor Strohman, Juliana Franco, Tim Green, Demis Hassabis, Koray Kavukcuoglu, Jeffrey Dean, and Oriol Vinyals. 2023. Gemini: A Family of Highly Capable Multimodal Models. Preprint, arXiv:2312.11805.
- Touvron et al. (2023) Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, Dan Bikel, Lukas Blecher, Cristian Canton Ferrer, Moya Chen, Guillem Cucurull, David Esiobu, Jude Fernandes, Jeremy Fu, Wenyin Fu, Brian Fuller, Cynthia Gao, Vedanuj Goswami, Naman Goyal, Anthony Hartshorn, Saghar Hosseini, Rui Hou, Hakan Inan, Marcin Kardas, Viktor Kerkez, Madian Khabsa, Isabel Kloumann, Artem Korenev, Punit Singh Koura, Marie-Anne Lachaux, Thibaut Lavril, Jenya Lee, Diana Liskovich, Yinghai Lu, Yuning Mao, Xavier Martinet, Todor Mihaylov, Pushkar Mishra, Igor Molybog, Yixin Nie, Andrew Poulton, Jeremy Reizenstein, Rashi Rungta, Kalyan Saladi, Alan Schelten, Ruan Silva, Eric Michael Smith, Ranjan Subramanian, Xiaoqing Ellen Tan, Binh Tang, Ross Taylor, Adina Williams, Jian Xiang Kuan, Puxin Xu, Zheng Yan, Iliyan Zarov, Yuchen Zhang, Angela Fan, Melanie Kambadur, Sharan Narang, Aurelien Rodriguez, Robert Stojnic, Sergey Edunov, and Thomas Scialom. 2023. Llama 2: Open Foundation and Fine-Tuned Chat Models. Preprint, arXiv:2307.09288.
- van der Ouderaa et al. (2024) Tycho F. A. van der Ouderaa, Markus Nagel, Mart Van Baalen, and Tijmen Blankevoort. 2024. The LLM surgeon. In The Twelfth International Conference on Learning Representations.
- Voita et al. (2019) Elena Voita, David Talbot, Fedor Moiseev, Rico Sennrich, and Ivan Titov. 2019. Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 5797–5808, Florence, Italy. Association for Computational Linguistics.
- Wang et al. (2019) Alex Wang, Yada Pruksachatkun, Nikita Nangia, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. 2019. SuperGLUE: A stickier benchmark for general-purpose language understanding systems. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, 294, pages 3266–3280. Curran Associates Inc., Red Hook, NY, USA.
- Wang et al. (2018) Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel Bowman. 2018. GLUE: A Multi-Task Benchmark and Analysis Platform for Natural Language Understanding. In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, pages 353–355, Brussels, Belgium. Association for Computational Linguistics.
- Wen et al. (2016) Wei Wen, Chunpeng Wu, Yandan Wang, Yiran Chen, and Hai Li. 2016. Learning structured sparsity in deep neural networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS’16, pages 2082–2090, Red Hook, NY, USA. Curran Associates Inc.
- Yin et al. (2024) Lu Yin, You Wu, Zhenyu Zhang, Cheng-Yu Hsieh, Yaqing Wang, Yiling Jia, Gen Li, Ajay Kumar Jaiswal, Mykola Pechenizkiy, Yi Liang, Michael Bendersky, Zhangyang Wang, and Shiwei Liu. 2024. Outlier Weighed Layerwise Sparsity (OWL): A Missing Secret Sauce for Pruning LLMs to High Sparsity. In Forty-First International Conference on Machine Learning.
- Zellers et al. (2019) Rowan Zellers, Ari Holtzman, Yonatan Bisk, Ali Farhadi, and Yejin Choi. 2019. HellaSwag: Can a Machine Really Finish Your Sentence? In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 4791–4800, Florence, Italy. Association for Computational Linguistics.
- Zeng et al. (2023) Qingcheng Zeng, Lucas Garay, Peilin Zhou, Dading Chong, Yining Hua, Jiageng Wu, Yikang Pan, Han Zhou, Rob Voigt, and Jie Yang. 2023. GreenPLM: Cross-Lingual Transfer of Monolingual Pre-Trained Language Models at Almost No Cost. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, pages 6290–6298, Macau, SAR China. International Joint Conferences on Artificial Intelligence Organization.
- Zhang et al. (2024) Honghe Zhang, XiaolongShi XiaolongShi, Jingwei Sun, and Guangzhong Sun. 2024. Structured Pruning for Large Language Models Using Coupled Components Elimination and Minor Fine-tuning. In Findings of the Association for Computational Linguistics: NAACL 2024, pages 1–12, Mexico City, Mexico. Association for Computational Linguistics.
- Zhang et al. (2021) Zhengyan Zhang, Fanchao Qi, Zhiyuan Liu, Qun Liu, and Maosong Sun. 2021. Know what you don’t need: Single-Shot Meta-Pruning for attention heads. AI Open, 2:36–42.
Appendix
Algorithm of Expert Pruning
Algorithms 1 and 2 describe the expert pruning we proposed. Note that we do not introduce any GPU inference in both two algorithms.
Implementation Details
We probe , except for the Snowflake Arctic, which is the biggest MoE we deal with, where we only consider , which means no GPU calls is needed for expert pruning. To get coactivation values , we utilize 1000 samples from the C4 dataset, each of which has 2048 sequence length. We evaluate on lm-evaluation-harness Gao et al. (2021) We use 4bit quantization Dettmers et al. (2023) for experiments with Mixtral-8x22B and Arctic, due to their model size. We use 20%, 12.5%, and 10% for Arctic, Mixtral-8x7B, and Mixtral-8x22B respectively, as the expert pruning ratio for STUN. These are the maximum values among 10, 12.5, 20, 25, and 35%, with minimum performance loss. We use for selective reconstruction. For Wanda and OWL, we use 128 C4 samples following the original papers Yin et al. (2024); Sun et al. (2024), while we use 4096 for sequence length. For OWL, we use the default setting, .
All experiments are conducted on H100 80GB GPUs, with a maximum of 4. Each evaluation is done within 4 hours, and each unstructured pruning requires less than 2 hours on one GPU. Evaluation is done only once, since we introduce no randomness in our experiment.
Other Clustering Algorithms
We also considered DSatur Brélaz (1979) as a clustering algorithm for Eq. 12, converting into clique-partitioning in a graph where edge connected if two experts are similar enough as follows,
| (15) |
where is some threshold to control the pruning ratio of MoE.
Ablation Studies Results
| ARC-c | ARC-e | BoolQ | HellaSwag | MMLU | OBQA | RTE | WinoGrande | Avg | |
|---|---|---|---|---|---|---|---|---|---|
| DSatur | 45.99 | 75.38 | 80.76 | 54.62 | 45.06 | 29.00 | 66.79 | 71.11 | 58.59 |
| Ours | 45.73 | 75.13 | 83.46 | 54.55 | 53.29 | 31.20 | 62.45 | 70.80 | 59.58 |
| ARC-c | ARC-e | BoolQ | HellaSwag | MMLU | OBQA | RTE | WinoGrande | Avg | |
|---|---|---|---|---|---|---|---|---|---|
| Always reconstruct () | 42.92 | 74.20 | 82.42 | 54.66 | 50.09 | 28.40 | 55.96 | 72.14 | 57.60 |
| No reconstruct () | 45.22 | 75.21 | 82.45 | 54.53 | 52.31 | 30.00 | 62.82 | 71.19 | 59.22 |
| Ours () | 45.73 | 75.13 | 83.46 | 54.55 | 53.29 | 31.20 | 62.45 | 70.80 | 59.58 |