Structured Convolutions for Efficient Neural Network Design

Consider a convolution with a Composite Kernel of size $C\!\times\!N\!\times\!N$, where $N$ is the spatial size and $C$ is the number of input channels. To compute an output, this kernel is convolved with a $C\!\times\!N\!\times\!N$ volume of the input feature map. Let’s call this volume $X$. Therefore, the output at this point will be:

where ‘$*$’ denotes convolution, ‘$\bullet$’ denotes element-wise multiplication. Since $\beta_{m}$ is a binary tensor, $sum(X\bullet\beta_{m})$ is same as adding the elements of $X$ wherever $\beta_{m}=1$, thus no multiplications are needed. Ordinarily, the convolution $X*W$ would involve $CN^{2}$ multiplications and $CN^{2}-1$ additions. In our method, we can trade multiplications with additions. From (1), we can see that we only need $M$ multiplications and the total number of additions becomes:

Depending on the structure, number of the additions per output can be larger than $CN^{2}-1$. For example, in Fig. 1(b) where $C=1,N=3,M=4$, we have $\sum_{m}sum(\beta_{m})-1=15>CN^{2}-1=8$). In Sec. 4.2, we show that the number of additions can be amortized to as low as $M-1$.

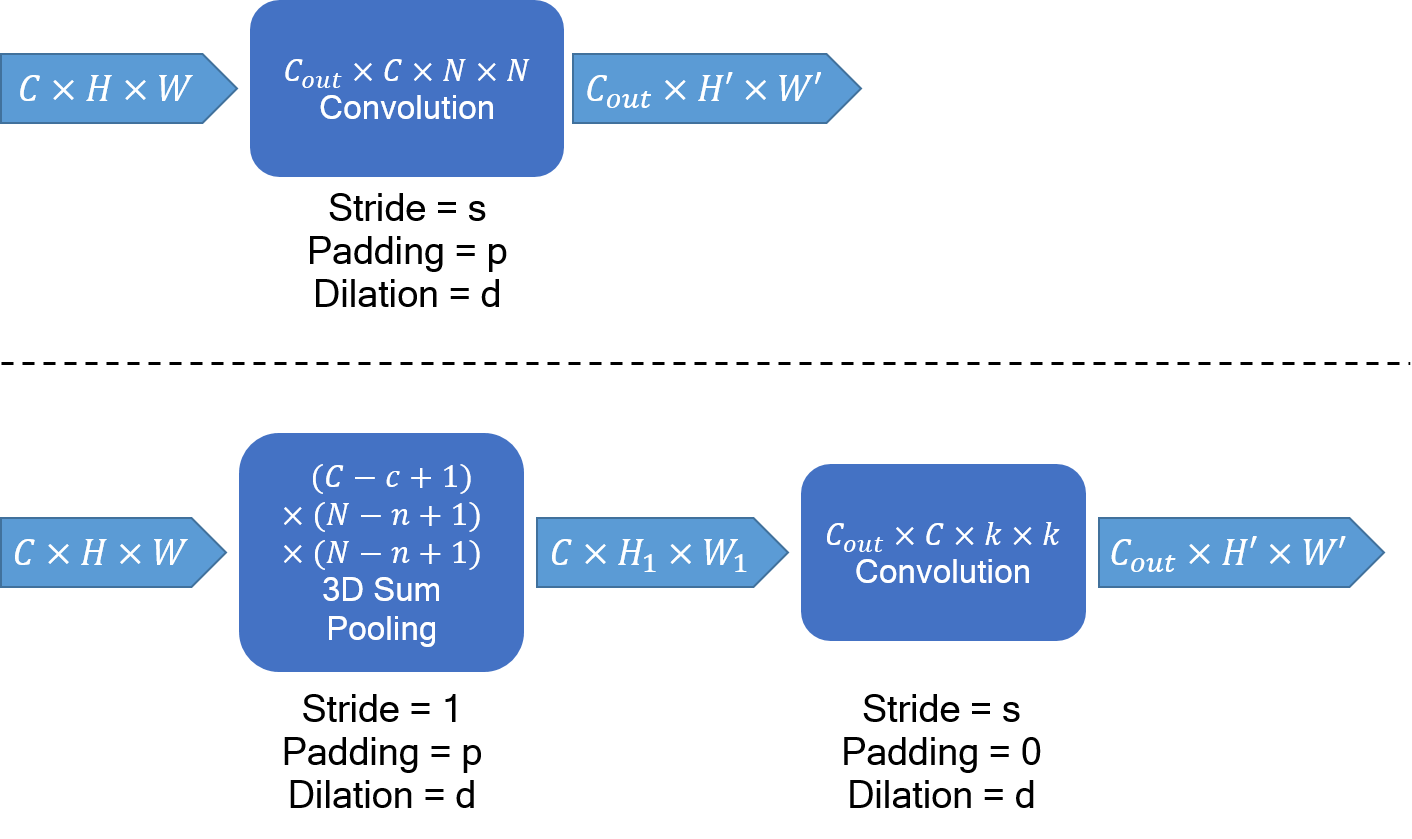
A major advantage of defining Structured Kernels this way is that all the basis elements are just shifted versions of each other (see Fig. 2 and Fig. 1(b)). This means, in Eq. (1), if we consider the convolution $X*W$ for the entire feature map $X$, the summed outputs $X*\beta_{m}$ for all $\beta_{m}$’s are actually the same (except on the edges of $X$). As a result, the outputs $\{X*\beta_{1},...,X*\beta_{cn^{2}}\}$ can be computed using a single sum-pooling operation on $X$ with a kernel size of $(C-c+1)\times(N-n+1)\times(N-n+1)$. Fig. 3 shows a simple example of how a convolution with a $3\!\times\!3$ structured kernel can be broken into a $2\!\times\!2$ sum-pooling followed by a $2\!\times\!2$ convolution with a kernel made of $\alpha_{i}$’s.

Furthermore, consider a convolutional layer of size $C_{out}\!\times\!C\!\times\!N\!\times\!N$ that has $C_{out}$ kernels of size $C{\mkern-1.0mu\times\mkern-1.0mu}N{\mkern-1.0mu\times\mkern-1.0mu}N$. In our design, the same underlying basis $\mathcal{B}=\{\beta_{1},...,\beta_{cn^{2}}\}$ is used for the construction of all $C_{out}$ kernels in the layer. Suppose any two structured kernels in this layer with coefficients $\boldsymbol{\alpha}^{(1)}$ and $\boldsymbol{\alpha}^{(2)}$, i.e. $W_{1}=\sum_{m}\alpha_{m}^{(1)}\beta_{m}$ and $W_{2}=\sum_{m}\alpha_{m}^{(2)}\beta_{m}$. The convolution output with these two kernels is respectively, $X*W_{1}=\sum_{m}\alpha_{m}^{(1)}(X*\beta_{m})$ and $X*W_{2}=\sum_{m}\alpha_{m}^{(2)}(X*\beta_{m})$. We can see that the computation $X*\beta_{m}$ is common to all the kernels of this layer. Hence, the sum-pooling operation only needs to be computed once and then reused across all the $C_{out}$ kernels.

A Structured Convolution can thus be decomposed into a sum-pooling operation and a smaller convolution operation with a kernel composed of $\alpha_{i}$’s. Fig. 4 shows the decomposition of a general structured convolution layer of size $C_{out}\!\times\!C\!\times\!N\!\times\!N$.

Notably, standard convolution ($C{\mkern-1.0mu\times\mkern-1.0mu}N{\mkern-1.0mu\times\mkern-1.0mu}N$), depthwise convolution ($1{\mkern-1.0mu\times\mkern-1.0mu}N{\mkern-1.0mu\times\mkern-1.0mu}N$), and pointwise convolution ($C{\mkern-1.0mu\times\mkern-1.0mu}1{\mkern-1.0mu\times\mkern-1.0mu}1$) kernels can all be constructed as 3D structured kernels, which means that this decomposition can be widely applied to existing architectures. See supplementary material for more details on applying the decomposition to convolutions with arbitrary stride, padding, dilation.

The sum-pooling component after decomposition requires no parameters. Thus, the total number of parameters in a convolution layer get reduced from $C_{out}CN^{2}$ (before decomposition) to $C_{out}cn^{2}$ (after decomposition). The sum-pooling component is also free of multiplications. Hence, only the smaller $c{\mkern-1.0mu\times\mkern-1.0mu}n{\mkern-1.0mu\times\mkern-1.0mu}n$ convolution contributes to multiplications after decomposition.

Before decomposition, computing every output element in feature map $Y\in\mathcal{R}^{C_{out}{\mkern-1.0mu\times\mkern-1.0mu}H^{\prime}{\mkern-1.0mu\times\mkern-1.0mu}W^{\prime}}$ involves $CN^{2}$ multiplications and $CN^{2}-1$ additions. Hence, total multiplications involved are $CN^{2}C_{out}H^{\prime}W^{\prime}$ and total additions involved are $(CN^{2}-1)C_{out}H^{\prime}W^{\prime}$.

After decomposition, computing every output element in feature map $Y$ involves $cn^{2}$ multiplications and $cn^{2}-1$ additions. Hence, total multiplications and additions involved in computing $Y$ are $cn^{2}C_{out}H^{\prime}W^{\prime}$ and $(cn^{2}-1)C_{out}H^{\prime}W^{\prime}$ respectively. Now, computing every element of the intermediate sum-pooled output $E\in\mathcal{R}^{c{\mkern-1.0mu\times\mkern-1.0mu}H_{1}{\mkern-1.0mu\times\mkern-1.0mu}W_{1}}$ involves $((C-c+1)(N-n+1)^{2}-1)$ additions. Hence, the overall total additions involved can be written as:

We can see that the number of parameters and number of multiplications have both reduced by a factor of $\mathbf{{cn^{2}}/{CN^{2}}}$. And in the expression above, if $C_{out}$ is large enough, the first term inside the parentheses gets amortized and the number of additions $\approx(cn^{2}-1)C_{out}H^{\prime}W^{\prime}$. As a result, the number of additions also reduce by approximately the same proportion $\approx cn^{2}/CN^{2}$. We will refer to $CN^{2}/cn^{2}$ as the compression ratio from now on.

Due to amortization, the additions per output are $\approx cn^{2}-1$, which is basically $M-1$ since $M=cn^{2}$.

For image classification networks, the last fully connected layer (sometimes called linear layer) dominates w.r.t. the number of parameters, especially if the number of classes is high. The structural decomposition can be easily extended to the linear layers by noting that a matrix multiplication is the same as performing a number of $1{\mkern-1.0mu\times\mkern-1.0mu}1$ convolutions on the input. Consider a kernel $W\in\mathcal{R}^{P\times Q}$ and input vector $X\in\mathcal{R}^{Q\times 1}$. The linear operation $WX$ is mathematically equivalent to the $1\times 1$ convolution $unsqueezed(X)*unsqueezed(W)$, where $unsqueezed(X)$ is the same as $X$ but with dimensions $Q\times 1\times 1$ and $unsqueezed(W)$ is the same as $W$ but with dimensions $P\times Q\times 1\times 1$. In other words, each row of $W$ can be considered a $1\times 1$ convolution kernel of size $Q\times 1\times 1$.

Now, if each of these kernels (of size $Q\times 1\times 1$) is structured with underlying parameter $R$ (where $R\leq Q$), then the matrix multiplication operation can be structurally decomposed as shown in Fig. 5.

Same as before, we get a reduction in both the number of parameters and the number of multiplications by a factor of $\mathbf{R/Q}$, as well as the number of additions by a factor of $\frac{R(Q-R)+(PR-1)P}{(PQ-1)P}$.

Now, for a structured kernel $W$ characterized by $\{C,N,c,n\}$, there exists a $cn^{2}$ length $\boldsymbol{\alpha}$ such that $W=A\boldsymbol{\alpha}$. Hence, a structured kernel $W$ satisfies the property: $W=AA^{+}W$, where $A^{+}$ is the Moore-Penrose inverse [2] of $A$. Based on this, we propose training a deep network with a Structural Regularization loss that can gradually push the deep network’s kernels to be structured via training:

where $\left\lVert\cdot\right\rVert_{F}$ denotes Frobenius norm and $l$ is the layer index. To ensure that regularization is applied uniformly to all layers, we use $\left\lVert W\right\rVert_{F}$ normalization in the denominator. It also stabilizes the performance of the decomposition w.r.t $\lambda$. The overall proposed training recipe is as follows:

Proposed Training Scheme:

• •

  Step 1: Train the original architecture with the Structural Regularization loss.

  • –

    After Step 1, all weight tensors in the deep network will be almost structured.

• •

  Step 2: Apply the decomposition on every layer and compute $\alpha_{l}=A_{l}^{+}W_{l}$.

  • –

    This results in a smaller and more efficient decomposed architecture with $\alpha_{l}$’s as the weights. Note that, every convolution / linear layer from the original architecture is now replaced with a sum-pooling layer and a smaller convolution / linear layer.

The proposed scheme trains the architecture with the original $C{\mkern-1.0mu\times\mkern-1.0mu}N{\mkern-1.0mu\times\mkern-1.0mu}N$ kernels in place but with a structural regularization loss. The structural regularization loss imposes a restrictive $cn^{2}$ degrees of freedom while training but in a soft or gradual manner (depending on $\lambda$):

1. 1.

   If $\lambda=0$, it is the same as normal training with no structure imposed.

2. 2.

   If $\lambda$ is very high, the regularization loss will be heavily minimized in early training iterations. Thus, the weights will be optimized in a restricted $cn^{2}$ dimensional subspace of $\mathcal{R}^{C{\mkern-1.0mu\times\mkern-1.0mu}N{\mkern-1.0mu\times\mkern-1.0mu}N}$.

3. 3.

   Choosing a moderate $\lambda$ gives the best tradeoff between structure and model performance.

We talk about training implementation details for reproduction, such as hyperparameters and training schedules, in Supplementary material, where we also show our method is robust to the choice of $\lambda$.

We present results for ResNets [10] in Tables 4 and 4. To demonstrate the efficacy of our method on modern networks, we also show results on MobileNetV2 [31] and EfficientNet¹¹1Our Efficientnet reproduction of baselines (B0 and B1) give results slightly inferior to [37]. Our Struct-EffNet is created on top of this EfficientNet-B1 baseline. [37] in Table 4 and 4.

To provide a comprehensive analysis, for each baseline architecture, we present structured counterparts, with version "A" designed to deliver similar accuracies and version "B" for extreme compression ratios. Using different $\{c,n\}$ configurations per-layer, we obtain structured versions with varying levels of reduction in model size and multiplications/additions (please see Supplementary material for details). For the "A" versions of ResNet, we set the compression ratio ($CN^{2}/cn^{2}$) to be 2$\times$ for all layers. For the "B" versions of ResNets, we use nonuniform compression ratios per layer. Specifically, we compress stages 3 and 4 drastically (4$\times$) and stages 1 and 2 by $2\times$. Since MobileNet is already a compact model, we design its "A" version to be $1.33\times$ smaller and "B" version to be $2\times$ smaller.

We note that, on low-level hardware, additions are much power-efficient and faster than multiplications [3, 13]. Since the actual inference time depends on how software optimizations and scheduling are implemented, for most objective conclusions, we provide the number of additions / multiplications and model sizes. Considering observations for sum-pooling on dedicated hardware units [44], our structured convolutions can be easily adapted for memory and compute limited devices.

Compared to the baseline models, the Struct-A versions of ResNets are $2\times$ smaller, while maintaining less than $0.65\%$ loss in accuracy. The more aggressive Struct-B ResNets achieve $60$-$70\%$ model size reduction with about $2$-$3\%$ accuracy drop. Compared to other methods, Struct-56-A is $0.75\%$ better than AMC-Res56 [11] of similar complexity and Struct-20-A exceeds ShiftResNet20-6 [42] by $0.45\%$ while being significantly smaller. Similar trends are observed with Struct-Res18 and Struct-Res50 on ImageNet. Struct-56-A and Struct-50-A achieve competitive performance as compared to the recent GhostNets [7]. For MobileNetV2 which is already designed to be efficient, Struct-MV2-A achieves further reduction in multiplications and model size with SOTA performance compared to other methods, see Table 4. Applying structured convolutions to EfficientNet-B1 results in Struct-EffNet that has comparable performance to EfficientNet-B0, as can be seen in Table 4.

The ResNet Struct-A versions have similar number of adds and multiplies (except ResNet50) because, as noted in Sec. 4.2, the sum-pooling contribution is amortized. But sum-pooling starts dominating as the compression gets more aggressive, as can be seen in the number of adds for Struct-B versions. Notably, both "A" and "B" versions of MobileNetV2 observe a dominance of the sum-pooling component. This is because the number of output channels are not enough to amortize the sum-pooling component resulting from the decomposition of the pointwise ($1\!\times\!1$ conv) layers.

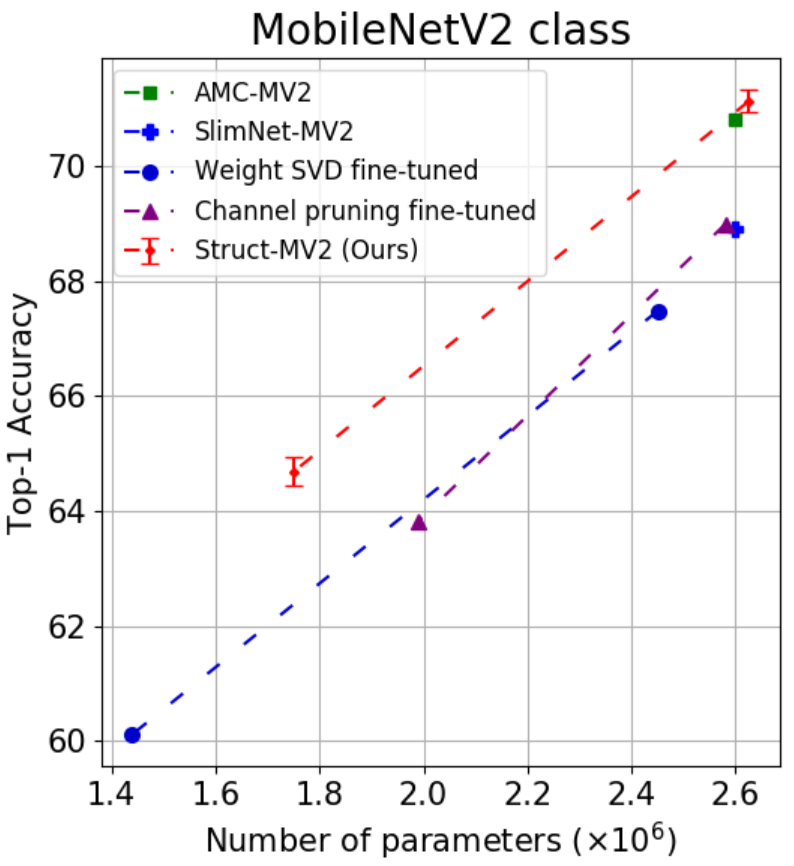
Fig. 6 compares our method with state-of-the-art structured compression methods - WeightSVD [48], Channel Pruning [12], and Tensor-train [35]. Note, the results were obtained from [19]. Our proposed method achieves approximately $1\%$ improvement over the second best method for ResNet18 ($2\times$) and MobileNetV2 ($1.3\times$). Especially for MobileNetV2, this improvement is valuable since it significantly outperforms all the other methods (see Struct-V2-A in Table 4).

After demonstrating the superiority of our method on image classification, we evaluate it for semantic segmentation that requires reproducing fine details around object boundaries. We apply our method to a recently developed state-of-the-art HRNet [39]. Table 5 shows that the structured convolutions can significantly improve our segmentation model efficiency: HRNet model is reduced by 50% in size, and 30% in number of additions and multiplications, while having only 1.5% drop in mIoU. More results for semantic segmentation can be found in the supplementary material.

The proposed method involves computing the Structural Regularization term (3) during training. Although the focus of this work is more on inference efficiency, we measure the memory and time-per-iteration for training with and w/o the Structural Regularization loss on an NVIDIA V100 GPU. We report these numbers for Struct-18-A and Struct-MV2-A architectures below. As observed, the additional computational cost of the regularization term is negligible for a batchsize of $256$. This is because, mathematically, the regularization term, $\sum_{l=1}^{L}\frac{\left\lVert(I-A_{l}A_{l}^{+})W_{l}\right\rVert_{F}}{\left\lVert W_{l}\right\rVert_{F}}$, is independent of the input size. Hence, when using a large batchsize for training, the regluarization term’s memory and runtime overhead is relatively small (less than $5\%$ for Struct-MV2-A and $10\%$ for Struct-18-A).

In our proposed method, we train the architecture with original $C\!\times\!N\!\times\!N$ kernels in place and the regularization loss imposes desired structure on these kernels. At the end of training, we decompose the $C\!\times\!N\!\times\!N$ kernels and replace each with a sum-pooling layer and smaller layer of $c\!\times\!n\!\times\!n$ kernels.

A more direct approach could be to train the decomposed architecture (with the sum-pooling + $c\!\times\!n\!\times\!n$ layers in place) directly. The regularization term is not required in this direct approach, as there is no decomposition step, hence eliminating the computation overhead shown in Table 6. We experimented with this direct training method and observed that the regularization based approach always outperformed the direct approach (by $1.5$% for Struct-18-A and by $0.9$% for Struct-MV2-A). This is because, as pointed out in Sec. 5.1, the direct method optimizes the weights in a restricted subspace of $c\!\times\!n\!\times\!n$ kernels right from the start, whereas the regularization based approach gradually moves the weights from the larger ($C\!\times\!N\!\times\!N$) subspace to the restricted subspace with gradual imposition of the structure constraints via the regularization loss.