Structure of bubbling solutions of Liouville systems with negative singular sources

In this article we consider the following Liouville system defined on Riemann surface $(M,g)$:

where $H_{1},\cdots,H_{n}$ are positive smooth functions on $M$, $p_{1},...,p_{N}$ are distinct points on $M$, $4\pi\gamma_{i}\delta_{p_{i}}$ ($i=1,...,N$) are Dirac masses placed at $p_{i}$ with each $-1<\gamma_{i}<0$, $\rho_{1},\cdots,\rho_{n}$ are nonnegative constants and without loss of generality, we assume $Vol(M)=1$. $\Delta_{g}$ is the Laplace-Beltrami operator ($-\Delta_{g}\geq 0$). Equation (1.1) is called Liouville system if all the entries in the coefficient matrix $A=(a_{ij})_{n\times n}$ are nonnegative. Here we point out that we assume the singular source on the right hand side is the same for all $i$ for simplicity.

Liouville systems have significant applications across various fields. In geometry, when the system reduces to a single equation ($n=1$), it generalizes the renowned Nirenberg problem, which has been extensively researched over the past few decades (see [2, 3, 4, 5, 11, 15, 38, 39, 40, 52, 53, 58, 59]). In physics, Liouville systems emerge from the mean field limit of point vortices in the Euler flow (see [7, 50, 51, 57]) and are intricately linked to self-dual condensate solutions of the Abelian Chern-Simons model with $N$ Higgs particles [37, 49]. In biology, they appear in the stationary solutions of the multi-species Patlak-Keller-Segel system [56] and are important for studying chemotaxis [20]. Understanding bubbling solutions, a significant challenge within Liouville systems, is crucial for advancing related fields.

The equation (1.1) is usually written in an equivalent form by removing the singular sources on the right hand side. Let $G(x,y)$ be the Green’s function of $-\Delta_{g}$ on $M$:

Note that in a neighborhood of $p$,

Using

we can write (1.1) as

where

In a neighborhood around each singular source, say, $p_{l}$, in local coordinates, $\mathfrak{h}_{j}$ can be written as

for some positive, smooth function $h_{j}(x)$.

Let $u=(u_{1},...u_{n})$ be a solution of (1.2), then it is standard to say $u$ belongs to ${}^{\text{\r{}}}H^{1,n}(M)=^{\text{\r{}}}H^{1}(M)\times....\times^{\text{\r{}}}H^{1}(M)$ where

Corresponding to   ${}^{\text{\r{}}}H^{1,n}$ there is a variational form whose Euler-Lagrange equation is (1.2).

In [42, 43], Lin and the second author completed a degree counting program to regular Liouville systems ( no singular source) under the following two assumptions on the matrix $A$: (recall that $I=\{1,...,n\}$)

where $(a^{ij})_{n\times n}$ is $A^{-1}$. $(H1)$ is a rather standard assumption for Liouville systems, $(H2)$ says the interaction between equations is strong, for example when $n=2$, the non-negative matrix $\left(\begin{array}[]{cc}a_{11}&a_{12}\\ a_{12}&a_{22}\end{array}\right)$ satisfies $(H1)$ and $(H2)$ if $a_{12}>\max\{a_{11},a_{22}\}$. Later Lin-Zhang’s work has been extended by the authors [27] for singular Liouville systems. Among other things we prove the following: Let $\Sigma$ be a set of critical values:

where $\mu_{l}=1+\gamma_{l}$ and $\mathbb{N}^{+}$ is the set of natural numbers. If $\Sigma$ is written as

then for $\rho=(\rho_{1},...,\rho_{n})$ satisfying

there is a priori estimate for all solution $u$ to (1.1), and the Leray-Schaudar degree $d_{\rho}$ for equation (1.1) is computed. The main result in [27] states that if the parameter $\rho=(\rho_{1},...,\rho_{n})$ is not on any of the critical hyper-surface $\Gamma_{L}$ below and if the manifold has a non-positive Euler characteristic, then there exists a solution. Let

be the L-th hypersurface, where

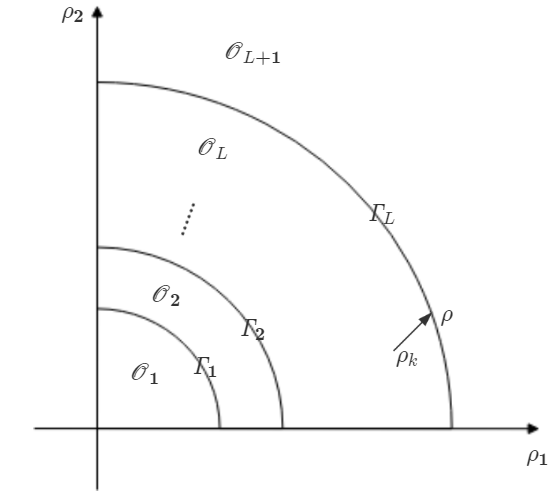
We use $\mathcal{O}_{L}$ to denote the region between $\Gamma_{L-1}$ and $\Gamma_{L}$, the main purpose of this article is to study the profile of bubbling solutions $u^{k}$ when $\rho^{k}=(\rho_{1}^{k},...,\rho_{n}^{k})\to\rho=(\rho_{1},..,\rho_{n})\in\Gamma_{L}$. Here $\rho\in\Gamma_{L}$ ($L\geq 1$) is a limit point, $\rho^{k}=(\rho_{1}^{k},..,\rho_{n}^{k})$ is a sequence of parameters corresponding to bubbling solutions $u^{k}=(u^{k}_{1},...,u^{k}_{n})$, which satisfies

where around each $p_{t}$ ($t=1,...,L$) $\mathfrak{h}_{t}^{k}=|x-p_{t}|^{2\gamma_{t}}h_{t}^{k}(x)$ for some smooth function $h_{t}^{k}(x)$ with uniform $C^{3}$ bound: There exists $c>0$ independent of $k$ such that

The aim of this article is to provide a complete and precise blowup analysis for $\rho^{k}\to\rho$ as $k\to\infty$. The information we shall provide includes comparison of bubbling heights, difference between energy integration around blowup points, leading term of $\rho^{k}-\rho$, location of regular blowup points and new relation on coefficient functions around different blowup points. First we observe that the normal vector at $\rho$ is proportional to

Based on our previous work [27] all these components are positive. For convenience we set

and we assume a controlled behavior of $\rho^{k}\to\rho$:

Note that $A_{k}\sim B_{k}$ means $CA_{k}\leq B_{k}\leq C_{1}A_{k}$ for some $C,C_{1}>0$ independent of $k$. We say $\rho^{k}$ tends to $\Gamma_{L}$ non-tangentially if (1.7) holds.

When $\rho^{k}\to\rho\in\Gamma_{L}$, if blowup occurs, let $p_{1}$,…,$p_{L_{2}}$ be blowup points, since singular sources may also be blowup points, we use $p_{1}.,,,p_{L_{1}}$ to denote regular blowup points and $p_{L_{1}+1}...,p_{L_{2}}$ to denote singular blowup points. It is proved (see [44, 27]) that they satisfy

where $\mu_{s}=1+\gamma_{s}$ (so $\mu_{s}=1$ if $p_{s}$ is a regular point),

Thus $(p_{1},...,p_{L_{1}})$ is a critical point of the following function:

Thus if $det(D^{2}f)$ is not zero at each critical point, the critical points are disjoint. As a consequence of the blowup analysis we shall carry out in this work, we present our main theorem as follows:

Theorem 1.1 follows naturally from the complete bubble interaction results in the next section. If the system is reduced to a single equation, a rather detailed blowup analysis has been done by many people [2, 3, 4, 5, 16, 17, 18, 19, 29, 38, 39, 52, 53, 54, 55, 58, 59]. For a single Liouville equation, the total energy of all solutions is just one number. However, for Liouville systems defined on $\mathbb{R}^{2}$, it is established in [21, 42] that total energy of all components form a $n-1$ dimensional hyper-surface similar to $\Gamma_{1}$. This continuum of energy brings great difficulty to blowup analysis. A simplest description is this: if $\rho^{k}\to\Gamma_{2}$ and there are two bubbling disks. Around each bubbling disk, the local energy tends to $\Gamma_{1}$, but in order to know exactly how $\rho^{k}\to\Gamma_{2}$ one needs precise information about how the local energy is tending to $\Gamma_{1}$ and the comparison of bubbling profiles around different blowup points. This seems to be a unique feature of Liouville systems. In 2013 Lin and the second author published an article [44] that describes $\rho^{k}\to\Gamma_{1}$, which avoided this major difficulty. So the main contribution in this article is to completely present the details of bubble interactions. To put our key idea in short, we show that first, bubbling solutions are sufficiently close to global solutions in a neighborhood of the blowup points. Since global solutions are radial, their behavior is determined by their initial conditions. In [42] Lin and Zhang established an important one-to-one correspondence between the initial condition and the total integration of Liouville system. It is based on this principle we are able to obtain the precise comparison among profiles at different blowup points. The reason in this article we require all the singular sources to have negative strength is because we have a classification theorem for such Liouville systems [45].

The organization of this article is as follows: In section two we state our results on bubble interactions, which lead to the proof of the main theorem at the end of this section. In section three we write the equation around a local blowup point, which happens to be a singular source. Then in section four we prove the main estimates that the profiles of bubbling solutions are extremely close around different blowup points. As a result of the main estimates of section four we prove Theorem 2.1,Theorem 2.6 and Theorem 2.2. Section five is dedicated to proving the leading terms in Theorem 2.3 and Theorem 2.5. All these results depend on a local estimate proved in section six.

It is established in [43] that when $\rho^{k}=(\rho_{1}^{k},..,\rho_{n}^{k})$ tends to $\rho\in\Gamma_{L}$ non-tangentially, suppose there are $L_{2}$ blowup solutions $p_{1},...,p_{N}$, some of them may be singular sources, some may be regular points. It is proved in [27] that

In [44] Lin-Zhang derived the leading term when there is no singular source and $\rho^{k}$ tends to the first critical hyper-surface $\rho^{k}\to\Gamma_{1}$. The main reason they can only discuss $\rho\to\Gamma_{1}$ is because there is only one blowup point in this case. Whether or not the same level of error estimate can still be obtained for multiple-bubble-situations ($\rho\to\Gamma_{N}$) was a major obstacle for Liouville systems in general. Recently Huang-Zhang [30] completely solved this problem by extending Lin-Zhang’s result to $\rho^{k}\to\Gamma_{N}$ for any $N$. But Huang-Zhang’s article does not include the singular cases. It is our goal to further extend all the theorems in [30] to singular Liouville systems.

One point on $\Gamma_{L}$ plays a particular role: Let $Q=(Q_{1},...Q_{n})$ be defined by $\sum_{j}a_{ij}Q_{j}=8\pi n_{L}$ for each $i$. Our approximating theorems depend on whether $\rho=Q$ or not.

For simplicity we set

thus we have

and

Let

be the maximum over $B(p_{t}^{k},\delta_{0})$ divided by $\mu_{l}$. Here $\delta_{0}$ is small enough so that $B(p_{t_{1}},\delta_{0})\cap B(p_{t_{2}},\delta_{0})=\emptyset$ for all $t_{1}\neq t_{2}$, $\gamma_{t}=0$ ($\mu_{t}=1$) if $p_{t}$ is a regular point. Let

One natural question is What is the relation between $M_{t}^{k}$?. The answer of this question is presented in this theorem:

It is proved in [27] that $\displaystyle{\int_{M\setminus\cup_{t}B(p_{t},\delta_{0})}\mathfrak{h}_{i}^{k}e^{\hat{u}_{i}^{k}}=o(1)}$. Moreover for any two blowup points $p,q$,

where $\delta>0$ is small to make bubbling disks mutually disjoint. The second main question is What is the exact difference between them?

Our next result is

Then we define $L_{2}$ open sets $\Omega_{t,\delta_{1}}$ such that they are mutually disjoint, each of them contains a bubbling disk and their union is $M$:

Next we set

where $\hat{\Omega}_{t,\delta}=\Omega_{t,\delta_{1}}\setminus B(p_{t}^{k},\delta)$. Then for fixed $k$ $\lim_{\delta\to 0}A_{i,\delta}$ exists because the leading term from the Green’s function is $-\frac{1}{2\pi}\log|x-p_{t}^{k}|$. In the next two theorems we identify the leading terms.

It can be observed that if $\rho^{k}$ tends to $\Gamma_{L}$ from $\mathcal{O}_{L}$ (that is, tending to $\Gamma_{L}$ from inside), $\Lambda_{L}(\rho^{k})>0$ for $\rho^{k}\in\mathcal{O}_{L}$ and $\Lambda_{L}(\rho^{k})<0$ for $\rho^{k}\in\mathcal{O}_{L+1}$. Thus, if $D\not=0$, the blowup solutions with $\rho^{k}$ occur as $\rho^{k}\to\rho\in\Gamma_{L}$ only from one side of $\Gamma_{L}$. Furthermore, it yields a uniform bound of solutions as $\rho^{k}$ converges to $\Gamma_{L}(\rho\not=Q)$ from $\mathcal{O}_{L}$ provided that $D<0$. The study of the sign of $D$ is another interesting fundamental question. Besides consideration on the compactness of solutions, the sign of $D$ is important for constructing blowup solutions with critical parameters and the uniqueness of bubbling solutions. These projects will be carried out in a different work.

The next result is concerned with the leading term of $\Lambda_{L}(\rho^{k})$ when $\rho^{k}\to Q$:

The fifth result is about the locations of the regular blowup points:

The sixth main result is a surprising restriction on coefficient function $h_{i}^{k}$.

Obviously Theorem 2.6 is not seen in the case of $L_{2}=1$ and reveals new relations on coefficient functions $h_{i}^{k}$. In other words, if one constructs bubbling solutions, the $h_{i}^{k}$s need to satisfy the statement of Theorem 2.6, in addition to other key information such as precise information about bubbling interactions, exact location of blowup points, accurate vanishing rate of coefficient functions and specific leading terms in asymptotic expansions. All these have been covered in the main results of this article. The construction of bubbling solutions will be carried out in other works in the future.

In this section we write the equation (1.4) around a singular source $p$, which is also a blowup point. Suppose that the strength of the singularity is $4\pi\gamma_{p}$ with $\gamma_{p}\in(-1,0)$, we derive an approximation theorem for blow-up solutions $u^{k}$ around $p$. To state more precise approximation results we write the equation in local coordinate around $p$. In this coordinate, $ds^{2}$ has the form

where

Also near $p$ we have

Here we invoke a result proved in our previous work [27] since $\gamma_{p}$ is not a positive integer, the spherical Harnack inequality holds around $p$ and $p$ is the only blowup point in $B(p,\delta)$. Here we recall that in a neighborhood of $p$, $\mathfrak{h}_{i}^{k}(x)=|x|^{2\gamma_{p}}h_{i}^{k}(x)$.

In this local coordinates, (1.4) is of the form

Going back to (3.1), we let $f_{i}^{k}$ be defined as

Then we have

which can be further written as

if we set

and

Now we introduce $\phi_{i}^{k}$ to be a harmonic function defined by the oscillation of $\tilde{u}_{i}^{k}$ on $B(p,\delta)$:

Obviously, $\phi_{i}^{k}(0)=0$ by the mean value theorem and $\phi_{i}^{k}$ is uniformly bounded on $B(0,\delta/2)$ because $u_{i}^{k}$ has finite oscillation away from blowup points. Now we set