Structure-Enhanced Deep Reinforcement Learning for Optimal Transmission Scheduling
††thanks: *Wanchun Liu is the corresponding author.
Abstract
Remote state estimation of large-scale distributed dynamic processes plays an important role in Industry 4.0 applications. In this paper, by leveraging the theoretical results of structural properties of optimal scheduling policies, we develop a structure-enhanced deep reinforcement learning (DRL) framework for optimal scheduling of a multi-sensor remote estimation system to achieve the minimum overall estimation mean-square error (MSE). In particular, we propose a structure-enhanced action selection method, which tends to select actions that obey the policy structure. This explores the action space more effectively and enhances the learning efficiency of DRL agents. Furthermore, we introduce a structure-enhanced loss function to add penalty to actions that do not follow the policy structure. The new loss function guides the DRL to converge to the optimal policy structure quickly. Our numerical results show that the proposed structure-enhanced DRL algorithms can save the training time by 50% and reduce the remote estimation MSE by 10% to 25%, when compared to benchmark DRL algorithms.
Index Terms:
Remote state estimation, deep reinforcement learning, sensor scheduling, threshold structure.I Introduction
Wireless networked control systems (WNCSs) consisting of distributed sensors, actuators, controllers, and plants are a key component for Industry 4.0 and have been widely applied in many areas such as industrial automation, vehicle monitoring systems, building automation and smart grids [1]. In particular, providing high-quality real-time remote estimation of dynamic system states plays an important role in ensuring control performance and stability of WNCSs [2]. For large-scale WNCSs, transmission scheduling of wireless sensors over limited bandwidth needs to be properly designed to guarantee remote estimation performance.
There are many existing works on the transmission scheduling of WNCSs. In [3], the optimal scheduling problem of a multi-loop WNCS with limited communication resources was investigated for minimizing the transmission power consumption under a WNCS stability constraint. In [4, 5], optimal sensor scheduling problems of remote estimation systems were investigated for achieving the best overall estimation mean-square error (MSE). In particular, dynamic decision-making problems were formulated as Markov decision processes (MDPs), which can be solved by classical methods, such as policy and value iterations. However, the conventional model-based solutions are not feasible in large-scale scheduling problems because of the curse of dimensionality caused by high-dimensional state and action spaces.111In [3, 4, 5], only the optimal scheduling of two-sensor systems has been solved effectively by the proposed methods.
In recent years, deep reinforcement learning (DRL) has been developed to deal with large MDPs by using deep neural networks as function approximators [6, 7]. Some works [8, 9] have used the deep Q-network (DQN), a simplest DRL method, to solve multi-sensor-multi-channel scheduling problems in different remote estimation scenarios. In particular, the sensor scheduling problems for systems with 6 sensors have been solved effectively, providing significant performance gains over heuristic methods in terms of estimation quality. More recent work [10] has introduced DRL algorithms with an actor-critic structure to solve the scheduling problem at a much larger scale (that cannot be handled by the DQN). However, existing works merely use the general DRL frameworks to solve specific scheduling problems, without questioning what features make sensor scheduling problems different from other MDPs. Also, we note that a drawback of general DRL is that it often cannot perform policy exploration effectively for specific tasks[11], which can lead to local minima or even total failure. Thus, the existing DRL-based solutions could be far from optimal.
Some recent works have shown that the optimal scheduling policies of remote estimation systems commonly have a “threshold structure” [12, 5], which means that there exist switching boundaries dividing the state space into multiple regions for different scheduling actions. In other words, the optimal policy has a structure where the action only changes at the switching boundaries of the state space. In [13], the threshold structure of an optimal scheduling policy has also been identified in a sensor scheduling system for minimizing the average age of information (AoI). Although these theoretical works have derived the structures of optimal policies, there is no existing work in the open literature utilizing the structural properties to guide DRL algorithms. This knowledge gap motivates us to investigate how knowledge of the optimal policy structure can be used to redesign DRL algorithms that find the optimal policy more effectively.
Contributions. In this paper, we develop novel structure-enhanced DRL algorithms for solving the optimal scheduling problem of a remote estimation system. Given the most commonly adopted DRL frameworks for scheduling, i.e., DQN and deep deterministic policy gradient (DDPG), we propose structure-enhanced DQN and DDPG algorithms. In particular, we design a structure-enhanced action selection method, which tends to select actions that obey the threshold structure. Such an action selection method can explore the action space more effectively and enhance the learning efficiency of DRL agents. Furthermore, we introduce a structure-enhanced loss function to add penalty to actions that do not follow the threshold structure. The new loss function guides the DRL to converge to the optimal policy structure quickly. Our numerical results show that the proposed structure-enhanced DRL algorithms can save the training time by 50%, while reducing the remote estimation MSE by 10% to 25% when compared to benchmark DRL algorithms.
II System Model
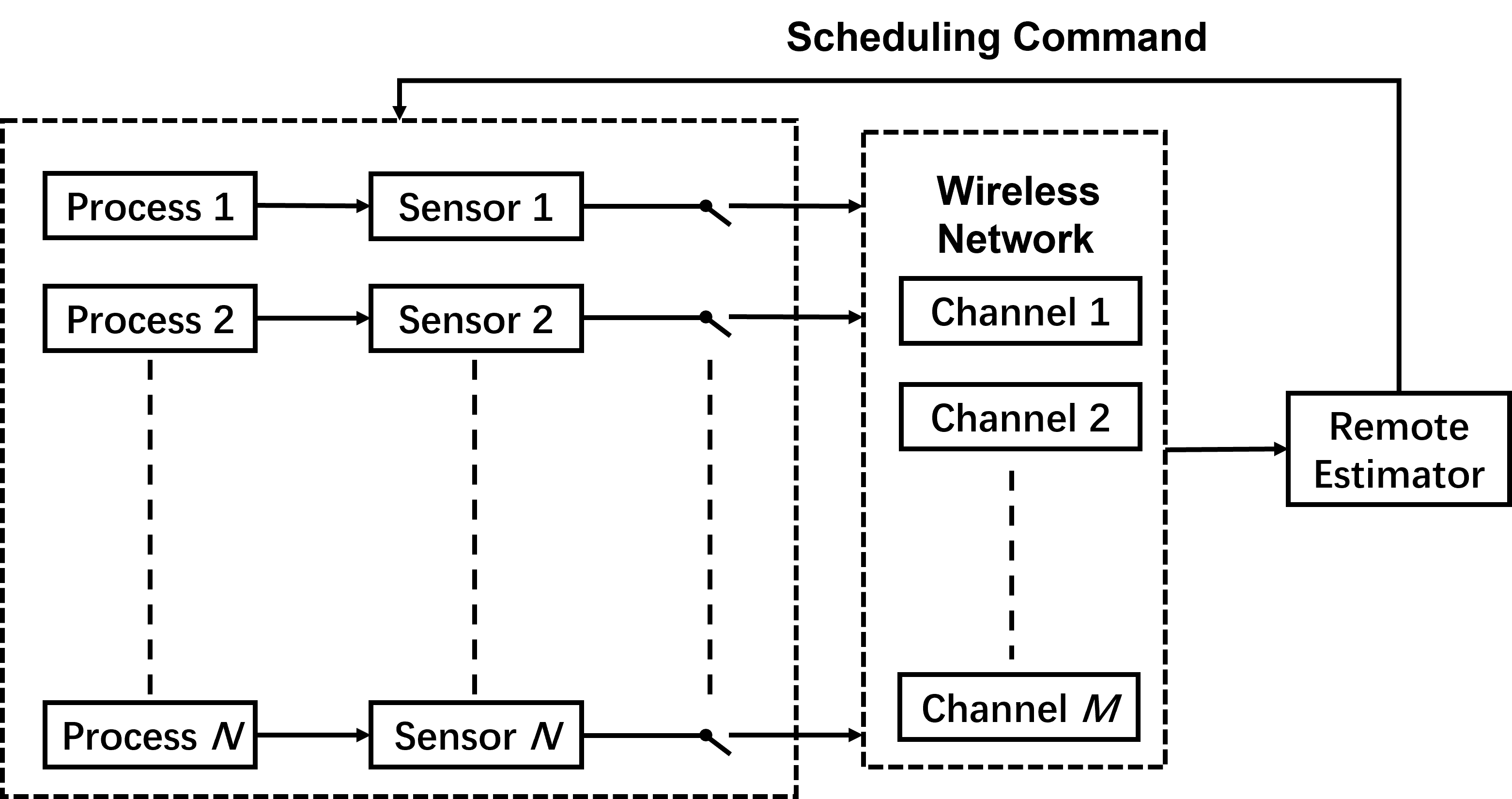
We consider a remote estimation system with dynamic processes each measured by a sensor, which pre-processes the raw measurements and sends its state estimates to a remote estimator through one of wireless channels, as illustrated in Fig. 1.
II-A Process Model and Local State Estimation
Each dynamic process is modeled as a discrete linear time-invariant (LTI) system as [8, 14, 15]
| (1) | ||||
where is process ’s state at time , and is the state measurement of the sensor , and are the system matrix and the measurement matrix, respectively, and are the process disturbance and the measurement noise modeled as independent and identically distributed (i.i.d) zero-mean Gaussian random vectors and , respectively. We assume that the spectral radius of , is greater than one, which means that the dynamic processes are unstable, making the remote estimation problem more interesting.
Due to the imperfect state measurement in (1), sensor executes a classic Kalman filter to pre-process the raw measurement and generate state estimate at each time [14]. Sensor sends to the remote estimator (not ) as a packet, once scheduled. The local state estimation error covariance matrix is defined as
| (2) |
We note that local Kalman filters are commonly assumed to operate in the steady state mode in the literature (see [14] and references therein222The th local Kalman filter is stable if and only if that is observable and is controllable.), which means the error covariance matrix converges to a constant, i.e., .
II-B Wireless Communications and Remote State Estimation
There are wireless channels (e.g., subcarriers) for the sensors’ transmissions, where . We consider independent and identically distributed (i.i.d.) block fading channels, where the channel quality is fixed during each packet transmission and varies packet by packet, independently. Let the matrix denote the channel state of the system at time , where the element in the th row and th column represents the channel state between sensor and the remote estimator at channel . In particular, there are quantized channel states in total. The packet drop probability at channel state is . Without loss of generality, we assume that . The instantaneous channel state is available at the remote estimator based on standard channel estimation methods. The distribution of is given as
| (3) |
where .
Due to the limited communication channels, only out of sensors can be scheduled at each time step. Let represent the channel allocation for sensor at time , where
| (4) |
In particular, we assume that each sensor can be scheduled to at most one channel and that each channel is assigned to one sensor [10]. Then, the constraints on are given as
| (5) |
where is the indicator function.
Considering schedule actions and packet dropouts, sensor ’s estimate may not be received by the remote estimator in every time slot. We define the packet reception indicator as
Considering the randomness of and assuming that the remote estimator performs state estimation at the beginning of each time slot, the optimal estimator in terms of estimation MSE is given as
| (8) |
where is the system matrix of process defined under (1). If sensor ’s packet is not received, the remote estimator propagates its estimate in the previous time slot to estimate the current state. From (1) and (8), we derive the estimation error covariance as
| (9) | ||||
| (12) |
where is the local estimation error covariance of sensor defined under (2).
Let denote the age-of-information (AoI) of sensor at time , which measures the amount of time elapsed since the latest sensor packet was received. Then, we have
| (13) |
If a sensor is frequently scheduled at good channels, the corresponding average AoI is small. However, due to the scheduling constraint (5), this is often not possible.
III Problem Formulation and Threshold structure
In this paper, we aim to find a dynamic scheduling policy that uses the AoI states of all sensors, as well as the channel states to minimize the expected total discounted estimation MSE of all processes over the infinite time horizon.
Problem 1.
| (15) |
where is the expected average value when adopting the policy and is a discount factor.
Problem 1 is a sequential decision-making problem with the Markovian property. This is because the expected estimation MSE only depends on the AoI state in (14), which has the Markovian property (13), and the channel states are i.i.d.. Therefore, we formulate Problem 1 as a Markov decision problem (MDP).
III-A MDP Formulation
We define the four elements of the MDP as below.
1) The state of the MDP is defined as , where is the AoI state vector. Thus, takes into account both the AoI and channel states.
2) The overall schedule action of the sensors is defined as under the constraint (5). There are actions in total. The stationary policy is a mapping between the state and the action, i.e., .
3) The transition probability is the probability of the next state given the current state and the action . Since we adopt stationary scheduling policies, the state transition is independent of the time index. Thus, we drop the subscript here and use and to represent the current and the next states, respectively. Due to the i.i.d. fading channel states, we have where can be obtained from (3) and , which is derived based on (3) and (13)
| (20) |
III-B Threshold Policies
Many works have proved that optimal scheduling policies have the threshold structure in Definition 1 for different problems, where the reward of an individual user is a monotonic function of its state [5, 12, 13]. Our problem has the same property, where the estimation MSE of sensor decreases with the decreasing AoI state and the increasing channel state.
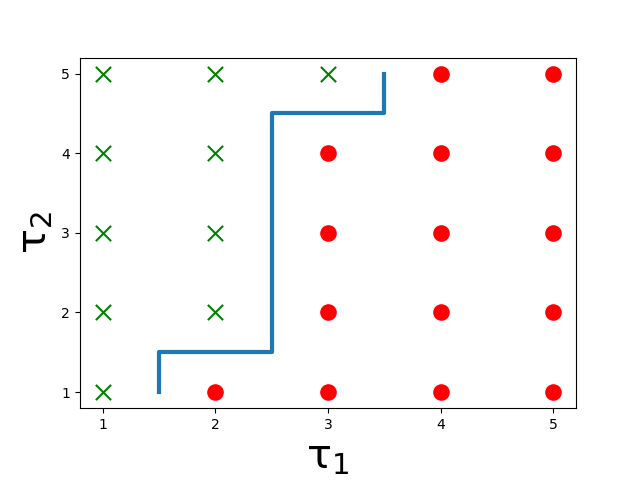
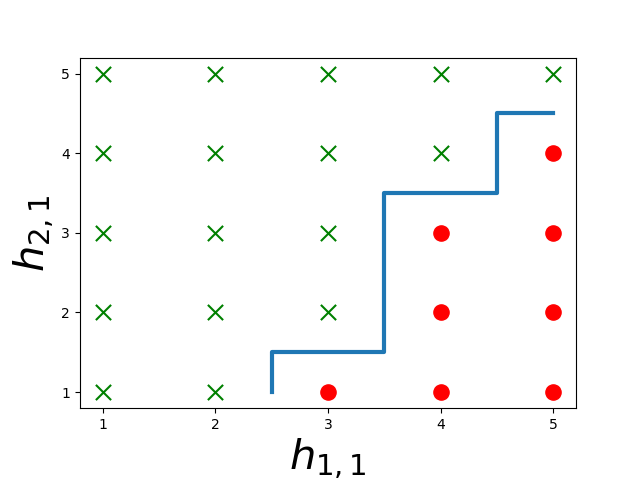
To verify whether the optimal policy of Problem 1 has the threshold structure, we consider a system with and and adopt the conventional value iteration algorithm to find the optimal policy. As illustrated in Fig. 2, we see action switching curves in both AoI and channel state spaces, and the properties in Definition 1 are observed. Due to space limitations, we here do not present formal proof that the optimal policy has a threshold structure, but will investigate it in our future work. In Section V, our numerical results also show that the optimized threshold policy is near optimal, confirming the conjecture.
Definition 1.
For a threshold policy of Problem 1, if channel is assigned to sensor at the state , then the following two properties must hold:
(i) for state , where is identical to except the sensor--channel- state with , then channel is still assigned to sensor ;
(ii) for state , where is idential to except sensor ’s AoI with , then either channel or a better channel is assigned to sensor .
For property (i), given that sensor is scheduled at channel at a certain state, if the channel quality of improves while the AoI and the other channel states are the same, then the threshold policy still assigns channel to sensor . The property is reasonable since the channel quality of sensor to channel is the only factor changed and improved.
For property (ii), if the AoI state of sensor is increased while the other states remain the same, the policy must schedule sensor to a channel that is no worse than the previous one. Such a scheduling policy does make sense, since a larger sensor ’s AoI leads to a lower reward, requiring a better channel for transmission to improve the reward effectively.
In the following, we will develop novel schemes that leverage the threshold structure to guide DRL algorithms for solving Problem 1 with improved training speed and performance.
IV Structure-Enhanced DRL
In the literature, DQN and DDPG are the most commonly adopted off-policy DRL algorithms for solving optimal scheduling problems (see [8, 10] and references therein), and they provide significant performance improvements over heuristic policies. Next, we develop threshold structure-enhanced (SE) DQN and DDPG for solving Problem 1.
IV-A Structure-Enhanced DQN
We define the Q-value as the expected discounted sum of the reward function
| (21) |
which measures the long-term performance of policy given the current state-action pair . Let denote the optimal policy of Problem 1. Then, the corresponding Q-value can, in principle, be obtained by solving the Bellman equation [16]
| (22) |
From the definition (21), the optimal policy generates the best action achieving the highest Q-value, and can be written as
| (23) |
A well-trained DQN uses a neural network (NN) with the parameter set to approximate the Q-values of the optimal policy in (23) as and use it to find the optimal action. Considering the action space defined in Section III-A, the DQN has Q-value outputs of different state-action pairs. To train the DQN, one needs to sample data (consisting of states, actions, rewards, and next states), define a loss function of based on the collected data, and minimize the loss function to find the optimized . However, the conventional DQN training method has never utilized structures of optimal policies before.
To utilize the knowledge of the threshold policy structure for enhancing the DQN training performance, we propose 1) an SE action selection method based on Definition 1 to select reasonable actions and hence enhance the data sampling efficiency; and 2) an SE loss function definition to add the penalty to sampled actions that do not follow the threshold structure.
Our SE-DQN training algorithm has three stages: 1) the DQN with loose SE action selection stage, which only utilizes part of the structural property, 2) the DQN with tight SE action selection stage utilizes the full structural property, and 3) the conventional DQN stage. The first two stages use the SE action selection schemes and the SE loss function to train the DQN fast, resulting in a reasonable threshold policy, and the last stage is for further policy exploration. In what follows, we present the loose and tight SE action selection schemes and the SE loss function.
IV-A1 Loose SE action selection
We randomly select an action from the entire action space with a probability of for action exploration; with a probability of , we generate the SE action as below. For simplicity, we drop the time index when describing action selections.
The threshold structure suggests that the actions of and the state with a smaller AoI or channel state are correlated. Thus, one can infer the action based on the action at the state with a smaller channel, or AoI state, based on property (i), or (ii), of Definition 1, respectively. We only consider property (ii) for loose SE action selection, as it is difficult to find actions that satisfy both structural properties (i) and (ii) at the beginning of training. We will utilize both (i) and (ii) in the tight SE action selection stage.
Given the state , we define the state with a smaller sensor ’s AoI as , where
| (24) |
For each , we calculate the corresponding action based on the Q-values as
| (25) |
Recall that is the channel index assigned to sensor at the state .
If , then property (ii) implies that channel or a better channel is assigned to sensor at the state . We define the set of channels with better quality as
| (26) |
Then, the SE action for sensor , say , is randomly chosen from the set with probability , and is equal to with probability .
If , then property (ii) can not help with determining the action. Then, we define the action selected by the greedy policy (i.e., the conventional DQN method) at the state as
| (27) |
Thus, we set the SE action of sensor identical to the one generated by the conventional DQN method, i.e., .
Now we can define the SE action for sensors as . If such an action meets the constraint
| (28) |
which is less restrictive than (5), we select the action as and assign the unused channels randomly to unscheduled sensors; otherwise, is identical to that of the conventional method as .
IV-A2 Tight SE action selection
By using the loose SE action selection, we first infer the scheduling action of sensor at the state based on the action of the state with a smaller AoI, . Then, we check whether the loose SE action satisfies the threshold property (i) as below.
For notation simplicity, we use to denote the SE channel selection for sensor . Given the state , we define the state with a smaller channel ’s state for sensor as , where and are identical except the element . Then, we calculate the corresponding action
| (29) |
From the structural properties (i) and (ii), the scheduling action should be identical to . Thus, if , then the SE action for sensor is ; otherwise, is identical to the conventional DQN action. The SE action satisfying the structural properties (i) and (ii) is . If such an action meets the constraint (5), then it is executed as ; otherwise, we select the greedy action .
IV-A3 SE loss function
During the training, each transition is stored in a replay memory, where denotes the immediate reward. Different from the conventional DQN, we include both the SE action and the greedy action , in addition to the executed action .
Let denote the th transition of a sampled batch from the replay memory. Same as the conventional DQN, we define the temporal-difference (TD) error of as
| (30) |
where is the estimation of Q-value at next step. This is to measure the gap between the left and right sides of the Bellman equation (22). A larger gap indicates that the approximated Q-values are far from the optimal. Different from DQN, we introduce the action-difference (AD) error as below to measure the difference of Q-value between actions selected by the SE strategy and the greedy strategy:
| (31) |
Since the optimal policy has the threshold structure, the inferred action should be identical to the optimal action . Thus, a well-trained should lead to a small difference in (31).
Based on (30) and (31), we define the loss function of as
| (32) |
where is a hyperparameter to balance the importance of and . In other words, if the SE action is executed, both the TD and AD errors are taken into account; otherwise, the conventional TD-error-based loss function is adopted.
Given the batch size , the overall loss function is
| (33) |
To optimize , we adopt the well-known gradient descent method and calculate the gradient as below
| (34) |
where is given as
| (35) |
The details of the SE-DQN algorithm are given in Algorithm 1.
IV-B Structure-Enhanced DDPG
Different from the DQN, which has one NN to estimate the Q-value, a DDPG agent has two NNs [17], a critic NN with parameter and an actor NN with the parameter . In particular, the actor NN approximates the optimal policy by , while the critic NN approximates the Q-value of the optimal policy by . In general, the critic NN judges whether the generated action of the actor NN is good or not, and the latter can be improved based on the former. The critic NN is updated by minimizing the TD error similar to the DQN. The actor-critic framework enables DDPG to solve MDPs with continuous and large action space, which cannot be handled by the DQN.
To solve our scheduling problem with a discrete action space, we adopt an action mapping scheme similar to the one adopted in [10]. We set the direct output of the actor NN with continuous values, ranging from to , corresponding to sensors to , respectively. Recall that the DQN has outputs. The values are sorted in descending order. The sensors with the highest ranking are assigned to channels to , respectively. The corresponding ranking values are then linearly normalized to as the output of the final outputs of the actor NN, named as the virtual action . It directly follows that the virtual action and the real scheduling action can be mapped from one to the other directly. Therefore, we use the virtual action , instead of the real action , when presenting the SE-DDPG algorithm.
Similar to the SE-DQN, the SE-DDPG has the loose SE-DDPG stage, the tight SE-DDPG stage, and the conventional DDPG stage. The th sampled transition is denoted as
| (36) |
We present the SE action selection method and the SE loss function in the sequel.
IV-B1 SE action selection
The general action selection approach for the SE-DDPG is identical to that of the SE-DQN, by simply converting , , , and to , , , and , respectively. Different from DQN with -greedy actions, the action generated by the DDPG based on the current state is
| (37) |
and the random action was generated by adding noise to the original continuous output of the actor NN.
| (38) | ||||
| (39) |
IV-B2 SE loss function
Different from the SE-DQN, the SE-DDPG needs different loss functions for updating the critic NN and the actor NN. For the critic NN, we use the same loss function as in (33), and thus the gradient for the critic NN update is identical to (34). Note that for DDPG, the next virtual action is the direct output of the actor NN given the next state , i.e., . Thus, when calculating the TD error (30), we have .
For the actor NN, we introduce the difference between actions selected by the SE strategy and the actor NN , when is executed, i.e., . If the SE action is not selected, then the loss function is the Q-value given the state-action pair, which is identical to the conventional DDPG. Given the hyperparameter , the loss function for the transition is defined as
| (40) |
and hence the overall loss function given the sampled batch is
| (41) |
By replacing (37) and (40) in (41) and applying the chain rule, we can derive the gradient of the overall loss function in terms of as
| (42) |
where is given by:
| (43) |
The details of the proposed SE-DDPG algorithm are given in Algorithm 2.
V Numerical Experiments
| Hyperparameters of SE-DQN and SE-DDPG | Value |
| Initial values of and | 1 |
| Decay rates of and | 0.999 |
| Minimum and | 0.01 |
| Mini-batch size, | 128 |
| Experience replay memory size, | 20000 |
| Discount factor, | 0.95 |
| Weight of SE-DQN and critic network loss function, | 0.5 |
| Hyperparameters of SE-DQN | |
| Learning rate | 0.0001 |
| Decay rate of learning rate | 0.001 |
| Target network update frequency | 100 |
| Input dimension of network, | |
| Output dimension of network, | |
| Hyperparameters of SE-DDPG | |
| Learning rate of actor network | 0.0001 |
| Learning rate of critic network | 0.001 |
| Decay rate of learning rate | 0.001 |
| Soft parameter for target update, | 0.005 |
| Weight of actor network loss function, | 0.9 |
| Input dimension of actor network, | |
| Output dimension of actor network, | |
| Input dimension of critic network, | |
| Output dimension of critic network, |
In this section, we evaluate and compare the performance of the proposed SE-DQN and SE-DDPG with the benchmark DQN and DDPG.
V-A Experiment Setups
Our numerical experiments run on a computing platform with an Intel Core i5 9400F CPU @ 2.9 GHz with 16GB RAM and an NVIDIA RTX 2070 GPU. For the remote estimation system, we set the dimensions of the process state and the measurement as and , respectively. The system matrices are randomly generated with the spectral radius within the range of . The entries of are drawn uniformly from the range , and are identity matrices. The fading channel state is quantized into levels, and the corresponding packet drop probabilities are and . The distributions of the channel states of each sensor-channel pair , i.e., are generated randomly.
During the training, we use the ADAM optimizer for calculating the gradient and reset the environment for each episode with steps. The episode numbers for the loose SE action, the tight SE action, and the conventional DQN stages are 50, 100, and 150, respectively. The settings of the hyperparameters for Algorithm 1 and Algorithm 2 are summarized in Table I.
V-B Performance Comparison
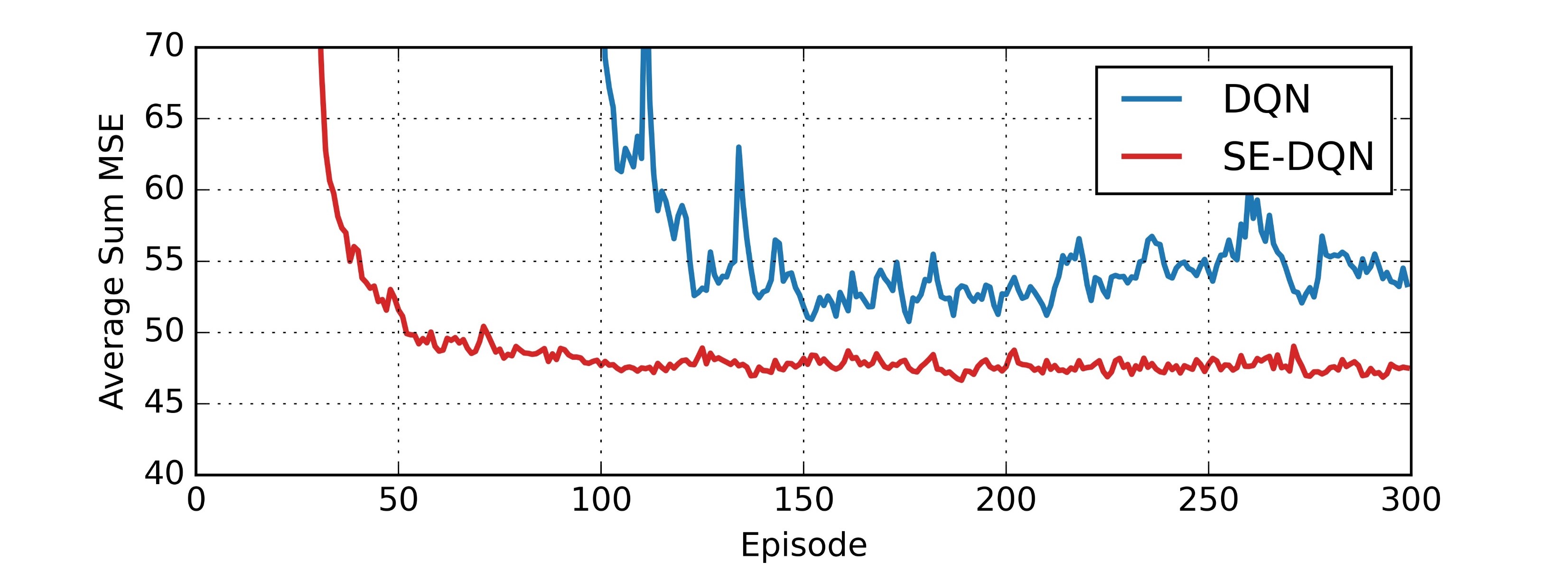
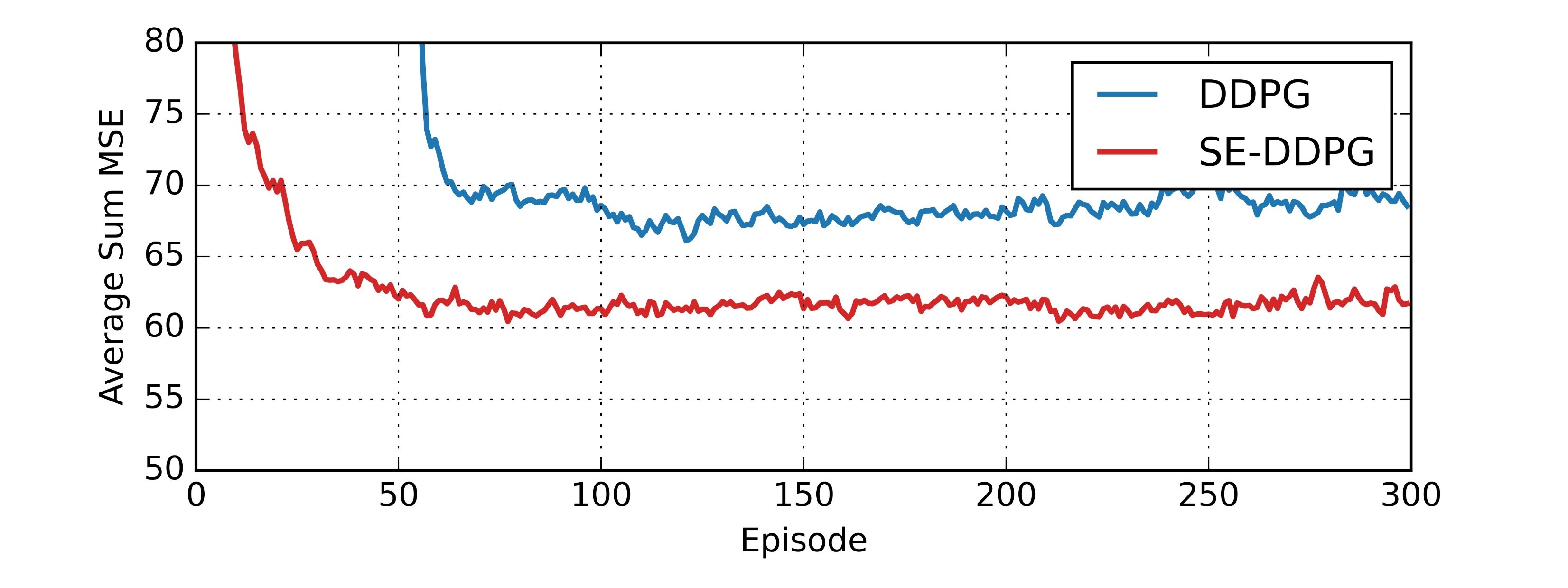
Fig. 3 and Fig. 4 illustrate the average sum MSE of all processes during the training achieved by the SE-DRL algorithms and the benchmarks under some system settings. Fig. 3 shows that the SE-DQN saves about training episodes for the convergence, and also decreases the average sum MSE for than the conventional DQN. Fig. 4 shows that the SE-DDPG saves about training episodes and reduces the average sum MSE by , when compared to the conventional DDPG. Also, we see that the conventional DQN and DDPG stages (i.e. the last 150 episodes) in Fig 3 and 4 cannot improve much of the training performance. This implies that the SE stages have found near optimal policies.
In Table II, we test the performance of well-trained SE-DRL algorithms for different numbers of sensors and channels, and different settings of system parameters, i.e., , , and , based on 10000-step simulations. We see that for 6-sensor-3-channel systems, the SE-DQN reduces the average MSE by to over DQN, while both DDPG and SE-DDPG achieve similar performance as the SE-DQN. This suggests that the SE-DQN is almost optimal and that the DDPG and the SE-DDPG cannot improve further. In 10-sensor-5-channel systems, neither the DQN nor the SE-DQN can converge, and the SE-DDPG achieves a MSE reduction over the DDPG. In particular, the SE-DDPG is the only converged algorithm in Experiment 12. In 20-sensor-10-channel systems, we see that the SE-DDPG can reduce the average MSE by to . Therefore, the performance improvement of the SE-DDPG appears significant for large systems.
| System Scale | Experiment | DQN | SE-DQN | DDPG | SE-DDPG |
|---|---|---|---|---|---|
| 1 | 52.4121 | 47.6766 | 48.4075 | 47.0594 | |
| 2 | 67.4247 | 49.8476 | 53.3675 | 44.7423 | |
| 3 | 84.1721 | 59.9127 | 56.9504 | 55.2409 | |
| 4 | 79.5902 | 65.1640 | 64.4313 | 58.5534 | |
| 9 | 68.0247 | 62.4727 | |||
| 10 | 89.6290 | 78.4138 | |||
| 11 | 90.2812 | 81.1148 | |||
| 12 | 147.2844 | ||||
| 13 | 181.4135 | 159.4321 | |||
| 14 | 163.1257 | 142.1850 | |||
| 15 | 173.0940 | 144.8166 | |||
| 16 | 215.2231 | 160.2304 |
VI Conclusion
We have developed the SE-DRL algorithms for optimal sensor scheduling of remote estimation systems. In particular, we have proposed novel SE action selection and loss functions to enhance training efficiency. Our numerical results have shown that the proposed structure-enhanced DRL algorithms can save the training time by 50% and reduce the estimation MSE by 10% to 25%, when benchmarked against conventional DRL algorithms. For future work, we will rigorously prove the threshold structure of the optimal scheduling policy for our system. Also, we will investigate other structural properties of the optimal policy to enhance the DRL.
References
- [1] P. Park, S. Coleri Ergen, C. Fischione, C. Lu, and K. H. Johansson, “Wireless network design for control systems: A survey,” IEEE Commun. Surv. Tutor., vol. 20, no. 2, pp. 978–1013, May 2018.
- [2] K. Huang, W. Liu, Y. Li, B. Vucetic, and A. Savkin, “Optimal downlink-uplink scheduling of wireless networked control for industrial IoT,” IEEE Internet Things J., vol. 7, no. 3, pp. 1756–1772, Mar. 2020.
- [3] K. Gatsis, M. Pajic, A. Ribeiro, and G. J. Pappas, “Opportunistic control over shared wireless channels,” IEEE Trans. Autom. Control, vol. 60, no. 12, pp. 3140–3155, Mar, 2015.
- [4] D. Han, J. Wu, H. Zhang, and L. Shi, “Optimal sensor scheduling for multiple linear dynamical systems,” Automatica, vol. 75, pp. 260–270, Jan, 2017.
- [5] S. Wu, X. Ren, S. Dey, and L. Shi, “Optimal scheduling of multiple sensors over shared channels with packet transmission constraint,” Automatica, vol. 96, pp. 22–31, Oct. 2018.
- [6] R. S. Sutton and A. G. Barto, Reinforcement learning: An introduction. MIT press, 2018.
- [7] Z. Zhao, W. Liu, D. E. Quevedo, Y. Li, and B. Vucetic, “Deep learning for wireless networked systems: a joint estimation-control-scheduling approach,” arXiv preprint, Oct, 2022. [Online]. Available: https://doi.org/10.48550/arXiv.2210.00673
- [8] A. S. Leong, A. Ramaswamy, D. E. Quevedo, H. Karl, and L. Shi, “Deep reinforcement learning for wireless sensor scheduling in cyber–physical systems,” Automatica, vol. 113, pp. 1–8, Mar. 2020. Art. no. 108759.
- [9] W. Liu, K. Huang, D. E. Quevedo, B. Vucetic, and Y. Li, “Deep reinforcement learning for wireless scheduling in distributed networked control,” submitted to Automatica, 2021. [Online]. Available: https://doi.org/10.48550/arXiv.2109.12562
- [10] G. Pang, W. Liu, Y. Li, and B. Vucetic, “DRL-based resource allocation in remote state estimation,” arXiv preprint, May. 2022. [Online]. Available: https://doi.org/10.48550/arXiv.2205.12267
- [11] Z. D. Guo and E. Brunskill, “Directed exploration for reinforcement learning,” arXiv preprint, Jun 2019. [Online]. Available: https://doi.org/10.48550/arXiv.1906.07805
- [12] S. Wu, K. Ding, P. Cheng, and L. Shi, “Optimal scheduling of multiple sensors over lossy and bandwidth limited channels,” IEEE Trans. Netw. Syst., vol. 7, no. 3, pp. 1188–1200, Jan. 2020.
- [13] Y.-P. Hsu, E. Modiano, and L. Duan, “Age of information: Design and analysis of optimal scheduling algorithms,” in Proc. IEEE Int. Symp. Inf. Theory, June. 2017, pp. 561–565.
- [14] W. Liu, D. E. Quevedo, Y. Li, K. H. Johansson, and B. Vucetic, “Remote state estimation with smart sensors over Markov fading channels,” IEEE Trans. Autom. Control, vol. 67, no. 6, pp. 2743–2757, June, 2022.
- [15] W. Liu, D. E. Quevedo, K. H. Johansson, B. Vucetic, and Y. Li, “Stability conditions for remote state estimation of multiple systems over multiple markov fading channels,” IEEE Trans. Autom. Control, early access, Aug. 2022.
- [16] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller, “Playing Atari with deep reinforcement learning,” in NIPS Deep Learning Workshop, 2013.
- [17] T. P. Lillicrap, et al., “Continuous control with deep reinforcement learning,” arXiv preprint, Sep. 2015. [Online]. Available: https://doi.org/10.48550/arXiv.1509.02971