Structural Superfluid-Mott Insulator Transition for a Bose Gas in Multi-Rods

Phase transitions are ubiquitous in condensed matter physics. In particular, at very low temperatures, quantum phase transitions are the onset to distinguish new phenomena in quantum many-body systems. Following the realization of a Bose-Einstein condensate (BEC) in 1995 [1, 2], a new and successful research line has been to study BEC within periodic optical lattices. It has been possible to study the properties and behavior of atomic gases trapped in three-dimensional (3D) multilayers, multi-tubes, or a simple cubic array of dots through the superposition of two opposing lasers in one, two, or three mutually perpendicular directions [3, 4], respectively. One of the most exciting achievements has been the observation of the superfluid (SF) to Mott insulator (MI) phase transition in a BEC with repulsive interactions, held both in a 3D [3, 5] and one-dimensional (1D) [6] optical lattices.

Although there have been great advances in the creation of many types of optical lattices, efforts are still being made to overcome their limited spatial resolution, which is of the order of one-half the laser wavelength $\lambda_{\mathrm{OL}}/2$, to manipulate atoms. Recently, there has been a notorious interest and advances in developing tools to surpass the diffraction limit, not only in the field of cold atoms but also in nanotechnology [7, 8]. Nowadays, the physical realization of optical lattices formed by subwavelength (ultranarrow) optical barriers of width below $\lambda_{\mathrm{OL}}/50$ [9, 10, 11, 12], is a reality. These so-called subwavelength optical lattices (SWOLs) can be seen as a very close experimental realization of a sequence of Dirac-$\delta$ functions, forming the well-known Dirac comb potential [13], and could be useful to test many mean-field calculations on the weakly-interacting Bose gas in this kind of potentials [14, 15, 16, 17, 18]. In the near future, we might see the realization of complex subwavelength optical lattices, including multiscale design, as a niche to observe new quantum phenomena [19, 11]. From the point of view of theoretical simplicity, adaptable periodic structures ranging from the subwavelength to typical optical lattices could be simulated and engineered by applying an external Kronig-Penney (KP) potential, for example, to a quantum gas.

In this paper, we analyze the physical properties of a degenerate interacting 1D Bose gas in a lattice formed by a succession of permeable rods at zero temperature. To create this multi-rod lattice, we apply the KP potential [20]

to the gas, where ${V_{0}}$ is the barrier height and $\Theta(z)$ the Heaviside step function. The rods, distributed along the $z$ direction, have width $b$, and are separated by empty regions of length $a$, such that the lattice period is $l\equiv a+b$. Here, we use the KP potential to study quantum gases due to its relatively simple shape, robustness, and versatility while preserving the system essence coming from the periodicity of its structure. We use it to model a typical optical lattice $V(z)={V_{0}}\sin^{2}(k_{\mathrm{OL}}z)$, with $k_{\mathrm{OL}}=2\pi/\lambda_{\mathrm{OL}}$, in the symmetric case $b=a$. Also, we model the subwavelength optical barriers in a SWOL through a Kronig-Penney lattice with $b\ll a$. Furthermore, we take advantage of the KP potential versatility by defining a new parameter $b/a$, and analyze how its variation affects the ground-state properties of the Bose gas within a fixed-period multi-rod lattice. Then, we show a new structural mechanism to induce a reentrant, commensurate SF-MI-SF quantum phase transition, by varying the ratio $b/a$ while keeping the interaction strength and lattice period fixed. We propose that this transition, infeasible in experiments with typical optical lattices under similar conditions, could be observed in experiments with cold atoms in SWOLs.

Our analysis relies on the ab-initio diffusion Monte Carlo (DMC) method [21], adapted for the calculation of pure estimators through the forward-walking technique. The DMC method solves stochastically the many-body Schrödinger equation, providing exact results for the ground-state of the system within some statistical noise. In Fig. 1, we show three faces of the KP potential depending on the ratio $b/a$ while keeping $V_{0}$ and $l$ fixed: (a) the symmetric case where $b=a$, which is our reference potential; (b) when the barriers become very thin, i.e. $b\ll a$; and (c) when $b\gg a$. The limits $b/a\to 0$ and $b/a\to\infty$ convert the KP potential in constant potentials $V_{\mathrm{KP}}=0$ and $V_{\mathrm{KP}}={V_{0}}$, respectively. The bosonic particles interact through a contact-like, repulsive potential of arbitrary magnitude. Consequently, our system corresponds to the Lieb-Liniger (LL) Bose gas [22] within the multi-rod lattice Eq. 1. The Hamiltonian of the system with $N$ bosons is

where $m$ is the mass of the particles, $g_{\mathrm{1D}}\equiv 2\hbar^{2}/ma_{\mathrm{1D}}$ is the interaction strength, and $a_{\mathrm{1D}}$ is the one-dimensional scattering length. In the absence of the multi-rod lattice, we recover the LL Bose gas, which is exactly solvable for any magnitude of the dimensionless interaction parameter $\gamma\equiv mg_{\mathrm{1D}}/\hbar^{2}n_{1}=2/n_{1}a_{\mathrm{1D}}$, with $n_{1}=N/L$ the linear density.

The presence of a lattice can produce a quantum phase transition in the system from a superfluid state to a Mott-insulator state or vice-versa, commonly known as Mott transition [5, 6, 23]. In deep optical lattices, that is, when the lattice height is way larger than the recoil energy $E_{\mathrm{R}}=\hbar^{2}k_{\mathrm{OL}}^{2}/2m$, the well-known Bose-Hubbard (BH) model [24, 3, 25, 5, 6, 26] captures the essence of the transition. According to this model, the competition between the on-site interaction $U$ and the hopping energy $J$ between adjacent lattice sites drives the transition from the SF to the MI state. In the Mott insulator state, each lattice site contains the same number of particles. On the other hand, the SF-MI transition can be also studied using the low-energy description of the system given by the Luttinger liquid theory and the quantum sine-Gordon (SG) Hamiltonian [27, 23, 28, 29]. In this approach, two system-dependent quantities, the speed of sound $c_{\mathrm{s}}$ and the Luttinger parameter $K=\hbar\pi n_{1}/mc_{\mathrm{s}}$, play a central role in the description of the ground-state. In particular, for any commensurate filling $n_{1}l={j}/{p}$, with $j$ and $p$ integers, the system can undergo a SF-MI transition when $K$ takes the critical value $K_{\mathrm{c}}=2/p^{2}$ [23, 28], where $p$ is the commensurability order. For $p=1$, i.e., for an integer number of bosons per lattice site, $K_{\mathrm{c}}=2$. The 1D Bose gas remains superfluid while $K>K_{\mathrm{c}}$, and variations in the interaction strength and the lattice height can push $K$ towards $K_{\mathrm{c}}$. The excitation energy spectrum is non-gapped and increases linearly with the quasimomentum as $E(k)=c_{\mathrm{s}}\hbar|k|$ in the SF state [30, 27], whereas it develops an excitation gap $\Delta$ in the MI phase, $E(k)=\sqrt{{\left(c_{\mathrm{s}}\hbar|k|\right)}^{2}+\Delta^{2}}$ [23]. Remarkably, in 1D gases, an arbitrarily weak periodic potential is enough to drive a Mott transition provided that the interactions are sufficiently strong [29, 6].

A fingerprint of the Mott transition can be obtained from the static structure factor $S(k)$ [31, 32],

where the operator $\boldsymbol{\hat{n}}_{1,k}$ is the Fourier transform of the density operator $\boldsymbol{\hat{n}}_{1}(z)\equiv\sum_{j=1}^{N}\delta(z-z_{j})$. For small momenta, $S(k)$ is sensitive to the collective excitations of the system. For high-$k$ values, $S(k)$ approximates to the model-independent value $\lim_{k\to\infty}S(k)=1$. Furthermore, the low-momenta behavior of the energy spectrum $E(k)$ is related to $S(k)$ through the well-known Feynman relation [33, 34, 32], $E(k)\equiv{\hbar^{2}k^{2}}/{(2mS(k))}$. This equation gives an upper bound to the excitation energies in terms of the static structure factor. Using this expression, we can estimate both the speed of sound $c_{\mathrm{s}}$ and the energy gap $\Delta$ from the low-momenta behavior of $S(k)$. In the SF phase, $\Delta=0$, and ${(c_{\mathrm{s}}/v_{\mathrm{F}})}^{-1}=2k_{\mathrm{F}}\lim_{k\to 0}{S(k)}/{k}$, where $k_{\mathrm{F}}=\pi n_{1}$ is the Fermi momentum and $v_{\mathrm{F}}=\hbar k_{\mathrm{F}}/m$ is the Fermi velocity. Also, $K={(c_{\mathrm{s}}/v_{\mathrm{F}})}^{-1}$. In contrast, in the MI phase, $S(k)$ grows quadratically with $k$ when $k\to 0$.

We study the SF-MI transition at unit-filling $n_{1}l=1$ and $b=a$, i.e., our system has, on average, one boson per lattice site. We determine the Mott transition by calculating $K$ as a function of the interaction strength $\gamma$ and the lattice height ${V_{0}}$. The boundary between the SF and MI phases corresponds to the condition $K(\gamma,{V_{0}})=2$. In Fig. 2a, we show the DMC zero-temperature phase diagram ${V_{0}}/E_{\mathrm{R}}$ vs. $\gamma^{-1}$ for a 1D Bose gas in a square multi-rod lattice (black circles). In the same figure, we also show experimental data [6] (orange and red squares) for a 1D Bose gas in an optical lattice at commensurability $n_{1}\sim 2/\lambda_{\mathrm{OL}}$, with $\lambda_{\mathrm{OL}}/2$ the spatial period of the optical potential. Note that the recoil energy is $E_{\mathrm{R}}=\hbar^{2}\pi^{2}/2ml^{2}$ since we require that both optical and multi-rod lattices have the same periodicity, that is $l=\lambda_{\mathrm{OL}}/2$.

We observe that our results are close to but below the experimental data in the deep lattices zone, where the BH model accurately describes the physics of the lattice. According to the 1D BH model, for an optical lattice the SF-MI transition occurs at the critical ratio ${(U/J)}_{\mathrm{c}}=3.85$ [37]. Since $U=(\sqrt{2\pi}/\pi^{2})E_{\mathrm{R}}\gamma(n_{1}\lambda_{\mathrm{OL}}/2){({V_{0}}/E_{\mathrm{R}})}^{1/4}$ and $J=(4/\sqrt{\pi})E_{\mathrm{R}}{({V_{0}}/E_{\mathrm{R}})}^{3/4}\exp[-2\sqrt{({V_{0}}/E_{\mathrm{R}})}]$, it is possible to define a relation between the lattice height ${V_{0}}$ and the interaction strength $\gamma$ at the transition [29, 38],

In Fig. 2a, we show Eq. 4 for the BH critical value ${(U/J)}_{\mathrm{c}}=3.85$ (dashed, red line). The BH transition line agrees with the experimental data for lattices as high as ${V_{0}}\geq 7E_{\mathrm{R}}$, but fails for shallow lattices, a behavior discussed in Ref. [6]. Remarkably, most of our DMC simulation results follow the law Eq. 4, with a smaller energy ratio, ${(U/J)}_{\mathrm{c}}=2.571(12)$ (dark-gray line), except close to the transition point $\gamma_{\mathrm{c}}^{-1}=0.28$ for ${V_{0}}=0$, where we do not expect a good fit since the BH model Eq. 4 predict $\gamma^{-1}\to\infty$ when $V_{0}\to 0$. The range of ${V_{0}}$ values for which the BH model fits the multi-rods DMC results is, in fact, quite large, starting from lattice heights as low as $\sim 2E_{\mathrm{R}}$. As we can see in Fig. 2a, the square multi-rod lattice is more insulating than an optical lattice with the same strength. Looking at the Fourier series expansion of $V_{\mathrm{KP}}(z)$, and considering only up to second order, we obtain that $V_{\mathrm{KP}}(z)\approx\tilde{V}_{0}(1-\cos(2\pi z/l))/2=\tilde{V}_{0}\sin^{2}(k_{\mathrm{OL}}z)$, where $\tilde{V}_{0}=4{V_{0}}/\pi$. Hence, the multi-rod lattice is roughly equivalent to an optical lattice with a larger height $\tilde{V}_{0}$; accordingly, the SF-MI transition in the former should occur at smaller ${V_{0}}$ than the latter; our numerical results corroborate this observation.

In Fig. 2b, we focus our analysis on shallow lattices only, where we do not include the data of Ref. [6] to avoid excessive piling of data. We compare our results with two additional relevant sources: first, experimental and numerical data reported in Ref. [35] (purple and pink squares), and second, DMC data reported in Ref. [36] (blue diamonds). Overall, there is a noticeable overlap between our DMC results and the data from Refs. [35] and [36], which is stronger as the lattices get shallower. The differences between the results for both lattices become smaller as $\gamma_{\mathrm{c}}^{-1}\to 0.28$ and ${V_{0}}\to 0$, just as expected since for both multi-rod and optical lattices the system resembles more the Lieb-Liniger gas. Experimental data from [6] and [35] in Figs. 2a and 2b seem to agree better with the BH model predictions for multi-rods (gray line) than Eq. 4 for an optical lattice with ${(U/J)}_{\mathrm{c}}=3.85$ (dashed, red line). On the other hand, Ref. [35] reports an estimation of ${(U/J)}_{\mathrm{c}}=3.36$, for which Eq. 4 agrees better with experimental data than the BH model for multi-rods. Given the above, it is clear that the experimental uncertainties in the data reported in Ref. [6] do not allow for a good estimation of ${(U/J)}_{\mathrm{c}}$ at the transition.

Complementary information on the MI phase can be obtained through the estimation of the energy gap $\Delta$. We calculate $\Delta$ as a function of ${V_{0}}$ for both the multi-rod and optical lattices, with $\gamma=11$. This particular value of $\gamma$ corresponds to the one for available experimental data [6]. Under these conditions, the system is a strongly interacting gas in the MI phase. We plot our results in Fig. 3, together with the experimental energy gap reported in Ref. [6]. We observe a good agreement between our simulation results (for both lattices) and the experimentally measured gap, better than similar results for an optical lattice shown in Ref. [36].

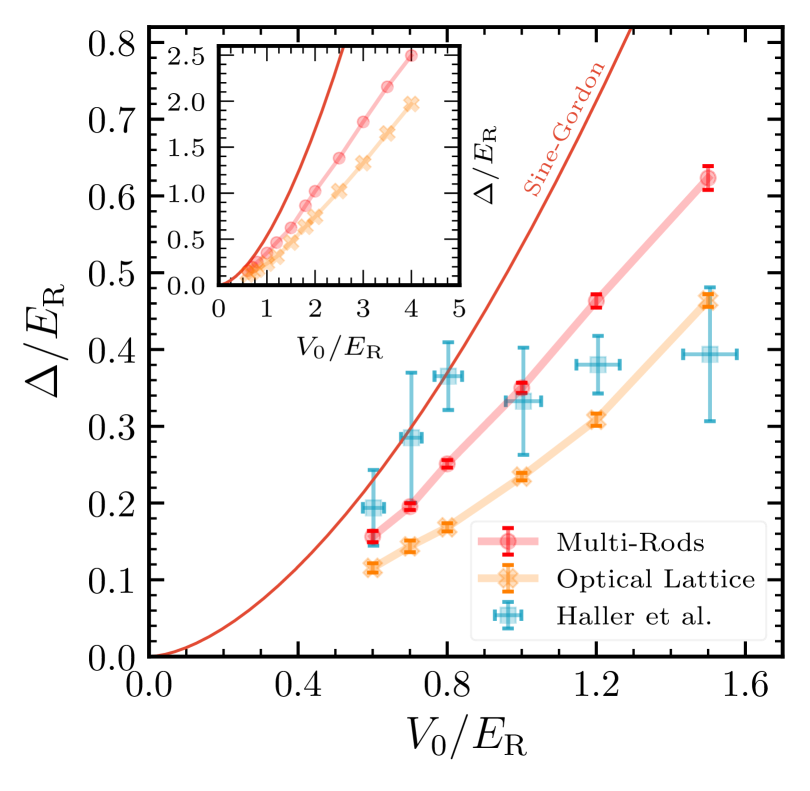
However, there is a clear qualitative discrepancy for ${V_{0}}>0.8E_{\mathrm{R}}$, since the experimental results show something like a plateau, while our results grow monotonically. For shallow lattices, the SG model correctly describes the system’s low-energy properties; in particular, it predicts that $\Delta$ increases with ${V_{0}}$, as our results. As commented in Ref. [36], the discussion on how good the modulation spectroscopy method for measuring $\Delta$ is, remains open. Finally, the gap as a function of ${V_{0}}$, for an optical lattice is smaller than the gap for a multi-rod lattice, so the latter is more insulating than the former, confirming the observation made after analyzing the results shown in Fig. 2.

Motivated by the recent studies on SWOLs, we extend the study of the interacting Bose gas within a square multi-rod lattice to a nonsquare multi-rod lattice, with special emphasis on describing the SF-MI quantum phase transition at commensurability $n_{1}l=1$. We performed our analysis for a fixed interaction strength $\gamma=1$. We calculate the speed of sound $c_{\mathrm{s}}$ from the low-momenta behavior of the static structure factor, and determine the ${V_{0}}$ and $b/a$ parameters such that $K(b/a,{V_{0}})=2$. In Fig. 4a, we show the dependence of the parameter $K={(c_{\mathrm{s}}/v_{\mathrm{F}})}^{-1}$ as a function of $b/a$ in four lattices with heights ${V_{0}}=3$, $3.5$, $4$, and $5$ times $E_{\mathrm{R}}$. First, we can see that, depending on the value of the lattice ratio $b/a$, $K$ can be greater or smaller than $K_{\mathrm{c}}=2$. This result shows that the SF-MI transition can be triggered by changing the lattices’s geometry if its height is large enough.

Variation of $b/a$ always affects $K$; however, although $K$ could diminish (starting from a SF state), a phase transition may not necessarily occur for relatively shallow lattices. As one can see, for $b/a\ll 1$ (thin barriers, see Fig. 1b) and $b/a\gg 1$ (thin wells, see Fig. 1c), the gas becomes superfluid independently of ${V_{0}}$. On the one hand, as $b/a$ diminishes and the barriers become thinner, the trapping effect of the lattice greatly reduces; in the limit $b/a\to 0$ the system becomes the LL gas. On the other hand, as $b/a$ increases, the system tends to resemble more to a succession of thin wells; in the limit $b/a\to\infty$, it becomes the LL gas subject to a constant potential of height ${V_{0}}$. Physically, there is no difference between both limits, except by a shift ${V_{0}}$ in the total energy. Also, in both limits, $K$ approaches to the corresponding value for the LL model, $K\approx 3.43$. It is worth noticing that the minimum $K$ in Fig. 4a occurs in the interval $1<b/a<2$, which interestingly shows that the largest trapping effect of the lattice does not correspond to the most symmetric case, i.e., the square lattice.

We show the zero-temperature phase transition diagram ${V_{0}}/E_{\mathrm{R}}$ vs. $b/a$ in Fig. 4b. As commented before, the minimum interaction ${V_{0}}$ to produce the Mott transition is slightly shifted to non-square potentials, $b/a\simeq 1.4$. When the asymmetry is $b/a<1$, the strength ${V_{0}}$ increases quite fast, favoring the stability of the SF phase. When $b/a>1.4$, ${V_{0}}$ also increases but with a slightly smaller slope. The blob in the phase diagram is therefore not symmetric and interestingly shows the possibility of a double transition SF-MI-SF for ${V_{0}}>3.4$ by just changing the relation $b/a$ keeping both ${V_{0}}$ and $\gamma$ constants. Note that the Fig. 4b is a cross-section of a MI tubular volume in the ${V_{0}}/E_{\mathrm{R}}$ vs. $\gamma^{-1}$ vs. $b/a$ diagram whose asymmetric V-boat-hull shape surface contains the SF-MI phase coexistence line shown in Fig. 2b.

Using the ab-initio DMC method we calculate the zero-temperature SF-MI quantum phase transition, in a ${V_{0}}/E_{\mathrm{R}}$ vs. $\gamma^{-1}$ diagram, for a 1D Bose gas with contact interactions within a square multi-rod lattice. We show and justify a notable similarity with the phase transition diagram of a Bose gas in a typical optical lattice by comparing it with several experimental and numerical data sources, finding that the multi-rod lattice favors the insulating phase. We also confirm that the BH model accurately predicts the transition in the regime of weak interactions and deep enough wells. For the Bose gas in both a multi-rod and optical lattices with the same strength and period, we calculate the energy gap $\Delta$ as a function of the lattice height ${V_{0}}$ for $\gamma=11$. As expected, the gap is larger within the multi-rods lattice than in the optical lattice, validating what has already been observed in the phase transition diagrams. In the range of ${V_{0}}$ values where experimental data exist for the gap, our results are of the same order of magnitude but do not match the experimental behavior that shows something similar to a saturation with ${V_{0}}$. Finally, we show a new structural mechanism to induce a robust reentrant, commensurate SF-MI-SF phase transition, triggered by the variation of the parameter $b/a$ at fixed interaction strength and lattice period. We propose that such a mechanism could be experimentally implemented using the recently realized SWOLs, so the SF-MI structural phase transition could be observed.