Stronger NAS with Weaker Predictors

Given a search space of network architectures $X$ and an architecture-to-performance mapping function $f:X\rightarrow P$ from the architecture set $X$ to the performance set $P$, the objective is to find the best neural architecture $x^{*}$ with the highest performance $f(x)$ in the search space $X$:

$\displaystyle x^{*}=\operatorname*{arg\,max}_{x\in X}f(x)$

(1)

A naïve solution is to estimate the performance mapping $f(x)$ through the full search space. However, this is prohibitively expensive since all architectures have to be exhaustively trained from scratch. To address this problem, predictor-based NAS learns a proxy predictor $\tilde{f}(x)$ to approximate $f(x)$ by using some architecture-performance pairs, which significantly reduces the training cost. In general, predictor-based NAS can be re-cast as a bi-level optimization problem:

$\displaystyle\begin{split}\quad x^{*}=\operatorname*{arg\,max}_{x\in X}\tilde{f}(x|S),\,\,\textrm{s.t.}\,\tilde{f}=\operatorname*{arg\,min}_{S,\tilde{f}\in\tilde{\mathcal{F}}}\sum_{s\in S}\mathcal{L}(\tilde{f}(s),f(s))\,\end{split}\vspace{-0.5em}$

(2)

where $\mathcal{L}$ is the loss function for the predictor $\tilde{f}$, $\tilde{\mathcal{F}}$ is a set of all possible approximation to $f$, $S:=\{S\subseteq X\mid|S|\leq C\}$ all architectures satisfying the sampling budget $C$. $C$ is directly related to the total training cost, e.g., the total number of queries. Our objective is to minimize the loss $\mathcal{L}$ based on some sampled architectures $S$.

Previous predictor-based NAS methods attempt to solve Equation 2 with two sequential steps: (1) sampling some architecture-performance pairs and (2) learning a proxy accuracy predictor. For the first step, a common practice is to sample training pairs $S$ uniformly from the search space $X$ to fit the predictor. Such sampling is however inefficient considering that the goal of NAS is only to find well-performed architectures without caring for the bad ones.

Optimization Insight: Instead of first (uniformly) sampling the whole space and then fitting the predictor, we propose to jointly evolve the sampling $S$ and fit the predictor $\tilde{f}$, which helps achieve better sample efficiency by focusing on only relevant sample subspaces. That could be mathematically formulated as solving Equation 2 in a new coordinate descent way, that iterates between optimizing the architecture sampling and predictor fitting subproblems:

	(Sampling)	$\displaystyle\tilde{P}^{k}=\{\tilde{f}_{k}(s)|s\in X\setminus S^{k}\},\,\,S_{M}\subset\text{Top}_{N}(\tilde{P}^{k}),\,\,S^{k+1}=S_{M}\cup S^{k},\,\,$		(3)
		$\displaystyle\text{where}\,\,\text{Top}_{N}(\tilde{P}^{k})\,\,\text{denote the set of top N architectures in}\,\,\tilde{P}^{k}$

$\displaystyle\textrm{(Predictor Fitting)}\quad x^{*}=\operatorname*{arg\,max}_{x\in X}\tilde{f}(x|S^{k+1}),\,\,\textrm{s.t.}\,\,\tilde{f}_{k+1}=\operatorname*{arg\,min}_{\tilde{f}_{k}\in\tilde{\mathcal{F}}}\sum_{s\in S^{k+1}}{\mathcal{L}}(\tilde{f}(s),f(s))\vspace{-0.9em}$

(4)

In comparison, existing predictor-based NAS methods could be viewed as running the above coordinate descent for just one iteration – a special case of our general framework.

As well known in optimization, many iterative algorithms only need to solve (subsets of) their subproblems inexactly [22, 23, 24] for properly ensuring convergence either theoretically or empirically. Here, using a strong predictor to fit the whole space could be treated as solving the predictor fitting subproblem relatively precisely, while adopting a weak predictor just imprecisely solves that. Previous methods solving Equation 2 truncate their solutions to “one shot" and hinge on solving subproblems with higher precision. Since we now take a joint optimization view and allow for multiple iterations, we can afford to only use weaker predictors for the fitting subproblem per iteration.

Implementation Outline: The above coordinate descent solution has clear interpretations and is straightforward to implement. Suppose our iterative methods has $K$ iterations. We initialize $S^{1}$ by randomly sampling a few samples from $X$, and train an initial predictor $\tilde{f}_{1}$. Then at iterations $k=2,\dots K$, we jointly optimize the sampling set $S^{k}$ and predictor $\tilde{f}_{k}$ in an alternative manner.

Our method can be alternatively regarded as a vastly simplified variant of Bayesian Optimization (BO). It does not refer to any explicit uncertainty-based modeling such as Gaussian Process (which are often difficult to scale up); instead it adopts a very simple step function as our acquisition function. For a sample $x$ in the search space $X$, our special “acquisition function" can be written as:

$$acq(x)=u(x-\theta)\cdot\epsilon$$

(5)

where the step function $u(x)$ is 1 if $x\geq\theta$, and 0 otherwise; $\epsilon$ is a random variable from the uniform distribution $U(0,1)$; and $\theta$ is the threshold to split Top$N$ from the rest, according to their predicted performance $\tilde{P}^{k}(x)$. We then choose the samples with the $M$ largest acquisition values:

$$S_{M}=\operatorname*{arg\,max}_{\text{Top}M}acq(x)$$

(6)

Why such “oversimplified BO" can be effectively for our framework? We consider the reason to be the inherently structured NAS search space. Specifically, existing NAS spaces are created either by varying operators from a pre-defined operator set (DARTS/NAS-Bench-101/201 Search Space) or by varying kernel size, width or depth (MobileNet Search Space). Therefore, as shown in Figure 4, the search spaces are often highly-structured, and the best performers gather close to each other.

Here comes our underlying prior assumption: we can progressively connect a piecewise search path from the initialization, to the finest subspace where the best architecture resides. At the beginning, since the weak predictor only roughly fits the whole space, the sampling operation will be “noisier", inducing more exploration. When it comes to the later stage, the weak predictors fit better on the current well-performing clusters, thus performing more exploitation locally. Therefore our progressive weak predictor framework provides a natural evolution between exploration and exploitation, without explicit uncertainty modeling, thanks to the prior of special NAS space structure.

Another exploration-exploitation trade-off is implicitly built in the adaptive sampling step of our subproblem 1 solution. To recall, at each iteration, instead of choosing all Top $N$ models by the latest predictor, we randomly sample $M$ models from Top $N$ models to explore new architectures in a stochastic manner. By varying the ratio $\epsilon=M/N$ and the sampling strategy (e.g., uniform, linear-decay or exponential-decay), we can balance the sampling exploitation and exploration per step, in a similar flavor to the $\epsilon$-greedy [27] approach in reinforcement learning.

Our framework is designed to be generalizable to various predictors and features. In predictor-based NAS, the objective of fitting the predictor $\tilde{f}$ is often cast as a regression [7] or ranking [5] problem. The choice of predictors is diverse, and usually critical to final performance [5, 6, 2, 7, 8, 9]. To illustrate our framework is generalizable and robust to the specific choice of predictors, we compare the following predictor variants.

• •

  Multilayer perceptron (MLP): MLP is the common baseline in predictor-based NAS [5] due to its simplicity. For our weak predictor, we use a 4-layer MLP with hidden layer dimension of (1000, 1000, 1000, 1000).

• •

  Regression Tree: tree-based methods are also popular [9, 28] since they are suitable for categorical architecture representations. As our weak predictor, we use the Gradient Boosting Regression Tree (GBRT) based on XGBoost [29], consisting of 1000 Trees.

• •

  Random Forest: random forests differ from GBRT in that they combines decisions only at the end rather than along the hierarchy, and are often more robust to noise. For each weak predictor, we use a random forest consisting of 1000 Forests.

The features representations to encode the architectures are also instrumental. Previous methods hand-craft various features for the best performance, e.g., raw architecture encoding [6], supernet statistics [30], and graph convolutional network encoding [7, 5, 8, 19] Our framework is also agnostic to various architecture representations, and we compare the following:

• •

  One-hot vector: In NAS-Bench-201 [31], its DARTS-style search space has fixed graph connectivity, hence the one-hot vector is commonly used to encode the choice of operator.

• •

  Adjacency matrix: In NAS-Bench-101, we used the same encoding scheme as in [32, 6], where a 7$\times$7 adjacency matrix represents the graph connectivity and a 7-dimensional vector represents the choice of operator on every node.

As shown in Figure 5, all predictor models perform similarly across different datasets. Comparing performance on NAS-Bench-101 and NAS-Bench-201, although they use different architecture encoding methods, our method still performs similarly well among different predictors. This demonstrates that our framework is robust to various predictor and feature choices.

We conduct a series of ablation studies on the effectiveness of proposed method on NAS-Bench-101. To validate the effectiveness of our iterative scheme, In Table 1, we initialize the initial Weak Predictor $\tilde{f}_{1}$ with 100 random samples, and set $M=10$, after progressively adding more weak predictors (from 1 to 191), we find the performance keeps growing. This demonstrates the key property of our method that probability of sampling better architectures keeps increasing as more iteration goes. It’s worth noting that the quality of random initial samples $M_{0}$ may also impact on the performance of WeakNAS, but if $|M_{0}|$ is sufficiently large, the chance of hitting good samples (or its neighborhood) is high, and empirically we found $|M_{0}|$=100 to already ensure highly stable performance at NAS-Bench-101: a more detailed ablation can be found in the Appendix Section D.

We then study the exploitation-exploration trade-off in Table 2 in NAS-Bench-101 (a similar ablation in Mobilenet Search space on ImageNet is also included in Appendix Table 13) by investigating two settings: (a) We gradually increase $N$ to allow for more exploration, similar to controlling $\epsilon$ in the epsilon-greedy [27] approach in the RL context; (b) We vary the sampling strategy from Uniform, Linear-decay to Exponential-decay (top models get higher probabilities by following either linear-decay or exponential-decay distribution). We empirically observed that: (a) The performance drops more (Test Regret 0.22% vs 0.08%) when more exploration (TopN=1000 vs TopN=10) is used. This indicates that extensive exploration is not optimal for NAS-Bench-101; (b) Uniform sampling method yields better performance than sampling method that biased towards top performing model (e.g. linear-decay, exponential-decay). This indicates good architectures are evenly distributed within the Top 100 predictions of Weak NAS, therefore a simple uniform sampling strategy for exploration is more optimal in NAS-Bench-101. To conclude, our Weak NAS Predictor strikes a good balance between exploration and exploration.

Apart from the above exploitation-exploration trade-off of WeakNAS, we also explore the possibility of integrating other meta-sampling methods. We found that the local search algorithm could achieve comparable performance, while using Semi-NAS [20] as a meta sampling method could further boost the performance of WeakNAS: more details are in Appendix Section G.

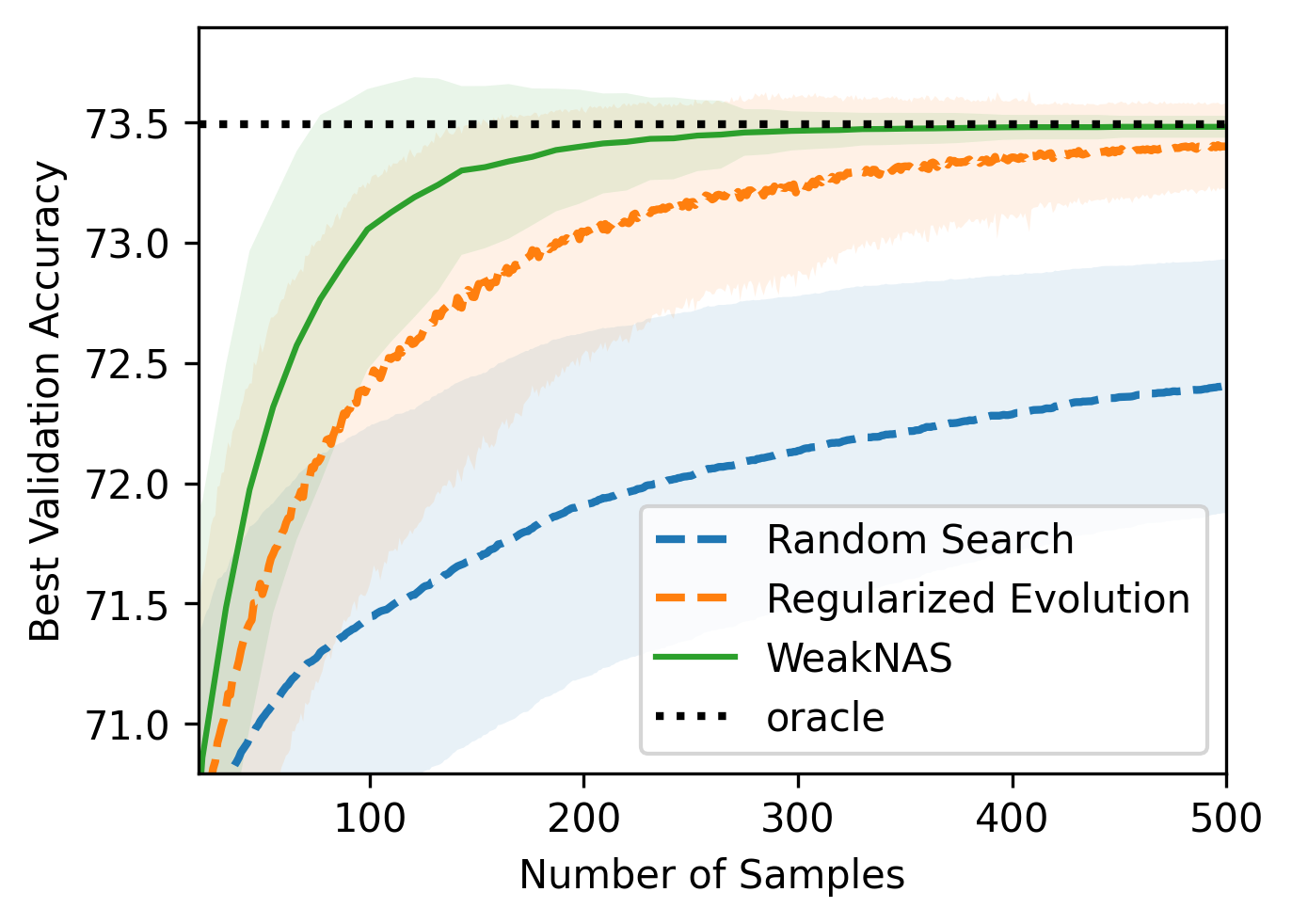
Table 5 shows that our method significantly outperforms baselines in terms of sample efficiency. Specifically, our method costs 964$\times$, 447$\times$, 378$\times$, 245$\times$, 58$\times$, and 7.5$\times$ less samples to reach the optimal architecture, compared to Random Search, Regularized Evolution [14], MCTS [40], Semi-NAS[20], LaNAS[21], BONAS[19], respectively. We then plot the best accuracy against number of samples in Table 4 and Figure 6 to show the sample efficiency on the NAS-Bench-101, from which we can see that our method consistently costs fewer sample to reach higher accuracy.

Compare with those BO-based method, our WeakNAS is an “oversimplified" version of BO as explained in Section 2.3. Interestingly, results in Table 4 suggests that WeakNAS is able to outperform BONAS [19], and is comparable to NASBOWLr [45] on NAS-Bench-101, showcasing that the simplification does not compromise NAS performance. We hypothesize that the following factors might be relevant: (1) the posterior modeling and uncertainty estimation in BO might be noisy; (2) the inherently structured NAS search space (shown in Figure 4) could enable a “shortcut" simplification to explore and exploit. In addition, the conventional uncertainty modeling in BO, such as the Gaussian Process used by [45], is not as scalable when the number of queries is large. In comparison, the complexity of WeakNAS scales almost linearly, as can be verified in Appendix Table 8. In our experiments, we observe WeakNAS to perform empirically more competitively than current BO-based NAS methods at larger query numbers, besides being way more efficient.

To further convince that WeakNAS is indeed an effective simplification compared to the explicit posterior modeling in BO, we report an apple-to-apple comparison, by use the same weak predictor from WeakNAS, plus obtaining its uncertainty estimation by calculating its variance using a deep ensemble of five model [49]; we then use the classic Expected Improvement (EI) [50] acquisition function. Table 3 confirms that such BO variant of WeakNAS is inferior our proposed formulation.

That said, we point out that our method can be complementary to those semi-supervised methods [20, 42], thus they can further be integrated as one, For example, Semi-NAS can be used as a meta sampling method, where at each iteration we further train a Semi-NAS predictor with pseudo labeling strategy to augment the training set of our weak predictors. We show in Appendix Table 12 that the combination of our method with Semi-NAS can further boost the performance of WeakNAS.