Strong Polynomiality of the Value Iteration Algorithm for Computing Nearly Optimal Policies for Discounted Dynamic Programming
Abstract
This note provides upper bounds on the number of operations required to compute by value iterations a nearly optimal policy for an infinite-horizon discounted Markov decision process with a finite number of states and actions. For a given discount factor, magnitude of the reward function, and desired closeness to optimality, these upper bounds are strongly polynomial in the number of state-action pairs, and one of the provided upper bounds has the property that it is a non-decreasing function of the value of the discount factor.
Keywords— Markov Decision Process, Discounting, Algorithm, Complexity, Optimal Policy.
1 Introduction
Value and policy iteration algorithms are the major tools for solving infinite-horizon discounted Markov decision processes (MDPs). Policy iteration algorithms also can be viewed as implementations of specific versions of the simplex method applied to linear programming problems corresponding to discounted MDPs [6, 17]. Ye [17] proved that for a given discount factor the policy iteration algorithm is strongly polynomial as a function of the total number of state-action pairs. Kitahara and Mizuno[7] extended Ye’s [17] results by providing sufficient conditions for strong polynomiality of a simplex method for linear programming, and Scherrer [13] improved Ye’s [17] bound for MDPs. For deterministic MDPs Post and Ye [10] proved that for policy iterations there is a polynomial upper bound on the number of operations, which does not depend on the value of the discount factor. Feinberg and Huang [4] showed that value iterations are not strongly polynomial for discounted MDPs. Earlier Tseng [16] proved weak polynomiality of value iterations.
In this note we show that the value iteration algorithm computes -optimal policies in strongly polynomial time. This is an important observation because value iterations are broadly used in applications, including reinforcement learning [1, 2, 15], for computing nearly optimal policies.
Let us consider an MDP with a finite state space and with a finite nonempty sets of actions available at each state Each action set consists of actions. Thus, the total number of actions is and this number can be interpreted as the total number of state-action pairs. Let be the discount factor. According to [13], the policy iteration algorithm finds an optimal policy within iterations, and each iterations requires at most operations with
| (1.1) |
This paper shows that for each , the value iteration algorithm finds an -optimal policy within iterations, and each iterations requires at most operations, where
| (1.2) |
where and are the constants defined by a one-step cost function and a function of terminal rewards . In addition, is non-decreasing in .
To define the values of and let us denote by the span seminorm of where is an -dimensional Euclidean space,
The properties of this seminorm can be found in [11, pp. 196].
Let be the reward collected if the system is at the state and the action is chosen. Let be the reward collected at the final state Then
| (1.3) |
We denote by
| (1.4) |
the maximal one-step reward that can be collected at the state Then
| (1.5) |
Observe that
Of course, the total number of operations to find an -optimal policy is bounded above by for the value iteration algorithm. The total number of operations to find an optimal policy is bounded above by for the policy iteration algorithm. Each iteration in the policy iteration algorithm requires solving a system of linear equations. This can be done by Gaussian elimination within operations. This is the reason the formula for in (1.1) depends on the term which can be reduced to with by using contemporary methods. For example, for Strassen’s algorithm[14]. According to [8], the best currently available but this method of solving linear equations is impractical due to the large value of the constant in In addition to (1.2), more accurate upper bounds on a number of iterations are presented in (3.5), (3.8), and (3.9), but they require additional definitions and calculations.
As well-known and clear from (1.1) and (1.2), the number of operations at each step is larger for the policy iteration algorithm than for the value iteration algorithm. If the number of states is large, then the difference can be significant. In order to accelerate policy iterations, the method of modified policy iterations was introduced in [12]. This method uses value iterations to solve linear equations. As shown in Feinberg et al. [5], modified policy iterations and their versions are not strongly polynomial algorithms for finding optimal policies.
2 Definitions
Let and be the sets of natural numbers and real numbers respectively. For a finite set , let denote the number of elements in the set . We consider an MDP with a finite state space where is the number of states, and nonempty finite action sets available at states Let be the action set. We recall that is the total number of actions at all states or, in slightly different terms, the number of all state-action pairs. For each if an action is selected at the state then a one-step reward is collected and the process moves to the next state with the probability where is a real number and The process continues over a finite or infinite planning horizon. For a finite-horizon problem, the terminal real-valued reward is collected at the final state
A deterministic policy is a mapping such that for each and, if the process is at a state then the action is selected. A general policy can be randomized and history-dependent; see e.g., Puterman [11, p. 154] for definitions of various classes of policies. We denote by the set of all policies.
Let be the discount factor. For a policy and for an initial state the expected total discounted reward for an -horizon problem is
and for the infinite-horizon problem it is
where is the expectation defined by the initial state and the policy and where is a trajectory of the process consisting of states and actions at epochs The value functions are defined for initial states as
for -horizon problems, and
for infinite-horizon problems. Note that for all and .
A policy is called optimal (-horizon optimal for ) if () for all . It is well-known that, for discounted MDPs with finite action sets, finite horizon problems have optimal policies and infinite horizon problems have deterministic optimal policies; see [11, p. 154].
A policy is called -optimal for if for all A -optimal policy is optimal. The objective of this paper is to estimate the complexity of the value iteration algorithm for finding a deterministic -optimal policy for .
3 Main Results
For a real-valued function let us define
| (3.1) |
We shall use the notation for a deterministic policy For we also define the optimality operator
| (3.2) |
Every real-valued function on can be identified with a vector Therefore, all real-valued functions on form the -dimensional Euclidean space
For each and all , the expected total discounted rewards and satisfy the equations
the value functions satisfy the optimality equations
and value iterations converge to the infinite-horizon expected total rewards and optimal values
| (3.3) | ||||
and a deterministic policy is optimal if and only if see, e.g., [3], [11, pp. 146-151]. Therefore, if we consider the nonempty sets
then a deterministic policy is optimal if and only if for all
For a given the following value iteration algorithm computes a deterministic -optimal policy. It uses a stopping rule based on the value of the span . As mentioned in [11, p. 205], this algorithm generates the same number of iterations as the relative value iteration algorithm originally introduced to accelerate value iterations.
Algorithm 1.
(Computing a deterministic -optimal policy by value iterations).
|
For given MDP, discount factor and constant :
|
||
|
1. select a vector and a constant (e.g., choose );
|
||
|
2. while compute and set endwhile;
|
||
|
3. choose a deterministic policy such that this policy is -optimal.
|
If then a deterministic policy is optimal if and only if As well-known, Algorithm 1 converges within a finite number of iterations (e.g., this follows from (3.3)) and returns an -optimal policy (e.g., this follows from [11, Proposition 6.6.5]).
Following Puterman [11, Theorem 6.6.6], let us define
| (3.4) |
We notice that . We assume since otherwise for any and If then we have again that a deterministic policy is optimal if and only if In this case Algorithm 1 stops at most after the second iteration and returns a deterministic optimal policy. If an MDP has deterministic probabilities and there are two or more deterministic policies with nonidentical stochastic matrices, then .
Computing the value of requires computing the sum in (3.4) for all couples of state-action pairs such that The identical pairs can be excluded since for such pairs the value of the function to be maximized in (3.4) is 0, which is the smallest possible value. The total number of such couples is . The number of arithmetic operations in (3.4), which are additions, is for each couple. Therefore, the straightforward computation of requires operations, which can be significantly larger than the complexity to compute an deterministic -optimal policy, which is the product of and defined in (1.2). Puterman [11, Eq. (6.6.16)] also provides an upper bound where whose computation requires operations.
Theorem 1.
For and , the number of iterations for Algorithm 1 to find a deterministic -optimal policy is bounded above by
| (3.5) |
if and If then and Algorithm 1 returns a deterministic optimal policy. If then and Algorithm 1 returns a deterministic optimal policy. In addition, each iteration uses at most operations.
Proof.
As follows from (3.1) and (3.2), each iteration uses at most arithmetic operations. Let be the actual number of iterations. According to its steps 2 snd 3, the algorithm returns the deterministic policy for which and
In view of [11, Proposition 6.6.5, p. 201], this is -optimal. By [11, Corollary 6.6.8, p. 204],
| (3.6) |
Therefore, the minimal number satisfying
| (3.7) |
leads to (3.5). The case is obvious, and the case is discussed above. ∎
Example 1.
This example shows that the bound in (3.5) can be exact, and it may not be monotone in the discount factor. Let the state space be and the action space be . Let , be the sets of actions available at states and respectively. The transition probabilities are given by . The one-step rewards are , and see Figure 1.

We set . As discussed above, for this MDP with deterministic transitions. Straightforward calculations imply that
where the -th coordinates of the vectors correspond to the states . The last displayed equality implies that inequality (3.6) holds in the form of an equality for this example. Therefore, the bound in (3.5) is also the actual number of iterations executed by Algorithm 1 for this MDP, which is
for and . If then Algorithm 1 stops after the first iteration. Let Then and , which shows that may not be monotone in .
Let us consider the vector defined in (1.4). Note that if . In the next corollary, we assume that and since otherwise Algorithm 1 stops after the first iteration and returns a deterministic optimal policy.
Theorem 2.
Proof.
Similarly, Therefore,
By the properties of seminorm provided in [11, p. 196],
which leads to where is defined in (3.5).
The formulae in (a) follow directly from (3.8). To prove (b), we recall that and see (1.5) and (1.3). By the assumption in the theorem,
The function is positive and decreasing in and the function is increasing in In addition, Therefore, the function
is increasing when , which is . This implies that is increasing on the interval where . Thus, if then the theorem is proved. Now let We choose an arbitrary Then which implies In view of (3.8), and the function is non-decreasing on ∎
As explained in the paragraph preceding Theorem 1, it may be time-consuming to find the actual value of for an MDP. The following corollaries provide additional bounds.
Corollary 1.
Let . For a fixed if , then
| (3.9) |
| (3.10) |
Proof.
We notice that, if the function from (3.8) is minimized in , than the smallest value is attained when which is The following corollary provides upper bounds for including
Corollary 2.
Let and let If then Algorithm 1 finds a deterministic -optimal policy after a finite number of iterations bounded above by
Proof.
This corollary follows from (3.10). ∎
Example 2.
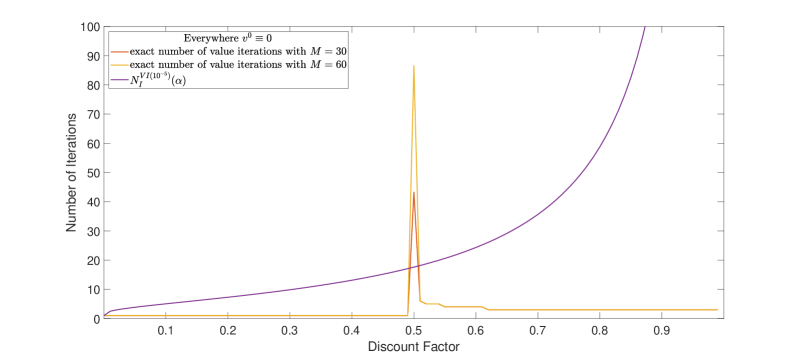
This example illustrates the monotonicity of the polynomial upper bound for computing -optimal policies and non-monotonicity of the number of calculations to find an optimal policy by value iterations. The following MDP is taken from [4]. Let the state space be and the action space be . Let , be the sets of actions available at states respectively; see Figure 2. The transition probabilities are given by . The one-step rewards are , and where . We set for .

As shown in [4], for the number of value iterations required to find an optimal policy increases to infinity as increases to infinity. This shows that the value iteration algorithm for computing the optimal policy is not strongly polynomial. However, does not change with the increasing in this example. As follows from Corollary 2, for fixed and with the number of required iterations for Algorithm 1 is uniformly bounded no matter how large is; see footnote 3.
Lewis and Paul [9] provide examples of MDPs for which the numbers of iterations required for computing an optimal policy by value iterations can tend to infinity even for discount factor bounded away from . Here we provide a significantly simpler example.
Example 3.
This example shows that the required number of value iterations to compute an optimal policy may be unbounded as a function of the discount factor when for some Consider an MDP with the state space with the action space and with the sets of actions and available at states and respectively; see Figure 4. The transition probabilities are given by . The one-step rewards are , and .
We set for .

There are only two deterministic policies denoted by and which differ only at state with and . Observe that for and all In addition,
Therefore, is optimal for and is optimal for Let us consider the number computed at the -th value iteration at step 2 of Algorithm 1, For this MDP, with and Observe that and for all If then . For
where and . Clearly is strictly decreasing as increases and . This implies that for the value iterations identify the optimal policy at the first iteration, and for every the value iterations identify the optimal policy at the -th iteration for .
4 Acknowledgement
This research was partially supported by the National Science Foundation grant CMMI-1636193.
References
- [1] D. P. Bertsekas, Reinforcement Learning and Optimal Control, Athena Scientific, Belmont, MA, 2019.
- [2] D. P. Bertsekas, J. N. Tsitsiklis, Neuro-Dynamic Programming, Athena Scientific, Belmont, MA, 1996.
- [3] E. A. Feinberg, Total reward criteria, in: E. A. Feinberg, A. Schwartz (Eds.), Handbook of Markov Decision Processes, Kluwer, Boston, MA, 2002, pp. 173-207.
- [4] E. A. Feinberg and J. Huang, The value iteration algorithm is not strongly polynomial for discounted dynamic programming, Oper. Res. Lett. 42 (2014) 130-131.
- [5] E. A. Feinberg, J. Huang, and B. Scherrer, Modified policy iteration algorithms are not strongly polynomial for discounted dynamic programming, Oper. Res. Lett. 42 (2014) 429-431
- [6] L.C.M. Kallenberg, Finite state and action MDPs, in: E. A. Feinberg, A. Schwartz (Eds.), Handbook of Markov Decision Processes, Kluwer, Boston, MA, 2002, pp. 21-87.
- [7] T. Kitahara and S. Mizuno, A bound for the number of different basic solutions generated by the simplex method, Math. Program. 137 (2013) 579-586.
- [8] J. F. Le Gall, Powers of tensors and fast matrix multiplication, Proc. of 39-th Int. Symp. Symb. Alge. Comput. (2014) 296-303.
- [9] M. E. Lewis and A. Paul, Uniform turnpike theorems for finite Markov decision processes, Math. Oper. Res. 44 (2019) 1145-1160.
- [10] I. Post and Y. Ye, The simplex method is strongly polynomial for deterministic Markov decision processes, Math. Oper. Res. 40 (2015) 859-868.
- [11] M. L. Puterman, Markov Decision Processes: Discrete Stochastic Dynamic Programming, John Wiley & Sons, Inc., New York, 1994.
- [12] M. L. Puterman and M. C. Shin, Modified policy iteration algorithms for discounted Markov decision problems, Manag. Sci. 24 (1978) 1127-1137.
- [13] B. Scherrer, Improved and generalized upper bounds on the complexity of policy iteration, Math. Oper. Res. 41 (2016) 758-774.
- [14] V. Strassen, Gaussian elimination is not optimal, Numer. Math. 13 (1969) 354-356.
- [15] R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, second ed., MIT Press, Cambridge, 2018.
- [16] P. Tseng, Solving h-horizon, stationary Markov decision problems in time proportional to log(h), Oper. Res. Lett. 9 (1990) 287-297.
- [17] Y. Ye, The simplex and policy-iteration methods are strongly polynomial for the Markov decision problem with a fixed discount rate, Math. Oper. Res. 36 (2011) 593-603.