Strong-field control of plasmonic properties in core-shell nanoparticles
Abstract
The strong-field control of plasmonic nanosystems opens up new perspectives for nonlinear plasmonic spectroscopy and petahertz electronics. Questions, however, remain regarding the nature of nonlinear light-matter interactions at sub-wavelength spatial and ultrafast temporal scales. Addressing this challenge, we investigated the strong-field control of the plasmonic response of Au nanoshells with a SiO2 core to an intense laser pulse. We show that the photoelectron energy spectrum from these core-shell nanoparticles displays a striking transition between the weak and strong-field regime. This observed transition agrees with the prediction of our modified Mie-theory simulation that incorporates the nonlinear dielectric nanoshell response. The demonstrated intensity-dependent optical control of the plasmonic response in prototypical core-shell nanoparticles paves the way towards ultrafast switching and opto-electronic signal modulation with more complex nanostructures.
The ability to reversibly manipulate the electronic structure and optical response of nanometer-sized materials has recently attracted substantial attention [1, 2, 3]. A hallmark property of nanostructures is the capacity to design and fabricate systems to take advantage of the tunable, size-, shape-, frequency-, and material-dependent properties as a means of tailoring specific optical responses. This holds the promise to both further our understanding of the transient electronic response in solid matter as well as enable new applications such as novel opto-electronics [3], plasmonically enhanced light harvesting [4], and photocatalysis [5, 6]. Among different configurations, composite nanostructures, such as core-shell nanoparticles, consisting of a dielectric core and a thin metallic shell, are of special interest for their exceptionally large plasmonic field enhancements and high tunability of absorption spectra [7, 8], generating novel applications in optical imaging and photothermal cancer therapy [9, 10]. Precise control of the optical response, typically achieved by manipulating the geometric structures [8], is the key to utilizing their unique plasmonic properties.
Investigations into such optical properties in nanostructures have been conducted by studying their plasmonic response, in particular, their plasmonic near-field enhancement [7, 11, 12, 13]. Photoelectrons provide an excellent window into understanding the dynamics of these interactions due to their sensitivity on the sub-wavelength spatial and ultrafast temporal scales. Photoelectron spectroscopy utilize these photoelectrons emitted during the interaction of a nanoparticle with an intense, femtosecond laser, allowing for the unraveling of the fundamental contributions to their acceleration, including enhanced near-fields, surface rescattering and charge interactions [14, 15, 16]. Experiments revealed the fundamental light-matter interaction processes during the optical response and associated electron dynamics in selected nanosystems, consistent with theoretical modeling of the induced plasmonic field near the nanostructure surface in the linear-response approximation [17, 18, 16, 19].
However, recent investigations of nanoscale thin films and metasufaces have revealed significant nonlinear (Kerr) effects [20, 21]. These motivate the study of such nonlinear effects in the optical response in composite nanostructures consisting of similar thin layers (e.g. core-shell nanoparticles).
Here, we investigate a type of core-shell nanoparticle specifically tailored to have a significant nonlinear effect which enables the intensity-dependent optical control of its plasmonic properties. This core-shell nanoparticle is comprised of a nanometer-thin gold coating encasing a larger dielectric silica core. We demonstrate, experimentally and theoretically, that as a function of the incident field intensity, a nonlinear response in the gold shell can be induced to control the plasmonic properties of the nanoparticle. At laser intensities below 0.1 TW/cm2, the linear response dominates, resulting in a large plasmonic near-field. However, with increasing intensity, the onset of a nonlinear component of the complex index of refraction for gold decreases the skin depth and effectively reduces the magnitude of the near-field. This ability to manipulate the plasmonic properties of core-shell nanoparticles solely by tuning the external-field intensity substantiates a new method of precise control over the optical response in layered nanomaterials.
I Results and Discussion
The photoelectron cut-off energy, defined as the highest observable electron energy, has been established as a gold standard for probing the induced plasmonic near-fields close to various nanostructure surfaces of different materials [12, 13, 22, 23]. This cut-off scales linearly with the cycle-averaged quiver energy of a free electron in a laser field, referred to as the "ponderomotive energy", ( and are electron charge and mass; , , , and designate the incident field strength, peak intensity, frequency, and wavelength of the laser pulse, respectively). Though near-fields are generally inhomogeneous (decreasing with distance), the fastest photoelectrons elastically rescatter and gain most of their kinetic energies near the nanoparticle surface [16, 24], well within the typical spatial range of the near-field enhancement [7, 25, 24]. Therefore, rescaling photoelectron cut-off energies with the incident-field reveals information about the plasmonic near-field enhancements, independent of the incident-field intensity.
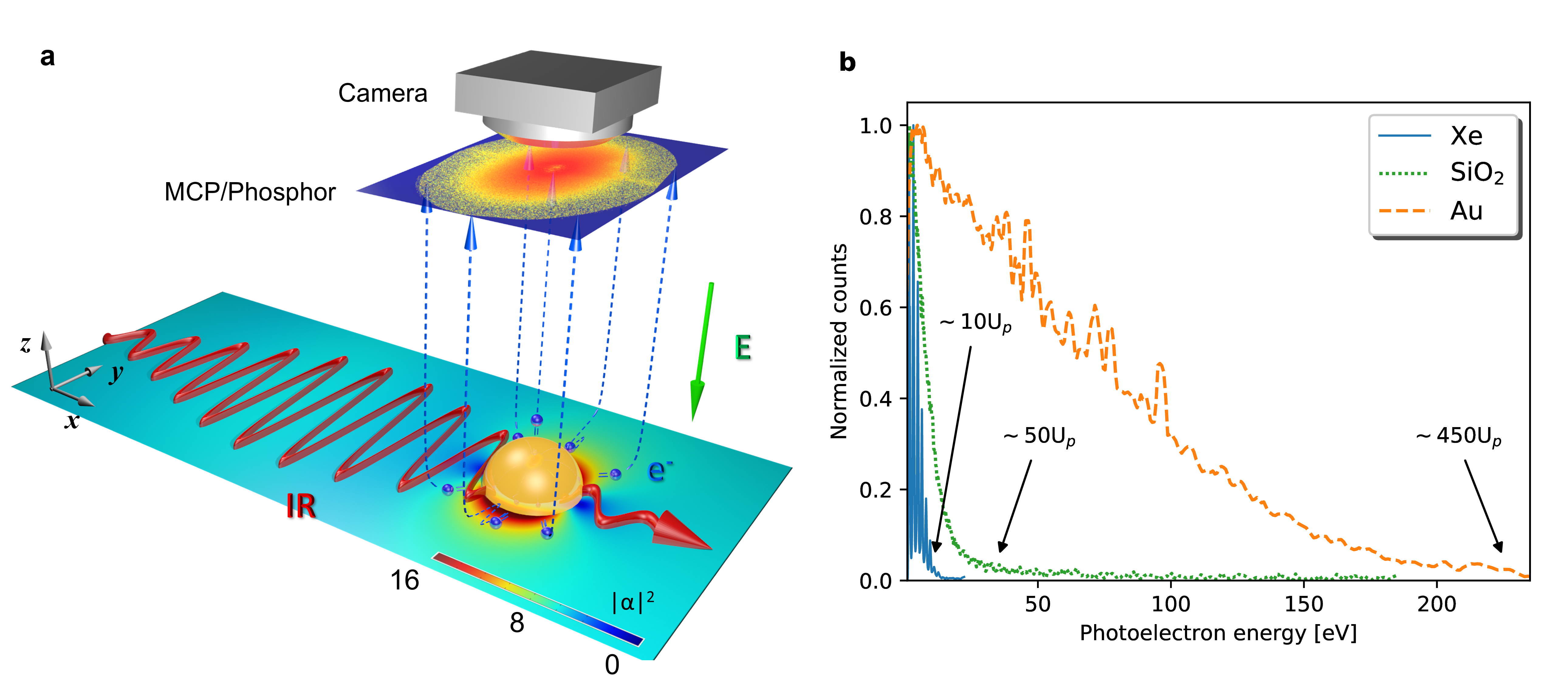
We determine the cut-off energies for single, isolated nanoparticles photoionized by femtosecond laser pulses, employing a high-energy velocity map imaging (VMI) spectrometer to measure the energy- and angle-resolved photoelectron spectra (see Methods for additional details). Figure 1a illustrates a simplified schematic of the interaction and subsequent electron propagation and detection. Figure 1b shows the comparison of typical photoelectron energy spectra and their respective cut-off energies for atomic Xe, SiO2 nanospheres, and Au nanospheres, exemplifying the substantial increase in the kinetic energy of electrons emitted from nanoparticles.
To demonstrate the feasibility of observing the signature of the near-field in these nanosystems, we measured the size-dependent photoelectron cut-off energies for solid Au nanospheres. Figure 2a shows the cut-off energies for diameters ranging from 5 nm to 400 nm at several intensities. The plasmonic near-field response was investigated by rescaling the cut-off energies to their respective incident-field ponderomotive energy , as shown in Fig. 2b. For comparison, the cut-off energies for SiO2 nanospheres at similar diameters and intensities are also plotted [15]. The -rescaled cut-off energies for both materials are shown to be independent of the laser field intensity, within the size and intensity range of this work, as evidenced in Fig. 2b by the overlap of the data points for each particular size. The cut-off energies for Au nanospheres indicates a prominent peak at diameter = 200 nm and more energetic photoelectrons than for SiO2 nanoparticles, for which only a slight, monotonic increase with diameter occurs.
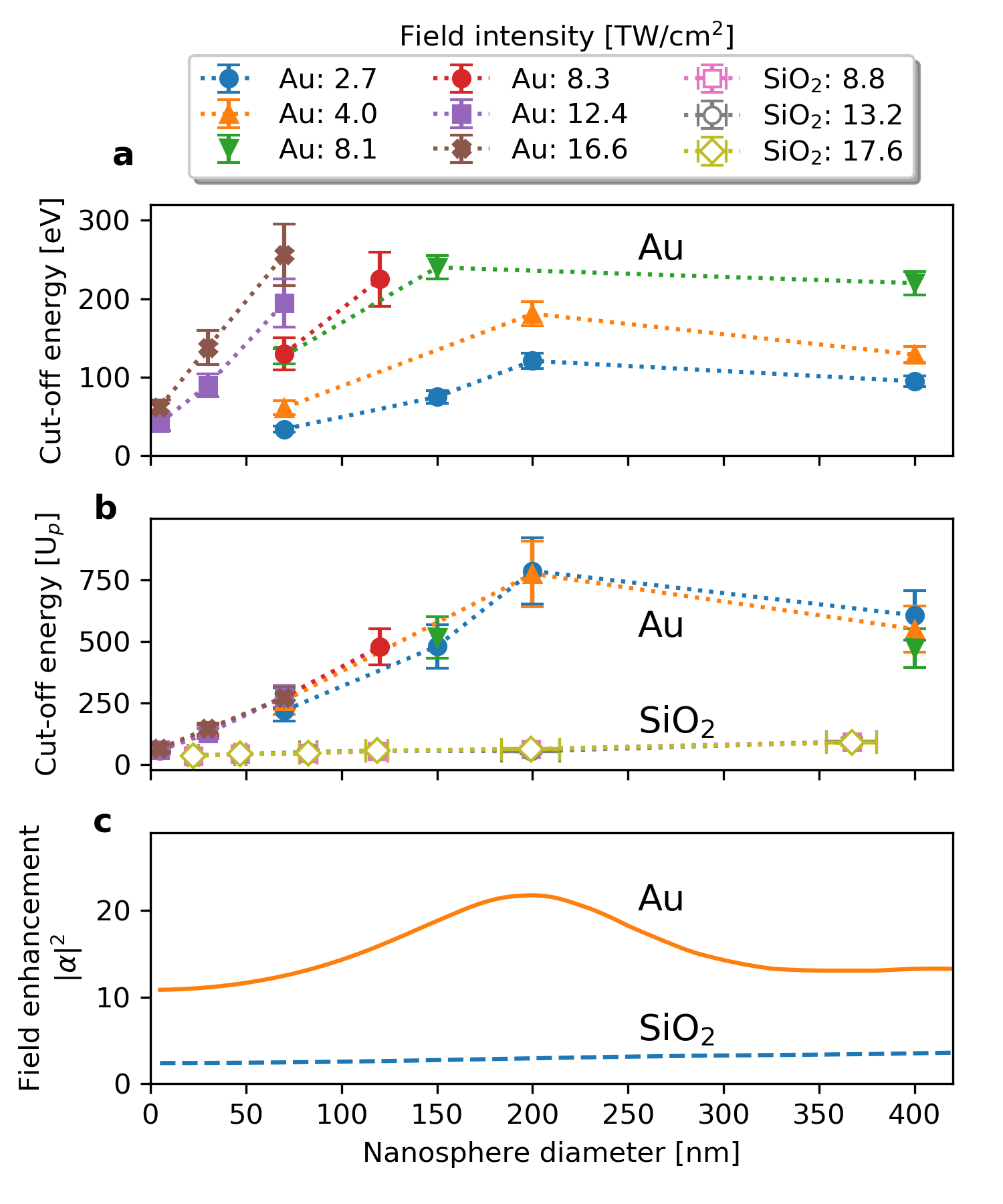
Further analysis in Fig. 2c reveals that the -rescaled cut-off energies resemble the maximum near-field intensity enhancement (which we refer to as “field enhancement” ), in Fig. 2b. For the results shown in Fig. 2c, we calculated the induced near-field by numerically solving the Mie equations [26, 27] using indices of refraction within the linear optical response for Au and SiO2 nanospheres [28]. The field enhancement is defined by the maximum total field intensity with respect to the incident intensity and typically located close to the particle surface [17, 18]. Though the exact dependence between the cut-off energy and field enhancement is determined by multiple effects (such as rescattering and Coulomb interactions) [14, 16], Fig. 2b and Fig. 2c reveal that the cut-off energy does, however, accurately reflect the dominant signature of field enhancement profiles for Au and SiO2 nanospheres (see Supplemental Note 2). This agreement supports our use of the cut-off energy as an indicator for observing changes in the magnitude of the plasmonic field enhancement.
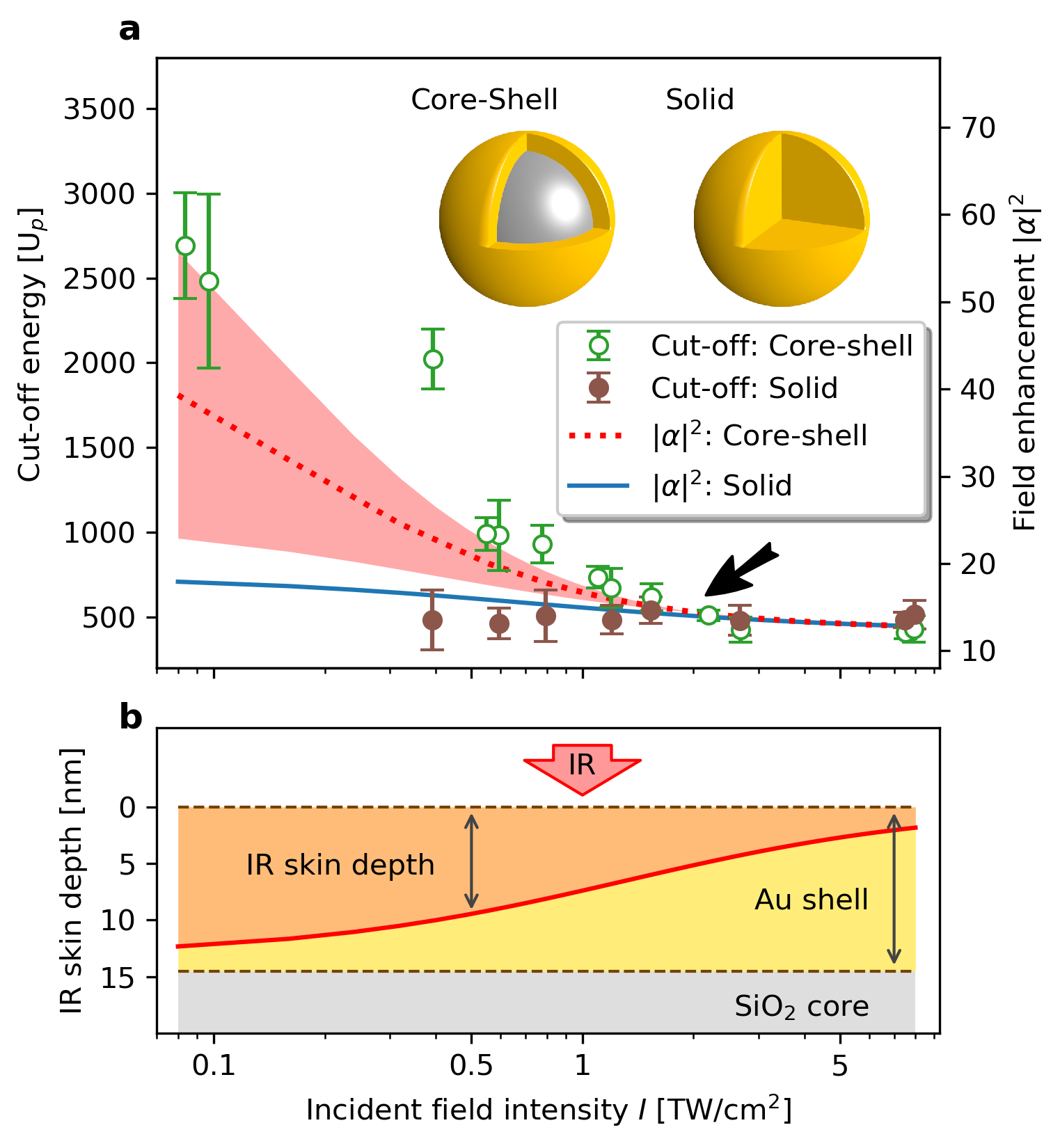
To investigate the strong-field control of the plasmonic properties in a layered nanostructure, we examined SiO2-core-Au-shell structures. Core-shell nanoparticles were specifically chosen to elucidate any intensity-related changes to the field enhancement due to their unique configuration in comparison with solid Au nanospheres of a comparable size. The nanometer-thin Au shell surrounding a dielectric core results in a stronger localization of the plasmonic near-field when compared to solid Au nanospheres. We neglect any laser-induced propagation effects as the nanoparticle radius is much smaller than the incident pulse wavelength. Figure 3a shows our measured intensity-dependent photoelectron cut-off energies, rescaled with the incident-field ponderomotive energy at 780 nm wavelength, for core-shell structures and solid Au nanospheres of approximately 150 nm diameter.
The -rescaled cut-off energy for solid Au nanospheres remains approximately unchanged ( 500 ) for different incident-field intensities, indicating that the field enhancement near solid Au nanospheres is nearly independent of the intensity (Fig. 3a). In contrast, the cut-off energy for the core-shell structures varies drastically within the intensity range sampled. At low intensities, this energy is large when scaled by (2000 3000 , approximately 10 eV). However, it rapidly decreases and converges to the nearly identical value of the solid Au nanospheres beyond 2 TW/cm2, as indicated by the black arrow in Fig. 3a. This implies that the field enhancement of the core-shell structure does not remain constant with the increasing laser intensity, but rather begins (at low intensity) at a value significantly higher for solid Au nanospheres, before quickly decreasing to a similar value at higher intensities. The contrast of these two particles is particularly strong at very low intensities ( 0.1 TW/cm2), where no photoemission is observed for solid Au nanospheres due to the extremely weak electromagnetic field. A measurable amount of photoelectrons with over 2000 cut-off energy are still observed from core-shell structures, further confirming that a large field enhancement is induced at low intensities.
The nonlinear optical response of the Au shell is the key to understanding the observed effects in core-shell nanoparticles. Note that only the linear optical response is included in Fig. 2c. To introduce the nonlinear response, we apply a simple and widely used model to account for intensity-dependent changes in the index of refraction for Au [29],
| (1) |
where , an experimentally determined complex number [28], is the linear index of refraction employed for our simulation results in Fig. 2. is related to the third-order susceptibility (or Kerr effect) [30],
| (2) |
is the real part of and , according to a measurement using 15 nm Au films [31], close to the Au shell thickness in our work. At 780 nm wavelength, is predominantly imaginary. When , the linear optical response dominates and . As the intensity increases, the imaginary part increases, and the nonlinear effect starts to emerge.
We estimate the normal-incident IR skin depth following [32] as,
| (3) |
where is the speed of light. Thus, the IR skin depth decreases with incident-field intensity in this particular situation. Figure 3b plots the intensity-dependent IR skin depth, in comparison with the Au shell thickness ( 14.5 nm) of the core-shell structures. At low intensities (< 0.1 TW/cm2), the skin depth is approximately 13 nm, comparable to the Au shell thickness, suggesting a considerable amount of the IR field reaches the SiO2 core. Since the optical response of a core-shell nanoparticle is extremely sensitive to the fields at both the inner and outer surfaces, their larger field enhancement results from the penetration of the external field into the Au-SiO2 interface. This effect is incorporated by applying the boundary conditions at both interfaces when solving the Mie equations [7]. However, as the intensity increases, rapidly drops and approaches 2 nm at 8 TW/cm2, well below the Au-shell thickness, preventing the IR field from penetrating the Au shell, i.e., shielding the SiO2 core. Therefore, the outer Au surface becomes the dominant factor for determining the optical response (and, thus, the field enhancement), causing the core-shell structures to appear to be indistinguishable from solid Au nanospheres of the same outer diameter.
Note that, while a recent study included the nonlinear response of SiO2 nanoparticles [19], we neglect such effects in the SiO2 core of the core-shell structures, since the field near the Au-SiO2 interface is too heavily dampened (not exceeding 1010 W/cm2) to induce any significant nonlinear response in this study.
Figure 3a also plots the Mie-simulated field enhancement for core-shell structures and solid Au nanospheres, including the nonlinear optical response. The field enhancement of solid Au nanospheres only decreases slightly from 18 to 13 as the intensity increases. This indicates that the nonlinear response, while present in solid Au nanospheres, is insignificant and does not induce a measurable difference exceeding experimental uncertainty in this work, justifying our calculation of the results in Fig. 2 using a linear-response approximation. The core-shell structures, on the other hand, start with a field enhancement up to 60 at low intensities, where linear response dominates. This large enhancement is responsible for the photoemission observed from core-shell structures at low intensities, which is absent in solid Au nanospheres, as well as the significantly larger cut-off energy. As the intensity increases, the nonlinear response results in a decreasing skin depth (Fig. 3b), leading to significantly smaller field enhancements that eventually converge with our results for the solid Au nanospheres beyond 2 TW/cm2. The profiles of the simulated field enhancements, especially the convergence at 2 TW/cm2, are in excellent agreement with that of the measured cut-off energies for both nanoparticles. This success validates the use of the simple model in Eq. (1) and shows that the laser intensity has a significant impact on the plasmonic response of core-shell structures, in contrast to their solid Au counterparts.
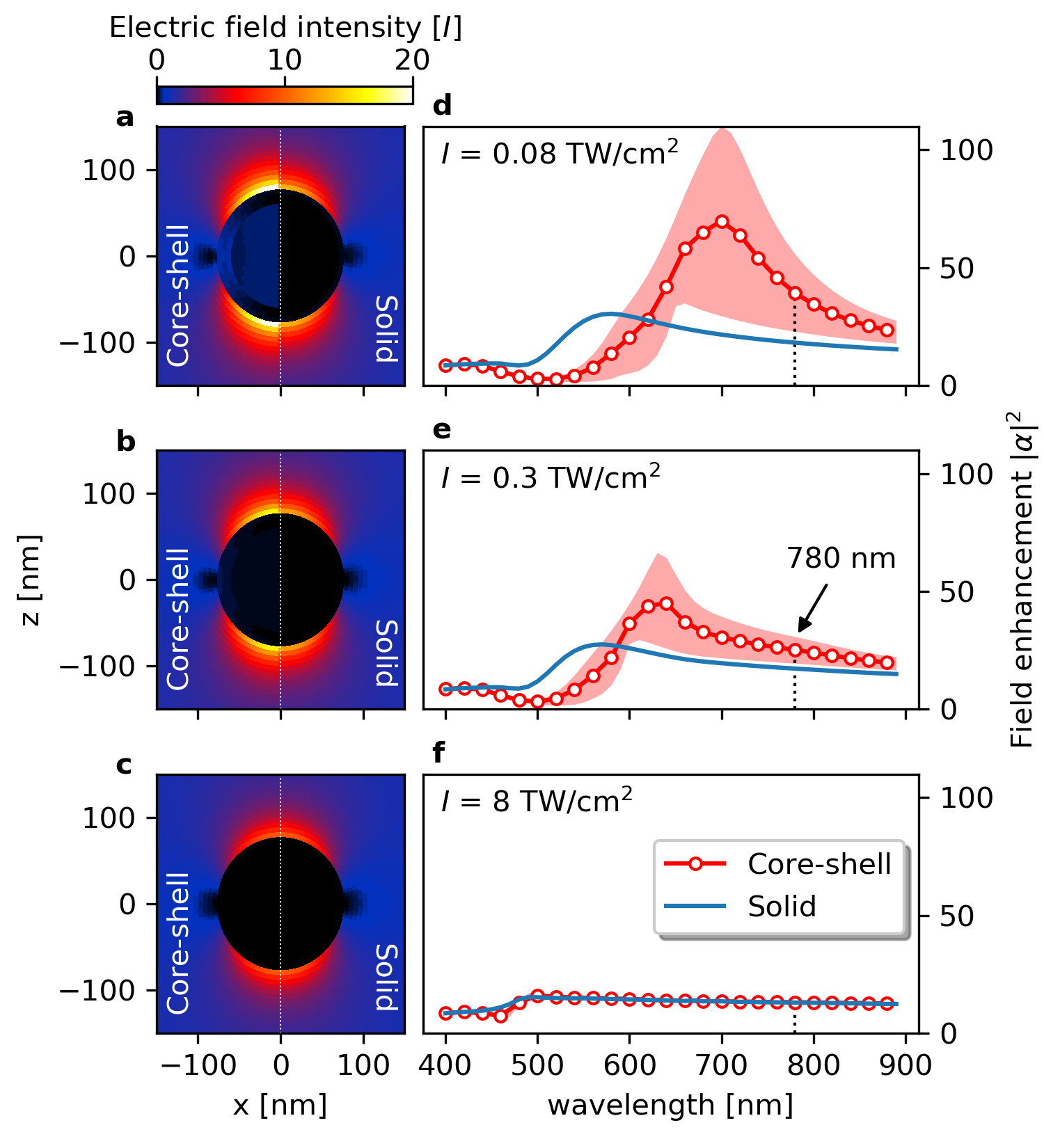
A more in-depth understanding of such an impact and the broader implications can be achieved by extending our line of investigation to a larger spectral range. Figures 4d-f show the calculated field enhancement of core-shell structures and solid Au nanospheres as a function of the incident-field wavelength for incident-field intensities of 0.08, 0.3, and 8 TW/cm2, respectively. For each corresponding incident-field intensity, Figs. 4a-c compare a section of our simulated electric-field-intensity distribution between the two types of nanoparticles for an incident field at 780 nm wavelength.
At 0.08 TW/cm2, where the linear optical response dominates, a weak yet noticeable field penetrates the Au shell of the core-shell structure. The propagation of the external field across the Au-SiO2 interface yields the significantly more intense and red-shifted resonant spectra, as compared with solid Au nanoparticles. Such pronounced differences show that the plasmonic response of core-shell structures, including the absorption resonance and the near-field magnitude, can be tuned by changing parameters in the production of the nanospheres (core diameter, shell thickness and composition) [7, 8, 9, 10].
As the incident-field intensity increases, due to the growing nonlinear response of the Au shell preventing penetration of the field, the resonance feature for the core-shell structures starts to blue shift and decrease in magnitude, before gradually becoming indistinguishable to solid Au nanospheres across the spectra. We thus demonstrate that for core-shell nanoparticles, the tunable plasmonic response can be effectively switched “on” and “off” by simply controlling the external field intensity. For intensities well below a threshold ( 2 TW/cm2 in this work), the tunable plasmonic response of core-shell structures is switched “on”, manifesting a large and red-shifted resonance. For intensities above the threshold, the response is effectively switched “off”, and the core-shell structures appear to be indistinguishable from the solid Au nanospheres. According to Eq. (3), for a chosen material, such a threshold is determined primarily by the shell thickness, where a thinner shell requires a larger intensity threshold to ensure the IR skin depth is smaller than the shell thickness. This shows core-shell nanoparticles can be carefully synthesized to have a designated intensity threshold so that their plasmonic properties are controllable by manipulating the external field intensity.
II Conclusions
We have demonstrated the ability to control the plasmonic response of a layered nanostructure solely by varying the laser intensity. This was accomplished by measuring the photoelectron cut-off energies from single, isolated core-shell nanoparticles and using them as a sensitive probe of the plasmonic field. Experimental signatures of a non-constant, intensity-dependent near-field were verified by a modified Mie theory as the direct result of the nonlinear optical response of the outer gold shell. Further analysis revealed that the decreasing skin depth into the nanoparticle surface at laser intensities above 2 TW/cm2 effectively shields the SiO2 core, rendering the magnitude of its near-field identical to that of a solid Au nanosphere. These results suggest a new intensity-dependent strong-field control of the plasmonic response in layered nanostructures. While such responses in layered nanostructures are known to be tunable by their physical structure, we demonstrated that they can further be effectively switched “on” and “off” solely by controlling the external-field intensity.
This intensity-dependent optical control of the plasmonic response could hold the keys to new lines of research and implementations based on layered nanostructures. For example, many applications require nanosystems such as core-shell structures to be tuned to precise resonant wavelengths [9, 10]. Our work unlocks a new tuning mechanism where a single core-shell structure can be manipulated to have an adjustable resonance and optical properties, dependent merely on the applied laser intensity. In other applications, such as photocatalysis [6] and field-induced molecular reactions [33], core-shell structures could be versatile substitutes for the currently used solid nanoparticles. Not only can they be tailored to provide larger field enhancements and substantially reduce the laser-intensity requirements, but such large enhancements can also be automatically turned “off” by the nonlinear response to avoid overexposure at high intensities. This can have significant impacts in areas such as metamaterials, plasmonics and opto-electronics.
References
- [1] Stockman, M. I. Nanoplasmonics: The physics behind the applications. Phys. Today 64, 39–44 (2011). URL http://scitation.aip.org/content/aip/magazine/physicstoday/article/64/2/10.1063/1.3554315.
- [2] Law, S., Yu, L., Rosenberg, A. & Wasserman, D. All-semiconductor plasmonic nanoantennas for infrared sensing. Nano Letters 13, 4569–4574 (2013). URL https://doi.org/10.1021/nl402766t. PMID: 23987983.
- [3] Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Photon. 8, 205–213 (2014). URL https://doi.org/10.1038/nphoton.2014.28.
- [4] Sheldon, M. T., van de Groep, J., Brown, A. M., Polman, A. & Atwater, H. A. Plasmoelectric potentials in metal nanostructures. Science 346, 828–831 (2014). URL http://science.sciencemag.org/content/346/6211/828.
- [5] Zhang, X., Chen, Y. L., Liu, R.-S. & Tsai, D. P. Plasmonic photocatalysis. Reports on Progress in Physics 76, 046401 (2013).
- [6] Wu, T. et al. Surface plasmon resonance-induced visible light photocatalytic reduction of graphene oxide: Using ag nanoparticles as a plasmonic photocatalyst. Nanoscale 3, 2142–2144 (2011). URL http://dx.doi.org/10.1039/C1NR10128E.
- [7] Li, J., Saydanzad, E. & Thumm, U. Imaging Plasmonic Fields with Atomic Spatiotemporal Resolution. Phys. Rev. Lett. 120, 223903 (2018). URL https://link.aps.org/doi/10.1103/PhysRevLett.120.223903.
- [8] Hirsch, L. R. et al. Metal nanoshells. Annals of Biomedical Engineering 34, 15–22 (2006). URL https://doi.org/10.1007/s10439-005-9001-8.
- [9] Rastinehad, A. R. et al. Gold nanoshell-localized photothermal ablation of prostate tumors in a clinical pilot device study. Proceedings of the National Academy of Sciences 116, 18590–18596 (2019). URL https://www.pnas.org/content/116/37/18590.
- [10] Chen, W. et al. Targeting of Pancreatic Cancer with Magneto-Fluorescent Theranostic Gold Nanoshells. Nanomedicine 9, 1209–1222 (2014). URL https://dx.doi.org/10.2217%2Fnnm.13.84.
- [11] Li, J. Spatiotemporally resolved photoemission from plasmonic nanoparticle. Ph.D. thesis, Kansas State University (2020). URL https://krex.k-state.edu/dspace/handle/2097/40310.
- [12] Thomas, S., Krüger, M., Förster, M., Schenk, M. & Hommelhoff, P. Probing of optical near-fields by electron rescattering on the 1 nm scale. Nano Letters 13, 4790–4794 (2013). URL https://doi.org/10.1021/nl402407r. PMID: 24032432.
- [13] Rácz, P. et al. Measurement of nanoplasmonic field enhancement with ultrafast photoemission. Nano Letters 17, 1181–1186 (2017). URL https://doi.org/10.1021/acs.nanolett.6b04893. PMID: 28094992.
- [14] Süßmann, F. et al. Field propagation-induced directionality of carrier-envelope phase-controlled photoemission from nanospheres. Nature Communications 6, 7944 (2015). URL https://doi.org/10.1038/ncomms8944.
- [15] Powell, J. A. et al. Interplay of pulse duration, peak intensity, and particle size in laser-driven electron emission from silica nanospheres. Opt. Express 27, 27124–27135 (2019). URL http://www.opticsexpress.org/abstract.cfm?URI=oe-27-19-27124.
- [16] Zherebtsov, S. et al. Controlled near-field enhanced electron acceleration from dielectric nanospheres with intense few-cycle laser fields. Nature Physics 7, 656–662 (2011). URL https://doi.org/10.1038/nphys1983.
- [17] Li, J., Saydanzad, E. & Thumm, U. Retrieving plasmonic near-field information: A quantum-mechanical model for streaking photoelectron spectroscopy of gold nanospheres. Phys. Rev. A 94, 051401 (2016). URL http://link.aps.org/doi/10.1103/PhysRevA.94.051401.
- [18] Li, J., Saydanzad, E. & Thumm, U. Attosecond time-resolved streaked photoelectron spectroscopy of transition-metal nanospheres. Phys. Rev. A 95, 043423 (2017). URL https://link.aps.org/doi/10.1103/PhysRevA.95.043423.
- [19] Rupp, P. et al. Few-cycle laser driven reaction nanoscopy on aerosolized silica nanoparticles. Nature Communications 10, 4655 (2019). URL https://doi.org/10.1038/s41467-019-12580-0.
- [20] Xiao, Y., Qian, H. & Liu, Z. Nonlinear metasurface based on giant optical kerr response of gold quantum wells. ACS Photonics 5, 1654–1659 (2018). URL https://doi.org/10.1021/acsphotonics.7b01140.
- [21] Nookala, N. et al. Ultrathin gradient nonlinear metasurface with a giant nonlinear response. Optica 3, 283–288 (2016). URL http://www.osapublishing.org/optica/abstract.cfm?URI=optica-3-3-283.
- [22] Wang, Z. et al. Universal high-energy photoelectron emission from nanoclusters beyond the atomic limit. Phys. Rev. Lett. 124, 173201 (2020). URL https://link.aps.org/doi/10.1103/PhysRevLett.124.173201.
- [23] Schötz, J. et al. Onset of space-charge effects in strong-field photocurrents from nanometric needle tips (2021). eprint 2106.00503.
- [24] Summers, A. M. Strong-field interactions in atoms and nanosystems: advances in fundamental science and technological capabilities of ultrafast sources. Ph.D. thesis, Kansas State University (2019). URL https://krex.k-state.edu/dspace/handle/2097/39413.
- [25] Süßmann, F. & Kling, M. F. Attosecond nanoplasmonic streaking of localized fields near metal nanospheres. Phys. Rev. B 84, 121406 (2011). URL http://link.aps.org/doi/10.1103/PhysRevB.84.121406.
- [26] Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Annalen der Physik 330, 377–445 (1908). URL http://dx.doi.org/10.1002/andp.19083300302.
- [27] Stratton, J. Electromagnetic theory, vol. 33 (Wiley, 2007). URL http://books.google.com/books?hl=en&lr=&id=zFeWdS2luE4C&oi=fnd&pg=PA1&dq=electromagnetic+theory+stratton&ots=8T5nXodjoo&sig=cv6oKO9UF6g8BZkPvqjCesJjSs8.
- [28] Johnson, P. B. & Christy, R. W. Optical Constants of the Noble Metals. Phys. Rev. B 6, 4370–4379 (1972). URL https://link.aps.org/doi/10.1103/PhysRevB.6.4370.
- [29] Boyd, R. W. Nonlinear optics (Academic Press, 2008).
- [30] Boyd, R. W., Shi, Z. & Leon, I. D. The third-order nonlinear optical susceptibility of gold. Optics Communications 326, 74–79 (2014). URL http://www.sciencedirect.com/science/article/pii/S0030401814002351.
- [31] Qian, H., Xiao, Y. & Liu, Z. Giant kerr response of ultrathin gold films from quantum size effect. Nature Communications 7, 13153 (2016). URL https://doi.org/10.1038/ncomms13153.
- [32] Hecht, E. Optics (Reading, Mass. : Addison-Wesley, Reading, Mass., 2002), 4th edition.. edn.
- [33] Rosenberger, P. et al. Near-field induced reaction yields from nanoparticle clusters. ACS Photonics 7, 1885–1892 (2020). URL https://doi.org/10.1021/acsphotonics.0c00823.
- [34] Kling, N. G. et al. Thick-lens velocity-map imaging spectrometer with high resolution for high-energy charged particles. Journal of Instrumentation 9, P05005–P05005 (2014). URL https://doi.org/10.1088%2F1748-0221%2F9%2F05%2Fp05005.
- [35] Powell, J. Strong-field driven dynamics of metal and dielectric nanoparticles. Ph.D. thesis, Kansas State University (2017).
- [36] Palik, E. Handbook of Optical Constants of Solids (Elsevier Science, 1985). URL http://books.google.com/books?id=h8mEd9no5-kC.
III Methods
III.1 Experimental setup
The laser setup and electron detection apparatus at the James R. Macdonald Laboratory at Kansas State University are described in more detail in [15]. Briefly, the experiments used a Ti:Sapphire-based chirped pulse amplification (CPA) system generating 25 fs pulses at 780 nm central wavelength. Photoelectron spectra were captured in a thick-lens, high-energy velocity map imaging (VMI) spectrometer [34] capable of gathering up to 350 eV electron energy. The custom nanoparticle source produces a continuous beam of nanoparticles into vacuum. Spherical nanoparticle samples were selected for their narrow size distribution and overall purity. The initial nanoparticle concentration was also carefully chosen to avoid the formation of clusters in the nanoparticle beam.
III.2 Laser intensity characterization
The peak laser intensity was determined by analyzing the above-threshold (ATI) photoelectron energy distribution of atomic Xe with the aforementioned VMI under similar experimental parameters. The ponderomotive shift of the Xe ATI comb was measured as a function of the input-laser pulse energy, in order to derive the ponderomotive energy, , and thus, the peak laser intensity [24, 35]. For intensities below the ionization threshold of Xe, the ratio of the pulse energies was used to extrapolate the peak intensity. See Supplementary Note 1 for more detail.
III.3 Photoelectron cut-off determination
The nanoparticle photolectron cut-off energy was extracted from the experimental VMI images in a method described in previous work [15, 35]. The detected elastically back-scattered photoelectrons are obtained from the non-inverted VMI images, for which the upper energy boundaries of the full 3D momentum sphere and the 2D projection are essentially the same. A radial distribution of these projections along the polarization direction accurately determines the maximum photoelectron energy.
III.4 Mie simulations
We simulated laser-induced plasmonic near-fields by solving the Mie equations [26, 27] for plane waves scattered by spherical objects. The linear terms of the dielectric response of Au and SiO2 enters as the frequency-dependent complex-valued index of refraction obtained from experiments [28, 36]. Our inclusion of nonlinear effects is discussed in the text. The original Mie equations apply only to the solid spheres. For the simulations of core-shell structures, we extended the traditional Mie theory as outlined in Supplementary Note 3.
IV Acknowledgment
This work was supported by the Air Force Office of Scientific Research under award number FA9550-17-1-0369. J.L., E.S. and U.T. acknowledge the support by the NSF Grant No. 1802085. A.S. and D.R. were supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U. S. Department of Energy under Award No. DEFG02-86ER13491, which also covered laser operational costs. M.F.K acknowledges support by the German Research Foundation (DFG) via SPP1840, and by the European Research Council (ERC) via the FETopen project PetaCOM.
V Author contributions
J.P. and J.L. contributed equally to this work. J.P., J.L., A.S., U.T. and A.R. conceptualized and conducted the study. J.P., A.S., S.J.R, M.D. and P.R. contributed to performing the experiment. J.P. and A.S. performed the data analysis. J.L. and U.T. developed the theoretical model, performed the simulations and interpreted the results. J.P., J.L., A.S., E.S., C.M.S., D.R., M.F.K., C.T.H., U.T. and A.R. discussed the results. J.L., J.P. and A.S. wrote the initial manuscript, which was revised with input from all authors.
VI Additional information
The authors declare no competing financial interests.