Strong current-state and initial-state opacity of
discrete-event systems
Abstract
Opacity, as an important property in information-flow security, characterizes the ability of a system to keep some secret information from an intruder. In discrete-event systems, based on a standard setting in which an intruder has the complete knowledge of the system’s structure, the standard versions of current-state opacity and initial-state opacity cannot perfectly characterize high-level privacy requirements. To overcome such a limitation, in this paper we propose two stronger versions of opacity in partially-observed discrete-event systems, called strong current-state opacity and strong initial-state opacity. Strong current-state opacity describes that an intruder never makes for sure whether a system is in a secret state at the current time, that is, if a system satisfies this property, then for each run of the system ended by a secret state, there exists a non-secret run whose observation is the same as that of the previous run. Strong initial-state opacity captures that the visit of a secret state at the initial time cannot be inferred by an intruder at any instant. Specifically, a system is said to be strongly initial-state opaque if for each run starting from a secret state, there exists a non-secret run of the system that has the same observation as the previous run has. To verify these two properties, we propose two information structures using a novel concurrent-composition technique, which has exponential-time complexity , where (resp., , , ) is the number of states (resp., events, observable events, unobservable events) of a system.
keywords:
Discrete-event system, Strong current-state opacity, Strong initial-state opacity, Observer, Concurrent composition, , , ,
1 Introduction
Opacity is a confidentiality property, which characterizes the scenario whether some “secret” of a system is ambiguous to a potential malicious intruder based on the evolution of the system. In other words, an opaque system always holds the plausible deniability for its “secret” during its execution. Opacity can be adapted to capture a variety of privacy and security requirements in cyber-physical systems, including event-driven dynamic systems [1, 2] and time-driven dynamic systems [3, 4].
The notion of opacity initially appeared in the computer science literature [5] to analyze cryptographic protocols. Whereafter, various versions of opacity were characterized in the context of discrete-event systems (DESs). For instance, in automata-based models, several notions of opacity have been proposed and studied, which include current-state opacity [6], initial-state opacity [7], -step opacity [8], infinite-step opacity [9], and language-based opacity [10, 11]. Some more efficient algorithms to check them have also been provided in [11, 12, 13]. Furthermore, when a given system is not opaque, its opacity enforcement problem has been extensively investigated using a variety of techniques, including supervisory control [14, 15, 16], insertion or edit functions [17, 18, 19, 20], dynamic observers [21], etc. Recently, verification and/or enforcement of opacity have been extended to other classes of settings, including Petri nets [22, 23, 24], stochastic systems [25, 26, 27], modular systems [28], networked systems [29, 30], etc. In recent literature [31, 32], the authors studied opacity preserving (bi)simulation relations using an abstraction-based technique for nondeterministic transition systems and metric systems, respectively. Some applications of opacity in real-world systems have also been provided in the literature, see, e.g., [33, 34, 35, 36].
In automata-based models, different notions of opacity can capture different security requirements. For example, current-state opacity (CSO) characterizes that an intruder cannot determine for sure whether a system is currently in a secret state. In Location-Based Services (LBS), a user may want to hide his/her initial location or his/her location (e.g., visiting a hospital or bank) at some specific previous instant. Such requirements can be characterized by initial-state opacity (ISO) and /infinite-step opacity (/Inf-SO)111For convenience, the notion originally named CSO (resp., ISO, -SO, and Inf-SO) is categorized as standard CSO (resp., standard ISO, standard -SO, and standard Inf-SO) in this paper.. However, these four standard versions of opacity have some limitations in practice. Specifically, they cannot capture the situation that an intruder can never infer for sure whether the system has passed through a secret state based on his/her observation. In other words, even though a system is “opaque” in the standard sense, the intruder may necessarily determine that a secret state must has been passed through. To this end, in [37], a strong version of opacity called strong -step opacity is proposed to capture that the visit of a secret state cannot be inferred within steps. Also, an algorithm that has complexity is provided to check it using so-called -delay trajectory estimators and R-verifiers, where is the number of states of a system.
Inspired by [37], in this paper we are interested in defining and verifying two other strong versions of opacity in partially-observed nondeterministic finite-state automata (NFAs), called strong current-state opacity (SCSO) and strong initial-state opacity (SISO), respectively. They mean that if a run passes through a secret state at the current time (resp., at the initial time), there exists another run that never passes through a secret state and has the same observation as the previous run has. Obviously, they have higher-level confidentiality than the standard versions. Note that, by the definition of strong -step opacity proposed in [37], we know readily that strong -step opacity reduces to standard CSO when . Thus, we conclude that SCSO implies the strong -step opacity but actually these two strong versions of opacity are incomparable when . Therefore, the proposed notions of SCSO and SISO are clearly different from all the existing ones in the literature. Further, we develop a novel method to verify SCSO and SISO from a span-new perspective. Specifically, the main contributions of this paper are summarized below.
-
•
To overcome the inadequacy that the standard CSO and ISO cannot perfectly characterize high-level privacy requirements, we propose two stronger versions of opacity, called SCSO and SISO. They can characterize higher-level confidentiality than the standard versions.
-
•
For SCSO, we construct an information structure using a novel concurrent-composition technique. And then, we propose a verification criterion of SCSO based on leaking secret states defined by us in the proposed structure. This verification approach costs time , where (resp., ) is the number of states (resp., events, observable events, unobservable events) of a system.
-
•
Regarding the verification problem of SISO, using the novel concurrent-composition technique, we propose another information structure in which the information that whether a system has passed through a secret initial state can be characterized. This approach has also time complexity .
The rest of this paper is arranged as follows. Section 2 provides preliminaries needed in this paper, including the system model, the formal definitions of standard CSO and ISO, and their limitations on confidentiality. Section 3 formalizes the notion of SCSO, and proposes a novel information structure for its verification. In Section 4, the notion of SISO is proposed, and its verification approach is reported. In Section 5, we conclude this paper with a brief discussion on how to use the proposed concurrent-composition structure to verify strong infinite-step opacity, which can be seen as a strong version of the standard Inf-SO.
2 Preliminaries
2.1 System model
A DES of interest is modeled as a nondeterministic finite-state automaton (NFA) , where is the finite set of states, is the finite set of events, is the set of initial states, is the transition function, which depicts the system dynamics: given states and an event , implies that there exists a transition labeled by from to . Note that for and , if there exists no such that , then . We can extend the transition function to in the usual manner, where denotes the Kleene closure of , consisting of all finite sequences composed of the events in (including the empty sequence ), see, e.g., [38] for more details on DESs. We use to denote the language generated by from state , i.e., . Therefore, the language generated by is . For a sequence , we denote its prefix closure by , i.e., . Further, for a prefix , we use the notation to denote the suffix of after its prefix . We without loss of generality assume that is accessible, i.e., all its states are reachable from .
As usual, we assume that the intruder can only see partially the system’s behavior. To this end, is partitioned into the set of observable events and the set of unobservable events, i.e., and . The natural projection is defined recursively by () , () , () , where . We extend the natural projection to by . We denote the inverse projection by a mapping , i.e., for any , we have .
To study opacity of , we assume that has a set of secret states, denoted by . We use to denote the set of non-secret initial states. Let and , . If , , we call a run generated by from to under . We write (resp., ) when (resp., ) are not specified. Note that there may be more than one run under a sequence based on nondeterminism of . In other words, may denote some runs. is called a non-secret run if , .
2.2 Standard current-state opacity and initial-state opacity
In this subsection, we first recall the formal definitions of standard CSO and ISO in [6] and [7, 11], respectively. And then, we discuss their limitations for characterizing information security.
Definition 2.1 (Standard CSO [6]).
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, is said to be current-state opaque (CSO)222For brevity, the terminology “CSO” (resp., ISO), is used as the acronym of both “current-state opacity” (resp., “initial-state opacity”) and “current-state opaque” (resp., “initial-state opaque”), adapted to the context. (w.r.t. and ), if for all and for all such that , it holds
| (1) |
Note that, in [6] the notion of standard CSO was defined for deterministic finite-state automata. Obviously, this property can be readily extended to the nondeterministic setting as in Definition 2.1.
Definition 2.2 (Standard ISO [7]).
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, is said to be initial-state opaque (ISO) (w.r.t. and ), if for all and for all , it holds
| (2) |
Remark 2.1.
Many results on the verification and enforcement of CSO and ISO have been obtained so far. However, the aforementioned two categories of opacity may not be able to characterize higher-level privacy requirements in some practical applications. The following two examples illustrate their limitations.
Example 2.1.
Let us consider the system shown in Fig. 1, in which the set of secret states is .
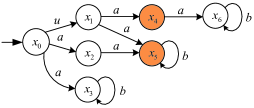
After observing the sequence , , can be in any state of (resp., ) when (reps., when ). For the sequences and , , we have , and P(s)=P(t). This means that, for each observation generated by , the intruder can never infer precisely whether is currently at secret states and/or . By Definition 2.1, is standard CSO w.r.t. and . Since an intruder has the perfect knowledge of the structure of , he/she immediately concludes that must have visited secret state or after observing , . This leads to some limitations that the security requirement characterized Definition 2.1 is not sufficiently strong to forbid the secret from being revealed.
Example 2.2.
Consider the system shown in Fig. 2, where the set of secret states is .

According to Definition 2.2, we conclude readily that is standard ISO. However, cannot keep the high-level secret based on the privacy condition characterized by Definition 2.2 since after observing the sequence () an intruder unambiguously determines that must have passed through secret initial state .
The phenomena in Examples 2.1 and 2.2 indicate that the standard versions of CSO and ISO have some limitations to some extent for characterizing high-level information security of a system. In order to overcome the aforementioned limitations, in this paper we propose two strong versions of opacity, called strong current-state opacity (SCSO) and strong initial-state opacity (SISO). Note that these two stronger notions of opacity provide high-level confidentiality.
3 Strong current-state opacity
In this section, we formally formulate the strong version of CSO for a system. And then, we propose a novel approach to verify it.
3.1 Notion of strong current-state opacity
Definition 3.1 (SCSO).
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, is said to be strongly current-state opaque (SCSO)333The terminology “SCSO” is the acronym of both “strong current-state opacity” and “strongly current-state opaque”, which depends on the context. (w.r.t. and ), if for all and for all such that , there exists a non-secret run such that , where , .
Note that if is a deterministic finite-state automaton, SCSO in Definition 3.1 can be rephrased as follows: is said to be SCSO (w.r.t. and ) if
Now we give a physical interpretation of Definition 3.1. The notion of SCSO captures that if a sequence is generated and a secret state is reached, then there exists a sequence that has the same projection as and its execution generates a run that never passes through a secret state. SCSO has a higher-level confidentiality than standard CSO. In other words, SCSO implies standard CSO, but the converse implication does not hold. For instance, the system in Example 2.1 is standard CSO, but not SCSO since after observing the sequence an intruder certainly concludes that has passed secret state or . This results in the following proposition for SCSO and CSO whose straightforward proof is omitted.
Proposition 3.1.
If system is SCSO w.r.t. and , then it is also standard CSO w.r.t. and . The converse is not true.
Remark 3.1.
In [37], the authors proposed the notion of strong -step opacity for a deterministic finite-state automaton . Specifically, is said to be strongly -step opaque (w.r.t. and ) if for all and for all such that and , there exists and such that and for all , if , then . Now we show that SCSO and strong -step opacity are incomparable when . Obviously, strong -step opacity does not imply SCSO based on their definitions. Also, the converse does not hold. Let us consider the system shown in Fig. 2, we conclude readily that is SCSO, but not strongly -step opaque for any .
In the following Subsection 3.2, we study the verification of SCSO based on a novel verification approach, which has time complexity .
3.2 Verifying strong current-state opacity
In this subsection, we focus on the verification of SCSO in Definition 3.1. In order to obtain the main result, we need to introduce three notions of non-secret subautomaton, observer and concurrent composition for a given system.
Given a system and a set of secret states, we construct a non-secret subautomaton by deleting all its secret states from , which is denoted by , where “” stands for the acronym of “deleting secret states”. Note that when we delete a secret state , all transitions attached to are also deleted. Formally,
| (3) |
where
-
•
stands for the set of states;
-
•
stands for the set of events;
-
•
stands for the transition function, i.e., for all ;
-
•
stands for the set of initial states.
Next, we recall the observer of that is defined by
| (4) |
where stands for the set of states; stands for the observable event set of ; stands for the (partial) deterministic transition function defined as follows: for any and , we have if it is nonempty, where ; stands for the (unique) initial state. For brevity, we only consider the accessible part of observer .
Note that the widely-used observer is an important information structure that can track all possible states of consistent with the current observation. Specifically, captures the observable behavior of , that is, . The time complexity of computing observer for is . We refer the reader to [38, 39] for more details on the notion of observer.
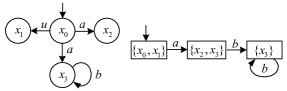
Example 3.1.
Consider the system depicted in Fig. 3, where the set of secret states is . The non-secret subautomaton and the observer for are shown in Fig. 4.


Now we are ready to introduce a novel information structure called the concurrent composition of system and observer , which will be used to verify SCSO in Definition 3.1.
Definition 3.2 (Concurrent Composition).
Given a system and a set of secret states, the concurrent composition of and is an NFA
| (5) |
where
-
•
stands for the set of states;
-
•
stands for the set of events;
-
•
is the transition function defined as follows: for any state and for any event ,
-
(i)
when ,
(a) if , then(b) if , then
-
(ii)
When ,
(a) if , then(b) if , then
-
(i)
-
•
stands for the set of initial states.
For a sequence , we utilize the notations and to denote its left and right components, respectively. A similar notation is employed to the language . Further, we use to denote or since for any , which depends on the context. Intuitively, characterizes the following two properties: (i) ; and (ii) it tracks a sequence from and an observation from (if exists) such that .
Remark 3.2.
The idea of concurrent composition was used in [40] to verify the so-called eventual strong detectability for a finite-state automaton. However, there are differences between the construction proposed in [40] and the above construction. First, the construction proposed in [40] is based on a system , while the concurrent composition defined in (5) is based on two different settings. Second, the two definitions of transition functions meet different requirements. Specifically, in [40], the concurrent composition aggregates each pair of transition sequences of generating the same projection. However, by Definition 3.2, captures that for any sequence , whether or not there exists an observation such that .
Example 3.2.
Consider again the system depicted in Fig. 3, the concurrent composition for is shown in Fig. 5, where is shown in Fig. 4. For brevity, for each state in , its first and second components are abbreviated by using their respective subscript sets. For example, state stands for state .

In order to present the first main result of this paper, we classify the states whose first components belong to in defined in (5) into two types:
-
•
leaking secret states: with ;
-
•
non-leaking secret states: with ;
The leaking and non-leaking secret states are interpreted physically as follows. If is a leaking secret state, then, by Definition 3.2, in there exists and such that , and there exists no observation such that . This means that an intruder certainly concludes that has reached/passed through at least one secret state by observing . If is a non-leaking secret state, then there exist , , and such that: (i) ; (ii) and have the same projection, i.e., ; (iii) there exists a non-secret run generated by from to under .
Based on the above preparation, now we are ready to introduce the main result on verification of SCSO for a system. It reveals that a system is SCSO if and only if its concurrent-composition structure does not contain any leaking secret state.
Theorem 3.1.
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, let be the concurrent composition of and . is SCSO w.r.t. and if and only if there exists no leaking secret state in .
Proof By contrapositive, assume that there exists a leaking secret state in . Let be a sequence that leads to from . Then, there exists an initial state such that . Further, by the construction of , we have that and is not well-defined. The former means and . The latter means that for all and for all with , it holds . By the construction of , we conclude that there exists no non-secret run in starting from with observation . Therefore, by Definition 3.1, is not SCSO w.r.t. and .
Also by contrapositive, assume that is not SCSO w.r.t. and . By Definition 3.1, there exists a run , where and , and there exist no and such that and generates a non-secret run starting from under . The former means . By the construction of , the latter means for all and for all with . This further means that is not well-defined. By the construction of , we conclude that there is with and such that . Therefore, a leaking secret state in .
Example 3.3.
(1) For the system depicted in Fig. 3, there exists no leaking state in shown in Fig. 5. By Theorem 3.1, is SCSO w.r.t. . (2) For the system depicted in Fig. 1, its concurrent composition is shown in Fig. 6 in which there exists a leaking secret states . By Theorem 3.1, is not SCSO w.r.t. and .

4 Strong initial-state opacity
In this section, we focus on the formulation of strong ISO and its verification problem for a system.
4.1 Notion of strong initial-state opacity
Definition 4.1 (SISO).
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, is said to be strongly initial-state opaque (SISO)444Similar to the terminology “SCSO”, in this paper “SISO” is the acronym of both “strong initial-state opacity” and “strongly initial-state opaque”, which also depends on the context. (w.r.t. and ), if for all and for all , there exists a non-secret run such that , where .
Intuitively, SISO in Definition 4.1 captures that for each sequence starting from any , there exists a sequence starting from some such that and generates a non-secret run starting from under . Note that, SISO, compared with standard ISO in Definition 2.2, has a higher-level confidentiality obviously. In other words, SISO implies standard ISO, but the converse is not true. Taking the system shown in Fig. 2 for example, by Definitions 2.2 and 4.1, we conclude readily that is standard ISO, but not SISO.
Next, we illustrate these two strong versions of opacity in Definitions 3.1 and 4.1 are incomparable. In other words, SCSO does not imply SISO, and vice versa. For instance, by Definitions 3.1 and 4.1, the system depicted in Fig. 2 is SCSO, but not SISO. On the other hand, let us consider the system shown in Fig. 8. We know that is SISO, but not SCSO.

4.2 Verifying strong initial-state opacity
Inspired by the verification of SCSO in Section 3, we, in this subsection, use a minor variant of the concurrent composition approach to verify SISO of a system.
Consider a system in which the set of secret states is denoted by . stands for the non-secret subautomaton obtained by deleting all secret states in , which is defined in Eq. (4). defined in Eq. (5) stands for the observer of . To check SISO in Definition 4.1, we construct an initial-secret subautomaton from , denoted by , as follows:
| (6) |
where
-
•
stands for the set of states;
-
•
stands for the set of events;
-
•
stands for the transition function, i.e., for all and , if ;
-
•
stands for the set of secret initial states.
Note that when we “delete” a state that is inaccessible from the set of secret initial states, we also delete all transitions attached to that state. Obviously, is a subautomaton of and is obtained by deleting all its states unreachable from .
Next, we construct the concurrent composition of and for , which also is an NFA, as follows.
| (7) |
where
-
•
stands for the set of states;
-
•
stands for the set of events, where (resp., ) is the set of observable (resp., unobservable) events of ;
-
•
is the transition function defined as follows: for any state , and for any event ,
-
(i)
when ,
(a) if , then(b) if , then
-
(ii)
when ,
(a) if , then(b) if , then
-
(i)
-
•
stands for the set of initial states.
In order to present the verification criterion of SISO in Definition 4.1, similarly to the argument in Section 3, we classify the states in defined in (7) into two types:
-
•
leaking states: for all with ;
-
•
non-leaking states: for all with ;
We now give an interpretation of leaking and non-leaking states as follows: if is a leaking state, by the construction of , then in there exists a secret initial state and a sequence such that , and there exists no and such that is a non-secret run and . If is a non-leaking state, then in there exists , , , and such that: (i) , and (ii) generates a non-secret run starting from under .
Theorem 4.1.
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, let be the concurrent composition of and . is SISO w.r.t. and if and only if there exists no leaking state in .
Proof This proof is analogous to that of Theorem 3.1 by contraposition.
Assume that there exists a leaking state in . Let be a sequence that leads to from . Then, there exists an initial state such that . By the construction of , one has , and is not well-defined. Since is the initial-secret subautomaton of , means . However, not well-defined implies that for all and for all with , it holds . By the construction of , we conclude that there do not exist a state and a sequence with such that generates a non-secret run starting from under . Therefore, by Definition 4.1, is not SISO w.r.t. and .
Assume that is not SISO w.r.t. and . By Definition 4.1, we know that: (1) in there exists a secret initial state and a sequence , and (2) there does not exist a sequence for any such that is a non-secret run and . By the construction of , the former means that there exists a state such that . By the construction of , the latter means for all and for all with . This further implies that is not well-defined. By the construction of , we conclude that there exists a sequence with and such that . Therefore, a leaking state in .
Remark 4.1.
We discuss the time complexity of checking SISO for using Theorem 4.1. From Subsection 3.2, has time complexity . By Eq. (6), the time complexity of constructing from is . Therefore, the time complexity of constructing is . This indicates that the time complexity of verifying SISO in Definition 4.1 is .
Example 4.1.
Let us consider the system depicted in Fig. 9, where the set of secret states is . The constructed automata , and for are shown in Fig. 10. Further, the concurrent composition is shown in Fig. 11 in which there exist two leaking states and 555Note that, similar to , for each state in , its first and second components are also abbreviated by using their respective subscript set. For instance, is the abbreviation of state .. By Theorem 4.1, is not SISO w.r.t. and .



5 Concluding remarks
In this paper, we characterized two strong versions of opacity called strong current-state opacity and strong initial-state opacity, respectively. They have higher-level confidentiality than the standard versions. Further, we constructed two information structures using a novel concurrent-composition technique to verify these two strong versions of opacity, which have (worst-case) time complexity .
Motivated by [37] and our work, a strong version of standard Inf-SO, called strong infinite-step opacity (Inf-SSO), is formally formulate in the context of nondeterministic settings as follows.
Definition 5.1 (Inf-SSO).
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, is said to be strongly infinite-step opaque (Inf-SSO) (w.r.t. and ), if for all and for all such that , there exists a non-secret run such that , where .
By Definition 5.1, one sees that is Inf-SSO if and only if for all and for all , there exists a non-secret run for some and some such that . We can use the concurrent composition of and constructed in Definition 3.2 to present the result on verification of Inf-SSO, which also has time complexity . We here omit its proof, which is similar to that of Theorem 3.1.
Theorem 5.1.
Given a system , a projection map w.r.t. the set of observable events, and a set of secret states, let be the concurrent composition of and . is Inf-SSO w.r.t. and if and only if there exists no such a state in whose right component is .
In the future, we plan to exploit the proposed concurrent-composition approach to design algorithms for enforcing strong current-state opacity, strong initial-state opacity and strong infinite-step opacity.
References
- [1] S. Lafortune, F. Lin, and C. Hadjicostis. On the history of diagnosability and opacity in discrete event systems. Annual Reviews in Control, 45:257–266, 2018.
- [2] C. Hadjicostis. Estimation and Inference in Discrete Event Systems. Springer, Switzerland AG, 2020.
- [3] L. An and G. Yang. Opacity enforcement for confidential robust control in linear cyber-physical systems. IEEE Transactions on Automatic Control, 265(3):1234–1241, 2020.
- [4] B. Ramasubramanian, W.R. Cleaveland, and S. Marcus. Notions of centralized and decentralized opacity in linear systems. IEEE Transactions on Automatic Control, 265(4):1442–1455, 2020.
- [5] L. Mazaré. Using unification for opacity prooperties. In: Proceeding of the Workshop on Issues in the Theory of Security, pages 165–176, 2004.
- [6] A. Saboori and C. Hadjicostis. Notions of security and opaicty in discrete event systems. In: Proceedings of 46th IEEE Conference on Decision and Control, pages 5056–5061, 2007.
- [7] A. Saboori and C. Hadjicostis. Verification of initial-state opacity in security appications of discrete event systems. Information Sciences, 246:115–132, 2013.
- [8] A. Saboori and C. Hadjicostis. Verification of -step opacity and analysis of its complexity. IEEE Transactions on Automation Science and Engineering, 8(3):549–559, 2011.
- [9] A. Saboori and C. Hadjicostis. Verification of infinite-step opacity and complexity considerations. IEEE Transactions on Automatic Control, 57(5):1265–1269, 2012.
- [10] F. Lin. Opacity of discrete event systems and its applications. Automatica, 47(3):496–503, 2011.
- [11] Y. Wu and S. Lafortune. Comparative analysis of related notions of opacity in centralized and coordinated architectures. Discrete Event Dynamic Systems, 23(3): 307–339, 2013.
- [12] X. Yin and S. Lafortune. A new approach for the verification of infinite-step and K-step opacity using two-way observers. Automatica, 80:162–171, 2017.
- [13] H. Lan, Y. Tong, J. Guo, and A. Giua. Comments on “A new approach for the verification of infinite-step and K-step opacity using two-way observers”. Automatica, 122:109290, 2020.
- [14] J. Dubreil, P. Darondeau, and H. Marchand. Supervisory control for opacity. IEEE Transactions on Automatic Control, 55(5):1089–1100, 2010.
- [15] A. Saboori and C. Hadjicostis. Opacity-enforcing supervisory strategies via state estimator constructions. IEEE Transactions on Automatic Control, 57(2):1155–1165, 2012.
- [16] Y. Tong, Z. Li, C. Seatzu, and A. Giua. Current-state opacity enforcement in discrete event systems under incomparable observations. Discrete Event Dynamic Systems, 28(2):161–182, 2018.
- [17] Y. Ji, Y. Wu, and S. Lafortune. Enforcement of opacity by public and private insertion functions. Automatica, 93:369–378, 2018.
- [18] Y. Ji, X. Yin, and S. Lafortune. Opacity enforcement using nondeterministic publicly-known edit functions. IEEE Transactions on Automatic Control, 64(10):4369–4376, 2019.
- [19] Y. Ji, X. Yin, and S. Lafortune. Enforcing opacity by insertion functions under multiple energy constraints and imperfect information. Automatica, 108:1–14, 2019.
- [20] X. Yin and S. Li. Synthesis of dynamic masks for infinite-step opacity. IEEE Transactions on Automatic Control, 65(4):1429–1441, 2020.
- [21] B. Zhang, S. Shu, and F. Lin. Maximum information release while ensuring opacity in discrete event systems. IEEE Transactions on Automation Science and Engineering, 12(4):1067–1079, 2015.
- [22] J. Bryans, M. Koutny, L. Mazaré, et al. Opacity generalised to transition systems. International Journal of Information Security, 7(6):421–435, 2008.
- [23] Y. Tong, Z. Li, C. Seatzu, et al. Verification of state-based opacity using Petri nets. IEEE Transactions on Automatic Control, 62(6):2823–2837, 2017.
- [24] X. Cong, M.P. Fanti, A.M. Mangini, and Z. Li. On-line verification of current-state opacity by petri nets and integer linear programming. Automatica, 94:205–213, 2018.
- [25] A. Saboori and C. Hadjicostis. Current-state opacity formulations in probabilistic finite automata. IEEE Transactions on Automatic Control, 59(1):120–133, 2014.
- [26] C. Keroglou and C. Hadjicostis. Probabilistic system opacity in discrete event systems. Discrete Event Dynamic Systems, 28:289–314, 2018.
- [27] X. Yin, Z. Li, W. Wang, et al. Infinite-step opacity and K-step opacity of stochastic discrete-event systems. Automatica, 99:266–274, 2019.
- [28] Y. Tong and H. Lan. Current-state opacity verification in modular discrete event systems. In: Proceedings of the 58th IEEE Conference on Decision and Control, pages 7665–7670, 2019.
- [29] X. Yin and S. Li. Opacity of networked supervisory control systems over insecure multiple channel networks. In: Proceedings of the 58th IEEE Conference on Decision and Control, pages 7641–7646, 2019.
- [30] J. Yang, W. Deng, C. Jiang, and D. Qiu. Opacity of networked discrete event systems. In: Proceedings of the 58th IEEE Conference on Decision and Control, pages 6736–6741, 2019.
- [31] K. Zhang, X. Yin, and M. Zamani. Opacity of nondeterministic transition systems: A (bi)simulation relation approach. IEEE Transactions on Automatic Control, 64(2):5116–5123, 2019.
- [32] X. Yin, M. Zamani, and S. Liu. On approximate opacity of Cyber-physical systems. IEEE Transactions on Automatic Control, DOI 10.1109/TAC.2020.2998733.
- [33] A. Saboori and C.N. Hadjicostis.. Coverage analysis of mobile agent trajectory via state-based opacity formulations. Control Engineering Practice, 19(9):967–977, 2011.
- [34] Y. Wu, K. Sankararaman, and S. Lafortune. Ensuring privacy in location-based services: An approach based on opacity enforcement. In: Proceedings of 12th International Workshop on Discrete Event Systems, pages 33–38, 2014.
- [35] A. Bourouis, K. Klai, N. Ben Hadj-Alouane, and Y. El Touati. On the verification of opacity in web services and their composition. IEEE Transactions on Services Computing, 10(1):66–79, 2017.
- [36] F. Lin, W. Chen, W. Wang, and F. Wang. Information control in networked discrete event systems and its application to battery management systems. Discrete Event Dynamic Systems, 30(2):243–268, 2020.
- [37] Y. Falcone and H. Marchand. Enforcement and validation (at runtime) of various notions of opacity. Discrete Event Dynamic Systems, 25:531–570, 2015.
- [38] C. G. Cassandras and S. Lafortune. Introduction to disctete event system. Springer, New York, 2nd Edition, 2008.
- [39] S. Shu, F. Lin, and H. Ying. Detectability of discrete event systems. IEEE Transactions on Automatic Control, 52(12):2356–2359, 2007.
- [40] K. Zhang and A. Giua. On detectability of labeled Petri nets and finite automata. Discrete Event Dynamic Systems, 30:465–497, 2020.