Stochastic Approximation Approaches to
Group Distributionally Robust Optimization and Beyond
Abstract
This paper investigates group distributionally robust optimization (GDRO) with the goal of learning a model that performs well over different distributions. First, we formulate GDRO as a stochastic convex-concave saddle-point problem, which is then solved by stochastic mirror descent (SMD) with samples in each iteration, and attain a nearly optimal sample complexity. To reduce the number of samples required in each round from to 1, we cast GDRO as a two-player game, where one player conducts SMD and the other executes an online algorithm for non-oblivious multi-armed bandits, maintaining the same sample complexity. Next, we extend GDRO to address scenarios involving imbalanced data and heterogeneous distributions. In the first scenario, we introduce a weighted variant of GDRO, enabling distribution-dependent convergence rates that rely on the number of samples from each distribution. We design two strategies to meet the sample budget: one integrates non-uniform sampling into SMD, and the other employs the stochastic mirror-prox algorithm with mini-batches, both of which deliver faster rates for distributions with more samples. In the second scenario, we propose to optimize the average top- risk instead of the maximum risk, thereby mitigating the impact of outlier distributions. Similar to the case of vanilla GDRO, we develop two stochastic approaches: one uses samples per iteration via SMD, and the other consumes samples per iteration through an online algorithm for non-oblivious combinatorial semi-bandits.
Keywords: Group distributionally robust optimization (GDRO), Stochastic convex-concave saddle-point problem, Non-oblivious online learning, Bandits, Average top- risk
1 Introduction
In the classical statistical machine learning, our goal is to minimize the risk with respect to a fixed distribution (Vapnik, 2000), i.e.,
| (1) |
where is a sample drawn from , denotes a hypothesis class, and is a loss measuring the prediction error of model on . During the past decades, various algorithms have been developed to optimize (1), and can be grouped in two categories: sample average approximation (SAA) and stochastic approximation (SA) (Kushner and Yin, 2003). In SAA, we minimize an empirical risk defined as the average loss over a set of samples drawn from , and in SA, we directly solve the original problem by using stochastic observations of the objective .
However, a model trained on a single distribution may lack robustness in the sense that (i) it could suffer high error on minority subpopulations, though the average loss is small; (ii) its performance could degenerate dramatically when tested on a different distribution. Distributionally robust optimization (DRO) provides a principled way to address those limitations by minimizing the worst-case risk in a neighborhood of (Ben-Tal et al., 2013). Recently, it has attracted great interest in optimization (Shapiro, 2017), statistics (Duchi and Namkoong, 2021), operations research (Duchi et al., 2021), and machine learning (Hu et al., 2018; Curi et al., 2020; Jin et al., 2021; Agarwal and Zhang, 2022). In this paper, we consider an emerging class of DRO problems, named as Group DRO (GDRO) which optimizes the maximum risk
| (2) |
over a finite number of distributions (Oren et al., 2019; Sagawa et al., 2020). Mathematically, GDRO can be formulated as a minimax stochastic problem:
| (3) |
where denote distributions. A motivating example is federated learning, where a centralized model is deployed at multiple clients, each of which faces a (possibly) different data distribution (Mohri et al., 2019).
Supposing that samples can be drawn from all distributions freely, we develop efficient SA approaches for (3), in favor of their light computations over SAA methods. As elaborated by Nemirovski et al. (2009, § 3.2), we can cast (3) as a stochastic convex-concave saddle-point problem:
| (4) |
where is the ()-dimensional simplex, and then solve (4) by their mirror descent stochastic approximation method, namely stochastic mirror descent (SMD). In fact, several recent studies have adopted this (or similar) strategy to optimize (4). But, unfortunately, we found that existing results are unsatisfactory because they either deliver a loose sample complexity (Sagawa et al., 2020), suffer subtle dependency issues in their analysis (Haghtalab et al., 2022; Soma et al., 2022), or hold only in expectation (Carmon and Hausler, 2022).
As a starting point, we first provide a routine application of SMD to (4), and discuss the theoretical guarantee. In each iteration, we draw sample from every distribution to construct unbiased estimators of and its gradient, and then update both and by SMD. The proposed method achieves an convergence rate in expectation and with high probability, where is the total number of iterations. As a result, we obtain an sample complexity for finding an -optimal solution of (4), which matches the lower bound (Soma et al., 2022, Theorem 5) up to a logarithmic factor, and tighter than the bound of Sagawa et al. (2020) by an factor. While being straightforward, this result seems new for GDRO. Additionally, we note that the aforementioned method requires setting the number of iterations in advance, which could be inconvenient in practice. To avoid this limitation, we further propose an anytime algorithm by using time-varying step sizes, and obtain an 111We use the notation to hide constant factors as well as polylogarithmic factors in . convergence rate at each iteration .
Then, we proceed to reduce the number of samples used in each iteration from to . We remark that a naive uniform sampling over distributions does not work well, and yields a higher sample complexity (Sagawa et al., 2020). As an alternative, we borrow techniques from online learning with stochastic observations, and explicitly tackle the non-oblivious nature of the online process, which distinguishes our method from that of Soma et al. (2022). Specifically, we use SMD to update , and Exp3-IX, a powerful algorithm for non-oblivious multi-armed bandits (MAB) (Neu, 2015), with stochastic rewards to update . In this way, our algorithm only needs sample in each round and attains an convergence rate, implying the same sample complexity. Similarly, we also put forward an anytime variant, achieving an convergence rate.
Subsequently, we extend GDRO to address two specific scenarios, as illustrated below.
1.1 Extension to Imbalanced Data
In the first extention, we investigate a more practical and challenging scenario in which there are different budgets of samples that can be drawn from each distribution, a natural phenomenon encountered in learning with imbalanced data (Amodei et al., 2016). Let be the sample budget of the -th distribution, and without loss of generality, we assume that . Now, the goal is not to attain the optimal sample complexity, but to reduce the risk on all distributions as much as possible, under the budget constraint. To achieve this goal, we propose a novel formulation of weighted GDRO, which weights each risk in (4) by a scale factor . For GDRO with different budgets, we develop two SA approaches based on non-uniform sampling and mini-batches, respectively.
In each iteration of the first approach, we draw sample from every with probability , and then construct stochastic gradients to perform mirror descent. Consequently, the budget will be satisfied in expectation after rounds, and our algorithm can be regarded as SMD for an instance of weighted GDRO. With the help of scale factors, we demonstrate the proposed algorithm enjoys distribution-dependent convergence in the sense that it converges faster for distributions with more samples. In particular, the excess risk on distribution reduces at an rate, and for , it becomes , which almost matches the optimal rate of learning from a single distribution with samples.
On the other hand, for distribution with budget , the above rate is worse than the rate obtained by learning from alone. In shape contrast with this limitation, our second approach yields nearly optimal convergence rates for multiple distributions across a large range of budgets. To meet the budget constraint, it runs for rounds, and in each iteration, draws a mini-batch of samples from every distribution . As a result, (i) the budget constraint is satisfied exactly; (ii) for distributions with a larger budget, the associated risk function can be estimated more accurately, making the variance of the stochastic gradient smaller. To benefit from the small variance, we leverage stochastic mirror-prox algorithm (Juditsky et al., 2011), instead of SMD, to update solutions, and again make use of the weighted GDRO formulation to obtain distribution-wise convergence rates. Theoretical analysis shows that the excess risk converges at an rate for each . Thus, we obtain a nearly optimal rate for distributions with , and an rate otherwise. Note that the latter rate is as expected since the algorithm only updates times.
1.2 Extension to Heterogeneous Distributions
In the second extension, we delve into another scenario where distributions exhibit heterogeneity, indicating significant variations in their risks (Li et al., 2019). The widely acknowledged sensitivity of the max operation to outliers implies that GDRO could be dominated by a single outlier distribution, while neglecting others (Shalev-Shwartz and Wexler, 2016). Inspired by the average top- loss for supervised learning (Fan et al., 2017), we modify our objective from the maximum risk in GDRO to the average top- risk:
| (5) |
where is the set of subsets of with size , i.e., . This modification aims to reduce the impact of outliers in heterogeneous distributions while still including GDRO as a special case.
We refer to the minimization of as average top- risk optimization (ATkRO), and develop two stochastic algorithms. Similar to GDRO, ATkRO can be formulated as a stochastic convex-concave saddle-point problem, akin to (4), with the only difference being that the domain of is the capped simplex instead of the standard simplex. Therefore, we can employ SMD to update and , which uses samples in each round. Theoretical analysis demonstrates that this approach achieves an convergence rate, implying an sample complexity. Furthermore, to circumvent the limitation of predefining the total number of iterations , we introduce an anytime version that attains an convergence rate.
Following the second approach for GDRO, we reduce the number of samples required in each round from to by casting ATkRO as a two-player game. In each round, we use the Dependent Rounding (DepRound) algorithm (Gandhi et al., 2006) to select distributions based on the current value of , and then draw sample from each selected distribution. Then, we construct unbiased stochastic gradients for , and apply SMD for updates. Since the domain of is the capped simplex, we model the online problem for as an instance of non-oblivious combinatorial semi-bandits, and extend Exp3-IX to develop its update rule. We prove that our algorithm achieves an convergence rate, yielding an sample complexity. Similarly, we have also designed an anytime approach, which uses sample per round and achieves an rate.
This paper extends our previous conference version (Zhang et al., 2023) by developing anytime algorithms, investigating a new scenario, and conducting more experiments, as detailed below.
-
•
First, we adapt the two SA algorithms for GDRO to operate in an anytime manner. In the conference paper, our algorithms for GDRO required predefining the total number of iterations to set step sizes. By adopting time-varying step sizes, we design anytime algorithms and provide the corresponding theoretical analysis.
-
•
Second, we explore the scenario of heterogeneous distributions, which involves outlier distributions with significantly high risks. To mitigate the impact of these outliers, we propose to solve the ATkRO problem and develop two algorithms: one employs SMD with samples per round, achieving a sample complexity of ; the other combines SMD with an algorithm for non-oblivious combinatorial semi-bandits, achieving a sample complexity of and using samples in each iteration. Furthermore, we have also extended these two algorithms into anytime versions.
-
•
Last, we construct a heterogeneous data set and perform experiments to verify the advantages of ATkRO. Additionally, we compare the performance of the anytime algorithms with their non-anytime counterparts, demonstrating the benefits of the anytime capability.
2 Related Work
Distributionally robust optimization (DRO) stems from the pioneering work of Scarf (1958), and has gained a lot of interest with the advancement of robust optimization (Ben-Tal et al., 2009, 2015). It has been successfully applied to a variety of machine learning tasks, including adversarial training (Sinha et al., 2018), algorithmic fairness (Hashimoto et al., 2018), class imbalance (Xu et al., 2020), long-tail learning (Samuel and Chechik, 2021), label shift (Zhang et al., 2021), etc.
In general, DRO is formulated to reflect our uncertainty about the target distribution. To ensure good performance under distribution perturbations, it minimizes the risk w.r.t. the worst distribution in an uncertainty set, i.e.,
| (6) |
where denotes a set of probability distributions around . In the literature, there mainly exist three ways to construct : (i) enforcing moment constraints (Delage and Ye, 2010), (ii) defining a neighborhood around by a distance function such as the -divergence (Ben-Tal et al., 2013), the Wasserstein distance (Kuhn et al., 2019), and the Sinkhorn distance (Wang et al., 2021), and (iii) hypothesis testing of goodness-of-fit (Bertsimas et al., 2018).
By drawing a set of samples from , we can also define an empirical DRO problem, which can be regarded as an SAA approach for solving (6). When the uncertainty set is defined in terms of the Cressie–Read family of -divergences, Duchi and Namkoong (2021) have studied finite sample and asymptotic properties of the empirical solution. Besides, it has been proved that empirical DRO can also benefit the risk minimization problem in (1). Namkoong and Duchi (2017) show that empirical DRO with the -divergence has the effect of variance regularization, leading to better generalization w.r.t. distribution . Later, Duchi et al. (2021) demonstrate similar behaviors for the -divergence constrained neighborhood, and provide one- and two-sided confidence intervals for the minimum risk in (1). Based on the Wasserstein distance, Esfahani and Kuhn (2018) establish an upper confidence bound on the risk of the empirical solution.
Since (6) is more complex than (1), considerable research efforts were devoted to develop efficient algorithms for DRO and its empirical version. For with finite support, Ben-Tal et al. (2013, Corollary 3) have demonstrated that (6) with -divergences is equivalent to a convex optimization problem, provided that the loss is convex in . Actually, this conclusion is true even when is continuous (Shapiro, 2017, § 3.2). Under mild assumptions, Esfahani and Kuhn (2018) show that DRO problems over Wasserstein balls can be reformulated as finite convex programs—in some cases even as linear programs. Besides the constrained formulation in (6), there also exists a penalized (or regularized) form of DRO (Sinha et al., 2018), which makes the optimization problem more tractable. In the past years, a series of SA methods have been proposed for empirical DRO with convex losses (Namkoong and Duchi, 2016), and DRO with convex loss (Levy et al., 2020) and non-convex losses (Jin et al., 2021; Qi et al., 2021; Rafique et al., 2022).
The main focus of this paper is the GDRO problem in (3)/(4), instead of the traditional DRO in (6). Sagawa et al. (2020) have applied SMD (Nemirovski et al., 2009) to (4), but only obtain a sub-optimal sample complexity of , because of the large variance in their gradients. In the sequel, Haghtalab et al. (2022) and Soma et al. (2022) have tried to improve the sample complexity by reusing samples and applying techniques from MAB respectively, but their analysis suffers dependency issues. Carmon and Hausler (2022, Proposition 2) successfully established an sample complexity by combining SMD and gradient clipping, but their result holds only in expectation. To deal with heterogeneous noise in different distributions, Agarwal and Zhang (2022) propose a variant of GDRO named as minimax regret optimization (MRO), which replaces the risk with “excess risk” . More generally, calibration terms can be introduced to prevent any single distribution from dominating the maximum (Słowik and Bottou, 2022). Efficient optimization of MRO has been investigated by Zhang et al. (2024).
In the context of federated learning, Mohri et al. (2019) have analyzed the generalization error of empricial GDRO when the number of samples from different distributions could be different. However, their convergence rate is unsatisfactory as it depends on the smallest number of samples and is distribution-independent. Finally, we note that GDRO has a similar spirit with collaborative PAC learning (Blum et al., 2017; Nguyen and Zakynthinou, 2018; Rothblum and Yona, 2021) in the sense that both aim to find a single model that performs well on multiple distributions.
3 SA Approaches to GDRO
In this section, we present two efficient SA approaches for GDRO, which achieve the same sample complexity but use a different number of samples in each round ( versus ).
3.1 Preliminaries
First, we state the general setup of mirror descent (Nemirovski et al., 2009). We equip the domain with a distance-generating function , which is -strongly convex with respect to certain norm . We define the Bregman distance associated with as
For the simplex , we choose the negative entropy (neg-entropy) function , which is -strongly convex with respect to the vector -norm , as the distance-generating function. Similarly, is the Bregman distance associated with .
Then, we introduce the standard assumptions about the domain, and the loss function.
Assumption 1
The domain is convex and its diameter measured by is bounded by , i.e.,
| (7) |
For , it is easy to verify that its diameter measured by the neg-entropy function is bounded by .
Assumption 2
For all , the risk function is convex.
To simplify presentations, we assume the loss belongs to , and its gradient is also bounded.
Assumption 3
For all , we have
| (8) |
Assumption 4
For all , we have
| (9) |
where is the dual norm of .
3.2 Stochastic Mirror Descent for GDRO
To apply SMD, the key is to construct stochastic gradients of the function in (4). We first present its true gradients with respect to and :
In each round , denote by and the current solutions. We draw one sample from every distribution , and define stochastic gradients as
| (12) |
Obviously, they are unbiased estimators of the true gradients:
where represents the expectation conditioned on the randomness until round . It is worth mentioning that the construction of can be further simplified to
| (13) |
where is drawn randomly according to the probability .
Then, we use SMD to update and :
| (14) | ||||
| (15) |
where and are two step sizes that will be determined later. The updating rule of depends on the choice of the distance-generating function . For example, if , (14) becomes stochastic gradient descent (SGD), i.e.,
where denotes the Euclidean projection onto the nearest point in . Since is defined in terms of the neg-entropy, (15) is equivalent to
| (16) |
which is the Hedge algorithm (Freund and Schapire, 1997) applied to a maximization problem. In the beginning, we set , and , where is the -dimensional vector consisting of ’s. In the last step, we return the averaged iterates and as final solutions. The complete procedure is summarized in Algorithm 1.
Based on the theoretical guarantee of SMD for stochastic convex-concave optimization (Nemirovski et al., 2009, § 3.1), we have the following theorem for Algorithm 1.
Theorem 1
Remark 1
Comparisons with Sagawa et al. (2020)
Given the fact that the number of samples used in each round of Algorithm 1 is , it is natural to ask whether it can be reduced to a small constant. Indeed, the stochastic algorithm of Sagawa et al. (2020) only requires sample per iteration, but suffers a large sample complexity. In each round , they first generate a random index uniformly, and draw sample from . The stochastic gradients are constructed as follows:
| (17) |
where is a vector with in position and elsewhere. Then, the two stochastic gradients are used to update and , in the same way as (14) and (15). However, it only attains a slow convergence rate: , leading to an sample complexity, which is higher than that of Algorithm 1 by a factor of . The slow convergence is due to the fact that the optimization error depends on the dual norm of the stochastic gradients in (17), which blows up by a factor of , compared with the gradients in (12).
Comparisons with Haghtalab et al. (2022)
To reduce the number of samples required in each round, Haghtalab et al. (2022) propose to reuse samples for multiple iterations. To approximate , they construct the stochastic gradient in the same way as (13), which needs sample. To approximate , they draw samples , one from each distribution, at round , , and reuse them for iterations to construct the following gradient:
| (18) |
Then, they treat and as stochastic gradients, and update and by SMD. In this way, their algorithm uses samples on average in each iteration. However, the gradient in (18) is no longer an unbiased estimator of the true gradient at rounds , making their analysis ungrounded. To see this, from the updating rule of SMD, we know that depends on , which in turn depends on the samples drawn at round , and thus
3.2.1 Anytime Extensions
The step sizes and in Theorem 1 depend on the total number of iterations , which complicates practical implementation as it requires setting beforehand. Additionally, the theorem only offers theoretical guarantees for the final solution. To avoid these limitations, we propose an anytime extension of Algorithm 1 by employing time-varying step sizes. We note that there is a long-standing history of designing anytime algorithms in optimization and related areas (Zilberstein, 1996; Horsch and Poole, 1998; Cutkosky, 2019).
Specifically, we replace the fixed step sizes and in (14) and (15) with time-varying step sizes (Nemirovski et al., 2009)
| (19) |
respectively. To enable anytime capability, we maintain the weighted averages of the iterates:
| (20) |
which can be returned as solutions whenever required, and provide the following theoretical guarantee for the solution at each round .
Theorem 2
Remark 2
The convergence rate of the anytime extension is slower by a factor of compared to Algorithm 1 with fixed step sizes. However, the modified algorithm possesses the anytime characteristic, indicating it is capable of returning a solution at any round.
3.3 Non-oblivious Online Learning for GDRO
In this section, we explore methods to reduce the number of samples used in each iteration from to . As shown in (13), we can use sample to construct a stochastic gradient for with small norm, since under Assumption 4. Thus, it is relatively easy to control the error related to . However, we do not have such guarantees for the stochastic gradient of . Recall that the infinity norm of in (17) is upper bounded by . The reason is that we insist on the unbiasedness of the stochastic gradient, which leads to a large variance. To control the variance, Carmon and Hausler (2022) have applied gradient clipping to , and established an sample complexity that holds in expectation. Different from their approach, we borrow techniques from online learning to balance the bias and the variance.
In the studies of convex-concave saddle-point problems, it is now well-known that they can be solved by playing two online learning algorithms against each other (Freund and Schapire, 1999; Rakhlin and Sridharan, 2013; Syrgkanis et al., 2015; Roux et al., 2021). This transformation allows us to exploit no-regret algorithms developed in online learning to bound the optimization error. To solve problem (4), we ask the 1st player to minimize a sequence of convex functions
| (22) |
under the constraint , and the 2nd player to maximize a sequence of linear functions
| (23) |
subject to the constraint . We highlight that there exists an important difference between our stochastic convex-concave problem and its deterministic counterpart. Here, the two players cannot directly observe the loss function, and can only approximate by drawing samples from . The stochastic setting makes the problem more challenging, and in particular, we need to take care of the non-oblivious nature of the learning process. Here, “non-oblivious” refers to the fact that the online functions depend on the past decisions of the players.
Next, we discuss the online algorithms that will be used by the two players. As shown in Section 3.2, the 1st player can easily obtain a stochastic gradient with small norm by using sample. So, we model the problem faced by the 1st player as “non-oblivious online convex optimization (OCO) with stochastic gradients”, and still use SMD to update its solution. In each round , with sample drawn from , the 2nd player can estimate the value of which is the coefficient of . Since the 2nd player is maximizing a linear function over the simplex, the problem can be modeled as “non-oblivious multi-armed bandits (MAB) with stochastic rewards”. And fortunately, we have powerful online algorithms for non-oblivious MAB (Auer et al., 2002; Lattimore and Szepesvári, 2020), whose regret has a sublinear dependence on . In this paper, we choose the Exp3-IX algorithm (Neu, 2015), and generalize its theoretical guarantee to stochastic rewards. In contrast, if we apply SMD with in (17), the regret scales at least linearly with .
The complete procedure is presented in Algorithm 2, and we explain key steps below. In each round , we generate an index from the probability distribution , and then draw a sample from the distribution . With the stochastic gradient in (13), we use SMD to update :
| (24) |
Then, we reuse the sample to update according to Exp3-IX, which first constructs the Implicit-eXploration (IX) loss estimator (Kocák et al., 2014):
| (25) |
where is the IX coefficient and equals to when the event is true and otherwise, and then performs a mirror descent update:
| (26) |
Compared with (15), the only difference is that the stochastic gradient is now replaced with the IX loss estimator . However, it is not an instance of SMD, because is no longer an unbiased stochastic gradient. The main advantage of is that it reduces the variance of the gradient estimator by sacrificing a little bit of unbiasedness, which turns out to be crucial for a high probability guarantee, and thus can deal with non-oblivious adversaries. Since we still use the entropy regularizer in (26), it also enjoys an explicit form that is similar to (16).
We present the theoretical guarantee of Algorithm 2. To this end, we first bound the regret of the 1st player. In the analysis, we address the non-obliviousness by the “ghost iterate” technique of Nemirovski et al. (2009).
By extending Exp3-IX to stochastic rewards, we have the following bound for the 2nd player.
Theorem 4
Combining the above two theorems directly leads to the following optimization error bound.
Theorem 5
Remark 3
The above theorem shows that with sample per iteration, Algorithm 2 is able to achieve an convergence rate, thus maintaining the sample complexity. It is worth mentioning that one may attempt to reduce the factor by employing mirror descent with the Tsallis entropy () for the 2nd player (Audibert and Bubeck, 2010, Theorem 13). However, even in the standard MAB problem, such an improvement only happens in the oblivious setting, and is conjectured to be impossible in the non-oblivious case (Audibert and Bubeck, 2010, Remark 14).
Comparisons with Soma et al. (2022)
In a recent work, Soma et al. (2022) have deployed online algorithms to optimize and , but did not consider the non-oblivious property. As a result, their theoretical guarantees, which build upon the analysis for oblivious online learning (Orabona, 2019), cannot justify the optimality of their algorithm for (4). Specifically, their results imply that for any fixed and that are independent from and (Soma et al., 2022, Theorem 3),
| (29) |
However, (29) cannot be used to bound in (10), because of the dependency issue. To be more clear, we have
where and depend on and , respectively.
Remark 4
3.3.1 Anytime Extensions
Similar to Algorithm 1, Algorithm 2 also requires the prior specification of the total number of iterations , as the values of in SMD, as well as and in Exp3-IX, are dependent on . Following the extension in Section 3.2.1, we can also adapt Algorithm 2 to be anytime by employing time-varying parameters in SMD and Exp3-IX. Specifically, in the -th round, we replace in (24), in (26), and in (25) with
| (30) |
respectively, and output and in (20) as the current solution.
Compared to the original Algorithm 2, our modifications are relatively minor. However, the theoretical analysis differs significantly. The reason is because the optimization error of is governed by the weighted average regret of the two players, rather than the standard regret. That is,
| (31) |
For the 1st player, we extend the analysis of SMD in Theorem 3, and obtain the results below for bounding .
Theorem 6
While Neu (2015) have analyzed the regret of Exp3-IX with time-varying step sizes, our focus is on the weighted average regret . To achieve this, we conduct a different analysis to bound , and establish the following theoretical guarantee.
Theorem 7
By directly integrating the above two theorems, we derive the following theorem for the optimization error at each round.
Theorem 8
4 Weighted GDRO for Imbalanced Data
When designing SA approaches for GDRO, it is common to assume that the algorithms are free to draw samples from every distribution (Sagawa et al., 2020), as we do in Section 3. However, this assumption may not hold in practice. For example, data collection costs can vary widely among distributions (Radivojac et al., 2004), and data collected from various channels can have different throughputs (Zhou, 2024). In this section, we investigate the scenario where the number of samples can be drawn from each distribution could be different. Denote by the number of samples that can be drawn from . Without loss of generality, we assume that . Note that we have a straightforward Baseline which just runs Algorithm 1 for iterations, and the optimization error .
4.1 Stochastic Mirror Descent with Non-uniform Sampling
To meet the budget, we propose to incorporate non-uniform sampling into SMD. Before getting into technical details, we first explain the main idea of using non-uniform sampling. One way is to draw sample from every distribution with probability in each iteration. Then, after iterations, the expected number of samples drawn from will be , and thus the budget is satisfied in expectation.
Specifically, in each round , we first generate a set of Bernoulli random variables with to determine whether to sample from each distribution. If , we draw a sample from . The question then becomes how to construct stochastic gradients from these samples. Let be the indices of selected distributions. If we stick to the original problem in (4), then the stochastic gradients should be constructed in the following way
| (34) |
to ensure unbiasedness. Then, they can be used by SMD to update and . To analyze the optimization error, we need to bound the norm of stochastic gradients in (34). To this end, we have and . Following the arguments of Theorem 1, we can prove that the error , which is even larger than the error of the Baseline.
In the following, we demonstrate that a simple twist of the above procedure can still yield meaningful results that are complementary to the Baseline. We observe that the large norm of the stochastic gradients in (34) is caused by the inverse probability . A natural idea is to ignore , and define the following stochastic gradients:
| (35) |
In this way, they are no longer stochastic gradients of (4), but can be treated as stochastic gradients of a weighted GDRO problem:
| (36) |
where each risk is scaled by a factor . Based on the gradients in (35), we still use (14) and (15) to update and . We summarize the complete procedure in Algorithm 3.
We omit the optimization error of Algorithm 3 for (36), since it has exactly the same form as Theorem 1. What we are really interested in is the theoretical guarantee of its solution on multiple distributions. To this end, we have the following theorem.
Theorem 9
Remark 6
While the value of is generally unknown, it can be regard as a small constant when there exists one model that attains small risks on all distributions. We see that Algorithm 3 exhibits a distribution-dependent convergence behavior: the larger the number of samples , the smaller the target risk , and the faster the convergence rate . Note that its rate is always better than the rate of SMD with (34) as gradients. Furthermore, it converges faster than the Baseline when . In particular, for distribution , Algorithm 3 attains an rate, which almost matches the optimal rate of learning from a single distribution. Finally, we would like to emphasize that a similar idea of introducing “scale factors” has been used by Juditsky et al. (2011, § 4.3.1) for stochastic semidefinite feasibility problems and Agarwal and Zhang (2022) for empirical MRO.
4.2 Stochastic Mirror-Prox Algorithm with Mini-batches
In Algorithm 3, distributions with more samples take their advantage by appearing more frequently in the stochastic gradients. In this section, we propose a different way, which lets them reduce the variance in the elements of stochastic gradients by mini-batches (Roux et al., 2008).
The basic idea is as follows. We run our algorithm for a small number of iterations that is no larger than . Then, in each iteration, we draw a mini-batch of samples from every distribution . For with more samples, we can estimate the associated risk and its gradient more accurately, i.e., with a smaller variance. However, to make this idea work, we need to tackle two obstacles: (i) the performance of the SA algorithm should depend on the variance of gradients instead of the norm, and for this reason SMD is unsuitable; (ii) even some elements of the stochastic gradient have small variances, the entire gradient may still have a large variance. To address the first challenge, we resort to a more advanced SA approach—stochastic mirror-prox algorithm (SMPA), whose convergence rate depends on the variance (Juditsky et al., 2011). To overcome the second challenge, we again introduce scale factors into the optimization problem and the stochastic gradients. And in this way, we can ensure faster convergence rates for distributions with more samples.
In SMPA, we need to maintain two sets of solutions: and . In each round , we first draw samples from every distribution , denoted by , . Then, we use them to construct stochastic gradients at of a weighted GDRO problem (36), where the value of will be determined later. Specifically, we define
| (37) |
Let’s take the stochastic gradient , whose variance will be measured in terms of , as an example to explain the intuition of inserting . Define . With a larger mini-batch size , will approximate more accurately, and thus have a smaller variance. Then, it allows us to insert a larger value of , without affecting the variance of , since is insensitive to perturbations of small elements. Similar to the case in Theorem 9, the convergence rate of depends on , and becomes faster if is larger.
Based on (37), we use SMD to update , and denote the solution by :
| (38) | ||||
| (39) |
Next, we draw another samples from each distribution , denoted by , , to construct stochastic gradients at :
| (40) |
Then, we use them to update again, and denote the result by :
| (41) | ||||
| (42) |
To meet the budget constraints, we repeat the above process for iterations. Finally, we return and as solutions. The complete procedure is summarized in Algorithm 4.
To analysis the performance of Algorithm 4, we further assume the risk function is smooth, and the dual norm satisfies a regularity condition.
Assumption 5
All the risk functions are -smooth, i.e.,
| (43) |
Note that even in the studies of stochastic convex optimization (SCO), smoothness is necessary to obtain a variance-based convergence rate (Lan, 2012).
Assumption 6
The dual norm is -regular for some small constant .
The regularity condition is used when analyzing the effect of mini-batches on stochastic gradients. For a formal definition, please refer to Juditsky and Nemirovski (2008). Assumption 6 is satisfied by most of papular norms considered in the literature, such as the vector -norm and the infinity norm.
Then, we have the following theorem for Algorithm 4.
Theorem 10
Remark 7
Compared with Algorithm 3, Algorithm 4 has two advantages: (i) the budget constraint is satisfied exactly; (ii) we obtain a faster rate for all distributions such that , which is much better than the rate of Algorithm 3, and the rate of the Baseline. For distributions with a larger budget, i.e., , it maintains a fast rate. Since it only updates times, and the best we can expect is the rate of deterministic settings (Nemirovski, 2004). So, there is a performance limit for mini-batch based methods, and after that increasing the batch-size cannot reduce the rate, which consists with the usage of mini-batches in SCO (Cotter et al., 2011; Zhang et al., 2013).
Remark 8
To further improve the convergence rate, we can design a hybrid algorithm that combines non-uniform sampling and mini-batches. Specifically, we run our algorithm for rounds, and for distributions with , we use mini-batches to reduce the variance, and for distributions with , we use random sampling to satisfy the budget constraint.
5 ATkRO for Heterogeneous Distributions
GDRO is effective in dealing with homogeneous distributions, where the risks of all distributions are roughly of the same order. However, its effectiveness diminishes when confronted with heterogeneous distributions. This stems from the sensitivity of the max operator to outlier distributions with significantly high risks, causing it to focus solely on outliers and overlook others (Shalev-Shwartz and Wexler, 2016). To address this issue, research in robust supervised learning has introduced the approach of minimizing the average of the largest individual losses (Fan et al., 2017; Curi et al., 2020). Inspired by these studies, we propose to optimize the average top- risk in (5), which can mitigate the influence of outliers.
5.1 Preliminaries
By replacing in (2) with , we obtain the average top- risk optimization (ATkRO) problem:
| (46) |
which reduces to GDRO when . Before introducing specific optimization algorithms, we present an example to illustrate the difference between GDRO and ATkRO.
Example 1
We define the hypothesis space as and the Bernoulli distribution as , which outputs 1 with probability and 0 with probability . Then, we consider 16 distributions: where is sequentially set to . The loss function is defined as for a random sample drawn from these distributions. We denote the solutions of GDRO and AT5RO by and , respectively. It is easy to show that and , as detailed in Appendix B.


To visualize the results, in Fig. 1 we plot a portion of the risk functions, the objectives of GDRO and AT5RO, as well as their respective solutions. From Fig. 1(a), it is evident that distribution is significantly different from the other 15 distributions, indicating it could be an outlier. Fig. 1(b) demonstrates that GDRO primarily focuses on , yielding the solution . Although its solution performs well on , it underperforms on the other 15 distributions. Note that a slight increase in leads to a noticeable reduction in , with the cost of a minor increase in . AT5RO offers a relatively balanced solution by considering the top- high-risk distributions. Specifically, the average risk of on distributions is 0.168 lower than that of , with a 0.09 increase in the risk on . Therefore, AT5RO effectively mitigates the influence of the outlier distribution , showing superior robustness compared to GDRO.
Similar to the case of GDRO, (46) can be cast as a stochastic convex-concave saddle-point problem:
| (47) |
where
is the capped simplex which can be viewed as the slice of the hyper-cube cut by a hyper-plane . The difference between (4) and (47) lies in the domain of , which is and respectively.
Note that a similar convex-concave optimization problem has been studied by Curi et al. (2020) and Roux et al. (2021). However, their works investigate the deterministic setting, whereas our paper considers a stochastic problem. Consequently, their algorithms are not applicable here, necessitating the design of efficient stochastic approaches for (47). By replacing in (10) with , we obtain the performance measure of an approximate solution to (47), i.e.,
| (48) |
which also controls the optimality of to (46) by replacing with in (11).
5.2 Stochastic Mirror Descent for ATkRO
Following the procedure in Section 3.2, we also use SMD to optimize (47), with the only difference being the update rule for .
Since the objectives of (47) and (4) are identical, the stochastic gradients and in (12) also serve as unbiased estimators of true gradients and , respectively. In the -th round, we reuse (14) to update , and modify the update of as
| (49) |
Because the domain is no longer the simplex , the explicit form in (16) does not apply to (49). In the following lemma, we demonstrate that (49) can be reduced to a neg-entropy Bregman projection problem onto the capped simplex (Si Salem et al., 2023).
Lemma 11
Consider a mirror descent defined as
| (50) |
where and is the Bregman distance defined in terms of the neg-entropy. Then, (50) is equivalent to where .
By Lemma 11, we can leverage existing algorithms for neg-entropy Bregman projections onto the capped simplex to compute
| (51) |
In particular, we choose Algorithm 2 of Si Salem et al. (2023), summarized in Appendix C.1, whose time complexity is .
We present the entire procedure in Algorithm 5, and have the following theorem.
Theorem 12
Remark 9
The above theorem indicates that Algorithm 5 attains an convergence rate. Since it requires samples in each iteration, the sample complexity is .
5.2.1 Anytime Extensions
As discussed in Section 3.2.1, we can adapt Algorithm 5 for anytime use by employing time-varying step sizes. In the -th round, we use step sizes
| (52) |
in (14) and (49)/(51) to update and , respectively. When required, we return and in (20) as outputs.
Similar to Theorem 2, we have the following theoretical guarantee for .
Theorem 13
Remark 10
Similar to previous cases, the convergence rate of the anytime extension is slower by a factor of .
5.3 Non-oblivious Online Learning for ATkRO
Building on the two-player game in Section 3.3, we can leverage online learning techniques to reduce the number of samples used in each round from to .
The 1st player faces the same problem, specifically minimizing the sequence of convex functions in (22) under the constraint . Therefore, it can still be framed as “non-oblivious OCO with stochastic gradients” and solved using SMD. In contrast, the 2nd player tackles a different challenge: maximizing the sequence of linear functions in (23), constrained by rather than . Because the domain is the capped simplex, it is natural to ask the 2nd player to select the highest-risk options from distributions, reflecting the combinatorial nature of the problem. After drawing one sample from each selected distribution, the 2nd player observes stochastic rewards, which fits into a semi-bandit structure. This leads to modeling the 2nd player’s problem as “non-oblivious combinatorial semi-bandits with stochastic rewards”. For the 2nd player, we can certainly apply existing algorithms designed for non-oblivious combinatorial semi-bandits (Audibert et al., 2014; Neu and Bartók, 2016; Vural et al., 2019). Here, to maintain consistency with Algorithm 2, we will extend the Exp3-IX algorithm to address this scenario.
In the following, we elaborate on the details and modifications compared to Algorithm 2. To select distributions from in each round, we require a sampling algorithm that, given the value of and a probability vector , can generate a set such that
| (53) |
For this purpose, we can use the DepRound algorithm (Gandhi et al., 2006), which satisfies the above requirement and has time and space complexities. A detailed description of its procedure is provided in Appendix C.2. We note that DepRound has been used by many combinatorial semi-bandit algorithms (Uchiya et al., 2010; Vural et al., 2019; Roux et al., 2021). In each round , we first invoke the DepRound algorithm with as inputs to generate a set containing the indices of selected distributions. For each , we then draw a sample from the corresponding distribution .
Next, the 1st player constructs the stochastic gradient as shown below:
| (54) |
which can be easily verified, based on (53), as an unbiased estimator of . Then, we update by applying the mirror descent (24) with in (54). For the 2nd player, we modify the IX loss estimator for the combinatorial semi-bandit setting:
| (55) |
and then update by mirror descent
| (56) |
Compared with (25), (55) incorporates two key changes. First, we replace with to utilize all the observed losses . Second, since , the denominator of is adjusted accordingly. By Lemma 11, we can similarly transform (56) into a neg-entropy Bregman projection problem:
| (57) |
which can be solved by Algorithm 2 of Si Salem et al. (2023). The complete procedure is presented in Algorithm 6.
Input: step sizes and , and IX coefficient
For the 1st player, Theorem 3 remains applicable because the only change in the proof of Theorem 3 is that , which does not alter the conclusion. For the 2nd player, we prove the following theorem.
Theorem 14
Theorem 15
Remark 11
5.3.1 Anytime Extensions
Based on the discussion in Section 3.3.1, it is natural to adopt time-varying parameters to make Algorithm 6 anytime. However, during the theoretical analysis, we encountered a technical obstacle. In the original paper of Exp3-IX, there are two concentration results concerning the IX loss estimator (25): one for fixed parameters and the other for time-varying parameters, i.e., Corollary 1 and Lemma 1 of Neu (2015) respectively. In Section 5.3, we successfully extended their Corollary 1 to combinatorial semi-bandits, resulting in Theorem 14. However, we are unable to extend their Lemma 1 to combinatorial semi-bandits,222In combinatorial semi-bandits, there are non-zero in each round . Consequently, we need to handle non-zero in (140), which renders the original analysis invalid, and it remains unclear how to resolve this issue. and therefore cannot provide theoretical guarantees for Algorithm 6 when using time-varying parameters. Additionally, we have not found any algorithms in the literature that utilize time-varying parameters in non-oblivious combinatorial semi-bandits.
To circumvent the aforementioned challenge, we present an anytime algorithm for ATkRO from a different perspective. The key observation is that we are not dealing with a true bandit problem but are instead exploiting bandit techniques to solve (47). During the execution of our algorithm, the 2nd player is not necessarily required to select distinct arms. It is perfectly fine to select just arm, as long as we can bound the regret in terms of the linear functions in (23), subject to the constraint . To this end, we propose to modify the anytime extension of Algorithm 2 described in Section 3.3.1.
In the following, we describe the key steps. Recall the three time-varying parameters , and in (30). In each round, we use SMD in (24) with a time-varying step size to update :
| (58) |
where is defined in (13). Similarly, we use a time-varying parameter to define the IX loss estimator
| (59) |
The only change required is to adjust the domain in the mirror descent (26) to :
| (60) |
which can also be reduced to a neg-entropy Bregman projection problem. If demanded, we will return in (20) as the current solution. We summarize the complete procedure in Algorithm 7.
Following the proof of Theorem 8, we establish the following theoretical guarantee regarding the optimization error.
Theorem 16
6 Analysis
In this section, we present proofs of main theorems, and defer the analysis of supporting lemmas to Appendix A.
6.1 Proof of Theorem 1
The proof is based on Lemma 3.1 and Proposition 3.2 of Nemirovski et al. (2009). To apply them, we show that their preconditions are satisfied under our assumptions.
Although two instances of SMD are invoked to update and separately, they can be merged as instance by concatenating and as a single variable , and redefine the norm and the distance-generating function (Nemirovski et al., 2009, § 3.1). Let be the space that lies in. We equip the Cartesian product with the following norm and dual norm:
| (61) |
We use the notation , and equip the set with the distance-generating function
| (62) |
It is easy to verify that is -strongly convex w.r.t. the norm . Let be the Bregman distance associated with :
| (63) |
where .
Then, we consider the following version of SMD for updating :
| (64) |
where is the step size. In the beginning, we set . From the decomposition of the Bregman distance in (63), we observe that (64) is equivalent to (14) and (15) by setting
Next, we show that the stochastic gradients are well-bounded. Under our assumptions, we have
As a result, the concatenated gradients used in (64) is also bounded in term of the dual norm :
| (65) |
6.2 Proof of Theorem 2
In a manner similar to the proof of Theorem 1 in Section 6.1, we combine the updates for and into a unified expression:
where the step size satisfying
Then, from (3.11) of Nemirovski et al. (2009), we have
| (66) |
where we set , and is defined in (65). Combining (66) with the following inequalities
| (67) |
we obtain
Next, we focus on the high-probability bound. Although Proposition 3.2 of Nemirovski et al. (2009) provides a high-probability bound only for a fixed step size, its proof actually supports time-varying step sizes. By setting in their analysis, we have
| (68) |
for any . Substituting into (68), we have
We complete the proof by setting .
6.3 Proof of Theorem 3
Our goal is to analyze SMD for non-oblivious OCO with stochastic gradients. In the literature, we did not find a convenient reference for it. A very close one is the Lemma 3.2 of Flaxman et al. (2005), which bounds the expected regret of SGD for non-oblivious OCO. But it is insufficient for our purpose, so we provide our proof by following the analysis of SMD for stochastic convex-concave optimization (Nemirovski et al., 2009, § 3). Notice that we cannot use the theoretical guarantee of SMD for SCO (Nemirovski et al., 2009, § 2.3), because the objective function is fixed in SCO.
From the standard analysis of mirror descent, e.g., Lemma 2.1 of Nemirovski et al. (2009), we have
| (69) |
Summing the above inequality over , we have
| (70) |
where the last step is due to (Nemirovski et al., 2009, (2.42))
| (71) |
By Jensen’s inequality, we have
Maximizing each side over , we arrive at
| (72) |
Next, we bound the last term in (72), i.e., . Because , is the sum of a martingale difference sequence for any fixed . However, it is not true for , because depends on the randomness of the algorithm. Thus, we cannot directly apply techniques for martingales to bounding . This is the place where the analysis differs from that of SCO.
To handle the above challenge, we introduce a virtual sequence of variables to decouple the dependency (Nemirovski et al., 2009, proof of Lemma 3.1). Imagine there is an online algorithm which performs SMD by using as the gradient:
| (73) |
where . By repeating the derivation of (70), we can show that
| (74) |
where in the last inequality, we make use of (71) and
| (75) |
Then, we have
| (76) |
From the updating rule of in (73), we know that is independent from , and thus is a martingale difference sequence.
Substituting (76) into (72), we have
| (77) |
Taking expectation over both sides, we have
where we set .
To establish high probability bounds, we make use of the Hoeffding-Azuma inequality for martingales stated below (Cesa-Bianchi and Lugosi, 2006).
Lemma 17
Let be a martingale difference sequence with respect to some sequence such that for some random variable , measurable with respect to and a positive constant . If , then for any ,
6.4 Proof of Theorem 4
Since we can only observe instead of , the theoretical guarantee of Exp3-IX (Neu, 2015) cannot be directly applied to Algorithm 2. To address this challenge, we generalize the regret analysis of Exp3-IX to stochastic rewards.
By the definition of in (4) and the property of linear optimization over the simplex, we have
| (80) |
where and the vector is defined as
| (81) |
To facilitate the analysis, we introduce a vector with
| (82) |
where denotes a random sample drawn from the -th distribution. Note that is only used for analysis, with the purpose of handling the stochastic rewards. In the algorithm, only is observed in the -th iteration.
Following the proof of Theorem 1 of Neu (2015), we have
| (83) |
which makes use of the property of online mirror descent with local norms (Bubeck and Cesa-Bianchi, 2012). From (5) of Neu (2015), we have
| (84) |
Combining (83) and (84), we have
| (85) |
From (80), we have
| (86) |
We proceed to bound the above three terms , and respectively.
To bound term , we need the following concentration result concerning the IX loss estimates (Neu, 2015, Lemma 1), which we further generalize to the setting with stochastic rewards.
Lemma 18
Let for all and , and be its IX-estimator defined as , where , , and the index is sampled from according to the distribution . Let be a fixed non-increasing sequence with and let be non-negative -measurable random variables satisfying for all and . Then, with probability at least ,
| (87) |
Furthermore, when for all , the following holds with probability at least ,
| (88) |
simultaneously for all .
Notice that our construction of in (25) satisfies that and is drawn from according to as well as , which meets the conditions required by Lemma 18. As a result, according to (88), we have
for all (including ) with probability at least .
To bound term , we can directly use Lemma 1 of Neu (2015), because our setting satisfies its requirement. Thus, with probability at least , we have
We now consider term in (86). Let . Then, it is easy to verify that . So, the process forms a martingale difference sequence and it also satisfies for all . Hence, we can apply Lemma 17 and have
with probability at least .
Combining the three upper bounds for the terms , and , and further taking the union bound, we have, with probability at least
where the third line holds because of our parameter settings and .
To obtain the expected regret upper bound based on high probability guarantee, we use the formula as follows (Bubeck and Cesa-Bianchi, 2012, § 3.2).
Lemma 19
For any real-valued random variable ,
6.5 Proof of Theorem 5
By Jensen’s inequality and the outputs and , we have
| (89) |
and thus
| (90) |
6.6 Proof of Theorem 6
The proof of Theorem 6 closely follows that of Theorem 3, with the difference being the use of a time-varying step size .
Similar to (69), by Lemma 2.1 of Nemirovski et al. (2009), we have
| (91) |
Summing (91) over , we have
| (92) |
By Jensen’s inequality, we get
Maximizing both sides over , we obtain
| (93) |
To handle the last term in (93), we also construct a virtual sequence of variable:
| (94) |
where . The difference between (94) and (73) lies in the use of the time-varying step size in (94). By repeating the derivation of (92), we have
| (95) |
6.7 Proof of Theorem 7
We will modify the proof of Theorem 4 to bound the weighted average regret .
By using the property of online mirror descent with local norms (Bubeck and Cesa-Bianchi, 2012, Theorem 5.5; Orabona, 2019, § 6.5 and § 6.6), we have
| (101) |
where the last step follows from the fact that . We rewrite (84) as
| (102) |
where is defined in (82). Then, we have
| (103) |
For term , recall that we set in (30). In Section 6.4, we have verified that our constructions of and satisfy the requirement of Lemma 18. Then, by setting in (87), with probability at least , we have
for each . Taking the union bound, we conclude that with probability at least
| (105) |
For term , we apply Lemma 1 of Neu (2015) with . It is easy to very that , and thus . Then, with probability at least , we have
| (106) |
To bound term , we define a martingale difference sequence , . Then, it can be shown that for all . Applying Lemma 17, with probability at least , we have
| (107) |
6.8 Proof of Theorem 8
According to (30), we can rewrite and with and . Then, we decompose the optimization error in the -th round using the convexity-concavity of :
| (109) |
where and are defined in (31). And thus
| (110) |
We derive (33) by substituting the high probability bounds in Theorems 6 and 7 into (131) and taking the union bound. Moreover, we obtain (32) by substituting the expectation bounds in Theorems 6 and 7 into (110).
6.9 Proof of Theorem 9
6.10 Proof of Theorem 10
We first provide some simple facts that will be used later. From Assumption 3, we immediately know that each risk function also belongs to . As a result, the difference between each risk function and its estimator is well-bounded, i.e., for all ,
| (113) |
From Assumption 4, we can prove that each risk function is -Lipschitz continuous. To see this, we have
| (114) |
As a result, we have
| (115) |
Furthermore, the difference between the gradient of and its estimator is also well-bounded, i.e., for all ,
| (116) |
Recall the definition of the norm and dual norm for the space in (61), and the distance-generating function in (62). Following the arguments in Section 6.1, the two updating rules in (38) and (39) can be merged as
where and . Similarly, (41) and (42) are equivalent to
Let be the monotone operator associated with the weighted GDRO problem in (36), i.e.,
From our constructions of stochastic gradients in (37) and (40), we clearly have
Thus, Algorithm 4 is indeed an instance of SMPA (Juditsky et al., 2011, Algorithm 1), and we can use their Theorem 1 and Corollary 1 to bound the optimization error.
Before applying their results, we show that all the preconditions are satisfied. The parameter defined in (16) of Juditsky et al. (2011) can be upper bounded by
| (117) |
Next, we need to demonstrate that is continuous.
Lemma 20
We proceed to show the variance of the stochastic gradients satisfies the light tail condition. To this end, we introduce the stochastic oracle used in Algorithm 4:
where
and is the -th sample drawn from distribution . The following lemma shows that the variance is indeed sub-Gaussian.
Lemma 21
Based on (117), Lemma 20, and Lemma 21, we can apply the theoretical guarantee of SMPA. Recall that the total number of iterations is in Algorithm 4. From Corollary 1 of Juditsky et al. (2011), by setting
we have
for all . Choosing such that and , we have with probability at least
Following the derivation of (112), we have
| (118) |
6.11 Proof of Theorem 12
The proof of Theorem 12 is almost identical to that of Theorem 1 in Section 6.1, with the only difference being the replacement of the simplex with the capped simplex .
To obtain specific convergence rates, we need to analyze the diameter of measured by the neg-entropy function. First, it is easy to verify that and . Note that is convex in , indicating that the maximum value is attained at the extreme points of , i.e., the vectors in that cannot be expressed as a convex combination of other vectors in (Roux et al., 2021, Section 4). Specifically, such vectors comprise elements equal to and the remaining elements equal to . Thus, . In summary, we have
6.12 Proof of Theorem 13
In anytime extensions, the difference between Algorithm 1 and Algorithm 5 also lies in the domain of . Thus, we can follow the proof of Theorem 2 in Section 6.2, where we only need to replace the simplex with the capped simplex . From Section 6.11, we know that the diameter of is upper bounded by . Therefore, we redefine , which leads to Theorem 13.
6.13 Proof of Theorem 14
Recall the definition of and in (81) and (82) of Section 6.4. Following the analysis of (80), we have
| (121) |
where . From the new construction of the IX loss estimator (55), we have
| (122) |
Similar to the derivation of (83) and (101), we make use the property of online mirror descent with local norms and proceed with the following steps:
| (123) |
where in the first step we make use the fact that the diameter of is upper bounded by . Moreover, (84) becomes
| (124) |
Combining (123) and (124), we have
| (125) |
From (121), we have
| (126) | ||||
Next, we sequentially bound the above three items , , and .
Lemma 22
Let for all and , and be its IX-estimator defined as , where , , , , and is sampled by . Then, with probability at least ,
| (127) |
simultaneously hold for all .
It is easy to verify that the construction of and satisfy the conditions outlined in Lemma 22. Therefore, with probability at least , we have
| (128) |
At the same time, we can also deliver an upper bound for . From (127), we have
implying
| (129) |
As for term , we denote . Since
we know that is a martingale difference sequence. Furthermore, under Assumption 3 and , we have for all . By Lemma 17, with probability at least , we have
| (130) |
6.14 Proof of Theorem 15
6.15 Proof of Theorem 16
Similar to the proof of Theorem 8 in Section 6.8, we decompose the optimization error in the -th round as
| (131) |
where is defined in (31) and
Note that the 1st player is identical to the one in Section 3.3.1, so we can directly use Theorem 6 to bound . For the 2nd player, due to the difference in the domain, we need to reanalyze and have proven the same upper bounds for as in Theorem 7.
Theorem 23
6.16 Proof of Theorem 23
We need to specifically adjust the proof of Theorem 7 in Section 6.7 based on the fact that the domain is the capped simplex .
First, we modify (100) as
| (132) |
where . Based on the property of online mirror descent with local norms and the fact that the diameter of is upper bounded by , (101) becomes
| (133) |
By using (133) in the derivation of (103), we obtain
| (134) |
Note that (105) in Section 6.7 holds for any possible value of . As a result, with probability at least , we have
| (136) |
To bound and , we can directly use the inequalities in (106) and (107). Substituting (136), (106) and (107) into (135), and taking the union bound, with probability at least , we have
| (137) |
Note that the final bound in (137) is exactly the same as that in (108), and therefore we can reach the same conclusion as Theorem 7.
7 Experiments
We present experiments to evaluate the effectiveness of the proposed algorithms.
| Algorithms | Notation | Highlights |
| Alg. 1 of Sagawa et al. (2020) | SMD(1) | SMD with 1 sample per round |
| Alg. 1 | SMD() | SMD with samples per round |
| Anytime extension of Alg. 1 | SMD()a | SMD() with time-varying step sizes |
| Alg. 2 | Online(1) | Online learning method with sample per round |
| Anytime extension of Alg. 2 | Online(1)a | Online(1) with time-varying step sizes |
| Alg. 3 | SMDr | SMD with random sampling |
| Alg. 4 | SMPAm | SMPA with mini-batches |
| Alg. 5 | ATkRO | SMD() for ATkRO |
| Anytime extension of Alg. 5 | ATkRO | SMD() with time-varying step sizes for ATkRO |
| Alg. 6 | ATkRO | Online learning method with samples per round for ATkRO |
| Alg. 7 | ATkRO | Anytime online method with sample per round for ATkRO |



7.1 Data Sets and Experimental Settings
Following the setup in previous work (Namkoong and Duchi, 2016; Soma et al., 2022), we use both synthetic and real-world data sets.
First, we create a synthetic data set with groups, each associated with a true classifier . The set is constructed as follows: we start with an arbitrary vector on the unit sphere; then, we randomly choose points on a sphere of radius centered at ; these points are projected onto the unit sphere to form . For distribution , the sample is generated by sampling from the standard normal distribution and setting with probability , or to its inverse with probability . We set in this data set.
To simulate heterogeneous distributions, we specifically construct another synthetic data set, which contains distributions. The classifiers s are generated in the same way as described above. For a sample , the distribution outputs with probability and with probability . We choose as the outlier distribution and set , while the remaining values are uniformly chosen from the range to . Additionally, we set to ensure that are close, emphasizing that the heterogeneity is primarily due to noise.
We also use the Adult data set (Becker and Kohavi, 1996), which includes attributes such as age, gender, race, and educational background of individuals. The objective is to determine whether an individual’s income exceeds USD or not. We set up groups based on the race and gender attributes, where each group represents a combination of {black, white, others} with {female, male}.
We set to be the logistic loss and utilize different methods to train a linear model. Table 1 lists the notation for the algorithms referenced in this section. When we need to estimate the risk , we draw a substantial number of samples from , and use the empirical average to approximate the expectation.
7.2 GDRO on Balanced Data
For experiments on the first synthetic data set, we will generate the random sample on the fly, according to the protocol in Section 7.1. For those on the Adult data set, we will randomly select samples from each group with replacement. In other words, is defined as the empirical distribution over the data in the -th group.
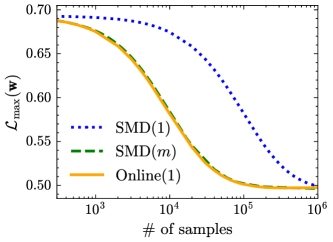
In the experiments, we compare SMD(1) with our algorithms SMD() and Online(). Fig. 3 plots the maximum risk , with respect to the number of iterations. We observe that SMD() is faster than Online(), which in turn outperforms SMD(). This observation is consistent with our theories, since their convergence rates are , , and , respectively. Next, we plot against the number of samples consumed by each algorithm in Fig. 3. As can be seen, the curves of SMD() and Online() are very close, indicating that they share the same sample complexity, i.e., . On the other hand, SMD() needs more samples to reach a target precision, which aligns with its higher sample complexity, i.e., .






7.3 Weighted GDRO on Imbalanced Data
For experiments on the first synthetic data set, we set the sample size for each group as . For those on the Adult data set, we first select samples randomly from each group, reserving them for later use in estimating the risk of each group. Then, we visit the remaining samples in each group once to simulate the imbalanced setting, where the numbers of samples in groups are , , , , , and . In this way, corresponds to the (unknown) underlying distribution from which the samples in the -th group are drawn.




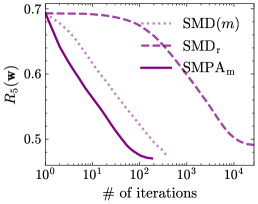

On imbalanced data, we will compare SMDr and SMPAm with the baseline SMD(), and examine how the risk on each individual distribution decreases with respect to the number of iterations. Recall that the total number of iterations of SMDr, SMPAm and SMD() are , and , respectively. We present the experimental results on the synthetic and the Adult data sets in Fig. 4 and Fig. 5, respectively. First, we observe that our SMPAm is faster than both SMDr and SMD() across all distributions, and finally attains the lowest risk in most cases. This behavior aligns with our Theorem 10, which reveals that SMPAm achieves a nearly optimal rate of for all distributions , after iterations. We also note that on distribution , the distribution with the most samples, although SMDr converges slowly, its final risk is the lowest, as illustrated in Fig. 4(a) and Fig. 5(a). This phenomenon is again in accordance with our Theorem 9, which shows that the risk of SMDr on reduces at a nearly optimal rate, after iterations. From Fig. 4(f) and Fig. 5(f), we can see that the final risk of SMD() on the last distribution matches that of SMPAm. This outcome is anticipated, as they exhibit similar convergence rates of and , respectively.







7.4 ATkRO on Heterogeneous Distributions
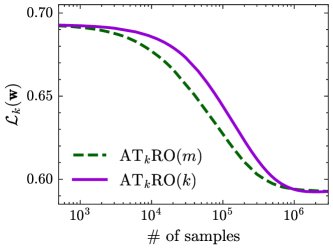
For experiments on heterogeneous distributions, we use the second synthetic data set described in Section 7.1. We first compare our two algorithms ATkRO() and ATkRO(), where , and plot the changes of the average top- risk in Fig. 7. From Theorems 12 and 15, we know that their convergence rates are and , respectively, and their sample complexities are and , respectively. Fig. 6(a) indicates that ATkRO() indeed converges faster than ATkRO(), and Fig. 6(b) shows that ATkRO() requires slightly fewer samples than ATkRO().
Additionally, to demonstrate the advantages of ATkRO, we examine the performance of directly applying the SMD() algorithm, which is designed for GDRO, to the synthetic data set. Fig. 7 presents the changes in risk across a subset of distributions for SMD(), ATkRO(), and ATkRO(). We observe that SMD() concentrates entirely on and achieves the lowest final risk on the outlier distribution , approximately lower than ATkRO() and lower than ATkRO(). However, for the remaining distributions , the risk of SMD() is approximately higher on average than those of the other two algorithms. Therefore, we conclude that ATkRO can mitigate the impact of the outlier distribution and deliver a more balanced model in heterogeneous distributions compared to GDRO.
7.5 Anytime Capability
To demonstrate the benefits of the anytime capability, we compare SMD() and Online(1) with their anytime extensions SMD()a and Online(1)a on the Adult data set under balanced settings, and ATkRO() and ATkRO with ATkRO and ATkRO on the second synthetic data set, where .
We assign a preset value of for SMD() and Online(1), and for ATkRO() and ATkRO(). When the actual number of iterations exceeds the preset number , we continue running the four algorithms with the initial parameters. As illustrated in Fig. 8, non-anytime algorithms initially reduce the objective (the maximum risk or the average top- risk) more rapidly than anytime algorithms before reaching the predetermined , where they achieve minimal values. However, as the number of iterations increases, their curves plateau or even increase due to sub-optimal parameters. In contrast, the anytime extensions, with time-varying step sizes, consistently reduce their targets over time, eventually falling below the risk attained by the corresponding non-anytime algorithms.




8 Conclusion
For the GDRO problem, we develop two SA approaches based on SMD and non-oblivious MAB, which consume and sample per round, respectively, and both achieve a nearly optimal sample complexity of . Then, we consider two special scenarios: imbalanced data and heterogeneous distributions. In the first scenario, we formulate a weighted GDRO problem and propose two methods by incorporating non-uniform sampling into SMD and using mini-batches with SMPA, respectively. These methods yield distribution-dependent convergence rates, and in particular, the latter one attains nearly optimal rates for multiple distributions simultaneously. In the second scenario, we formulate an ATkRO problem and propose two algorithms: one using SMD with samples per round, obtaining an sample complexity, and the other combining SMD with non-oblivious combinatorial semi-bandits, using samples per round and achieving an sample complexity. For both GDRO and ATkRO, we have also developed SA algorithms with anytime capabilities.
Appendix A Supporting Lemmas
A.1 Proof of Lemma 11
We first define as
| (138) |
Then, we have
Recall that is defined in terms of the neg-entropy, i.e., , we have . Therefore, the -th component of can be computed as
A.2 Proof of Lemma 18
The proof follows the argument of Neu (2015, Proof of Lemma 1), and we generalize it to the setting with stochastic rewards. First, observe that for any and ,
| () | ||||
| (139) |
where the last step is due to the inequality for and we introduce the notations and to simplify the presentation.
Define the notation and . Then, we have
| ( by assumption) | ||||
| (140) |
where the second inequality is by the inequality that holds for all and , the equality follows from the fact that holds whenever , and the last line is due to and the inequality for all .
As a result, from (140) we conclude that the process is a supermartingale. Indeed, . Thus, we have . By Markov’s inequality,
holds for any . By setting and solving the value, we complete the proof for (87). And the inequality (88) for the scenario can be immediately obtained by setting and taking the union bound over all .
A.3 Proof of Lemma 20
From the definition of norms in (61), we have
A.4 Proof of Lemma 21
The light tail condition, required by Juditsky et al. (2011), is essentially the sub-Gaussian condition. To this end, we introduce the following sub-gaussian properties (Vershynin, 2018, Proposition 2.5.2).
Proposition 1 (Sub-gaussian properties)
Let be a random variable. Then the following properties are equivalent; the parameters appearing in these properties differ from each other by at most an absolute constant factor.
-
(i)
The tails of satisfy
-
(ii)
The moments of satisfy
-
(iii)
The moment generating function (MGF) of satisfies
-
(iv)
The MGF of is bounded at some point, namely
From the above proposition, we observe that the exact value of those constant is not important, and it is very tedious to calculate them. So, in the following, we only focus on the order of those constants. To simplify presentations, we use to denote an absolute constant that is independent of all the essential parameters, and its value may change from line to line.
Since
we proceed to analyze the behavior of and . To this end, we have the following lemma.
Lemma 24
A.5 Proof of Lemma 22
The proof is built upon that of Corollary 1 of Neu (2015). Let and . First, we have
| (142) |
where the first inequality follows from and last inequality from the elementary inequality that holds for all . Second, from the property of DepRound, we have
| (143) |
Then, we have
Then, by repeating the subsequent analysis from Corollary 1 of Neu (2015), we can derive this lemma.
A.6 Proof of Lemma 24
To analyze , we first consider the approximation error caused by samples from :
Under the regularity condition of in Assumption 6, we have, for any ,
| (144) |
which is a directly consequence of the concentration inequality of vector norms (Juditsky and Nemirovski, 2008, Theorem 2.1.(iii)) and (116). Then, we introduce the following lemma to simplify (144).
Lemma 25
Suppose we have
where is nonnegative. Then, we have
From (144) and Lemma 25, we have
which satisfies the Proposition 1.(i). From the equivalence between Proposition 1.(i) and Proposition 1.(iv), we have
Inserting the scaling factor , we have
| (145) |
To simplify the notation, we define
By Jensen’s inequality, we have
where we use the fact that , and are convex, and the last two functions are increasing in .
To analyze , we consider the approximation error related to :
Note that the absolute value is -regular (Juditsky and Nemirovski, 2008). Following (113) and the derivation of (145), we have
| (146) |
To prove that is also sub-Gaussian, we need to analyze the effect of the infinity norm. To this end, we develop the following lemma.
Lemma 26
Suppose
| (147) |
Then,
where is an absolute constant, and .
A.7 Proof of Lemma 25
When , we have
When , we have
where we use the fact . Thus, we always have
A.8 Proof of Lemma 26
Appendix B Details of Example 1
According to our constructions, the -th risk function is given by
We first derive the objective of GDRO, i.e., in (2). When , with corresponding , and when , with corresponding . Then, it can be easily verified from Fig. 1(b) that .
Then, we analyze the objective of AT5RO, i.e., in (5). Denote . We discuss the following two situations:
-
1.
When , we have , and . In this case, attains the minimum objective ;
-
2.
When , we have , and . In this case, attains the minimum objective .
In summary, .
Appendix C Supporting Algorithms
C.1 Projection onto the Capped Simplex
Input: size , and non-negative vector
C.2 Sampling Rule: DepRound
The original DepRound algorithm (Gandhi et al., 2006) takes an input vector that satisfies and . Here, we modify it to require .
Input: size , and probability vector
References
- Agarwal and Zhang (2022) Alekh Agarwal and Tong Zhang. Minimax regret optimization for robust machine learning under distribution shift. In Proceedings of 35th Conference on Learning Theory, pages 2704–2729, 2022.
- Amodei et al. (2016) Dario Amodei, Sundaram Ananthanarayanan, Rishita Anubhai, and et al. Deep speech 2 : End-to-end speech recognition in english and mandarin. In Proceedings of the 33rd International Conference on Machine Learning, pages 173–182, 2016.
- Audibert and Bubeck (2010) Jean-Yves Audibert and Sébastien Bubeck. Regret bounds and minimax policies under partial monitoring. Journal of Machine Learning Research, 11:2785–2836, 2010.
- Audibert et al. (2014) Jean-Yves Audibert, Sébastien Bubeck, and Gábor Lugosi. Regret in online combinatorial optimization. Mathematics of Operations Research, 39(1):31–45, 2014.
- Auer et al. (2002) Peter Auer, Nicolò Cesa-Bianchi, Yoav Freund, and Robert E. Schapire. The nonstochastic multiarmed bandit problem. SIAM Journal on Computing, 32(1):48–77, 2002.
- Becker and Kohavi (1996) Barry Becker and Ronny Kohavi. Adult. UCI Machine Learning Repository, 1996. DOI: https://doi.org/10.24432/C5XW20.
- Ben-Tal et al. (2009) Aharon Ben-Tal, Laurent El Ghaoui, and Arkadi Nemirovski. Robust Optimization. Princeton University Press, 2009.
- Ben-Tal et al. (2013) Aharon Ben-Tal, Dick den Hertog, Anja De Waegenaere, Bertrand Melenberg, and Gijs Rennen. Robust solutions of optimization problems affected by uncertain probabilities. Management Science, 59(2):341–357, 2013.
- Ben-Tal et al. (2015) Aharon Ben-Tal, Elad Hazan, Tomer Koren, and Shie Mannor. Oracle-based robust optimization via online learning. Operations Research, 63(3):628–638, 2015.
- Bertsimas et al. (2018) Dimitris Bertsimas, Vishal Gupta, and Nathan Kallus. Robust sample average approximation. Mathematical Programming, 171:217–282, 2018.
- Blum et al. (2017) Avrim Blum, Nika Haghtalab, Ariel D. Procaccia, and Mingda Qiao. Collaborative PAC learning. In Advances in Neural Information Processing Systems 30, pages 2389–2398, 2017.
- Bubeck and Cesa-Bianchi (2012) Sébastien Bubeck and Nicolò Cesa-Bianchi. Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Foundations and Trends in Machine Learning, 5(1):1–122, 2012.
- Carmon and Hausler (2022) Yair Carmon and Danielle Hausler. Distributionally robust optimization via ball oracle acceleration. In Advances in Neural Information Processing Systems 35, pages 35866–35879, 2022.
- Cesa-Bianchi and Lugosi (2006) Nicolò Cesa-Bianchi and Gábor Lugosi. Prediction, Learning, and Games. Cambridge University Press, 2006.
- Cotter et al. (2011) Andrew Cotter, Ohad Shamir, Nati Srebro, and Karthik Sridharan. Better mini-batch algorithms via accelerated gradient methods. In Advances in Neural Information Processing Systems 24, pages 1647–1655, 2011.
- Curi et al. (2020) Sebastian Curi, Kfir Y. Levy, Stefanie Jegelka, and Andreas Krause. Adaptive sampling for stochastic risk-averse learning. In Advances in Neural Information Processing Systems 33, pages 1036–1047, 2020.
- Cutkosky (2019) Ashok Cutkosky. Anytime online-to-batch, optimism and acceleration. In Proceedings of the 36th International Conference on Machine Learning, pages 1446–1454, 2019.
- Delage and Ye (2010) Erick Delage and Yinyu Ye. Distributionally robust optimization under moment uncertainty with application to data-driven problems. Operations Research, 58(3):595–612, 2010.
- Duchi and Namkoong (2021) John C. Duchi and Hongseok Namkoong. Learning models with uniform performance via distributionally robust optimization. The Annals of Statistics, 49(3):1378–1406, 2021.
- Duchi et al. (2021) John C. Duchi, Peter W. Glynn, and Hongseok Namkoong. Statistics of robust optimization: A generalized empirical likelihood approach. Mathematics of Operations Research, 46(3):946–969, 2021.
- Esfahani and Kuhn (2018) Peyman Mohajerin Esfahani and Daniel Kuhn. Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Mathematical Programming, 171:115–166, 2018.
- Fan et al. (2017) Yanbo Fan, Siwei Lyu, Yiming Ying, and Baogang Hu. Learning with average top-k loss. In Advances in Neural Information Processing Systems 30, pages 497–505, 2017.
- Flaxman et al. (2005) Abraham D. Flaxman, Adam Tauman Kalai, and H. Brendan McMahan. Online convex optimization in the bandit setting: Gradient descent without a gradient. In Proceedings of the 16th Annual ACM-SIAM Symposium on Discrete Algorithms, pages 385–394, 2005.
- Freund and Schapire (1997) Yoav Freund and Robert E Schapire. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences, 55(1):119–139, 1997.
- Freund and Schapire (1999) Yoav Freund and Robert E. Schapire. Adaptive game playing using multiplicative weights. Games and Economic Behavior, 29(1):79–103, 1999.
- Gandhi et al. (2006) Rajiv Gandhi, Samir Khuller, Srinivasan Parthasarathy, and Aravind Srinivasan. Dependent rounding and its applications to approximation algorithms. Journal of the ACM, 53(3):324–360, 2006.
- Haghtalab et al. (2022) Nika Haghtalab, Michael I. Jordan, and Eric Zhao. On-demand sampling: Learning optimally from multiple distributions. In Advances in Neural Information Processing Systems 35, pages 406–419, 2022.
- Haghtalab et al. (2023) Nika Haghtalab, Michael I. Jordan, and Eric Zhao. On-demand sampling: Learning optimally from multiple distributions. ArXiv e-prints, arXiv:2210.12529v2, 2023.
- Hashimoto et al. (2018) Tatsunori Hashimoto, Megha Srivastava, Hongseok Namkoong, and Percy Liang. Fairness without demographics in repeated loss minimization. In Proceedings of the 35th International Conference on Machine Learning, pages 1929–1938, 2018.
- Horsch and Poole (1998) Michael C. Horsch and David Poole. An anytime algorithm for decision making under uncertainty. In Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence, pages 246–255, 1998.
- Hu et al. (2018) Weihua Hu, Gang Niu, Issei Sato, and Masashi Sugiyama. Does distributionally robust supervised learning give robust classifiers? In Proceedings of the 35th International Conference on Machine Learning, pages 2029–2037, 2018.
- Jin et al. (2021) Jikai Jin, Bohang Zhang, Haiyang Wang, and Liwei Wang. Non-convex distributionally robust optimization: Non-asymptotic analysis. In Advances in Neural Information Processing Systems 34, pages 2771–2782, 2021.
- Juditsky et al. (2011) Anatoli Juditsky, Arkadi Nemirovski, and Claire Tauvel. Solving variational inequalities with stochastic mirror-prox algorithm. Stochastic Systems, 1(1):17–58, 2011.
- Juditsky and Nemirovski (2008) Anatoli B. Juditsky and Arkadi S. Nemirovski. Large deviations of vector-valued martingales in 2-smooth normed spaces. ArXiv e-prints, arXiv:0809.0813, 2008.
- Kocák et al. (2014) Tomás Kocák, Gergely Neu, Michal Valko, and Rémi Munos. Efficient learning by implicit exploration in bandit problems with side observations. In Advances in Neural Information Processing Systems 27, pages 613–621, 2014.
- Kuhn et al. (2019) Daniel Kuhn, Peyman Mohajerin Esfahani, Viet Anh Nguyen, and Soroosh Shafieezadeh-Abadeh. Wasserstein distributionally robust optimization: Theory and applications in machine learning. Operations Research Management Science in the Age of Analytics, pages 130–166, 2019.
- Kushner and Yin (2003) Harold J. Kushner and G. George Yin. Stochastic Approximation and Recursive Algorithms and Applications. Springer, second edition, 2003.
- Lan (2012) Guanghui Lan. An optimal method for stochastic composite optimization. Mathematical Programming, 133:365–397, 2012.
- Lattimore and Szepesvári (2020) Tor Lattimore and Csaba Szepesvári. Bandit Algorithms. Cambridge University Press, 2020.
- Levy et al. (2020) Daniel Levy, Yair Carmon, John C. Duchi, and Aaron Sidford. Large-scale methods for distributionally robust optimization. In Advances in Neural Information Processing Systems 33, pages 8847–8860, 2020.
- Li et al. (2019) Liping Li, Wei Xu, Tianyi Chen, Georgios B. Giannakis, and Qing Ling. RSA: Byzantine-robust stochastic aggregation methods for distributed learning from heterogeneous datasets. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence, pages 1544–1551, 2019.
- Mohri et al. (2019) Mehryar Mohri, Gary Sivek, and Ananda Theertha Suresh. Agnostic federated learning. In Proceedings of the 36th International Conference on Machine Learning, pages 4615–4625, 2019.
- Namkoong and Duchi (2016) Hongseok Namkoong and John C. Duchi. Stochastic gradient methods for distributionally robust optimization with -divergences. In Advances in Neural Information Processing Systems 29, pages 2216–2224, 2016.
- Namkoong and Duchi (2017) Hongseok Namkoong and John C. Duchi. Variance-based regularization with convex objectives. In Advances in Neural Information Processing Systems 30, pages 2971–2980, 2017.
- Nemirovski et al. (2009) A. Nemirovski, A. Juditsky, G. Lan, and A. Shapiro. Robust stochastic approximation approach to stochastic programming. SIAM Journal on Optimization, 19(4):1574–1609, 2009.
- Nemirovski (2004) Arkadi Nemirovski. Prox-method with rate of convergence for variational inequalities with lipschitz continuous monotone operators and smooth convex-concave saddle point problems. SIAM Journal on Optimization, 15(1):229–251, 2004.
- Neu (2015) Gergely Neu. Explore no more: Improved high-probability regret bounds for non-stochastic bandits. In Advances in Neural Information Processing Systems 28, pages 3168–3176, 2015.
- Neu and Bartók (2016) Gergely Neu and Gábor Bartók. Importance weighting without importance weights: An efficient algorithm for combinatorial semi-bandits. Journal of Machine Learning Research, 17(154):1–21, 2016.
- Nguyen and Zakynthinou (2018) Huy Lê Nguyen and Lydia Zakynthinou. Improved algorithms for collaborative PAC learning. In Advances in Neural Information Processing Systems 31, pages 7642–7650, 2018.
- Orabona (2019) Francesco Orabona. A modern introduction to online learning. ArXiv e-prints, arXiv:1912.13213v6, 2019.
- Oren et al. (2019) Yonatan Oren, Shiori Sagawa, Tatsunori B. Hashimoto, and Percy Liang. Distributionally robust language modeling. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, pages 4227–4237, 2019.
- Qi et al. (2021) Qi Qi, Zhishuai Guo, Yi Xu, Rong Jin, and Tianbao Yang. An online method for a class of distributionally robust optimization with non-convex objectives. In Advances in Neural Information Processing Systems 34, pages 10067–10080, 2021.
- Radivojac et al. (2004) Predrag Radivojac, Nitesh V. Chawla, A. Keith Dunker, and Zoran Obradovic. Classification and knowledge discovery in protein databases. Journal of Biomedical Informatics, 37(4):224–239, 2004.
- Rafique et al. (2022) Hassan Rafique, Mingrui Liu, Qihang Lin, and Tianbao Yang. Weakly-convex-concave min-max optimization: Provable algorithms and applications in machine learning. Optimization Methods and Software, 37(3):1087–1121, 2022.
- Rakhlin and Sridharan (2013) Sasha Rakhlin and Karthik Sridharan. Optimization, learning, and games with predictable sequences. In Advances in Neural Information Processing Systems 26, pages 3066–3074, 2013.
- Rothblum and Yona (2021) Guy N. Rothblum and Gal Yona. Multi-group agnostic PAC learnability. In Proceedings of the 38th International Conference on Machine Learning, pages 9107–9115, 2021.
- Roux et al. (2021) Christophe Roux, Elias Wirth, Sebastian Pokutta, and Thomas Kerdreux. Efficient online-bandit strategies for minimax learning problems. ArXiv e-prints, arXiv:2105.13939, 2021.
- Roux et al. (2008) Nicolas Le Roux, Pierre-Antoine Manzagol, and Yoshua Bengio. Topmoumoute online natural gradient algorithm. In Advances in Neural Information Processing Systems 20, pages 849–856, 2008.
- Sagawa et al. (2020) Shiori Sagawa, Pang Wei Koh, Tatsunori B. Hashimoto, and Percy Liang. Distributionally robust neural networks for group shifts: On the importance of regularization for worst-case generalization. In International Conference on Learning Representations, 2020.
- Samuel and Chechik (2021) Dvir Samuel and Gal Chechik. Distributional robustness loss for long-tail learning. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, pages 9475–9484, 2021.
- Scarf (1958) Herbert Scarf. A min-max solution of an inventory problem. Studies in the Mathematical Theory of Inventory and Production, pages 201–209, 1958.
- Shalev-Shwartz and Wexler (2016) Shai Shalev-Shwartz and Yonatan Wexler. Minimizing the maximal loss: How and why. In Proceedings of the 33rd International Conference on Machine Learning, pages 793–801, 2016.
- Shapiro (2017) Alexander Shapiro. Distributionally robust stochastic programming. SIAM Journal on Optimization, 27(4):2258–2275, 2017.
- Si Salem et al. (2023) Tareq Si Salem, Giovanni Neglia, and Stratis Ioannidis. No-regret caching via online mirror descent. ACM Transactions on Modeling and Performance Evaluation of Computing Systems, 8(4), 2023.
- Sinha et al. (2018) Aman Sinha, Hongseok Namkoong, and John Duchi. Certifying some distributional robustness with principled adversarial training. In International Conference on Learning Representations, 2018.
- Słowik and Bottou (2022) Agnieszka Słowik and Léon Bottou. On distributionally robust optimization and data rebalancing. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, pages 1283–1297, 2022.
- Soma et al. (2022) Tasuku Soma, Khashayar Gatmiry, and Stefanie Jegelka. Optimal algorithms for group distributionally robust optimization and beyond. ArXiv e-prints, arXiv:2212.13669, 2022.
- Syrgkanis et al. (2015) Vasilis Syrgkanis, Alekh Agarwal, Haipeng Luo, and Robert E. Schapire. Fast convergence of regularized learning in games. In Advances in Neural Information Processing Systems 28, pages 2989–2997, 2015.
- Uchiya et al. (2010) Taishi Uchiya, Atsuyoshi Nakamura, and Mineichi Kudo. Algorithms for adversarial bandit problems with multiple plays. In Algorithmic Learning Theory, pages 375–389, 2010.
- Vapnik (2000) Vladimir N. Vapnik. The Nature of Statistical Learning Theory. Springer, second edition, 2000.
- Vershynin (2018) Roman Vershynin. High-Dimensional Probability: An Introduction with Applications in Data Science. Cambridge University Press, 2018.
- Vural et al. (2019) Nuri Mert Vural, Hakan Gokcesu, Kaan Gokcesu, and Suleyman S. Kozat. Minimax optimal algorithms for adversarial bandit problem with multiple plays. IEEE Transactions on Signal Processing, 67(16):4383–4398, 2019.
- Wang et al. (2021) Jie Wang, Rui Gao, and Yao Xie. Sinkhorn distributionally robust optimization. ArXiv e-prints, arXiv:2109.11926, 2021.
- Xu et al. (2020) Ziyu Xu, Chen Dan, Justin Khim, and Pradeep Ravikumar. Class-weighted classification: Trade-offs and robust approaches. In Proceedings of the 37th International Conference on Machine Learning, pages 10544–10554, 2020.
- Zhang et al. (2021) Jingzhao Zhang, Aditya Krishna Menon, Andreas Veit, Srinadh Bhojanapalli, Sanjiv Kumar, and Suvrit Sra. Coping with label shift via distributionally robust optimisation. In International Conference on Learning Representations, 2021.
- Zhang et al. (2013) Lijun Zhang, Tianbao Yang, Rong Jin, and Xiaofei He. projections for stochastic optimization of smooth and strongly convex functions. In Proceedings of the 30th International Conference on Machine Learning, pages 1121–1129, 2013.
- Zhang et al. (2023) Lijun Zhang, Peng Zhao, Zhenhua Zhuang, Tianbao Yang, and Zhi-Hua Zhou. Stochastic approximation approaches to group distributionally robust optimization. In Advances in Neural Information Processing Systems 37, pages 52490–52522, 2023.
- Zhang et al. (2024) Lijun Zhang, Haomin Bai, Wei-Wei Tu, Ping Yang, and Yao Hu. Efficient stochastic approximation of minimax excess risk optimization. In Proceedings of the 41st International Conference on Machine Learning, pages 58599–58630, 2024.
- Zhou (2024) Zhi-Hua Zhou. Learnability with time-sharing computational resource concerns. National Science Review, nwae204, 2024.
- Zilberstein (1996) Shlomo Zilberstein. Using anytime algorithms in intelligent systems. AI Magazine, 17(3):73–83, 1996.