Stellar Population Synthesis with Distinct Kinematics: Multi-Age Asymmetric Drift in SDSS-IV MaNGA Galaxies
Abstract
We present the first asymmetric drift (AD) measurements for unresolved stellar populations of different characteristic ages above and below 1.5 Gyr. These measurements sample the age-velocity relation (AVR) in galaxy disks. In this first paper we develop two efficient algorithms to extract AD on a spaxel-by-spaxel basis from optical integral-field spectroscopic (IFS) data-cubes. The algorithms apply different spectral templates, one using simple stellar populations and the other a stellar library; their comparison allows us to assess systematic errors in derived multi-component velocities, such as template-mismatch. We test algorithm reliability using mock spectra and Monte Carlo Markov Chains on real data from the MaNGA survey in SDSS-IV. We quantify random and systematic errors in AD as a function of signal-to-noise and stellar population properties with the aim of applying this technique to large subsets of the MaNGA galaxy sample. As a demonstration of our methods, we apply them to an initial sample of seven galaxies with comparable stellar mass and color to the Milky Way. We find a wide range of distinct AD radial profiles for young and old stellar populations.
Subject headings:
galaxies: spiral – galaxies: stellar content – galaxies: kinematicsI. Introduction
It has long been known that there exists a correlation between stellar population age and their vertical scale height in the Milky Way (MW) solar neighborhood (Strömberg, 1925; Wielen, 1977). The dynamical linkage between scale-height to velocity dispersion and tangential speed has led to this correlation being referred to as the age–velocity or age–velocity-dispersion relation (AVR). This relationship has been studied exhaustively in the Milky Way’s Solar neighborhood, but it still remains unclear whether disk populations form a discrete or continuous dynamical and chemical distribution (Nordström et al., 2004; Holmberg et al., 2007; Seabroke & Gilmore, 2007; Aumer & Binney, 2009). AVR measurements are critical for understanding disk evolution because AVR modulates in response to chemo-dynamical processes. AVR measurements are essential for accurate dynamical estimates of stellar disk mass because AVR encapsulates vertical population gradients.
AVR’s have been detected in M31 (Collins et al., 2011; Dorman et al., 2015; Quirk et al., 2019), M33 (Beasley et al., 2015), several other Local Group (LG) dwarf galaxies (compiled by Leaman et al., 2017), and inferred indirectly via photometric means in a handful of nearby, low-mass edge-on galaxies (Seth et al., 2005). Despite a consistent general trend – older disk stellar populations are dynamically hotter than their younger cohort – the slope and normalization of AVR in other galaxies is found to be significantly different from that seen in the Milky Way. No consensus has been reached regarding the shape (or amplitude) of the relationship and its dependence on other galaxies properties.
The origin of the AVR remains uncertain. Three processes have been suggested. One invokes scattering with giant molecular clouds, spiral arms or bars within galaxies (Spitzer & Schwarzschild, 1951, 1953; Kokubo & Ida, 1992; Carlberg et al., 1985), or by minor mergers (Toth & Ostriker, 1992; Walker et al., 1996; Huang & Carlberg, 1997; Benson et al., 2004; House et al., 2011; Helmi et al., 2012; Few et al., 2012; Ruiz-Lara et al., 2016). A second suggests accretion of dynamically hot debris from mergers of old and metal poor satellites (Abadi et al., 2003; Pinna et al., 2019), raising the possibility for discrete chemical enrichment patterns between thin and thick disks. A third suggests older stellar populations formed in a thicker, more turbulent star-forming gas layer, i.e., older populations were dynamically hotter ab initio (Brook et al., 2004; Bournaud et al., 2009; Forbes et al., 2012). The observed velocity dispersions of ionized gas in star-forming galaxy disks at higher redshift (Weiner et al., 2006; Law et al., 2007; Förster Schreiber et al., 2009; Wisnioski et al., 2015) make this a compelling if perhaps incomplete scenario. Simulations suggest several mechanisms can be at play even in individual galaxies (e.g., Bird et al., 2013; Martig et al., 2014), while Leaman et al. (2017) suggest the interplay between heating mechanisms correlates with galaxy mass, based on eight LG galaxies, only two of which have stellar masses above 10.
The aim of this paper is to develop reliable methods toward measuring AVR in the galaxy population at large, as observed by the MaNGA survey (Bundy et al., 2015). This work can potentially be extended to other surveys such as SAMI (Croom et al., 2012) or CALIFA (Sánchez et al., 2012). However, these surveys resolve physical scales of 1 kpc and 70 (stellar ), and do not typically achieve signal-to-noise ratios (S/N) ample to recover scales below the instrumental resolution (e.g., Toloba et al., 2011; Ryś et al., 2013). For reference, MW vertical velocity dispersions for the older disk at the solar radius are 30 to 50 while the younger counterpart has vertical velocity dispersions of 10 to 20 . Hence, the boundary conditions for such a method are that it cannot depend on resolved stellar populations (available for only LG and very nearby galaxies), nor can it depend on stellar velocity dispersions.
A compelling solution is found in the asymmetric drift (AD) that relates in-plane stellar velocity dispersion components to the lag of the stellar tangential speed from the circular speed of the potential. The latter is well-estimated from ionized or neutral gas velocities when these gas-phase components are observed to have very small velocity dispersions. In early-type disk systems where sometimes small corrections for pressure support are needed to bring ionized-gas tangential speeds in line with circular speeds (e.g., Davis et al., 2013), such corrections can be estimated from gas density gradients without recourse to velocity dispersion information (Dalcanton & Stilp, 2010). Stellar and gas velocity centroids are robust kinematic measures far below the instrumental resolution, and the former are relatively immune (compared to higher-order moments) to systematics from template mismatch. Hence this paper develops methods to measure multi-component asymmetric drift as a function of population age to determine AVR.
Using asymmetric drift is not without its challenges in disentangling multiple kinematic components from spectra of integrated star-light. Previous work attempting to disentangle kinematic components have focused mainly on counter-rotating disks (e.g., Coccato et al., 2011; Johnston et al., 2013) or early-type galaxies (e.g., De Bruyne et al., 2004; Tabor et al., 2017; Poci et al., 2019), although these studies have availed themselves of higher-order moments. The work of Poci et al. (2019) combines detailed Schwarzchild dynamical modeling and stellar population synthesis to correlate the relative weights of stellar orbits and single stellar populations, thus generating a decomposed model for the galaxy structure. This technique provides a powerful approach to investigate the underlying structures in galaxies, but is sensitive to the reliable identification and modeling of all structures in a galaxy and hence may not be ideal for scaling to large galaxy samples. The work of Tabor et al. (2017) is of particular relevance because of its use of disk-bulge decompositions as further constraints and its application intended for MaNGA. In contrast to this work we use an age constraint instead, and limit ourselves to a metric which depends on velocity only.
This paper uses optical IFS of nearby galaxies from the MaNGA survey (Bundy et al., 2015; Yan et al., 2016a) in SDSS-IV (Blanton et al., 2017). MaNGA uses fiber integral-field units (Drory et al., 2015) with the BOSS spectrographs (Smee et al., 2013) on the Sloan 2.5m telescope (Gunn et al., 2006). The MaNGA observing strategy, target selection, spectrophotometric calibration and data reduction pipeline are described in Law et al. (2015), Wake et al. (2017), Yan et al. (2016b), and Law et al. (2016), respectively. Salient features of the spectroscopic data are given in relevant sections below. We take advantage of existing gas and stellar kinematic measurements from the Data Analysis Pipeline (Westfall et al. submitted) to select targets and define geometries.
After defining our data sets and basic fitting methods in Section II, we demonstrate that a differential asymmetric-drift signal between young and old stellar populations can be measured in MaNGA spectra (Section III). This initial demonstration uses simple stellar populations (SSPs) from stellar population synthesis models in a Markov-Chain Monte Carlo (MCMC) implementation of the penalized pixel fitting code (pPXF) code of Cappellari (2017). This implementation is computationally inefficient and, at low signal-to-noise, sensitive to degeneracies in stellar population fitting. For these reasons, in the next three sections we motivate and develop two efficient and robust algorithms, also based on pPXF, that do not depend on MCMC. These algorithms avoid stellar population fitting degeneracies via a combination of a local minimizer and priors. One of these algorithms employs SSPs, while the other employs an empirical stellar library; they have comparable performance, and together they provide a means to estimate systematics due to template mismatch.
Readers interested only in the performance and results of these two final algorithms may skip to Section VII. In this Section we derive estimates of random and systematic errors for our algorithms, and present our asymmetric drift measurements for seven MaNGA galaxies with near-MW mass in this context. Section VIII summarizes our findings and conclusions.
Reader interested in the algorithm development will find the presentation in the intervening sections: In Section IV we define the metrics used to determine algorithm performance. We then construct an efficient SSP-based algorithm using pPXF that robustly measures the differential asymmetric-drift signal between young and old stellar populations. This algorithm is successful in avoiding local minima in the likelihood space, while also avoiding global degeneracies in population-synthesis fitting noted above. We identify the potential for non-negligible systematics from template mismatch in velocities in Section V. Consequently we construct a second algorithm to measure the differential asymmetric-drift signal between young and old stellar populations using empirical stellar libraries rather than SSPs (Section VI). Appendices provide details of our stellar library selection (A), mock spectra (C), MCMC analysis (B), and kinematic maps for the studied galaxy sample (D).
II. Sample, Data and Fitting Methods
II.1. Galaxy Sample
| MID | plate-IFU | redshift | b/a | M* | nS | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (kpc) | (mag) | (mag) | (mag) | (mag) | () | |||||
| 1-339041 | 8138-12704 | 0.031 | 0.69 | 6.7 | 0.67 | -21.73 | 4.06 | -22.09 | 6.62 | 4.14 |
| 1-209537 | 8486-12701 | 0.038 | 0.63 | 8.6 | 0.74 | -21.44 | 4.52 | -21.79 | 5.27 | 6.00 |
| 1-532459 | 8320-9102 | 0.052 | 0.67 | 7.6 | 0.60 | -21.63 | 3.07 | -21.90 | 4.77 | 2.72 |
| 1-251279 | 8332-12705 | 0.033 | 0.81 | 3.6 | 0.69 | -21.16 | 4.10 | -21.52 | 3.88 | 3.33 |
| 1-542358 | 8482-3702 | 0.040 | 0.93 | 3.9 | 0.63 | -21.25 | 3.62 | -21.58 | 3.74 | 3.19 |
| 1-265988 | 8329-6103 | 0.031 | 0.64 | 4.0 | 0.62 | -20.30 | 3.68 | -20.63 | 1.65 | 1.47 |
| 1-209199 | 8485-9102 | 0.026 | 0.72 | 4.1 | 0.56 | -20.33 | 3.30 | -20.68 | 1.61 | 2.26 |
We selected seven galaxies from the MaNGA survey to develop and test the algorithms in this study. The galaxies were chosen to have exceptionally regular gas and stellar kinematics (in terms of azimuthal symmetry, with little evidence for bar distortions), moderate inclinations (), and clear evidence for asymmetric drift between their (single component) stellar velocities and ionized gas (as reckoned by the MaNGA data analysis pipeline data products; hereafter DAP). This list is by no means exhaustive of good candidates.
These galaxies were also chosen to have stellar masses and colors similar to the Milky Way (MW).111MW stellar mass is estimated to be (Licquia et al., 2016), with an -band absolute magnitude of mag and color of mag (Licquia et al., 2015). Photometric properties of these galaxies, sorted by stellar mass, are summarized in Table 1, where redshift, b/a (minor to major axis ratio), half-light radius, rest-frame and NUV- colors, SDSS - and -band absolute magnitude, stellar mass and Sersic index (nS) are from the NASA-Sloan Atlas (NSA, Blanton et al., 2011).222http://www.nsatlas.org Except for nS, all photometric quantities report their elliptical Petrosian aperture measurements. Magnitudes and colors have AB zero-points; absolute magnitudes and masses are scaled to H Mpc-1 throughout. A value of n is a hard upper limit in the Blanton et al. (2011) analysis. The NUV- color range is blueward of the red sequence (e.g., Figure 2 of Yan et al., 2016a) but in the redder half of the blue cloud. As we will see, the sample has peak rotation speeds between 200 to 300 , with both slow- and fast-rising rotation curves.
We refer to these galaxies by their plate-IFU (integral field unit) designation throughout the paper. Table 1 provides their corresponding, unique MaNGA ID (MID).
II.2. MaNGA Data Cubes
For the spectral analysis throughout this paper we use the “LOGCUBE” datacube from the Data Reduction Pipeline (DRP) of MaNGA (Law et al., 2016) from an internal release333MaNGA Product Launch (MPL) 5, v2_0_1. closely related to the versions in Data Release (DR)14 (Abolfathi et al., 2018). We spot-checked our analysis to verify that subsequent subtle changes in the data-processing through DR15 (Aguado et al., 2019) and the next internal data release444MPL 8, v2_5_3 do not alter the results in any significant way. Given the significant investment in MCMC analysis, we have retained the results from the older release.
MaNGA datacubes contain the reduced and combined spectra from the dithered IFU observations of a single galaxy. Spaxels have been resampled to a logarithmic bin of 70 and to a common wavelength grid.555For reference, the median instrumental resolution (FWHM) varies between 250 at the blue limit of 362 nm to 125 at 950 nm, with a median FWHM value close to 150 characteristic of the performance between 500 and 750 nm Law et al. (2016); Yan et al. (2016a). Data cubes also contain information on the mean and variance of the spectral line spread function (LSF). We use this LSF to match the resolution of our spectral templates to the data, spaxel-by-spaxel, before fitting. We measure the S/N of individual spaxels in MaNGA datacubes using the median of the spectra and inverse variance (IVAR in the datacube) within the wavelength range of 360-940 nm. In our analysis we ignore spaxels with S/N per Å less than 1.
II.3. General Considerations for pPXF

Throughout this paper we conduct full-spectrum fitting of the observed spectra between 350 and 940 nm. The extensive wavelength coverage yields a wide range of stellar features including the full Balmer series dominated by hot young stars as well as strong stellar features from Ca H&K to the NIR triplet which are dominated by cool stars; together these features should contain the significant information on the the kinematics of the young and old populations.
Full-spectrum fitting uses pPXF. This code fits an observed spectrum with a set of spectral templates, convolved with a line-of-sight velocity distribution (LOSVD) in pixel-space. Throughout this study, we fit for the velocity and velocity dispersion moments of the LOSVD of all kinematic components. The code allows multiple kinematic components to be fit simultaneously; in our analysis we have leveraged this to fit the observed galaxy spectrum with a single component for the observed gas emission features and a single or multiple stellar kinematic components.
During our full-spectrum fitting of observed galaxy spectra, we fit for the following gas emission features; H, H, H, H, [OII], [OII], [OIII], [OIII], [OI], [OI], [NII], [NII], [SII] and [SII]. The gas emission lines are modeled as Gaussian features and are treated as a single kinematic component independent of that measured for the stellar component(s). While we fix the relative flux ratio between the [OIII], [OI] and [NII] doublets, based on atomic physics, the fluxes of the gas emission lines are free parameters during the fitting process.
When fitting two stellar components we take advantage of the pPXF feature to constrain the relative weight of two kinematic components, referred to in the code as fraction but shortened to yfrac in this study. This parameter is a light-weighted quantity defined as the relative weight in the first kinematic component to that in all components:
| (1) |
where are the weights of the first component while are the weights of second component. In our analysis the first component will always correspond to the young stellar population and hence the use of the subscript ’y.’ We flux normalize the template spectra for our stellar components and hence, if the first (second) component represents the young (old) stellar population, yfrac is a relative indicator of star formation history. Though by default pPXF limits the user to constrain the relative weight of two kinematic components, in the course of our analysis we removed this limit to allow the development the algorithm in Section VI. This allowed us to constrain the relative weight of more than two kinematic components simultaneously during our full-spectrum fitting by providing a vector of relative fractional values (fracn for the element), i.e.:
| (2) |
where is the number of kinematic components being fit, is the sum of the weights of the component and is the sum of the weights of all components. Throughout our study, we allow the relative weight of the gas component to be free and unconstrained by yfrac.
The pPXF code can also minimize errors caused by imperfect spectral calibration, template mismatch, or scattered light by fitting multiplicative and/or additive Legendre polynomials or trigonometric series. In our analysis we simultaneously use additive and multiplicative polynomials of order 8 when fitting MaNGA galaxy spectra for their stellar kinematics with independent stellar population templates.666This order is based on experience gained from analysis of MaNGA data (Westfall et al. submitted) as well as analysis of SAURON data of galaxies in the Coma cluster (Shetty et al. submitted). When fitting mock spectra using the same stellar population templates we do not use any polynomials.
II.4. Choice of SSPs
For our analysis, we adopt the SSPs of MIUSCAT (Vazdekis et al., 2012) as our template spectra for the stellar components. These models were developed using empirical stellar spectral libraries, particularly the MILES (Falcón-Barroso et al., 2011), Indo-US Library of Coudé Feed Stellar spectra (Valdes et al., 2004), and the CaT Stellar Library (Cenarro et al., 2001). These models were selected primarily due to their significant overlap in rest-frame wavelength coverage with MaNGA. The 346.5-946.9 nm span for MIUSCAT almost exactly matches the 360-1030 nm span for MaNGA at the typical redshift of the MaNGA sample. The spectral resolution (0.251 nm FWHM) is slightly higher at all wavelengths than the MaNGA data (cf. Law et al., 2016; Yan et al., 2016a, respectively their Figures 18 and 20), which is important for properly convolving the data to the MaNGA instrumental resolution for kinematic analysis, as described in Westfall et al. (submitted). MIUSCAT SSPs used in our analysis cover an age range 0.03-14 Gyrs in 53 steps, metallicities ([M/H]) -0.66, -0.35, -0.25, 0.06, 0.15 and 0.26 (without -enhancement), and use the BaSTI isochrones (Pietrinferni et al., 2004) and a Kroupa initial mass function (IMF) (Kroupa, 2001). The metallicity range of these SSPs encompass the observed range of metallicities seen in large integral-field surveys sampling all galaxy types over a wide range of luminosity and radius (e.g., Sánchez-Blázquez et al., 2014; González Delgado et al., 2015; Zheng et al., 2017).
II.5. Defining Young and Old Components
For the old stellar population we use SSPs older than 1.5 Gyrs as template spectra, and the remaining for the young stellar population modeling. This choice is motivated in Figure 1. Here we conduct a light-weighted full spectrum fit of each MIUSCAT SSP with a set of empirical stellar spectra representative of a broad range of stellar spectral types (see Appendix A) and sum the weights for the presented bins of stellar types. The plot demonstrates that except for the lowest metallicity models the relative weight in hot stars (O, B, and A type) falls below 10% above ages of 1.5 Gyrs, while the coolest stars begin to contribute substantially (30%) after this time, namely the times-scale for the formation of the red-giant branch.
It is also the case that the intermediate stars (F,G) peak around 1 Gyr. While the hottest of these (F0 V) will still have significant Balmer absorption and Main Sequence (MS) anlifetimes of roughly 3 Gyr, for regions with on-going or recent star-foration the F-star contribution to the Balmer absorption equivalent width will be small compared contributions from hotter, more luminous MS stars. Nonetheless, based on this Figure, an argument can be made for an intermediate age range, say, between 0.5 and 3 Gyr, particularly for modeling galaxies or regions of galaxies that have not had recent star-formation. We take advantage of the multimodel distributions in Figure 1 to constrain the mix of stars used in the stellar library algorithms (Section VI.4). However, while an additional time-bin would greatly aid in determining the AVR, for simplicity of our development in this work we distinguish only between two age bins for measuring differential asymmetric drift signals.
In the MW solar cylinder from Aumer & Binney (2009) or from MW and M33 star clusters (Beasley et al., 2015) there is observed to be roughly a factor of 3 change in velocity dispersion between t=0 and 1.5 Gyr (assuming the birth population has the same dispersion as the molecular gas – something that is not clearly the case for the star-cluster measurements), and about a factor of 2 increase between 1.5 and 10 Gyr; in M31 (Dorman et al., 2015) the increase in velocity dispersion is roughly the same during these two time periods. Hence our choice of age bins appears a sensible starting point if the three large galaxies in the Local Group are representative of the larger population of intermediate-to-massive spiral disks.



III. A Robust Two-component AD Signal
| plate-IFU | xoff | yoff | PAkin | ikin | iphot |
|---|---|---|---|---|---|
| (arcsec) | (arcsec) | (deg) | (deg) | (deg) | |
| (1) | (2) | (3) | (4) | (5) | (6) |
| 8138-12704 | +0.100.01 | +0.020.01 | 165.920.04 | 53.40.1 | 46.8 |
| 8486-12701 | -0.040.01 | +0.030.01 | 309.720.04 | 59.30.1 | 51.3 |
| 8320-9102 | +0.030.01 | -0.070.01 | 111.560.05 | 50.10.2 | 48.0 |
| 8332-12705 | +0.040.01 | +0.000.01 | 146.250.05 | 42.60.2 | 36.6 |
| 8482-3702 | -0.000.02 | -0.200.01 | 14.750.11 | 27.10.9 | 22.1 |
| 8329-6103 | +0.170.01 | -0.170.01 | 207.070.06 | 54.90.2 | 50.6 |
| 8485-9102 | -0.230.01 | -0.090.01 | 181.540.06 | 49.80.2 | 44.6 |
Note. — Column (1) gives the galaxy plate-IFU identifier matching Table 1. Columns (2) and (3) give the x- and y-offsets of the galaxy barycenter from the IFU center in arcsec from kinematic modeling described in the text. Column (4) gives the position angle from the same kinematic modeling. Column (5) gives the inclination from the same kinematic modeling. Column (6) give the photometric inclination derived from the b/a values in Table 1 assuming an intrinsic disk oblateness of 0.2.
Outside of the Milky Way’s solar neighborhood and few of the nearest galaxies in the Local Group, we lack evidence demonstrating the presence of an AVR in other galaxies. All existing evidence is based on measurements of resolved stellar populations. Before developing a technique to measure AVR in spectra of integrated star-light as observed by MaNGA, we demonstrate that this information is present and extractable from such spectra. The purpose of this section is to show unequivocally, via MCMC analysis, that a stellar population model with at least two kinematic components can be robustly constrained by the data.
The MCMC analysis undertakes full-spectrum fitting of the observed galaxy spectrum using three kinematic components; a young stellar component (age Gyrs), an old stellar component (age 1.5 Gyrs) and a gas component – as defined in the previous section. The MCMC helps us explore how robust the pPXF likelihood maximization is at deriving distinct kinematics of a young and old stellar populations. This is important given the degrees of freedom in the fitting, the subtlety of the signal (a few 10’s of in velocity difference expected between young and old populations), the degeneracies in stellar population synthesis (e.g., age and metallicity), and a range of data quality – all of which contribute to introducing local minima in space. We use Bayesian inference to sample the posterior probability distribution of the kinematics, employing an implementation of Affine-Invariant Markov-Chain Monte-Carlo (MCMC) proposed by Goodman & Weare (2010) and encoded by Foreman-Mackey et al. (2013). This technique minimizes the need for a lengthy “burn-in” phase which, given the extensive computation time of the full spectrum fit with the complete set of SSP models, requires significant computing time.
Here, the MCMC uses 14 independent ‘walkers’ to sample for a model with two stellar populations and gas with distinct kinematics. Each step of the chain fixes the kinematics (velocity and dispersion) and the yfrac of the two stellar populations and allows pPXF to optimize the SSP weights, polynomials, and gas emission line intensities. The kinematics of the young and old stellar components are then randomly ‘walked’ through in order to sample and determine the location and shape of the global minima of this parameter space777In what follows we assume all models have equal probability so probability scaling can be ignored.. If the kinematics of the young and old stellar populations in the galaxy are similar, then we expect to see so within the posterior distribution sampled by the MCMC. However if this is not the case, then the peaks of the posterior distributions should not overlap.
The MCMC parameterizes over the six kinematic parameters of the components, i.e. the velocities and dispersions for the young and old stellar component and gas component, and yfrac (defined in Equation 1). The initial starting values for the Markov Chain are randomly generated using the results from an initial full-spectrum fit of the galaxy spectrum with a single stellar component and a gas component. We hypothesize that the kinematics of the young stellar component is close to that derived for the gas component, and the kinematics of the old component is close to that of the single stellar component. Hence the initial kinematics for the two components are randomly generated from a normal distribution centered at the measured kinematics and with a standard deviation of 25 for the velocities and 50 for the velocity dispersions. The initial starting values for yfrac is also randomly generated from a normal distribution centered at total relative weight in the young SSP templates in the initial fit, with a standard deviation of 0.1. For each step of the MCMC, we bound the parameters of the fit such that the velocities of the components are within 250 , while the velocity dispersions are within 200 of the starting values. The parameter yfrac is bound to values between 0 and 1. Within these bounds, we assume no prior on the parameters.




III.1. MCMC Results
We applied the MCMC algorithm to our sample of seven galaxies on a spaxel-by-spaxel basis. Figure 2 shows the measured, line-of-sight (projected) velocity and velocity dispersion maps for one galaxy for young and old stellar components in the second to fourth columns of the top row. (Maps for the remaining six galaxies in our sample are in Appendix D.) There is no smoothing applied to these maps; the color of each data point in the image corresponds to the kinematics of individual spaxels. Blank spaxels in these maps within the MaNGA IFU footprint are either regions masked in the DRP as foreground stars or, in the case of the MCMC only, represent spaxels where the MCMC did not converge within the maximum run-time permitted for jobs on the computer cluster to which we had access.888Job run-times were limited to 72 hours. Each job consisted of processing for several contiguous spaxels, leading sometimes to vertical sets of incompletion. For comparison we also show the derived velocity and velocity dispersion maps for gas and stars for a single stellar component. (In later sections these serve as the initial fitting step in multi-step alrgorithms.) These were measured directly from pPXF. Note the coherency of the velocity fields with the expected spider-diagram of isovels, as well as the smoothness of the kinematics on scales much larger than the beam size (2 arcsec fiber diameter). This smoothness and coherency persists for both single and two-component stellar kinematics. Keeping in mind that the kinematics are derived independently for each spaxel, this coherency indicates that our two-component stellar solutions from the MCMC algorithm are robust and measuring astrophysical kinematic signals. While there is much more scatter in the velocity dispersion maps, our approach is to avoid using these and higher kinematic moments.999NB: stellar velocity dispersion maps provided for the young and old components, denoted by a cross, are presented as qualitative metric to guide the development of the algorithm and are considered quantitatively unreliable much below the instrumental resolution until forthcoming improvements in the accuracy in the instrumental line-spread-function are concluded (D. Law, private communication). It is reassuring nonetheless to see that on average the younger component has lower dispersions than the older component as anticipated, and the old component has the qualitatively expected radial decline in value. These trends are seen for all galaxies in our sample.
While the asymmetric drift signal is readily apparent from Figure 2 to the practiced eye, this is more easily seen by extracting rotation curves using some fiducial geometry. Accordingly, Figure 3 shows the results of our MCMC algorithm in decoupling the deprojected tangential speeds of young and old stellar populations. In most cases and at most radii we see that both young and old stellar components lag in their tangential speed relative to the ionized gas (i.e., this is asymmetric drift), with the old component lag being larger, as one would expect from the presence of AVR. For comparison we show the deprojected tangential speeds for gas and stars for a single stellar component (again, derived directly from pPXF), from which the asymmetric drift signal also is readily apparent.
For Figure 3 we adopt geometric parameters derived from full, two-dimensional kinematic modeling of a monolithic inclined-disk. We use the method described in Westfall et al. (2011) and Andersen & Bershady (2013), applied simultaneously to the DAP gas and stellar kinematics. These parameters are summarized in Table 2. However, these geometric parameters are only used to define radial and azimuthal bins and deproject the kinematics; the individual fits to each spaxel are independent of these geometric parameters. Consequently the rotation curves in Figure 3 make no assumptions about kinematic or rotation-curve models except insofar as they share the geometries given in Table 2. Figure 2 and associated Figures in Appendix D are completely independent of any assumed geometric or rotation-curve model.
We focus on two fairly extreme cases: 8138-12704 and 8329-6103. Both galaxies have S/N above 10 Å-1 even at large radii, and yfrac values between 0.1 to 0.2 (in the central regions) and 0.4 to 0.55 in the outer regions. The radial trend in yfrac is qualitatively what is to be expected for age gradients in spiral galaxies where the older population is centrally more concentrated.
The former galaxy 8138-12704 was chosen because of its exceptionally large asymmetric drift signal as measured for a single stellar kinematic component with respect to the ionized gas, yet clear presence of young and old stellar populations. At R = Re, Dn4000 = 1.42 while . Of a sample of nearly 500 galaxies in MPL-5 selected to have regular kinematics and moderate inclinations (see Section II.1), this galaxy is in the upper quartile in terms of deprojected gas rotation speed ( ). Since in general the asymmetric drift signal scales with velocity, it is useful to also look at the fractional difference between tangential speed of the stars and gas relative to the gas (). For 8138-12704 this fraction is 13.7%, and it too is in the upper quartile.
In contrast 8329-6103 has an asymmetric drift signal that is in the lowest quartile for the sample of galaxies in both an absolute and relative sense: , and is only 6%. The galaxy has about 25% of the total stellar mass and 41% of the dynamical mass at R = Re ( ) compared to 8138-12704, yet has a comparable Dn4000 of 1.36. Indeed, our analysis shows the two galaxies have yfrac values of 0.42 and 0.53 respectively. Compared to the MW (e.g., Licquia et al., 2016), 8329-6103 is almost a factor of two less luminous.
For the more massive galaxy, 8138-12704, the differential asymmetric drift signal is readily apparent at all radii sampled. To quantify this excellent kinematic separation of young and old stellar populations, Figure 4 shows the bivariate posterior probability distribution for velocity and velocity dispersion of two spaxels selected from near the major axis. One spaxel is on the approaching side at 0.3 Re (3.5 arcsec radius) and the other is on the receding side at 1.1 Re (12 arcsec radius). In both cases the peaks and 99.7% contours are well separated with the relative velocities and dispersions for the two populations. Moreover, they are differentiated as expected toward higher dispersions and lower speeds for the old population and vice versa for the younger population. While this is consistent with our priors, the presence of these distinct, age-dependent kinematics independently determined for all spaxels using an unconstrained model suggests there is ample information to extract a quantitative measure consistent with our qualitative astrophysical expectations.
For the less massive galaxy 8329-6103, Figure 3 shows the kinematics for the young and old populations are differentiated at smaller radii, as expected, but at larger radii the differentiation is less evident. This is reflected in Figure 4 as well. One spaxel is on the receding side at 0.6 Re (4 arcsec radius) and the other is on the approaching side at 1.3 Re (8.5 arcsec radius). For the inner spaxel, we see the anticipated velocity difference between young and old population, although the velocity dispersions are flipped in the opposite sense of what we might physically expect, i.e., the faster-rotating (young component) has a larger dispersion. However, the 67% probability contours are quite broad, and both components are at, or well below, the instrumental resolution. At the larger radius the young stellar component continues to appear to rotate more quickly, even though the probability contours substantially overlap. The velocity dispersions are well below the instrumental resolution in this limit.
These results are promising, indicating we should be able to derive separate kinematics for most of the MaNGA sample that have regular disk kinematics. Clearly Figure 3 shows some irregularities in the tangential speeds of young and old components at large radii, which correspond to low S/N. The behavior reflects an increasing frequency with decreasing signal-to-noise where the measured kinematics of the young stellar populations are dynamically hotter and rotate slower than the old stellar component. In Appendix B we demonstrate this behavior is due to degeneracies in disentangling the kinematics of the young and old stellar populations in this regime when using a global minimizer (i.e., MCMC) with a very broad range of template age and metallicity. Our subsequent algorithms that use a local minimizer with carefully constructed initial conditions largely eliminate this problem.
IV. SSP-Based Algorithms to Measure AD
While MCMC provides a robust means for determining the kinematic parameters of our two-component stellar kinematic model, it is also computationally too time-consuming for application to data-cubes of hundreds to tens-of-thousands of galaxies in e.g., MaNGA. In this section we explore how we can make this measurement by directly using the likelihood maximization technique of pPXF since this reduces computation times by factors of order a thousand. To evaluate the performance of such efficient algorithms we rely on two different metrics:
-
1.
Quantitative comparison of algorithm recovered velocities and yfrac to model or MCMC values: In the early stages of algorithm development we used 2,500 MaNGA-like mock spectra with realistic star formation histories. We summarize the key results for this metric in the main text and refer the reader to Appendix C for further details. Since the mocks and fitting spectra were based on the same SSPs, they mocks were less useful for refinning our algorithms. Consequently we also compared the young and old stellar-component velocities derived by our efficient algorithms to those quantities derived from our MCMC results on real data. This served as our summary performance metric, with results given in Table 3 and discussed throughout this Section and in Section VI for the stellar library algorithm.
-
2.
Qualitative comparison of velocity and velocity dispersion maps: We used the smoothness of velocity and velocity dispersion maps (e.g., Figure 2) as a qualitative assessment of our algorithms. The smoothness of the field maps are suggestive of astrophysically real and observationally reliable results since each spaxel is analyzed independently. This second metric, only available for real data, is particularly useful because the quantitative metrics don’t capture systemmatic uncertainties in measured velocities.
| Algorithm | S/N | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Range | med | med | med | med | ||||||||
| () | () | |||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |||
| Simple SSP | [10,35] | -1.9 | 18.3 | 0.7 | 9.9 | 0.84 | 0.66 | 0.040 | 0.088 | |||
| Simple SSP | [35,50] | -3.3 | 7.5 | 1.6 | 4.6 | 0.81 | 0.32 | 0.057 | 0.058 | |||
| Simple SSP | 50 | -0.1 | 7.1 | 1.7 | 4.8 | 0.82 | 0.29 | 0.038 | 0.044 | |||
| 2-Step SSP | [10,35] | -2.7 | 13.5 | 0.4 | 9.3 | 0.82 | 0.59 | 0.018 | 0.050 | |||
| 2-Step SSP | [35,50] | -4.9 | 3.9 | 1.4 | 3.8 | 0.88 | 0.18 | 0.019 | 0.022 | |||
| 2-Step SSP | 50 | -2.1 | 3.5 | 1.4 | 3.2 | 0.88 | 0.12 | 0.023 | 0.016 | |||
| 3-Step SSP | [10,35] | -0.1 | 10.8 | 0.7 | 7.6 | 0.93 | 0.47 | 0.006 | 0.038 | |||
| 3-Step SSP | [35,50] | -0.5 | 2.3 | 0.8 | 2.2 | 0.96 | 0.09 | 0.005 | 0.014 | |||
| 3-Step SSP | 50 | 0.4 | 2.1 | 1.8 | 2.0 | 0.98 | 0.08 | 0.005 | 0.013 | |||
Note. — SSP algorithms (column 1) are defined in Sections IV.1 and IV.2. Three S/N bins (column 2) contain 12945, 587, and 512 spaxels, respectively from low to high S/N. Spaxels are culled from the seven galaxies in our sample to be at radii greater than 2 arcsec in radius (to avoid low values of yfrac) and to available MCMC solutions. The MCMC measurements use the Maximum Likelihood solutions. The metrics include the median (med) and mean absolute deviation () scaled by a factor of 1.4 for in columns (3) and (4); in columns (5) and (6); the ratio in columns (7) and (8), where ; and in columns (9) and (10).
In the following sub-sections, we first present the simplest possible SSP-based algorithm for measuring efficiently the two-component velocities of young and old stellar populations (Section IV.1). This involves a single fitting step. Its shortcomings motivate using better initial conditions for the kinematics and constraints on yfrac in algorithms that involve two fitting steps (Section IV.2). A third fitting step that leaves yfrac unconstrained is found to improve metric performance further, and yield results that are within the uncertainties of the MCMC algorithm results. This final, three-step, algorithm is summarized in Section IV.3.
IV.1. A Simple SSP Algorithm
The simplest scheme for measuring the kinematics of two discrete stellar population components consists of giving pPXF the set of SSPs described in Section II. We again split the assignment of stellar population components at 1.5 Gyr regardless of metallicity. There are no constraints placed on yfrac; pPXF is free to assign weights to the templates as needed to minimize . A single full-spectrum fit to the galaxy spectrum is made with these two (young and old) stellar kinematic components and, in the case of real galaxy spectra (as opposed to emission-line free mocks) a kinematically independent gas component. The initial velocities and velocity dispersions for the two stellar components are identical and are set at 0 and 210 respectively.
This simple algorithm performs well on our mock spectra (metric 1), yielding derived AD signals within 10% of the expected value 67% of the time even for AD signals as low as 5-10 (see Appendix C.1 and Table C1). While these results look promising, the test is highly idealized, absent noise and using the same templates in the mocks and the fitting templates. Consequently, we turn to apply this simple algorithm to real MaNGA spectra as a more definitive performance test. In applying the simple SSP algorithm to real galaxy data, we fit for the gas kinematic component simultaneously along with the stellar kinematic components and match the LSF of the SSP templates to that of the spaxels.101010We use the PRESPECRES datacube extension providing each spaxels’ pre-pixelized (PRE) spectral resolution (SPECRES).
Application of the simple SSP algorithm to 8138-12704 (Section III) indicates the algorithm does not appear to reliably converge to the kinematics measured by the MCMC (metric 2). In Figure 2 we observe that for both the MCMC results and the simple SSP algorithm the younger component appears to have on average faster rotation than its older counterpart, as expected. However, the young velocities for the simple SSP algorithm are systematically lower (in amplitude) than derived from MCMC, while the older velocities are systematically higher; both young and old velocity fields are less smooth as well. Further, the maps are noisy, particularly for the young component, and lack the expected structure of being azimuthally smooth with a radial decline. These qualitative conclusions for 8138-12704 are also found in the remaining six galaxies in our sample (Appendix D). This is quantified in the first three lines of Table 3.
Given that the more robust MCMC technique derived a solution for the kinematics different from our simple SSP algorithm, this suggests that the spectral fitting code (pPXF), which uses a Levenberg-Marquardt technique to find the local minima, is not able to converge to the global minima with real data.
IV.2. Multi-step SSP Algorithms
To circumvent the pitfalls of a complex terrain we augment our simple SSP algorithm by adding an additional fitting step. This additional step allow us to improve initial conditions to position pPXF fairly close to where the global minimum is expected.
In a new first step, we conduct a full spectrum fit with only one stellar kinematic component and one gas emission-line component, using all SSPs (regardless of age) as templates for the single stellar component. This fit is essentially a stellar population synthesis of the spaxel and, accordingly, we use only multiplicative Legendre polynomials during this fit. Expectations based on the MW AVR are that the kinematics of the young stellar population should be close to that of the gas. Simultaneously the kinematics of the old stellar component should be similar to that from a single stellar component than the gas kinematics. Results from our MCMC analysis support these expectations. Hence, in the second fit we use the derived gas kinematics from our first fit as the initial conditions for the young component, and the derived stellar kinematics from our first fit as the initial conditions for the old component. During this second fit, we fix the kinematics of the gas to that derived from the first fit and use additive and multiplicative polynomials during the fit. We refer to this algorithm as ‘2-Step SSP’ in Table 3.
As seen in the Table this two-step SSP algorithm exhibits some modest quantitative improvement in the derived kinematics compared to the simple SSP algorithm. This demonstrates that the irregular space of the solution affects the reliability of the kinematic decomposition unless reasonable initial conditions can be placed on the kinematics. However, some observable differences persist in the velocities of the young component. The discrepancy suggests a lack of full convergence of the two-step SSP algorithms to the global minima of the space identified by the MCMC analysis. We find that although yfrac determined in the first step of the two-step SSP algorithm correlates well with that determined by the MCMC analysis, the relation has significant scatter; better initial conditions on yfrac could also be beneficial. Previously Katkov & Chilingarian (2012) used a Monte-Carlo technique to demonstrate that when conducting a spectral decomposition of co-spatial components an incorrect estimation of the relative light contribution of the components could bias the results.
To test if constraining the relative weights of the young and old components further improves results we provide a data-driven constraint on yfrac by using the template weights from the first full spectrum fit with a single stellar component. From this weight distribution yfrac is set in the second fitting step to the sum of the weights associated with the young SSP models ( 1.5 Gyrs) over the sum of the weights of all SSPs. This constraint is imposed independently for each spaxel. We then add a third full spectrum fitting step to our SSP algorithm (i) where we update the initial conditions for the kinematics to that measured in the second step, but (ii) we remove the constraint on yfrac for the fit. The motivation for this step is to assume that the kinematic solution obtained in the second step is close enough to the global minima that the final step can free the fit to converge onto the global minima without constrains put in place on yfrac. We refer to this algorithm as ‘3-Step SSP’ in Table 3. It is immediately evident that across the board, all of the metrics improve significantly, and hence we adopt this as our final SSP algorithm. Figure 2 and Appendix D show the velocity and velocity dispersion fields for MCMC, simple and 3-step SSP algorithms.
The aim of using a multi-step approach to nudge pPXF toward a global minimum using iteratively improved initial conditions appears to be on target. In contrast, the initial two-step SSP algorithm had less refined initial conditions on the kinematics produced nosier kinematic maps for the two stellar components – compared both to this three-step algorithm and the MCMC results.
IV.3. SSP Algorithm Summary
Our final SSP algorithm used to measure the two-component AD is a three-step process as follows:
-
1.
Use full spectral fitting with pPXF with one stellar and one gas (emission-line) kinematic component. The entire suite of SSP models are used as templates for the single stellar component. Since each SSP is normalized, the resulting spectral fitting weight distribution is light-weighted. The gas emission-line components assume Gaussian line profiles, and the kinematics for all lines are tied to a single value for velocity and dispersion per spaxel. During this fit, the initial conditions for the kinematic for all components are zero velocity with respect to the NSA redshift and velocity dispersion of 210 . All stellar kinematic fitting is done assuming a Gaussian LOSVD and multiplicative Legendre polynomials of order eight are used to match continuum shapes between observed and template spectra. The resulting kinematics and weight distribution of this fit provide informed constraints for the second fitting step.
-
2.
Use full spectral fitting with pPXF with two stellar kinematic components (young and old) and one gas (emission-line) kinematic component. The young kinematic component is restricted to use only SSP models with ages 1.5 Gyrs, while the remainder are used as templates for the old component; yfrac is constrained by the ratio of these weights derived in the first step. The initial kinematics of the young component is set to the derived gas kinematics from the first fit and the old component are set to those of the single stellar component. The kinematics of the gas component in this second fit is constrained to that derived by the previous fit, however the fitting code is free to optimize the relative weights of the different emission line features. Similarly, pPXF is allowed to optimize the relative weights of SSPs within young and old age bins, but the sum of these weights is constrained by yfrac from the first fit.
-
3.
Repeat the full spectral fitting in the same setup as the previous step with the initial kinematics of the stellar components updated to those derived in step 2, but with no constraint on yfrac. This full spectrum fitting provides the final measured kinematics for the two stellar components, and the weights in the two components provides the yfrac in the spaxel.
V. Systematics from Template Mismatch

Template mismatch (Rix & White, 1992; Statler, 1995, and references therein) can lead to potential systematics in the derived kinematics caused by the inability of the templates to accurately reproduce the true galaxy spectrum. This may arise due to the lack of knowledge of the stellar IMF, incomplete parameter coverage in the stellar libraries making up the the SSPs, or systematic errors in the isochrone of the stellar population synthesis models. Notably, the SAURON survey switched from using SSPs to a subset of stellar-library template Cappellari et al. (2007) principally to minimize template-mismatch errors on the derived kinematics. Previous analyses have focused on the impact of template mismatch on systematics in velocity dispersion and higher moments, while we are primarily interested in velocities. It is reasonable to expect that the impact of template mismatch on velocities will be relatively small, but since the asymmetric drift signal is also small, it is worthy of exploration.
To create a situation where template mismatch induced systematics in the recovered velocities we convolved the oldest and most metal rich SSP model spectrum (14 Gyrs, 0.26 [Z/H]) with an LOSVD prescribed by a velocity of 0 and a dispersion of 250 .111111Results using a 13 Gyr model are comparable. We then attempted to derive the kinematics of this mock by fitting the spectra using only SSPs with ages less than 4 Gyrs and metallicities less than solar. Since the purpose of this test is to demonstrate the effect template mismatch has on the measured kinematics, we do not include any polynomials during these tests. Figure 5 illustrates the quality of the best fit (red) against the mock (black) in a feature-rich region including H, MgI, and NaD (recall, however, the full fit is between 360 and 745 nm). As one would expect the H feature at 486.2 nm is very poorly fit while the metal features, NaD at 589.0 nm and 589.6 nm and MgI at 517.6 nm, are significantly better fit but with notable features being visible in their residuals. The best fit clearly does not reproduce the mock spectra very well, so it is unsurprising the recovered velocity from the this fit is off (in this instance) by 18 off the mock’s model value. The bottom panel of Figure 5 demonstrates a significantly better fit to the same model spectrum for a more typical case of template mismatch where we allow fitting the mock spectrum with all sub-solar metallicity, 10Gyr old templates.

We quantified the effect on the systematic errors in recovered velocity for this extreme scenario that induces strong template mismatch. Results for 500 mock spectra with different LOSVDs selected randomly with velocities between , to remove any effect due to pixelization, and velocity dispersions between 5 and 300 are summarized in Figure 6. The plot suggests there is bias in the recovered velocities that correlates with the mock velocity dispersion. This is likely due to the blending of spectral features as the mock velocity dispersion increases, thereby reducing sharp spectral features and the signal available to measure velocity. The cause of the correlation between measured velocity and velocity dispersion however is unclear.
recovered velocities also are biased towards under-estimating the velocity of the mock, for reasons which are not clear.
Were we to use this extreme case as a guide, we would note that the upper values for the stellar dispersion in most disk galaxies should be (for example 50 would be typical of the old, thick disk of the Milky Way at the solar circle). The effect of template mismatch on velocity is, in this extreme case, , as reckoned from Figure 6. Since this case is extreme, in Figure 6 we also present the more typical case for template mismatch described above. In this more typical case the effect of template mismatch is substantially reduced relative to the extreme case at large dispersions, but is comparable for dispersions below 150 . Examining residuals observed for fitting real galaxies with SSP models indicates that in practice template mismatch is more in line with our typical case. The results summarized in Figure 6, however, shows that the resulting template mis-match is comparable in the velocity dispersion regime of interest.
It is likely that the systematics found here are underestimates when fitting real galaxies because in this analysis both the mocks and fitting templates are based on the same SSPs. The differences in our results for mock and real spectra, as illustrated in our SSP algorithm performance, supports this conclusion. Since we are attempting to measure a small differential velocity between different stellar populations in integrated starlight, this potential for template-mismatch velocity systematics cannot be ignored. It is widely accepted that using an empirical stellar library that efficiently samples the stellar parameter space – rather than SSPs – diminishes the effect of template mismatch when fitting for observed galaxy spectra. We have therefore taken the extra step to create an algorithm based on stellar libraries in the following Section VI. We use this algorithm in Section VII to compare to our simpler, SSP-based algorithm using real data.

VI. Stellar Library-based Algorithms to Measure AD
This section presents key steps in developing algorithms based on stellar libraries assessed with the same metrics defined in Section IV. We construct a representative set of empirical stellar spectra (Section VI.1), incorporated first into a set of simple algorithms to disentangle kinematics of young and old stellar components of mock spectra (Section VI.2). To guide development, we identify the origins of the strengths and deficiencies in these algorithms specific to using stellar libraries rather than SSPs. As we found for SSP-based algorithms, initial conditions for the kinematics are important in directing pPXF away from local minima in application to real data (Section VI.3). In the context of stellar library algorithms these local minima are exacerbated by the presence of cooler stars in both young and old populations. To overcome this problem we implement constraints based on expectations from stellar evolution in Section VI.4. These constraints are minimally imposed to retain the flexibility gained using stellar spectral libraries rather than SSPs. What emerges is a well-motivated and robust two-step algorithm that disentangles the kinematics of young and old stellar components and provides results qualitatively on par with the final SSP algorithm. The final stellar library algorithm is summarized in Section VI.5.
| Set | Young templates | Old templates |
|---|---|---|
| A | OBA | F-M |
| B | OBAFG | F-M |
| C | all | F-M |
| D | all | K-M |
VI.1. Young and Old Stellar Templates
We use a representative subset of 51 stars from the empirical Indo-US Library of Coudé Feed Stellar Spectra (Valdes et al., 2004). As described in Appendix A these are well suited for our purposes of analyzing MaNGA spectra. Similar to what was done for the SSP algorithms, we begin by defining the templates for the two age components being fit.
In the context of SSPs (Section II.5) we define the young-component templates to be those containing significant Balmer features. For a stellar library, however this definition excludes stars cooler than late-F which we know are present in young stellar populations for any plausible present-day stellar initial mass function. This is quantified in Figure 7. Since the younger populations have both hot and cool stars, with metal lines contributed to the spectra by the latter, we select three ranges that always include the hottest stars but extended to progressively cooler limits in cases labeled A, B and C. Our aim is to include the smallest possible range of cool stars to minimize degeneracy with the older stellar populations, and hence simplify the fitting algorithm.
The choice of stellar templates for the old component is simpler since hot, Main Sequence stars are short lived and hence only present in young stellar populations, where they dominate the spectral continuum in the blue and visible portion of the spectrum. We therefore exclude hot stars (hotter than F) from the templates for the old component, effectively ignoring the possibility of extreme (very metal poor) blue Horizontal Branch stars from contributing significantly to the integrated light of a mixed stellar population. In one case (D) we restrict the older population to have only K and M type stars to understand if there is any sensitivity to the giant-branch effective temperature.
Table 4 summarizes the four distinct combinations of stellar templates we explore for the young and old stellar components. These template combinations place no restrictions on luminosity class.
VI.2. Simple Stellar Library Algorithms
As a starting point for the development of our algorithm, we test the following simple algorithms to identify pitfalls to be ameliorated by more complex techniques. These pitfalls highlight subtle but important aspects of fitting multiple kinematic components where velocities are offset by values comparable to the spectral resolution. There are no constraints on yfrac in any of these algorithms.

-
1.
Full Spectrum Fitting (Full): pPXF fits two kinematic components to the provided (mock or real) spectrum over the full wavelength range using the above mentioned template sets.
-
2.
Feature Fitting (Feature): Based on the knowledge that we expect to see hot stars only within young stellar populations, the kinematics of the young component are fit with pPXF using only wavelength regions of 1500 about Balmer lines up to n=18 in the spectra while masking out the remainder, as shown in Figure 8. Because of the strong contamination from Ca H, we exclude H; and because of the G band (CN), we only use 500 for H. Given the 1500 velocity width, the region contain H (n=9) and above form a continuous band from 385.36 to 367.21 nm. During this fit, two kinematic components are still applied in pPXF despite the dominance of Balmer features in these regions for young populations, there remains an imprint of the kinematics of the older population in these regions, both in the Balmer lines as well as the metal lines within these windows. This fit is then followed by a fit using pPXF that excludes the Balmer regions. During this second fit, the velocity moments of the young component are kept fixed to the values derived from the first step.
| Algorithm | S/N | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Range | med | med | med | median | ||||||||
| () | () | () | ||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |||
| Simple SL | [10,35] | 13.76 | 51.44 | 4.02 | 14.21 | 0.90 | 1.18 | 0.09 | 0.12 | |||
| Simple SL | [35,50] | 21.50 | 43.47 | 8.21 | 10.88 | 0.88 | 1.38 | 0.13 | 0.07 | |||
| Simple SL | 50 | 69.56 | 87.29 | 5.23 | 8.82 | 1.05 | 2.36 | 0.05 | 0.05 | |||
| 2-Step 1-Bin SL | [10,35] | 1.70 | 29.94 | 3.70 | 15.27 | 0.73 | 0.81 | 0.05 | 0.12 | |||
| 2-Step 1-Bin SL | [35,50] | 1.50 | 17.25 | 6.13 | 7.86 | 1.00 | 0.40 | 0.10 | 0.07 | |||
| 2-Step 1-Bin SL | 50 | 0.90 | 24.86 | 5.46 | 6.69 | 1.09 | 0.74 | 0.04 | 0.06 | |||
| 2-Step 3-Bin SL | [10,35] | -2.02 | 26.27 | 6.17 | 18.38 | 0.62 | 0.87 | 0.01 | 0.08 | |||
| 2-Step 3-Bin SL | [35,50] | 0.66 | 11.50 | 5.44 | 6.54 | 0.98 | 0.35 | 0.05 | 0.05 | |||
| 2-Step 3-Bin SL | 50 | 1.45 | 26.45 | 7.56 | 5.54 | 1.16 | 0.70 | 0.03 | 0.04 | |||
Based on our tests using mock spectra (Appendix C.2) and Table C2), we find the performance of these two algorithms is comparable. This confirms expectations about where most of spectral information is stored for discriminating between young and old stellar populations. For simplicity and consistency with the SSP algorithms we adopt the Full algorithm.
Table C2 also reveals important performance differences between templates: Velocity systematics for the young component are minimized for template set C, while velocity systematics for the old component are minimized for template set B. Perhaps this is unsurprising given Figures 1 and 7. However it is concerning that neither template set optimizes both young and old component systematics. A further concern arises with template sets C and D. In these cases there are many occurrences where yfrac >0.85, i.e., the best-fitting solution yields too large a young-component contribution. This is due to the degeneracy in the contribution of cool stars in the young and old components; the pPXF likelihood minimization falls into a local minima where the stellar kinematics of the mock spectra is almost entirely modeled by the young component. An example of this is given in Appendix C.2, Figure C2. We to conclude that template set B is the best compromise. This leaves us with performance results, based on mocks, that are somewhat unsatisfactory.
VI.3. Basic Two-Step Stellar Library Algorithm
Following the success of adding additional steps to improve the kinematic initial conditions with our SSP-based algorithms, we further developed the Full algorithm using the template set B by adding a step to provide initial conditions in an identical fashion as our two-step SSP algorithm. Foreshadowing further development, we refer to this algorithm as ‘2-Step 1-Bin SL’, where the ‘1-Bin’ designation refers to the grouping of the templates as a single unit for each of the stellar components.
An evaluation of the performance of this algorithm using mocks (Appendix C.2, Table C3) indicates no improvement, but we suspect this is due to systematics between the mocks generated by SSPs and the fits using the stellar library. We turn instead, and henceforth, to a comparison with the MCMC for real data. Velocity and velocity dispersion maps (Figure 2 and Appendix D) show marked qualitative improvement in the smoothness of the kinematic maps between our one-step and two-step stellar library algorithms. Table 5 quantifies this contrast, most pronounced for the young component velocities. There also are performance improvements also for the old-component velocities.
However, further inspection of the kinematic maps reveals velocities and velocity dispersions are quite noisy for the young component of galaxies with lower mass () or bluer color (). (These properties are correlated in general, and particularly so for our small sample). It is also the case that for 33% of the spaxels with both the simple and two-step 1-bin algorithms find very high values of yfrac compared to MCMC results. This is indicative of an incorrect allocation of cool stars to the young kinematic component in the stellar library algorithms, and suggests further algorithm improvement is desirable.
VI.4. Two-Step Stellar Library Algorithm with Constraints from Stellar Evolution
Since problems with our stellar library algorithms arise due to incorrect allocation of cool stars to the young kinematic component, we need an objective mechanism to appropriately assign weights for these stars in young and old components. The above stellar library algorithms attempt to steer the allocation of weights via a prescriptive template set (B). Additional constraint on the relative weights of the young and old component (yfrac) fails to improve algorithm performance with nearly all our quantitative metrics. Further improvement requires a better guided approach.
An astrophysically motivated mechanism to properly weight stellar contributions to young and old stellar populations is to assign priors based on what we would expect from stellar evolution. A limiting case is just to use SSPs but since the entire exercise here is to not restrict ourselves the specific weights produced by the mapping of theoretical isochrones to a template library, we aim to impose a less restrictive scheme that still is informed by the relative weights of different stellar types as we would expect from stellar evolution. As we show, it is possible to do this by coarsely categorizing stellar types in effective temperature while leaving pPXF the freedom to optimize template weights within these coarse (broad) categories.
Figure 7 shows the derived weights for our stellar library from fitting SSPs with pPXF; these results broadly match our expectations for stellar evolution and the impact of metallicity on, e.g., the temperature of the giant branch. The youngest populations, dominated by the hottest stars, indeed have most of their weight in B and A templates, but do contain significant weight in cooler stars. As the populations age (and the Main Sequence burns down while the asymptotic and then red giant branches are populated), the relative weight of the cooler stars gradually increases and the weight of the hotter stars decrease. The oldest SSPs are entirely dominated by the coldest stars, but the specific age where this occurs depends on metallicity because of the temperature of the stars on the horizontal and giant branches. Hence by constraining the relative weights of the templates used in the kinematic fitting such that they are at least consistent with that expected from stellar evolution at some granularity, we could disentangle the the relative weight of the cool stars in the two kinematic components in our fit. Just what granularity should be adopted is one question we answer.
To constrain the relative weights of the stellar templates in the two kinematic components we use pPXF to do a full spectrum fit of the target spectrum with SSPs for a single stellar kinematic component (plus a second component for gas, if the target is a real galaxy spectrum; see Section II). The resulting SSP weight distribution is translated into weights of our stellar templates for a young and old population via a reference look-up table containing the stellar weights derived from fitting our Indo-US stellar subset to each SSP (Figure 7). The weights are divided between young and old populations by summing over SSP weights younger or older than 1.5 Gyrs.
While this scheme provides reasonable estimates for individual stellar template weights, the detailed result can be strongly effected by noise in the galaxy spectra. Further, fixing the relative weights is almost equivalent to using the SSP spectra as templates themselves, which defeats the purpose of this algorithm. To relax these constraints we divided the stellar template into temperature bins. The purpose of this division is to constrain the relative weights only between but not within these bins for young and old populations during the full-spectrum fitting of the galaxy spectrum. The detailed distribution of weights for the individual stellar templates within each bin is a free parameter, tuned (by pPXF) to optimize the likelihood of the solution.

We divide templates into three temperature bins (each contains stars with a range of luminosity classes and metallicity) motivated by the fact that the young and old kinematic components both have cooler stellar types (F-M) as common templates, but the mix of intermediate-temperature stars (F-G) changes strongly with population age (see Figure 1), while only the young component has the hottest stellar types (O-A). The three bins are: Hot (which contains templates of stellar types O, B and A with roughly above 9000∘ K), Intermediate (F, G with roughly between 5000∘ and 9000∘ K) and Cold (K and M roughly below 5000∘ K). Since the unrealistic distribution of weights for the cool stellar types is causing the catastrophic failure in yfracwhen deriving the kinematics of the young and old kinematic components for our simple and 2-step 1-bin algorithms, this three-bin division fix the hot : intermediate : cool contributions in each kinematic component to reasonable values consistent with both the observed spectra and rough expectations from stellar evolution. Consequently we can dispense with the restrictions of the template sets A-D from Section VI.1. We refer to this as our 2-step 3-bin stellar library algorithm.
To implement constraints on the relative weights of the bins we utilize features in pPXF that (i) allow the relative weight to be fixed between multiple kinematic components, and (ii) grants the user the ability to tie together the kinematics of different components. Effectively we fit a set of template bins with tied kinematics for each stellar component. By fixing the relative weights of the bins of the young and old components we can avoid unrealistic template weights while giving freedom for template optimization. Nominally pPXF limits users to fixing the relative weight between only two kinematic components. For this study we modified the pPXF code to disable this limit, enabling us to split the templates for each component into as many bins as needed.
We find the addition of these multiple constraints on yfrac yield a significant qualitative improvements in the smoothness of the velocity and velocity dispersion maps for the lowest-mass and bluest galaxies in Appendix D. As seen in these Figures, this stellar library algorithm provides comparable qualitative performance to the SSP algorithm, and based on this we adopt this three-bin approach. Further comparison with the SSP algorithm is presented in Section VII.
VI.5. Stellar Library Algorithm Summary
The final algorithm (SL hereafter) can be summarized as a two-step process. The first step is identical to what is described in Section IV.3; it is a full-spectrum fit for a single stellar kinematic component using SSPs. This step is used to constrain the relative weights of empirical stellar spectra via a decomposition of the SSPs into relative weights for the empirical stellar spectra. Henceforth SSPs are not used. A second and final, two-stellar-component fit (also full-spectrum) uses the empirical stellar spectra with weights broadly constrained in three effective-temperature classes (Hot, Intermediate, and Cool). The second step uses a modified version of pPXF with fixed fractional contributions to the total fit for two stellar kinematic components, each with three different sub-populations. By definition, the three sub-populations for each kinematic component share the same kinematics. In detail:
-
1.
The relative weights for the Hot, Intermediate and Cool stellar bins for each (young and old) kinematic components are derived from the decomposition of the SSPs into individual stellar templates, as illustrated in Figure 1. The stellar template weights for the SSPs younger or older than 1.5 Gyr, respectively, are assigned to the young and old stellar components via the look-up table generated from the decomposition of each SSP (Figure 7).
-
2.
The initial kinematics of the young component are set to the derived gas kinematics from the initial fit, and the old component are set to those of the single stellar component.
-
3.
The kinematics of the gas component in this second fit is constrained to that derived by in the first fit. The fitting code is free to optimize the relative fluxes of the different emission lines.
-
4.
The fitting code is allowed to optimize the relative weights of the stellar templates within each temperature bin for each age component (young and old) but the relative sum of these weights is constrained by six yfrac values defined above. This flexibility minimizes the effect of template mismatch.
VII. Results
In this section we explore the random and systematic uncertainties in the our methods to disentangle the tangential velocities of young and old stellar populations in spiral galaxies observed by MaNGA. Section VII.1 presents the measured velocities for our seven test galaxies. Section VII.2 and Section VII.3, respectively, explore the behavior of random and systematic uncertainties in our measurements. Finally, Section VII.4 puts these uncertainties into the astrophysical context of a two-component asymmetric drift signal.
VII.1. Measured Kinematics
The velocity and velocity dispersion maps in Figure 2 and Appendix D show that our different algorithms display qualitatively similar kinematics. We focus further analysis on kinematics from spaxels within a wedge of each galaxies’ major axis, defined using the geometry in Table 2. Tangential velocities for each galaxy and tracer are corrected for their own systemic velocity determined by minimizing the difference in the approaching and receding components, excluding data at radii less than 2 arcsec. We find these systemic velocity values are consistent (at the 1 level, on average) with values estimated from full two-dimensional kinematic modeling of a monolithic inclined-disk using the method described in (Westfall et al., 2011; Andersen & Bershady, 2013). There are variations between systemic velocities between tracers that are of order 3 to 5 . These differences are consistent with random errors, and they are negligible in our overall error budget.
VII.2. Random Errors
Our two algorithms (SSP, SL) both use pPXF to minimize . Because pPXF does not map the shape of the minima in space, these algorithms do not provide a direct estimate of the measurement uncertainty. In contrast the Markov-Chain Monte Carlo analysis we conducted for our sample galaxies do provide this information. From the MCMC chains we have marginalized the posterior probability distribution (PPD) for the kinematics (velocities, velocity dispersions) and relative light contribution of the young and old stellar populations of the galaxies. As mentioned in Appendix B, the shapes of the PPD for individual spaxels can sometimes be multi-modal, particularly at low S/N. We quantify the PPD width using a standard deviation (rather than, e.g., the median absolute deviation) specifically to include the impact of multi-modality.
We find that the uncertainty in the measured velocities of the two components correlates with the S/N of the spectra and yfrac. Figure 9 illustrates these trends by plotting the median width of the PPDs () as a function of yfrac and S/N. The middle-panel shows that for the lowest values of yfrac the uncertainty in the measured velocity of young stellar component is the lowest for a given S/N. This is expected given that lower value of yfrac corresponds to lower contribution of the young stellar component to observed galaxy spectrum. Likewise, the right-panel illustrates that at a given S/N the reliability of the measured velocity of the old stellar component is higher when yfrac is lower, the relative contribution of the old stellar component is higher. Both panels illustrate the expected correlation between and S/N. Since the systematic differences (seen in the next section) and the scatter between methods is smaller than the random errors exhibited in Figure 9, these values are well suited for characterizing the random errors in appplication of either the SSP or SL algorithms.
For reference, at a S/N (Å-1) = 10 and yfrac = 0.4, the random errors in the young and old velocities are roughly 30 , while at S/N (Å-1) = 30 the errors are between 5 and 10 for young and old components respectively. On-line tables of quantities plotted in the middle and left panels of Figure 9 are available.

VII.3. SL vs SSP: Systematics
Figure 10 compares the median difference (spaxel by spaxel) between the derived velocities from our two algorithms binned in S/N and yfrac. This shows that the systematic differences are small in absolute value, but nonetheless non-zero. The SL algorithm’s (Section VI.5) measurement of the velocity of the young component is consistent with that of the SSP algorithm (Section IV.3) across S/N and yfrac to within 8, with an overall median difference of -5 such that the SL algorithm tends to find the young component rotating faster. For the old component, the median difference is 7 such that the SL algorithm tends to find the old component rotating slower.These systematic differences may reflect template mismatch or systematics in the final yfrac values of the two algorithms. We will further explore the cause of these systematics in future work, but it suffices to conclude here that the systematics are small and have little correlation with S/N or yfrac. As shown in the bottom panels of Figure 10, random errors almost always dominate over systematic differences between algorithms at the spaxel level.
VII.4. Summary Two-component Asymmetric Drift Measurements
As a summary measurement of asymmetric drift for two independent stellar components differentiated by age, we take the mean velocity from our two algorithms (SSP and SL), spaxel by spaxel, as our measure. For each spaxel we take as the random error, and half the difference between the velocities from the two algorithms as the systematic error. When averaging the kinematics derived from, e.g., a radial bin of spaxels, we assume the random errors diminish with the usual quadrature averaging, while the systematic errors do not. Systematic errors in the binned data are taken as the median of the systematic error for individual spaxels in the bin.
Figure 11 shows the implementation of this summary scheme to a measure of asymmetric drift for young and old components relative to the ionized gas velocity for the seven galaxies in our sample. Line ratios (e.g., [OIII]5007/H versus [NII]/H) are consistent with HII-like regions for most galaxies at radii outside several arcsec; hence ionized gas velocities should be close to the circular speed of the potential. Results from Section VII.2 indicate that young-component velocities are unreliable for yfrac0.15, and both young- and old-component velocities are unreliable when individual spaxels have S/N10. These radial points have been indicated with open symbols. Referring to Figure 3, we see that most of the observed radial range for the galaxies in our sample are above these limits.
This final figure shows that we can indeed measure a distinct asymmetric drift for two stellar components for this sample of galaxies. Systematic errors dominate random errors in radial bins, but in most cases and at most radii the errors are substantially smaller than the difference between the asymmetric drift of young and old components. While the difference between ionized gas and young stellar component is small, it is non-zero ( in the mean, with a median value of 8 ). In all cases the asymmetric drift signals for young and old components straddle what is measured for a single stellar component, as one would expect. The asymmetric drift signal for the young component is generally small, with value of order 20 or less, also as one might expect. The net effect of isolating the two population components by age is to elevate the asymmetric drift signal for the old component relative to the single-component asymmetric drift signal.

VII.5. Discussion
The results from Figure 11, combined with population age information will be exploited in future work to measure the AVR in MaNGA galaxies. However, it is already interesting to remark on the large range of AD signals observed in our sample of seven galaxies. There is also some indication of a trend with mass: The differential asymmetry drift signal for older populations is largest in the more massive galaxies, but this trend is far less regular (noting the small and large AD signals for 83320-9102 and 8482-3702, respectively) compared to the standard mass–rotation-speed scaling seen in Figure 3. While the addition of age estimates may transform the AD signal into a smoother trend in AVR with mass, the rather uniform colors of our sample suggests this expectation may be illusory. Given that there are at least three likely astrophysical paths to generating an AVR (see Section I), perhaps it is unsurprising to see a wide range in AD over such a modest range of stellar mass. Application of our methods to larger samples will provide statistics on the distribution of AD as a function of galaxy mass.
It is worth noting the limitations of the present methods and scope of analysis. We have selected galaxies with regular kinematics and with modest values of yfrac. One may well expect that interpretation of AD measurements will be problematic in cases where the kinematics are less regular or there are significant bar or oval distortions. It is imperative, therefore, to have an assessment of galaxy kinematic regularity, and to limit analysis to galaxies or radial zones within galaxies where the gas is on near-circular orbits and low-order distortions (e.g., m=1,2 modes) are weak or absent for both stars and gas.
We have also seen that our algorithms are limited in precision once the continuum S/N falls much below Å-1. However, there is nothing preventing the methods described here to be applied in a more sophisticated analysis that fits multiple spaxels simultaneously in a parameterized model to increase the effective S/N; even a relatively simple tilted-ring approach would likely improve upon the S/N limitations of our current spaxel-by-spaxel scheme, e.g., at larger radii.
Nonetheless, the kinematics of the young component are not well measured for yfrac . This means that the AVR within the centers of galaxies with prominent, old bulge or pseudo-bulge populations, while typically observed at sufficient S/N, are not easily accessible given our current methods. While we have not probed yfrac with our modest sample, we can expect that at least in the outskirts of later-type galaxies this condition will exist. We can also expect that measuring the kinematics for the old component will be difficult in this regime. Hence there is likely to be a sweet spot for our methods at intermediate radius, where both young and old disk components are comparably present. Such a sweet-spot is likely well-matched to a comparison with the MW solar neighborhood.
Finally, while we cannot offer a definitive recommendation between our SSP and SL algorithms, our preference is for the SL algorithm. Despite its greater complexity, the SL algorithm in principle should suffer less from template-mismatch systematics. Possibly supporting this statement is the observation that the SL algorithms’ velocity-dispersion maps for the young stellar component look smoother and more realistic (in amplitude) than for the SSP algorithm (Figure 2 and Appendix D).
VII.5.1 Gas Kinematics
It has become increasingly apparent that diffuse ionized gas (DIG) contributes significantly to the projected area of many early-type galaxies as well as the centers of some intermediate-type galaxies (e.g., Belfiore et al., 2016). Recent studies have shown that in some cases the ionized gas of even rotationally supported systems lags behind that of the molecular gas (Levy et al., 2018). In general this is not the case for intermediate and late-type galaxies where the emission from ionized gas is dominated from HII regions; in these systems the agreement between H and HI velocities is excellent (e.g., Martinsson et al., 2016). Unsurprisingly, the discrepancy tends to occur in more massive systems or early-type dwarfs where the specific star-formation is depressed. As recently shown by den Brok et al. (2020) when the ionized gas is DIG like not HII-like (as reckoned by e.g., line ratios of [OI], [NII] or [SII] to H.) In these cases the ionized gas cannot be used as an accurate surrogate for the potential’s circular speed, and hence also cannot be used to estimate the absolute amplitude of asymmetric drift in the stars. However the differential asymmetric drift between young and old can be measured regardless.
For the galaxy sample in this paper, as we noted in the previous Section, we find the ionized gas is predominately HII-like at most radii outside of the central regions. We note that application of our technique broadly should consider the limitations of using ionized gas as a tracer of circular speed; the situations where the ionized gas is predominantly DIG-like can be readily determined with the same spectroscopy used to measure velocities.
VIII. Summary and Conclusions
The study of the stellar age–velocity-dispersion relationship (AVR) in galaxies has been limited to date to a handful of nearby galaxies where individual stars are spatially resolved. This limitation has been a significant obstacle in understanding the processes of galaxy evolution that give rise to the phenomenon. With the advent of large IFS surveys, such as MaNGA, we have an opportunity to spectroscopically resolve the spatial profiles of galaxy populations on an unprecedented scale, but not to spatially resolve the individual stars therein, nor necessarily to spectroscopically resolve their velocity dispersions at radii of interest. Consequently no tool has existed to probe the AVR in these galaxies despite the recent wealth of IFS data.
In this paper we have developed two algorithms to efficiently measure the asymmetric drift (which depends only on an accurate measure of tangential speed) in modern IFS data for spatially-unresolved stellar populations. Using these algorithms we have presented the first measurements of asymmetric drift in two stellar age components for seven galaxies from the MaNGA survey. Since asymmetric drift can be used as a proxy for velocity dispersion, combined with age information for multiple components, the measurement of AVR in external galaxies is now possible in unresolved star-light. Future efforts to increase the number of age components will further enhance our ability to broadly constrain AVR.
In Section III we tested the hypothesis via a MCMC analysis that the observed MaNGA galaxy spectra contain sufficient information between 360 to 940 nm to constrain velocities for a young and old stellar component, as well as a gas component. We demonstrate not only that the two stellar components have distinct kinematics but also that the best-fitting kinematics for our galaxy sample have velocity and velocity dispersion maps that are reasonably smooth and have the expected trends with radius and azimuth. The measured tangential velocities for the two stellar components are also qualitatively consistent with that observed for nearby galaxies with resolved stellar populations, i.e., the young stellar component has a higher measured tangential velocity than its older counterpart. The radial profiles of the derived fraction of young to old stellar components (yfrac), which for the purpose of our analysis was split at an age of 1.5 Gyr, rise with radius, also in agreement with expectations. These results demonstrate, respectively, that the random and systematic errors in measured velocities for young and old stellar populations are small. We show these errors are sufficiently small to independently measure the asymmetric drift for at least two age-components in spiral galaxies using MaNGA IFU data. This opens the possibility for the whole-sale exploration of thin and thick-disk properties in today’s galaxy population.
Since our MCMC analysis is computationally prohibitive for application to large data-sets, in Section IV we developed an algorithm using SSP models to disentangle the kinematics of the young and old component as accurately as the MCMC method at a fraction of the computational cost. Due to the astrophysical degeneracies between age and metallicity on the appearance of the integrated-light spectra, our more efficient SSP algorithm – that uses a local minimizer based on pPXF – is more robust at lower S/N than the global minimization inherent to the MCMC analysis.
While the results of our SSP-based algorithm are promising, because the asymmetric drift signal is small (of order 10’s of ), there remains the perennial but rarely addressed concern in studies of galaxy kinematics of what systematic effects template-mismatch could have on our conclusions. Rather than dismiss the concern out of hand, we present an estimate of what we might expect for systematics on tangential velocity due to template mismatch (Section V). The potential effect is large enough to warrant attention. We therefore developed an independent algorithm in Section VI based on empirical stellar spectra rather than SSPs; the former are known to minimize the effect of template mismatch. This algorithm is also computationally efficiency and robust at low S/N.
Leveraging the results from the analysis of our seven galaxy sample in Section VII, we use (i) the posterior probability distribution from our MCMC analysis to estimate random errors on our derived two-age component stellar tangential velocities; and (ii) and the difference between our SSP and stellar-library algorithms to estimate our systematic errors. This analysis indicates that reliable measurements require S/N (per Å) above 10. While random errors dominate at the spaxel level, systematic errors (which are of order 5 to 20 deprojected) dominate in radial bins containing 10’s of spaxels.
We find the measured asymmetric drift for the young and old components are clearly distinct for 6 of our 7 galaxies with rotation speeds above 200 . The asymmetric drift for the young stellar component is always close to zero, as expected, but in some cases is consistent with non-zero values (10 to 20 ). The old stellar component has significantly (roughly a factor of 2) larger asymmetric drift value than what would be inferred from an asymmetric drift measurement adopting only a single stellar component. There is a wide range in old-component asymmetric drift signals from 20 to 150 (a factor of 7) at large radii in disks with rotation speeds varying only from 200 to 350 (a factor 2). This indicates there is much to learn about the statistical properties and potentially a wide range of evolutionary histories of disk populations with MaNGA and other IFS surveys.
Appendix A Stellar Template Library
| Spectral type | ||||||
|---|---|---|---|---|---|---|
| Index | HD | SIMBAD | Pickles | [Fe/H] | ||
| 0 | 30614 | O9.5Iae | A0I | 29647 | 3.05 | |
| 1 | 34816 | B0.5IV | B2IV | 29890 | 4.22 | |
| 2 | 180163 | B2.5IV | B2IV | 17360 | 3.38 | |
| 3 | 207330 | B3III | B3III | 19470 | 3.49 | |
| 4 | 51309 | B3Ib/II | B3I | 17390 | 2.7 | |
| 5 | 41692 | B5IV | B6IV | 14400 | 3.12 | |
| 6 | 155763 | B6III | B5III | 12900 | 3.9 | |
| 7 | 35497 | B7III | B9III | 13622 | 3.8 | |
| 8 | 34797 | B8/B9IV: | B8V | 14000 | 4.5 | |
| 9 | 175640 | B9III | B9III | 12100 | 4.0 | |
| 10 | 105262 | B9 | A0I | 8542 | 1.5 | |
| 11 | 18296 | B9p… | B9III | 11200 | 3.0 | |
| 12 | 87737 | A0Ib | A0I | 9700 | 2.0 | |
| 13 | 183324 | A0V | A0V | 9260 | 4.22 | |
| 14 | 198001 | A1V | A2V | 9470 | 3.64 | |
| 15 | 14489 | A2Ia | A2I | 9000 | 1.4 | |
| 16 | 223385 | A3Iae | A2I | 9333 | 1.0 | |
| 17 | 34578 | A5II | A5III | 8300 | 1.85 | |
| 18 | 36673 | F0Ib | F0I | 7400 | 1.1 | |
| 19 | 25291 | F0II | F0II | 7600 | 1.5 | |
| 20 | 90277 | F0V | F0V | 7412 | 3.46 | |
| 21 | 33276 | F2IV | F02IV | 7099 | 3.3 | |
| 22 | 184266 | F2V | F2V | 5713 | 2.64 | |
| 23 | 168151 | F5V | F5V | 6587 | 4.09 | |
| 24 | 134083 | F5V | F5V | 6632 | 4.5 | |
| 25 | 108954 | F9V | F8V | 6060 | 4.35 | |
| 26 | 92125 | G2.5IIa | G5II | 5600 | 2.1 | |
| 27 | 126868 | G2IV | G2IV | 5521 | 3.3 | |
| 28 | 106210 | G3V | G2V | 5337 | 4.0 | |
| 29 | 117176 | G5V | G5V | 5480 | 3.83 | |
| 30 | 47731 | G5Ib | G5I | 4990 | 1.0 | |
| 31 | 131156 | G8V | G8V | 5500 | 4.6 | |
| 32 | 106714 | G8III | G8III | 4897 | 2.34 | |
| 33 | 107383 | G8III | G8III | 4690 | 2.91 | |
| 34 | 104985 | G9III | G8III | 4658 | 2.2 | |
| 35 | 191026 | K0IV | K0IV | 5150 | 3.49 | |
| 36 | 124897 | K1.5III | K1III | 4300 | 1.5 | |
| 37 | 149661 | K2V | K2V | 5362 | 4.56 | |
| 38 | 121146 | K2IV | K3IV | 4400 | 1.85 | |
| 39 | 105043 | K2III | K2III | 4374 | 2.67 | |
| 40 | 175545 | K2III | K2III | 4429 | 2.94 | |
| 41 | 110281 | K5 | K5V | 3950 | 0.2 | |
| 42 | 113996 | K5III | K5III | 3970 | 1.69 | |
| 43 | 237903 | K7V | K7V | 4070 | 4.7 | |
| 44 | 102212 | M1III | M1III | 3761 | 1.5 | |
| 45 | 39801 | M1 | M2I | 3540 | 0.0 | |
| 46 | 36389 | M2Iab: | M2I | 3706 | 0.7 | |
| 47 | 112300 | M3III | M3III | 3700 | 1.3 | |
| 48 | 44478 | M3III | M3III | 3450 | 1.0 | |
| 49 | 148783 | M6III | M6III | 3250 | 0.2 | |
| 50 | 126327 | M7.5 | M8III | 3000 | 0.0 | |
The Indo-US Library of Coudé Feed Stellar Spectra (Valdes et al., 2004) is an empirical stellar spectral library of 1,273 stars with broad coverage of stellar types and with spectra spanning from 346.5–946.9 nm with a resolution (FWHM) of 0.135 nm sampled at 0.044 nm pixel-1. The wavelength range is important because it includes strong metal features in the red, such as the Ca Triplet, which we anticipate will constrain the kinematics of old populations in galaxy spectra that are dominated in the blue by younger stellar populations. The spectral resolution is roughly twice the spectral resolution as MaNGA data. Using a library with higher spectral resolution to that of MaNGA allows for a simple accounting of the difference in the line spread function between the galaxy spectra and templates. For this reason we have not used the MaStar library (Yan et al., 2019) which otherwise is superior in stellar parameter coverage and calibration. While the diversity of stellar types is important to minimize effects of template mismatch we believe the Indo-US Library is sufficient for our purposes. From this library we select a subset of 51 stars which represent and span the stellar parameters in and of the complete library.
The sub-sample of 51 stars from the Indo-US Coudé Feed Stellar Library (Valdes et al., 2004) covers stellar spectral types O to M. Table A1 gives the internal index used in this analysis and corresponding HD number; classification and spectral types and atmospheric parameters are repeated from Table 3 of Valdes et al. (2004, references for these parameters are therein). We have included both the Simbad database121212SIMBAD is operated at CDS, Strasbourg, France. and Pickles (1998) spectral types to point out inconsistencies between different spectral types and temperatures, although luminosity classes and surface-gravities appear to be more consistent. Of particular note is HD 30614, which is plainly an O-star given the relative strength of He to H lines, but also suffers from significant redenning given its continuum shape; the SIMBAD spectral type is preferred, as corroborated by its estimated surface temperature. This illustrates some of the perils of mapping stellar libraries for population synthesis and also why polynomials are often required in, e.g., pPXF, to both fit the relative line-strengths and continuum shape. A number of other stars are clearly mis-typed according to their surface-temperature, but given the coarse binning into hot, intermediate and cool stars for this study, this is not of significance for our purposes.
As Table A1 shows, we have selected a wide range of luminosity classes for all spectral types, although Main Sequence stars dominate at intermediate temperatures (late-A through mid-G), and giants dominating for the cooler stars (late-G and later). Our thinking in this selection was as follows. All of the earliest-types are massive, short-lived stars. At the other extreme in temperature, we expect the light to be dominated by giants, with the exception of very early ages where red super-giants may be significant, depending on metallicity. There is, in principle, an uncomfortable intermediate temperature (types A-F) where significant contributions can come either from the Main Sequence or a blue horizontal branch from old, metal-poor populations. The selected subset should offer sufficient flexibility to cover these various conditions.
In the pPXF decompositions of the MIUSCAT SSPs we find five stars are given zero or near-zero maximum weight (#4,10,12,15,44,50). These are either hot super-giants (3) or cool giants (2). In contrast there are 11 stars (#8,9,14,21,23,24,25,29,33,37,40) that either contribute more than 20% of the weight in a single SSP or an average weight above 5% across all SSPs (the mean values for the full sample is 11% and 2% respectively). These contain stellar types between late-B and early K, with mostly main-sequence B,A,F,G, stars and late-G and early-K giants. The remainder of the stars appear significant in aggregate, but we have made no attempt to define a minimal subset, and certainly would not want to do so based on SSPs. The purpose here is to indicate that this library, while not unique, should be capable of representing of a broad range of stellar populations, and the stars selected by pPXF to represent SSPs seem sensible.
Appendix B MCMC Posterior Probability Distribution: Bi-modality

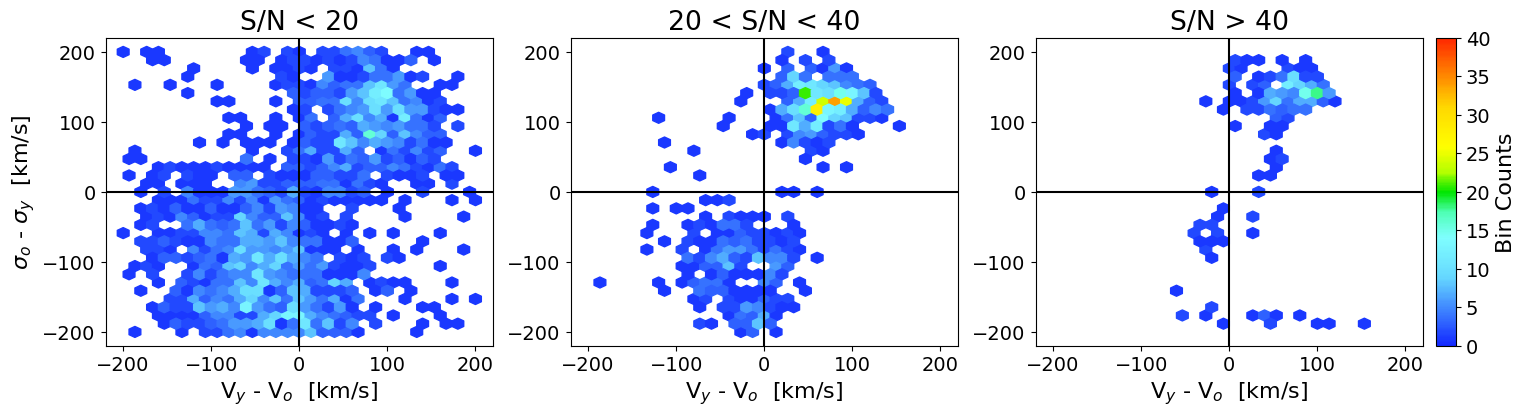
We take advantage of the MCMC posterior probability distribution (PPD) to understand the complexity of the likelihood space of the two-component kinematic model tested in Section III. We use this understanding to assess the reliability of the MCMC results.
For a normally distributed PPD, the best-fitting parameter and its uncertainty can be quantified by the mean and standard deviation of the PPD. However, such a quantification becomes problematic when the PPD is not unimodal; the first moment may not correspond to a parameter value at either a local or global minima in . We find there are cases where the PPD displays a bimodal distribution in the difference between young and old stellar population velocities () and the difference between old and young velocity dispersions (). Figure B1 presents examples of this behavior within the steps of the MCMC walkers. These steps are color-coded by the relative likelihood of the solution at that step. In each case the steps outline two very different combinations of parameters with near-equal high likelihood. We have therefore adopted the best-fitting parameters from the MCMC analysis as those which have the maximum likelihood. In these particular cases the maximum likelihood occurs where and , i.e., where the old population is rotating more quickly and is dynamically colder than the young population. We refer to this as a ‘flipped’ solution.
Figure B2 illustrates and from the maximum likelihood solution of the MCMC for all seven of our galaxies as a function of S/N. At low S/N a portion of the spaxels the maximum likelihood solution from the MCMC is in the bottom-left quadrant (with negative and ); the kinematics of young and old components are flipped in a significant fraction of low S/N spaxels. The spatial distribution of the flipped spaxels appears random, and there are no significant correlations observed with other parameters, e.g., yfrac. These facts suggest that the presence of these flipped results aren’t astrophysical, but rather they demonstrate the sensitivity of the spectral-fitting maximum likelihood solution. This sensitivity is due to the presence of multiple (principally two), discrete local minima, as seen in Figure B1. Based on a bootstrap analysis we find these minima become shallower at lower S/N. Since we begin the walkers in the upper-right portion of the parameter space (Section III), at lower S/N the walkers will more easily find a maximum likelihood solution in a flipped portion of parameter space.
The presence of these two local minima with discrete kinematics is not fully understood. One possible cause may be the degeneracy of the spectral features in the components of the young and old stellar population. Upon inspection of the derived young and old spectra in these flipped cases, we find they retain their overall spectral energy distribution: The young spectrum is bluer than the old spectrum. While there are more subtle differences in the strengths of the spectral features when comparing the spectrum of each stellar component, these differences have not yet pointed to a solution for eliminating the degeneracy in the kinematic solutions.
Results from previous studies and theoretical expectations of the AVR of galaxies (see Section I) strongly suggest that the older stellar populations of the galaxy disk tend to a lower tangential velocity and be dynamically hotter than their young counterparts, i.e. and . Placing this prior upon our MCMC results and noting the near-equal of the two minima, we believe that we have a strong case to ignore the spaxels with flipped kinematics. For our non-MCMC algorithms, where we use local minimization, we rely successfully on initial conditions to largely eliminate these flipped cases and converge onto solution consistent with previous studies and theoretical expectations. Hence for quantitative comparison between our algorithms and the MCMC results we ignore spaxels where the measured maximum likelihood solution has negative and .
Appendix C Mock Spectra
Mock spectra were generated to assess the effectiveness of different techniques to measure the kinematics of multiple stellar-population components. These consist of ‘Simple’ and ‘Realistic’ mocks, as follows. The ‘Simple’ mocks were useful in the early of our stellar-library algorithm development, while the ‘Realistic’ mocks provided an early check on our SSP algorithms.
‘Simple mocks’ are composite stellar populations made up of two SSPs with differing kinematics. For each mock one SSP is selected at random from a subset of SSPs with young ages ( 1.5Gyr), and a second from a subset with ages greater than 1.5 Gyrs (see Section II.5). Each SSP in a mock is shifted in velocity and convolved with a Gaussian to mimic a LOSVD for each population. The velocity and velocity dispersion of the young population is determined at random within the bounds of 100-350 and 5-50 respectively. The velocity dispersion of the old population is randomly assigned between the velocity dispersion of the young population and 100 . The velocity of the old population is then determined such that the quadrature sum of the velocity and velocity dispersion of the two populations are equal. The convolved spectra are then added together after being randomly normalized randomly between the wavelength range 360-900A nm, allowing our simple mock spectra to crudely approximate a range star formation histories.
‘Realistic’ mocks aim to simulate what we expect to observe in MaNGA spectra of external galaxies in terms of more realistic star-formation histories (SFH) but retaining a simple prescription for the age-velocity relation (AVR).131313We also constructed mocks with a range of realistic AVRs, but we found this added complexity made the interpretation of recovered values more ambigous, and hence of less use for algorithm development. Our mocks consist of a set of 2,500 spectra using the MIUSCAT SSP library described in Section II.4 with randomly generated parameters for their SFH, chemical evolution and AVR relationship.
We adopt the parametric star-formation model recommended by Simha et al. (2014) based on their analysis of smooth-particle hydrodynamical simulations. This model accurately recovers the physical properties of their simulated data in terms of mass-to-light ratio, population ages, and specific star formation rates. The star-formation model is a combination of one function describing an initial burst with time-scale initiated at and a normalization factor , followed by a linear function with slope after a transition-time :

| Algorithm | Failure Fraction | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Range | med | med | med | median | Cat | Flip | High | |||||||||
| () | () | () | ||||||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | ||||
| Simple SSP | [10,35] | 0.12 | 0.20 | 0.08 | 0.13 | 1.00 | 0.02 | -0.03 | 0.01 | 0.00 | 0.00 | 0.02 | ||||
| Simple SSP | [35,50] | 0.22 | 0.16 | 0.16 | 0.24 | 1.00 | 0.01 | -0.03 | 0.01 | 0.00 | 0.01 | 0.06 | ||||
| Simple SSP | 50 | 0.23 | 0.15 | 0.15 | 0.28 | 1.00 | 0.01 | -0.03 | 0.01 | 0.00 | 0.02 | 0.03 | ||||
Note. — The Simple SSP algorithm (column 1) is described in Section IV.1. Three bins in for the mocks () given in column (2) contain 678, 263, and 996 mocks, respecitvely from low to high . Columns (3) to (10) are defined identically to the corresponding columns in Table 5 except they are referenced to the ‘Realistic’ mock model values instead of the MCMC results. Columns (11) to (13) are defined in the text.
| (C1) |
The time of the initial burst () and the transition time () are randomly selected from normal distributions centered at Gyr and Gyr, respectively; the timescale of the initial burst () is randomly selected from a uniform distribution within the bounds 1 and 10 Gyr; is randomly selected from an uniform distribution between -0.5 and 0.5.
We implement a simple model for chemical evolution. The oldest stellar population in the mocks begin with a metallicity of -0.66 dex, i.e., the lowest metallicity of the MIUSCAT SSP models (Section II.4). At every stellar age increment the metallicity of the SSP model to be added to the mock (and those that will follow) may increase by one step in metallicity index with a probability of 0.15, up to the maximum metallicity of 0.26 dex.
The AVR model changes the stellar kinematics as a step function: the velocity and velocity dispersion of the young stellar population, ages 1.5 Gyrs and younger, are derived randomly from a uniform distribution within the range of 100 to 250 for velocity and 10 to 30 for velocity dispersion. The velocity dispersion of the old stellar population, with ages more than 1.5 Gyrs, is also randomly drawn from a uniform distribution between 50 and 100 . Based on these already drawn kinematics, the velocity for the older populations is derived such that the quadrature sum of the velocity and velocity dispersion of the spectra remains constant, i.e. . Hence within the two categories of ages, the SSP models are assigned identical kinematics. The purpose of this AVR model is to test the impact of providing realistic SFH in the context of clearly defined, albeit simple, model kinematics. The range of kinematics of the mocks are similar to those seen in real galaxies.
C.1. Performance of the Simple SSP Algorithm on Mock Spectra
‘Realistic’ mock spectra were used to test the abilities of the simple (1-step) SSP algorithm to disentangle the velocities of young and old stellar populations. We define metrics similar to those given in Tables 3 and 5, presented here in Table C1; these metrics reference the mock spectra model values rather than the MCMC derived values from real data. We also tabulate failure fractions defined as follows: ‘Cat’ are instances where either one of the measured velocities is more than 100 from the model velocity. ‘Flip’ are instances where . ‘High’ are instances where yfrac . High yfrac values are indicative of an incorrect allocation of cool stars to the young kinematic component.
| Algorithm | TPL | Failure Fraction | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| set | Range | med | med | med | median | Cat | Flip | High | |||||||||
| () | () | () | |||||||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | ||||
| Feature | A | [10,35] | 26.8 | 14.8 | -6.8 | 5.5 | -0.92 | 1.07 | 0.24 | 0.13 | 0.09 | 0.82 | 0.00 | ||||
| Feature | A | [35,50] | 21.5 | 13.4 | -19.9 | 11.2 | -0.05 | 0.58 | 0.20 | 0.12 | 0.10 | 0.52 | 0.00 | ||||
| Feature | A | 50 | 20.8 | 10.5 | -44.1 | 24.4 | 0.10 | 0.42 | 0.21 | 0.13 | 0.09 | 0.43 | 0.00 | ||||
| Feature | B | [10,35] | 18.9 | 10.4 | -7.3 | 7.0 | -0.78 | 1.06 | 0.10 | 0.11 | 0.02 | 0.74 | 0.00 | ||||
| Feature | B | [35,50] | 14.4 | 6.0 | -8.6 | 11.1 | 0.47 | 0.40 | 0.01 | 0.08 | 0.02 | 0.35 | 0.00 | ||||
| Feature | B | 50 | 13.2 | 4.6 | -7.1 | 13.2 | 0.72 | 0.22 | -0.03 | 0.05 | 0.05 | 0.23 | 0.01 | ||||
| Feature | C | [10,35] | 14.0 | 5.1 | 44.0 | 66.2 | 3.01 | 4.17 | -0.20 | 0.19 | 0.43 | 0.29 | 0.45 | ||||
| Feature | C | [35,50] | 13.4 | 5.5 | 15.8 | 27.2 | 1.21 | 0.81 | -0.13 | 0.06 | 0.26 | 0.15 | 0.22 | ||||
| Feature | C | 50 | 13.6 | 4.7 | 18.3 | 16.6 | 1.10 | 0.26 | -0.11 | 0.04 | 0.22 | 0.08 | 0.21 | ||||
| Feature | D | [10,35] | 15.7 | 4.5 | 49.7 | 104.0 | 2.72 | 5.64 | -0.32 | 0.21 | 0.46 | 0.28 | 0.65 | ||||
| Feature | D | [35,50] | 18.0 | 6.7 | 34.7 | 37.3 | 1.44 | 0.96 | -0.28 | 0.14 | 0.31 | 0.12 | 0.54 | ||||
| Feature | D | 50 | 17.9 | 6.5 | 57.6 | 45.2 | 1.49 | 0.55 | -0.21 | 0.11 | 0.38 | 0.06 | 0.47 | ||||
| Full | A | [10,35] | 17.4 | 4.4 | -5.9 | 5.1 | -0.26 | 0.36 | 0.24 | 0.12 | 0.04 | 0.69 | 0.00 | ||||
| Full | A | [35,50] | 17.1 | 4.8 | -20.2 | 10.5 | 0.12 | 0.32 | 0.21 | 0.12 | 0.04 | 0.40 | 0.00 | ||||
| Full | A | 50 | 15.8 | 5.6 | -43.8 | 23.8 | 0.23 | 0.32 | 0.21 | 0.13 | 0.05 | 0.32 | 0.00 | ||||
| Full | B | [10,35] | 15.8 | 4.7 | -6.7 | 6.0 | -0.33 | 0.50 | 0.03 | 0.09 | 0.03 | 0.69 | 0.02 | ||||
| Full | B | [35,50] | 15.1 | 5.8 | -8.7 | 11.4 | 0.39 | 0.46 | 0.00 | 0.07 | 0.06 | 0.36 | 0.01 | ||||
| Full | B | 50 | 11.4 | 5.0 | -4.7 | 13.1 | 0.79 | 0.24 | -0.02 | 0.04 | 0.08 | 0.23 | 0.03 | ||||
| Full | C | [10,35] | 12.1 | 4.0 | 160.5 | 177.1 | 9.11 | 10.04 | -0.30 | 0.22 | 0.57 | 0.21 | 0.60 | ||||
| Full | C | [35,50] | 12.2 | 6.4 | 27.7 | 69.3 | 1.58 | 2.20 | -0.16 | 0.10 | 0.44 | 0.16 | 0.42 | ||||
| Full | C | 50 | 10.7 | 4.6 | 26.7 | 27.0 | 1.27 | 0.42 | -0.12 | 0.04 | 0.36 | 0.10 | 0.31 | ||||
| Full | D | [10,35] | 13.4 | 3.6 | 265.2 | 375.5 | 18.06 | 24.56 | -0.36 | 0.22 | 0.66 | 0.18 | 0.71 | ||||
| Full | D | [35,50] | 16.2 | 6.9 | 158.5 | 164.1 | 4.13 | 3.77 | -0.38 | 0.22 | 0.59 | 0.17 | 0.69 | ||||
| Full | D | 50 | 16.1 | 7.6 | 109.5 | 99.4 | 2.18 | 1.17 | -0.26 | 0.15 | 0.55 | 0.10 | 0.60 | ||||
Note. — Simple stellar library algorithms (column 1) are described in Section VI.2; the Full algorithm using template set B is identified as ‘Simple SL’ in Tables 5 and C3. Column definitions and mock number are the same as in Table C1, with the addition of the template set in column (2) and the referencing of ‘Simple’ rather than ‘Realistic’ mocks.
Figure C1 presents the performance for on of the metrics, where , the ‘mock’ values are the input velocities used to generate the models, and the ‘algorithm’ values are the recovered values. The histograms are divided into four groups based on the strength of the signal in the mock spectra: , , and . For this metric, a value of 1 suggests a successful disentanglement of the velocities of the two components, while other values can give clues to the cause of failure in the measurement. As examples: A value of -1 indicates instances when the derived velocities of the two components are flipped (the velocity of the young is measured by the old component and vice versa). Values between -1 and 1 are likely caused by an over estimation of the velocity dispersion of one component. Very large positive or negative values suggest the observed spectrum has been reproduced by only one component and the other has been used only to minimize the of the solution.
For all mock groups, the distribution of the performance metric peaks at 1, as it should, consistent with the result seen in Section III where we demonstrate that MaNGA/MaNGA-like spectra of galaxies can contain sufficient information on the kinematics of co-spatial stellar populations for disentanglement. The distribution width increases at smaller model velocity differences, , because the uncertainty in the measured velocity difference is constant in . Even for AD signals as low as 5-10 , 67% of the derived AD signals are within 10% of the expected value. Performance evaluation of this algorithm against real data is presented in SectionIV.1.
| Algorithm | Failure Fraction | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| range | med | med | med | median | Cat | Flip | High | |||||||||
| () | () | () | ||||||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | ||||
| Simple SL | [10,35] | 10.66 | 2.26 | -4.68 | 5.19 | -0.14 | 0.43 | 0.02 | 0.07 | 0.00 | 0.57 | 0.00 | ||||
| Simple SL | [35,50] | 6.20 | 3.52 | -4.34 | 7.61 | 0.74 | 0.25 | 0.01 | 0.04 | 0.00 | 0.26 | 0.00 | ||||
| Simple SL | 50 | 4.07 | 2.63 | -0.86 | 8.30 | 0.91 | 0.15 | -0.02 | 0.02 | 0.04 | 0.22 | 0.00 | ||||
| 2-Step 1-Bin SL | [10,35] | 12.06 | 3.43 | -4.52 | 4.86 | -0.18 | 0.41 | 0.10 | 0.11 | 0.00 | 0.60 | 0.00 | ||||
| 2-Step 1-Bin SL | [35,50] | 6.39 | 3.88 | -3.54 | 7.40 | 0.75 | 0.25 | 0.01 | 0.05 | 0.00 | 0.30 | 0.00 | ||||
| 2-Step 1-Bin SL | 50 | 3.62 | 2.35 | 1.14 | 5.46 | 0.96 | 0.09 | -0.02 | 0.02 | 0.02 | 0.17 | 0.00 | ||||
| 2-Step 3-Bin SL | [10,35] | 8.46 | 8.87 | -4.06 | 4.75 | 0.41 | 0.54 | -0.04 | 0.03 | 0.02 | 0.36 | 0.04 | ||||
| 2-Step 3-Bin SL | [35,50] | 8.93 | 8.73 | -17.1 | 15.54 | 0.41 | 0.39 | -0.05 | 0.03 | 0.02 | 0.26 | 0.07 | ||||
| 2-Step 3-Bin SL | 50 | 8.11 | 7.80 | -25.8 | 27.23 | 0.54 | 0.36 | -0.07 | 0.04 | 0.06 | 0.19 | 0.05 | ||||
C.2. Performance of Stellar Library Algorithms on Mock Spectra
Table C2 presents metrics using our ‘simple’ mocks for all simple stellar library algorithms described and discussed in Section VI.2. The adopted best simple algorithm corresponds to ‘Full’ with template set B.
Figure C2 shows two instances of a failed and successful fit of the simple stellar library algorithm using template set C, where the failed case is characterized by a high yfrac value .
Table C3 presents metrics using ‘realistic’ mocks for the best simple stellar library algorithm (Full with template set B); the two-step stellar library algorithm (2-Step 1-Bin S); and our final two-step stellar library algorithm that constrains the relative weight of young and old stellar components in three stellar temperature bins (2-Step 3-Bin).


Appendix D Maps
Figures D1-D6 contain maps of the following information for remaining six galaxies in our sample, formatted as Figure 2. Maps are displayed at the pixel level with no interpolation between pixels.
First (left) column: Kinematics (velocity and dispersion) of the ionized gas and single-component stellar population as well as the decomposition of the single-component stellar population into young and old, as presented by yfrac are presented in the following Figures. These are derived as the initial step of all algorithms developed in this paper.
Second column: Stellar velocity for the young stellar component for the five methods outlining the development in this paper. Top to bottom these are the simple SSP algorithm, and then two-step SSP algorithms with inferred initial conditions, and then constraints on yfrac; the two- and three-bin stellar library algorithms (with similar inferred initial conditions and constraints on yfrac.
Third column: Stellar velocity dispersion for the young stellar component, ordered as the previous column.
Fourth column: Stellar velocity for the old stellar component, ordered as the previous column.
Fifth column: Stellar velocity dispersion for the old stellar component, ordered as the previous column.






References
- Abadi et al. (2003) Abadi, M. G., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003, ApJ, 597, 21
- Abolfathi et al. (2018) Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42
- Aguado et al. (2019) Aguado, D. S., Ahumada, R., Almeida, A., et al. 2019, ApJS, 240, 23
- Andersen & Bershady (2013) Andersen, D. R., & Bershady, M. A. 2013, ApJ, 768, 41
- Aumer & Binney (2009) Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286
- Beasley et al. (2015) Beasley, M. A., San Roman, I., Gallart, C., Sarajedini, A., & Aparicio, A. 2015, MNRAS, 451, 3400
- Belfiore et al. (2016) Belfiore, F., Maiolino, R., Maraston, C., et al. 2016, MNRAS, 461, 3111
- Benson et al. (2004) Benson, A. J., Lacey, C. G., Frenk, C. S., Baugh, C. M., & Cole, S. 2004, MNRAS, 351, 1215
- Bird et al. (2013) Bird, J. C., Kazantzidis, S., Weinberg, D. H., et al. 2013, ApJ, 773, 43
- Blanton et al. (2011) Blanton, M. R., Kazin, E., Muna, D., Weaver, B. A., & Price-Whelan, A. 2011, AJ, 142, 31
- Blanton et al. (2017) Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28
- Bournaud et al. (2009) Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1
- Brook et al. (2004) Brook, C. B., Kawata, D., Gibson, B. K., & Freeman, K. C. 2004, ApJ, 612, 894
- Bruzual & Charlot (2003) Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000
- Bundy et al. (2015) Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7
- Cappellari (2017) Cappellari, M. 2017, MNRAS, 466, 798
- Cappellari et al. (2007) Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418
- Carlberg et al. (1985) Carlberg, R. G., Dawson, P. C., Hsu, T., & Vandenberg, D. A. 1985, ApJ, 294, 674
- Cenarro et al. (2001) Cenarro, A. J., Cardiel, N., Gorgas, J., et al. 2001, MNRAS, 326, 959
- Coccato et al. (2011) Coccato, L., Morelli, L., Corsini, E. M., et al. 2011, MNRAS, 412, L113
- Collins et al. (2011) Collins, M. L. M., Chapman, S. C., Ibata, R. A., et al. 2011, MNRAS, 413, 1548
- Croom et al. (2012) Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872
- Dalcanton & Stilp (2010) Dalcanton, J. J., & Stilp, A. M. 2010, ApJ, 721, 547
- Davis et al. (2013) Davis, T. A., Alatalo, K., Bureau, M., et al. 2013, MNRAS, 429, 534
- De Bruyne et al. (2004) De Bruyne, V., De Rijcke, S., Dejonghe, H., & Zeilinger, W. W. 2004, MNRAS, 349, 461
- den Brok et al. (2020) den Brok, M., Carollo, C. M., Erroz-Ferrer, S., et al. 2020, MNRAS, 491, 4089
- Dorman et al. (2015) Dorman, C. E., Guhathakurta, P., Seth, A. C., et al. 2015, ApJ, 803, 24
- Drory et al. (2015) Drory, N., MacDonald, N., Bershady, M. A., et al. 2015, AJ, 149, 77
- Falcón-Barroso et al. (2011) Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95
- Few et al. (2012) Few, C. G., Gibson, B. K., Courty, S., et al. 2012, A&A, 547, A63
- Forbes et al. (2012) Forbes, J., Krumholz, M., & Burkert, A. 2012, ApJ, 754, 48
- Foreman-Mackey et al. (2013) Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306
- Förster Schreiber et al. (2009) Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364
- González Delgado et al. (2015) González Delgado, R. M., García-Benito, R., Pérez, E., et al. 2015, A&A, 581, A103
- Goodman & Weare (2010) Goodman, J., & Weare, J. 2010, Communications in Applied Mathematics and Computational Science, Vol. 5, No. 1, p. 65-80, 2010, 5, 65
- Gunn et al. (2006) Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332
- Helmi et al. (2012) Helmi, A., Sales, L. V., Starkenburg, E., et al. 2012, ApJ, 758, L5
- Holmberg et al. (2007) Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519
- House et al. (2011) House, E. L., Brook, C. B., Gibson, B. K., et al. 2011, MNRAS, 415, 2652
- Huang & Carlberg (1997) Huang, S., & Carlberg, R. G. 1997, ApJ, 480, 503
- Johnston et al. (2013) Johnston, E. J., Merrifield, M. R., Aragón-Salamanca, A., & Cappellari, M. 2013, MNRAS, 428, 1296
- Katkov & Chilingarian (2012) Katkov, I. Y., & Chilingarian, I. V. 2012, in IAU Symposium, Vol. 284, The Spectral Energy Distribution of Galaxies - SED 2011, ed. R. J. Tuffs & C. C. Popescu, 69–71
- Kokubo & Ida (1992) Kokubo, E., & Ida, S. 1992, PASJ, 44, 601
- Kroupa (2001) Kroupa, P. 2001, MNRAS, 322, 231
- Law et al. (2007) Law, D. R., Steidel, C. C., Erb, D. K., et al. 2007, ApJ, 669, 929
- Law et al. (2015) Law, D. R., Yan, R., Bershady, M. A., et al. 2015, AJ, 150, 19
- Law et al. (2016) Law, D. R., Cherinka, B., Yan, R., et al. 2016, AJ, 152, 83
- Leaman et al. (2017) Leaman, R., Mendel, J. T., Wisnioski, E., et al. 2017, MNRAS, 472, 1879
- Levy et al. (2018) Levy, R. C., Bolatto, A. D., Teuben, P., et al. 2018, ApJ, 860, 92
- Licquia et al. (2016) Licquia, T. C., Newman, J. A., & Bershady, M. A. 2016, ApJ, 833, 220
- Licquia et al. (2015) Licquia, T. C., Newman, J. A., & Brinchmann, J. 2015, ApJ, 809, 96
- Martig et al. (2014) Martig, M., Minchev, I., & Flynn, C. 2014, MNRAS, 443, 2452
- Martinsson et al. (2016) Martinsson, T. P. K., Verheijen, M. A. W., Bershady, M. A., et al. 2016, A&A, 585, A99
- Nordström et al. (2004) Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989
- Pickles (1998) Pickles, A. J. 1998, PASP, 110, 863
- Pietrinferni et al. (2004) Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168
- Pinna et al. (2019) Pinna, F., Falcón-Barroso, J., Martig, M., et al. 2019, A&A, 623, A19
- Poci et al. (2019) Poci, A., McDermid, R. M., Zhu, L., & van de Ven, G. 2019, MNRAS, 487, 3776
- Quirk et al. (2019) Quirk, A., Guhathakurta, P., Chemin, L., et al. 2019, ApJ, 871, 11
- Rix & White (1992) Rix, H.-W., & White, S. D. M. 1992, MNRAS, 254, 389
- Ruiz-Lara et al. (2016) Ruiz-Lara, T., Few, C. G., Gibson, B. K., et al. 2016, A&A, 586, A112
- Ryś et al. (2013) Ryś, A., Falcón-Barroso, J., & van de Ven, G. 2013, MNRAS, 428, 2980
- Sánchez et al. (2012) Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8
- Sánchez-Blázquez et al. (2014) Sánchez-Blázquez, P., Rosales-Ortega, F. F., Méndez-Abreu, J., et al. 2014, A&A, 570, A6
- Seabroke & Gilmore (2007) Seabroke, G. M., & Gilmore, G. 2007, MNRAS, 380, 1348
- Seth et al. (2005) Seth, A. C., Dalcanton, J. J., & de Jong, R. S. 2005, AJ, 130, 1574
- Simha et al. (2014) Simha, V., Weinberg, D. H., Conroy, C., et al. 2014, ArXiv e-prints, arXiv:1404.0402
- Smee et al. (2013) Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32
- Spitzer & Schwarzschild (1951) Spitzer, Jr., L., & Schwarzschild, M. 1951, ApJ, 114, 385
- Spitzer & Schwarzschild (1953) —. 1953, ApJ, 118, 106
- Statler (1995) Statler, T. 1995, AJ, 109, 1371
- Strömberg (1925) Strömberg, G. 1925, ApJ, 61, 363
- Tabor et al. (2017) Tabor, M., Merrifield, M., Aragón-Salamanca, A., et al. 2017, MNRAS, 466, 2024
- Toloba et al. (2011) Toloba, E., Boselli, A., Cenarro, A. J., et al. 2011, A&A, 526, A114
- Toth & Ostriker (1992) Toth, G., & Ostriker, J. P. 1992, ApJ, 389, 5
- Valdes et al. (2004) Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251
- Vazdekis et al. (2012) Vazdekis, A., Ricciardelli, E., Cenarro, A. J., et al. 2012, MNRAS, 424, 157
- Wake et al. (2017) Wake, D. A., Bundy, K., Diamond-Stanic, A. M., et al. 2017, AJ, 154, 86
- Walker et al. (1996) Walker, I. R., Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121
- Weiner et al. (2006) Weiner, B. J., Willmer, C. N. A., Faber, S. M., et al. 2006, ApJ, 653, 1027
- Westfall et al. (2011) Westfall, K. B., Bershady, M. A., Verheijen, M. A. W., et al. 2011, ApJ, 742, 18
- Wielen (1977) Wielen, R. 1977, A&A, 60, 263
- Wisnioski et al. (2015) Wisnioski, E., Förster Schreiber, N. M., Wuyts, S., et al. 2015, ApJ, 799, 209
- Yan et al. (2016a) Yan, R., Bundy, K., Law, D. R., et al. 2016a, AJ, 152, 197
- Yan et al. (2016b) Yan, R., Tremonti, C., Bershady, M. A., et al. 2016b, AJ, 151, 8
- Yan et al. (2019) Yan, R., Chen, Y., Lazarz, D., et al. 2019, ApJ, 883, 175
- Zheng et al. (2017) Zheng, Z., Wang, H., Ge, J., et al. 2017, MNRAS, 465, 4572