Statistical Guarantees for Link Prediction using Graph Neural Networks
Abstract
This paper derives statistical guarantees for the performance of Graph Neural Networks (GNNs) in link prediction tasks on graphs generated by a graphon. We propose a linear GNN architecture (LG-GNN) that produces consistent estimators for the underlying edge probabilities. We establish a bound on the mean squared error and give guarantees on the ability of LG-GNN to detect high-probability edges. Our guarantees hold for both sparse and dense graphs. Finally, we demonstrate some of the shortcomings of the classical GCN architecture, as well as verify our results on real and synthetic datasets.
1 Introduction
Graph Neural Networks (GNNs) have emerged as a powerful tool for link prediction (Zhang & Chen, 2018; Zhang, 2022). A significant advantage of GNNs lies in their adaptability to different graph types. Traditional link prediction heuristics tend to presuppose network characteristics. For example, the common neighbors heuristic presumes that nodes that share many common neighbors are more likely to be connected, which is not necessarily true in biological networks (Kovács, 2019). In contrast, GNNs inherently learn predictive features through the training process, presenting a more flexible and adaptable method for link prediction.
This paper provides statistical guarantees for link prediction using GNNs, in graphs generated by the graphon model. A graphon is specified by a symmetric measurable kernel function . A graph with the vertex set is sampled from as follows: (i) each vertex draws latent feature for some probability distribution on ; (ii) the edges of are generated independently and with probability where is a constant called the sparsifying factor111Throughout the paper, we will assume . This is without loss of generality. For any graphon with features in some arbitrary sampled from on , there exists some graphon with latent features drawn from so that the graphs generated from these two graphons are equivalent in law. See Remark 4 in (Davison & Austern, 2023) for more details..
The graphon model includes various widely researched graph types, such as Erdos-Renyi, inhomogeneous random graphs, stochastic block models, degree-corrected block models, random exponential graphs, and geometric random graphs as special cases; see (Lovász, 2012) for a more detailed discussion.
This paper’s key contribution is the analysis of a linear Graph Neural Network model (LG-GNN) which can provably estimate the edge probabilities in a graphon model. Specifically, we present a GNN-based algorithm that yields estimators, denoted as , that converge to true edge probabilities . Crucially, these estimators have mean squared error converging to 0 at the rate . To our knowledge, this work is the first to rigorously characterize the ability of GNNs to estimate the underlying edge probabilities in general graphon models.
The estimators are constructed in two main steps. We first employ LG-GNN (Algorithm 1), to embed the vertices of . Concretely, for each vertex , LG-GNN computes a set where and is the embedding dimension. Then, are used to construct estimators for the moments of . We refer the reader to Section 4 for the formal definition of the moments. Intuitively, the th moment represents the probability that there is a path of length between vertices with latent features and in .
The next step is to show that when the number of distinct nonzero eigenvalues of , denoted , is finite, then the edge probabilities can be written as a linear function of the moments . This naturally motivates Algorithm 2, which learn the ’s from the moment estimators , using a constrained regression. The regression coefficients are then used to produce estimators for .
The main result of the paper (stated in Theorem 4.4) presents the convergence rate of the mean square error of . It shows that if , the number of message-passing layers in LG-GNN, is at least , then the mean square error converges to 0. That implies that our estimators for the edge probabilities are consistent. For , the theorem provides the rate at which the mean square error decreases when increases. The second main result, stated in Proposition 4.5, gives statistical guarantees on how well LG-GNN can detect in-community edges in a symmetric stochastic block model. A notable feature of this theorem is that the implied convergence rate is much faster than that of Theorem 4.4, which demonstrates mathematically that ranking high and low probability edges is easier than estimating the underlying probabilities of edges.
Finally, we would like to highlight two key aspects of the results of the paper. Firstly, our statistical guarantees for edge prediction are proven for scenarios when node features are absent and the initial node embeddings are chosen at random. This underscores that effective link prediction can be achieved solely through the appropriate selection of GNN architecture, even in the absence of additional node data. The second point relates to graph sparsity: although graphons typically produce dense graphs, introducing the sparsity factor results in vertex degrees of , facilitating the exploration of sparse graphs. Our findings are pertinent for . Note that a sparsity of is the necessary threshold for connectivity (Spencer, 2001), highlighting the generality of our results.
While the primary focus of this paper is theoretical, we complement our theoretical analysis with experimental evaluations on real-world datasets (specifically, the Cora dataset) and graphs derived from random graph models. Our empirical observations reveal that in scenarios where node features are absent, LG-GNN exhibits performance comparable to the traditional Graph Convolutional Network (GCN) on simple random graphs, and surpasses GCN in more complex graphs sampled from graphons. Additionally, LG-GNN presents two further benefits: LG-GNN does not involve any parameter tuning (e.g., through the minimization of a loss function), resulting in significantly faster operation, and it avoids the common oversmoothing issues associated with the use of numerous message-passing layers.
1.1 Organization of the Paper
Section 2 discusses related works and introduces the motivation for our paper. Section 3 introduces our notation and presents an outline for our exposition. Section 4 presents our main results and Section 5 states a negative result for naive GNN architectures with random embedding initialization. Lastly, Section 6 discusses the issues of identifiability, and Section 7 presents our experimental results.
2 Related Works
Link prediction on graphs have a wide range of applications in domains ranging from social network analysis to drug discovery (Hasan & Zaki, 2011; Abbas et al., 2021). A survey of techniques and applications can be found in (Kumar et al., 2020; Martínez et al., 2016; Djihad Arrar, 2023).
Much of the existing theory on GNNs is regarding their expressive power. For example, (Xu et al., 2018; Morris et al., 2021) show that GNNs with deterministic node initializations have expressive power bounded by that of the 1-dimensional Weisfeiler-Lehman (WL) graph isomorphism test. Generalizations such as -GNN (Morris et al., 2021) have been proposed to boost the expressive power higher in the WL-hierarchy. The Structural Message Passing GNN (SGNN) (Vignac et al., 2020) was also proposed and was shown to be universal on graphs with bounded degrees, and converges to continuous ”c-SGNNs” (Keriven et al., 2021), which were also shown to be universal on many popular random graph models. Lastly, (Abboud et al., 2020) showed that GNNs that use random node initializations are universal, in that they can approximate any function defined on graphs with fixed order.
A recent wave of works focus on deriving statistical guarantees for graph representation algorithms. A common data-generating model for the graph is a graphon model (Lovász & Szegedy, 2006; Borgs et al., 2008, 2012). A large literature has been devoted to establishing guarantees for community detection on graphons such as the stochastic block model; see (Abbe, 2018) for an overview. For this task, spectral embedding methods have long been proposed (see (Deng et al., 2021; Ma et al., 2021) for some recent examples). Lately, statistical guarantees for modern random walk-based graph representation learning algorithms have also been obtained. Notably (Davison & Austern, 2021; Barot et al., 2021; Qiu et al., 2018; Zhang & Tang, 2021) characterize the asymptotic properties of the embedding vectors obtained by deepwalk, node2vec, and their successors and obtain statistical guarantees for downstream tasks such as edge prediction. Recently, some works also aim at obtaining learning guarantees for GNNs. Stability and transferability of certain untrained GNNs have been established in (Ruiz et al., 2021; Maskey et al., 2023; Ruiz et al., 2023; Keriven et al., 2020). For example (Keriven et al., 2020) shows that for relatively sparse graphons, the embedding produced by an untrained GNN will converge in to a limiting embedding that depends on the underlying graphon. They use this to study the stability of the obtained embeddings to small changes in the training distribution. Other works established generalization guarantees for GNNs. Those depend respectively on the number of parameters in the GNN (Maskey et al., 2022), or on the VC dimension and Radamecher complexity (Esser et al., 2021) of the GNN.
Differently from those two lines of work, our paper studies when link prediction is possible using GNNs, establishes statistical guarantees for link prediction, and studies how the architecture of the GNN influences its performance. More similar to our paper is (Kawamoto et al., 2018), which exploits heuristic mean-field approximations to predict when community detection is possible using an untrained GNN. Note, however, that contrary to us, their results are not rigorous and the accuracy of their approximation is instead numerically evaluated. (Lu, 2021) formally established guarantees for in-sample community detection for two community SBMs with a GNN trained via coordinate descent. However, our work establishes learning guarantees for general graphons beyond two-community SBMs, both in the in-sample and out-sample settings. Moreover, the link prediction task we consider, while related to community detection, is still significantly different. (Baranwal et al., 2021) studies node classification for contextual SBMs and shows that an oracle GNN can significantly boost the performance of linear classifiers. Another related work (Magner et al., 2020) studies the capacity of GNN to distinguish different graphons when the number of layers grows at least as . Interestingly they find that GNN struggles in differentiating graphons whose expected degree sequence is not sufficiently heterogeneous, which unfortunately occurs for many graphon models, including the symmetric SBM. It is interesting to note that in Proposition 5.1 we will show that this is also the regime where the classical GCN fails to provide reliable edge probability prediction. Finally, some learning guarantees have also been derived for other graph models. Notably (Alimohammadi et al., 2023) studied the convergence of GraphSAGE and related GNN architectures under local graph convergence.
3 Notation and Preliminaries
In this section, we present our assumptions, some background regarding GNNs, and the link prediction goals that we focus on.
3.1 Assumptions
As mentioned in the introduction, the random graph with the vertex set is sampled from a graphon , where each vertex draws latent feature and the edges are generated independently and with probability We let denote the adjacency matrix. When the graph and context are clear, we let , and let . We make the following three assumptions:
| () | |||
| () | |||
| is a Hölder-by-parts function | () |
We refer the reader to Appendix B for a more detailed discussion.
3.2 Graph Neural Networks
An -layer GNN, comprised of processing layers, transforms graph data into numerical representations, or embeddings, of each each vertex. Concretely, a GNN associates each vertex to some where we call the embedding dimension. The learned embeddings are then used for downstream tasks such as node prediction, graph classification or link prediction, as investigated in this paper.
A GNN computes the embeddings iteratively through message passing. We let denote the embedding produced for vertex after GNN iterations. As such, denotes the initialization of the embedding for vertex . The message passing layer can be expressed generally as
where is the set of neighbors of vertex , are continuous functions, is the feature of the edge , and is some permutation-invariant aggregation operator, for example, the sum (Wu et al., 2022).
One classical architecture is the Graph Convolutional Network (GCN) (Kipf & Welling, 2017), whose update equation is given by
| (1) |
where is a non-linear function and are matrices. These matrices are chosen by minimizing some empirical risk during a training process, typically through gradient descent.
In some settings, additional node features for each vertex are given, and the initialization is chosen to incorporate this information. In this paper, we focus on the setting when no node features are present, and a natural way to initialize our embeddings is at random. One of our key messages is that even without additional node information, link prediction is provably possible with a correct choice of GNN architecture.
3.3 Link Prediction
Given a graph generated from a graphon, potential link prediction tasks are (a) to determine which of the non-edges are most likely to occur, or (b) to estimate the underlying probability of a particular edge according to the graphon. Here, we make the careful distinction between two different link prediction evaluation tasks. One task is regarding the ranking of a set of test edges. Suppose a set of test edges has underlying probabilities according to . The prediction algorithm assigns a predicted probability for each edge and is evaluated on how well it can extract the true ordering (e.g., the AUC-ROC metric).
Another link prediction task is to estimate the underlying probabilities of edges in a random graph model. For example, in a stochastic block model, a practitioner might wish to determine the underlying connection probabilities, as opposed to simply determine the ranking. We will refer to this task as graphon estimation. It is important to note that the latter task is generally more difficult.
We also distinguish between two link prediction settings, i.e., the in-sample and out-sample settings. In in-sample prediction, the aim is to discover potentially missing edges between two vertices already present at training time. On the contrary, in out-of-sample prediction, the objective is to predict edges among vertices that were not present at training. If are the set of vertices not present at training, the goal is to use the trained GNN to predict edges for , or for and
4 Main Results
We introduce the Linear Graphon Graph Neural Network, or LG-GNN in Algorithm 1. The algorithm starts by assigning each node a random feature where is the embedding dimension. The first message passing layer computes by summing for all , scaled by The subsequent layers normalize the ’s by before adding them to . We show in Proposition D.3 and Lemma D.4 that this procedure essentially counts the number of paths between pairs of vertices. Specifically, is a linear combination of the ”empirical moments” of (Equation 7). The second stage of Algorithm 1 then recovers these empirical moments by decoupling the aforementioned linear equations. We refer the reader to Section D.2 for more details and intuition behind LG-GNN.
We note that the scaling of in the first message passing layer is crucial in allowing the embedding vectors to learn information about the latent features asymptotically. We show in Proposition 5.1 that without this construction, the classical GCN is unable to produce meaningful emebddings with random feature initializations.
4.1 Statistical Guarantees for Moment Estimation
Define the th moment of a sparsified graphon as
which is the probability that there is a path of a length between two vertices with latent features , averaging over the latent features of the vertices in the path. As with the graphon itself, we denote The following proposition shows that the estimators are consistent estimators for these moments
Proposition 4.1.
Input: a Graph ;
Output: estimators for the th moments
Sample
GNN Iteration:
for do
Computing Estimators for : for do
4.2 Edge Prediction Using the Moments of the Graphon
Proposition 4.1 relates the embeddings produced by LG-GNN to the underlying graph moments. We show in Theorem 4.4 that the s can be used to derive consistent estimators for the underlying edge probability between vertices and .
The key observation is that for any Hölder-by-parts graphon , there exists some such that
for some sequence of eigenvalues with and eigenfunctions orthonormal in . This, coupled with the Cayley-Hamilton theorem (Hamilton, 1853), implies that can be re-expressed as a linear combination of its moments. We will refer to the number of distinct nonzero eigenvalues of as , which we call the distinct rank.
Proposition 4.2.
Suppose that is a Hölder-by-parts graphon. Then, there exists a vector such that for all ,
| (3) |
The above suggests the following algorithm for edge prediction using the embedding produced by LG-GNN.
Input: Graph , search space , threshold ; .
Output: Set of predicted edges
Using Algorithm 1, compute for every vertex
Compute:
Compute: for all
Return: the set of predicted edges.
Algorithm 2 estimates the edge probabilities by regressing the moment estimators onto the ’s. The coefficients of the regression are chosen through constrained optimization. This is necessary due to high multi-collinearity among the observations . Other methods to control the multi-collinearity include using Partial Least Squares (PLS) regression in Algorithm 2. This leads to an alternative algorithm presented in Algorithm 3, called PLSG-GNN, that is also evaluated in the experiments section.
Before stating our main theorem, we define a few quantities.
Definition 4.3 (MSE error).
For any vector , define the mean squared error
where the expectation is taken with respect to the randomness in . We interpret as being two new vertices that were not present at training time. We also define the following quantity, used in the statement of Theorem 4.4:
For some set , we can interpret as the “ projection” of onto the subspace spanned by . In particular, if contains a vector satisfying Equation 3, then In the context of Algorithm 2, this suggests that we can obtain a consistent estimator for Hence, since Proposition 4.2 guarantees that such a exists when , the intuition is that if both the search space and number of layers are sufficiently large, then Algorithm 2 should produce estimators that are consistent.
The following theorem shows that this intuition is indeed true. It states that is a consistent estimator for the edge probability if the number of LG-GNN layers is large enough, and characterizes its convergence rate. We will show this when the search space is a rectangle of the form for some . We discuss the implications of this result after its statement.
Theorem 4.4 (Main Theorem).
Let be sampled from some graphon , where satisfies () and (). Take to be the estimators given by Algorithm 2. Define to be the population minimizer. Then, with probability at least the MSE converges at rate
where and .
We remark that when increases quickly enough, the inequality in Theorem 4.4 implies that
In particular, when , and increases fast enough, then i.e. the MSE decreases faster than the sparsity of the graph.
As mentioned in the discussion preceeding Theorem 4.4, if the search space is large enough to contain some vector such that for all , then , and the MSE converges to 0. Notably, Proposition 4.2 implies that this search space exists for . In this sense, captures the “complexity” of , and each layer of LG-GNN extracts an additional order of complexity.
When , in order for the search space to contain the defined in Proposition 4.2, we require that where is defined in Theorem 4.4. Considering the proof of Proposition 4.2, if , then is on the order of , and hence the constant in Proposition 4.2 is on this order as well. This dependence on the inverse of small eigenvalues is a statistical bottleneck; it turns out, however, that if we are concerned only with edge ranking, instead of graphon estimation, this dependence can be greatly reduced. This is outlined in Proposition 4.5.
If Algorithm 2 is used for predicting all the edges that have a probability of more than of existing, then the - loss will also go to zero. Indeed for almost every we have
Furthermore, if is smaller than the number of distinct eigenvalues of , then we have
implying that the the in Theorem 4.4 decreases as increases. This latter bound is proved in Lemma F.1.
4.3 Preserving Ranking in Link Prediction
Theorem 4.4 states that under general conditions, LG-GNN yields a consistent estimator for the underlying edge probability However, estimating edge probabilities is strictly harder than discovering a set of high-probability edges. In practical applications, one often cares about ranking the underlying edges, i.e., whether an algorithm can assign higher probabilities to positive test edges than to negative ones. Metrics such as the AUC-ROC and Hits@k capture this notion. The following proposition characterizes the performance of LG-GNN in ranking edges in a -community symmetric SBM. See Section A.3 for more details about SBMs.
Before stating the proposition, we define the following notation for a -community symmetric SBM. Let , and define
to be the event that the predicted probabilities for all of the in-community edges are greater than all of the predicted probabilities for the across-community edges, i.e., LG-GNN achieves perfect ranking of the graph edges. We will prove that this event happens with high probability. See Proposition G.1 for the full proposition.
Proposition 4.5 (Informal).
Consider a -community symmetric stochastic block model with parameters and sparsity factor Let be the eigenvalues of the associated graphon. Suppose that the search space is such that .
Produce probability estimators for the probability of an edge between vertices and using Algorithm 1 and Algorithm 2 with parameters where . Then, there exists a constant such that when
holds, then with high probability, occurs, i.e., LG-GNN correctly predicts higher probability for all of the in-community edges than for cross-community edges.
Proposition 4.5 gives conditions under which LG-GNN achieves perfect ranking on a -community symmetric SBM. One subtle but important point is the implied convergence rate. In Proposition 4.5, the size of the search space is required only to be on the order of . In the notation of Theorem 4.4, this means that the constant is upper bounded by , which indicates a much faster rate of converge than the rate that is required by Theorem 4.4 to define consistent estimators. This confirms the intuition that ranking is easier than graphon estimation, and in particular, should be less sensitive to small eigenvalues. Proposition 4.5 demonstrates the extent to which ranking is easier than graphon estimation.
5 Performance of the Classical GCN Architecture
As mentioned in Section 4, in the context of random node initializations, a naive choice of GNN architecture can cause learning to fail. In the following proposition, we demonstrate that for a large class of graphons, the Classical GCN architecture with random initializations results in embeddings that cannot be informative in out-of-sample graphon estimation. To make this formal, we assume that at training, only vertices are observable. We denote by the induced subgraph with vertex set . And we consider graphons that are such that
| () |
Note that many graphons satisfy this assumption, including symmetric SBMs.
Proposition 5.1.
Suppose that the graph is generated according to a graphon . Moreover assume that Assumptions (), (), () hold.
Suppose that the initial embeddings are so that each coordinate is generated i.i.d. from a sub-Gaussian distribution. Assume that the subsequent embeddings are computed iteratively according to Equation 1, where is taken to be Lipschitz and where the weight matrices are trained on and satisfy .
Then, there exist random variables , that are independent of such that for a certain with probability at least ,
| (4) |
where is an absolute constant.
We show that this leads to suboptimal risk for graphon estimation. For simplicity we show this for dense graphons, e.g when .
Proposition 5.2.
Suppose that the conditions of Proposition 5.1 hold. Moreover assume that the graphon is not constant and that for all . Then, there exists some constant such that for any Lipchitz prediction rule , for all vertices we have
| (5) |
Proposition 5.1 and Proposition 5.2 imply that in the out-of-sample setting, the embeddings produced by Equation 1 with random node feature initializations will lead to sub-optimal estimators for the edge probability . A key feature of the proof of Proposition 5.1 is that concentrates to 0 very quickly with random node initializations. This demonstrates the importance of the (subtle) construction of the first round of message passing in Algorithm 1. We also note that Proposition 5.2 doesn’t necessarily imply that predicted probabilities will be ineffective at ranking test edges, though we do see in the experiments that the performance is decreased for the out-of-sample case.
6 Identifiability and Relevance to Common Random Graph Models
We remark that a key feature of LG-GNN is that it uses the embedding vector produced at each layer. Indeed depends on all of the terms . This is in contrast to many classical ways of using GNNs for link prediction that depend only on The following proposition shows that this construction is necessary to obtain consistent estimators.
Proposition 6.1.
For any , there exists a 2-community stochastic block model, such that for every continuous function we have
This notably implies that
To illustrate this, consider the following example for
Example 6.2.
Consider an 2 community symmetric SBM with edge connection probability matrix The matrix of second moments, that is, the matrix of probabilities of paths of length two between members of the two communities is Hence for any continuous function and every vertex belonging respectively to communities for and for then we have that and have the same limit. Hence this implies that no consistent estimator of can be built by using only
While this result is for the specific case of Algorithm 1, which in particular contains no non-linearities, we anticipate that this general procedure of learning a function that maps a set of dot products to a predicted probability, instead of just , can lead to better performance for practioners on various types of GNN architectures.
7 Experimental Results
We compare experimentally a GCN, LG-GNN, and PLSG-GNN. We perform experiments on the Cora dataset (McCallum et al., 2000) in the in-sample setting. We also show results for various random graph models. The results for random graphs below are in the out-sample setting, more results are in Appendix I. We report the AUC-ROC and Hits@k metric, and also a custom metric called the Probability Ratio@k, which is more suited to the random graph setting. We refer the reader to Appendix I for a more complete discussion.
LG-GNN and PLSG-GNN perform similarly to the classical GCN in settings with no node features and can outperform it on more complex graphons. One major advantage of LG-GNN/PLSG-GNN is that they do not require extensive tuning of hyperparameters (e.g., through minimizing a loss function) and hence run much faster and are easier to fit. For example, training the 4-layer GCN resulted in convergence issues, even on a wide set of learning rates.
7.1 Real Data: Cora Dataset
The following results are in the in-sample setting. We consider when (a) the GCN has access to node features (b) the GCN does not.
| Params | Model | Hits@50 | Hits@100 |
|---|---|---|---|
| layers=2 | GCN | 0.496 0.025 | 0.633 0.023 |
| LG-GNN | 0.565 0.012 | 0.637 0.006 | |
| PLSG-GNN | 0.591 0.014 | 0.646 0.013 | |
| layers=4 | GCN | 0.539 0.008 | 0.665 0.007 |
| LG-GNN | 0.564 0.005 | 0.620 0.008 | |
| PLSG-GNN | 0.578 0.014 | 0.637 0.013 |
| Params | Model | Hits@50 | Hits@100 |
|---|---|---|---|
| layers=2 | GCN | 0.753 0.019 | 0.898 0.021 |
| LG-GNN | 0.555 0.027 | 0.603 0.034 | |
| PLSG-GNN | 0.577 0.033 | 0.626 0.042 | |
| layers=4 | GCN | 0.609 0.072 | 0.776 0.069 |
| LG-GNN | 0.560 0.013 | 0.601 0.012 | |
| PLSG-GNN | 0.574 0.025 | 0.625 0.024 |
7.2 Synthetic Dataset: Random Graph Models
7.2.1 10-Community Symmetric SBM
The following are results for a 10-community stochastic block model with parameter matrix that has randomly generated entries. The diagonal entries are generated as , and is generated as . The specific connection matrix that was used is in Appendix I.
| Params | Model | P-Ratio@100 | AUC-ROC |
|---|---|---|---|
| layers=2 | GCN | 0.709 0.125 | 0.716 0.019 |
| LG-GNN | 0.883 0.016 | 0.734 0.005 | |
| PLSG-GNN | 0.886 0.016 | 0.735 0.005 | |
| layers=4 | GCN | 0.645 0.025 | 0.578 0.109 |
| LG-GNN | 0.879 0.011 | 0.786 0.002 | |
| PLSG-GNN | 0.883 0.013 | 0.732 0.001 |
| Params | Model | P-Ratio@100 | AUC-ROC |
|---|---|---|---|
| layers=2 | GCN | 0.344 0.021 | 0.493 0.004 |
| LG-GNN | 0.580 0.020 | 0.497 0.009 | |
| PLSG-GNN | 0.586 0.035 | 0.521 0.008 | |
| layers=4 | GCN | 0.285 0.016 | 0.486 0.006 |
| LG-GNN | 0.589 0.016 | 0.532 0.003 | |
| PLSG-GNN | 0.578 0.013 | 0.508 0.011 |
7.2.2 Geometric Graph
Each vertex has latent feature generated uniformly at random on , Two vertices and are connected if corresponding to a connection probability Higher sparsity is achieved by adjusting the threshold .
| Params | Model | P-Ratio@100 | AUC-ROC |
|---|---|---|---|
| layers=2 | GCN | 1.000 0.000 | 0.873 0.020 |
| LG-GNN | 1.000 0.000 | 0.915 0.007 | |
| PLSG-GNN | 0.997 0.005 | 0.917 0.010 | |
| layers=4 | GCN | 0.813 0.021 | 0.591 0.016 |
| LG-GNN | 1.000 0.000 | 0.956 0.001 | |
| PLSG-GNN | 1.000 0.000 | 0.958 0.001 |
| Params | Model | P-Ratio@100 | AUC-ROC |
|---|---|---|---|
| layers=2 | GCN | 0.333 0.017 | 0.840 0.008 |
| LG-GNN | 0.523 0.037 | 0.818 0.022 | |
| PLSG-GNN | 0.423 0.054 | 0.842 0.017 | |
| layers=4 | GCN | 0.313 0.021 | 0.848 0.021 |
| LG-GNN | 0.570 0.016 | 0.823 0.010 | |
| PLSG-GNN | 0.510 0.014 | 0.843 0.013 |
8 Impact Statement
This paper presents work whose goal is to advance the field of Machine Learning. There are many potential societal consequences of our work, none which we feel must be specifically highlighted here.
9 Acknowledgements
The first author would like to thank Qian Huang for helpful discussions regarding the experiments. The authors would also like to thank the Simons Institute for the Theory of Computing, specifically the program on Graph Limits and Processes on Networks. Part of this work was done while Austern and Saberi were at the Simon’s Institute for the Theory of Computing.
This research is supported in part by the AFOSR under Grant No. FA9550-23-1-0251, and by an ONR award N00014-21-1-2664.
References
- Abbas et al. (2021) Abbas, K., Abbasi, A., Dong, S., Niu, L., Yu, L., Chen, B., Cai, S.-M., and Hasan, Q. Application of network link prediction in drug discovery. BMC bioinformatics, 22:1–21, 2021.
- Abbe (2018) Abbe, E. Community detection and stochastic block models: recent developments. Journal of Machine Learning Research, 18(177):1–86, 2018.
- Abboud et al. (2020) Abboud, R., Ceylan, I. I., Grohe, M., and Lukasiewicz, T. The surprising power of graph neural networks with random node initialization. arXiv preprint arXiv:2010.01179, 2020.
- Abdi (2010) Abdi, H. Partial least squares regression and projection on latent structure regression (pls regression). Wiley interdisciplinary reviews: computational statistics, 2(1):97–106, 2010.
- Alimohammadi et al. (2023) Alimohammadi, Y., Ruiz, L., and Saberi, A. A local graph limits perspective on sampling-based gnns. arXiv preprint arXiv:2310.10953, 2023.
- Baranwal et al. (2021) Baranwal, A., Fountoulakis, K., and Jagannath, A. Graph convolution for semi-supervised classification: Improved linear separability and out-of-distribution generalization. arXiv preprint arXiv:2102.06966, 2021.
- Barot et al. (2021) Barot, A., Bhamidi, S., and Dhara, S. Community detection using low-dimensional network embedding algorithms. arXiv preprint arXiv:2111.05267, 2021.
- Bellec (2019) Bellec, P. C. Concentration of quadratic forms under a bernstein moment assumption. arXiv preprint arXiv:1901.08736, 2019.
- Borgs et al. (2008) Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T., and Vesztergombi, K. Convergent sequences of dense graphs i: Subgraph frequencies, metric properties and testing. Advances in Mathematics, 219(6):1801–1851, 2008.
- Borgs et al. (2012) Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T., and Vesztergombi, K. Convergent sequences of dense graphs ii. multiway cuts and statistical physics. Annals of Mathematics, pp. 151–219, 2012.
- Davison & Austern (2021) Davison, A. and Austern, M. Asymptotics of network embeddings learned via subsampling. arXiv preprint arXiv:2107.02363, 2021.
- Davison & Austern (2023) Davison, A. and Austern, M. Asymptotics of network embeddings learned via subsampling, 2023.
- Deng et al. (2021) Deng, S., Ling, S., and Strohmer, T. Strong consistency, graph laplacians, and the stochastic block model. The Journal of Machine Learning Research, 22(1):5210–5253, 2021.
- Djihad Arrar (2023) Djihad Arrar, Nadjet Kamel, A. L. A comprehensive survey of link prediction methods. The Journal of Supercomputing, 80:3902–3942, 2023.
- Esser et al. (2021) Esser, P., Chennuru Vankadara, L., and Ghoshdastidar, D. Learning theory can (sometimes) explain generalisation in graph neural networks. Advances in Neural Information Processing Systems, 34:27043–27056, 2021.
- Fabian et al. (2013) Fabian, M., Habala, P., Hajek, P., Santalucia, V., Pelant, J., and Zizler, V. Functional Analysis and Infinite-Dimensional Geometry. CMS Books in Mathematics. Springer New York, 2013. ISBN 9781475734805. URL https://books.google.com/books?id=TWLaBwAAQBAJ.
- Goemans (2015) Goemans, L. M. Chernoff bounds, and some applications. https://math.mit.edu/~goemans/18310S15/chernoff-notes.pdf, 2015.
- Hamilton (1853) Hamilton, W. R. Lectures on Quaternions: Containing a Systematic Statement of a New Mathematical Method; of which the Principles Were Communicated in 1843 to the Royal Irish Academy; and which Has Since Formed the Subject of Successive Courses of Lectures, Delivered in 1848 and Subsequent Years, in the Halls of Trinity College, Dublin: with Numerous Illustrative Diagrams, and with Some Geometrical and Physical Applications. Hodges and Smith, 1853.
- Hasan & Zaki (2011) Hasan, M. A. and Zaki, M. J. A survey of link prediction in social networks. Social network data analytics, pp. 243–275, 2011.
- Hoeffding (1963) Hoeffding, W. Probability inequalities for sums of bounded random variables. Journal of the American Statistical Association, 58(301):13–30, 1963. ISSN 01621459. URL http://www.jstor.org/stable/2282952.
- Kawamoto et al. (2018) Kawamoto, T., Tsubaki, M., and Obuchi, T. Mean-field theory of graph neural networks in graph partitioning. Advances in Neural Information Processing Systems, 31, 2018.
- Keriven et al. (2020) Keriven, N., Bietti, A., and Vaiter, S. Convergence and stability of graph convolutional networks on large random graphs. Advances in Neural Information Processing Systems, 33:21512–21523, 2020.
- Keriven et al. (2021) Keriven, N., Bietti, A., and Vaiter, S. On the universality of graph neural networks on large random graphs, 2021.
- (24) Kim, J. and Vu, V. Concentration of multivariate polynomials and applications. Combinatorica, to appear.
- Kipf & Welling (2017) Kipf, T. N. and Welling, M. Semi-supervised classification with graph convolutional networks, 2017.
- Kovács (2019) Kovács, István A., e. a. Network-based prediction of protein interactions. Nature Communiations, 2019.
- Kumar et al. (2020) Kumar, A., Singh, S. S., Singh, K., and Biswas, B. Link prediction techniques, applications, and performance: A survey. Physica A: Statistical Mechanics and its Applications, 553:124289, 2020.
- Lovász (2012) Lovász, L. Large networks and graph limits, volume 60. American Mathematical Soc., 2012.
- Lovász & Szegedy (2006) Lovász, L. and Szegedy, B. Limits of dense graph sequences. Journal of Combinatorial Theory, Series B, 96(6):933–957, 2006.
- Lu (2021) Lu, W. Learning guarantees for graph convolutional networks on the stochastic block model. In International Conference on Learning Representations, 2021.
- Ma et al. (2021) Ma, S., Su, L., and Zhang, Y. Determining the number of communities in degree-corrected stochastic block models. The Journal of Machine Learning Research, 22(1):3217–3279, 2021.
- Magner et al. (2020) Magner, A., Baranwal, M., and Hero, A. O. The power of graph convolutional networks to distinguish random graph models. In 2020 IEEE International Symposium on Information Theory (ISIT), pp. 2664–2669. IEEE, 2020.
- Martínez et al. (2016) Martínez, V., Berzal, F., and Cubero, J.-C. A survey of link prediction in complex networks. ACM computing surveys (CSUR), 49(4):1–33, 2016.
- Maskey et al. (2022) Maskey, S., Levie, R., Lee, Y., and Kutyniok, G. Generalization analysis of message passing neural networks on large random graphs. Advances in neural information processing systems, 35:4805–4817, 2022.
- Maskey et al. (2023) Maskey, S., Levie, R., and Kutyniok, G. Transferability of graph neural networks: an extended graphon approach. Applied and Computational Harmonic Analysis, 63:48–83, 2023.
- McCallum et al. (2000) McCallum, A. K., Nigam, K., Rennie, J., and Seymore, K. Automating the construction of internet portals with machine learning. Information Retrieval, 3(2):127–163, 2000.
- Morris et al. (2021) Morris, C., Ritzert, M., Fey, M., Hamilton, W. L., Lenssen, J. E., Rattan, G., and Grohe, M. Weisfeiler and leman go neural: Higher-order graph neural networks, 2021.
- Qiu et al. (2018) Qiu, J., Dong, Y., Ma, H., Li, J., Wang, K., and Tang, J. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In Proceedings of the eleventh ACM international conference on web search and data mining, pp. 459–467, 2018.
- Ruiz et al. (2021) Ruiz, L., Wang, Z., and Ribeiro, A. Graphon and graph neural network stability. In ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 5255–5259. IEEE, 2021.
- Ruiz et al. (2023) Ruiz, L., Chamon, L. F., and Ribeiro, A. Transferability properties of graph neural networks. IEEE Transactions on Signal Processing, 2023.
- Spencer (2001) Spencer, J. The Strange Logic of Random Graphs. Algorithms and Combinatorics. Springer Berlin Heidelberg, 2001. ISBN 9783540416548. URL https://books.google.com/books?id=u2c3LpjWs7EC.
- Stein & Shakarchi (2009) Stein, E. and Shakarchi, R. Real Analysis: Measure Theory, Integration, and Hilbert Spaces. Princeton University Press, 2009. ISBN 9781400835560. URL https://books.google.com/books?id=2Sg3Vug65AsC.
- Vershynin (2018) Vershynin, R. High-dimensional probability: An introduction with applications in data science, volume 47. Cambridge university press, 2018.
- Vignac et al. (2020) Vignac, C., Loukas, A., and Frossard, P. Building powerful and equivariant graph neural networks with structural message-passing, 2020.
- Wu et al. (2022) Wu, L., Cui, P., Pei, J., and Zhao, L. Graph Neural Networks: Foundations, Frontiers, and Applications. Springer Singapore, Singapore, 2022.
- Xu et al. (2018) Xu, K., Hu, W., Leskovec, J., and Jegelka, S. How powerful are graph neural networks? arXiv preprint arXiv:1810.00826, 2018.
- Zhang (2022) Zhang, M. Graph neural networks: Link prediction. In Wu, L., Cui, P., Pei, J., and Zhao, L. (eds.), Graph Neural Networks: Foundations, Frontiers, and Applications, pp. 195–223. Springer Singapore, Singapore, 2022.
- Zhang & Chen (2018) Zhang, M. and Chen, Y. Link prediction based on graph neural networks. Advances in neural information processing systems, 31, 2018.
- Zhang & Tang (2021) Zhang, Y. and Tang, M. Consistency of random-walk based network embedding algorithms. arXiv preprint arXiv:2101.07354, 2021.
Appendix A Notation and Preliminaries
We let be the vector Euclidean norm. The norm over the probability space will be denoted .
A.1 Graph Notation
We let be the adjacency matrix of the graph. Let be the latent features of the vertices, generated from Let be the graphon, and let be the sparsifying factor. We denote (we will typically be concerned only with , since that is the graphon from which the graph is generated). Let be the set of neighbors of a vertex , and hence is the degree of .
We define the th moment of a graphon to be the function from given by
| (6) |
Heuristically, if one fixes two vertices with latent features , then this is the probability of a particular path of length from , when averaging over the possible latent features of the vertices in the path. Correspondingly, we define the empirical th moment between two vertices and to be
| (7) |
A.2 GNN Notation
We let be the embedding for the th vertex produced by the GNN after the th layer. The linear GNN architecture is given by Equation 58:
| (8) |
where and denote the weight matrices of the GNN at the th layer. We remark that LG-GNN corresponds to being the identity matrix. Let
| (9) |
which is a quantity that shows up naturally in the GNN iteration. The classical GCN architecture we consider is also given in Equation 1.
A.3 Stochastic Block Model
We define the stochastic block model, as it is a running model in this paper.
A stochastic block model is parameterized by the number of vertices in the graph and a connection matrix . Each vertex belongs in a particular community, labeled . We assign each vertex to belong to community with probability . In this paper, we choose for all . Let denote the community of the th vertex. The graph is generated as follows. For each pair of vertices , we connect them with an edge with probability . We also denote the symmetric stochastic block model by . The SSBM is a stochastic block model with only two parameters: the parameter matrix is so that , if .
The following lemma details how to represent a SBM using a graphon.
Lemma A.1.
Consider a stochastic block model . Suppose that is a symmetric matrix and that has spectral decomposition where Let be the corresponding graphon.
Then can be represented by a graphon as follows. if and The eigenvalues of are given by with corresponding eigenfunctions , where if
This further implies that the eigenfunctions are bounded above pointwise by , in that for all and since , implying that each entry of has norm bounded above by 1.
This proof of this lemma is a simple verification of the properties. We note that the eigenfunctions are scaled by because they integrate to in
A.4 PLSG-GNN Algorithm
We state the PLSG-GNN Algorithm, which is an analog of Algorithm 2 that uses Partial Least Squares Regression (PLS). Let be an enumeration of the pairs , In the algorithm below, let PLS denote the Partial Least Squares algorithm as introduced in (Abdi, 2010).
Input: Graph , set , threshold ; .
Output: Set of predicted edges
Using Algorithm 1, compute for every vertex . Define the matrix and vector , as , , and .
Compute:
Compute: for all
Return: the set of predicted edges.
Appendix B Properties of Holder-by-Parts Graphons
Here, we discuss properties of symmetric, piecewise-Holder graphons. This section is largely from (Davison & Austern, 2023), Appendix H. Refer to that text for a more complete exposition; we just present the details most relevant to our needs.
Let be the Lebesgue measure. We define a partition of to be a finite collection of pairwise disjoint, connected sets whose union is , such that , for all , and This induces a partition of We say that a graphon lies in the Holder class if is Holder continuous in each All graphons in question in this paper are assumed to belong to this class.
A graphon can be viewed as an operator between spaces. In this paper, we focus on the case of In particular, for a fixed Graphon , one can define the Hilbert-Schmidt operator
Since is symmetric, is self-adjoint. Furthermore, because is a compact operator, as in (Stein & Shakarchi, 2009) page 190. Hence, the spectral theorem (for example, in (Fabian et al., 2013), Theorem 7.46) states that there exists a sequence of eigenvalues and eigenvectors (that form an orthonormal basis of , such that
| (10) |
and We note also that This is because if is an eigenvalue, then
where the last inequality is true because is bounded by and integrates to 1. Then, since also integrates to 1, this shows the result.
B.1 Linear Relationship Between Moments and (Proof of Proposition 4.2)
Proof of Proposition 4.2.
Suppose that is the number of distinct nonzero eigenvalues of , and label them by Recall that
We first prove via induction that
Assume that this is true for . Now we show that . Because the are orthonormal in we can compute
where the last equality is due to the orthonormality of the in This completes the induction. We now argue that there is a linear relationship between and i.e., there exists some such that
for all In light of the above discussion, we can observe that the vector is simply the solution (if it exists) to the system of equations
To observe that a solution indeed exists, it suffices to observe that the matrix on the LHS is of full rank, i.e., has nonzero determinant. To see this, we note that the th row is a multiple of We note that the matrix whose th row is is a Vandermonde matrix, which has nonzero determinant if all of the variables are distinct. Then, since multiplying each row by a constant changes the determinant only by a multiplicative factor, this suffices for the proof. ∎
Appendix C Proof of Proposition 5.1 and Proposition 5.2
We let denote the adjacency matrix. In the proof, for random variables and Borel sets , we might write quantities of the form . This denotes a conditional probability, where we condition on the realization of the graph. A notation we also use is , which denotes the conditional distribution of a random variable , conditioned on the realization of the graph. We first state the following Lemma, used in the proof of Proposition 5.1.
Lemma C.1.
Suppose that is generated from the graphon . Write . Then we have that
| (11) |
Proof of Lemma C.1.
We first show the above result for a fixed vertex (without loss of generality, let ), and then conclude the proof through a union bound. We first state
Lemma C.2 ((Goemans, 2015), Theorem 4).
Let , where and all the are independent. Let Then
for all
Now suppose that the latent feature is fixed. For any vertex , we have
| (12) | ||||
| (13) |
Recall that hence . We show that concentrates around . In this goal, remark that is distributed as a sum of independent Bernoulli random variables with probabilities . Therefore, according to Lemma C.2, for all we have
| (14) |
Moreover, we remark that conditionally on , the random variables are i.i.d. Therefore, according to Hoeffding’s inequality, we remark that for all , we have
| (15) |
Using the union bound this directly implies that for all we have
| (16) |
∎
Proof of Proposition 5.1.
The proof proceeds through induction. Let be a constant such that . We denote the event
We remark that according to Lemma C.1 we have . For the remainder of the proof we will work under the event . Note that when holds this also implies that
| (17) |
For ease of notation we define and write
We will then show that there is a constant so that, conditional on holding, with a probability of at least there exists embedding vectors that are independent from such that for every we have
To do so we proceed by induction. Firstly, since is Lipschitz, we observe that for all that we have
| (18) |
which we will show is bounded by with high probability. Using the hypothesis that , we note that
| (19) | ||||
| (20) |
To bound this last quantity, we note that conditioned on , we have that is a-sub-Gaussian vector with i.i.d entries. We will therefore use the following lemma
Lemma C.3.
Suppose that is a sub-Gaussian vector with i.i.d coordinates. There exists some universal constant such that
| (21) |
We remark that
Therefore we obtain that there exists a universal constant such that
| (22) |
and from this, setting we can deduce that with probability at least
| (23) | ||||
| (24) | ||||
| (25) |
where to get (a) we used the fact that under we have that .
We denote
and remark that the random variables are independent from since are assumed to be independent from . We remark in addition that for all we have We know that is a sub-Gaussian vector with i.i.d coordinates. Therefore by using Lemma C.3 again, we obtain that there exists such that with probability of at least we have
Denote the event
Taking a union bound over all vertices, we know that holds, conditionally on holding, with a probability of at least . We now suppose that both and hold. Suppose that for some the following event is true: for all , there exists some set of vectors independent of the latent features such that
| (26) |
We will show that the same statement holds for . In this goal, we denote by the event
For ease of notation, for each , write . We write where the norm of is bounded, under the event , by . Furthermore, we note that
| (27) | ||||
| (28) | ||||
| (29) |
Under the event we have
As is Lipschitz, this implies that
| (30) | |||
| (31) |
Moreover we also remark that as and holds we have
| (32) | |||
| (33) | |||
| (34) | |||
| (35) |
Note however that we have assumed that is a constant function. This therefore implies that is independent from . Defining
| (36) |
we have that
| (37) |
Moreover we note that
| (38) | ||||
| (39) | ||||
| (40) |
where to get (a) we used the fact that we assumed that holds. Hence we obtain that
Hence if and hold this implies that and hold which completes the induction. We hence have that
Choosing yields the desired result. ∎
We then prove Proposition 5.2
Proof.
Suppose that is Lipchtiz with respect to the Euclidean distance in . Using Proposition 5.1, we know that there exists and embeddings that are independent from such that with a probability of at least we have,
| (41) |
where is an absolute constant. As is assumed to be a Lipchitz function we obtain that
Now denote the event and define . We will obtain two different bounds respectively when
-
•
-
•
.
Firstly, if we remark that
| (42) | |||
| (43) |
Now assume instead . This implies that
| (44) | |||
| (45) | |||
| (46) | |||
| (47) | |||
| (48) | |||
| (49) |
where to get (a) we used the fact that under we have
and
Hence we obtain that
However as are independent from we have that is independent from . Hence if we write we obtain that
| (50) | |||
| (51) | |||
| (52) | |||
| (53) |
Now we have assumed that and we know that . Hence we obtain that
Now we have assumed that is not the constant graphon but assumes that is a constant function. Hence by choosing
we obtain that
∎
Appendix D Proof of Proposition 4.1
We proceed in two main steps. The first step is to establish a high-probability bound for This bound is then used to establish a bound on . The main goal is to prove Proposition D.8, which is a restatement of Proposition 4.1.
We will do these steps separately in the below subsections.
D.1 Proof of Proposition 4.1, Part 1
The goal of this subsection is to prove the following lemma.
Lemma D.1.
With probability at least , we have that for all ,
where where are some absolute positive constants.
We proceed in three steps. We first establish a high probability bound for Then, we establish a high probability bound for We then bound
D.1.1 Bounding
We use the following
Lemma D.2 ((Kim & Vu, )).
Let be a sequence of independent Bernouilli random variables. Let be an integer and be a polynomial of degree . For a subset we write by the partial derivative of with respect to the indexes . Define and let . Then,
| (54) |
where and is an absolute constant.
We will apply Lemma D.2 to obtain the desired result. We first fix . In this goal we set and define to be the following polynomial:
We remark that conditionally on the features , the random variables are independent Bernouili random variables. We note that our goal is to give a high probability bound on the difference between and its expectation . We first bound . We note that this is maximized when contains only one element. This is because when differentiating by , all of the terms that do not include this edge vanish, hence differentiating by more will cause more edges to vanish.
Furthermore, is maximized by choosing to be an edge that appears most often, such that as many terms as possible are preserved. Because the endpoints are fixed as , it suffices to bound the desired quantity for (without loss of generality, assume ; note the choice of was arbitrary). For each string , if it contains , then the number of terms in the string will be lowered by 1 upon differentiation (otherwise it equals 0 identically), hence after differentiating, the maximum number of terms in the string is
We now upper-bound the number of strings that contain and also have exactly distinct edges.
-
1.
Case 1: . Then, there are free indices remaining. However, since there are distinct edges, that means edges are repeated (appear at least more than once). Note that each repeated edge removes one free index. Hence, the remaining number of degrees of freedom is
-
2.
Case 2: Then, since the edge needs to appear in the sequence, there are at most locations for it to appear, and then ways to orient it (it can either be or ). So, there are ways to choose the edge , and then there remain ways degrees of freedom remaining.
Combining the two cases, there are at most ways to choose the set of indices Then, there are at most ways to choose the values of among this set, which is upper bounded by . Hence, the number of configurations with exactly distinct edges is upper bounded by . Hence, we can bound
where the last inequality follows if We now bound We first upper-bound the number of paths from to of length with exactly distinct edges. For convenience, denote and . Firstly, we note that if there are exactly distinct edges, then Since there are at most ways to choose a superset in which lies. Then, there are at most ways to choose the indices among this set. Hence, there are most paths of length with exactly distinct edges from to . Hence,
Now we apply Lemma D.2 to obtain
for some absolute constant , where Choosing , and union bounding over all and , we have that with probability at least , for all
where where is from the constant in the Big O factor, and is some constant.
D.1.2 Step 2: bounding
We now bound using McDiarmid’s Inequality. For ease of notation, we assume WLOG that and , and denote and . To use McDiarmid’s inequality; we first bound the maximum deviation in altering one of the coordinates. WLOG we alter the th coordinate and bound
Recalling the definition
denote We first bound each individually over different choices of the indices . We note that if none of the , then . Hence, we need consider only the terms in the summation for which at least one of the equals .
If corresponds to a path with exactly distinct edges, then We upper bound the number of paths of length that have exactly distinct edges. Note that , since our we are considering terms such that there exist that equal , so there cannot be less than two distinct edges. We note that if there are exactly distinct edges, then the number of distinct numbers among the set is at most . Because and , and must be one of the must equal , there are at most ways to choose the remaining vertices. Then, the number of ways to choose the values of among these options is bounded by Hence, the total number of options is upper bounded by Lastly, we note that Hence, the constant in the exponential bound of McDiarmid’s Inequality is given by
| (55) |
if , since then and for all Then, the McDiarmid Inequality states that
| (56) |
Hence, choosing and union bounding over , , we have that with probability at least for all ,
| (57) |
D.1.3 Step 3: bounding
Recall
We see that
Firstly, we claim that the number of paths of length starting from vertex to that have no repeated edges is lower bounded by . This is simply because if no vertex is passed through twice along the path, then there cannot exist repeated edges. There are choices for , then choices for etc., which shows this assertion. This implies that the number of paths with distinct edges is , where Note that this also implies that the number of paths of length is of order Hence, we can write
To proceed with the triangle inequality, we first upper-bound the number of paths from to of length with exactly distinct edges. For convenience, denote and . Firstly, we note that if there are exactly distinct edges, then Since there are at most ways to choose a superset in which lies. Then, there are at most ways to choose the indices among this set. Hence, there are most paths of length with exactly distinct edges from to . Hence,
where this last line is true because
D.1.4 Step 4: Combining the Bounds
Combining the three steps and using the triangle inequality, we have that with probability at least , we have that for all ,
for sufficiently large , as we note that the second term is the dominating one when . This suffices for the proof of Lemma D.1.
D.2 Proof of Proposition 4.1, Part 2
The main goal of this subsection is to prove Proposition D.8. Before proving that, we first present general properties of the GNN embedding vectors our proposed algorithm produces (where we consider a more general version of our proposed GNN in which the weight matrices are not the identity). Uninterested readers can skip directly to Proposition D.8 to see the main result, and those who interested in more details can continue to read the exposition below.
In this appendix, we consider a version of our proposed GNN architecture with general weight matrices, given by
| (58) |
where are matrices that can be freely chosen. Note also that , and hence the normalization by . As proposed in Algorithm 1, we initialize the embeddings by first sampling , and then computing the first layer through
| (59) |
We compute a total of GNN iterations and for all vertices , produce the sequence
In this appendix, we prove Proposition D.8 in a series of steps:
-
1.
We first give a general formula for , and then demonstrate that is a linear combination of the empirical moments of the graphon . This is done in Lemma D.4.
-
2.
We then show in Lemma D.5 that can be written in the simpler form
-
3.
We then use the above observation to establish a concentration result for in Proposition D.8.
D.3 Formula for the Embedding Vectors
Proposition D.3.
Consider the GNN Architecture defined in Algorithm 1, and recall the definition of the empirical moment between vertices and ,
as in Equation 7. Then for we have
| (61) |
Proof of Proposition D.3.
We proceed through induction. The induction base case of is satisfied by definition of . Now, suppose for induction that, for
We use the definition of our GNN iteration to compute In particular, we observe that will be a linear combination of the where the coefficient of is given by
| (62) |
To arrive at the desired result, we first make a few observations. Firstly, we note that
| (63) |
which allows us to simplify the analogous quantities in the last two terms. To simplify the second term, we use the definition of and note that
To see this, we note that
which allows us to simplify the second term. Finally, we see that the coefficient of is given by
Hence, we obtain that
| (64) |
as desired. ∎
D.4 Expectation of Dot Products and their Concentration
The following lemma shows that the expectation of the dot products of the embedding vectors, conditional on the graph, is a linear combination of the empirical moments .
Lemma D.4.
Suppose that are produced through Algorithm 1. Then, conditional on the latent features and the adjacency matrix , we have
| (65) |
Proof of Lemma D.4.
Firstly, we note that if then . Then, we can compute
| (66) | ||||
| (67) | ||||
| (68) |
∎
Now that these properties of the embedding vectors have been shown, we now return to the setting of our algorithm, where the weight matrices are chosen to be the identity. We now prove that the algorithm to produce estimators for in Algorithm 1 is asymptotically consistent, and we establish the convergence rate. For the reader’s convenience, we rewrite the algorithm below. The following lemma explains the intuition as to why we expect to be an estimator for
Input: a Graph ;
Output: estimators for the edge probability
Computing Estimators for :
for do
Lemma D.5.
As in Algorithm 1, define (with the weight matrices )
Then
Under the heuristic that , then we see that
Proof of Lemma D.5.
We first show that we can write
| (69) |
Note equivalently this can be written as
We show this using induction. Assume this is true for all for some . We can compute using the formula in Algorithm 1. Using the definition of we can compute that the coefficient of in is given by
To compute this, we first argue that
We use generating functions. We note that is the coefficient of in the expansion of Then, we note that is the coefficient of in the expansion of Hence, this summation simply represents the coefficient of in the expansion of However, since is a degree polynomial, the coefficient is simply 0. Hence, this implies that
Thus, we have shown that the coefficient of in is of the desired form, which suffices to prove Equation 69. Now, continuing with the proof, we recall that Proposition D.3 states that
so
We analyze the second term in the dot product more closely. The coefficient of in the second term is equal to (ignoring the factor of for now)
Hence it suffices to argue that if , and 0 otherwise. We argue this in Lemma D.6. Assuming that this is true, then we see that
as desired. To conclude the proof, we present and prove Lemma D.6.
Lemma D.6.
Let be an integer. Then
Proof.
Consider the formal series
Multiplying these two series, we notice that the desired quantity is exactly the coefficient of in the product of the two series, which is However, is a monomial of degree , and hence has coefficient 0 in , which has degree when . The notable exception is when , and then the coefficient (of the constant term) in is exactly equal to 1. This suffices for the proof. ∎
∎
We now establish the main concentration result, Proposition D.8. Before doing so, we first state the following lemma.
Lemma D.7.
Let and let be independent, zero-mean normal random variables with for all Let Let be any real matrix. Then for all
| (70) |
Proof of Lemma D.7.
We adapt Proposition 1 from (Bellec, 2019), which states the following.
Let and let be independent, zero-mean normal random variables with for all Let Let be any real matrix. Then for any ,
To adapt this proposition into the form in Lemma D.7, we firstly note that so
| (71) | ||||
| (72) |
Then
| (73) | |||
| (74) | |||
| (75) | |||
| (76) |
which implies that
| (77) |
as desired. ∎
Proposition D.8 (Proposition 4.1).
We first introduce the following lemma:
Lemma D.9.
Proof of Lemma D.9.
We use the following lemma about sums of independent Bernoulli random variables:
Lemma D.10 ((Goemans, 2015), Theorem 4).
Let , where and all the are independent. Let Then
for all
Fix . We note that the random variables are independent conditioned on the Using these variables directly in this lemma above yields
Then, noting that , and substiting , we obtain
A union bound over all concludes the proof.
∎
Proof of Proposition D.8.
In the remainder of this proof, we condition on the event in Lemma D.1, which is that
This contributes the probability of For simplicity of notation, denote We also condition on the event in Lemma D.9, which contributes the probability of .
Fix some . We prove the claim for this particular choice of , and then union bound over all pairs at the end of the proof. Recall that Lemma D.5 states that
We first note that because we have that
where this is the expectation is over the randomness in the Gaussian vectors Hence, to show the desired result, it suffices just to show the concentration of a quadratic form of Gaussian vectors. Concretely, writing we can write where
and
To show the concentration of the quadratic form we employ Lemma D.7 to do this. In order to apply Lemma D.7, we first bound the Frobenius norm of . Noting that
we can write
For ease of notation, we will write for some constant We now use Lemma D.7. Noting that each element of is an independent random variable, then Lemma D.7 states that when we have
Choose Then
Now, union bounding over all and we have that with probability at least , for all (assuming ), conditional on ,
Taking , we have that with probability for all conditional on , and using that
Now, recall that
Hence, the triangle inequality implies that for all with probability at least ,
as desired. ∎
Appendix E Proof of Theorem 4.4
In this section, we prove Theorem 4.4. We first review some notation used below.
Define the vectors
and recall that denotes Define
We note that when The term in the parentheses in the first equation is simply the bound on presented in Proposition 4.1. will be a natural quantity that appears later in this section.
We also define
where the expectation is over and define the empirical risk as
We also define the out-of-sample test error as
| (79) |
The following proposition is the main component of Theorem 4.4.
Proposition E.1 (Theorem 4.4).
Let be a subset of where for some Let be a positive integer and define
Define Then with probability at least
where and the constant depends on
Proof of Theorem 4.4.
We write
| (80) |
We first bound
We note that the LHS is by definition of We note that the second term on the RHS is by definition of Hence, it follows that
Lemma E.2 states that
so hence
| (81) |
where the last inequality follows from Lemma E.2. We now bound For any , write
which implies that (using similar arguments as in the proof of Lemma F.4),
| (82) |
Substituting Equation 81 and Equation 82 into Equation 80 yields the desired result.
∎
The following lemma is used directly in the above proof of Theorem 4.4. We state it and prove it below.
Lemma E.2.
Let be a subset of where for some Let be arbitrary. Define Then
Furthermore, employing Lemma F.2, Lemma F.4, and Lemma F.5 implies that with probability at least
where and the constant depends on We note that this is the probability at which this lemma holds, since Lemma F.2, Lemma F.4, and Lemma F.5 all condition on the same events, so the probabilities in their respective statements do not add.
Appendix F Proofs of Lemma F.1, Lemma F.2, Lemma F.4, and Lemma F.5
This section presents Lemma F.1, which is used in Theorem 4.4, and its proof. We also present Lemma F.2, Lemma F.4, and Lemma F.5, which are used in the proof of Theorem 4.4.
F.1 Proof of Lemma F.1
Lemma F.1.
Suppose that has finite distinct rank and let so that
Let denote the vector that minimizes
Then
Proof of Lemma F.1.
By definition of being a minimizer of , this quantity would be bounded by the error incurred if we replace with the vector . This would yield
∎
F.2 Proof of Lemma F.2
Lemma F.2.
Let be a subset of where for some Define and define
Let
Then with probability at least , we have
| (86) |
where hides logarithmic factors.
Proof of Lemma F.2.
In the proof of this lemma, we are inherently conditioning on all of the events that the proof of Proposition D.8 conditions on. Specifically, we are conditioning on the event that
and that
Firstly, we note that See the proof of Lemma F.4 for a more detailed calculation.
We use an -net argument to obtain the desired uniform concentration result over the entire space. We first bound the cardinality of an -net needed to cover , where the covering sets are -balls in the norm in . We then establish a high-probability bound for the quantity using a concentration inequality for U-statistics, for a fixed . Then, the continuity of will yield a bound for for all in the same -ball as . We then take a union bound over all balls in the -net to arrive at the conclusion.
We note that a hypercube with side length centered at some is contained in the -ball centered at , so bounding the cardinality of a covering with hypercubes of side length would also bound the cardinality of a covering with -balls. To determine this cardinality, we can simply consider the construction of tiling (which is a hyper-rectangle) with hypercubes simply by packing the cubes side-to-side. Hence, we obtain an -net of size bounded by
| (87) |
Now, we bound . In this goal we define
and
We remark that . Using the triangle inequality, we notice that it is enough to show concentration of and around their respective expectations.
We first remark that and show concentration around its expectation. In this goal, notice that conditional on , the random variables are i.i.d Bernoulli random variables. Moreover we notice that conditionally on the features we have that is a polynomial of degree one of the Bernoulli random variables . Hence, we use Lemma D.2. We note that and the first derivative with respect to is Then, for all we have
Think it should be
| (88) |
where is some constant from Lemma D.2. Moreover we notice that . Therefore, we obtain that
| (89) |
Then, we derive a concentration bound for , for a fixed vector The randomness in term comes from the latent features and we observe that it is a U-Statistic with two variables. To bound the desired quantity, we use the following
Lemma F.3 (Equation (5.7) from (Hoeffding, 1963)).
Let be independent random variables. For , consider a random variable of the form
Then if , it follows that
To use this quantity, we first bound Using Equation 108, we have
| (90) | |||
| (91) | |||
| (92) |
Hence, for a fixed , we have that
| (93) |
We now use continuity to argue that is bounded for all in the -ball containing . we derive a bound on for when We can use the triangle inequality and bound and separately.
We can write
| (94) | ||||
| (95) | ||||
| (96) |
where the term is from the first term: the norm of is bounded by and each entry in the vector is bounded by The factor of is using Equation 108.
In a similar way, we can bound . We first bound the quantity
| (97) | |||
| (98) | |||
| (99) |
Then we can bound
| (100) | |||
| (101) | |||
| (102) | |||
| (103) |
where the last inequality comes from conditioning on the event mentioned at the beginning of the proof. From here, we can see that
| (104) |
This implies that
| (105) | |||
| (106) |
Choosing
we have that with probability
Choose Recall that
Then, we conclude that with probability at least ,
where the Big-O constant depends on
∎
Lemma F.4.
Let be a subset of where for some Define and for define
Then with probability at least
| (107) |
where
Proof of Lemma F.4.
In the proof of this lemma, we are inherently conditioning on all of the events that the proof of Proposition D.8 conditions on. Specifically, we are conditioning on the event that
and that
We first consider for some arbitrary .
We write
| (108) |
This yields the bound
where ∎
Lemma F.5.
Let be a subset of where for some Define and for define
Then with probability at least
Appendix G Proof of Proposition 4.5
In this section, we state a formal version of Proposition 4.5 and provide the proof.
Proposition G.1 (Proposition 4.5, Formal).
Consider a -community symmetric stochastic block model (see Section A.3 for the definition) with parameters and sparsity factor which has eigenvalues Fix some and define .
Produce probability estimators for the probability of an edge between vertices and using Algorithm 1 and Algorithm 2. Let be defined as in Theorem 4.4. Suppose that satisfy
where is a constant that depends on , for some positive constant
Let and Then, with probability at least the following event occurs:
Proof of Proposition 4.5.
Consider a -community symmetric SBM with connection matrix , where for all and for all . We first write the eigen-decomposition of this matrix; there are two eigenvalues and we write an orthogonal basis for their eigenspaces.
According to Lemma A.1, the eigenvalues of the corresponding graphon representation are and Call the eigenvalues and , and let without loss of generality. The eigenfunctions of are also given by Lemma A.1, and are essentially scaled versions of the above eigenvectors. For the remainder of this proof, we assume that the graph was generated from for some sparsity factor .
Define , Using that we see that
Now suppose that a graph is generated from We demonstrate that under the conditions mentioned in Proposition 4.5, Algorithm 1 and Algorithm 2 results in probability predictions so that when and . In other words, the probability predictions for all of the intra (within) community edges are higher than the probability predictions for all of the inter (across) community edges.
As in the proposition statement, define , and suppose that is the number of layers that are computed. In other words, LG-GNN computes the set of embeddings for all , and for each pair of vertices , it computes moment estimators
Then, in Algorithm 2, we solve the optimization problem
For and any , define where the subscript makes implicit that there is dependence on Defining
we note that for any fixed , we have that
Let be the latent features of two vertices that both correspond to being in community 1, and let be the latent features of two vertices that correspond to being in communities 1 and 2, respectively. Now, suppose that for the edges and , LG-GNN assigns them predicted probabilities respectively, and suppose that Consider
where we simplified the first term this way in the last equality by using the form of the eigenvectors , and noting that both correspond to vertices in community 1. In a similar way, we have that
Hence, if , then noting that we have
We note that Proposition 4.1 states that with probability at least we have that for all ,
for some constants , and also that the conclusion from Lemma F.2 holds. We will be conditioning on these events for the remainder of the proof. We also note that
Using these definitions, noting that we have that
Define to have as the first component, and 0 everywhere else. Now, we note that Lemma E.2 states, with the same probability above, that
where
where and is some constant that depends on . We also note that because is the minimizer of the empirical risk. This implies that So, noting that , and noting that
However, this is a contradiction when Consider the bounds
Hence, when
the result follows. Dividing both sides by , and multiplying by the above is equivalent to
The result follows.
∎
Appendix H Proof of Proposition 6.1
Note that in this proof, we assume that the sparisity factor . Consider a 2-community stochastic block model (see Section A.3 for more details) parameterized by the matrix The eigenvalues and eigenvectors are given by
where Then, recall that Lemma A.1 states that the eigenvalues of the graphon representation of this SBM has eigenvalues We also use the eigenfunctions for as written in Lemma A.1. We recall that Lemma D.4 states that for all , we have
Then, the proof of Proposition D.8 implies that for all ,
In this proof, we let denote the community of vertex and let denote all of the vertices in community . In the graphon reprentation of this 2-community SBM, if is the latent feature for vertex , then if and only if vertex belongs to community 1, and if and only if vertex belongs to community 2. To reflect this and simplify notation, we let , where and are any so that correspond to the appropriate communities. For example, , which is the probability that two vertices in community 1 are connected. We write the above as
In the remainder of the proof, we choose parameters so that , but (this last equality indicates that the connection probability between two vertices in community 2 is different than the connection probability between a vertex in community 1 and a vertex in community 2). This would suffice for the proof, since the continuous mapping theorem would imply that for any continuous function ,
and we note that With this in mind, consider
Substituting in the forms of the eigenvectors , it suffices to show that there exist values of , with , so that
which would suffice for the proof. Recall that and Choosing and substituting these values in, we obtain that the above is equivalent to
We show that there exist values and , , so that there exists a root for some We will fix to be some small number to be decided later. might depend on . Since this function is continuous in all variables, we use the intermediate value theorem (by varying ) to deduce that there exists a root for some sufficiently small Firstly, we observe that . On the other hand, This implies that for sufficiently small . Then, it suffices to argue that for , as then the intermediate value theorem implies the desired result.
Let Taylor’s theorem implies that Hence, we can write as
We can also write
We note that the first two terms in both and are of constant order (the constants are difference, but both of constant order). However, the third term in is of constant order, but the third term in is of order This implies that for sufficiently small , . This suffices to imply that for this small enough , there is some so that has a root. This suffices for the proof.
Appendix I Experiments
We present three different sets of results. The first is for real-data (the Cora dataset), and we use the in-sample train/test splitting scheme for this. The second are in-sample experiments for a variety of random graph models, and the third set are out-sample experiments for these random graph models. For clarity, we explain and define the metrics we are using in the experiments. For the real-data experiments, we consider only the in-sample setting, while for the random graph experiments, we consider both the in-sample and out-of-sample settings.
One point of clarification is that our link prediction procedure is not simply to guess a particular edge to be a positive edge if its predicted probability is over 0.5. If the graphon , then this doens’t make sense because the LG-GNN estimates the underlying probability of edges.
Instead, we concern ourselves more with the ranking of the edges and choose evaluation metrics to reflect that. Concretely, we evaluate our algorithms on whether they are able to assign higher probabilities to edges with higher underlying probabilities (and in the real-data case, whether they are able to assign higher probabilities to the positive edges than to the negative edges in the testing set).
To reflect this, the principle metrics we use are the AUC-ROC, Hits@k (as is standard for link prediction tasks in the Stanford Open Graph Benchmark) for the real data experiments. For the random graphs, introduce a new metric called the Probability Ratio@k, defined below, which is inspired by the Hits@K metric.
I.1 Train/Test Splits
We first describe our train/test split procedures.
I.1.1 In-Sample (random graph)
We generate a graph with ( vertices). Let be the set of non-edges. Concretely, We then split the edges into a train, validation, and testing set as follows.
For each edge , we remove it from the graph (independently from all the other edges) with probability . The edges that are not removed are labelled The set will be the set of positive training edges. Among the edges that were removed, half of those will be the set of positive validation edges and the remaining will be the set of positive test edges. Call these and respectively. During training, message passing only occurs along the edges in
Now, we select the negative edges among the set of edges Specifically, fraction of these edges will be the negative training edges, fraction will be the negative validation edges, and the remaining fraction will be the negative testing edges.
It is important to pick the negative training edges from the set , as opposed to simply from . If the negative training edges were sampled only from , then this would give implicit information about where the edges are in the graph. The model should not have access to which edges are in vs in a priori; if the negative training edges that were given to it are only from , then it would implicitly know that the edges in are less likely to be negative edges. Indeed, when we trained the GCN on a 2-community SBM with parameters 80 and 20 in the setting in which the negative training edges were sampled only from , it was able to estimate the underlying parameters and almost perfectly, which should be impossible if it only had access to a graph with edges removed.
I.1.2 In-Sample (real data)
For real data, we use the same train/test split procedure as described above. However, during training and testing, we do not use the entire set of negative edges. This is because the graph is very sparse, and hence there are many more negative edges than positive edges. This makes link prediction difficult and causes the training procedure to be erratic.
I.1.3 Out-Sample
For each random graph model, we generate a graph with ( vertices). We partition where contains a random -fraction of the original set of vertices, and contains the remaining fraction. Let be the subgraph induced by (i.e., the set of all positive and negative edges with both endpoints in ). Let be the set of edges that have both endpoints in Let be the set of edges that have at least one vertex in , and let be the set of negative edges with at least one vertex in
We pick a random fraction of the positive and negative edges from to be the training positive and negative edges, and the remaining fraction to be the validation edges. Then, we pick fraction of the positive edges in and fraction of the negative edges in to be the testing edges. The remaining edges in and we will refer to as message-passing edges.
We first train the models on the positive + validation edges. Then once the model is trained, we compute the embedding vectors by running message passing on the set of train + message passing edges. Finally, we do edge prediction on the testing edges.
I.2 Definition of Probability Ratio
Let be the underlying probability of an edge . In the graphon model, and note that we have access to these values. Given a set of edges , we say that a link prediction algorithm ranks the edges as if where is the probability that the algorithm predicts for the edge . Given some edge ranking as above, define the total predicted probability as
and the maximum probability as
In other words, the is the sum of the probabilities of the top most likely edges in . Then, the probability ratio is defined as
In essence, the Probability Ratio@k captures what fraction of the top probabilities a link prediction algorithm can capture. For example, suppose that there are three testing edges with underlying probabilities , respectively. Suppose that some edge prediction algorithm ranks the edges as Then the Probability Ratio@2 is equal to
I.3 Real-Data: Cora
For the dataset, we perform a train/test split using the StellarGraph edge splitter, which randomly removes positive edges while ensuring that the resulting graph remains connected. For the negative training edges, we sample an equal number of negative edges as positive edges to train on. For the negative testing edges, we sample an equal number of negative edges as positive testing edges.
I.3.1 Results without Node Features
| Parameter Set | Model | Cross Entropy | Hits@50 | Hits@100 |
|---|---|---|---|---|
| layers=2 | GCN | 0.645 0.043 | 0.496 0.025 | 0.633 0.023 |
| LG-GNN | 2.953 0.013 | 0.565 0.012 | 0.637 0.006 | |
| PLSG-GNN | 0.679 0.012 | 0.591 0.014 | 0.646 0.013 | |
| layers=4 | GCN | 0.689 0.002 | 0.539 0.008 | 0.665 0.007 |
| LG-GNN | 2.682 0.010 | 0.564 0.005 | 0.620 0.008 | |
| PLSG-GNN | 0.660 0.030 | 0.578 0.014 | 0.637 0.013 |
I.3.2 Results with Node Features (GCN has access to node features)
| Parameter Set | Model | Cross Entropy | Hits@50 | Hits@100 |
|---|---|---|---|---|
| layers=2 | GCN | 0.487 0.003 | 0.753 0.019 | 0.898 0.021 |
| LG-GNN | 3.034 0.285 | 0.555 0.027 | 0.603 0.034 | |
| PLSG-GNN | 0.679 0.027 | 0.577 0.033 | 0.626 0.042 | |
| layers=4 | GCN | 0.661 0.041 | 0.609 0.072 | 0.776 0.069 |
| LG-GNN | 2.711 0.213 | 0.560 0.013 | 0.601 0.012 | |
| PLSG-GNN | 0.677 0.019 | 0.574 0.025 | 0.625 0.024 |
Figure 1 shows histograms of the predicted probabilities by each of the algorithms (with the two cases of the GCN having access or not having access to the node features). This is to give a visual demonstrate as to what PLSG-GNN is doing. There is a ”low probability” hump around 0.25, but then smaller peaks of high-probability predictions. The humps clearly separate the edges in regimes of how connected they are and show clearly the properties of the graph topology.
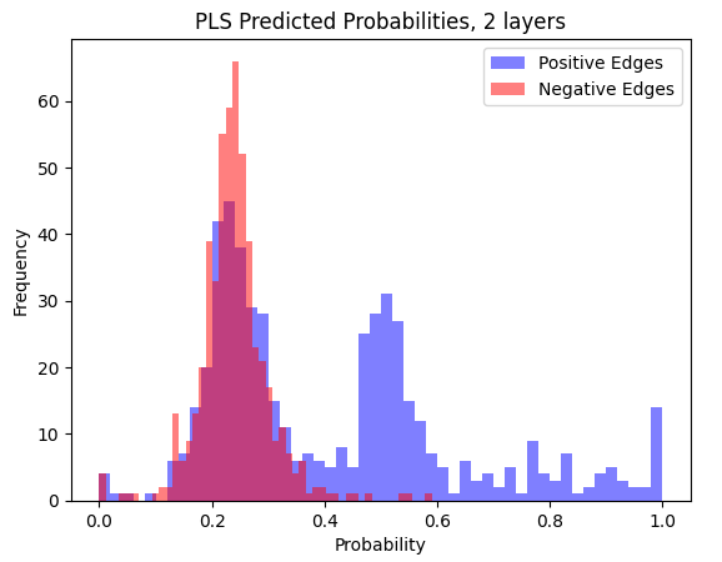
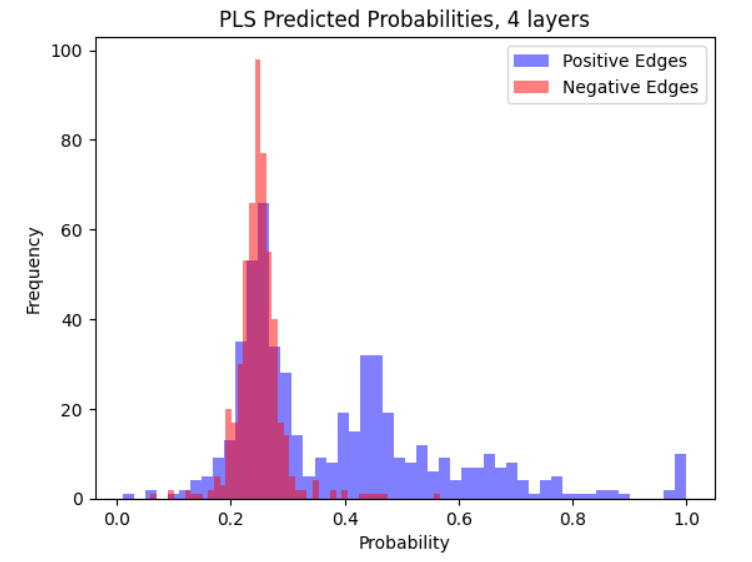
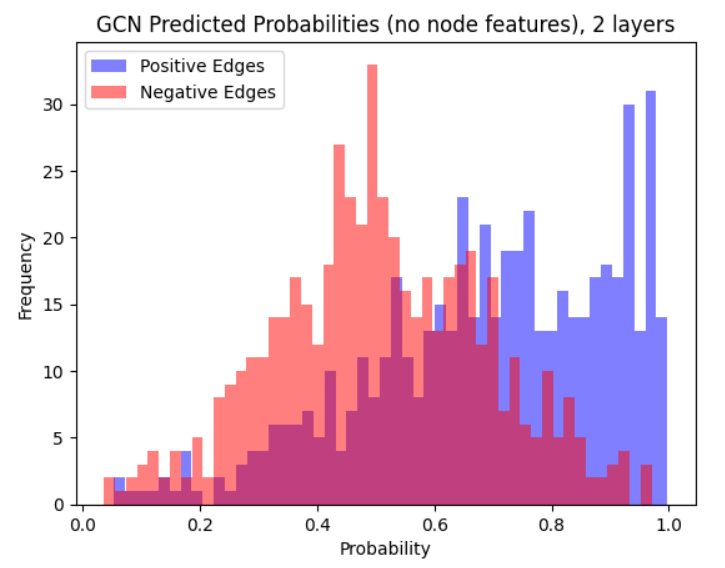
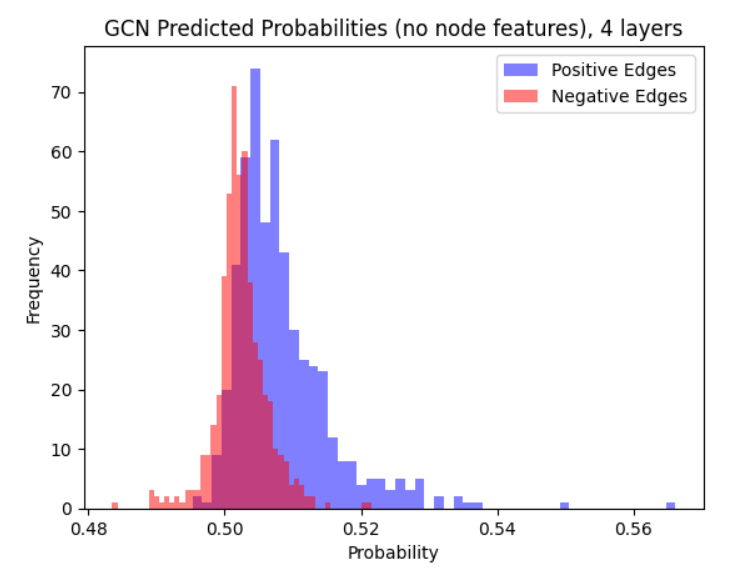
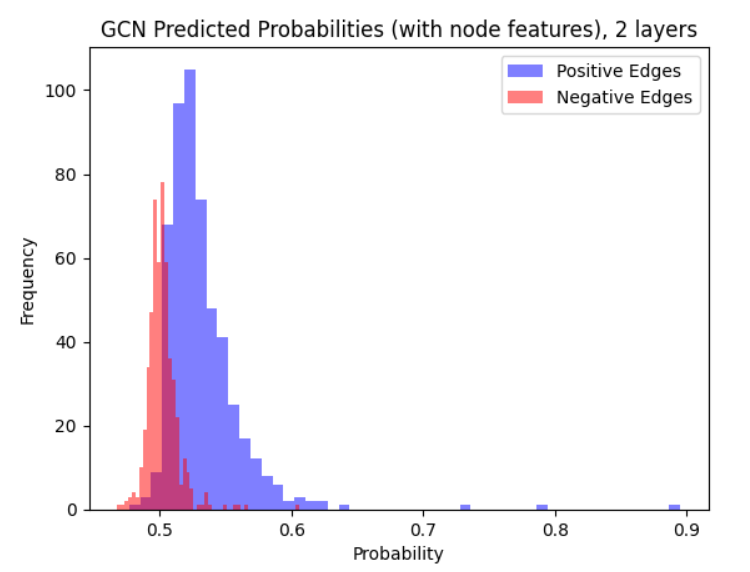
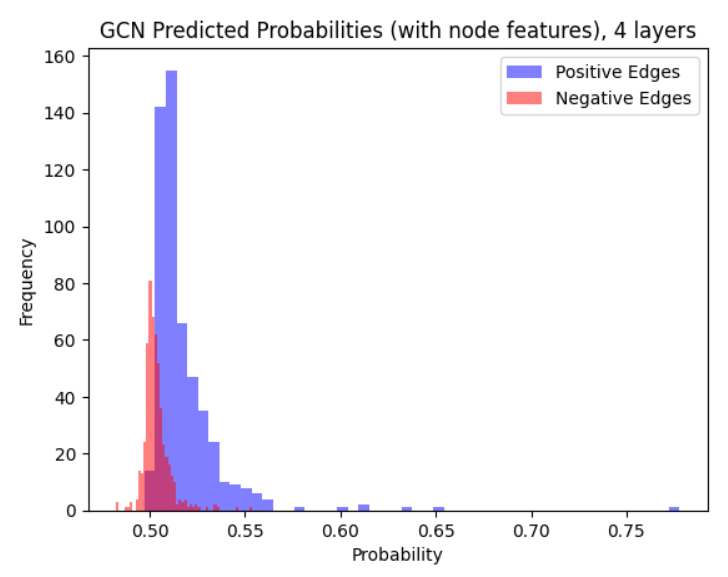
Appendix J Experiments (In-Sample)
J.1 6SSBM (80-20)
6-community symmetric stochastic block model with connection probabilities 0.8 and 0.2.
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.587 0.010 | 1.000 0.000 | 1.000 0.000 | 0.697 0.002 |
| LG-GNN | 0.563 0.001 | 1.000 0.000 | 1.000 0.000 | 0.677 0.003 | |
| PLSG-GNN | 0.583 0.004 | 1.000 0.000 | 1.000 0.000 | 0.673 0.004 | |
| rho=1, layers=4 | GCN | 0.693 0.000 | 0.973 0.009 | 0.978 0.006 | 0.640 0.029 |
| LG-GNN | 0.532 0.000 | 1.000 0.000 | 1.000 0.000 | 0.697 0.001 | |
| PLSG-GNN | 0.579 0.002 | 1.000 0.000 | 0.999 0.001 | 0.680 0.002 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.388 0.058 | 0.408 0.006 | 0.503 0.007 |
| LG-GNN | 0.090 0.001 | 0.458 0.035 | 0.450 0.006 | 0.503 0.007 | |
| PLSG-GNN | 0.091 0.002 | 0.398 0.014 | 0.393 0.010 | 0.491 0.007 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.383 0.009 | 0.376 0.004 | 0.499 0.007 |
| LG-GNN | 0.088 0.000 | 0.430 0.016 | 0.439 0.013 | 0.505 0.004 | |
| PLSG-GNN | 0.089 0.001 | 0.388 0.009 | 0.388 0.012 | 0.507 0.001 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.382 0.009 | 0.376 0.012 | 0.458 0.014 |
| LG-GNN | 0.021 0.001 | 0.367 0.004 | 0.389 0.002 | 0.517 0.006 | |
| PLSG-GNN | 0.019 0.000 | 0.370 0.027 | 0.374 0.012 | 0.521 0.004 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.405 0.007 | 0.380 0.005 | 0.496 0.010 |
| LG-GNN | 0.021 0.000 | 0.470 0.007 | 0.410 0.003 | 0.505 0.017 | |
| PLSG-GNN | 0.019 0.000 | 0.380 0.004 | 0.375 0.007 | 0.513 0.010 |
J.2 6SSBM (55-45)
6-community symmetric stochastic block model with edge connection probabilities 0.55 and 0.45.
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.693 0.000 | 0.859 0.004 | 0.852 0.001 | 0.500 0.001 |
| LG-GNN | 0.695 0.000 | 0.849 0.006 | 0.849 0.003 | 0.500 0.002 | |
| PLSG-GNN | 0.693 0.000 | 0.849 0.006 | 0.849 0.003 | 0.500 0.002 | |
| rho=1, layers=4 | GCN | 0.693 0.000 | 0.847 0.000 | 0.846 0.003 | 0.500 0.000 |
| LG-GNN | 0.695 0.000 | 0.848 0.005 | 0.850 0.002 | 0.500 0.001 | |
| PLSG-GNN | 0.693 0.000 | 0.853 0.005 | 0.851 0.002 | 0.501 0.001 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.847 0.005 | 0.848 0.001 | 0.502 0.002 |
| LG-GNN | 0.130 0.000 | 0.852 0.001 | 0.849 0.000 | 0.503 0.006 | |
| PLSG-GNN | 0.130 0.001 | 0.850 0.011 | 0.848 0.004 | 0.506 0.003 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.848 0.002 | 0.847 0.002 | 0.502 0.006 |
| LG-GNN | 0.121 0.001 | 0.849 0.007 | 0.849 0.001 | 0.502 0.010 | |
| PLSG-GNN | 0.131 0.001 | 0.848 0.005 | 0.852 0.002 | 0.495 0.004 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.853 0.002 | 0.850 0.002 | 0.489 0.000 |
| LG-GNN | 0.031 0.000 | 0.845 0.007 | 0.850 0.003 | 0.508 0.008 | |
| PLSG-GNN | 0.030 0.001 | 0.852 0.005 | 0.850 0.002 | 0.496 0.006 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.851 0.004 | 0.848 0.002 | 0.487 0.004 |
| LG-GNN | 0.031 0.001 | 0.847 0.001 | 0.848 0.003 | 0.492 0.005 | |
| PLSG-GNN | 0.030 0.001 | 0.856 0.007 | 0.852 0.003 | 0.508 0.017 |
J.3 10 SBM
10-community stochastic block model with parameter matrix that has randomly generated entries. The diagonal entries are generated as , and is generated as . The connection matrix is
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.599 0.001 | 0.878 0.007 | 0.872 0.007 | 0.764 0.001 |
| LG-GNN | 0.588 0.001 | 0.908 0.008 | 0.867 0.009 | 0.726 0.002 | |
| PLSG-GNN | 0.588 0.001 | 0.909 0.007 | 0.867 0.006 | 0.727 0.001 | |
| rho=1, layers=4 | GCN | 0.677 0.003 | 0.737 0.094 | 0.758 0.106 | 0.672 0.011 |
| LG-GNN | 0.562 0.008 | 0.868 0.042 | 0.868 0.037 | 0.780 0.002 | |
| PLSG-GNN | 0.588 0.001 | 0.896 0.038 | 0.858 0.023 | 0.728 0.001 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.288 0.022 | 0.315 0.008 | 0.505 0.003 |
| LG-GNN | 0.111 0.002 | 0.561 0.015 | 0.546 0.023 | 0.515 0.003 | |
| PLSG-GNN | 0.110 0.001 | 0.610 0.008 | 0.577 0.005 | 0.520 0.005 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.298 0.048 | 0.312 0.043 | 0.512 0.014 |
| LG-GNN | 0.105 0.003 | 0.584 0.036 | 0.564 0.011 | 0.516 0.008 | |
| PLSG-GNN | 0.110 0.002 | 0.589 0.022 | 0.564 0.003 | 0.517 0.011 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.300 0.017 | 0.307 0.014 | 0.478 0.019 |
| LG-GNN | 0.026 0.000 | 0.486 0.010 | 0.494 0.005 | 0.525 0.009 | |
| PLSG-GNN | 0.024 0.000 | 0.493 0.012 | 0.490 0.004 | 0.514 0.018 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.312 0.013 | 0.303 0.010 | 0.517 0.019 |
| LG-GNN | 0.026 0.002 | 0.498 0.004 | 0.494 0.007 | 0.517 0.014 | |
| PLSG-GNN | 0.025 0.001 | 0.496 0.008 | 0.501 0.006 | 0.514 0.013 |
J.4 Geometric Graph
Each vertex has a latent feature generated uniformly at random on , Two vertices and are connected if corresponding to a connection probability Higher sparsity is achieved by adjusting .
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.537 0.012 | 1.000 0.000 | 1.000 0.000 | 0.886 0.015 |
| LG-GNN | 0.354 0.005 | 1.000 0.000 | 1.000 0.000 | 0.916 0.004 | |
| PLSG-GNN | 0.343 0.006 | 1.000 0.000 | 0.996 0.003 | 0.918 0.005 | |
| rho=1, layers=4 | GCN | 0.693 0.000 | 0.900 0.127 | 0.767 0.075 | 0.759 0.039 |
| LG-GNN | 0.305 0.002 | 1.000 0.000 | 1.000 0.000 | 0.950 0.002 | |
| PLSG-GNN | 0.301 0.002 | 1.000 0.000 | 0.999 0.001 | 0.956 0.002 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.333 0.062 | 0.232 0.030 | 0.848 0.007 |
| LG-GNN | 0.046 0.002 | 0.637 0.059 | 0.379 0.020 | 0.822 0.012 | |
| PLSG-GNN | 0.046 0.002 | 0.453 0.076 | 0.293 0.035 | 0.844 0.012 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.410 0.016 | 0.275 0.021 | 0.883 0.003 |
| LG-GNN | 0.045 0.001 | 0.637 0.054 | 0.377 0.024 | 0.827 0.003 | |
| PLSG-GNN | 0.045 0.001 | 0.530 0.079 | 0.345 0.012 | 0.848 0.003 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.003 0.005 | 0.019 0.005 | 0.624 0.018 |
| LG-GNN | 0.019 0.001 | 0.163 0.021 | 0.247 0.005 | 0.607 0.019 | |
| PLSG-GNN | 0.019 0.000 | 0.100 0.024 | 0.097 0.014 | 0.611 0.009 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.003 0.005 | 0.011 0.009 | 0.608 0.018 |
| LG-GNN | 0.019 0.001 | 0.170 0.022 | 0.237 0.029 | 0.609 0.032 | |
| PLSG-GNN | 0.018 0.001 | 0.133 0.019 | 0.154 0.023 | 0.634 0.022 |
Appendix K Out-Sample Experiments
K.1 6SSBM (80-20)
6-community symmetric stochastic block model with connection probabilities 0.8 and 0.2.
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.610 0.022 | 1.000 0.000 | 1.000 0.000 | 0.699 0.001 |
| LG-GNN | 0.569 0.004 | 0.998 0.004 | 0.998 0.001 | 0.682 0.002 | |
| PLSG-GNN | 0.730 0.184 | 0.998 0.004 | 0.999 0.001 | 0.677 0.002 | |
| rho=1, layers=4 | GCN | 0.693 0.000 | 0.623 0.106 | 0.581 0.090 | 0.520 0.004 |
| LG-GNN | 0.545 0.004 | 1.000 0.000 | 1.000 0.000 | 0.698 0.001 | |
| PLSG-GNN | 0.585 0.014 | 1.000 0.000 | 0.997 0.003 | 0.680 0.001 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.448 0.028 | 0.423 0.005 | 0.502 0.008 |
| LG-GNN | 0.092 0.002 | 0.450 0.031 | 0.436 0.013 | 0.508 0.004 | |
| PLSG-GNN | 0.091 0.002 | 0.405 0.004 | 0.387 0.003 | 0.503 0.003 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.415 0.006 | 0.387 0.004 | 0.506 0.006 |
| LG-GNN | 0.088 0.002 | 0.460 0.011 | 0.436 0.008 | 0.501 0.014 | |
| PLSG-GNN | 0.089 0.001 | 0.390 0.019 | 0.382 0.011 | 0.496 0.007 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.382 0.018 | 0.371 0.008 | 0.488 0.010 |
| LG-GNN | 0.021 0.001 | 0.355 0.024 | 0.371 0.012 | 0.510 0.019 | |
| PLSG-GNN | 0.019 0.001 | 0.387 0.049 | 0.377 0.015 | 0.491 0.030 | |
| rho=log(n)/n, layers=4 | GCN | 0.694 0.000 | 0.377 0.022 | 0.379 0.014 | 0.506 0.015 |
| LG-GNN | 0.021 0.000 | 0.460 0.054 | 0.384 0.011 | 0.499 0.015 | |
| PLSG-GNN | 0.018 0.000 | 0.395 0.013 | 0.376 0.021 | 0.511 0.011 |
K.2 6SSBM (55-45)
6-community symmetric stochastic block model with edge connection probabilities 0.55 and 0.45.
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.693 0.000 | 0.848 0.006 | 0.850 0.002 | 0.500 0.002 |
| LG-GNN | 0.698 0.002 | 0.845 0.005 | 0.846 0.003 | 0.500 0.001 | |
| PLSG-GNN | 0.694 0.001 | 0.844 0.003 | 0.846 0.003 | 0.500 0.001 | |
| rho=1, layers=4 | GCN | 0.693 0.000 | 0.848 0.004 | 0.850 0.001 | 0.498 0.001 |
| LG-GNN | 0.702 0.001 | 0.847 0.012 | 0.848 0.004 | 0.499 0.001 | |
| PLSG-GNN | 0.695 0.000 | 0.844 0.011 | 0.850 0.004 | 0.499 0.001 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.851 0.004 | 0.850 0.002 | 0.496 0.004 |
| LG-GNN | 0.131 0.003 | 0.859 0.010 | 0.851 0.005 | 0.505 0.011 | |
| PLSG-GNN | 0.131 0.002 | 0.844 0.007 | 0.850 0.001 | 0.505 0.003 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.842 0.008 | 0.847 0.001 | 0.500 0.009 |
| LG-GNN | 0.123 0.001 | 0.850 0.003 | 0.849 0.001 | 0.497 0.016 | |
| PLSG-GNN | 0.130 0.002 | 0.852 0.008 | 0.848 0.001 | 0.498 0.012 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.844 0.007 | 0.850 0.001 | 0.488 0.031 |
| LG-GNN | 0.030 0.000 | 0.842 0.002 | 0.846 0.005 | 0.484 0.011 | |
| PLSG-GNN | 0.029 0.001 | 0.851 0.001 | 0.849 0.002 | 0.505 0.008 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.851 0.004 | 0.847 0.002 | 0.493 0.024 |
| LG-GNN | 0.030 0.002 | 0.844 0.005 | 0.845 0.003 | 0.488 0.015 | |
| PLSG-GNN | 0.028 0.000 | 0.845 0.009 | 0.846 0.004 | 0.504 0.002 |
K.3 10 SBM
10-community stochastic block model with parameter matrix that has randomly generated entries. The diagonal entries are generated as , and is generated as . The connection matrix is
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.635 0.014 | 0.709 0.125 | 0.726 0.108 | 0.716 0.019 |
| LG-GNN | 0.586 0.004 | 0.883 0.016 | 0.843 0.014 | 0.734 0.005 | |
| PLSG-GNN | 0.586 0.004 | 0.886 0.016 | 0.844 0.013 | 0.735 0.005 | |
| rho=1, layers=4 | GCN | 0.801 0.193 | 0.645 0.025 | 0.633 0.027 | 0.578 0.109 |
| LG-GNN | 0.564 0.011 | 0.879 0.011 | 0.886 0.004 | 0.786 0.002 | |
| PLSG-GNN | 0.592 0.004 | 0.883 0.013 | 0.836 0.015 | 0.732 0.001 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.344 0.021 | 0.318 0.013 | 0.493 0.004 |
| LG-GNN | 0.115 0.002 | 0.580 0.020 | 0.557 0.007 | 0.497 0.009 | |
| PLSG-GNN | 0.112 0.004 | 0.586 0.035 | 0.561 0.001 | 0.521 0.008 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.285 0.016 | 0.275 0.006 | 0.486 0.006 |
| LG-GNN | 0.105 0.000 | 0.589 0.016 | 0.563 0.003 | 0.532 0.003 | |
| PLSG-GNN | 0.111 0.002 | 0.578 0.013 | 0.544 0.009 | 0.508 0.011 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.312 0.011 | 0.316 0.006 | 0.503 0.017 |
| LG-GNN | 0.026 0.000 | 0.528 0.029 | 0.504 0.006 | 0.506 0.015 | |
| PLSG-GNN | 0.023 0.002 | 0.511 0.017 | 0.501 0.013 | 0.519 0.002 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.304 0.027 | 0.304 0.015 | 0.518 0.005 |
| LG-GNN | 0.026 0.000 | 0.498 0.017 | 0.486 0.015 | 0.500 0.013 | |
| PLSG-GNN | 0.024 0.000 | 0.546 0.018 | 0.505 0.018 | 0.498 0.016 |
K.4 Geometric Graph
We generate points uniformly on and connect two points if For the following experiment, we chose and This corresponds to a probability of about 0.15.
| Cross Entropy | Prob Ratio @ 100 | Prob Ratio @ 500 | AUC ROC | ||
|---|---|---|---|---|---|
| Parameters | Model | ||||
| rho=1, layers=2 | GCN | 0.573 0.015 | 1.000 0.000 | 0.996 0.002 | 0.873 0.020 |
| LG-GNN | 0.358 0.009 | 1.000 0.000 | 0.999 0.001 | 0.915 0.007 | |
| PLSG-GNN | 0.350 0.013 | 0.997 0.005 | 0.999 0.002 | 0.917 0.010 | |
| rho=1, layers=4 | GCN | 0.693 0.000 | 0.813 0.021 | 0.733 0.079 | 0.591 0.016 |
| LG-GNN | 0.303 0.004 | 1.000 0.000 | 1.000 0.000 | 0.956 0.001 | |
| PLSG-GNN | 0.298 0.004 | 1.000 0.000 | 1.000 0.000 | 0.958 0.001 | |
| rho=1/sqrt(n), layers=2 | GCN | 0.693 0.000 | 0.333 0.017 | 0.216 0.017 | 0.840 0.008 |
| LG-GNN | 0.046 0.003 | 0.523 0.037 | 0.311 0.021 | 0.818 0.022 | |
| PLSG-GNN | 0.045 0.002 | 0.423 0.054 | 0.244 0.020 | 0.842 0.017 | |
| rho=1/sqrt(n), layers=4 | GCN | 0.693 0.000 | 0.313 0.021 | 0.207 0.013 | 0.848 0.021 |
| LG-GNN | 0.045 0.001 | 0.570 0.016 | 0.311 0.010 | 0.823 0.010 | |
| PLSG-GNN | 0.045 0.001 | 0.510 0.014 | 0.289 0.003 | 0.843 0.013 | |
| rho=log(n)/n, layers=2 | GCN | 0.693 0.000 | 0.003 0.005 | 0.012 0.004 | 0.610 0.026 |
| LG-GNN | 0.018 0.000 | 0.210 0.029 | 0.276 0.005 | 0.616 0.018 | |
| PLSG-GNN | 0.018 0.001 | 0.063 0.037 | 0.123 0.033 | 0.631 0.027 | |
| rho=log(n)/n, layers=4 | GCN | 0.693 0.000 | 0.007 0.009 | 0.035 0.007 | 0.607 0.002 |
| LG-GNN | 0.019 0.000 | 0.147 0.012 | 0.191 0.017 | 0.569 0.015 | |
| PLSG-GNN | 0.018 0.000 | 0.107 0.012 | 0.143 0.018 | 0.607 0.010 |