Stable Higher-Order Topological Dirac Semimetals with $\mathbb{Z}_{2}$ Monopole Charge in Alternating-twisted Multilayer Graphenes and beyond

The breakthrough in magic angle twisted bilayer graphene (TBG) makes it clear that the twist, as a powerful control method, can dramatically manipulate the physical properties of layered materials [1, 2, 3, 4]. In the rapid development of this field, numerous new twisted systems have been experimentally prepared, such as twisted trilayer graphene [5, 6], twisted double-bilayer graphene [7, 8], alternating- twisted four-layer and five-layer graphene [9], twisted transition metal dichalcogenide [10], twisted hexagonal boron nitride [11, 12], etc. It opens exciting possibilities for engineering exotic quantum states by the twist. A variety of novel quantum states are predicted or observed experimentally in the twisted systems, including unconventional superconducting states [2, 3], topological superconducting states [13, 14], quantum anomalous Hall states [4], quantum spin Hall states [15], high order topological insulating states [16, 17], and so on [18, 19, 20, 21, 22].

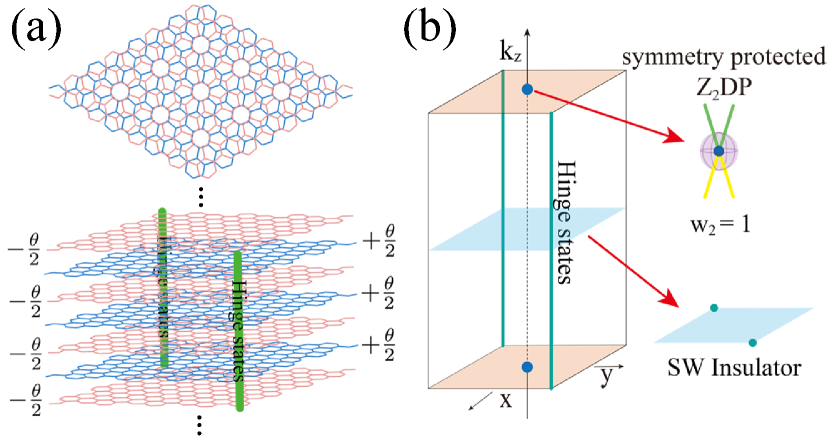
Topological semimetals (TSMs)[23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35] are materials whose band structures own gap-closing points, lines, or surfaces near the Fermi level. Recent studies show that the TSMs with nodal lines [36, 37, 38, 39, 40], or Dirac points (DPs) [38, 41, 40] can bear a 2D topological invariant called $\mathbb{Z}_{2}$ monopole charge protected by the space-time inversion ($\mathcal{P}\mathcal{T}$) symmetry in the absence of spin-orbital coupling. The topology of the $\mathbb{Z}_{2}$ monopole charge Dirac semimetals ($\mathbb{Z}_{2}$DSMs) is characterized by the second Stiefel-Whitney (SW) number $w_{2}$ (also called as the real Chern number) [42, 37, 43, 38]. Unlike the conventional Dirac semimetals, which do not belong to any of the four common characteristic classes, i.e., Chern class, Stiefel-Whitney class, Pontrjagin class, and Euler class, the $\mathbb{Z}_{2}$DSMs belong to the Stiefel-Whitney class [44, 37]. Previous studies mainly focused on the $\mathbb{Z}_{2}$ monopole charge nodal line ($\mathbb{Z}_{2}$NL) semimetals [37, 41, 40], since the $\mathbb{Z}_{2}$NLs are doubly charged, characterized by 1D winding number and the second Stiefel-Whitney number, and the two topological charges result in different boundary states at distinct boundaries, i.e., 2D drumhead surface states and 1D hinge states. In contrast, the $\mathbb{Z}_{2}$ monopole charge Dirac point ($\mathbb{Z}_{2}$DP) phase was considered a critical phase in the evolution of $\mathbb{Z}_{2}$NLs, unstable in real materials, and having only surface Fermi arcs. However, such surface Fermi arcs are not topologically protected [45].

In this Letter, we demonstrate the stability of $\mathbb{Z}_{2}$DPs with crystal symmetries and clearly show the topological-protected robust hallmark higher-order bulk-boundary correspondence in the $\mathbb{Z}_{2}$DP phase. We predict the alternating-twisted multilayer graphene (ATMG), which is plotted in Fig. 1(a) and considered as 3D TBG, as the first example of such stable $\mathbb{Z}_{2}$DSM materials from density functional theory (DFT) calculations and analytic analysis. We take the ATMG with a large twist angle (21.78^∘) and thus strong intervalley scattering as an instance to explicitly show the DPs, $\mathbb{Z}_{2}$ monopole charge, and higher-order hinge states. The stable DPs are protected by $\mathcal{P}\mathcal{T}$ and other crystalline symmetry operations. We build the effective models for the 3D TBGs. By applying strain or pressure we are able to access $\mathbb{Z}_{2}$NLs or introduce another pair of $\mathbb{Z}_{2}$DPs resulting in the hinge states with adjustable length. Furthermore, we generalize our discussion, tabulate all possible space groups supporting the stable $\mathbb{Z}_{2}$DPs and present the corresponding effective models. We suggest such stable $\mathbb{Z}_{2}$DSMs can also be realized in phonon and metamaterials, such as acoustics, photonics, and electrical circuits, with the allowable space groups.

We first introduce the crystal structures and symmetry of 2D TBGs. The TBG is constructed by rotating the two layers of $AA$-stacked bilayer graphene around the center of the hexagonal lattice by $-\theta/2$ and $+\theta/2$, respectively. For generic $\theta$, the translation symmetry is broken by the twist. The moiré translational symmetry is retained for the specific twist angles, which can take the form of $\theta(m,n)=\operatorname{arccos}[(3m^{2}+3mn+n^{2}/2)/(3m^{2}+3mn+n^{2})]$, where $m$ and $n$ are coprime positive integers [46]. The corresponding lattice constant of the moiré unit cell is $L=a\sqrt{\left(3m^{2}+3mn+n^{2}\right)/[\operatorname{gcd}(n,3)]}$, where $a$ is the original lattice constant and gcd represents the greatest common divisor. Then, we consider a structure of ATMG where the twisted angles of adjacent layers have the same magnitude but opposite direction as shown in Fig. 1(a). The ATMG can be viewed as a 3D TBG with two layers of graphene in each unit cell.

The 2D TBG crystalizes in the hexagonal symmorphic space group P622 with $C_{6z}$ and $C_{2x}$ symmetry about the out-of-plane $z$ and in-plane $x$ axes but no inversion symmetry ($\mathcal{P}$). The 3D TBG belongs to the nonsymmorphic space group P6/mmc (No. 192), which includes $C_{6z}$, $\mathcal{P}$ and $C_{2xy}^{{}^{\prime}}=\{C_{2xy}|00\frac{1}{2}\}$. Stacking gives 3D TBG some symmetry operations that 2D TBG does not have, which dramatically affects the topology and band degeneracy of the system.

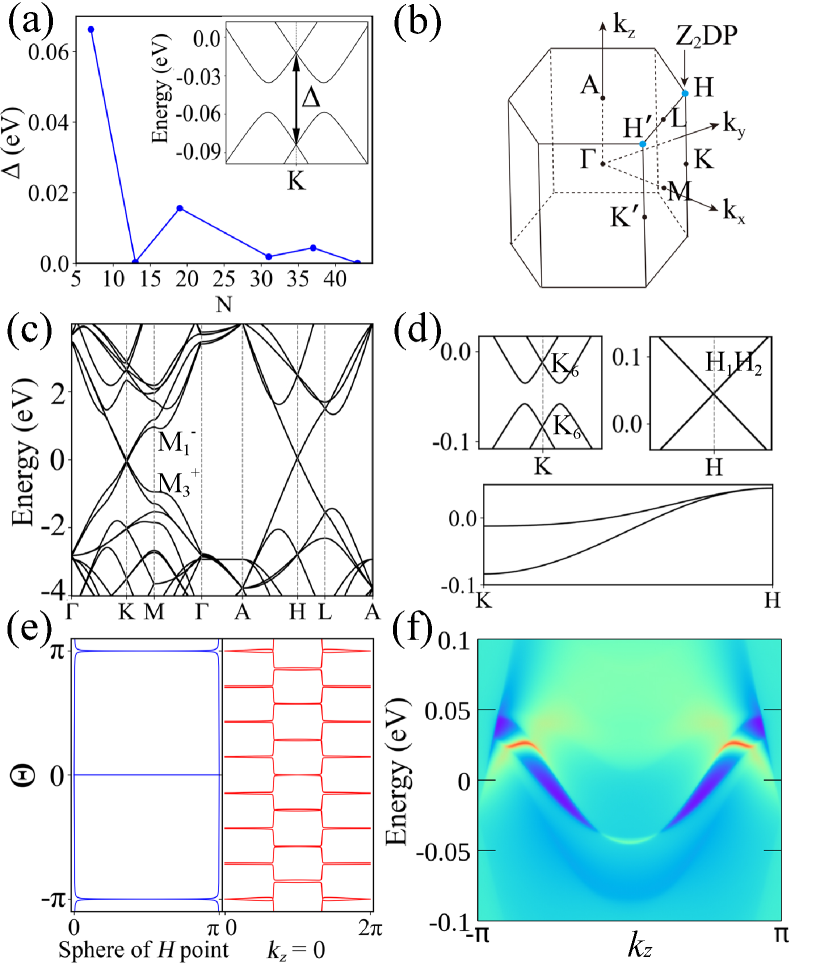
In stark contrast to the small twist angle limit ($\lesssim 1^{\circ}$), the $U(1)$ valley symmetry in TBGs is broken at a large angle with a gap opened at $K$ point due to the intervalley scattering[47, 16]. The size of the gap at $K$ depends on the size of the commensuration cell $N$ with $N=(L/a)^{2}$ and decays rapidly as $N$ increases, as shown in Fig. 2(a), and the 3D TBG with $N=7$ has the largest band gap at $K$ point, about 60 meV. Figure 2(c) shows the DFT band structure of $\sqrt{7}\times\sqrt{7}$ ($N=7$, $\theta=21.78^{\circ}$) 3D TBG. The magnified views of the regions near $K$, $H$, and high symmetric line $KH$ are plotted in Fig. 2(d). The corresponding band representations are also given. The band gap is about 20 meV near $K$. As the $k_{z}$ increases, the band gap becomes smaller and smaller and finally the bands close at $H$. The bands are double degenerate along the $KH$ line protected by the $C_{3z}$ and $\mathcal{PT}$ symmetry and become a four-fold degenerate point at $H$. The band gap of 3D TBG around $K$ point is dramatically affected by the layer distance. Under pressure, the band gap near $K$ can reach 0.1 eV at the layer distance of 2.95 Å (3.3 Å without pressure) [See details in Supplemental Material (SM) [48]].

The $\mathbb{Z}_{2}$ monopole topology for a $\mathbb{Z}_{2}$DP or $\mathbb{Z}_{2}$NL can be characterized by the second Stiefel-Whitney number $w_{2}$, which can be calculated efficiently by using the Wilson loop method [37]. We calculate the Wilson loop of the sphere enclosing the DP ($H$ point), as shown in the left panel of Fig. 2(e). This Wilson loop spectrum exhibits $w_{2}=1$ with the characteristic winding of a $\mathbb{Z}_{2}$DP, as it only has one crossing point on $\Theta=\pi$. Normally, a nontrivial $\mathbb{Z}_{2}$NL can shrink to a $\mathbb{Z}_{2}$DP with only critical parameters. Such $\mathbb{Z}_{2}$DPs are not stable under the protection of $\mathcal{P}\mathcal{T}$ symmetry. We point out that one new kind of $\mathbb{Z}_{2}$DPs can stably exist at certain high symmetric points with additional crystalline symmetry operations forming essential degenerate points, such as in the 3D TBG. These $\mathbb{Z}_{2}$DPs are even more stable than $\mathbb{Z}_{2}$NLs because they are pinned at high symmetric points and therefore cannot be annihilated without symmetry broken.

The ATMGs (3D TBGs) with nontrivial $\mathbb{Z}_{2}$ monopole topology have a higher-order bulk-boundary correspondence with a hallmark hinge state, which is shown in Fig. 2(f) and calculated by the recursive hinge Green function method, as described in SM [48]. To better understand the higher-order bulk-boundary correspondence, we further calculate the Wilson loop spectrum at the planes of $k_{z}\in(-\pi,\pi)$, with the $k_{z}=0$ plane shown in the right panel of Fig. 2(e). The crossing points on $\Theta=0$ and $\Theta=\pi$ in the Wilson loop are both odd numbers, which indicates the $w_{2}=1$. Each slice with a specific $k_{z}$ in the Brillouin zone (BZ) is a torus and can be taken as a 2D subsystem. In the 3D TBG, the entire $k_{z}$ slices except $k_{z}=\pm\pi$ carry nontrivial $w_{2}=1$. Therefore, each slice in the region of (-$\pi,\pi$) is a 2D Stiefel-Whitney insulator, which has a pair of topologically protected corner zero modes, as schematically shown in Fig. 1(b). Such zero modes from all of these nontrivial $k_{z}$ slices make up the topological protected hinge states on a pair of $\mathcal{P}\mathcal{T}$-related hinges [49].

At $H/H^{\prime}$ points of 3D TBG, the $\mathbb{Z}_{2}$DPs are protected by not only $\mathcal{P}\mathcal{T}$ symmetry but also $C_{3z}^{\pm}$, $\widetilde{\mathcal{\sigma}}_{d}=\{\sigma_{d}|00\frac{1}{2}\}$ and $M_{z}$. We first demonstrate an essential degenerate DP at $H$ with these symmetry operations. The algebra of these symmetry operations can be written as $(M_{z}\mathcal{P}\mathcal{T})^{2}\equiv\mathcal{A}^{2}=1,\widetilde{\mathcal{\sigma}}_{d}^{2}=-1,C_{3z}^{\pm}\mathcal{A}=\mathcal{A}C_{3z}^{\pm},C_{3z}^{\pm}\widetilde{\mathcal{\sigma}}_{d}=\widetilde{\mathcal{\sigma}}_{d}C_{3z}^{\mp},\mathcal{A}\widetilde{\mathcal{\sigma}}_{d}=\widetilde{\mathcal{\sigma}}_{d}\mathcal{A}$ [48]. The Bloch states can be chosen as the eigenstates of $C_{3z}^{+}$, denoted as $|\phi\rangle$ with the eigenvalues $\phi=1,e^{\pm i\frac{2\pi}{3}}$. Since $C_{3z}^{+}$ commutes with $\mathcal{A}$ and $\mathcal{A}i=-i$, the two states $|e^{i\frac{2\pi}{3}}\rangle$ and $\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$ would be degenerate, as $C_{3}^{+}\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle=e^{-i\frac{2\pi}{3}}\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$. Similarly, the two states $\widetilde{\mathcal{\sigma}}_{d}|e^{i\frac{2\pi}{3}}\rangle$ and $\widetilde{\mathcal{\sigma}}_{d}\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$ are degenerate. Since $(\widetilde{\mathcal{\sigma}}_{d}\mathcal{A})^{2}=-1$ and $\langle e^{i\frac{2\pi}{3}}|\widetilde{\mathcal{\sigma}}_{d}\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$ = 0, the two degenerate states $|e^{i\frac{2\pi}{3}}\rangle$ and $\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$ and their Kramers-like partner $\widetilde{\mathcal{\sigma}}_{d}\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$ and $\widetilde{\mathcal{\sigma}}_{d}|e^{i\frac{2\pi}{3}}\rangle$ are linearly independent. Consequently, the four states $\{|e^{i\frac{2\pi}{3}}\rangle$, $\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle$, $\widetilde{\mathcal{\sigma}}_{d}|e^{i\frac{2\pi}{3}}\rangle$, $\widetilde{\mathcal{\sigma}}_{d}\mathcal{A}|e^{i\frac{2\pi}{3}}\rangle\}$ must be degenerate at the same energy, forming an essential degenerate DP.

Constrained by these symmetry operations [48], the $\mathbf{k}\cdotp\mathbf{p}$ model around $H$ expanded to the first order of $q=k-H$ reads

$$H_{DP}=\alpha(q_{x}\Gamma_{x,z}-q_{y}\Gamma_{y,0})+q_{z}(\beta_{1}\Gamma_{x,x}+\beta_{2}\Gamma_{y,x}),$$

(1)

where $\alpha$ and $\beta_{i}$ are real parameters and $\Gamma_{i,j}=\sigma_{i}\otimes\sigma_{j}$. The energy eigenvalues are $E_{DP}=\pm\sqrt{\alpha^{2}\rho^{2}+\beta^{2}q_{z}^{2}\pm 2\alpha\left|\beta_{2}q_{z}\right|\rho}$ with $\rho=\sqrt{q_{x}^{2}+q_{y}^{2}}$ and $\beta=\sqrt{\beta_{1}^{2}+\beta_{2}^{2}}$. One can see the four-fold degenerate DP located at $q_{x}=q_{y}=q_{z}=0$ [Fig. 3(a)]. To confirm the $\mathbb{Z}_{2}$ topological charge of the model, we calculate the Wilson loop of a sphere enclosing the DP, which is nontrivial with $w_{2}=1$ [Fig. 3(a)]. A perturbation term $m_{0}\sigma_{0}\otimes\sigma_{z}$, which breaks the $\widetilde{\mathcal{\sigma}}_{d}$, is added on the $H_{DP}$ and the energy eigenvalues are $E_{NL}=\pm\sqrt{\left(\sqrt{\beta_{2}^{2}q_{z}^{2}+m_{0}^{2}}\pm\alpha\rho\right)^{2}+\beta_{1}^{2}q_{z}^{2}}$. One can see that the valence and conduction bands touch at $q_{z}=0$ and $\rho=\lvert m_{0}/\alpha\rvert$, indicating that the $\mathbb{Z}_{2}$DP is split into a NL [Fig. 3(a)]. Moreover, the $\mathbb{Z}_{2}$ monopole charge is preserved in the NL, resulting in a $\mathbb{Z}_{2}$NL [Fig. 3(a)]. The other NLs ($\rho=0$) from two valence or conduction bands link with the $\mathbb{Z}_{2}$NL.

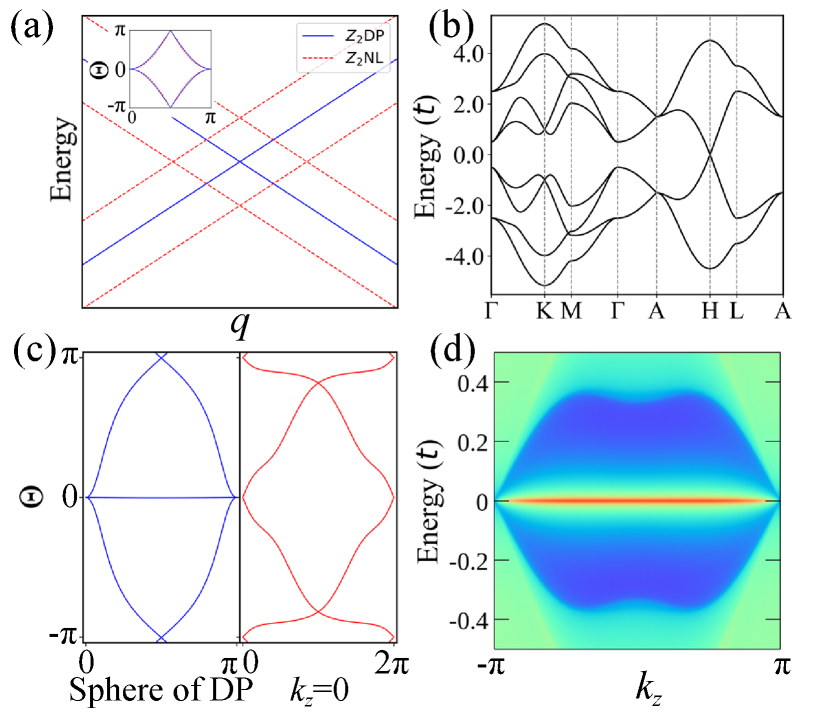
To further explore the higher-order bulk-boundary correspondence of the $\mathbb{Z}_{2}$DPs and get a better fitting with the 3D TBG in the band representation, we construct a minimal tight-binding (TB) lattice model. The model assumes $d_{xz}$ and $d_{yz}$ symmetry orbitals at the Wyckoff position 4$d$ of a hexagonal lattice with nonsymmorphic space group P6/mmc. This model can be viewed as two layers of honeycomb lattice in a unit cell. The intra-layer hopping integrals between $d_{xz,yz}$-like orbitals on each layer of the honeycomb lattice are constructed via the Slater-Koster formalism, which reflects coexisting $\sigma$ and $\pi$ bonds.

The intra-layer Hamiltonian with only nearest neighbor hopping of each layer reads

$$H_{intra}=\sum_{i\mu,j\nu}t_{i\mu,j\nu}c_{i\mu}^{\dagger}c_{j\nu},$$

(2)

where $\mu,\nu=x,y$ represent the $d_{xz}$ and $d_{yz}$ orbitals, $i$, $j$ stand for the two sublattices of one layer honeycomb lattice. The hopping integrals $t_{i\mu,j\nu}$ read

$$t_{i\mu,j\nu}=t_{\sigma}^{ij}\cos\theta_{\mu,ij}\cos\theta_{\nu,ij}+t_{\pi}^{ij}\sin\theta_{\mu,ij}\sin\theta_{\nu,ij},$$

(3)

where $\theta_{\mu,ij}$ represents the angle between the direction of $\mu$ and $\mathbf{r}_{j}-\mathbf{r}_{i}$ [48]. The Slater-Koster parameters $t_{\sigma/\pi}^{ij}$ denote the hopping integrals contributed by $\sigma/\pi$ bonds. The interlayer hopping has the form of

$$H_{inter}=r_{2}\cos\left(\frac{k_{z}}{2}\right)s_{0}\sigma_{0}\tau_{x}+r_{1}\cos\left(\frac{k_{z}}{2}\right)s_{y}\sigma_{0}\tau_{y}$$

(4)

where the Pauli matrices $s$, $\sigma$, and $\tau$ act on the orbital, sublattice, and layer degree of freedom, respectively. The $r_{1}$ and $r_{2}$ denote the hopping integrals between the orbitals in different layers.

Therefore, the minimal eight-band model reads

$$H_{8}=H_{intra}\tau_{0}+H_{inter}.$$

(5)

The Hamiltonian belongs to the space group P6/mmc, which is demonstrated in SM [48]. The band structure shows that a couple of DPs are pinned at $H/H^{\prime}$ and at the Fermi level [Fig. 3(b)]. The degeneracy at $H$ and the band representations are both consistent with the 3D TBG. The nontrivial monopole charge of the DPs are confirmed by the Wilson loop [left panel of Fig. 3(c)]. Similar to the above analysis, each slice in the region of (-$\pi,\pi$) is a 2D Stiefel-Whitney insulator [right panel of Fig. 3(c)], whose corner zero modes constitute the hinge Fermi arc, as shown in Fig. 3(d).

We also construct a Slater-Koster TB model with only $p_{z}$ orbitals of carbon, which has good agreements with the DFT results [48].

Manipulation of $\mathbb{Z}_{2}$ topological quantum states— One can induce novel topological child phases from the $\mathbb{Z}_{2}$DP parent phase. Adding different onsite energy of the two layers in the minimal TB model, the symmetry $C_{2xy}^{{}^{\prime}}$ is broken and a $\mathbb{Z}_{2}$NL emerges and links with other NLs formed by two valence or conduction bands, as shown in Figs. 4(a, b) [48]. Similar to the DP phase case, each slice of $k_{z}\in(-\pi,\pi)$ is a 2D Stiefel-Whitney insulator with a pair of topologically protected corner zero modes. These zero modes will constitute the topologically protected hinge states, as shown in Fig. 4(c). Such scenario to induce the $\mathbb{Z}_{2}$NL phase can be realized in 3D TBG with uniaxial strain applied, as demonstrated in SM [48].

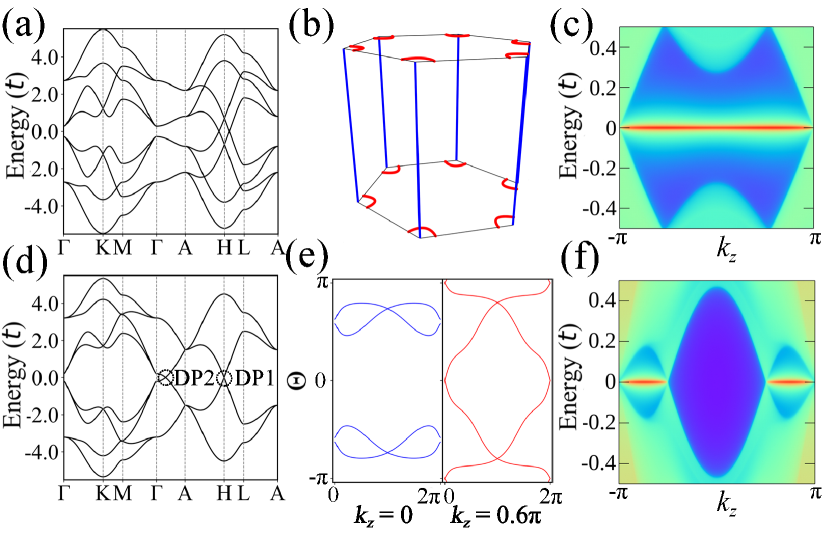
Tailoring the parameters of interlayer coupling can result in another pair of DPs along the high symmetric line $\Gamma A$ in addition to the pair of DPs at the points $H/H^{\prime}$, which are labeled as DP2 and DP1 respectively [Fig. 4(d)]. The DP2 is an accidental degenerate point while the DP1 is an essential degenerate point. Both types of DPs have nontrivial $\mathbb{Z}_{2}$ topology. The $w_{2}$ of the $k_{z}$ slices between two accidental degenerate $\mathbb{Z}_{2}$DPs become trivial [Fig. 4(e)], and the hinge states are split into two pieces [Fig. 4(f)] [48]. As a result, one can tailor the length of the hinge Fermi arc by tuning the interlayer hopping parameters.

Since the DPs are protected by the crystal symmetry at (along) high-symmetric points (lines), we can check their topology of $\mathbb{Z}_{2}$ monopole charge by calculating the Wilson loop of all DPs in the 230 type-II magnetic space groups [50, 51, 52]. Finally, we find six space groups can protect essential degenerate $\mathbb{Z}_{2}$DPs and six space groups can protect accidental degenerate $\mathbb{Z}_{2}$DPs, as given in Table 1. The corresponding $\mathbf{k}\cdot\mathbf{p}$ effective models, band structures, and Wilson loop spectra are presented in SM [48].

The $\mathbb{Z}_{2}$DPs are widely present in the electronic band structures and phonon spectra of materials which belong to these space groups. For example, besides the ATMG, the $\mathbb{Z}_{2}$DPs are also present in the band structure at the $P$ point of Si [53] with the space group No. 206, the $H$ point of the phonon spectrum in LaF₃ [54] with the space group No. 165, and in the phonon spectrum of KSn [55] with the space group No. 142, as shown in SM [48]. Moreover, one can also construct metamaterials such as photonic and phononic crystals to realize $\mathbb{Z}_{2}$DP phases based on these space groups.

We demonstrate that $\mathbb{Z}_{2}$DPs can stably exist in real materials and give all possible space groups to allow the existence of $\mathbb{Z}_{2}$DPs. The nontrivial $\mathbb{Z}_{2}$ monopole charge topology is characterized by the second Stiefel-Whitney number $w_{2}$. Our research shows that the $\mathbb{Z}_{2}$DP phase is stable and even can be observed more readily in experiments than the $\mathbb{Z}_{2}$NL phase. This is because the $\mathbb{Z}_{2}$NL phase easily undergoes the pair annihilation, whereas the $\mathbb{Z}_{2}$DPs stably exist in specific high-symmetric points for all materials in the twelve allowable space groups, which we point out explicitly. Specifically, we propose ATMGs as the first example of such stable $\mathbb{Z}_{2}$DSM with higher-order hinge Fermi arcs, which can be probed by scanning tunneling spectroscopy, as exploring the higher-order topology in Bismuth [56]. The $\mathbb{Z}_{2}$DSM in 3D TBG enriches the topological phases in twistronics. Based on our effective models and proposed list of allowed space groups, the new and stable kinds of $\mathbb{Z}_{2}$DSM phases are expected to be realized in metamaterials, such as acoustics, photonics, and electrical circuits, thanks to the flexibility of the building blocks.

The work is supported by the National Key R&D Program of China (Grant No. 2020YFA0308800) and the NSF of China (Grants No. 11922401).