Stable Atomic Magnetometer in Parity-Time Symmetry Broken Phase

Introduction.—Measurement of extremely weak signals requires sensors with high sensitivity and high stability. High sensitivity allows the sensor to generate large enough signal against background noise. However, the signal-to-noise ratio is ultimately limited by the measurement time. During a long measurement, even if the detected signal is actually unchanged, the sensor output is prone to vary over time due to the imperfect control of measurement conditions (e.g., the low frequency drift of electronic devices). In this sense, the ability of rejection or compensation of long-term drift, i.e. the stability, of a sensor is essential for measuring extremely weak signals.

Atomic spins are useful in the sensing of weak magnetic fields [1] or signals which are regarded as effective magnetic fields, such as inertial rotations [2] and extraordinary interactions of fundamental physics [3, 4, 5, 6, 7]. These fields to be detected will manifest themselves by shifting the precession frequency of atomic spins. For atoms in liquid or gas phases, their spatial motion is usually governed by the diffusion law. With inevitable magnetic field inhomogeneity, the diffusion causes spin relaxation and decoherence, which increase the uncertainty of the spin precession frequency and degrade the weak field sensing.

The spin precession with spatial motion has been extensively studied decades ago [8, 9, 10]. The dynamics of diffusive atomic spins is governed by the Torrey equation [10]. When confined in a finite volume, the atomic motion is described by a series of eigenmodes with complex eigenvalues. Stoller, Happer and Dyson [11] gave the exact solution to the Torrey equation with a linear magnetic field gradient and demonstrated the branch behavior of the eigenvalue spectrum due to the non-Hermitian nature of the Torrey equation.

The spin diffusion in non-uniform magnetic field is an ideal platform for studying the non-Hermitian physics. The branch spectrum of the Torrey equation proposed in ref. [11] is indeed the signature of the $PT$ transition [12, 13]. Among a number of experimental demonstrations of the $PT$ transition in various physical systems [14, 15, 16, 17, 18, 19, 20, 21, 22, 23], Zhao, Schaden and Wu [24, 25, 26, 27, 28] observed the $PT$ transition in system of diffusive electron spin of Rb atoms using ultra-thin vapor cells. Here, we study the $PT$ transition process of diffusive nuclear spins. The full eigenvalue spectrum in both $PT$-symmetric and $PT$-broken phases and, particularly, the mode localization (also known as edge-enhancement [29]) behavior in the $PT$-broken phase are observed.

We further demonstrate the application of the $PT$ transition of diffusive spins in magnetometry. In contrast to previous studies on the improvement of sensitivity near the exceptional points (EPs) [35, 36, 37, 38, 39, 40, 41], we show that, the spatial motion of spins in the $PT$-broken phase could be a resource for improving measurement stability.

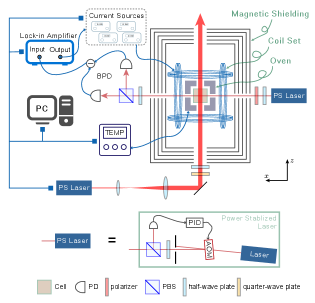
$PT$ Transition of Diffusive Spins.—We observe the $PT$ transition of diffusive nuclear spins by using the experimental setup shown in Fig. 1. Two isotopes of noble gas ($\rm{}^{129}Xe$ and $\rm{}^{131}Xe$), both carrying nuclear spins, are sealed in a cubic glass cell with inner side length $L=0.8~{}{\rm cm}$. The free-induction decay (FID) signal of the Xe nuclear spins is measured to explore their dynamics.

The dynamics of the Xe nuclear spins is governed by the Torrey equation [10]

where $K_{+}(\mathbf{r},t)\equiv K_{x}+iK_{y}$ is the transverse component of the Xe nuclear spin magnetization $\mathbf{K}(\mathbf{r},t)$, $D$ is the diffusion constant, $\gamma$ is the gyromagnetic ratio of Xe nuclear spins, $B_{z}(\mathbf{r})$ is the magnetic field along $z$ direction and $\Gamma_{\rm 2c}$ is the intrinsic spin relaxation rate due to inter-atom collisions. We present a detailed solution of Eq. (1) in Section LABEL:SMsec:theoreticalModel of Supplemental Material (SM).

Consider the special case where $B_{z}(\mathbf{r})=B_{0}+G\cdot z$ and the boundary condition is $\hat{\mathbf{n}}\cdot\nabla K_{+}(\mathbf{r})=0$ on the cell walls. The eigen-problem corresponding to Eq. (1) can simplify to

Here, we ignore the $x,y$ directions because $B_{z}$ is uniform along these directions, and thus $M_{k}(\mathbf{r})=M_{k}(z)$ for the ground modes. The $i\gamma B_{0}$ and $\Gamma_{\rm 2c}$ terms are dropped because they only contribute a constant shift to all eigenvalues $\{s_{k}\}$.

The $PT$ operation changes Eq. (2) into

meaning that both $\{s_{k},M_{k}(z)\}$ and $\{s_{k}^{*},M_{k}^{*}(-z)\}$ solve Eq. (2).

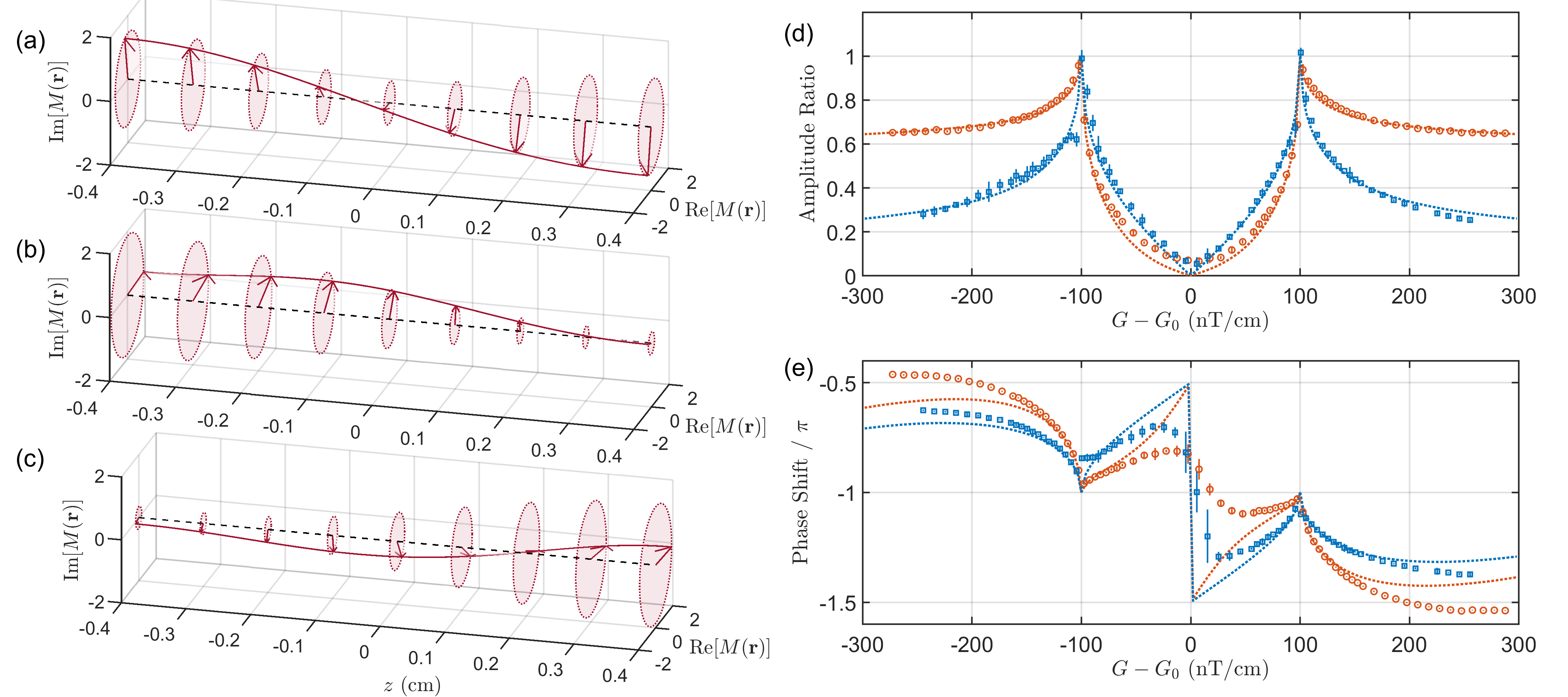
In the small gradient region, all $\{s_{k}\}$ are purely real and no degeneracy exists, which means the eigenmodes should have $PT$ symmetry, i.e. $M_{k}(z)=M_{k}^{*}(-z)$. Figure. 2(a) shows an example of $M_{1}(z)$ in this region. The eigenmodes extend over the whole cell, mode localization at the boundary is prevented by the $PT$ symmetry.

However, predicted by the solution in ref. [11], there is a critical gradient called exceptional point (EP) where $s_{0}$ and $s_{1}$ become the same. In the region $G>G_{\rm EP}$, the imaginary part of $s_{0}$ and $s_{1}$ are non-zero, and the $PT$ symmetry of $M_{0}(z)$ and $M_{1}(z)$ breaks. Instead, $PT$ operation transforms $M_{0}(z)$ into $M_{1}^{*}(-z)$. As the gradient gets larger, $M_{0}(z)$ and $M_{1}(z)$ start to localize on the opposite ends of the cell. This lead to the splitting of resonance frequency of these eigenmodes since they “feel” a different average field. Figure. 2(b)(c) show an example of $M_{0}(z)$ and $M_{1}(z)$ in this region. (For more details, see Section LABEL:SMsec:PT_explanation of SM.)

Based on the symmetry of eigenmodes, the $G<G_{\rm EP}$ region is named as $PT$-symmetric phase and the $G>G_{\rm EP}$ region is $PT$-broken phase. The theoretical prediction of EP for ${\rm{}^{129}Xe}$ in our experiment is $G_{\rm EP}=99.4~{}{\rm nT/cm}$. The EP for ${\rm{}^{131}Xe}$ ($\sim 335~{}{\rm nT/cm}$) is larger than the gradient region we can reach.

The evolution of $K_{+}$ can be expanded using the eigenmodes as $K_{+}(\mathbf{r},t)=\sum_{k}c_{k}M_{k}(\mathbf{r}){\rm e}^{-s_{k}t}$, where $\{c_{k}\}$ are expansion coefficients determined by the initial spin distribution. The FID signal is proportional to (see Eq. (LABEL:Eq:FIDSignal_twoModeSolution) of SM):

where $z_{\rm p}$ is the position of probe beam (on $z$ axis), $A_{k}(z_{\rm p})\equiv|c_{k}M_{k}(z_{\rm p})|$, $\theta_{k}(z_{\rm p})\equiv-\arg[c_{k}M_{k}(z_{\rm p})]$ and $s_{k}\equiv\Gamma_{k}+i\omega_{k}$. Since higher excited modes decays very fast, only $M_{0}$ and $M_{1}$ have experimentally observable effect. In the following, the subscript $k=1$ and $0$ is replaced by “$+$” and “$-$” signs, respectively.

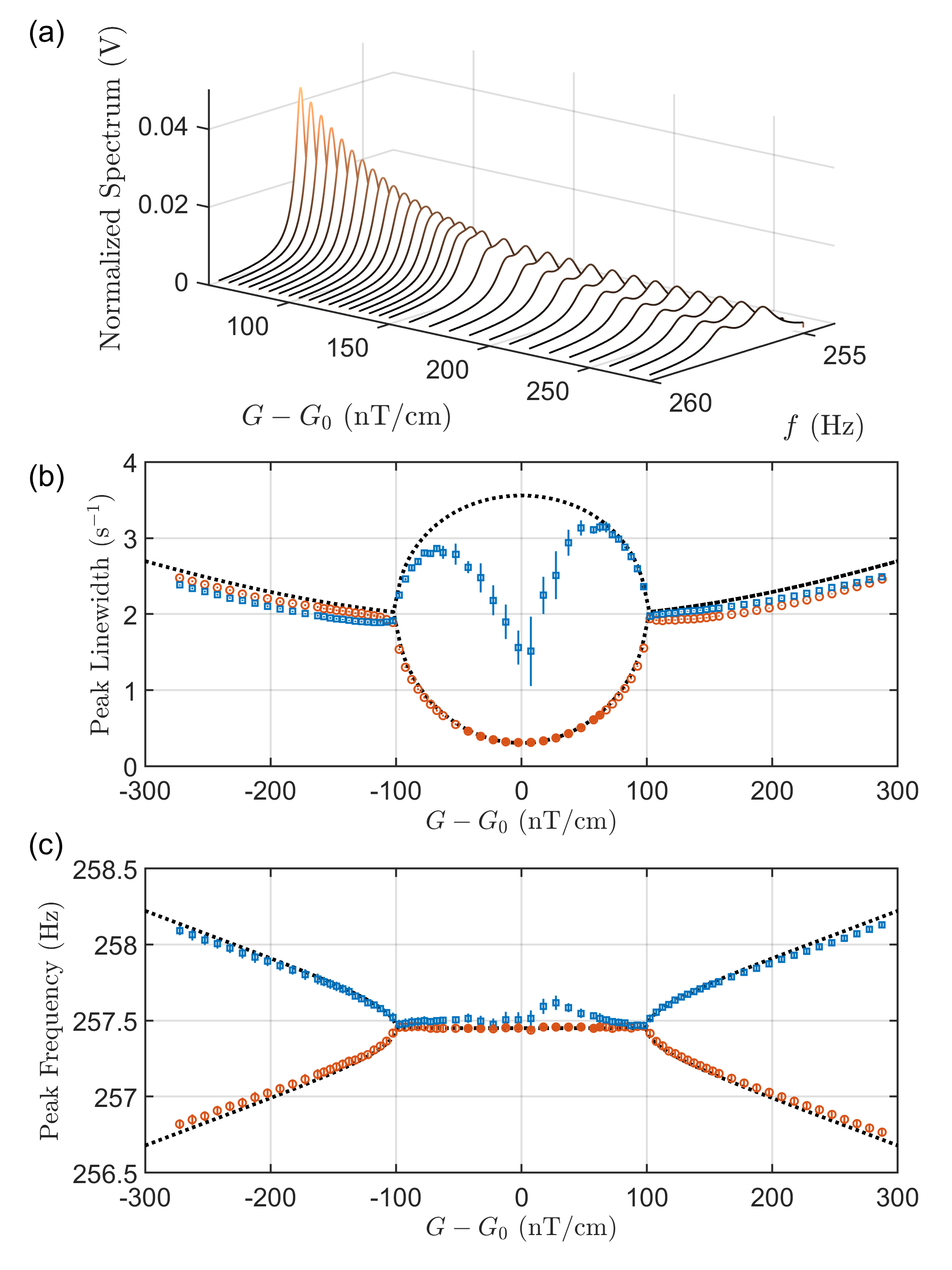
Figure 3(a) shows the spectrum of FID signals at different gradient. The resonance peak splits as gradient gets larger. Figures 3(b)(c) compare the measured eigenvalues $s_{\pm}$ with the theoretical values. The behavior of $\Gamma_{\pm}$ and $\omega_{\pm}$ fits well with theory. Figures 2(d)(e) show the amplitude ratio $\eta(z_{\rm p})\equiv A_{\rm min}/A_{\rm max}$ and phase shift $\delta\theta(z_{\rm p})\equiv\pm\left(\theta_{+}-\theta_{-}\right)$ of the two eigenmodes $M_{\pm}$, where $A_{\rm max}$ ($A_{\rm min}$) is the larger (smaller) amplitude between $A_{\pm}(z_{\rm p})$. Two probe beam positions are used to verify the spatial distribution of eigenmodes. The amplitude ratio $\eta$ fits well with theory, and is sensitive to $z_{\rm p}$ in the $PT$-broken phase due to the localization of eigenmodes. The phase shift fits not so good with theory because of the fitting accuracy and the difficulty on determining the precise time origin of an FID signal.

Stable Comagnetometer in $PT$ Broken Phase.—One can utilize the split spin precession frequencies in the $PT$-broken phase to stabilize the output of the atomic magnetometers. In general, the precession frequency $\omega_{\alpha}$ of a given spin species $\alpha$ is usually influenced by a number of input variables and is expressed by a multivariate function $\omega_{\alpha}=\omega_{\alpha}(\mathbf{x})$ of the input vector $\mathbf{x}=[x_{1},x_{2},…,x_{M}]^{\rm T}$. Among the $M$ components of $\mathbf{x}$, only one is the real signal we want to detect (e.g., the unknown magnetic field). The remaining $M-1$ variables will cause systematic error if they are not well controlled. Comagnetometers use $M$ precession frequencies $\bm{\omega}=[\omega_{1},\omega_{2},…,\omega_{M}]^{\rm T}$ of different spin species to determine the $M$ variables in $\mathbf{x}$ unambiguously. As long as the Jacobian matrix $J=[\partial\omega_{i}/\partial x_{j}]_{i,j=1\dots M}$ of the multidimensional function $\bm{\omega}=\bm{\omega}(\mathbf{x})$ is invertible, the comagnetometer is immune to the drift of all the variables in $\mathbf{x}$.

The dual-species nuclear magnetic resonance gyroscope (NMRG) [2], a kind of comagnetometer, uses the precession frequencies $\bm{\omega}=[\omega_{129},\omega_{131}]^{\rm T}$ of $\rm{}^{129}Xe$ and $\rm{}^{131}Xe$ nuclear spin to determine the rotation rate $\Omega_{\rm rot}$ of the system. The precession frequencies $\bm{\omega}$ depend on $\mathbf{x}=[B,\Omega_{\rm rot}]^{\rm T}$ through the relation $\omega_{\alpha}=\gamma_{\alpha}B+\Omega_{\rm rot}$, where $\gamma_{\alpha}$ is the gyromagnetic ratio of $\rm{}^{129}Xe$ or $\rm{}^{131}Xe$ nuclear spin and $B$ is the magnetic field along $z$ direction. The rotation rate is estimated by (assume $B>0$)

with $R\equiv\gamma_{129}/\gamma_{131}\approx-3.373417$ the ratio of gyromagnetic ratios [42].

The above relation $\omega_{\alpha}=\gamma_{\alpha}B+\Omega_{\rm rot}$ is only valid when the magnetic field $B$ is spatially uniform. Due to the difference of boundary conditions and gyromagnetic ratios, the diffusive $\rm{}^{129}Xe$ and $\rm{}^{131}Xe$ spins can have different responses to a non-uniform magnetic field. The spin precession frequencies are actually $\omega_{\alpha}=\gamma_{\alpha}B_{0}+\Omega_{\rm rot}+\gamma_{\alpha}\bar{B}_{\rm A,\alpha}$, where $\bar{B}_{\rm A,\alpha}$ is an isotope-dependent effective magnetic field originated from the inhomogeneity of $B(\mathbf{r})$ [43] and $B_{0}$ is the mean value of $B(\mathbf{r})$. The differential part $b_{\rm A}\equiv\bar{B}_{\rm A,129}-\bar{B}_{\rm A,131}$ of the isotope-dependent effective field produces a systematic error on the estimator Eq. (5) as

One origin of the inhomogeneity of $B(\mathbf{r})$ is the polarization field generated by the spin-exchange collisions between Xe and Rb atoms. In our experiment, the $\bar{B}_{\rm A,\alpha}$ from polarization field is in the order of $\sim 10^{1}~{}{\rm nT}$, and the observed value of $b_{\rm A}$ can be as large as $\sim 10^{0}~{}{\rm nT}$. More importantly, $b_{\rm A}=b_{\rm A}(P_{\rm pump},f_{\rm pump},T,\dots)$ depends on several control parameters such as the laser power $P_{\rm pump}$, laser frequency $f_{\rm pump}$ and cell temperature $T$, etc. The drift of these control parameters will eventually limit the long-term stability of $\Omega_{\rm rot}$ measurement. Great efforts based on pulse control of the alkali-metal atoms have been made to eliminate the influence of the polarization field [44, 45, 46]. Here we demonstrate a new method utilizing the $PT$ transition.

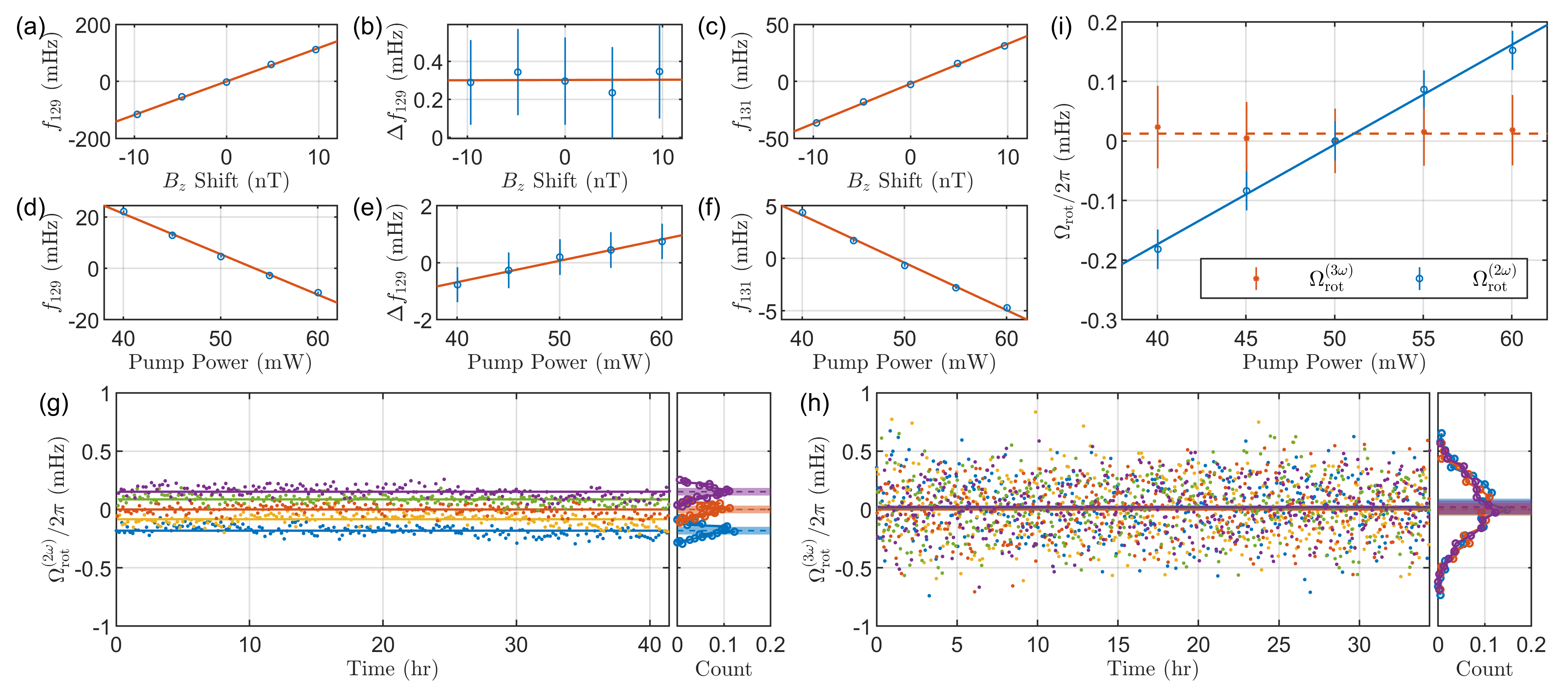
The $PT$ transition extends the dual-species NMRG to a 3-component comagnetometer. Particularly, we measure three frequencies $\bm{\omega}=[\omega_{129},\Delta\omega_{129},\omega_{131}]^{\rm T}$ as functions of three input variables $\mathbf{x}=[B_{0},\Omega_{\rm rot},P_{\rm pump}]^{\rm T}$, where $\omega_{129}\equiv(\omega_{+}+\omega_{-})/2$ and $\Delta\omega_{129}\equiv|\omega_{+}|-|\omega_{-}|$ are the mean frequency and the $PT$ splitting of $\rm{}^{129}Xe$. As a proof-of-principle experiment, we assumed the pump power $P_{\rm pump}$ to be the dominating parameter which affects the non-uniform magnetic field, i.e., $b_{\rm A}=b_{\rm A}(P_{\rm pump})$. The Jacobian matrix is experimentally determined and the gyroscope signal $\Omega_{\rm rot}^{\rm(3\omega)}$ of 3-component comagnetometer is calculated by solving the following linear equation

where $\chi_{1}$, $\chi_{2}$ and $\chi_{3}$ are the fitted slopes in Figs. 4(d)-(f), respectively. The $PT$ splitting $\Delta\omega_{129}$ is insensitive to $B_{0}$ but proportional to the change of $P_{\rm pump}$. This can be understood by noticing that the spatial distribution of the polarization field relies on $P_{\rm pump}$. The $\rm{}^{129}Xe$ spins sense the change of the inhomogeneous polarization field and manifest it as the splitting $\Delta\omega_{129}$ between the two localized modes in the $PT$-broken phase.

Figures 4(g)(h)(i) compare the measurement stability of $\Omega_{\rm rot}$ against the change of $P_{\rm pump}$. During the whole measurement, the actual rotation rate $\Omega_{\rm rot}$ is unchanged. The traditional dual-species NMRG estimator $\Omega_{\rm rot}^{(\rm 2\omega)}$ shows a $17~{}{\rm\mu Hz/mW}$ dependence on $P_{\rm pump}$, while slope almost vanishes for our 3-component comagnetometer estimator $\Omega_{\rm rot}^{\rm(3\omega)}$. This result demonstrates the great potential for improving comagnetometer stability.

We have demonstrated the stability of 3-component comagnetometer against the fluctuation of pumping power, but the key idea is that we can choose two arbitrary parameters $x_{1}$ and $x_{2}$, and then configure the 3-component comagnetometer to be stable against the fluctuation of both $x_{1}$ and $x_{2}$. $x_{1}$, $x_{2}$ can be any continuous scalar parameters of the experimental system such as laser power, laser wavelength, cell temperature, coil current or even linear combination of them. Due to the mode localization nature in $PT$-broken phase, $\Delta\omega_{129}$ is directly sensitive to the non-uniform distribution of magnetic field. Conversely, $\omega_{129}$ and $\omega_{131}$ are mainly determined by the average magnetic field, non-uniformity only contributes perturbative corrections. These make the $\Delta\omega_{129}$ a good indicator for monitoring the change of parameters that can induce non-uniform magnetic field, and then to suppress their influence on $\omega_{129}$ and $\omega_{131}$.

Discussion and Outlook.—In this paper, we report the observation of the $PT$ transition of diffusive nuclear spins. Particularly, the spin precession frequency splitting and the mode localization are measured in the $PT$-broken phase. In this phase, boundary between coherent and incoherent spin motion is blurred. The random spin diffusion in a gradient field behaves like a coherent coupling (e.g., spin-orbit coupling) in a Hermitian system, rather than a pure dissipation as in the $PT$-symmetric phase. The diffusive nuclear spin system provides an excellent testbed for further exploring the non-Hermitian physics.

We also demonstrate the application of $PT$ transition in sensing of weak signals. Comagnetometer in the $PT$-broken phase is sensitive to magnetic field gradient, which enables the design of gradiometer [47, 48] measuring the magnitude and gradient of magnetic field in a single atomic cell. Furthermore, the $PT$ transition was shown to be useful in improving the sensitivity of parameter estimation near the EPs previously [35, 36, 37, 38, 39, 40, 41], although the signal-to-noise ratio and the fundamental precession limit are still under debate [49, 50, 51, 52]. Our work show that, assisted by the $PT$ transition, the spatial motion is engaged in the sensing process and the sensor stability, another important aspect of high-precession measurement, is significantly enhanced. This paves the way to develop stable comagnetometers for the detection of extremely weak signals.

Supplemental Material (SM) is provided on [url], which includes Refs. [53, 54, 55, 56, 57, 58, 59].