Stabilizer codes for Open Quantum Systems

Francisco Revson F. Pereira¹¹1[email protected]; current affiliation: IQM, Nymphenburgerstr. 86, 80636 Munich, Germany. School of Science and Technology, University of Camerino, I-62032 Camerino, Italy INFN, Sezione di Perugia, I-06123 Perugia, Italy Stefano Mancini School of Science and Technology, University of Camerino, I-62032 Camerino, Italy INFN, Sezione di Perugia, I-06123 Perugia, Italy Giuliano G. La Guardia Department of Mathematics and Statistics, State University of Ponta Grossa, 84030-900 Ponta Grossa, PR, Brazil

Abstract

The Lindblad master equation describes the evolution of a large variety of open quantum systems. An important property of some open quantum systems is the existence of decoherence-free subspaces. A quantum state from a decoherence-free subspace will evolve unitarily. However, there is no procedural and optimal method for constructing a decoherence-free subspace. In this paper, we develop tools for constructing decoherence-free stabilizer codes for open quantum systems governed by Lindblad master equation. This is done by pursuing an extension of the stabilizer formalism beyond the celebrated group structure of Pauli error operators. We then show how to utilize decoherence-free stabilizer codes in quantum metrology in order to attain the Heisenberg limit scaling with low computational complexity.

Keywords: Open Quantum Systems, Decoherence-free Subspaces, Stabilizer Codes, Heisenberg Limit Scaling

1 Introduction

The second quantum revolution emerges from the possibility of designing and controlling quantum systems. The complexity of controlling quantum systems can be reduced by decreasing the noise due to system-environment interaction. This can be achieved by resorting to quantum error correcting codes. Among them are the stabilizer codes [18]. These codes were proposed by Gottesman [18]. Several works have extended the original construction method in order to incorporate Hilbert spaces and quantum systems with different structures [9, 19, 32, 5, 23, 8, 7, 14, 31]. As an important result, it was shown that stabilizer codes exist if and only if there exist classical block codes obeying an orthogonality rule; e.g., Euclidean and Hermitian self-orthogonality [23]. Such a duality between stabilizer codes and classical block codes has stimulated several works [23, 8, 7, 20, 14, 35, 33, 31, 34]. Nevertheless, there is still room for novelties. In particular, we can find at least two relevant points not envisioned in previous works.

Firstly, consider the error set and the algebraic structure associated with it. One will see that the errors obey a group structure with the composition of operators as the group operation. However, in several practical cases, one has an additional operation in play, which is the sum of operators. In these applications, a ring or vector space structure is needed. This is the framework we are going to consider in this paper. As a consequence of this new and intricate formulation, the standard dual structure of stabilizer codes will not be block codes in the general case. We need to abandon the idea of classical codes as vector spaces and work with additive groups. For these additive groups, we introduce a new sum operation that corresponds to the sum and composition of operators. A homomorphism is given between operators and additive codes.

Secondly, stabilizer codes are often designed for a specific quantum channel, or anyway their performance vary from channel to channel [6]. Having a dynamical evolution means to deal with time varying Kraus operators, or equivalently with time varying quantum channels. Hence, in such a case it might be not satisfactory to resort to the standard stabilizer codes construction. In this paper, we consider an open quantum system described by a Lindblad master equation. This class of equations is the most general form for the generator of a quantum dynamical semigroup. We construct stabilizer codes able to eliminate the dissipator part of the Lindblad master equation, thus turning the evolution into unitary. As we are going to show, this is possible since the stabilizer code corresponds to a decoherence-free subspace. A state from a decoherence-free subspace will evolve unitarily; i.e., the dissipator part of the Lindblad master equation will not contribute to the evolution of the state [22]. Even though the stabilizer code constructed is a subspace of the corresponding decoherence-free subspace, an important advancement is made here. Using the stabilizer code construction we can derive a procedural and optimal method, in terms of computational complexity, for constructing the decoherence-free subspace that corresponds to the stabilizer code.

Decoherence-free subspace can be regarded as a particular case of subsystem codes [2]. Suppose we decompose the Hilbert space as $\mathcal{H}=(\mathcal{C}\otimes\mathcal{D})\oplus\mathcal{B}$ , where the subsystem code belongs to $\mathcal{C}$ , $\mathcal{D}$ is a second subsystem, and we are partitioning $\mathcal{H}$ into two subspaces, $\mathcal{B}$ and $\mathcal{C}\otimes\mathcal{D}$ . The concept of a noiseless subsystem is that symmetries on the system-environment evolution factor the interaction Hamiltonian with respect to some subsystem structure on the Hilbert space $\mathcal{H}$ [2]. One can describe decoherence-free subspaces as a subsystem code where there is no subsystem $\mathcal{D}$ and the code relies on symmetries that factor the interaction Hamiltonian with respect to system and environment.

Quantum metrology aims at using quantum systems in order to improve the estimation of parameters. It is possible to show that the reduction one can obtain in terms of the number of probes a quantum system can achieve is quadratically faster than the best classical strategy [16]. This is characterized by the Heisenberg limit (HL). In this paper, as an application of the developed theory, we present a method to achieve the HL using decoherence-free stabilizer codes. It differs quite significantly from the existing methods in the literature. In previous works, under the hypothesis that the Hamiltonian is not in Lindblad span (HNLS), joint encoding and decoding schemes are presented in order to obtain the Heisenberg limit [10, 37, 25, 17, 11]. In our method, using decoherence-free subspaces for quantum metrology, the dissipator part of the open quantum system does not contribute to the evolution. Hence, under certain hypothesis, we demonstrate that it is possible to achieve the HL using decoherence-free stabilizer codes. Furthermore, since the system evolves unitarily without any interaction between the system and environment, there is no need for a decoding process. Therefore, we are free of any further errors that could arrive in the decoding process. It is also clear that the computational complexity is reduced when compared with other schemes.

This paper is organized as follows. In Section 2 we present the preliminary concepts used to elaborate the results in this paper. The mathematical tools needed to construct the stabilizer codes for noise operators having a tensor product description and a more general description are shown in Sections 3 and 4, respectively. A connection between stabilizer codes and decoherence-free subspaces is made. We also illustrate some of the new structures by presenting several examples. Next, Section 5 demonstrates the applicability of the stabilizer codes in the area of quantum metrology. A condition for probing a quantum system using stabilizer codes in order to obtain the Heisenberg limit scaling is stated and analyzed. The final remarks and future perspectives are given in Section 6.

2 Preliminaries

In this section, we review some formulations needed to understand the main results of the paper. Firstly, we review the evolution of open quantum systems and describe the idea of decoherence-free subspace in Lindblad master equations. Secondly, the stabilizer formalism is presented. We focus on the main aspect considered in this paper, which is the algebraic structure obeyed by the errors. The first result of the paper is also given, connecting decoherence-free subspaces and stabilizer codes.

2.1 Open Quantum Systems and Decoherence-free Subspace

In this paper we deal with open quantum systems evolving by means of a Markovian master equation. Suppose $q$ is a prime power and let $S$ be a system modeled by a $q$ -dimensional Hilbert space $\mathcal{H}_{S}$ (we also use the notation $\mathcal{H}_{q}$ when it is clear which system is considered) interacts with a reservoir system $R$ associated with a Hilbert space $\mathcal{H}_{R}$ . Then the full Hamiltonian can be decomposed as

H=H_{S}\otimes\mathbb{I}+\mathbb{I}\otimes H_{R}+H_{\text{int}},

(1)

with $H_{S}$ , $H_{R}$ , and $H_{\text{int}}$ the system, reservoir, and interaction Hamiltonians, respectively, and $\mathbb{I}$ is the identity operator. Instead of analyzing the full system-reservoir evolution, we are only interested in the evolution of a reduced system density operator $\rho$ . This is obtained by tracing over the reservoir in the full density operator. As a result, the dynamics of the reduced density operator $\rho$ is given by [21]

\frac{\partial\rho}{\partial t}=-i[H_{S},\rho]+L_{D}(\rho),

(2)

where

L_{D}(\rho)=\frac{1}{2}\sum_{l=1}^{M}\lambda_{l}([J_{l},\rho J_{l}^{\dagger}]+[J_{l}\rho,J_{l}^{\dagger}])

(3)

is the decoherence evolution originated from the system-reservoir coupling, with $M\leq N^{2}-1$ where $N$ is the number of qudit systems, $q=d^{N}$ , and $\{J_{l}\}_{l=1}^{M}$ are the Lindblad operators. We call this part of the evolution throughout the paper as the dissipator part.

Definition 1.

[22] Let the time evolution of an open quantum system with Hilbert space $\mathcal{H}_{S}$ be described by means of a Markovian master equation and $D(\mathcal{H})$ be the set of density matrices of a given Hilbert space $\mathcal{H}$ . Then a decoherence-free subspace (DFS) $\mathcal{H}_{\text{DFS}}$ of $\mathcal{H}_{S}$ is such that all pure states $\rho(t)\in D(\mathcal{H}_{\text{DFS}})$ satisfies

\frac{d\text{Tr}\{\rho^{2}(t)\}}{dt}=0,\forall t\geq 0,\qquad\text{ with }\qquad\text{Tr}\{\rho^{2}(0)\}=1.

(4)

On the other hand, a subspace $\mathcal{H}_{\text{sDFS}}$ is called strong decoherence-free subspace (sDFS) if for all pure $\rho(t)\in D(\mathcal{H}_{\text{sDFS}})$ one has

L_{D}(\rho(t))=0,\qquad\text{ and }\qquad\rho^{2}(t)=\rho(t),\forall t.

(5)

From Definition 5, it is clear that strong DFS is a sufficient but not necessary condition to have a DFS.

Proposition 2.

[22, Theorem 4, Proposition 5, Theorem 6] Let the time evolution be given by the Markovian open system dynamics shown in Eq. (2). Assume $\Gamma=\sum_{l=1}^{M}\lambda_{l}J_{l}^{\dagger}J_{l}$ . On the one hand, the space $\mathcal{P}=\text{span}\{\ket{\psi_{i}}\}_{i=1,\ldots,K}$ is a DFS for all time $t$ if and only if $J_{l}\ket{\psi_{k}}=c_{l}\ket{\psi_{k}}$ , for all $l=1,\ldots,M$ and $k=1,\ldots,K$ , and the commutator $[H_{ev},J_{l}]$ has eigenvalues equal to zero for all $\ket{\psi_{k}}\in\mathcal{P}$ , and $l=1,\ldots,M$ . Here

H_{ev}=H_{S}+\frac{i}{2}\sum_{l=1}^{M}\lambda_{l}(c_{l}^{*}J_{l}-c_{l}J_{l}^{\dagger}).

(6)

On the other hand, $\mathcal{P}$ is sDFS if the commutators $[H_{S},J_{l}]$ , for $l=1,...,M$ , and $[H_{S},\Gamma]$ have eigenvalues equal to zero for all $\ket{\psi_{k}}\in\mathcal{P}$ . Furthermore, $J_{l}\ket{\psi_{k}}=c_{l}\ket{\psi_{k}}$ , and $\Gamma\ket{\psi_{k}}=g\ket{\psi_{k}}$ , for all $l=1,\ldots,M$ and $k=1,\ldots,K$ , where $g=\sum_{l=1}^{M}\lambda_{l}|c_{l}|^{2}$ .

We are going to show below a case study in which the operators in the dissipator part of the evolution cannot be described in a tensor product form of Pauli operators. Later, we will show that a stabilizer code can be derived from the (strong) DFS, but one cannot rely on the standard stabilizer formalism, which will be explained in the next subsection, for such codes.

Example 3.

Consider an $N$ -qubit quantum system with the dynamics described by the master equation

\frac{\partial\rho}{\partial t}=-i[H_{S},\rho]+\frac{\gamma}{2}(2J\rho J^{\dagger}-J^{\dagger}J\rho-\rho J^{\dagger}J),

(7)

with

J=\sum_{j=1}^{N}J_{j}\qquad\text{ and }\qquad J_{j}=\frac{s+c}{2}(\sigma_{xj}+i\sigma_{yj}+\sigma_{zj}),

(8)

where $\sigma_{xj},\sigma_{yj},\sigma_{zj}$ are the Pauli operators on the $j$ -th qubit, $s=\sinh(r)$ , $c=\cosh(r)$ , and $r$ is the (real) squeezing parameter derived from the assumption that the reservoir is given by a squeezed vacuum state. For $r\neq 0$ , the eigenvectors of $J$ are all possible tensor products of $\ket{\psi_{+}}$ and $\ket{\psi_{-}}$ , where $\ket{\psi_{+}}=\ket{0}$ and $\ket{\psi_{-}}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}$ . For each $J_{j}$ , the eigenvalue of $\ket{\psi_{\pm}}$ is equal to $\pm(\frac{s+c}{2})$ . Thus, if the number of $\ket{\psi_{+}}$ in the eigenvector of $J$ is $n_{+}$ , then the eigenvalue of such eigenvector is $(n_{+}-n_{-})\frac{s+c}{2}$ , where $n_{-}=N-n_{+}$ . Notice that it is not possible to describe $J$ as only tensor products of Pauli operators. This forbid us to use standard constructions of stabilizer codes in the theory that follows. Therefore, before presenting our main results, we need to extend the stabilizer formulation to a suitable type of errors, in conjunction with the operations allowed between them. Now, to compute the expression for $H_{S}$ so that there exists a nonempty (strong) DFS of the eigenspace of $J$ , we use the commutativity condition on $H_{S}$ given in Proposition 2. From it, one possible solution is to have the system Hamiltonian with the form

H_{S}=\sum_{j=1}^{N}\frac{\gamma}{4}(n_{+}-n_{-})(s+c)^{2}\sigma_{yj},

(9)

where $n_{+}\neq n_{-}$ . Observe that the choice of $H_{S}$ implies that $H_{ev}=0$ and, therefore, the space spanned by $\ket{\psi_{+}}$ and $\ket{\psi_{-}}$ is sDFS.

2.2 Stabilizer Codes

The theory of stabilizer codes, introduced by Gottesman, has been long studied, analyzed, and extended [13, 29, 27]. However, the physical environment over which the stabilizer code will be used is commonly ignored, relying on the error-correction capability only over the minimal distance of the code. Before presenting the approach taken in this paper, we recall the stabilizer formalism. Actually, we refer to the stabilizer formalism introduced by Gottesman, the connection between the stabilizer group and associated additive code by standard stabilizer formalism.

A stabilizer code $\mathcal{Q}$ is a subspace of a $N$ -qubit system described by $\mathbb{C}^{2^{N}}$ stabilized by the elements of an abelian subgroup $S$ of the error group $G_{N}$ over $N$ qubits. We can mathematically describe a stabilizer code as

\mathcal{Q}=\bigcap_{E\in S}\{\ket{\psi}\in\mathcal{H}_{q}\colon E\ket{\psi}=\ket{\psi}\}.

(10)

For the characterization of correctable and uncorrectable errors, we need to introduce the concept of centralizer of a subgroup of $G_{N}$ and center of $G_{N}$ . The subgroup $C_{G_{N}}(S)$ of $G_{N}$ , given by

C_{G_{N}}(S)=\{E\in G_{N}\colon EF=FE\text{ for all }F\in S\},

(11)

is called the centralizer of $S$ in $G_{N}$ . Observe that the commutativity property of $S$ implies $S\leq C_{G_{N}}(S)$ . The center of $G_{N}$ , denoted by $Z(G_{N})$ , is the subgroup $Z(G_{N})=C_{G_{N}}(G_{N})$ . The group $SZ(G_{N})$ is given by the elements $Ez$ , where $E\in S$ and $z\in Z(G_{N})$ . The following lemma characterizes the relation among correctable errors, stabilizer, centralizer, and the center of a quantum code.

Lemma 4.

[23, Lemma 11] Let $S\leq G_{N}$ be the stabilizer group of a stabilizer code $\mathcal{Q}$ of dimension greater than one. An error $E\in G_{N}$ is detectable by the stabilizer code $\mathcal{Q}$ if and only if $E$ is an element of $SZ(G_{N})$ or $E$ does not belong to the centralizer $C_{G_{N}}(S)$ .

An important achievement of standard stabilizer formalism is showing the equivalence of stabilizer codes and additive classical codes. For a $K$ -dimensional quantum code with minimum distance $d$ and living in the Hilbert space $\mathcal{H}_{q}^{\otimes N}$ ; i.e., with parameters $((N,K,d))_{q}$ , there exists an additive classical code $C$ (and its symplectic dual $C^{\perp_{s}}$ ) which is equivalent to the stabilizer code. As shown in Proposition 5, the minimum distance of the stabilizer code is computed from the symplectic weight. We define the symplectic weight of a vector $(\bm{a}|\bm{b})\in\mathbb{F}_{q}^{2N}$ as $\text{swt}((\bm{a}|\bm{b}))=|\{k\colon(a_{k},b_{k})\neq(0,0)\}|.$ One of the main results of this paper is the extension the equivalence between classical codes and quantum stabilizer codes to more general errors, in particular non-Pauli errors. Due to the complex algebraic structure describing the errors, we show sufficient conditions for a classical code to be equivalent to a stabilizer code.

Proposition 5.

[23, Theorem 13] An $((N,K,d))_{q}$ stabilizer code exists if and only if there exists an additive code $C\subseteq\mathbb{F}_{q}^{2N}$ of size $|C|=q^{N}/K$ such that $C\subseteq C^{\perp_{s}}$ and $\text{swt}(C^{\perp_{s}}\setminus C)=d$ if $K>1$ (and $\text{swt}(C^{\perp_{s}})=d$ if $K=1$ ), where swt denotes the symplectic weight, and the symplectic weight of a set is the minimum symplectic weight of the elements in the set.

Now, we are going to describe in detail the error basis and error vector space used through the paper. A set $\mathcal{E}$ of operators on $\mathbb{C}^{2}$ is denoted a nice error basis if it attains three conditions: (a) it contains the identity operator, (b) it is closed under the composition of operators, (c) the trace $\text{Tr}\{A^{\dagger}B\}=0$ for distinct elements $A,B\in\mathcal{E}$ . In this paper, we consider the error basis

\mathcal{E}=\{\mathbb{I},\sigma_{x},\sigma_{y},\sigma_{z}\},

(12)

where $\mathbb{I}$ is the identity operator and $\sigma_{i}$ , for $i=1,2,3$ , are the Pauli matrices. The inner product of two distinct elements $A,B$ in $\mathcal{E}$ is given by

\langle A,B\rangle=\text{Tr}\{A^{\dagger}B\}.

(13)

Clearly, $\mathcal{E}$ is a nice error basis. Additionally, we have that if $\mathcal{E}_{1}$ and $\mathcal{E}_{2}$ are nice error bases, then $\mathcal{E}^{2}=\{\sf{E_{1}}\otimes\sf{E_{2}}\colon E_{1}\in\mathcal{E}_{1},E_{2}\in\mathcal{E}_{2}\}$ is a nice error basis as well.

Proposition 6.

Let $A=a_{0}\mathbb{I}+a_{1}\sigma_{x}+a_{2}\sigma_{y}+a_{3}\sigma_{z}$ and $B=b_{0}\mathbb{I}+b_{1}\sigma_{x}+b_{2}\sigma_{y}+b_{3}\sigma_{z}$ be two elements generated by $\mathcal{E}$ . Then

[A,B]=2i\Big{(}(a_{2}b_{3}-b_{2}a_{3})\sigma_{x}+(a_{3}b_{1}-b_{3}a_{1})\sigma_{y}+(a_{1}b_{2}-b_{1}a_{2})\sigma_{z}\Big{)}.

(14)

Proof.

It follows from the commutation relations of the Pauli operators $[\sigma_{i},\sigma_{j}]=2i\epsilon_{ijk}\sigma_{k}$ , for $i,j,k=1,2,3$ . ∎

Definition 7.

Let $\mathcal{E}^{N}$ be the error basis constructed as $N$ -fold tensor product of the Pauli matrices shown in Eq. (12). The error group, denoted by $G_{N}$ , is the vector space over $\mathbb{C}$ consisting of elements in $\mathcal{E}^{N}$ .

For explicit examples of the error vector space $G_{N}$ , see Section 4.

In the definition of error set and operations allowed among its elements, there is a significant turn concerning the one utilized in standard stabilizer formalism. There, only the composition of operators is considered. Here, we also have the sum of operators, thus obtaining a vector space structure for the error set. Notice, however, that to define the stabilizer set in both approaches (the standard one and the one used in this paper) only composition of operators is necessary, besides the commutativity of its elements.

Suppose the evolution of a state $\rho(t)$ is given by a Markovian master equation with dissipator part described by operators from the set $\mathcal{J^{\prime}}=\{J_{l}\colon l=1,\dots,M\}$ . Add the operator $\Gamma=\sum_{l=1}^{M}\lambda_{l}J_{l}^{\dagger}J_{l}$ to the set $\mathcal{J^{\prime}}$ so that $\mathcal{J}=\mathcal{J^{\prime}}\cup\Gamma$ . Assume the existence of a DFS or sDFS satisfying the assumptions of Proposition 2. Then we can construct the following stabilizer sets

\mathcal{S}_{\text{sDFS}}:=\langle S_{1},\ldots,S_{M+1}\colon S_{l}=c_{l}^{-1}J_{l},\text{ for }l=1,\ldots,M+1,\text{ where }J_{l}\in\mathcal{J}\rangle,

(15)

\mathcal{S}_{\text{DFS}}:=\langle S_{1},\ldots,S_{M}\colon S_{l}=c_{l}^{-1}J_{l},\text{ for }l=1,\ldots,M,\text{ where }J_{l}\in\mathcal{J^{\prime}}\rangle.

(16)

Suppose $\mathcal{Q}$ is the joint eigenspace with eigenvalue $+1$ for every element in $\mathcal{S}_{\text{sDFS}}$ ; i.e., $\mathcal{S}_{\text{sDFS}}$ stabilizes $\mathcal{Q}$ . If $[S_{i},S_{j}]=0$ , for all $i,j=1,\ldots,M+1$ , then $\mathcal{S}_{\text{sDFS}}$ is an abelian group. Furthermore, if the system Hamiltonian $H_{S}$ belongs to the centralizer $C_{G_{N}}(\mathcal{S}_{\text{sDFS}})$ , then we can conclude from Proposition 2 that $\mathcal{Q}$ is sDFS. Similar arguments can be used for DFS, where the stabilizer group is given by $\mathcal{S}_{\text{DFS}}$ and the commutativity condition is imposed over $H_{ev}$ . A stabilizer code that is also (sDFS) DFS will be called a (strong) decoherence-free stabilizer code.

Theorem 8.

Let the time evolution of the quantum system be given by the Markovian master equation shown in Eq. (2). Suppose there exists a nontrivial maximal joint $+1$ -eigenspace $\mathcal{Q}$ of the abelian group $\mathcal{S}_{\text{sDFS}}$ or $\mathcal{S}_{\text{DFS}}$ constructed in Eq. (15) and (16), respectively. If

1.

$H_{S}+\frac{i}{2}\sum_{l=1}^{M}\lambda_{l}(c_{l}^{*}J_{l}-c_{l}J_{l}^{\dagger})$ belongs to $C_{G_{N}}(\mathcal{S}_{\text{DFS}})$ , then $\mathcal{Q}$ is a stabilizer code and a decoherence-free subspace;
2.

$H_{S}$ belongs to $C_{G_{N}}(\mathcal{S}_{\text{sDFS}})$ and $S_{M+1}\in\mathcal{S}_{\text{sDFS}}$ stabilizes $\mathcal{Q}$ , then $\mathcal{Q}$ is a stabilizer code and a strong decoherence-free subspace.

We call $\mathcal{Q}$ a (strong) decoherence-free stabilizer code.

Proof.

Consider Claim $1$ . First of all, notice that the claim $\mathcal{Q}$ is a stabilizer code of $\mathcal{S}_{\text{DFS}}$ follows from the fact that $\mathcal{Q}$ is the nontrivial maximal $+1$ -eigenspace of $\mathcal{S}_{\text{DFS}}$ . Secondly, for any $\ket{\psi}\in\mathcal{Q}$ and $S_{l}\in\mathcal{S}_{\text{sDFS}}$ we have

J_{l}\ket{\psi}=c_{l}S_{l}\ket{\psi}=c_{l}\ket{\psi}.

(17)

Since $H_{S}+\frac{i}{2}\sum_{l=1}^{M}\lambda_{l}(c_{l}^{*}J_{l}-c_{l}J_{l}^{\dagger})$ belongs to $C_{G_{N}}(\mathcal{S}_{\text{DFS}})$ , then the commutator of $H_{S}+\frac{i}{2}\sum_{l=1}^{M}\lambda_{l}(c_{l}^{*}J_{l}-c_{l}J_{l}^{\dagger})$ with any element in $\mathcal{S}_{\text{DFS}}$ has eigenvalue equal to zero. Therefore, from Eq. (17) and Proposition 2, we have that $\mathcal{Q}$ is also a decoherence-free subspace.

Claim $2$ follows the same reasoning. ∎

A connection between stabilizer codes and decoherence-free subspace is given in Theorem 8. Differently from previous works, such as Ref. [26], we give a direct algebraic relation between the Lindblad operators, DFSs, and stabilizer codes. It is shown in Ref. [26] that DFSs are a specific class of quantum error correcting codes, but no constructive method to derive the stabilizer set from the Lindblad operators is shown. Furthermore, as will be shown in the following sections, we extend the stabilizer description to classical error-correcting codes defined over the complex number field. More precisely, the standard theory of quantum error-correcting code contains quantum codes derived from classical codes, i.e., codes defined over finite fields. In this new context, we consider classical codes defined over $\mathbb{C}$ , the complex field which has characteristic zero, and this fact modifies completely the techniques to be applied in the constructions of our results. To the best of the author’s knowledge, this is the first work presenting such a formulation. In particular, there are DFS that have a stabilizer code as subspace. This inclusion may or may not be proper. However, dealing with stabilizer codes can produce results that we could not obtain otherwise. In fact, one can find encoding methods for stabilizer codes that are procedural and optimum algorithms for creating the corresponding code space. Additionally, set membership can be optimally implemented by decoding methods. Later in the paper we construct an algorithm for quantum metrology that uses set membership as one of the important steps. Therefore, dealing with decoherence-free stabilizer code instead of the whole decoherence-free subspace is computationally relevant for several applications.

The connection between decoherence-free subspaces and stabilizer codes is expanded in the following two sections. Firstly, errors with a particular structure are considered. The considered structure simplifies the stabilizer formalism and the connection between stabilizers and classical codes. Afterwards, the restriction is relaxed and generalized errors are considered.

3 Decoherence-Free Stabilizer Codes for Tensor-Product Noise

We have seen necessary and sufficient conditions for a subspace $\mathcal{P}\subseteq\mathcal{H}_{S}$ to be decoherence-free or strong decoherence-free in Proposition 2. Additionally, we established conditions for a (strong) decoherence-free subspace to be a stabilizer code. In this section we are going to elaborate over these conditions in order to connect (strong) decoherence-free stabilizer code, defined over a particular type of errors, with classical code. For this purpose, this section is divided in three parts. In the first part, we present some motivations for the tools constructed in the second part. Then, in the second part, it is put forward a vector space where the sum of vectors is related to the composition of operators. Lastly, part three connects stabilizer codes to these vector spaces by means of an isomorphism.

3.1 Motivation

In order to illustrate the connection between DFS (sDFS) and $\mathcal{S}_{\text{DFS}}$ ( $\mathcal{S}_{\text{sDFS}}$ ), we present the example below.

Example 9.

Consider the same evolution as in Example 3, but with

J=\frac{s+c}{2}\bigotimes_{j=1}^{5}(\sigma_{xj}+i\sigma_{yj}+\sigma_{zj}),

(18)

For $r\neq 0$ , the eigenvectors of $J$ are all possible tensor products of $\ket{\psi_{+}}$ and $\ket{\psi_{-}}$ , where $\ket{\psi_{+}}=\ket{0}$ and $\ket{\psi_{-}}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}$ . The eigenvalue of $\ket{\psi_{\pm}}$ is equal to $\pm(\frac{s+c}{2})$ . Thus, if the number of $\ket{\psi_{\pm}}$ in the eigenvector of $J$ is $n_{\pm}$ , the eigenvalue of such eigenvector is $\frac{s+c}{2}$ if $n_{+}>n_{-}$ or $-\frac{s+c}{2}$ if $n_{+}<n_{-}$ . For $n_{+}>n_{-}$ , the stabilizer set is given by

\mathcal{S}_{\text{DFS}}=\Big{\langle}\frac{2J}{s+c}\Big{\rangle}=\Big{\{}\Big{(}\frac{2J}{s+c}\Big{)}^{i}\colon i\in\mathbb{N}\Big{\}}.

(19)

It is clear that $\mathcal{S}_{\text{DFS}}$ is abelian. Hence, we can construct a stabilizer code form $\mathcal{S}_{\text{DFS}}$ . Additionally, from the commutation relation of Proposition 14 and $J=\frac{s+c}{2}\bigotimes_{j=1}^{5}\Big{(}\sigma_{xj}+i\sigma_{yj}+\sigma_{zj}\Big{)}$ , the system Hamiltonian with the form

H_{S}=\bigotimes_{j=1}^{5}\eta_{0}\sigma_{yj},

(20)

where $\eta_{0}=\frac{\gamma(s+c)^{2}}{4}$ , belongs to $C_{G_{N}}(\mathcal{S}_{\text{DFS}})$ . Observe that if we have derived the form of $H_{S}$ in a similar way as the method in Example 3; i.e., by imposing that the eigenvalue of $[H_{S}+\frac{i\gamma(s+c)}{4}(J-J^{\dagger}),J]$ over the subspace $\mathcal{Q}$ is equal to zero, we would obtain the same result as in the current example, which imposes the stronger condition $[H_{S}+\frac{i\gamma(s+c)}{4}(J-J^{\dagger}),J]=0$ . This means that for the model of $N$ qubits considered, the existence of a decoherence-free subspace is equivalent to the existence of a decoherence-free stabilizer code.

There are several interesting aspects of dealing with stabilizer groups. One is the complexity reduction in defining the stabilizer code, i.e., instead of using vector space basis we can use the group generator of the stabilizer group. Encoding, error detection, error correction, and decoding schemes can also be computationally-efficient constructed from the stabilizer group. Another one is the connection between stabilizer groups and additive codes. This connection is implemented by means of an isomorphism. Thus, statements over the equivalent additive code are directly translated to the stabilizer group and, more importantly, to the stabilizer code. This approach is largely utilized to show existence or non-existence of stabilizer codes with specific parameters or properties. In the following, we sketch the connection between stabilizer groups constructed from open quantum systems and additive codes. In particular, the isomorphism utilized to connect them is introduced.

Example 10.

Following Example 9, the stabilizer elements $S_{1}$ and $S_{2}$ in $\mathcal{S}_{\text{DFS}}$ can be written as

	$\displaystyle S_{1}$	$\displaystyle=$	$\displaystyle\bigotimes_{j=1}^{5}\Big{(}\sigma_{xj}+i\sigma_{yj}+\sigma_{zj}\Big{)},$		(21)
	$\displaystyle S_{2}$	$\displaystyle=$	$\displaystyle\mathbb{I}\otimes\mathbb{I}\otimes\mathbb{I}\otimes\mathbb{I}\otimes\mathbb{I}.$		(22)

Now, we can create a map that represents errors as vectors. Let us consider

	$\displaystyle\zeta\colon\tilde{G}_{N}$	$\displaystyle\rightarrow$	$\displaystyle\mathbb{C}^{4N},$
	$\displaystyle\bigotimes_{j=1}^{N}\Big{(}a_{0j}\mathbb{I}_{j}+a_{1j}\sigma_{xj}+a_{2j}\sigma_{yj}+a_{3j}\sigma_{zj}\Big{)}$	$\displaystyle\mapsto$	$\displaystyle(a_{01},\ldots,a_{0N},a_{11},\ldots,a_{1N},a_{21},\ldots,a_{2N},a_{31},\ldots a_{3N}),$		(23)

where $\tilde{G}_{N}\subseteq{G}_{N}$ has elements with the above description. As an example, applying the map $\zeta$ to the generators of $\mathcal{S}_{\text{DFS}}$ gives

\displaystyle\bm{v}_{S_{1}}=\zeta(S_{1})=

\displaystyle\setcounter{MaxMatrixCols}{20}\begin{pmatrix}0,&0,&0,&0,&0,&1,&1,&1,&1,&1,&i,&i,&i,&i,&i,&1,&1,&1,&1,&1\end{pmatrix}

(24)

and $\bm{v}_{S_{2}}=\zeta(S_{2})=(1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)$ . We can also examine the image of $H_{S}$ , given in Eq. (20), by the map $\zeta$ ,

\displaystyle\bm{v}=\zeta(H_{S})=

\displaystyle\setcounter{MaxMatrixCols}{20}\begin{pmatrix}0,&0,&0,&0,&0,&0,&0,&0,&0,&0,&1,&1,&1,&1,&1,&0,&0,&0,&0,&0\end{pmatrix}.

(25)

The commutativity property between $H_{ev}$ and $J$ can also be described using our representation. Let $\bm{v}_{H_{ev}}=\zeta(H_{S}+\frac{i\gamma}{2}\sqrt{sc}(J-J^{\dagger}))$ and write it as

\bm{v}_{H_{ev}}=\begin{pmatrix}\bm{b}_{0},&\bm{b}_{1},&\bm{b}_{2},&\bm{b}_{3}\end{pmatrix},

(26)

where $\bm{b}_{j}\in\mathbb{C}^{5}$ , for all $j=0,1,2,3$ . Similarly, $\bm{v}_{S_{1}}$ is given by

\bm{v}_{S_{1}}=\begin{pmatrix}\bm{a}_{0},&\bm{a}_{1},&\bm{a}_{2},&\bm{a}_{3}\end{pmatrix},

(27)

where $\bm{a}_{j}\in\mathbb{C}^{5}$ , for all $j=0,1,2,3$ . Then the commutation relation of Proposition 14 can be extended by defining

$\displaystyle\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(1,j)}}$	$\displaystyle:=$	$\displaystyle(a_{2j}b_{3j}-a_{3j}b_{2j}),$	(28)
$\displaystyle\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(2,j)}}$	$\displaystyle:=$	$\displaystyle(a_{3j}b_{1j}-a_{1j}b_{3j}),$	(29)
$\displaystyle\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(3,j)}}$	$\displaystyle:=$	$\displaystyle(a_{1j}b_{2j}-a_{2j}b_{1j}),$	(30)

for $j=1,\ldots,N$ . We can see that $[H_{ev},J]=0$ if and only if $\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(1,j)}}=\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(2,j)}}=\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(3,j)}}=0$ , for $j=1,\ldots,N$ . In our example, we have $\bm{v}_{H_{ev}}=(0,0,\ldots,0)\in\mathbb{C}^{20}$ , which gives $\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(1,j)}}=\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(2,j)}}=\langle\bm{v}_{H_{ev}},\bm{v}_{S_{1}}\rangle_{\zeta_{(3,j)}}=0$ , for $j=1,\ldots,N$ .

Consider the composition of operators. Let $E_{1},E_{2}\in G^{N}$ be two errors written as

	$\displaystyle E_{1}$	$\displaystyle=$	$\displaystyle\bigotimes_{j=1}^{N}\Big{(}a_{0j}\mathbb{I}_{j}+a_{1j}\sigma_{xj}+a_{2j}\sigma_{yj}+a_{3j}\sigma_{zj}\Big{)},$		(31)
	$\displaystyle E_{2}$	$\displaystyle=$	$\displaystyle\bigotimes_{j=1}^{N}\Big{(}b_{0j}\mathbb{I}_{j}+b_{1j}\sigma_{xj}+b_{2j}\sigma_{yj}+b_{3j}\sigma_{zj}\Big{)}.$		(32)

Then,

E_{1}E_{2}=\bigotimes_{j=1}^{N}\Big{(}c_{0j}\mathbb{I}_{j}+c_{1j}\sigma_{xj}+c_{2j}\sigma_{yj}+c_{3j}\sigma_{zj}\Big{)},

(33)

where


$\displaystyle c_{0j}$	$\displaystyle=$	$\displaystyle a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j},$	(34a)
$\displaystyle c_{1j}$	$\displaystyle=$	$\displaystyle(a_{1j}b_{0j}+a_{0j}b_{1j})+i(a_{2j}b_{3j}-a_{3j}b_{2j}),$	(34b)
$\displaystyle c_{2j}$	$\displaystyle=$	$\displaystyle(a_{2j}b_{0j}+a_{0j}b_{2j})+i(a_{3j}b_{1j}-a_{1j}b_{3j}),$	(34c)
$\displaystyle c_{3j}$	$\displaystyle=$	$\displaystyle(a_{3j}b_{0j}+a_{0j}b_{3j})+i(a_{1j}b_{2j}-a_{2j}b_{1j}),$	(34d)

for $j=1,\ldots,N$ . Thus, we need to impose over the map $\zeta$ the following condition for composition of operators

\displaystyle\zeta(E_{1}E_{2})=\setcounter{MaxMatrixCols}{12}\begin{pmatrix}c_{01},&\ldots,&c_{0N},&c_{11},&\ldots,&c_{1N},&c_{21},&\ldots,&c_{2N},&c_{31},&\ldots,&c_{3N}\end{pmatrix},

(35)

where $c_{ij}$ , for $i\in\{0,1,2,3\}$ and $j\in\{1,\ldots,N\}$ , is defined in Eq. (34). Further details of this operation will be given below and in the following subsections.

Let us introduce the map $\zeta$ in formal terms and derive an additive operation from this definition.

Definition 11.

Let $E_{1},E_{2}\in G^{N}$ be two errors written as

	$\displaystyle E_{1}$	$\displaystyle=$	$\displaystyle\bigotimes_{j=1}^{N}\Big{(}a_{0j}\mathbb{I}_{j}+a_{1j}\sigma_{xj}+a_{2j}\sigma_{yj}+a_{3j}\sigma_{zj}\Big{)},$		(36)
	$\displaystyle E_{2}$	$\displaystyle=$	$\displaystyle\bigotimes_{j=1}^{N}\Big{(}b_{0j}\mathbb{I}_{j}+b_{1j}\sigma_{xj}+b_{2j}\sigma_{yj}+b_{3j}\sigma_{zj}\Big{)}.$		(37)

Then we define the map

	$\displaystyle\zeta\colon\tilde{G}_{N}$	$\displaystyle\rightarrow$	$\displaystyle\mathbb{C}^{4N},$
	$\displaystyle\bigotimes_{j=1}^{N}\Big{(}a_{0j}\mathbb{I}_{j}+a_{1j}\sigma_{xj}+a_{2j}\sigma_{yj}+a_{3j}\sigma_{zj}\Big{)}$	$\displaystyle\mapsto$	$\displaystyle(a_{01},\ldots,a_{0N},a_{11},\ldots,a_{1N},a_{21},\ldots,a_{2N},a_{31},\ldots a_{3N})$		(38)

via the operation

\displaystyle\zeta(E_{1}E_{2})=\setcounter{MaxMatrixCols}{12}\begin{pmatrix}c_{01},&\ldots,&c_{0N},&c_{11},&\ldots,&c_{1N},&c_{21},&\ldots,&c_{2N},&c_{31},&\ldots,&c_{3N}\\ \end{pmatrix},

(39)

where


$\displaystyle c_{0j}$	$\displaystyle=$	$\displaystyle a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j},$	(40a)
$\displaystyle c_{1j}$	$\displaystyle=$	$\displaystyle(a_{1j}b_{0j}+a_{0j}b_{1j})+i(a_{2j}b_{3j}-a_{3j}b_{2j}),$	(40b)
$\displaystyle c_{2j}$	$\displaystyle=$	$\displaystyle(a_{2j}b_{0j}+a_{0j}b_{2j})+i(a_{3j}b_{1j}-a_{1j}b_{3j}),$	(40c)
$\displaystyle c_{3j}$	$\displaystyle=$	$\displaystyle(a_{3j}b_{0j}+a_{0j}b_{3j})+i(a_{1j}b_{2j}-a_{2j}b_{1j}),$	(40d)

for $j=1,\ldots,N$ .

Definition 12.

Let $N$ be a positive integer, and $\bm{v}_{1},\bm{v}_{2}\in\mathbb{C}^{4N}$ be two vectors given, respectively, by

	$\displaystyle\bm{v}_{1}$	$\displaystyle=$	$\displaystyle\setcounter{MaxMatrixCols}{12}\begin{pmatrix}a_{01},&\ldots,&a_{0N},&a_{11},&\ldots,&a_{1N},&a_{21},&\ldots,&a_{2N},&a_{31},&\ldots,&a_{3N}\end{pmatrix},$		(41)
	$\displaystyle\bm{v}_{2}$	$\displaystyle=$	$\displaystyle\setcounter{MaxMatrixCols}{12}\begin{pmatrix}b_{01},&\ldots,&b_{0N},&b_{11},&\ldots,&b_{1N},&b_{21},&\ldots,&b_{2N},&b_{31},&\ldots,&b_{3N}\end{pmatrix}.$		(42)

Define the binary operation $+_{\zeta}$ as

\bm{v}_{1}+_{\zeta}\bm{v}_{2}:=\setcounter{MaxMatrixCols}{12}\begin{pmatrix}c_{01},&\ldots,&c_{0N},&c_{11},&\ldots,&c_{1N},&c_{21},&\ldots,&c_{2N},&c_{31},&\ldots,&c_{3N}\end{pmatrix},

(43)

where


$\displaystyle c_{0j}$	$\displaystyle=$	$\displaystyle a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j},$	(44a)
$\displaystyle c_{1j}$	$\displaystyle=$	$\displaystyle(a_{1j}b_{0j}+a_{0j}b_{1j})+i(a_{2j}b_{3j}-a_{3j}b_{2j}),$	(44b)
$\displaystyle c_{2j}$	$\displaystyle=$	$\displaystyle(a_{2j}b_{0j}+a_{0j}b_{2j})+i(a_{3j}b_{1j}-a_{1j}b_{3j}),$	(44c)
$\displaystyle c_{3j}$	$\displaystyle=$	$\displaystyle(a_{3j}b_{0j}+a_{0j}b_{3j})+i(a_{1j}b_{2j}-a_{2j}b_{1j}),$	(44d)

for $j=1,\ldots,N$ .

Considering the $+_{\zeta}$ operation defined above as the sum operation of the additive codes, we derive some constraint over the coordinates of the elements in these codes.

Proposition 13.

Let $C$ be an $+_{\zeta}$ -additive code. If $\bm{v}_{1}=(\bm{a}_{0},\bm{a}_{1},\bm{a}_{2},\bm{a}_{3})$ and $\bm{v}_{2}=(\bm{b}_{0},\bm{b}_{1},\bm{b}_{2},\bm{b}_{3})$ are elements in $C$ , then


$\displaystyle a_{2j}b_{3j}$	$\displaystyle=$	$\displaystyle a_{3j}b_{2j},$	(45a)
$\displaystyle a_{3j}b_{1j}$	$\displaystyle=$	$\displaystyle a_{1j}b_{3j},$	(45b)
$\displaystyle a_{1j}b_{2j}$	$\displaystyle=$	$\displaystyle a_{2j}b_{1j},$	(45c)

and the following system of equations must also be satisfied


$\displaystyle a_{lj}$	$\displaystyle=$	$\displaystyle 0,$	(46a)
$\displaystyle a_{ij}$	$\displaystyle=$	$\displaystyle\pm ia_{kj},$	(46b)

for pairwise distinct $l,i,k\in\{1,2,3\}$ and each $j=1,\ldots,N$ .

Proof.

The set of conditions presented in Eq. (45) follows by imposing commutativity of $\bm{v}_{1}+_{\zeta}\bm{v}_{2}$ and $\bm{v}_{2}+_{\zeta}\bm{v}_{1}$ in Eq. (44). To derive the conditions in Eq. (46), notice that Eq. (45) can be described as


$\displaystyle a_{2j}b_{3j}-a_{3j}b_{2j}$	$\displaystyle=$	$\displaystyle 0,$	(47a)
$\displaystyle a_{3j}b_{1j}-a_{1j}b_{3j}$	$\displaystyle=$	$\displaystyle 0,$	(47b)
$\displaystyle a_{1j}b_{2j}-a_{2j}b_{1j}$	$\displaystyle=$	$\displaystyle 0,$	(47c)

which has nontrivial solution if and only if $a_{1j}a_{2j}a_{3j}=0$ . Substituting this condition in Eq. (47) and imposing nontriviality to the solution again, we obtain $a_{ij}^{2}=-a_{kj}^{2}$ and $a_{lj}=0$ for pairwise distinct $l,i,k\in\{1,2,3\}$ . Notice that for each $j$ , we have independent conditions. ∎

We have presented some intuitions on how to relate operators and vectors. Some constraints on the coordinates of the vectors have been presented. However, we need to develop further tools and properties to derive a stabilizer formalism connecting stabilizer code and additive codes. In particular, three points are covered in the following subsection. Firstly, we demonstrate that the map $\langle\cdot,\cdot\rangle_{\zeta}$ is a symplectic form. Using this fact, we show that the map $\zeta$ is an isomorphism between abelian sets of operators and additive codes. Lastly, we introduce symplectic dual codes and the stabilizer formalism connecting quantum stabilizer codes with $+_{\zeta}$ -additive codes.

3.2 Symplectic form and Additive Codes

A symplectic form connects the centralizer of a stabilizer group to the dual code of the classical code corresponding to the stabilizer group. Symplectic forms can be defined over vector spaces or groups. In the following we consider a symplectic form over groups. Thus, the dual code obtained is an additive code.

Definition 14.

A symplectic form over an additive group $\mathcal{G}$ to a field $F$ is a function

	$\displaystyle f\colon\mathcal{G}\times\mathcal{G}$	$\displaystyle\rightarrow$	$\displaystyle F$		(48)
	$\displaystyle(g_{1},g_{2})$	$\displaystyle\mapsto$	$\displaystyle f(g_{1},g_{2}),$		(49)

such that


$\displaystyle f(g_{1}+g_{2},g_{3})$	$\displaystyle=$	$\displaystyle f(g_{1},g_{3})+f(g_{2},g_{3}),$	(50a)
$\displaystyle f(g_{1},g_{2})$	$\displaystyle=$	$\displaystyle-f(g_{2},g_{1}),$	(50b)
$\displaystyle f(g_{1},g_{1})$	$\displaystyle=$	$\displaystyle 0,$	(50c)

for all $g_{1},g_{2},g_{3}\in\mathcal{G}$ .

For the operation in Eq. (30) to be a symplectic form, the first point we need to show is that the image of $\zeta$ equipped with a proper additive operation forms an additive group.

We claim that the set $\mathcal{V}=\zeta(C_{G_{N}}(\mathcal{S}))$ , where $\mathcal{S}$ is a stabilizer group, equipped with $+_{\zeta}$ operation from Definition 12 is an additive group. Indeed, let $\bm{v}_{A},\bm{v}_{B},\bm{v}_{C}\in\mathcal{V}$ , then the following axioms are satisfied:

1.

$\mathcal{V}$ is closed under $+_{\zeta}$ ;
2.

$\bm{v}_{A}+_{\zeta}\bm{v}_{B}=\bm{v}_{B}+_{\zeta}\bm{v}_{A}$ ;
3.

$(\bm{v}_{A}+_{\zeta}\bm{v}_{B})+_{\zeta}\bm{v}_{C}=\bm{v}_{A}+_{\zeta}(\bm{v}_{B}+_{\zeta}\bm{v}_{C})$ ;
4.

there exists an element $\bm{v}_{\mathbb{I}}$ such that $\bm{v}_{A}+_{\zeta}\bm{v}_{\mathbb{I}}=\bm{v}_{A}$ ;
5.

For each $\bm{v}_{A}\in\mathcal{V}$ , there exists an element $\bm{v}_{B}\in\mathcal{V}$ such that $\bm{v}_{A}+_{\zeta}\bm{v}_{B}=\bm{v}_{\mathbb{I}}=\bm{v}_{B}+_{\zeta}\bm{v}_{A}$ .

The first point is clearly true. For the second point, we have that $\mathcal{V}$ is the image of $\zeta$ over $C_{G_{N}}(\mathcal{S})$ . From Proposition 14, we have


	$\displaystyle a_{2j}b_{3j}-a_{3j}b_{2j}=0,$		(51a)
	$\displaystyle a_{3j}b_{1j}-a_{1j}b_{3j}=0,$		(51b)
	$\displaystyle a_{1j}b_{2j}-a_{2j}b_{1j}=0,$		(51c)

for $j=1,\ldots,N$ , where $a_{lj}$ and $b_{pj}$ are the coordinates of the vectors $\bm{v}_{A}$ and $\bm{v}_{B}$ , respectively, for $l,p=1,2,3$ . Thus, we can see from Definition 12 that $+_{\zeta}$ is abelian. For the third point, let $\bm{v}_{D}=\bm{v}_{A}+_{\zeta}\bm{v}_{B}$ and $\bm{v}_{E}=\bm{v}_{B}+_{\zeta}\bm{v}_{C}$ , where each coordinate is given by


	$\displaystyle d_{0j}=a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j},$		(52a)
	$\displaystyle d_{1j}=a_{1j}b_{0j}+a_{0j}b_{1j},$		(52b)
	$\displaystyle d_{2j}=a_{2j}b_{0j}+a_{0j}b_{2j},$		(52c)
	$\displaystyle d_{3j}=a_{3j}b_{0j}+a_{0j}b_{3j},$		(52d)

and


	$\displaystyle e_{0j}=b_{0j}c_{0j}+b_{1j}c_{1j}+b_{2j}c_{2j}+b_{3j}c_{3j},$		(53a)
	$\displaystyle e_{1j}=b_{1j}c_{0j}+b_{0j}c_{1j},$		(53b)
	$\displaystyle e_{2j}=b_{2j}c_{0j}+b_{0j}c_{2j},$		(53c)
	$\displaystyle e_{3j}=b_{3j}c_{0j}+b_{0j}c_{3j},$		(53d)

for $j=1,\ldots,N$ . Then, the result of the sum $\bm{v}_{F}=\bm{v}_{D}+\bm{v}_{C}$ can be described by

$\displaystyle f_{0j}$	$\displaystyle=$	$\displaystyle(a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j})c_{0j}+(a_{1j}b_{0j}+a_{0j}b_{1j})c_{1j}$
	$\displaystyle+$	$\displaystyle(a_{2j}b_{0j}+a_{0j}b_{2j})c_{2j}+(a_{3j}b_{0j}+a_{0j}b_{3j})c_{3j},$
$\displaystyle f_{1j}$	$\displaystyle=$	$\displaystyle(a_{1j}b_{0j}+a_{0j}b_{1j})c_{0j}+(a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j})c_{1j},$
$\displaystyle f_{2j}$	$\displaystyle=$	$\displaystyle(a_{2j}b_{0j}+a_{0j}b_{2j})c_{0j}+(a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j})c_{2j},$
$\displaystyle f_{3j}$	$\displaystyle=$	$\displaystyle(a_{3j}b_{0j}+a_{0j}b_{3j})c_{0j}+(a_{0j}b_{0j}+a_{1j}b_{1j}+a_{2j}b_{2j}+a_{3j}b_{3j})c_{3j}.$	(54)

Similarly, it follows that the sum $\bm{v}_{F^{\prime}}=\bm{v}_{A}+\bm{v}_{E}$ is equal to

$\displaystyle f^{\prime}_{0j}$	$\displaystyle=$	$\displaystyle a_{0j}(b_{0j}c_{0j}+b_{1j}c_{1j}+b_{2j}c_{2j}+b_{3j}c_{3j})+a_{1j}(b_{1j}c_{0j}+b_{0j}c_{1j})$
	$\displaystyle+$	$\displaystyle a_{2j}(b_{2j}c_{0j}+b_{0j}c_{2j})+a_{3j}(b_{3j}c_{0j}+b_{0j}c_{3j}),$
$\displaystyle f^{\prime}_{1j}$	$\displaystyle=$	$\displaystyle a_{1j}(b_{0j}c_{0j}+b_{1j}c_{1j}+b_{2j}c_{2j}+b_{3j}c_{3j})+a_{0j}(b_{1j}c_{0j}+b_{0j}c_{1j}),$
$\displaystyle f^{\prime}_{2j}$	$\displaystyle=$	$\displaystyle a_{2j}(b_{0j}c_{0j}+b_{1j}c_{1j}+b_{2j}c_{2j}+b_{3j}c_{3j})+a_{0j}(b_{2j}c_{0j}+b_{0j}c_{2j}),$
$\displaystyle f^{\prime}_{3j}$	$\displaystyle=$	$\displaystyle a_{3j}(b_{0j}c_{0j}+b_{1j}c_{1j}+b_{2j}c_{2j}+b_{3j}c_{3j})+a_{0j}(b_{3j}c_{0j}+b_{0j}c_{3j}).$	(55)

Rearranging the terms in Eq. (55) and utilizing the relation from Eq. (51), we see that $f_{ij}=f^{\prime}_{ij}$ for $i=0,1,2,3$ and $j=1,\ldots,N$ . Therefore, we have proven Property 3. From the definition of $+_{\zeta}$ and the relation from Eq. (51), we have that the identity element exists. In particular, the identity element is given by $\bm{v}_{\mathbb{I}}=(\bm{1}_{N},\bm{0}_{N},\bm{0}_{N},\bm{0}_{N})$ , where $\bm{1}_{N}$ and $\bm{0}_{N}$ are $N$ -dimensional vectors with all coordinates equal to $1$ and $0$ , respectively. The same approach can be used to show Property 5.

Now, we can use the previous algebraic structure to show that the expression given in Eq. (30) is a symplectic form.

Proposition 15.

Let $N$ be a positive integer and $\mathcal{V}=\{\bm{v}\in\mathbb{C}^{4N}|\bm{v}=(\bm{x}_{0},\bm{x}_{1},\bm{x}_{2},\bm{x}_{3})\text{ where }\bm{x}_{0}=(1,1,\ldots,1)\in\mathbb{C}^{N}\text{ and }\bm{x}_{1},\bm{x}_{2},\bm{x}_{3}\in\mathbb{C}^{N}\}$ be a group under $+_{\zeta}$ . Then the maps

	$\displaystyle\langle\cdot,\cdot\rangle_{\zeta_{(1,j)}}\colon\mathbb{C}^{4N}\times\mathbb{C}^{4N}$	$\displaystyle\rightarrow$	$\displaystyle\mathbb{C}$
	$\displaystyle(\bm{v}_{A},\bm{v}_{B})$	$\displaystyle\mapsto$	$\displaystyle\langle\bm{v}_{A},\bm{v}_{B}\rangle_{\zeta_{(1,j)}}=(a_{2j}b_{3j}-a_{3j}b_{2j}),$		(56)

	$\displaystyle\langle\cdot,\cdot\rangle_{\zeta_{(2,j)}}\colon\mathbb{C}^{4N}\times\mathbb{C}^{4N}$	$\displaystyle\rightarrow$	$\displaystyle\mathbb{C}$
	$\displaystyle(\bm{v}_{A},\bm{v}_{B})$	$\displaystyle\mapsto$	$\displaystyle\langle\bm{v}_{A},\bm{v}_{B}\rangle_{\zeta_{(2,j)}}=(a_{3j}b_{1j}-a_{1j}b_{3j}),$		(57)

	$\displaystyle\langle\cdot,\cdot\rangle_{\zeta_{(3,j)}}\colon\mathbb{C}^{4N}\times\mathbb{C}^{4N}$	$\displaystyle\rightarrow$	$\displaystyle\mathbb{C}$
	$\displaystyle(\bm{v}_{A},\bm{v}_{B})$	$\displaystyle\mapsto$	$\displaystyle\langle\bm{v}_{A},\bm{v}_{B}\rangle_{\zeta_{(3,j)}}=(a_{1j}b_{2j}-a_{2j}b_{1j}),$		(58)

are symplectic forms over $\mathcal{V}$ , where $\bm{v}_{A}=(\bm{x}_{0},\bm{a}_{1},\bm{a}_{2},\bm{a}_{3})$ , $\bm{v}_{B}=(\bm{x}_{0},\bm{b}_{1},\bm{b}_{2},\bm{b}_{3})$ , and $j=1,\ldots,N$ .

Proof.

Let $\bm{v}_{A}=(\bm{x}_{0},\bm{a}_{1},\bm{a}_{2},\bm{a}_{3}),\bm{v}_{B}=(\bm{x}_{0},\bm{b}_{1},\bm{b}_{2},\bm{b}_{3}),$ and $\bm{v}_{C}=(\bm{x}_{0},\bm{c}_{1},\bm{c}_{2},\bm{c}_{3})\in\mathcal{V}$ . From the clear relation between Eqs. (56-58), we only need to show that one of these functions is a symplectic form. Then,

$\displaystyle\langle\bm{v}_{A}+_{\zeta}\bm{v}_{B},\bm{v}_{C}\rangle_{\zeta_{(1,j)}}$	$\displaystyle=$	$\displaystyle(a_{2j}x_{0j}+x_{0j}b_{2j})c_{3j}-(a_{3j}x_{0j}+a_{0j}x_{3j})c_{2j}$	(59)
	$\displaystyle=$	$\displaystyle(a_{2j}c_{3j}-a_{3j}c_{2j})x_{0j}+(b_{2j}c_{3j}-b_{3j}c_{2j})x_{0j}$
	$\displaystyle=$	$\displaystyle\langle\bm{v}_{A},\bm{v}_{C}\rangle_{\zeta_{(1,j)}}+\langle\bm{v}_{B},\bm{v}_{C}\rangle_{\zeta_{(1,j)}},$

where $j=1,\ldots,N$ and we have used the fact that $\bm{x}_{0}=(1,1,\ldots,1)$ . It is also possible to see that

$\displaystyle\langle\bm{v}_{A},\bm{v}_{B}\rangle_{\zeta_{(1,j)}}$	$\displaystyle=$	$\displaystyle a_{2j}b_{3j}-a_{3j}b_{2j}$	(60)
	$\displaystyle=$	$\displaystyle-(a_{3j}b_{2j}-a_{2j}b_{3j})$
	$\displaystyle=$	$\displaystyle-\langle\bm{v}_{B},\bm{v}_{A}\rangle_{\zeta_{(1,j)}},$

and $\langle\bm{v}_{A},\bm{v}_{A}\rangle_{\zeta_{(1,j)}}=0$ . Thus, we have shown that $\langle\cdot,\cdot\rangle_{\zeta_{(1,j)}}$ is, in fact, a symplectic form. ∎

Example 16.

Let $G_{3}$ be the error set for three qubit systems and $A,B\in G_{3}$ be operators given by

	$\displaystyle A$	$\displaystyle=$	$\displaystyle(\mathbb{I}+i\sigma_{y}+\sigma_{z})\otimes(\mathbb{I}+\sigma_{x}-i\sigma_{y})\otimes\mathbb{I}$		(61)
	$\displaystyle B$	$\displaystyle=$	$\displaystyle\mathbb{I}\otimes\mathbb{I}\otimes(\mathbb{I}+\sigma_{x}-i\sigma_{z}).$		(62)

Then, on the one hand, we have that

AB=(\mathbb{I}+i\sigma_{y}+\sigma_{z})\otimes(\mathbb{I}+\sigma_{x}-i\sigma_{y})\otimes(\mathbb{I}+\sigma_{x}-i\sigma_{z}),

(63)

which implies

\displaystyle\zeta(AB)=(1,1,1,0,1,1,i,-i,0,1,0,-i).

(64)

On the other hand, the action of $\zeta$ on $A$ and $B$ is given by

	$\displaystyle\bm{v}_{A}$	$\displaystyle=$	$\displaystyle\zeta(A)=(1,1,1,0,1,0,i,-i,0,1,0,0)$		(65)
	$\displaystyle\bm{v}_{B}$	$\displaystyle=$	$\displaystyle\zeta(B)=(1,1,1,0,0,1,0,0,0,0,0,-i).$		(66)

Therefore,

\displaystyle\bm{v}_{A}+_{\zeta}\bm{v}_{B}=(1,1,1,0,1,1,i,-i,0,1,0,-i),

(67)

where we used Definition 12. From Eqs. (64) and (67) we see that

\zeta(AB)=\bm{v}_{A}+_{\zeta}\bm{v}_{B}.

(68)

Now, we have the tools to define the symplectic dual of a $+_{\zeta}$ -additive code.

Definition 17.

Let $N$ be a positive integer and $C=\{\bm{c}\in\mathbb{C}^{4N}|\bm{c}=(\bm{c}_{0},\bm{c}_{1},\bm{c}_{2},\bm{c}_{3}),\text{ where }\bm{c}_{0}=(1,1,\ldots,1)\in\mathbb{C}^{N}\text{ and }\bm{c}_{1},\bm{c}_{2},\bm{c}_{3}\in\mathbb{C}^{N}\}$ be an $+_{\zeta}$ -additive code. The symplectic dual of $C$ is given by

C^{\perp_{\zeta}}:=\{\bm{c}\in\mathbb{C}^{4N}\colon\langle\bm{c},\bm{d}\rangle_{\zeta_{(l,j)}}=0,\text{ for all }\bm{d}\in C,l=1,2,3,\text{ and }j=1,\ldots,N\}.

(69)

Similar to previous works on stabilizer codes, we are going to derive a connection between stabilizer codes and classical error-correcting codes. This approach enables us to derive algebraic conditions for the construction and existence of decoherence-free stabilizer codes. We can use it to show nonexistence of decoherence-free stabilizer codes with some specific parameters.

Theorem 18.

Let $\mathcal{V}_{\mathcal{S}_{\text{DFS}}}=\zeta(\mathcal{S}_{\text{DFS}})$ or $\mathcal{V}_{\mathcal{S}_{\text{sDFS}}}=\zeta(\mathcal{S}_{\text{sDFS}})$ be a basis of the $+_{\zeta}$ -additive code of the form $C=\{\bm{c}\in\mathbb{C}^{4N}|\bm{c}=(\bm{c}_{0},\bm{c}_{1},\bm{c}_{2},\bm{c}_{3})\text{ where }\bm{c}_{0}=(1,1,\ldots,1)\in\mathbb{C}^{N}\text{ and }\bm{c}_{1},\bm{c}_{2},\bm{c}_{3}\in\mathbb{C}^{N}\}$ . Then,

1.

A decoherence-free stabilizer code $\mathcal{Q}$ exists if there exists an $+_{\zeta}$ -additive code $C$ over $\mathbb{C}$ generated by $\mathcal{V}_{\mathcal{S}_{\text{DFS}}}$ such that $C\leq C^{\perp_{\zeta}}$ and $\zeta(H_{ev})\in C^{\perp_{\zeta}}$ ;
2.

A strong decoherence-free stabilizer code $\mathcal{Q}$ exists if there exists an $+_{\zeta}$ -additive code $C$ over $\mathbb{C}$ generated by $\mathcal{V}_{\mathcal{S}_{\text{sDFS}}}$ such that $C\leq C^{\perp_{\zeta}}$ and $\zeta(H_{S})\in C^{\perp_{\zeta}}$ .

Proof.

First of all, since $C\leq C^{\perp_{\zeta}}$ , then for all $S_{1},S_{2}\in\mathcal{S}_{\text{DFS}}$ we have $[S_{1},S_{2}]=0$ . This implies the existence of a maximum jointly eigenspace of all operators in $\mathcal{S}_{\text{DFS}}$ . Let us denote it by $\mathcal{Q}$ . In particular, $\mathcal{Q}$ is a stabilizer code with stabilizer given by $\mathcal{S}_{\text{DFS}}$ . On the other hand, the hypothesis $\zeta(H_{ev})\in C^{\perp_{\zeta}}$ leads to $[H_{ev},S_{i}]=0$ for any $S_{i}\in\mathcal{S}_{\text{DFS}}$ . Therefore, the eigenvalue of the commutator of $H_{ev}$ with any operator in $\mathcal{S}_{\text{DFS}}$ is equal to zero. Using Proposition 2, we have that $\mathcal{Q}$ is also a decoherence-free subspace.

The same strategy can be used to deduce the second claim. ∎

4 Decoherence-Free Stabilizer Codes for General Noise

This section extends the previous results to general error operators. The approach followed to connect operators and classical codes is based on matrix vectorization. After showing the corresponding vectorized operations, we demonstrate that the formulation of Section 3 is indeed a particular case of the current formulation. Additionally, the standard stabilizer formalism can also be derived from our formalism.

4.1 Motivation

Suppose we wish to extend the formulation of the previous section to operators of the form

E=\sum_{l=1}^{L}\bigotimes_{j=1}^{N}(a_{0j}^{l}\mathbb{I}_{j}+a_{1j}^{l}\sigma_{xj}+a_{2j}^{l}\sigma_{yj}+a_{3j}^{l}\sigma_{zj}),

(70)

where $L$ is the number of terms in the sum describing the operator $E$ , and $N$ is the number of physical systems. A naïve approach would be to map operators to matrices. There are some problems with this strategy. First of all, one should impose an ordering over the terms in the sum going from $l=1,\ldots,L$ as a means to make a uniquely correspondence between each term in the sum and a row in the matrix. Secondly, the composition of errors could result in a sum of matrices giving a matrix with more rows than the original matrices that are being summed; e.g., suppose we have $E_{1}$ with $L_{1}$ terms in the sum and $E_{2}$ with $L_{2}$ terms in the sum, then $E_{1}\circ E_{2}$ can produce up to $L_{1}\times L_{2}$ terms. This can be solved since there is a maximum $L^{\prime}$ of terms with which any operator can be described. Third, and more importantly, the above representation is not unique. To see this, consider the operator

A=(\mathbb{I}+\sigma_{x}+\sigma_{z})\otimes\sigma_{y}+\sigma_{z}\otimes\sigma_{x},

(71)

which can also be written as

A=(\mathbb{I}+\sigma_{x})\otimes\sigma_{y}+\sigma_{z}\otimes(\sigma_{x}+\sigma_{y}).

(72)

The issue of uniqueness in representing an operator and, consequently, its matrix representation may be solved by introducing equivalence classes over matrix spaces similar to the equivalence classes utilized in the definition of tensor product of vector spaces [24]. Even tough these problem may be solved, the formulation seems not straightforward. Therefore, in the following we use matrix vectorization to avoid all these complications.

Let $\{\ket{i}\}_{i=1}^{q}$ be a basis of a Hilbert space $\mathcal{H}_{q}$ , and $\outerproduct{i}{j}\in\mathcal{L}(\mathcal{H}_{q})$ be a linear operator over the Hilbert space $\mathcal{H}_{q}$ . Vectorization is a bijective linear map from $\mathcal{L}(\mathcal{H}_{q})$ to $\mathcal{H}_{q}^{\otimes 2}$ defined as [1]

\text{vec}(\outerproduct{i}{j}):=\ket{i}\ket{j}.

(73)

Vectorization can be extended to any operator space. Let $\outerproduct{i_{1}}{j_{1}}\otimes\outerproduct{i_{2}}{j_{2}}\otimes\cdots\otimes\outerproduct{i_{N}}{j_{N}}\in\mathcal{L}(\mathcal{H}_{q}^{\otimes N})$ , then

\text{vec}(\outerproduct{i_{1}}{j_{1}}\otimes\outerproduct{i_{2}}{j_{2}}\otimes\cdots\otimes\outerproduct{i_{N}}{j_{N}})=\ket{i_{1}}\otimes\ket{i_{2}}\otimes\cdots\otimes\ket{i_{N}}\otimes\ket{j_{1}}\otimes\ket{j_{2}}\otimes\cdots\otimes\ket{j_{N}}.

(74)

Since $\outerproduct{i_{1}}{j_{1}}\otimes\outerproduct{i_{2}}{j_{2}}\otimes\cdots\otimes\outerproduct{i_{N}}{j_{N}}$ forms a basis for the space and the vectorization is a bijective linear map, it can be applied to any operator in $\mathcal{L}(\mathcal{H}_{q}^{\otimes N})$ .

Several properties can be derived for matrix vectorization. Two operations we have used are composition and commutation of operators. For the first, we can use the relation

\text{vec}(ABC)=(A\otimes C^{T})\text{vec}(B).

(75)

In particular, we have $\text{vec}(AB)=(A\otimes\mathbb{I})\text{vec}(B)$ . The commutator can be easily obtained from the above relation and the linearity of the vectorization. We have

\text{vec}([A,B])=(A\otimes\mathbb{I}-\mathbb{I}\otimes A^{T})\text{vec}(B).

(76)

Definition 19.

Let $A,B\in\mathcal{L}(\mathcal{H}_{q}^{N})$ be operators. We define the sum of the vectors $\text{vec}(A)$ and $\text{vec}(B)$ by

\text{vec}(A)+_{\text{vec}}\text{vec}(B)=(A\otimes\mathbb{I})\text{vec}(B).

(77)

If $A$ commutes with $B$ , then it is clear that $\text{vec}(A)+_{\text{vec}}\text{vec}(B)=\text{vec}(B)+_{\text{vec}}\text{vec}(A)$ . Note that $+_{\text{vec}}$ is not the traditional sum of vectors, which always commutes.

We utilize this relation to show that the result from the previous section and the standard stabilizer formalism can be derived from the formulation presented below. Furthermore, the vectorization of the commutator between two operators is used later to construct the symplectic form and the dual code of the additive code.

Proposition 20.

Let $\mathcal{S}$ be a stabilizer set with operators satisfying the structure of the previous section. Assume that $\mathcal{C}_{\zeta}=\zeta(\mathcal{S})$ and $\mathcal{C}_{\text{vec}}=\text{vec}(\mathcal{S})$ , where the composition of operators in $\mathcal{S}$ corresponds to the respective operation of the additive group. Then $\mathcal{C}_{\zeta}\equiv\mathcal{C}_{\text{vec}}$ .

Proof.

First of all, consider a quantum system with $N=1$ . An operator $E$ can be written as $E=e_{01}\mathbb{I}+e_{11}\sigma_{x}+e_{21}\sigma_{y}+e_{31}\sigma_{z}$ or $E=e_{00}^{1}\outerproduct{0}{0}+e_{01}^{1}\outerproduct{0}{1}+e_{10}^{1}\outerproduct{1}{0}+e_{11}^{1}\outerproduct{1}{1}$ , where $e_{i1}$ , $i=0,1,2,3$ , and $e_{pq}^{1}$ , $p,q=0,1$ , satisfy the relations


$\displaystyle e_{00}^{1}$	$\displaystyle=$	$\displaystyle e_{01}+e_{31},$	(78a)
$\displaystyle e_{01}^{1}$	$\displaystyle=$	$\displaystyle e_{11}-ie_{21},$	(78b)
$\displaystyle e_{10}^{1}$	$\displaystyle=$	$\displaystyle e_{11}+ie_{21},$	(78c)
$\displaystyle e_{11}^{1}$	$\displaystyle=$	$\displaystyle e_{01}-e_{31},$	(78d)

and


$\displaystyle e_{01}$	$\displaystyle=$	$\displaystyle(e_{00}^{1}+e_{11}^{1})/2,$	(79a)
$\displaystyle e_{11}$	$\displaystyle=$	$\displaystyle(e_{01}^{1}+e_{10}^{1})/2,$	(79b)
$\displaystyle e_{21}$	$\displaystyle=$	$\displaystyle(e_{10}^{1}-e_{01}^{1})/2i,$	(79c)
$\displaystyle e_{31}$	$\displaystyle=$	$\displaystyle(e_{00}^{1}-e_{11}^{1})/2.$	(79d)

Extending these relations to any positive integer $N$ , taking into account that the relations are independent from one to another qubit, we obtain


$\displaystyle e_{00}^{l}$	$\displaystyle=$	$\displaystyle e_{0l}+e_{3l},$	(80a)
$\displaystyle e_{01}^{l}$	$\displaystyle=$	$\displaystyle e_{1l}-ie_{2l},$	(80b)
$\displaystyle e_{10}^{l}$	$\displaystyle=$	$\displaystyle e_{1l}+ie_{2l},$	(80c)
$\displaystyle e_{11}^{l}$	$\displaystyle=$	$\displaystyle e_{0l}-e_{3l},$	(80d)

and


$\displaystyle e_{0l}$	$\displaystyle=$	$\displaystyle(e_{00}^{l}+e_{11}^{l})/2,$	(81a)
$\displaystyle e_{1l}$	$\displaystyle=$	$\displaystyle(e_{01}^{l}+e_{10}^{l})/2,$	(81b)
$\displaystyle e_{2l}$	$\displaystyle=$	$\displaystyle(e_{10}^{l}-e_{01}^{l})/2i,$	(81c)
$\displaystyle e_{3l}$	$\displaystyle=$	$\displaystyle(e_{00}^{l}-e_{11}^{l})/2.$	(81d)

for $l=1,\ldots,N$ .Thus, it is clear that one can describe a vector in the vec formulation in terms of the coordinates of the vector in the $\zeta$ formulation. In order to show that these two formulations are equivalent, we need to show that the additive operation in one formulation can be described by the vectors in the other formulation. Let

	$\displaystyle A$	$\displaystyle=$	$\displaystyle\sum_{i_{1},j_{1}}\cdots\sum_{i_{N},j_{N}}a^{1}_{i_{1}j_{1}}\cdots a^{N}_{i_{N}j_{N}}\outerproduct{i_{1}}{j_{1}}\cdots\outerproduct{i_{N}}{j_{N}},$		(82)
	$\displaystyle B$	$\displaystyle=$	$\displaystyle\sum_{p_{1},r_{1}}\cdots\sum_{p_{N},r_{N}}b^{1}_{p_{1}r_{1}}\cdots b^{N}_{p_{N}r_{N}}\outerproduct{p_{1}}{r_{1}}\cdots\outerproduct{p_{N}}{r_{N}}.$		(83)

Then,

$\displaystyle\text{vec}(AB)$	$\displaystyle=$	$\displaystyle\sum_{p_{1},r_{1}}\cdots\sum_{p_{N},r_{N}}b^{1}_{p_{1}r_{1}}\cdots b^{N}_{p_{N}r_{N}}(A\ket{p_{1}}\cdots\ket{p_{N}})\ket{r_{1}}\cdots\ket{r_{N}}$	(84)
	$\displaystyle=$	$\displaystyle\sum_{i_{1},\ldots,i_{N}}\sum_{r_{1},\ldots,r_{N}}\Big{(}\sum_{p_{1},\ldots,p_{N}}a^{1}_{i_{1}p_{1}}b^{1}_{p_{1}r_{1}}\cdots a^{N}_{i_{N}p_{N}}b^{N}_{p_{N}r_{N}}\Big{)}\ket{i_{1}}\cdots\ket{i_{N}})\ket{r_{1}}\cdots\ket{r_{N}}$
	$\displaystyle=$	$\displaystyle\sum_{i_{1},\ldots,i_{N}}\sum_{r_{1},\ldots,r_{N}}\Big{[}(\sum_{p_{1}}a^{1}_{i_{1}p_{1}}b^{1}_{p_{1}r_{1}})\cdots(\sum_{p_{N}}a^{N}_{i_{N}p_{N}}b^{N}_{p_{N}r_{N}})\Big{]}\ket{i_{1}}\cdots\ket{i_{N}})\ket{r_{1}}\cdots\ket{r_{N}}.$

We can describe each coordinate by

\text{vec}(AB)_{i_{1},\ldots,i_{N},r_{1},\ldots,r_{N}}=(\sum_{p_{1}}a^{1}_{i_{1}p_{1}}b^{1}_{p_{1}r_{1}})\cdots(\sum_{p_{N}}a^{N}_{i_{N}p_{N}}b^{N}_{p_{N}r_{N}}).

(85)

From Eq. (80), denoting $\lambda_{i_{2},\ldots,i_{N},r_{2},\ldots,r_{N}}=(\sum_{p_{2}}a^{2}_{i_{2}p_{2}}b^{2}_{p_{2}r_{2}})\cdots(\sum_{p_{N}}a^{N}_{i_{N}p_{N}}b^{N}_{p_{N}r_{N}})$ , we obtain


$\displaystyle\text{vec}(AB)_{0,i_{2},\ldots,i_{N},0,r_{2},\ldots,r_{N}}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{01}+b_{31})+(a_{11}-ia_{21})(b_{11}+ib_{21})]\lambda_{i_{2},\ldots,i_{N},r_{2},\ldots,r_{N}},$	(86a)
$\displaystyle\text{vec}(AB)_{0,i_{2},\ldots,i_{N},1,r_{2},\ldots,r_{N}}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{11}-ib_{21})+(a_{11}-ia_{21})(b_{01}-b_{31})]\lambda_{i_{2},\ldots,i_{N},r_{2},\ldots,r_{N}},$	(86b)
$\displaystyle\text{vec}(AB)_{1,i_{2},\ldots,i_{N},0,r_{2},\ldots,r_{N}}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{01}+b_{31})+(a_{01}-a_{31})(b_{11}+ib_{21})]\lambda_{i_{2},\ldots,i_{N},r_{2},\ldots,r_{N}},$	(86c)
$\displaystyle\text{vec}(AB)_{1,i_{2},\ldots,i_{N},1,r_{2},\ldots,r_{N}}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{11}-ib_{21})+(a_{01}-a_{31})(b_{01}-b_{31})]\lambda_{i_{2},\ldots,i_{N},r_{2},\ldots,r_{N}}.$	(86d)

Expanding $\lambda_{i_{2},\ldots,i_{N},r_{2},\ldots,r_{N}}$ in terms of $a_{ij}$ and $b_{ij}$ , we see that $\text{vec}(AB)$ can be computed from the vector representation given in Definition 11. Similarly, Eq. (81) can be applied in order to describe $\zeta(AB)$ in terms of $\text{vec}(A)$ and $\text{vec}(B)$ . ∎

Proposition 21.

Let $\mathcal{S}$ be a stabilizer group with operators satisfying the structure of the standard stabilizer formalism. Assume that $\mathcal{C}$ is the additive group constructed using the standard stabilizer formalism and $\mathcal{C}_{\text{vec}}=\text{vec}(\mathcal{S})$ , where the composition of operators in $\mathcal{S}$ corresponds to the respective operation of the additive group. Then $\mathcal{C}\equiv\mathcal{C}_{\text{vec}}$ .

Proof.

Consider the single qubit $N=1$ case. Let $A=X(a)Z(b)$ , for $a,b\in\mathbb{Z}_{2}$ . Then we can write

A=A_{00}\outerproduct{0}{0}+A_{01}\outerproduct{0}{1}+A_{10}\outerproduct{1}{0}+A_{11}\outerproduct{1}{1},

(87)

where $A_{00}=1-a$ , $A_{01}=(-1)^{b}a$ , $A_{10}=a$ , $A_{11}=(-1)^{b}(1-a)$ . These equalities are clearly invertible. Now, consider the case where $N>1$ . The coordinates of $\text{vec}(AB)$ are given by

	$\displaystyle\text{vec}(AB)_{i_{1},\ldots,i_{N},r_{1},\ldots,r_{N}}$	$\displaystyle=$	$\displaystyle(\sum_{p_{1}}a^{1}_{i_{1}p_{1}}b^{1}_{p_{1}r_{1}})\cdots(\sum_{p_{N}}a^{N}_{i_{N}p_{N}}b^{N}_{p_{N}r_{N}})$		(88)
		$\displaystyle=$	$\displaystyle AB_{i_{1}r_{1}}^{1}\cdots AB_{i_{N}r_{N}}^{N}.$		(89)

Then we can see that


$\displaystyle AB_{00}^{j}$	$\displaystyle=$	$\displaystyle(1-a_{1}^{j})(1-(-1)^{b_{1}^{j}})+(-1)^{b_{1}^{j}}a_{2}^{j}a_{1}^{j},$	(90a)
$\displaystyle AB_{01}^{j}$	$\displaystyle=$	$\displaystyle(1-a_{1}^{j})(-1)^{b_{1}^{j}+b_{2}^{j}}+(1-(-1)^{b_{1}^{j}})(-1)^{b_{2}^{j}}a_{2}^{j}a_{1}^{j},$	(90b)
$\displaystyle AB_{10}^{j}$	$\displaystyle=$	$\displaystyle(1-(-1)^{b_{1}^{j}})a_{1}^{j}+(-1)^{b_{1}^{j}}a_{2}^{j}(1-a_{1}^{j}),$	(90c)
$\displaystyle AB_{11}^{j}$	$\displaystyle=$	$\displaystyle a_{1}^{j}(-1)^{b_{1}^{j}+b_{2}^{j}}+(1-(-1)^{b_{1}^{j}})(-1)^{b_{2}^{j}}(1-a_{1}^{j})a_{2}^{j}.$	(90d)

Since the above equalities are invertible, we have that both formulations are equivalent. ∎

Example 22.

Consider the operator $A=X\otimes\mathbb{I}+\mathbb{I}\otimes X$ . The operator A can be written in the computational basis as

$\displaystyle A$	$\displaystyle=$	$\displaystyle(\outerproduct{0}{1}+\outerproduct{1}{0})\otimes(\outerproduct{0}{0}+\outerproduct{1}{1})+(\outerproduct{0}{0}+\outerproduct{1}{1})\otimes(\outerproduct{0}{1}+\outerproduct{1}{0})$
	$\displaystyle=$	$\displaystyle\outerproduct{0}{0}\otimes\outerproduct{0}{1}+\outerproduct{0}{1}\otimes\outerproduct{0}{0}+\outerproduct{0}{0}\otimes\outerproduct{1}{0}+\outerproduct{0}{1}\otimes\outerproduct{1}{1}$
	$\displaystyle+$	$\displaystyle\outerproduct{1}{0}\otimes\outerproduct{0}{0}+\outerproduct{1}{1}\otimes\outerproduct{0}{1}+\outerproduct{1}{0}\otimes\outerproduct{1}{1}+\outerproduct{1}{1}\otimes\outerproduct{1}{0}.$	(92)

Thus, the vectorization of $A$ is given by

	$\displaystyle\text{vec}(A)$	$\displaystyle=$	$\displaystyle\ket{0001}+\ket{0010}+\ket{0100}+\ket{0111}$		(93)
		$\displaystyle+$	$\displaystyle\ket{1000}+\ket{1011}+\ket{1101}+\ket{1110}.$		(93)

Example 23.

In this example we show the equivalence between the vectorization representation and the $\zeta$ -representation. Consider $A=X\otimes\mathbb{I}$ and $B=\mathbb{I}\otimes Z$ . It is clear that $AB=X\otimes Z$ . The $\zeta$ and vec representations of $A$ , $B$ , and $AB$ are

	$\displaystyle\zeta(A)$	$\displaystyle=$	$\displaystyle(0,1,1,0,0,0,0,0),$		(94)
	$\displaystyle\text{vec}(A)$	$\displaystyle=$	$\displaystyle(0,0,1,0,0,0,0,1,1,0,0,0,0,1,0,0),$		(95)

	$\displaystyle\zeta(B)$	$\displaystyle=$	$\displaystyle(1,0,0,0,0,0,0,1),$		(96)
	$\displaystyle\text{vec}(B)$	$\displaystyle=$	$\displaystyle(1,0,0,0,0,-1,0,0,0,0,1,0,0,0,0,-1),$		(97)

and

	$\displaystyle\zeta(AB)$	$\displaystyle=$	$\displaystyle(0,0,1,0,0,0,0,1),$		(98)
	$\displaystyle\text{vec}(AB)$	$\displaystyle=$	$\displaystyle(0,0,1,0,0,0,0,-1,1,0,0,-1,0,0,0,0).$		(99)

To show the correspondence between these two representations, we are going to describe $\text{vec}(AB)$ in terms of the elements in $\zeta(A)$ and $\zeta(B)$ using Eq. (86). In particular, we have

$\displaystyle\text{vec}(AB)_{0,0,0,0}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{01}+b_{31})+(a_{11}-ia_{21})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{02}+b_{32})+(a_{12}-ia_{22})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{0,0,0,1}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{01}+b_{31})+(a_{11}-ia_{21})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{12}-ib_{22})+(a_{12}-ia_{22})(b_{02}-b_{32})],$
$\displaystyle\text{vec}(AB)_{0,1,0,0}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{01}+b_{31})+(a_{11}-ia_{21})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{02}+b_{32})+(a_{02}-a_{32})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{0,1,0,1}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{01}+b_{31})+(a_{11}-ia_{21})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{12}-ib_{22})+(a_{02}-a_{32})(b_{02}-b_{32})],$

$\displaystyle\text{vec}(AB)_{0,0,1,0}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{11}-ib_{21})+(a_{11}-ia_{21})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{02}+b_{32})+(a_{12}-ia_{22})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{0,0,1,1}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{11}-ib_{21})+(a_{11}-ia_{21})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{12}-ib_{22})+(a_{12}-ia_{22})(b_{02}-b_{32})],$
$\displaystyle\text{vec}(AB)_{0,1,1,0}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{11}-ib_{21})+(a_{11}-ia_{21})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{02}+b_{32})+(a_{02}-a_{32})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{0,1,1,1}$	$\displaystyle=$	$\displaystyle[(a_{01}+a_{31})(b_{11}-ib_{21})+(a_{11}-ia_{21})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{12}-ib_{22})+(a_{02}-a_{32})(b_{02}-b_{32})],$

$\displaystyle\text{vec}(AB)_{1,0,0,0}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{01}+b_{31})+(a_{01}-a_{31})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{02}+b_{32})+(a_{12}-ia_{22})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{1,0,0,1}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{01}+b_{31})+(a_{01}-a_{31})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{12}-ib_{22})+(a_{12}-ia_{22})(b_{02}-b_{32})],$
$\displaystyle\text{vec}(AB)_{1,1,0,0}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{01}+b_{31})+(a_{01}-a_{31})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{02}+b_{32})+(a_{02}-a_{32})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{1,1,0,1}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{01}+b_{31})+(a_{01}-a_{31})(b_{11}+ib_{21})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{12}-ib_{22})+(a_{02}-a_{32})(b_{02}-b_{32})],$

$\displaystyle\text{vec}(AB)_{1,0,1,0}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{11}-ib_{21})+(a_{01}-a_{31})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{02}+b_{32})+(a_{12}-ia_{22})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{1,0,1,1}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{11}-ib_{21})+(a_{01}-a_{31})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{02}+a_{32})(b_{12}-ib_{22})+(a_{12}-ia_{22})(b_{02}-b_{32})],$
$\displaystyle\text{vec}(AB)_{1,1,1,0}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{11}-ib_{21})+(a_{01}-a_{31})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{02}+b_{32})+(a_{02}-a_{32})(b_{12}+ib_{22})],$
$\displaystyle\text{vec}(AB)_{1,1,1,1}$	$\displaystyle=$	$\displaystyle[(a_{11}+ia_{21})(b_{11}-ib_{21})+(a_{01}-a_{31})(b_{01}-b_{31})]$
	$\displaystyle\times$	$\displaystyle[(a_{12}+ia_{22})(b_{12}-ib_{22})+(a_{02}-a_{32})(b_{02}-b_{32})].$

From the above relations and the representation $\zeta(A)$ and $\zeta(B)$ , we see that the same result for $\text{vec}(AB)$ is obtained.

In the previous two examples we have seen vectorization applied to operators and that the $\zeta(\cdot)$ and $\text{vec}(\cdot)$ are indeed equivalent. As can be noticed, the computations to implement the representations and to show equivalence are not complicate but tedious. Therefore, such task can be delegated to a computer.

4.2 Additive Codes

As explained in the previous section, we need to have a symplectic form in order to construct the additive code related to the stabilizer code and its centralizer. We can use Eq. (76) to construct the symplectic form used through this section.

Definition 24.

Let $A,B\in\mathcal{L}(\mathcal{H}_{2}^{\otimes N})$ be linear operators. We define the map

	$\displaystyle\langle\cdot,\cdot\rangle_{\text{vec}}\colon\mathbb{C}^{2N}\times\mathbb{C}^{2N}$	$\displaystyle\rightarrow$	$\displaystyle\mathbb{C},$		(100)
	$\displaystyle(\text{vec}(A),\text{vec}(B))$	$\displaystyle\mapsto$	$\displaystyle\langle\text{vec}(A),\text{vec}(B)\rangle_{\text{vec}}=\sum_{i=1}^{2N}[(A\otimes\mathbb{I}-\mathbb{I}\otimes A^{T})\text{vec}(B)]_{i}.$		(101)

Proposition 25.

The map from Definition 24 is a symplectic form over $\mathbb{C}$ .

Proof.

We show that the properties of Definition 24 are satisfied. Let $A,B,C\in\mathcal{L}(\mathcal{H}_{2}^{\otimes N})$ be operators. First of all, we see that

$\displaystyle\langle\text{vec}(A)+\text{vec}(B),\text{vec}(C)\rangle_{\text{vec}}$	$\displaystyle=$	$\displaystyle\sum_{i=1}^{2N}([(A+B)\otimes\mathbb{I}-\mathbb{I}\otimes(A+B)^{T}]\text{vec}(C))_{i}$	(102)
	$\displaystyle=$	$\displaystyle\sum_{i=1}^{2N}[(A\otimes\mathbb{I}-\mathbb{I}\otimes A^{T})\text{vec}(C)]_{i}+\sum_{i=1}^{2N}[(B\otimes\mathbb{I}-\mathbb{I}\otimes B^{T})\text{vec}(C)]_{i}$
	$\displaystyle=$	$\displaystyle\langle\text{vec}(A),\text{vec}(C)\rangle_{\text{vec}}+\langle\text{vec}(B),\text{vec}(C)\rangle_{\text{vec}}.$

The second point follows from

$\displaystyle\langle\text{vec}(A),\text{vec}(B)\rangle_{\text{vec}}$	$\displaystyle=$	$\displaystyle\sum_{i=1}^{2N}[\text{vec}([A,B])]_{i}$	(103)
	$\displaystyle=$	$\displaystyle\sum_{i=1}^{2N}[\text{vec}(AB)-\text{vec}(BA)]_{i}$	(104)
	$\displaystyle=$	$\displaystyle-\sum_{i=1}^{2N}(\text{vec}(BA)-\text{vec}(AB))_{i}$	(105)
	$\displaystyle=$	$\displaystyle-\sum_{i=1}^{2N}[\text{vec}([B,A])]_{i}$	(106)
	$\displaystyle=$	$\displaystyle-\langle\text{vec}(B),\text{vec}(A)\rangle_{\text{vec}}.$	(107)

We used the linearity of the vectorization in the second equality. The last point follows by expanding an operator $A$ in an eigenbasis and computing $(A\otimes\mathbb{I}-\mathbb{I}\otimes A^{T})\text{vec}(A)$ . ∎

Since the Definition 24 gives a symplectic form, we can define the dual code of an additive code. Furthermore, we can extend the stabilizer formulation presented in the previous section to a larger set of errors.

Definition 26.

Let $C$ be an $+_{\text{vec}}$ -additive code. The symplectic dual of $C$ is given by

C^{\perp_{\text{vec}}}:=\{\bm{c}\in\mathbb{C}^{2N}\colon\langle\bm{c},\bm{d}\rangle_{\text{vec}}=0,\text{ for all }\bm{d}\in C\}.

(108)

Theorem 27.

Let $\mathcal{V}_{\mathcal{S}_{\text{DFS}}}=\text{vec}(\mathcal{S}_{\text{DFS}})$ or $\mathcal{V}_{\mathcal{S}_{\text{sDFS}}}=\text{vec}(\mathcal{S}_{\text{sDFS}})$ be a basis of the $+_{\text{vec}}$ -additive code $C$ . Then,

1.

A decoherence-free stabilizer code $\mathcal{Q}$ exists if there exists an $+_{\text{vec}}$ -additive code $C$ over $\mathbb{C}$ generated by $\mathcal{V}_{\mathcal{S}_{\text{DFS}}}$ such that $C\leq C^{\perp_{\text{vec}}}$ and $\text{vec}(H_{ev})\in C^{\perp_{\text{vec}}}$ ;
2.

A strong decoherence-free stabilizer code $\mathcal{Q}$ exists if there exists an $+_{\text{vec}}$ -additive code $C$ over $\mathbb{C}$ generated by $\mathcal{V}_{\mathcal{S}_{\text{sDFS}}}$ such that $C\leq C^{\perp_{\text{vec}}}$ and $\text{vec}(H_{S})\in C^{\perp_{\text{vec}}}$ .

Proof.

It follows the same reasoning used in the proof of Theorem 18. ∎

5 Application to Parameter Estimation

In this section we consider the framework of quantum metrology and see how the stabilizer codes introduced previously can be used as a tool within it. As it will be shown, one can reach the Heisenberg limit once the stabilizer codes attain an eigenvector condition.

Suppose we have an unitary evolution given by $U=\exp(-iH_{S})$ , where $H_{S}=\eta H$ , $\eta$ is a parameter to be estimated, and $H$ is the generator of $U$ . One of the goals of quantum metrology is to reduce the variance obtained in estimating $\eta$ when compared to classical strategies. To attain this goal, we need to optimize the probing and measuring strategies. To decrease the estimating variance, we use $N$ identical and independent probes, measure them in the channel output, and average the results. Such scheme has the estimation precision lower bounded by [4, 3]

\Delta\eta\Delta h\geq\frac{1}{2},

(109)

where $\Delta A$ is the variance of the random variable $A$ , and $h=\sum_{j=1}^{N}H_{j}$ , $H_{j}$ acting on the $j$ -th probe, stands for the generator of the unitary evolution $U^{\otimes N}$ . Furthermore, it is shown in Ref. [16] that there exists a probing state and a measurement strategy such that

\Delta\eta\geq\frac{1}{N(\lambda_{\text{Max}}-\lambda_{\text{Min}})},

(110)

where $\lambda_{\text{Max}}$ and $\lambda_{\text{Min}}$ are the maximum and minimum eigenvalues of $h$ . This is accomplished with the use of general probe states, which may be entangled states, and local or joint measurements, after the unitary evolution $U^{\otimes N}$ . When the variance (110) scales like $1/N$ , we say that it attains the Heisenberg limit (HL) scaling.

A crucial assumption used in the above methodology to attain the HL is that the evolution is unitary. For Markovian noise, one alternative approach is to use a quantum error-correcting code to achieve the HL under the assumption that the Hamiltonian is not in the spanned space generated by the Lindblad operators [36, 10, 37, 25, 17]. Refs [36, 10] show that lower bounds can be constructed from a simple algebraic condition involving solely the operators appearing in the quantum master equation. a preliminary protocol considering the requirements that quantum error-correcting codes must satisfy in order to achieve HL is also described in Ref. [10]. This protocol has been extended considering necessary and sufficient conditions for achieving the HL when the probing system has a Markovian noise and noiseless ancilla systems are available. This proposal has been further extended for general adaptive multi-parameter estimation schemes in presence of Markovian noise [17]. Lastly, Ref. [25] gives a semidefinite program for finding optimal ancilla-free sensing codes.

The proposed protocol of this paper is described as follows. The first part is the construction of the stabilizer code from the open quantum system evolution. Let $\rho_{\text{Max-Min}}$ be the equally weighted superposition of the eigenvectors relative to the maximum and minimum eigenvalues of $\sum_{i=1}^{N}\mathbbm{1}^{\otimes i-1}_{S}\otimes H_{S}\otimes\mathbbm{1}^{\otimes N-i}_{S}$ . Next, we see if the stabilizer code contains the state $\rho_{\text{Max-Min}}$ . If so, then we use it to probe the quantum system. As shown in Theorem 8, we are going to have an unitary evolution described by $H_{S}$ . Therefore, using the optimal measurement described in Ref. [16] over the channel outputs, one obtains the HL scaling.

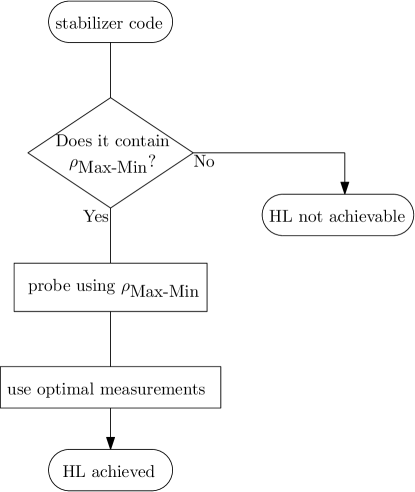
Refer to caption — Figure 1: Flowchart of the proposed protocol for achieving HL limit using the stabilizer codes of previous section.

The present idea differs from the literature on the use of quantum codes to attain the HL [36, 10, 17, 37] in terms of computational complexity. Here, we do not need to implement a decoding process, which is the case of Refs. [36, 10, 37, 25]. However, this decoder-free approach is not novel in the literature, e.g. Ref. [17] proposes a semidefinite program design to identify the optimal quantum error-correcting protocol, without the need for a decoding algorithm, to achieve the best estimation precision in the case where the Heisenberg scaling is achievable. The quantum state will not change by the environmental noise since it belongs to the DFS. Therefore, there is no error to be detected or corrected. Removing the decoder from the picture, we have a reduced number of operations to be implemented and a faster probing strategy.

Theorem 28.

Consider a quantum system with evolution given by a Markovian master equation with Lindblad operators $\{J_{l}\}$ . Let $\mathcal{S}$ be a stabilizer set constructed from the Lindblad operators. Let $\ket{\psi_{\text{max}}}$ and $\ket{\psi_{\text{min}}}$ be eigenvectors of the system Hamiltonian $H_{S}$ with maximum and minimum eigenvalues, respectively. Then, Heisenberg limit scaling is achievable if

\ket{\psi^{(N)}}=\frac{1}{\sqrt{2}}(\ket{\psi_{\text{max}}}^{\otimes N}+\ket{\psi_{\text{min}}}^{\otimes N})

belongs to the stabilizer code for any $N>N^{*}$ , where $N^{*}\in\mathbb{N}$ .

Proof.

Since $\ket{\psi^{(N)}}$ belongs to the stabilizer code, then it also belongs to the DFS, hence its evolution is unitary and the technique of Ref. [16] can be applied. ∎

We use Theorem 28 in the example below to show achievability of the HL using the protocol of Fig. 1. The proposed protocol relies on $\rho_{\text{Max-Min}}$ as a codeword of the DFS stabilizer code. The existence of a DFS stabilizer code is equivalent to the commutativity between the Lindblad operators and the system Hamiltonian. This is satisfied whenever we have environments acting locally on each subsystem. Therefore, we expect that the proposed protocol can be applied to most of the relevant physical systems.

Example 29.

Consider a quantum system with a similar dynamics as in the previous examples,

\frac{\partial\rho}{\partial t}=-i[H_{S},\rho]+\frac{\gamma}{2}(2J\rho J^{\dagger}-J^{\dagger}J\rho-\rho J^{\dagger}J),

(111)

with

J=\frac{s+c}{2}(\mathbb{I}\otimes\mathbb{I}+\sigma_{z}\otimes\sigma_{z}),

(112)

and

H_{S}=\frac{\gamma(s+c)^{2}}{4}(\sigma_{x}\otimes\sigma_{x}).

(113)

where $s=\sinh(r)$ , $c=\cosh(r)$ , and $r$ is the (real) squeezing parameter. The stabilizer set constructed from the dissipator part is given by $\mathcal{S}=\langle(\mathbb{I}\otimes\mathbb{I}+\sigma_{z}\otimes\sigma_{z})^{i}\colon i=0,1\rangle$ . Consider an eigenvector with maximum eigenvalue and an eigenvector with minimum eigenvalue of the operator $H_{S}$ . Such a pair is

\ket{\psi_{\text{Max}}}=\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})\qquad\text{and}\qquad\ket{\psi_{\text{Min}}}=\frac{1}{\sqrt{2}}(\ket{00}-\ket{11}).

(114)

Suppose we are going to probe the system $N$ times with the state

\rho_{\text{Max-Min}}=\ket{\psi^{(N)}}\bra{\psi^{(N)}}=\frac{1}{2}\Big{(}\ket{\psi_{\text{Max}}}^{\otimes N}+\ket{\psi_{\text{Min}}}^{\otimes N}\Big{)}\Big{(}\bra{\psi_{\text{Max}}}^{\otimes N}+\bra{\psi_{\text{Min}}}^{\otimes N}\Big{)}.

(115)

It is possible to see that $\ket{\psi^{(N)}}$ is a codeword of the stabilizer code $\mathcal{Q}$ , since $S\ket{\psi_{\text{Max}}}=\ket{\psi_{\text{Max}}}$ and $S\ket{\psi_{\text{Min}}}=\ket{\psi_{\text{Min}}}$ , for all $S\in\mathcal{S}$ . Now, the achievability of the HL scaling can by seen in two ways. Firstly from Theorem 28, where state membership in the stabilizer code is verified in the quantum or classical realms using the tools presented previously in this paper. Secondly from Eq. (111), where we have that the dissipator part does not contribute to the evolution since

2J\rho_{\text{Max-Min}}J^{\dagger}-J^{\dagger}J\rho_{\text{Max-Min}}-\rho_{\text{Max-Min}}J^{\dagger}J=2\rho_{\text{Max-Min}}-\rho_{\text{Max-Min}}-\rho_{\text{Max-Min}}=0.

(116)

6 Final Remarks

In this work we have constructed stabilizer codes for open quantum systems governed by Lindblad master equations. To achieve this goal, we had to go beyond the tools that exist for stabilizer codes in the literature. As an important step, we have extended the formulation of stabilizer codes under the influence of errors forming a group to those forming a vector space. Using stabilizer codes as tools, we were able to determine conditions under which decoherence-free subspaces exist. As an application of the results shown, a novel algebraic method for attaining the Heisenberg limit scaling is given by means of stabilizer codes. Explanations of tools and codes created in the paper are illustrated through a variety of examples. The algebraic approach developed to attain the Heisenberg limit scaling paves the way to attack this quantum metrology problem by reservoir engineering.

This paper suggests future lines of investigation from coding theory perspective. Firstly, by considering the construction of parameter bounds by connecting the physical constraints over Lindblad operators to the stabilizer code parameters. A quantification of goodness for decoherence-free subspaces can be obtained from this topic. One could also show the non-existence of decoherence-free subspaces, which could lead to a more effective approach to investigate open quantum systems. Secondly, identifying decoherence-free subspaces as stabilizer codes generates the possibility to classify some evolutions of open quantum systems. One approach is connecting some evolutions to families of classical codes. Lastly, because of the novel approach presented, we expect quantum evolutions with decoherence-free stabilizer codes leading to classical codes that have not been discovered yet.

7 Acknowledgments

The authors acknowledge the funding from the European Union’s Horizon 2020 research and innovation programme, under grant agreement QUARTET No 862644.

References

[1] Karim M. Abadir and Jan R. Magnus “Matrix Algebra” Cambridge University Press, 2005, pp. 464
[2] Dave Bacon “Operator quantum error-correcting subsystems for self-correcting quantum memories” In Physical Review A 73.1 American Physical Society (APS), 2006, pp. 012340 DOI: 10.1103/physreva.73.012340
[3] Samuel L. Braunstein and Carlton M. Caves “Statistical distance and the geometry of quantum states” In Physical Review Letters 72.22 American Physical Society (APS), 1994, pp. 3439–3443 DOI: 10.1103/physrevlett.72.3439
[4] Samuel L. Braunstein, Carlton M. Caves and Gerard J. Milburn “Generalized Uncertainty Relations: Theory, Examples, and Lorentz Invariance” In Annals of Physics 247.1 Elsevier BV, 1996, pp. 135–173 DOI: 10.1006/aphy.1996.0040
[5] Todd Brun, Igor Devetak and Min-Hsiu Hsieh “Correcting Quantum Errors with Entanglement” In Science 314.5798 American Association for the Advancement of Science (AAAS), 2006, pp. 436–439 DOI: 10.1126/science.1131563
[6] Carlo Cafaro, Sonia L’Innocente, Cosmo Lupo and Stefano Mancini “Quantifying the Performance of Quantum Codes” In Open Systems & Information Dynamics 18.01 World Scientific Pub Co Pte Lt, 2011, pp. 1–31 DOI: 10.1142/s1230161211000029
[7] Carlo Cafaro, Federico Maiolini and Stefano Mancini “Quantum stabilizer codes embedding qubits into qudits” In Physical Review A 86.2 American Physical Society (APS), 2012 DOI: 10.1103/physreva.86.022308
[8] Carlo Cafaro and Stefano Mancini “Quantum stabilizer codes for correlated and asymmetric depolarizing errors” In Physical Review A 82.1 American Physical Society (APS), 2010 DOI: 10.1103/physreva.82.012306
[9] A. Robert Calderbank, Eric M. Rains, Peter M. Shor and Neil J.A. Sloane “Quantum error correction via codes over GF(4)” In IEEE Transactions on Information Theory 44.4 Institute of ElectricalElectronics Engineers (IEEE), 1998, pp. 1369–1387 DOI: 10.1109/18.681315
[10] Rafał Demkowicz-Dobrzański, Jan Czajkowski and Pavel Sekatski “Adaptive Quantum Metrology under General Markovian Noise” In Physical Review X 7.4 American Physical Society (APS), 2017 DOI: 10.1103/physrevx.7.041009
[11] Rafał Demkowicz-Dobrzański, Wojciech Górecki and Mădălin Guţă “Multi-parameter estimation beyond quantum Fisher information” In Journal of Physics A: Mathematical and Theoretical 53.36 IOP Publishing, 2020, pp. 363001 DOI: 10.1088/1751-8121/ab8ef3
[12] Robert H. Dicke “Coherence in Spontaneous Radiation Processes” In Physical Review 93.1 American Physical Society (APS), 1954, pp. 99–110 DOI: 10.1103/physrev.93.99
[13] Frank Gaitan “Quantum error correction and fault tolerant quantum computing” Boca Raton, FL: CRC Press, 2008 URL: https://www.routledge.com/Quantum-Error-Correction-and-Fault-Tolerant-Quantum-Computing/Gaitan/p/book/9780849371998
[14] Carlos Galindo, Fernando Hernando, Ryutaroh Matsumoto and Diego Ruano “Entanglement-assisted quantum error-correcting codes over arbitrary finite fields” In Quantum Information Processing 18.4 Springer ScienceBusiness Media LLC, 2019 DOI: 10.1007/s11128-019-2234-5
[15] Vittorio Giovannetti, Seth Lloyd and Lorenzo Maccone “Advances in quantum metrology” In Nature Photonics 5.4 Springer ScienceBusiness Media LLC, 2011, pp. 222–229 DOI: 10.1038/nphoton.2011.35
[16] Vittorio Giovannetti, Seth Lloyd and Lorenzo Maccone “Quantum Metrology” In Physical Review Letters 96.1 American Physical Society (APS), 2006 DOI: 10.1103/physrevlett.96.010401
[17] Wojciech Górecki, Sisi Zhou, Liang Jiang and Rafał Demkowicz-Dobrzański “Optimal probes and error-correction schemes in multi-parameter quantum metrology” In Quantum 4 Verein zur Forderung des Open Access Publizierens in den Quantenwissenschaften, 2020, pp. 288 DOI: 10.22331/q-2020-07-02-288
[18] Daniel Gottesman “Stabilizer codes and quantum error correction”, 1997
[19] Daniel Gottesman, Alexei Kitaev and John Preskill “Encoding a qubit in an oscillator” In Physical Review A 64.1 American Physical Society (APS), 2001 DOI: 10.1103/physreva.64.012310
[20] Giuliano G. La Guardia and Francisco Revson F. Pereira “Good and asymptotically good quantum codes derived from algebraic geometry” In Quantum Information Processing 16.6 Springer ScienceBusiness Media LLC, 2017 DOI: 10.1007/s11128-017-1618-7
[21] Francesco Petruccione Heinz-Peter Breuer “The Theory of Open Quantum Systems” Oxford University Press, 2007 URL: https://www.ebook.de/de/product/6212122/heinz_peter_breuer_francesco_petruccione_the_theory_of_open_quantum_systems.html
[22] Raisa I. Karasik, Karl-Peter Marzlin, Barry C. Sanders and K. Birgitta Whaley “Criteria for dynamically stable decoherence-free subspaces and incoherently generated coherences” In Physical Review A 77.5 American Physical Society (APS), 2008 DOI: 10.1103/physreva.77.052301
[23] Avanti Ketkar, Andreas Klappenecker, Santosh Kumar and Pradeep K. Sarvepalli “Nonbinary Stabilizer Codes Over Finite Fields” In IEEE Transactions on Information Theory 52.11 Institute of ElectricalElectronics Engineers (IEEE), 2006, pp. 4892–4914 DOI: 10.1109/tit.2006.883612
[24] Serge Lang “Algebra” Springer New York, 2005 URL: https://www.ebook.de/de/product/3251791/serge_lang_algebra.html
[25] David Layden, Sisi Zhou, Paola Cappellaro and Liang Jiang “Ancilla-Free Quantum Error Correction Codes for Quantum Metrology” In Physical Review Letters 122.4 American Physical Society (APS), 2019 DOI: 10.1103/physrevlett.122.040502
[26] D. A. Lidar, D. Bacon and K. B. Whaley “Concatenating Decoherence-Free Subspaces with Quantum Error Correcting Codes” In Physical Review Letters 82.22 American Physical Society (APS), 1999, pp. 4556–4559 DOI: 10.1103/physrevlett.82.4556
[27] “Quantum Error Correction” Cambridge University Press, 2014 URL: https://www.ebook.de/de/product/20579019/quantum_error_correction.html
[28] Alfredo Luis “Breaking the weak Heisenberg limit” In Physical Review A 95.3 American Physical Society (APS), 2017 DOI: 10.1103/physreva.95.032113
[29] Stefano Mancini and Andreas Winter “A Quantum Leap in Information Theory” WORLD SCIENTIFIC, 2020 DOI: 10.1142/11314
[30] Isaac L. Chuang Michael A. Nielsen “Quantum Computation and Quantum Information” Cambridge University Pr., 2010 URL: https://www.ebook.de/de/product/13055864/michael_a_nielsen_isaac_l_chuang_quantum_computation_and_quantum_information.html
[31] Kyungjoo Noh and Christopher Chamberland “Fault-tolerant bosonic quantum error correction with the surface–Gottesman-Kitaev-Preskill code” In Physical Review A 101.1 American Physical Society (APS), 2020 DOI: 10.1103/physreva.101.012316
[32] Harold Ollivier and Jean-Pierre Tillich “Description of a Quantum Convolutional Code” In Physical Review Letters 91.17 American Physical Society (APS), 2003 DOI: 10.1103/physrevlett.91.177902
[33] Francisco Revson F. Pereira and Stefano Mancini “Entanglement-Assisted Quantum Codes from Cyclic Codes” In Entropy 25.1 MDPI AG, 2022, pp. 37 DOI: 10.3390/e25010037
[34] Francisco Revson F. Pereira, Ruud Pellikaan, Giuliano Gadioli La Guardia and Francisco Marcos Assis “Entanglement-Assisted Quantum Codes From Algebraic Geometry Codes” In IEEE Transactions on Information Theory 67.11 Institute of ElectricalElectronics Engineers (IEEE), 2021, pp. 7110–7120 DOI: 10.1109/tit.2021.3113367
[35] Francisco Revson Fernandes Pereira, Giuliano Gadioli La Guardia and Francisco Marcos Assis “Classical and Quantum Convolutional Codes Derived From Algebraic Geometry Codes” In IEEE Transactions on Communications 67.1 Institute of ElectricalElectronics Engineers (IEEE), 2019, pp. 73–82 DOI: 10.1109/tcomm.2018.2875754
[36] Pavel Sekatski, Michalis Skotiniotis, Janek Kołodyński and Wolfgang Dür “Quantum metrology with full and fast quantum control” In Quantum 1 Verein zur Forderung des Open Access Publizierens in den Quantenwissenschaften, 2017, pp. 27 DOI: 10.22331/q-2017-09-06-27
[37] Sisi Zhou, Mengzhen Zhang, John Preskill and Liang Jiang “Achieving the Heisenberg limit in quantum metrology using quantum error correction” In Nature Communications 9.1 Springer ScienceBusiness Media LLC, 2018 DOI: 10.1038/s41467-017-02510-3